A Critical Comparison of Shape Sensing Algorithms: The Calibration Matrix Method versus iFEM
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Demonstration: Benchmark Problems
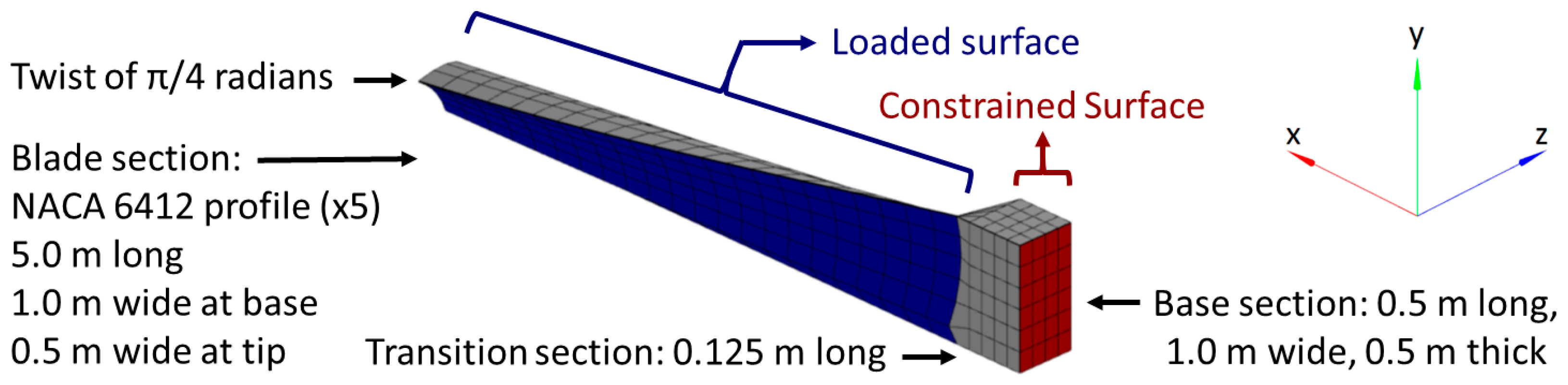
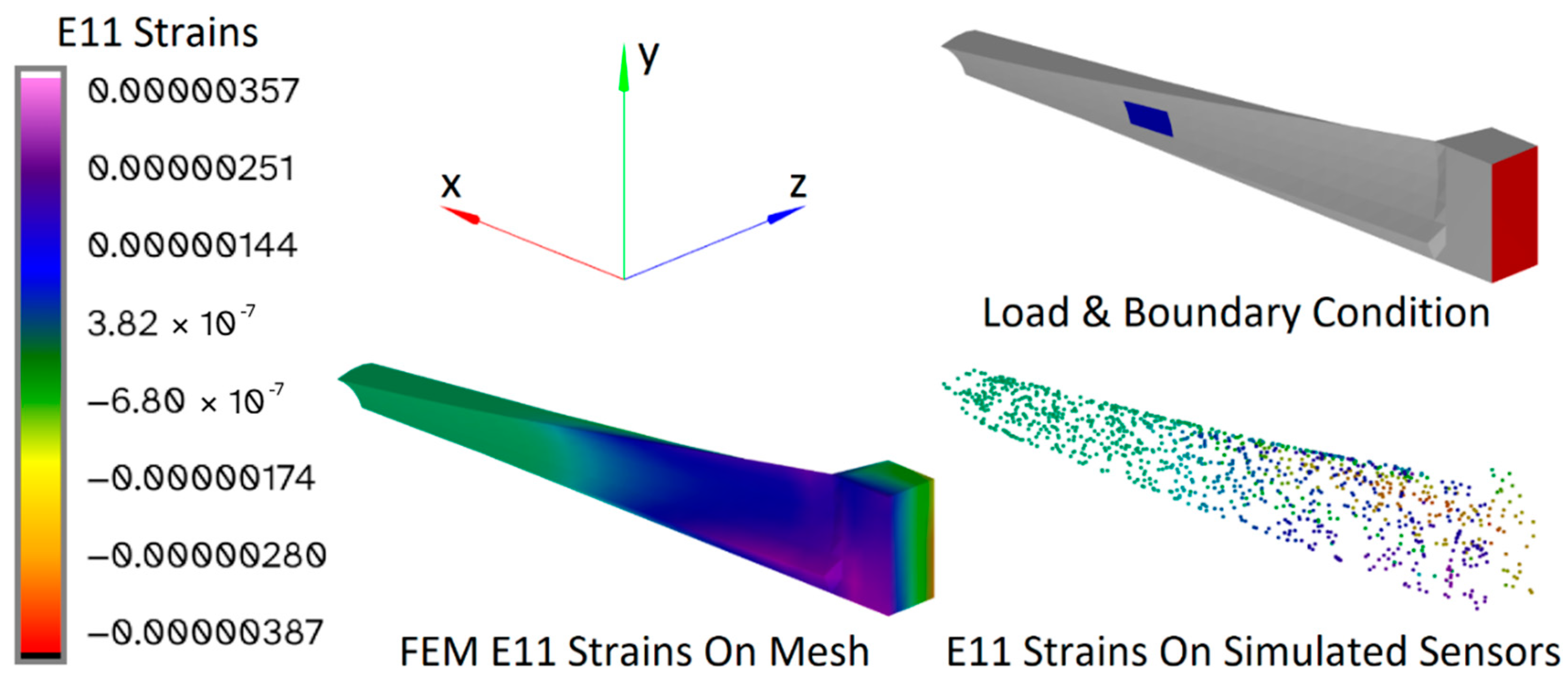
2.2. Numerical Demonstration: Representative Aerospace Structure
2.3. Assumptions
2.4. Calibration Matrix
2.5. iFEM Methodology
2.6. FEM Methodology
Converge Study
2.7. Sufficient Number of Strain Sensors
2.8. Computational Efficiency
3. Results
3.1. Convergence Study
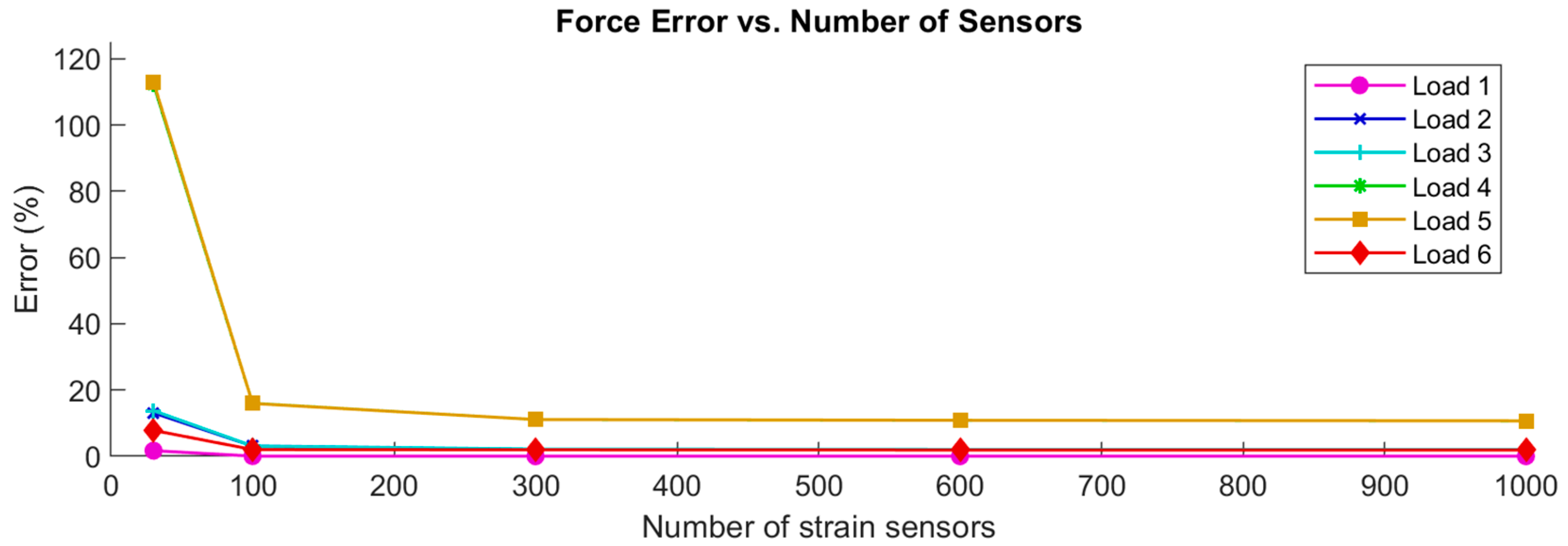
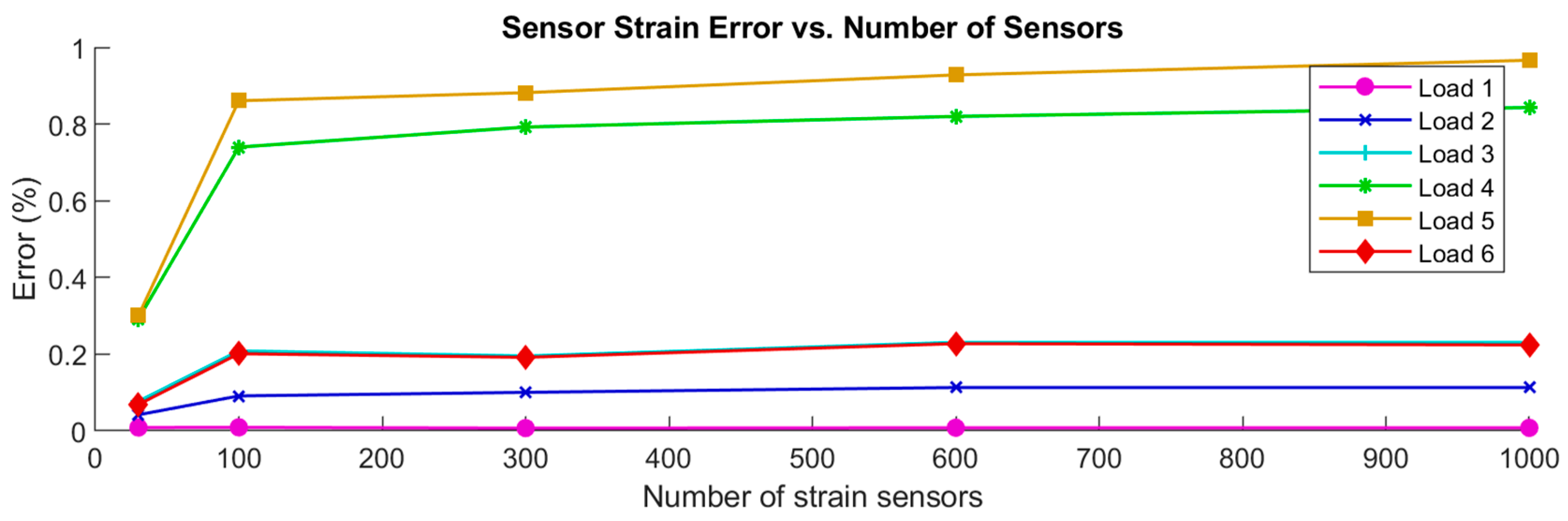
3.2. Sufficient Number of Strain Sensors
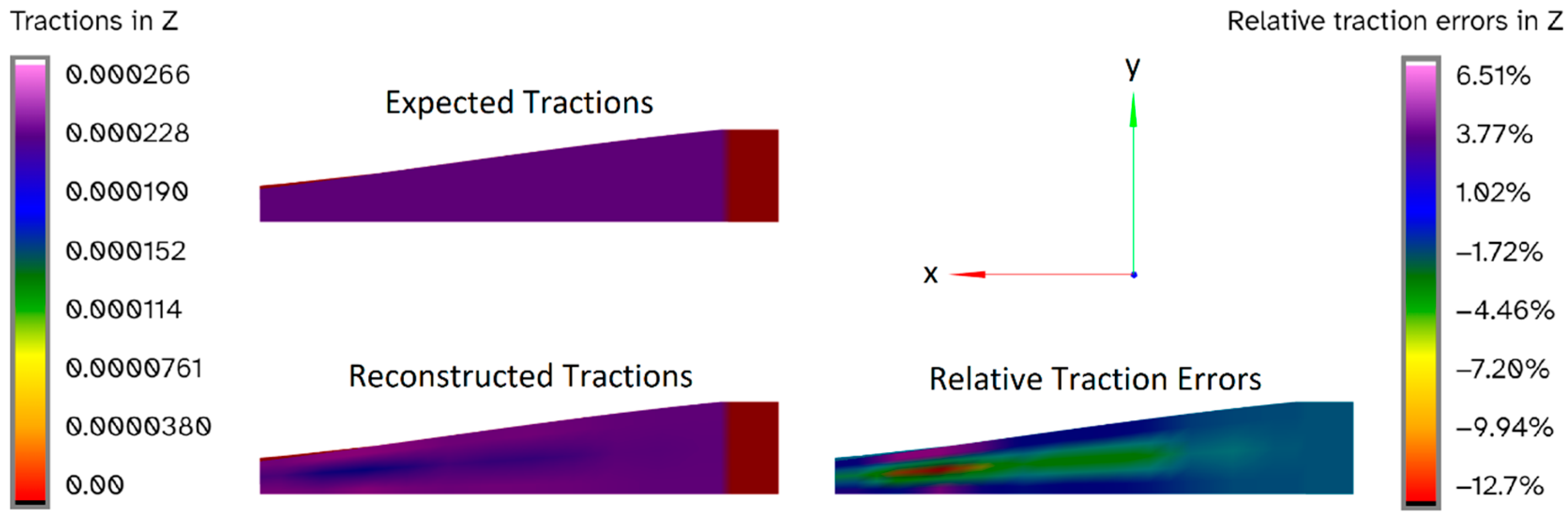
3.3. Errors between Reconstructed and Actual Load Cases
3.4. Computational Efficiency
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tuegel, E.J.; Ingraffea, A.R.; Eason, T.G.; Spottswood, S.M. Reengineering Aircraft Structural Life Prediction Using a Digital Twin. Int. J. Aerosp. Eng. 2011, 2011, 14. [Google Scholar] [CrossRef]
- Glaessgen, E.; Stargel, D. The Digital Twin Paradigm for Future NASA and U.S. Air Force Vehicles. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar]
- Kefal, A. An efficient curved inverse-shell element for shape sensing and structural health monitoring of cylindrical marine structures. Ocean Eng. 2019, 188, 106262. [Google Scholar] [CrossRef]
- Saunders, C.G. Reconstruction of Anatomical Shapes from Moire Contourographs. In Proceedings of the Biostereometrics’ 82, San Diego, CA, USA, 24–27 August 1982. [Google Scholar]
- Saunders, C.F.G. Automated Prosthetic Fitting. In Proceedings of the Second International Conference on Rehabilitation Engineering, Ottawa, ON, Canada, 17–22 June 1984. [Google Scholar]
- Fernie, G.; Griggs, G.; Bartlett, S.; Lunau, K. Shape sensing for computer aided below-knee prosthetic socket design. Prosthet. Orthot. Int. 1985, 9, 12–16. [Google Scholar] [CrossRef] [PubMed]
- Fernie, G.; Halsall, A.; Ruder, K. Shape sensing as an educational aid for student prosthetists. Prosthet. Orthot. Int. 1984, 8, 87–90. [Google Scholar] [CrossRef] [PubMed]
- Weathers, J.; Foster, W.; Swinson, W.; Turner, J. Integration of laser-speckle and finite-element techniques of stress analysis. Exp. Mech. 1985, 25, 60–65. [Google Scholar] [CrossRef]
- Maniatty, A.; Zabaras, N.; Stelson, K. Finite Element Analysis of Some Inverse Elasticity Problems. J. Eng. Mech. 1989, 115, 1303–1317. [Google Scholar] [CrossRef]
- Balas, J.; Sladek, J.; Drzik, M. Stress Analysis by Combination of Holographic Interferometry and Boundary-integral Method. Exp. Mech. 1983, 23, 196–202. [Google Scholar] [CrossRef]
- Hadamard, J. Lectures on Cauchy’s Problem in Linear Partial Differential Equations; Yale University Press: New Haven, CT, USA; Oxford University Press: London, UK, 1923. [Google Scholar]
- Tikhonov, A.; Arsenin, V. Solution of Ill-Posed Problems; V. H. Winston and Sons: Washington, DC, USA, 1977. [Google Scholar]
- Payne, L. Improperly Posed Problems in Partial Differential Equations; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1975; p. 76. [Google Scholar]
- Romanov, V. Inverse Problems of Mathematical Physics; VNU Science Press: Utrecht, The Netherlands, 1987. [Google Scholar]
- Maniatty, A.M.; Zabaras, N.J. Investigation of Regularization Parameters and Error Estimating in Inverse Elasticity Problems. Int. J. Numer. Methods Eng. 1994, 37, 1039–1052. [Google Scholar] [CrossRef]
- Schnur, D.; Zabaras, N. Finite Element Solution of Two-Dimensional Inverse Elastic Problems Using Spatial Smoothing. Int. J. Numer. Methods Eng. 1990, 30, 57–75. [Google Scholar] [CrossRef]
- Jones, R.; Bellemore, D.; Berkoff, T.; Sirkis, J.; Davis, M.; Putnam, M.; Friebele, E.; Kersey, A. Determination of cantilever plate shapes using wavelength division multiplexed fiber Bragg grating sensors and a least-squares strain-fitting algorithm. Smart Mater. Struct. 1998, 7, 178–188. [Google Scholar] [CrossRef]
- Martinez, M.; Rocha, B.; Li, M.; Shi, G.; Beltempo, A.; Rutledge, R.; Yanishevsky, M. Load Monitoring of Aerospace Structures Using Micro-Electro-Mechanical Systems (MEMS). In Proceedings of the ASME 2012 Conference on Smart Materials, Adaptive Structures and Intelligent Systems SMASIS2012, Stone Mountain, GA, USA, 19–21 September 2012. [Google Scholar]
- Martinez, M.; Rocha, B.; Li, M.; Shi, G.; Beltempo, A.; Rutledge, R.; Yanishevsky, M. Load monitoring of aerospace structures utilizing micro-electro-mechanical systems for static and quasi-static loading conditions. Smart Mater. Struct. 2012, 21, 115001. [Google Scholar] [CrossRef]
- Trujillo, D. Application Of Dynamic Programming To The General Inverse Problem. Int. J. Numer. Methods Eng. 1978, 12, 613–624. [Google Scholar] [CrossRef]
- Bogert, P.B.; Haugse, E.; Gehrki, R.E. Structural Shape Identification From Experimental Strains Using A Modal Transformation Technique. In Proceedings of the Structures, Structural Dynamics and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar]
- Duncan, R.; Froggatt, M.; Kreger, S.; Seeley, R.; Gifford, D.; Sang, A.; Wolfe, M. High-accuracy fiber-optic shape sensing. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 18–22 March 2007. [Google Scholar]
- Burnett, J.; Blanchard, P.; Greenaway, A. Optical Fibre-based Vectoral Shape Sensor. Strain 2000, 36, 127–133. [Google Scholar] [CrossRef]
- Gander, M.; MacPherson, W.; McBride, R.; Jones, J.; Zhang, L.; Bennion, I.; Blanchard, P.; Burnett, J.; Greenaway, A. Bend measurement using Bragg gratings in multicore fibre. Electron. Lett. 2000, 36, 120–121. [Google Scholar] [CrossRef]
- Shapiro, Y.; Kosa, G.; Wolf, A. Shape Tracking of Planar Hyper-Flexible Beams via Embedded PVDF Deflection Sensors. Trans. Mechatron. 2014, 19, 1260–1267. [Google Scholar] [CrossRef]
- Shkarayev, S.; Krashanitsa, R.; Tessler, A. An Inverse Interpolation Method Utilizing In-Flight Strain Measurements for Determining Loads and Structural Response of Aerospace Vehicles. In Proceedings of the Third International Workshop on Structural Health Monitoring, Stanford, CA, USA, 12–14 September 2001. [Google Scholar]
- Tessler, A.; Spangler, J. An Inverse Finite Element Method for Application to Structural Health Monitoring. In Proceedings of the 14th US National Congress of Theoretical and Applied Mechanics, Blacksburg, VA, USA, 23–28 June 2002. [Google Scholar]
- Shkarayev, S.; Raman, A.; Tessler, A. Computational and Experimental Validation Enabling a Viable in-Flight Structural Health Monitoring Technology. In Proceedings of the First European Workshop, Structural Health Monitoring, Paris, France, 10–12 July 2002. [Google Scholar]
- Tessler, A.; Spangler, J. A Variational Principle for Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells; NASA Langley Research Center: Hampton, VA, USA, 2003. [Google Scholar]
- Tessler, A.; Spangler, J. An Inverse Finite Element Method for Reconstruction of Elastic Deformations in Beam, Plate, and Shell Structures. In Proceedings of the Mathematics of Finite Elements and Applications (MAFELAP), London, UK, 21–23 June 2003. [Google Scholar]
- Tessler, A.; Spangler, J. Inverse FEM for Full-Field Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells. In Proceedings of the Second European Workshop on Structural Health Monitoring, Munich, Germany, 7–9 July 2004. [Google Scholar]
- Tessler, A.; Spangler, J. A least-squares variational method for full-field reconstruction of elastic deformations in shear-deformable plates and shells. In Proceedings of the 11th Conference on the Mathematics of Finite Elements and Applications, London, UK, 21–23 June 2003. [Google Scholar]
- Quach, C.; Vazquez, S.; Tessler, A.; Moore, J.; Cooper, E.; Spangler, J. Structural Anomaly Detection Using Fiber Optic Sensors and Inverse Finite Element Method. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar]
- Vazquez, S.; Tessler, A.; Quach, C.; Cooper, E.; Parks, J.; Spangler, J. Structural Health Monitoring Using High-Density Fiber Optic Strain Sensor and Inverse Finite Element Methods; NASA, Langley Research Center: Hampton, VA, USA, 2005. [Google Scholar]
- Tessler, A. Structural Analysis Methods for Structural Health Management of Future Aerospace Vehicle; NASA: Hampton, VA, USA, 2007. [Google Scholar]
- Tessler, A. Inverse Finite Element Method for Integrated Vehicle Health Management; Politecnico Di Torino: Turin, Italy, 2009. [Google Scholar]
- De Mooij, C.; Martinez, M.; Benedictus, R. iFEM benchmark problems for solid elements. Smart Mater. Struct. 2019, 28, 065003. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Dynamic shape reconstruction of three-dimensional frame structures using the inverse finite element method. In Proceedings of the III ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Corfu, Greece, 26–28 May 2011. [Google Scholar]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Beam Shape Sensing Using Inverse Finite Element Method: Theory and Experimental Validation. In Proceedings of the VIII International Workshop on Structural Health Monitoring, Stanford, CA, USA, 13–15 September 2011. [Google Scholar]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Shape sensing of 3D frame structures using an inverse Finite Element Method. Int. J. Solids Struct. 2012, 49, 3100–3112. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. An inverse finite element method for beam shape sensing: Theoretical framework and experimental validation. Smart Mater. Struct. 2014, 23, 045027. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; Di Sciuva, M.; Tessler, A. Shape and stress sensing of multilayered composite and sandwich structures using an inverse finite element method. In Proceedings of the V International Conference on Computational Methods for Coupled Problems in Science and Engineering, Ibiza, Spain, 17–19 June 2013. [Google Scholar]
- Cerracchio, P.; Gherlone, M.; Di Sciuva, M.; Tessler, A. A novel approach for displacement and stress monitoring of sandwich structures based on the inverse Finite Element Method. Compos. Struct. 2015, 127, 69–76. [Google Scholar] [CrossRef]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. A refined zigzag beam theory for composite and sandwich beams. J. Compos. Mater. 2009, 43, 1051–1081. [Google Scholar] [CrossRef]
- Tessler, A.; Di Sciuva, M.; Gherlone, M. A consistent refinement of first-order shear deformation theory for laminated composite and sandwich plates using improved zigzag kinematics. J. Mech. Mater. Struct. 2010, 5, 341–367. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E.; Tessler, A.; Spangler, J. A quadrilateral inverse-shell element with drilling degrees of freedom for shape sensing and structural health monitoring. Eng. Sci. Technol. Int. J. 2016, 19, 1299–1313. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method. Ocean Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a Panamax containership using inverse finite element method. Ocean Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
- Kefal, A.; Yildiz, M. Modeling of Sensor Placement Strategy for Shape Sensing and Structural Health Monitoring of a Wing-Shaped Sandwich Panel Using Inverse Finite Element Method. Sensors 2017, 17, 2775. [Google Scholar] [CrossRef] [PubMed]
- Maincon, P.; Barnardo-Viljoen, C. An inverse finite element method for the analysis of VIV data. Mar. Struct. 2013, 33, 143–159. [Google Scholar] [CrossRef]
- Cooperman, A.; Martinez, M. Load monitoring for active control of wind turbines. Renew. Sustain. Energy Rev. 2015, 41, 189–201. [Google Scholar] [CrossRef]
- Skopinski, T.; Aiken, W.S.J.; Huston, W.B. Calibration of Strain-Gage Installations in Aircraft Structures for the Measurement of Flight Loads; NASA: Langley Field, VA, USA, 1954. [Google Scholar]
- Nakamura, T.; Igawa, H.; Kanda, A. Inverse identification of continuously distributed loads using strain data. Aerosp. Sci. Technol. 2011, 23, 75–84. [Google Scholar] [CrossRef]
- Anton, H.; Rorres, C. Elementary Linear Algebra, 9th ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- MacNeal, R.H.; Harder, R.L. A Proposed Standard Set Of Problems To Test Finite Element Accuracy. Finite Elem. Anal. Des. 1985, 1, 3–20. [Google Scholar] [CrossRef]
- Fourier, J.B.J. Théorie Analytique de la Chaleur (The Analytical Theory of Heat); Firmin Didot Père et Fils: Paris, France, 1822; p. xxii. [Google Scholar]
- Hooke, R. De Potentia Restitutiva, or of Spring. Explaining the Power of Springing Bodies; The Royal Society: London, UK, 1678. [Google Scholar]
- De Borst, R.; Crisfield, M.; Remmers, J.J.; Verhoosel, C.V. Non-Linear Finite Element Analysis of Solids and Structures, 2nd ed.; Wiley: Chichester, UK, 2012; pp. 63–66. [Google Scholar]
- Felippa, C.A. Introduction to Finite Element Methods; University of Colorado: Boulder, CO, USA, 2004; pp. 294–306. [Google Scholar]
- Legendre, A.M. Nouvelles Méthodes Pour la Détermination des Orbites des Comètes (New Methods for the Determination of the Orbits of Comets); F. Didot: Paris, France, 1805; p. 80. [Google Scholar]
- Roache, P. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. ASME J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Slater, J.W. Examining Spatial (Grid) Convergence. NASA. 2021. Available online: https://www.grc.nasa.gov/www/wind/valid/tutorial/spatconv.html (accessed on 10 July 2022).
- Bos, J.; Klein, J.; Froggatt, M.; Sanborn, E.; Gifford, D. Fiber optic strain, temperature and shape sensing via OFDR for ground, air and space applications. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 25–29 August 2013; Volume 8876, no. VII. pp. 14–28. [Google Scholar]
- Martinez Bueno, P.; Martinez, M.; Rans, C.; Benedictus, R. Strain Monitoring using a Rayleigh Backscattering System for a Composite UAV Wing Instrumented with an Embedded Optical Fiber. Adv. Mater. Res. 2016, 1135, 1–10. [Google Scholar] [CrossRef]
- Backman, D.; Martinez, M. Validation of a Structural Health and Loads Monitoring Platform Using Digital Image Correlation. In Proceedings of the 27th ICAF Symposium, Jerusalem, Israel, 5–7 June 2013. [Google Scholar]













| Name | Element Shape | E (Pa) and (ν) (-) | Dimensions (m) | Load Case and BCs | Mesh Size |
|---|---|---|---|---|---|
| Cantilever | Regular, Parallelogram, Trapezoidal | 1.0 × 107 (0.30) | 6.0 × 0.2 × 0.1 | Unit loads (N) on tip: extension, in-plane shear, out-of-plane shear or twist (unit moment (Nm)) and clamped | 6 elements |
| Curved Beam | Regular | 1.0 × 107 (0.25) | radius: 4.12 to 4.32 thickness: 0.1 span: 90° | Unit loads (N) on tip: in-plane shear or out-of-plane shear and clamped | 6 elements |
| Plate Patch Test | Irregular | 1.0 × 106 (0.25) | 0.12 × 0.24 × 0.001 | Prescribed uniform stretch (m) or bending (m) | 5 elements |
| Solid Patch Test | Irregular | 1.0 × 106 (0.25) | 1 × 1 × 1 | Prescribed boundary displacements (m) | 7 elements |
| Thick-walled Cylinder | Regular | 1000 (ν: 0.49, 0.499, 0.4999) | radius: 3.0 to 9.0 thickness: 1.0 | Unit pressure (Pa) at the inner radius | 5 elements per 10° |
| Twisted Beam | Regular | 29.0 × 106 (0.22) | 12.0 × 1.1 × 0.32 twist: 90° | In-plane shear (N) or out-of-plane shear (N) and clamped | 12 × 2 |
| Normalized Grid Spacing | Elements along x Axis | Elements along y Axis | Elements along z Axis | Elements |
|---|---|---|---|---|
| 1 | 80 | 16 | 8 | 10,240 |
| 2 | 40 | 8 | 4 | 1280 |
| 4 | 20 | 4 | 2 | 160 |
| Load Case | Description | Load Magnitude Distribution (N) |
|---|---|---|
| 1x, 1y, 1z | Constant load | |
| 2x, 2y, 2z | Linear ramp, −x to +x | |
| 3x, 3y, 3z | Linear ramp, +x to −x | |
| 4x, 4y, 4z | Linear ramp, −y to +y | |
| 5x, 5y, 5z | Linear ramp, +y to −y | |
| 6x, 6y, 6z | Quadratic over x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Mooij, C.; Martinez, M. A Critical Comparison of Shape Sensing Algorithms: The Calibration Matrix Method versus iFEM. Sensors 2024, 24, 3562. https://doi.org/10.3390/s24113562
de Mooij C, Martinez M. A Critical Comparison of Shape Sensing Algorithms: The Calibration Matrix Method versus iFEM. Sensors. 2024; 24(11):3562. https://doi.org/10.3390/s24113562
Chicago/Turabian Stylede Mooij, Cornelis, and Marcias Martinez. 2024. "A Critical Comparison of Shape Sensing Algorithms: The Calibration Matrix Method versus iFEM" Sensors 24, no. 11: 3562. https://doi.org/10.3390/s24113562
APA Stylede Mooij, C., & Martinez, M. (2024). A Critical Comparison of Shape Sensing Algorithms: The Calibration Matrix Method versus iFEM. Sensors, 24(11), 3562. https://doi.org/10.3390/s24113562








