An Enhanced Indoor Three-Dimensional Localization System with Sensor Fusion Based on Ultra-Wideband Ranging and Dual Barometer Altimetry †
Abstract
1. Introduction
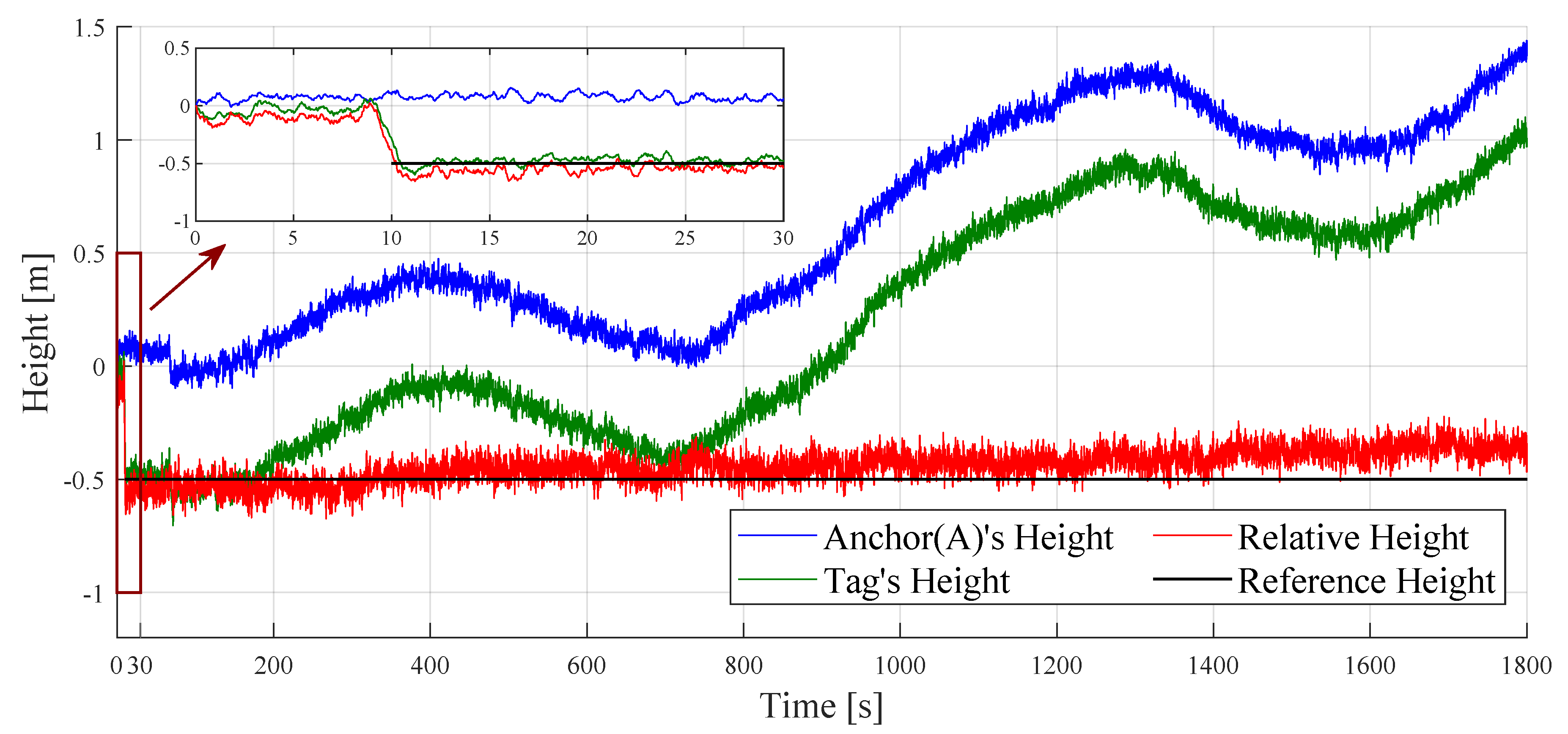
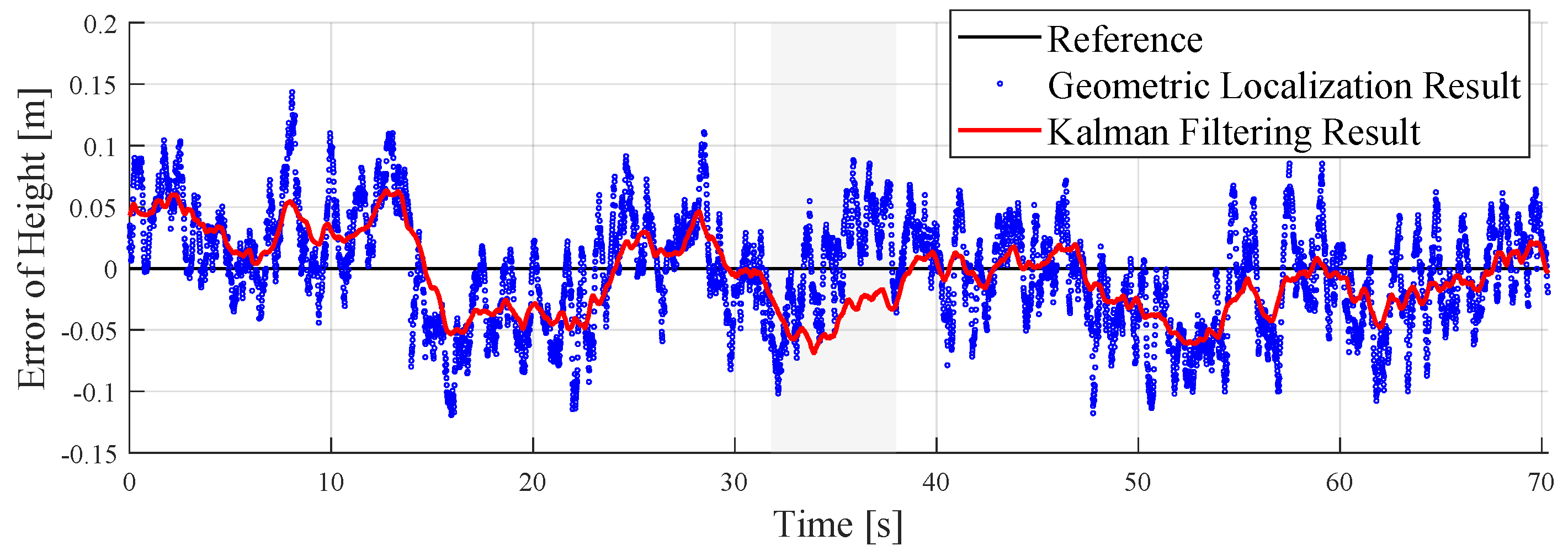
- Proposed and validated a method for estimating tag height based on dual BMP sensors, effectively compensating for most indoor barometric pressure deviations, and providing a more accurate height estimation than achievable with a single BMP sensor. For the challenge of indoor height estimation, our accuracy is approximately ±0.05 m, with an RMSE of 0.0282 m.
- Developed a hardware framework that enhances the system to be more efficient and stable, with a localization output rate reaching 37 Hz, a nine-fold increase compared to earlier designs.
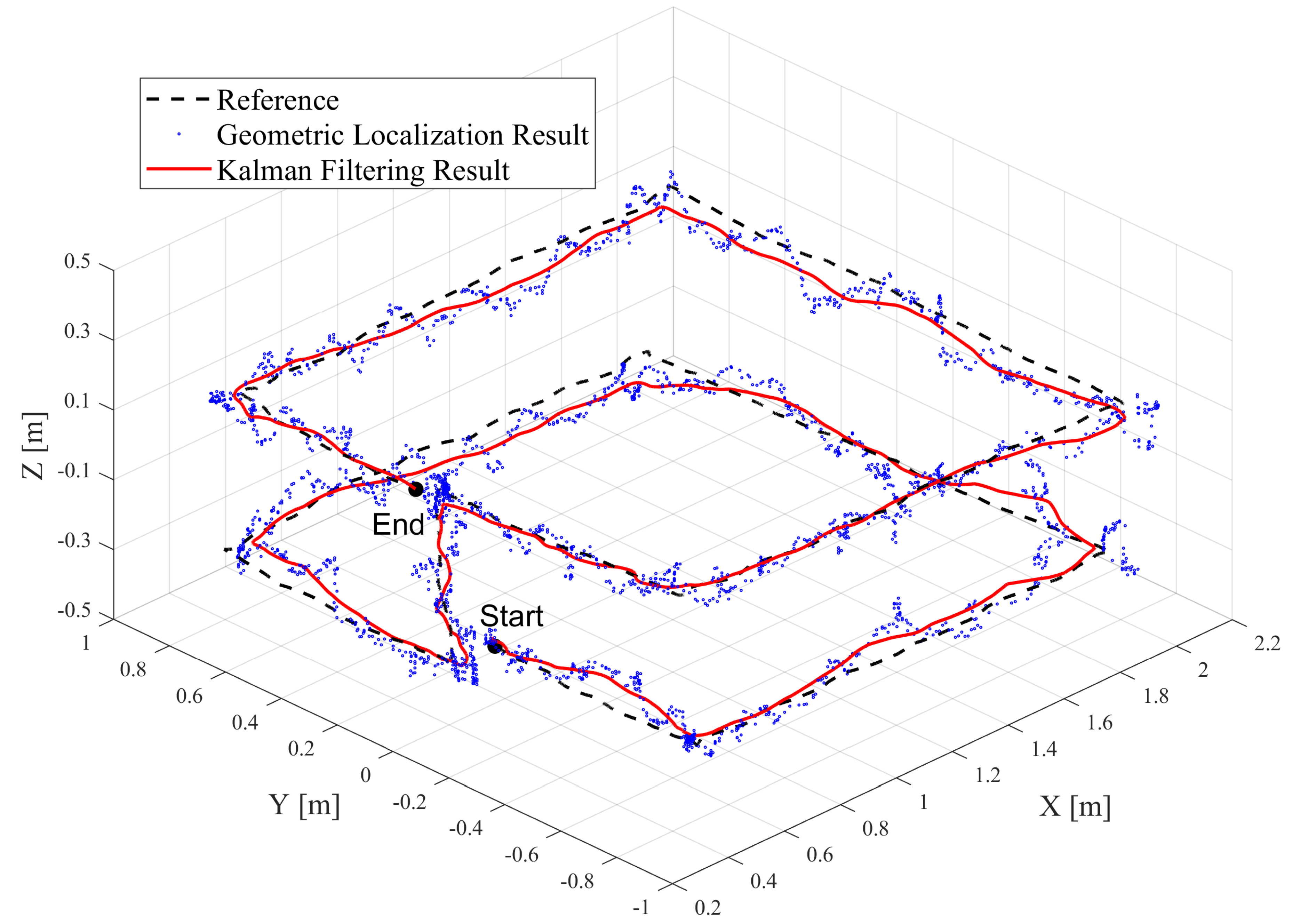
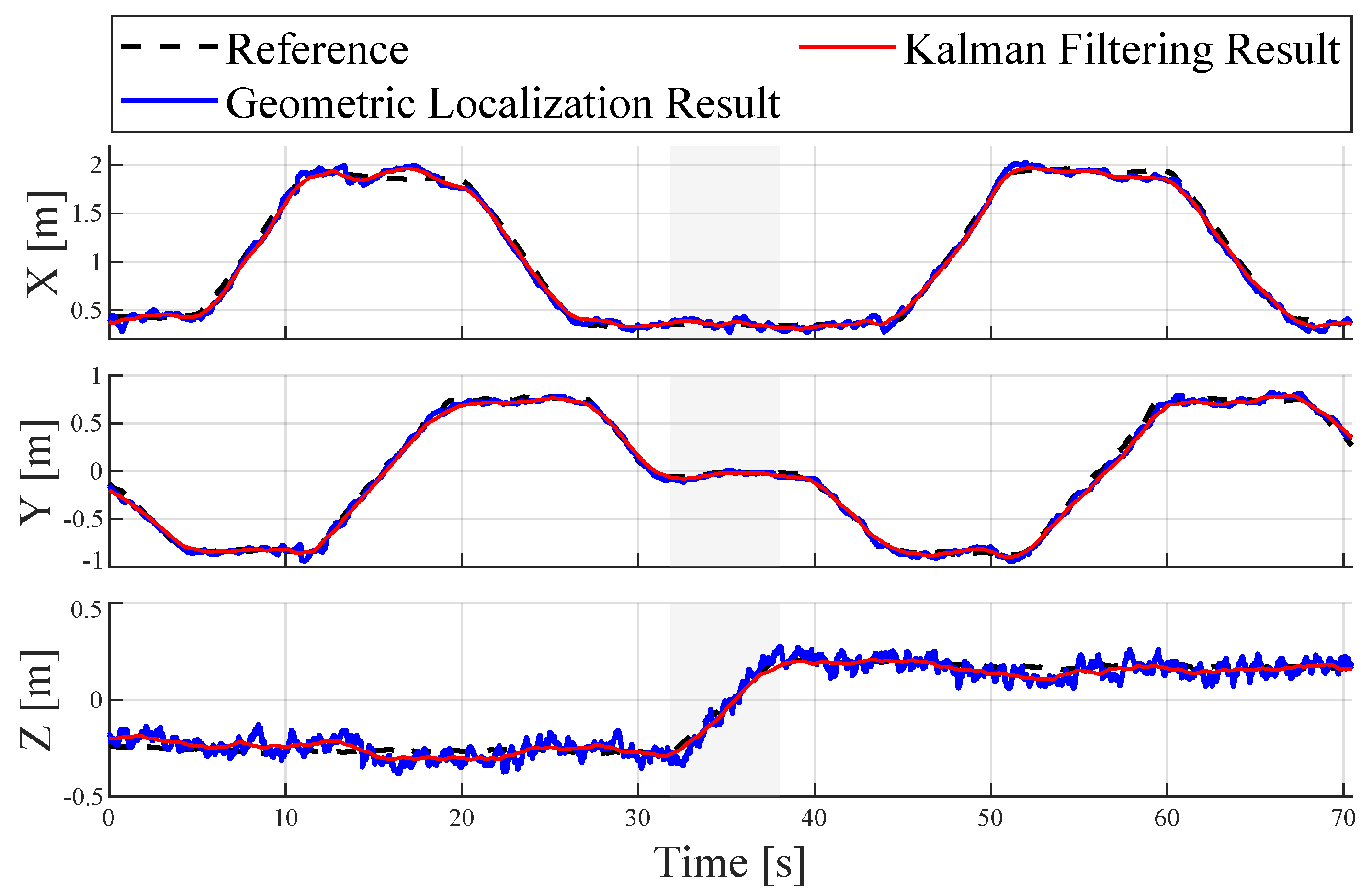
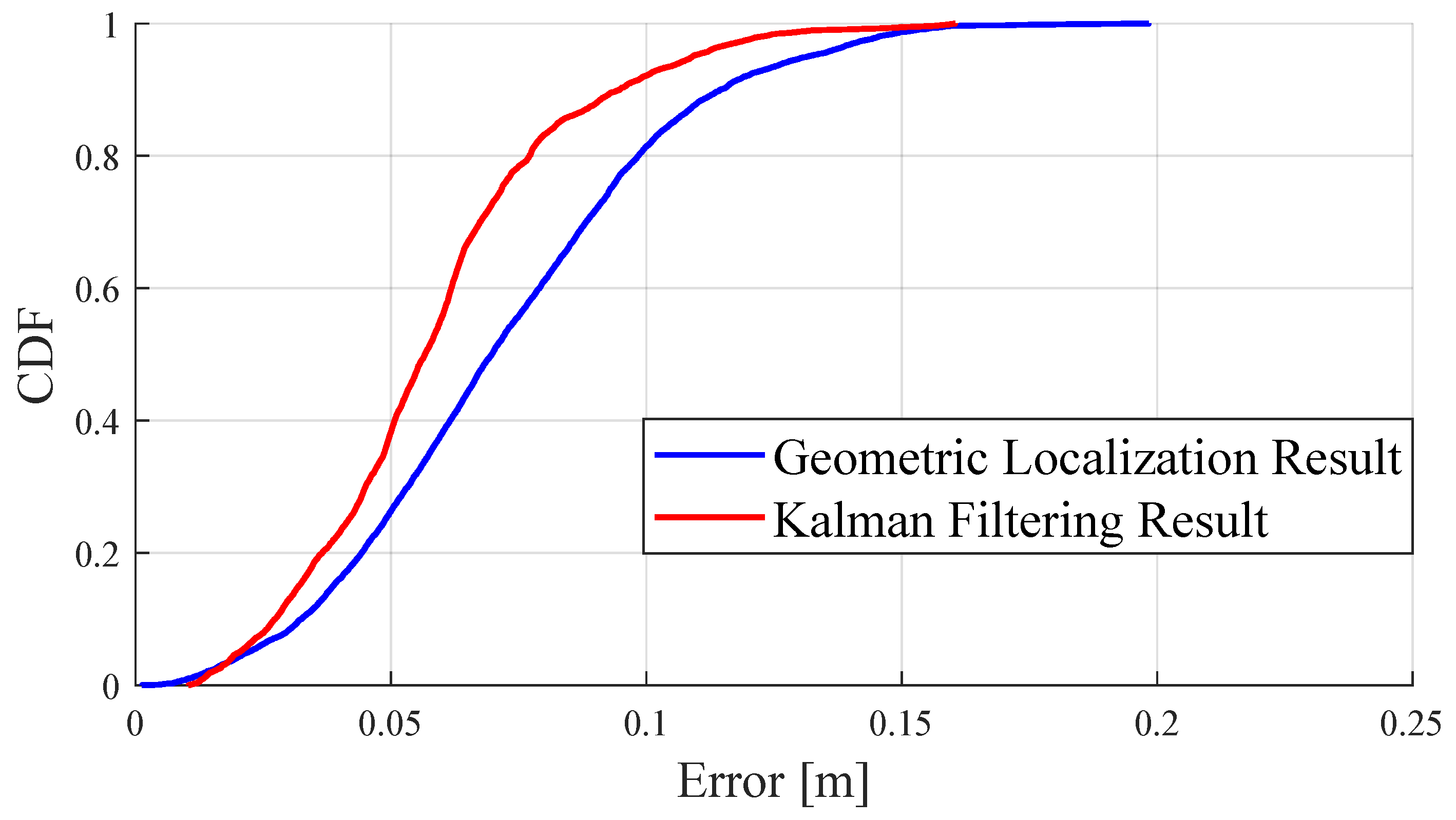
- Our portable localization system covers a larger measurable range. The proposed geometric localization model and the Kalman filtering technique are empirically validated, showing a 2D localization RMSE of 0.0585 m, and a 3D localization RMSE of 0.0740 m. Compared to indoor localization systems with a similar number of anchors, ours offers an extended measurable range and superior accuracy.
2. Hardware System Design
3. Spatial Distance Measurement
3.1. Height Measurement with Dual BMP Sensors
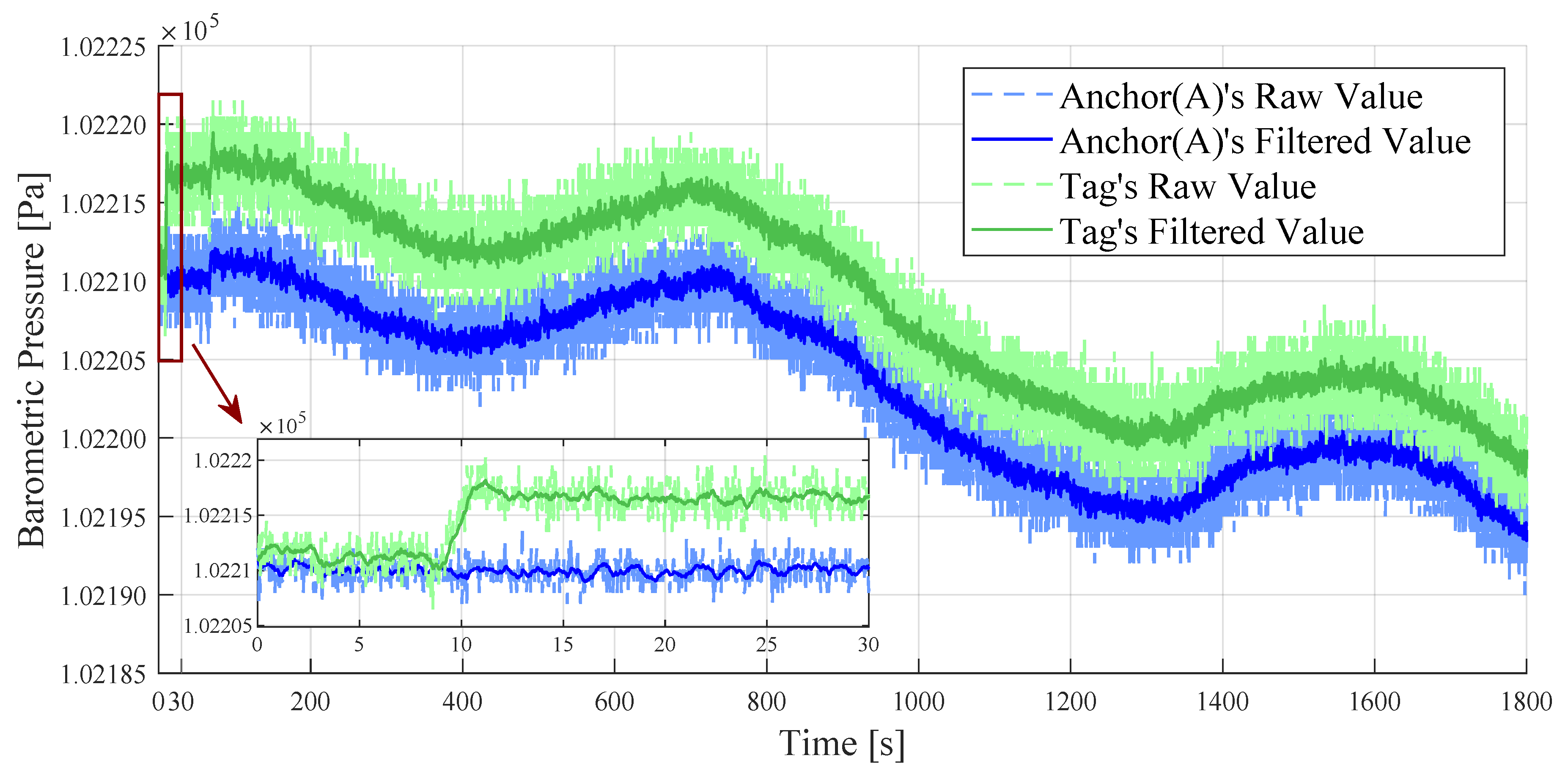
3.1.1. Observation of Indoor Barometric Pressure Measurements
3.1.2. Relative Height Estimation Based on Dual BMP Sensors
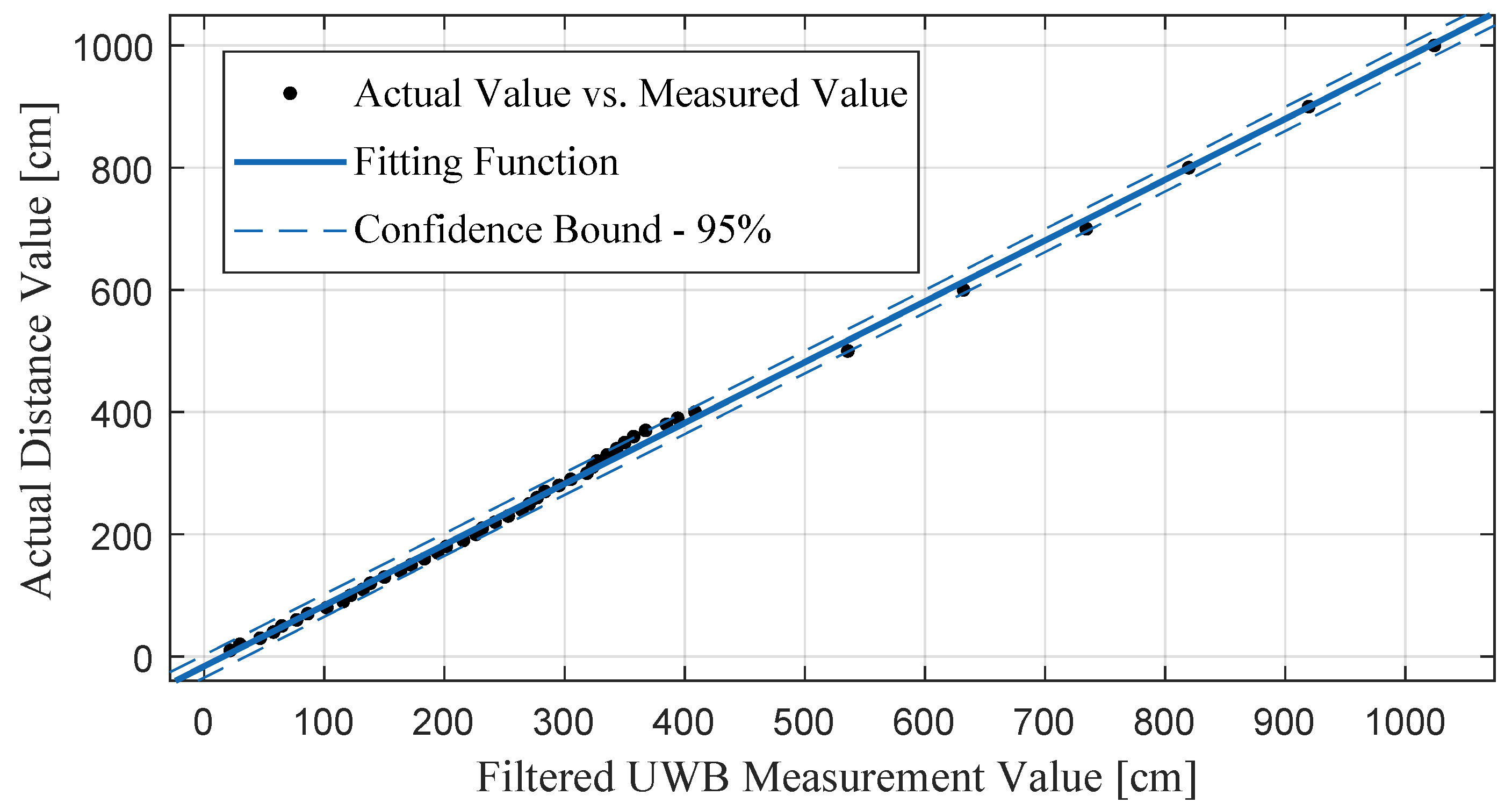
3.2. Distance Measurement Optimization for UWB Sensors
4. Indoor 3D Localization Method
| Algorithm 1 Indoor 3D localization method. |
| Input: Distance values measured by UWB sensors: . Barometric pressure values measured by BMP sensors: . Output: The coordinates of the tag’s 3D indoor location: .
|
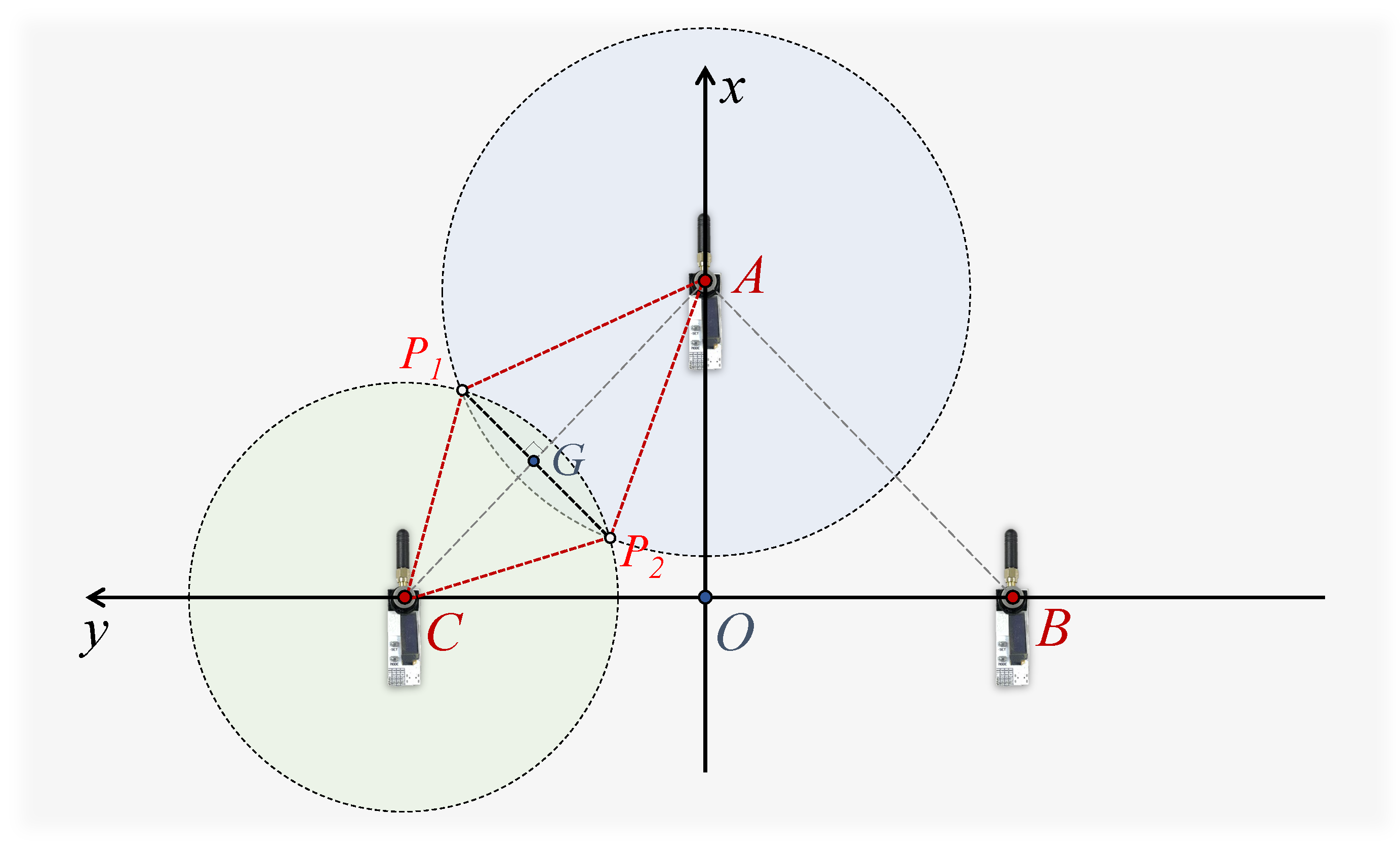
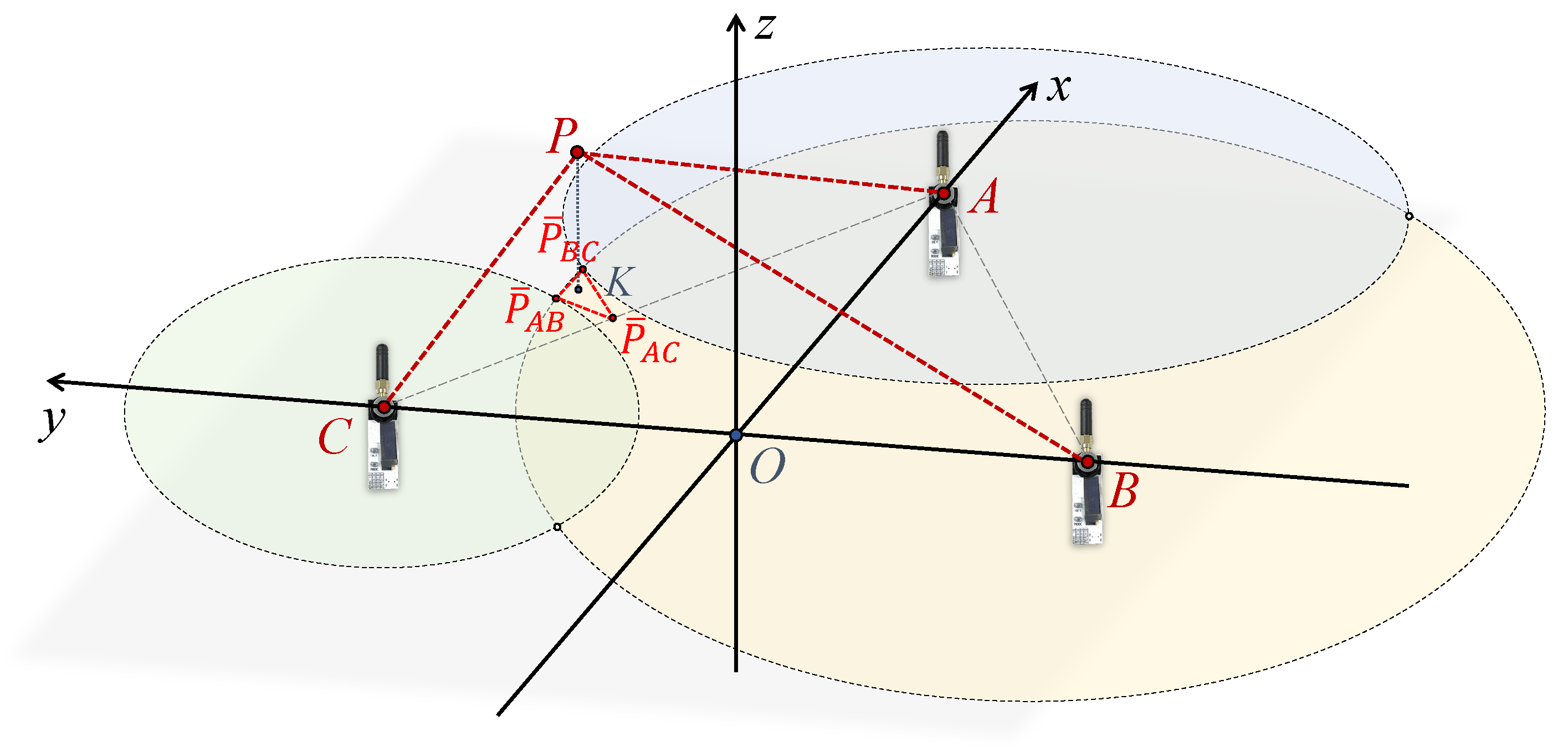
4.1. Geometric Localization Model
4.2. Optimization of Location Estimation Based on Kalman Filtering
5. Experiments and Evaluations
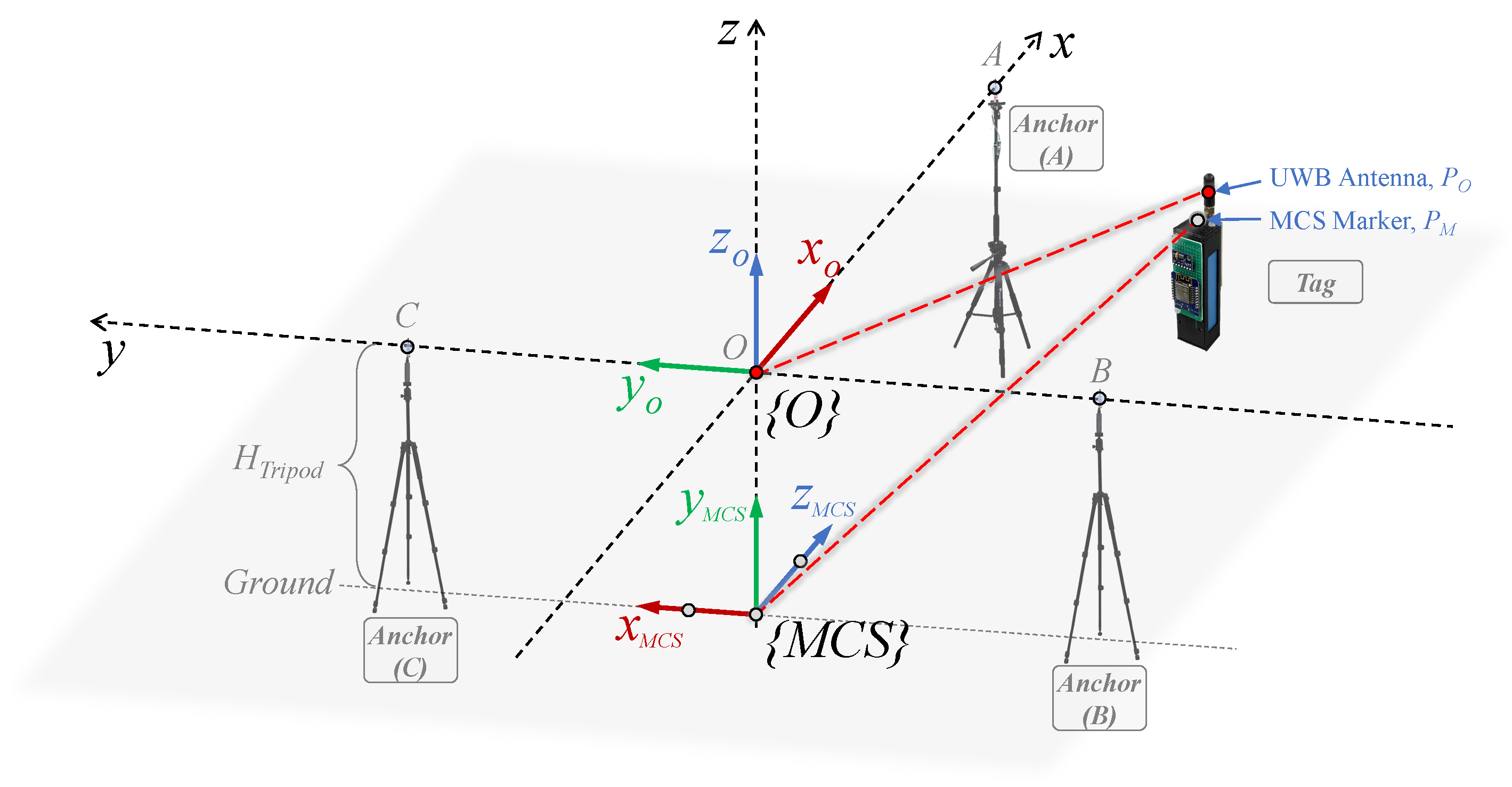
5.1. Experimental Setup
- Errors on different coordinate axes (, , ):
- Two-dimensional localization error on the X-Y plane ():
- Three-dimensional localization error across the X-Y-Z axes ():where , , are the tag’s reference location data collected by the motion capture system. , , and are the estimated location data of the proposed localization system.
5.2. Indoor 3D Localization Experiment
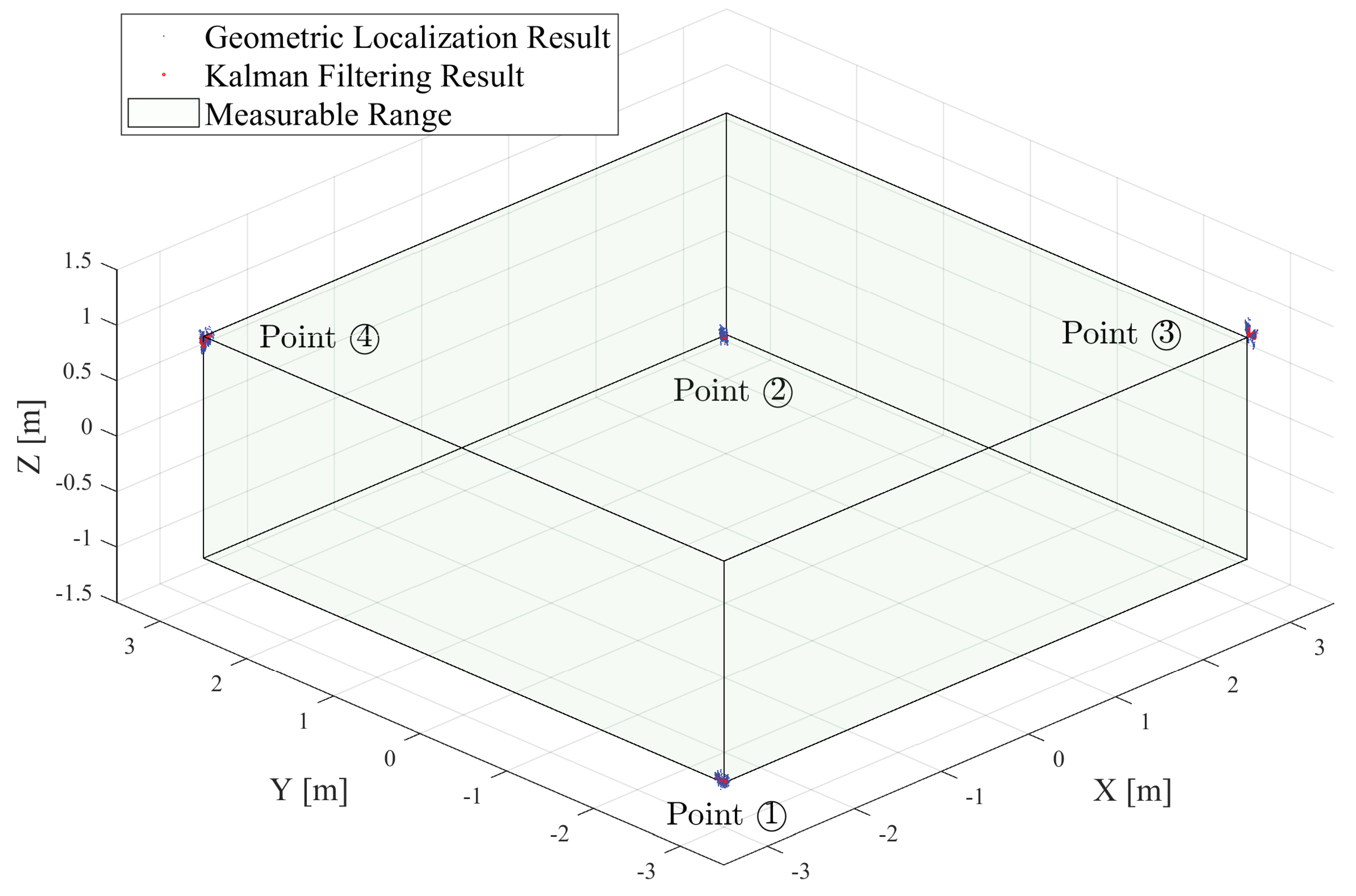
5.3. Locatable Range Verification Experiment
6. Discussion
6.1. Comparison with Our Previous Study
- In terms of hardware, the UWB sensor was upgraded from a patch type to an antenna type. To account for the propagation direction and range of the antenna signal, a short antenna with 2 dBi gain was selected to enhance the indoor omnidirectional ranging capability for the UWB sensors.
- Additionally, the main controller was upgraded from ESP8266 to the dual-core ESP32 chip. By rationally allocating tasks through the software, one core was specifically used for Wi-Fi data reading, thus making the data output of the localization system faster and more stable. The localization output rate reached 37 Hz, which was a nine-fold increase.
- The dispersed arrangement of the anchors allowed the locatable area of the new localization framework to expand. The verified locatable range of the system was 6 m (length) × 6 m (width) × 2 m (height), which was approximately three times larger compared to the previous localization device.
- In particular, the RMSE of the 3D localization system reached 0.074 m, which improved the localization accuracy by 40.7% compared to our previous study.
6.2. Comparison with Other Related Studies
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| BMP | Barometric Pressure |
| UWB | Ultra-Wideband |
| MCS | Motion Capture System |
| CDF | Cumulative Distribution Function |
| RMSE | Root Mean Square Error |
References
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Ledergerber, A.; Hamer, M.; D’Andrea, R. A robot self-localization system using one-way ultra-wideband communication. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 3131–3137. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y.; Lyu, J.; Dai, X.; Huang, R.; Zhang, Q.; Jing, H. Nuclear Power Plant Indoor Personnel Positioning Scheme and Test. In Proceedings of the 2023 5th International Conference on Electronics and Communication, Network and Computer Technology (ECNCT), Guangzhou, China, 18–20 August 2023; pp. 289–292. [Google Scholar] [CrossRef]
- Laoudias, C.; Moreira, A.; Kim, S.; Lee, S.; Wirola, L.; Fischione, C. A Survey of Enabling Technologies for Network Localization, Tracking, and Navigation. IEEE Commun. Surv. Tutor. 2018, 20, 3607–3644. [Google Scholar] [CrossRef]
- Li, J.; Bi, Y.; Li, K.; Wang, K.; Lin, F.; Chen, B.M. Accurate 3D Localization for MAV Swarms by UWB and IMU Fusion. In Proceedings of the 2018 IEEE 14th International Conference on Control and Automation (ICCA), Anchorage, AK, USA, 12–15 June 2018; pp. 100–105. [Google Scholar] [CrossRef]
- Si, M.; Wang, Y.; Zhou, N.; Seow, C.; Siljak, H. A Hybrid Indoor Altimetry Based on Barometer and UWB. Sensors 2023, 23, 4180. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Dehaene, W.; Gielen, G. A 3-tier UWB-based indoor localization system for ultra-low-power sensor networks. IEEE Trans. Wirel. Commun. 2009, 8, 2813–2818. [Google Scholar] [CrossRef]
- Xu, S.; Chen, R.; Guo, G.; Li, Z.; Qian, L.; Ye, F.; Liu, Z.; Huang, L. Bluetooth, Floor-Plan, and Microelectromechanical Systems-Assisted Wide-Area Audio Indoor Localization System: Apply to Smartphones. IEEE Trans. Ind. Electron. 2022, 69, 11744–11754. [Google Scholar] [CrossRef]
- Piciarelli, C. Visual Indoor Localization in Known Environments. IEEE Signal Process. Lett. 2016, 23, 1330–1334. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, C.; Lyu, Y. DMLL: Differential-Map-Aided LiDAR-Based Localization. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Zeng, Q.; Tao, X.; Yu, H.; Ji, X.; Chang, T.; Hu, Y. An Indoor 2-D LiDAR SLAM and Localization Method Based on Artificial Landmark Assistance. IEEE Sens. J. 2024, 24, 3681–3692. [Google Scholar] [CrossRef]
- Bochem, A.; Zhang, H. Robustness Enhanced Sensor Assisted Monte Carlo Localization for Wireless Sensor Networks and the Internet of Things. IEEE Access 2022, 10, 33408–33420. [Google Scholar] [CrossRef]
- Strohmeier, M.; Walter, T.; Rothe, J.; Montenegro, S. Ultra-Wideband Based Pose Estimation for Small Unmanned Aerial Vehicles. IEEE Access 2018, 6, 57526–57535. [Google Scholar] [CrossRef]
- Buck, L.; Vargas, M.F.; McDonnell, R. The Effect of Spatial Audio on the Virtual Representation of Personal Space. In Proceedings of the 2022 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW), Christchurch, New Zealand, 12–16 March 2022; pp. 354–356. [Google Scholar] [CrossRef]
- Kumar, C.P.; Poovaiah, R.; Sen, A.; Ganadas, P. Single access point based indoor localization technique for augmented reality gaming for children. In Proceedings of the 2014 IEEE Students’ Technology Symposium, Kharagpur, India, 28 February–2 March 2014; pp. 229–232. [Google Scholar] [CrossRef]
- Lan, Y.S.; Sun, S.W.; Shih, H.C.; Hua, K.L.; Chang, P.C. O-Shooting: An Orientation-based Basketball Shooting Mixed Reality Game Based on Environment 3D Scanning and Object Positioning. In Proceedings of the 2018 IEEE 7th Global Conference on Consumer Electronics (GCCE), Nara, Japan, 9–12 October 2018; pp. 678–679. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, X.; Xu, C.Z.; Li, X. ER-CRLB: An Extended Recursive Cramér–Rao Lower Bound Fundamental Analysis Method for Indoor Localization Systems. IEEE Trans. Veh. Technol. 2017, 66, 1605–1618. [Google Scholar] [CrossRef]
- Liu, X.; Cen, J.; Zhan, Y.; Tang, C. An Adaptive Fingerprint Database Updating Method for Room Localization. IEEE Access 2019, 7, 42626–42638. [Google Scholar] [CrossRef]
- Bouhdid, B.; Akkari, W.; Belghith, A. Accuracy/Cost Trade-Off in Localization Problem for Wireless Sensor Networks. In Proceedings of the 2018 International Conference on Control, Automation and Diagnosis (ICCAD), Marrakech, Morocco, 19–21 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Bao, L.; Li, K.; Li, W.; Shin, K.; Kim, W. A Sensor Fusion Strategy for Indoor Target Three-dimensional Localization based on Ultra-Wideband and Barometric Altimeter Measurements. In Proceedings of the 2022 19th International Conference on Ubiquitous Robots (UR), Jeju, Republic of Korea, 4–6 July 2022; pp. 181–187. [Google Scholar] [CrossRef]
- Sesyuk, A.; Ioannou, S.; Raspopoulos, M. A Survey of 3D Indoor Localization Systems and Technologies. Sensors 2022, 22, 9380. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, W.; Xu, H.; Kang, H. Research on Indoor Sports Positioning Algorithm Based on UWB. In Proceedings of the 2021 International Conference on Control, Automation and Information Sciences (ICCAIS), Xi’an, China, 14–17 October 2021; pp. 638–643. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Y.; Wang, G. On the anti-multipath performance of UWB signals in indoor environments. In Proceedings of the ICMMT 4th International Conference on, Proceedings Microwave and Millimeter Wave Technology, Beijing, China, 18–21 August 2004; pp. 163–166. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, J.; Wang, J. A multi-sensor fusion method based on EKF on granary robot. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 4838–4843. [Google Scholar] [CrossRef]
- Li, Y.; Chen, W.; Wang, J.; Nie, X. Precise Indoor and Outdoor Altitude Estimation Based on Smartphone. IEEE Trans. Instrum. Meas. 2023, 72, 9513111. [Google Scholar] [CrossRef]
- West, J.B. Torricelli and the Ocean of Air: The First Measurement of Barometric Pressure. Physiology 2013, 28, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Bhadoria, G.; Thomas, C.K.; Panchal, S.; Nayak, S. Multi Purpose Flight Controller for UAV. In Proceedings of the 2023 3rd International Conference on Advancement in Electronics & Communication Engineering (AECE), Ghaziabad, India, 23–24 November 2023; pp. 79–82. [Google Scholar] [CrossRef]
- Bao, X.; Xiong, Z.; Sheng, S.; Dai, Y.; Bao, S.; Liu, J. Barometer measurement error modeling and correction for UAH altitude tracking. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 3166–3171. [Google Scholar] [CrossRef]
- Bo, L.; Chao, X.; Xiaohui, L.; Wenli, W. Research and experimental validation of the method for barometric altimeter aid GPS in challenged environment. In Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–23 October 2017; pp. 88–92. [Google Scholar] [CrossRef]
- Kalamees, T.; Kurnitski, J.; Jokisalo, J.; Eskola, L.; Jokiranta, K.; Vinha, J. Measured and simulated air pressure conditions in Finnish residential buildings. Build. Serv. Eng. Res. Technol. 2010, 31, 177–190. [Google Scholar] [CrossRef]
- Ma, J.; Duan, X.; Shang, C.; Ma, M.; Zhang, D. Improved Extreme Learning Machine Based UWB Positioning for Mobile Robots with Signal Interference. Machines 2022, 10, 218. [Google Scholar] [CrossRef]
- Pierleoni, P.; Belli, A.; Maurizi, L.; Palma, L.; Pernini, L.; Paniccia, M.; Valenti, S. A Wearable Fall Detector for Elderly People Based on AHRS and Barometric Sensor. IEEE Sens. J. 2016, 16, 6733–6744. [Google Scholar] [CrossRef]
- Mondal, R.; Reddy, P.S.; Sarkar, D.C.; Sarkar, P.P. Compact ultra-wideband antenna: Improvement of gain and FBR across the entire bandwidth using FSS. IET Microw. Antennas Propag. 2020, 14, 66–74. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, X.; Zhao, Z.; Liu, Y.; Yang, S. High Accuracy Positioning System Based on Multistation UWB Time-of-Flight Measurements. In Proceedings of the 2020 IEEE International Conference on Computational Electromagnetics (ICCEM), Singapore, 24–26 August 2020; pp. 268–270. [Google Scholar] [CrossRef]
- Feng, T.; Yu, Y.; Wu, L.; Bai, Y.; Xiao, Z.; Lu, Z. A Human-Tracking Robot Using Ultra Wideband Technology. IEEE Access 2018, 6, 42541–42550. [Google Scholar] [CrossRef]
- Lazzari, F.; Buffi, A.; Nepa, P.; Lazzari, S. Numerical Investigation of an UWB Localization Technique for Unmanned Aerial Vehicles in Outdoor Scenarios. IEEE Sens. J. 2017, 17, 2896–2903. [Google Scholar] [CrossRef]
- Guo, H.; Li, M. Indoor Positioning Optimization Based on Genetic Algorithm and RBF Neural Network. In Proceedings of the 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 28–30 July 2020; pp. 778–781. [Google Scholar] [CrossRef]
- Pan, H.; Qi, X.; Liu, M.; Liu, L. Map-aided and UWB-based anchor placement method in indoor localization. Neural Comput. Appl. 2021, 33, 11845–11859. [Google Scholar] [CrossRef]
- Oğuz-Ekim, P. TDOA based localization and its application to the initialization of LiDAR based autonomous robots. Robot. Auton. Syst. 2020, 131, 103590. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, S.; Leng, C.T. A Study on the Location System Based on Zigbee for Mobile Robot. Appl. Mech. Mater. 2014, 651, 612–615. [Google Scholar] [CrossRef]
- Tiemann, J.; Ramsey, A.; Wietfeld, C. Enhanced UAV Indoor Navigation through SLAM-Augmented UWB Localization. In Proceedings of the 2018 IEEE International Conference on Communications Workshops (ICC Workshops), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Yoon, P.K.; Zihajehzadeh, S.; Kang, B.S.; Park, E.J. Robust Biomechanical Model-Based 3-D Indoor Localization and Tracking Method Using UWB and IMU. IEEE Sens. J. 2017, 17, 1084–1096. [Google Scholar] [CrossRef]
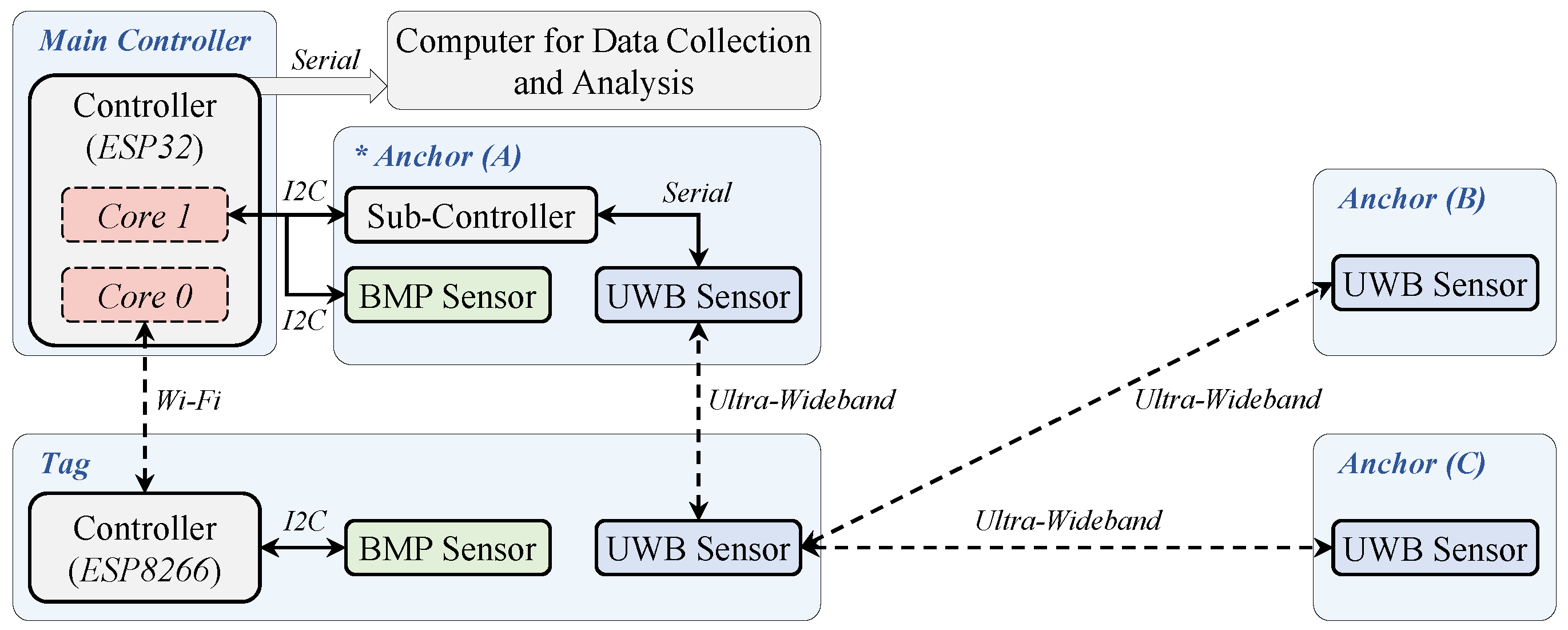
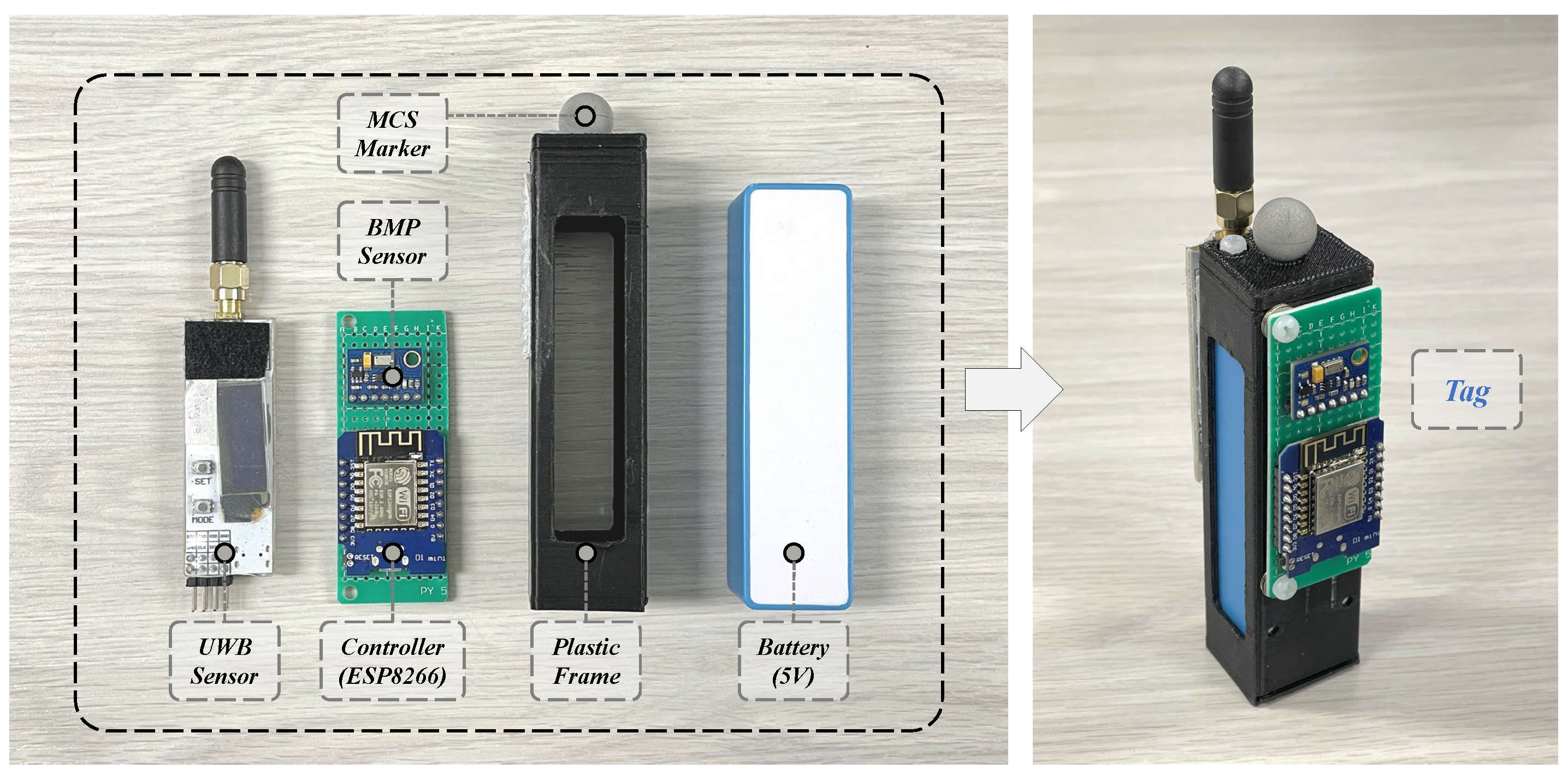




| Device | Microchip | Board Model | Communication Mode |
|---|---|---|---|
| Controller (ESP32) | ESP32 | Arduino Nano ESP32 | Serial, I2C, Wi-Fi |
| Controller (ESP8266) | ESP8266 | ESP8266 D1 Mini | I2C, Wi-Fi |
| Sub-Controller | ATmega2560 | Arduino Mega | Serial, I2C |
| BMP Sensor | MS5611 | GY-63 | I2C |
| UWB Sensor | DW3000 | D-DWM-PG3.9 | Serial, UWB |
| 1.5 m | 2.8 m | 2.4 m | 2.4 m |
| Coordinate Axis | Localization Result | Maximum Error [m] | * RMSE [m] |
|---|---|---|---|
| X | Geometric | 0.1524 | 0.0516 |
| Filtering | 0.1137 | 0.0415 | |
| Y | Geometric | 0.1374 | 0.0402 |
| Filtering | 0.1403 | 0.0392 | |
| Z | Geometric | 0.1434 | 0.0451 |
| Filtering | 0.0616 | 0.0282 | |
| X-Y (2D) | Geometric | 0.1781 | 0.0649 |
| Filtering | 0.1602 | 0.0578 | |
| X-Y-Z (3D) | Geometric | 0.1983 | 0.0790 |
| Filtering | 0.1604 | 0.0643 |
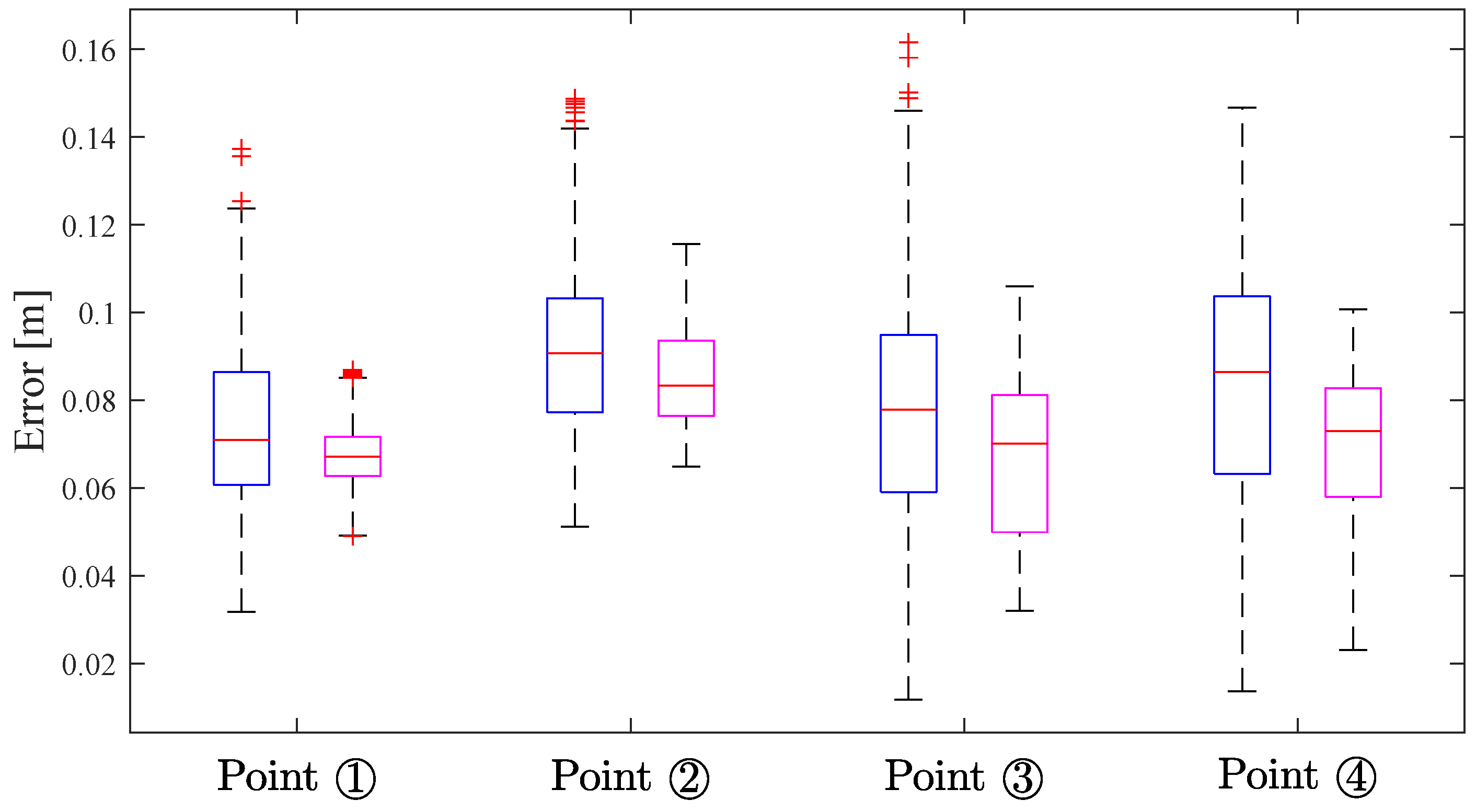
| Point | Localization Methods | RMSE (2D) [m] | RMSE (3D) [m] |
|---|---|---|---|
| ① | Geometric | 0.0575 | 0.0777 |
| Filtering | 0.0541 | 0.0688 | |
| ② | Geometric | 0.0797 | 0.0928 |
| Filtering | 0.0778 | 0.0856 | |
| ③ | Geometric | 0.0599 | 0.0835 |
| Filtering | 0.0592 | 0.0696 | |
| ④ | Geometric | 0.0626 | 0.0900 |
| Filtering | 0.0430 | 0.0720 | |
| Average Value | Geometric | 0.0649 | 0.0860 |
| Filtering | 0.0585 | 0.0740 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, L.; Li, K.; Lee, J.; Dong, W.; Li, W.; Shin, K.; Kim, W. An Enhanced Indoor Three-Dimensional Localization System with Sensor Fusion Based on Ultra-Wideband Ranging and Dual Barometer Altimetry. Sensors 2024, 24, 3341. https://doi.org/10.3390/s24113341
Bao L, Li K, Lee J, Dong W, Li W, Shin K, Kim W. An Enhanced Indoor Three-Dimensional Localization System with Sensor Fusion Based on Ultra-Wideband Ranging and Dual Barometer Altimetry. Sensors. 2024; 24(11):3341. https://doi.org/10.3390/s24113341
Chicago/Turabian StyleBao, Le, Kai Li, Joosun Lee, Wenbin Dong, Wenqi Li, Kyoosik Shin, and Wansoo Kim. 2024. "An Enhanced Indoor Three-Dimensional Localization System with Sensor Fusion Based on Ultra-Wideband Ranging and Dual Barometer Altimetry" Sensors 24, no. 11: 3341. https://doi.org/10.3390/s24113341
APA StyleBao, L., Li, K., Lee, J., Dong, W., Li, W., Shin, K., & Kim, W. (2024). An Enhanced Indoor Three-Dimensional Localization System with Sensor Fusion Based on Ultra-Wideband Ranging and Dual Barometer Altimetry. Sensors, 24(11), 3341. https://doi.org/10.3390/s24113341









