3D Indoor Position Estimation Based on a UDU Factorization Extended Kalman Filter Structure Using Beacon Distance and Inertial Measurement Unit Data †
Abstract
1. Introduction
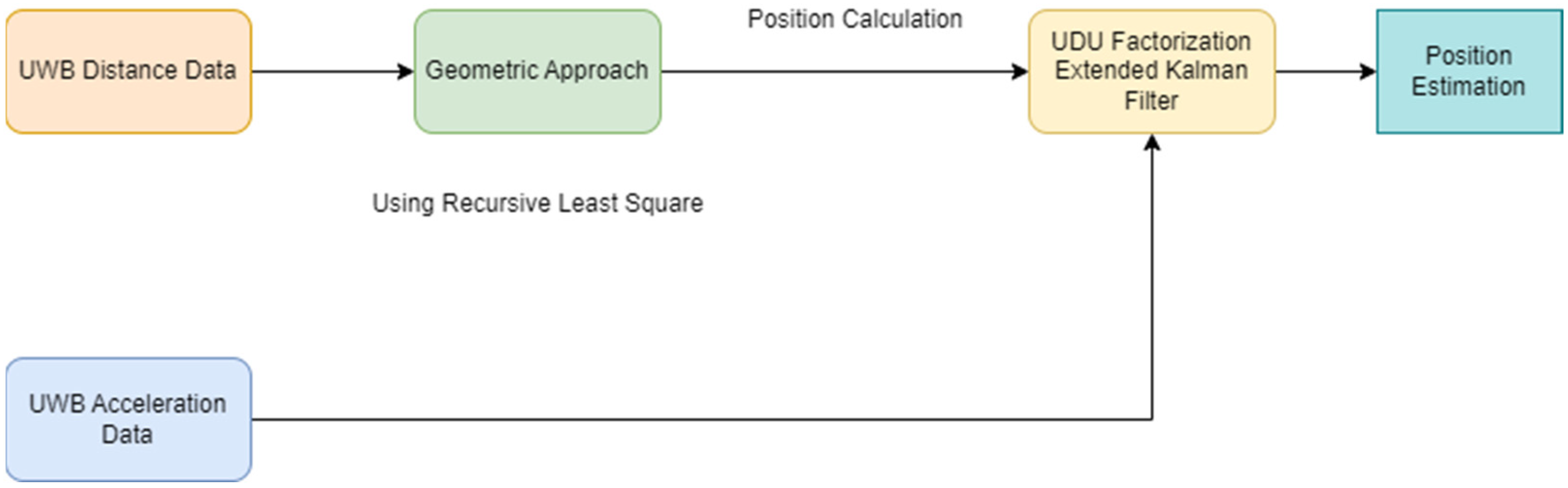
- The use of a sensor fusion algorithm, utilizing the EKF structure, in conjunction with acceleration data from IMU sensors, to enhance the accuracy of position information obtained from distance data provided by beacon sensors via the RLS algorithm.
- The incorporation of a UDU factorization structure to reduce computation costs in embedded systems, in addition to the utilization of the EKF structure for sensor fusion.
- The ability of the designed algorithm to produce a solution even under suboptimal conditions, such as the use of only three beacon sensors instead of the ideal four.
2. Position Estimation Algorithm
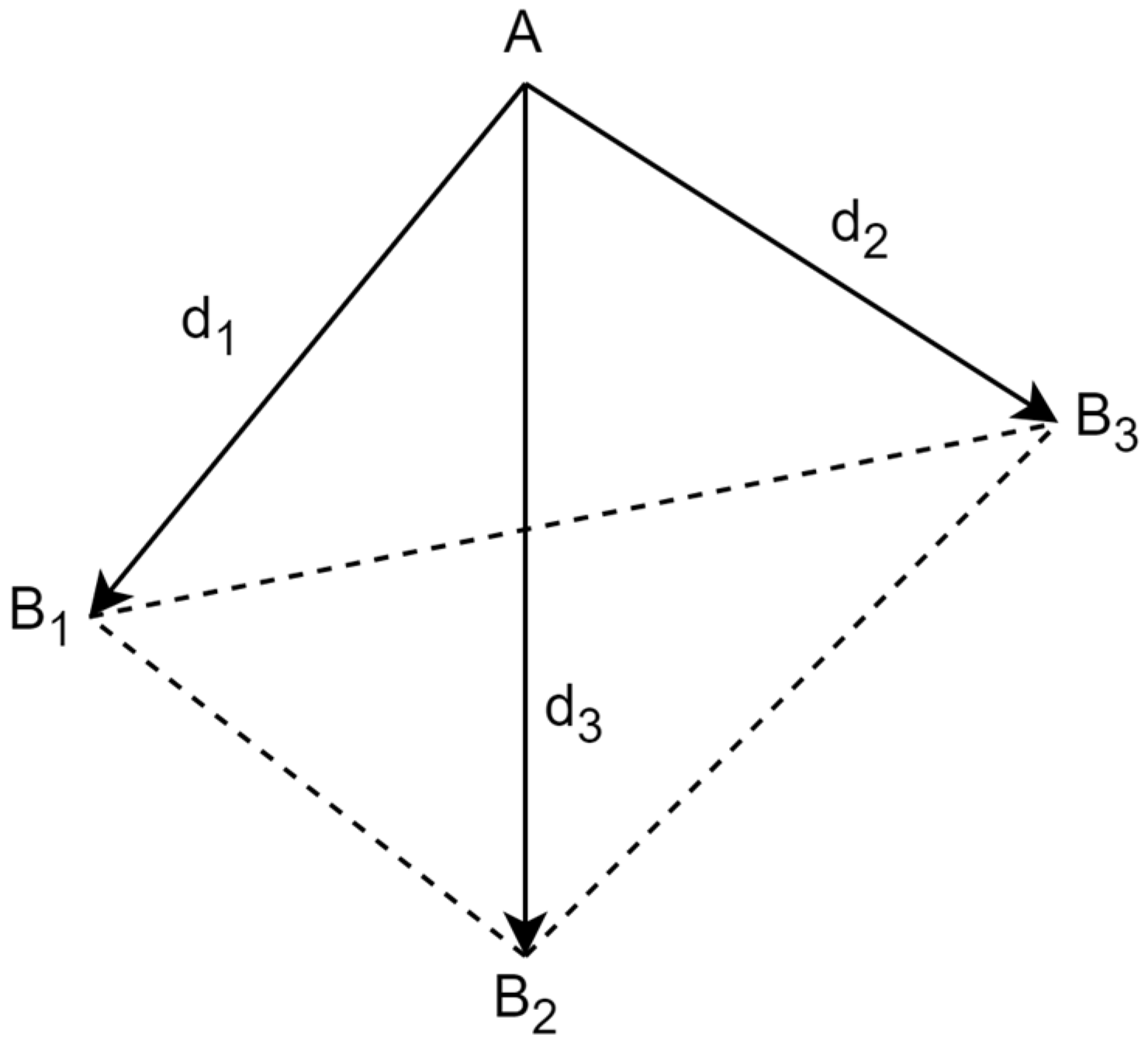
2.1. Geometric Approach
2.1.1. Solution Based on Three Reference Points
- Case 1. B1, B2, and B3 are not in a straight line.
- The rank of matrix A0 is 3.
- The dimension of the null space of A0 is 1.
- Case 2. B1, B2, and B3 are in a straight line.
- The rank of matrix A0 is 2.
- The dimension of the null space of A0 is 2.
2.1.2. Solution Based on More Than Three Reference Points
2.2. Sensor Fusion Algorithm
- (1)
- Prediction of state:
- (2)
- Prediction of state covariance:
- (3)
- Gain calculation of the EKF:
- (4)
- State correction:
- (5)
- State covariance correction:
2.3. UDU Factorization
2.4. UDU Measurement Update
2.5. UDU Time Update
3. Data Acquisition
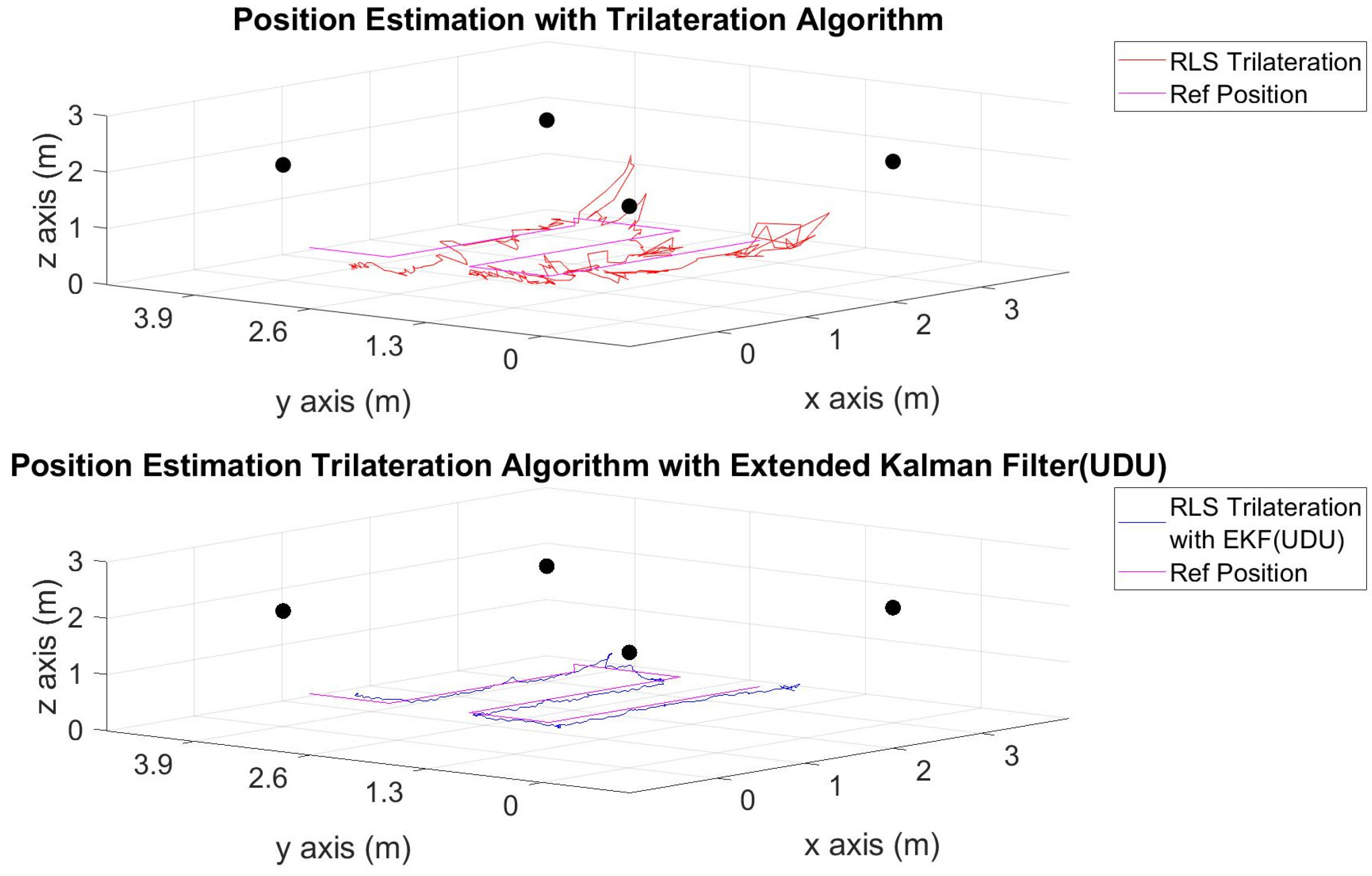
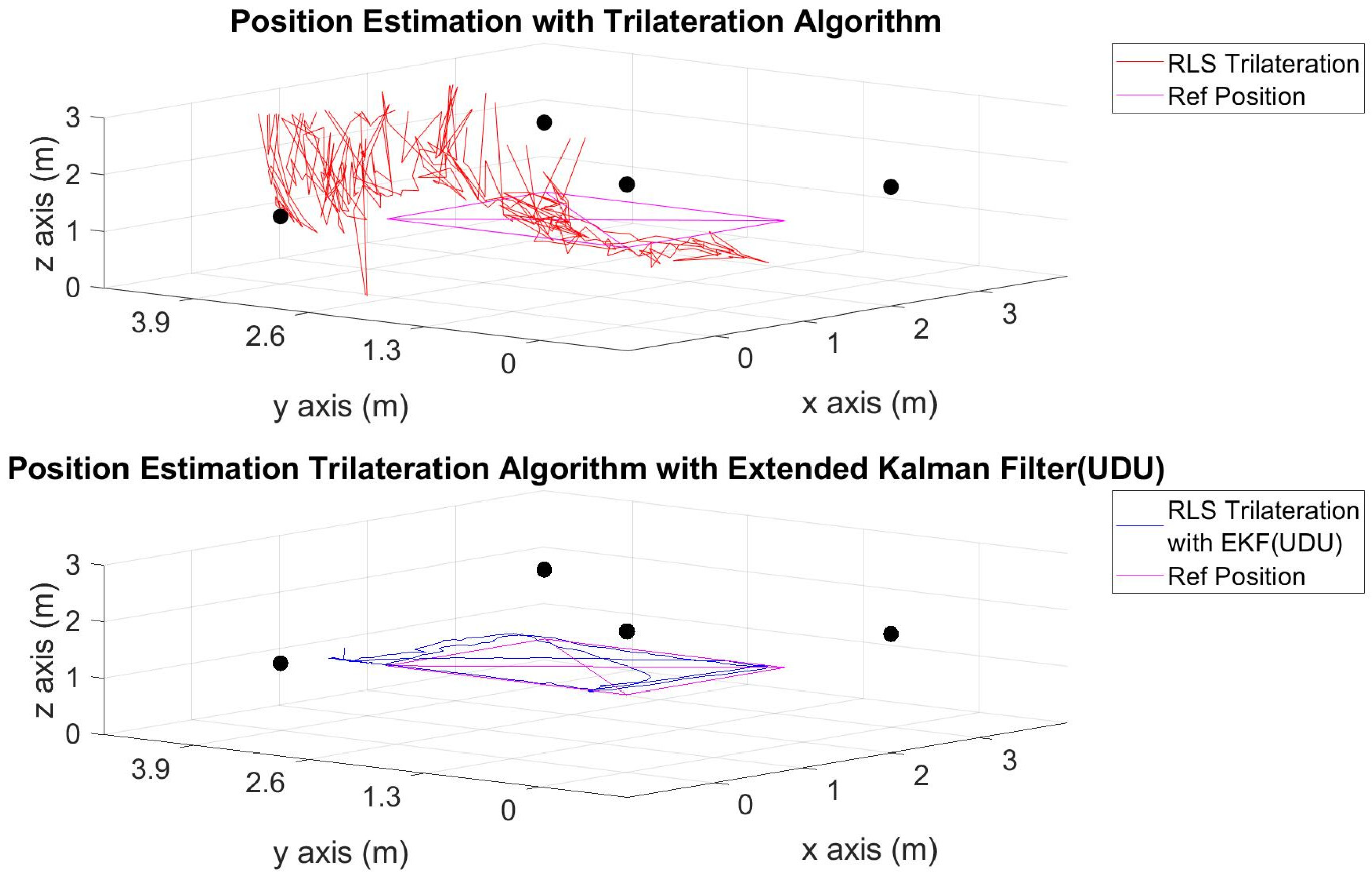
4. Testing Algorithm and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nirjon, S.; Liu, J.; DeJean, G.; Priyantha, B.; Jin, Y.; Hart, T. COIN-GPS: Indoor localization from direct GPS receiving. In Proceedings of the 12th Annual International Conference on Mobile Systems, Applications, and Services—MobiSys 2014, Bretton Woods, NH, USA, 16–19 June 2014; pp. 301–314. [Google Scholar]
- Vasisht, D.; Kumar, S.; Katabi, D. Decimeter-Level Localization with a Single WiFi Access Point. In Proceedings of the USENINX Symposium on Networked Systems Design and Implementation, Santa Clara, CA, USA, 16–18 March 2016; pp. 165–178. [Google Scholar]
- Zafari, F.; Papapanagiotou, I.; Christidis, K. Microlocation for internet-of-things-equipped smart buildings. IEEE Internet Things J. 2016, 3, 96–112. [Google Scholar] [CrossRef]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved techniques for grid mapping with rao-blackwellized particle filters. IEEE Trans. Robot. 2007, 23, 34–46. [Google Scholar] [CrossRef]
- Kohlbrecher, S.; von Stryk, O.; Meyer, J.; Klingauf, U. A flexible and scalable SLAM system with full 3D motion estimation. In Proceedings of the IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 1–5 November 2011; pp. 155–160. [Google Scholar]
- Ren, R.; Fu, H.; Wu, M. Large-scale outdoor SLAM based on 2D lidar. Electronics 2019, 8, 613. [Google Scholar] [CrossRef]
- Chintalapudi, K.; Padmanabha Iyer, A.; Padmanabhan, V.N. Indoor localization without the pain. In Proceedings of the Annual International Conference on Mobile Computing and Networking, MOBICOM, Chicago, IL, USA, 20–24 September 2010; pp. 173–184. [Google Scholar]
- Gomez, C.; Oller, J.; Paradells, J. Overview and evaluation of bluetooth low energy: An emerging low-power wireless technology. Sensors 2012, 12, 11734–11753. [Google Scholar] [CrossRef]
- Aiello, G.R.; Rogerson, G.D. Ultra-wideband wireless systems. IEEE Microw. Mag. 2003, 4, 36–47. [Google Scholar] [CrossRef]
- Chehri, A.; Fortier, P.; Tardif, P.M. UWB-based sensor networks for localization in mining environments. Ad Hoc Netw. 2009, 7, 987–1000. [Google Scholar] [CrossRef]
- Norrdine, A. An Algebraic Solution to the Multilateration Problem. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; pp. 1–4. [Google Scholar]
- Bodrumlu, T.; Caliskan, F. Indoor Position Estimation Using Ultrasonic Beacon Sensors and Extended Kalman Filter. Eng. Proc. 2022, 27, 16. [Google Scholar]
- Bodrumlu, T.; Çalışkan, F. Enhancing Indoor Position Estimation Accuracy: Integration of IMU, Raw Distance Data, and Extended Kalman Filter with Comparison to Vicon Indoor Positioning System Data. In Proceedings of the 10th International Electronic Conference on Sensors and Applications, Online, 15–30 November 2023; MDPI: Basel, Switzerland, 2023. [Google Scholar] [CrossRef]
- Fung, M.L.; Chen, M.Z.Q.; Chen, Y.H. Sensor fusion: A review of methods and applications. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 3853–3860. [Google Scholar]
- Krishnaveni, B.V.; Reddy, K.S.; Reddy, P.R. Indoor Tracking by Adding IMU and UWB Using Unscented Kalman Filter. Wirel. Pers. Commun. 2022, 123, 3575–3596. [Google Scholar] [CrossRef]
- You, W.; Li, F.; Liao, L.; Huang, M. Data Fusion of UWB and IMU Based on Unscented Kalman Filter for Indoor Localization of Quadrotor UAV. IEEE Access 2020, 8, 64971–64981. [Google Scholar] [CrossRef]
- Benini, A.; Mancini, A.; Marinelli, A.; Longhi, S. A Biased Extended Kalman Filter for Indoor Localization of a Mobile Agent using Low-Cost IMU and UWB Wireless Sensor Network. In Proceedings of the 10th IFAC Symposium on Robot Control International Federation of Automatic Control, Dubrovnik, Croatia, 5–7 September 2012. [Google Scholar]
- Kwon, S.-G.; Kwon, O.-J.; Kwon, K.-R.; Lee, S.-H. UWB and MEMS IMU Integrated Positioning Algorithm for a Work-Tool Tracking System. Appl. Sci. 2021, 11, 8826. [Google Scholar] [CrossRef]
- Oh, K.H.; Ahn, H.S. Extended Kalman Filter with Multi-frequency Reference Data for Quadrotor Navigation. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS 2015), Busan, Republic of Korea, 13–16 October 2015. [Google Scholar]
- Asl, H.G.; Pourtakdoust, S.H. UD Covariance Factorization for Unscented Kalman Filter using Sequential Measurements Update. Int. J. Aerosp. Mech. Eng. 2007, 1, 564–572. [Google Scholar]
- D’souza, C.; Zanetti, R. Information Formulation of the UDU Kalman Filter. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Carlson, N. Fast triangular factorization of the square root filter. AIAA J. 1973, 11, 1259–1265. [Google Scholar] [CrossRef]
- Marvelmind Indoor Navigation System Operating Manual. Available online: https://marvelmind.com/wp-content/uploads/2017/08/marvelmind_navigation_system_manual.pdf (accessed on 20 July 2017).
- PixHawk and Marvelmind Integration Manual. Available online: https://marvelmind.com/pics/PixHawk_Marvelmind_Integration_Manual.pdf (accessed on 1 December 2017).






| Message | Message Variable | Data Type | Description of Data |
|---|---|---|---|
| beacon_distance | dist_m | float64 | Raw distance data of beacon, in meters |
| add_hedge | uint8 | Address no of mobile beacon | |
| add_beacon | uint8 | Address no of stationary beacon | |
| hedge_imu_raw | time_var | int64 | Timestamp of IMU data |
| accel_x | int16 | Accelerometer of x data | |
| accel_y | int16 | Accelerometer of y data | |
| accel_z | int16 | Accelerometer of z data |
| Trajectory ID | Beacon Number | Trajectories |
|---|---|---|
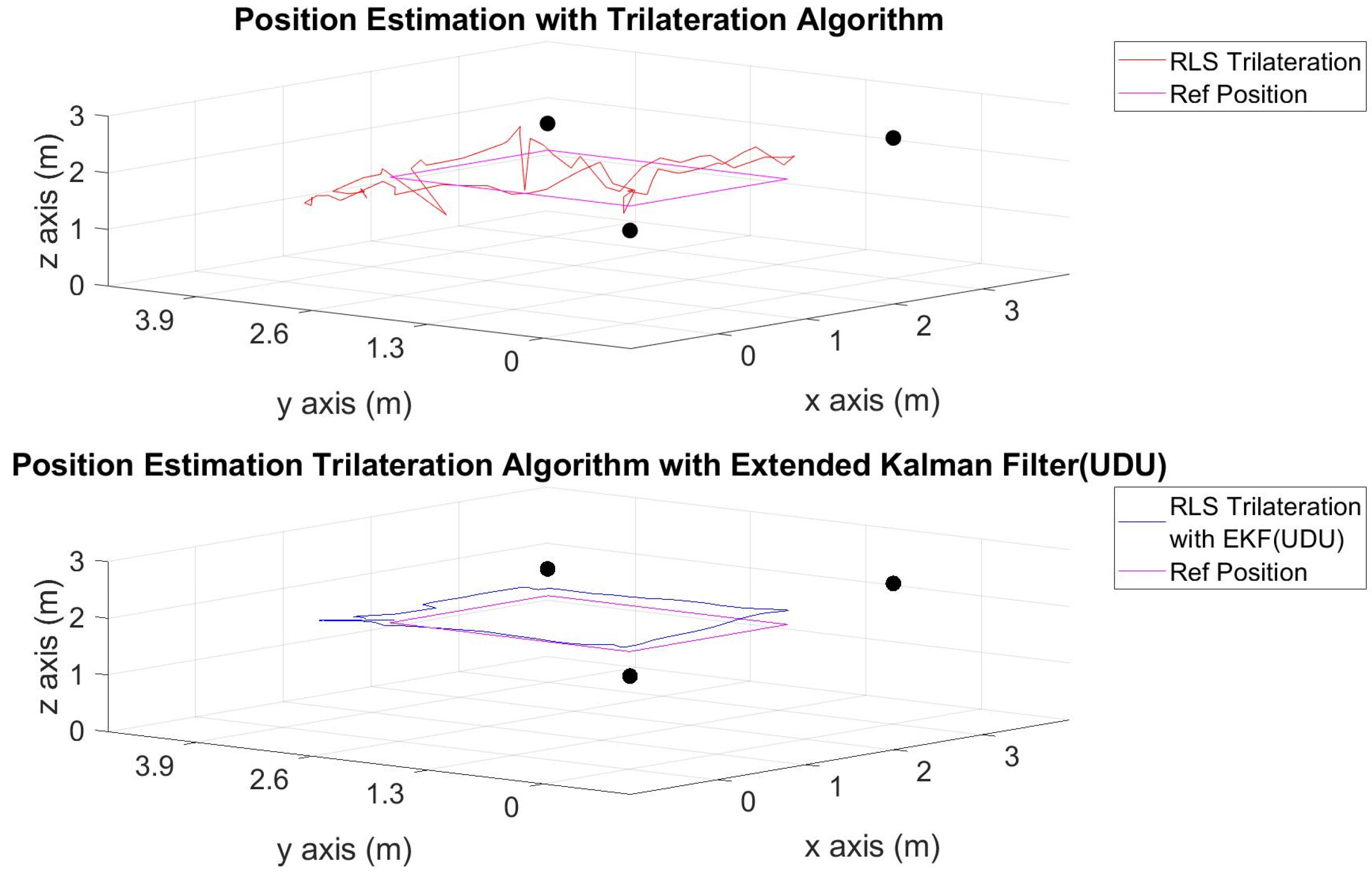
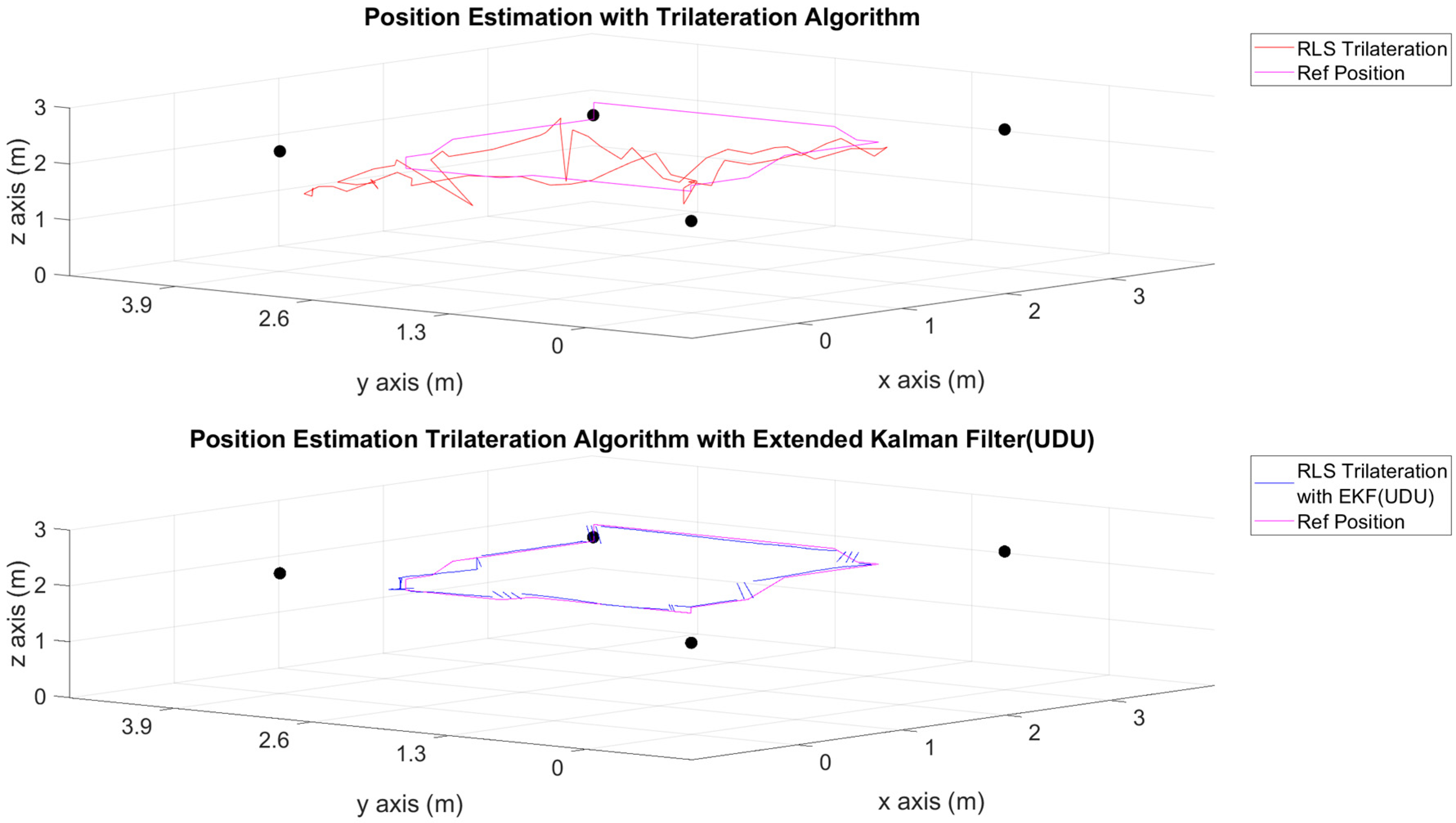
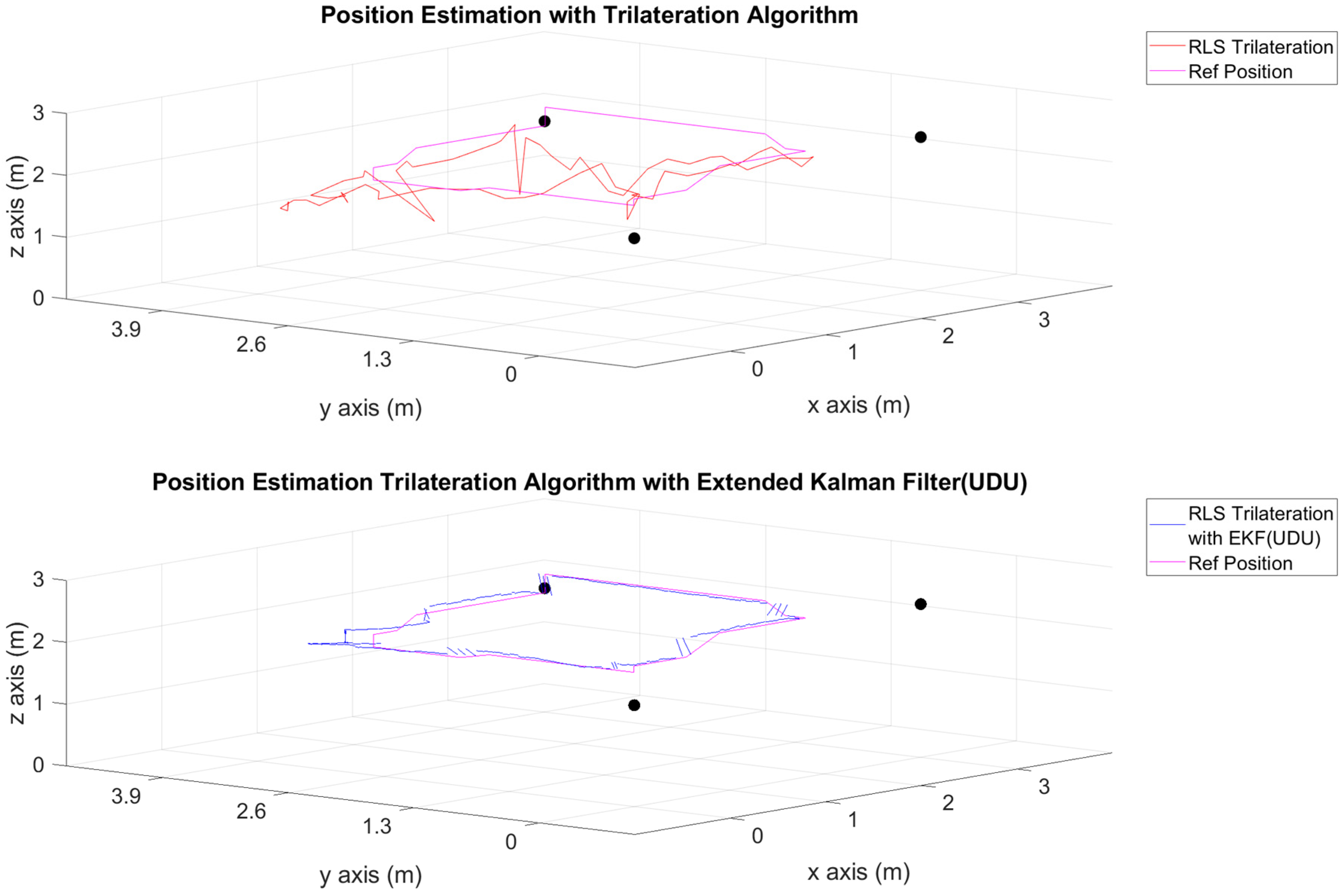
| 1 | 5 (4 stationary + 1 mobile) |  |
| 2 | 5 (4 stationary + 1 mobile) |  |
| 3 | 5 (4 stationary + 1 mobile) |  |
| 4 | 4 (3 stationary + 1 mobile) |  |
| 5 | 4 (3 stationary + 1 mobile) |  |
| 6 | 4 (3 stationary + 1 mobile) |  |
| 7 | 5 (4 stationary + 1 mobile) | With a different z value |
| 8 | 4 (3 stationary + 1 mobile) | With a different z value |
| Trajectory ID | Algorithm | Min Error (m) | Mean Error (m) | Max Error (m) |
|---|---|---|---|---|
| 1 | Only geometric approach | 0.0734 | 0.3356 | 0.9940 |
| 1 | Geometric approach with the EKF (UDU) | 0.0272 | 0.0617 | 0.1439 |
| 2 | Only geometric approach | 0.0776 | 0.4533 | 1.7680 |
| 2 | Geometric approach with the EKF (UDU) | 0.0177 | 0.0827 | 0.1686 |
| 3 | Only geometric approach | 0.3536 | 1.2583 | 5.0031 |
| 3 | Geometric approach with the EKF (UDU) | 0.0191 | 0.1034 | 0.2148 |
| 4 | Only geometric approach | 0.1142 | 0.3628 | 1.1472 |
| 4 | Geometric approach with the EKF (UDU) | 0.0430 | 0.2070 | 0.4387 |
| 5 | Only geometric approach | 0.1348 | 0.5312 | 2.1322 |
| 5 | Geometric approach with the EKF (UDU) | 0.0752 | 0.1660 | 0.3361 |
| 6 | Only geometric approach | 0.4612 | 1.436 | 5.4721 |
| 6 | Geometric approach with the EKF (UDU) | 0.1141 | 0.2378 | 0.4796 |
| 7 | Only geometric approach | 0.0682 | 0.3781 | 1.2343 |
| 7 | Geometric approach with the EKF (UDU) | 0.0305 | 0.1312 | 0.1980 |
| 8 | Only geometric approach | 0.0836 | 0.4116 | 1.3841 |
| 8 | Geometric approach with the EKF (UDU) | 0.0504 | 0.2162 | 0.3226 |
| Trajectory | UDU-EKF (s) | EKF (s) | Percentage of Difference |
|---|---|---|---|
| 1 | 0.0094 | 0.0119 | 21% |
| 2 | 0.0076 | 0.0101 | 25% |
| 3 | 0.0099 | 0.0121 | 18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodrumlu, T.; Caliskan, F. 3D Indoor Position Estimation Based on a UDU Factorization Extended Kalman Filter Structure Using Beacon Distance and Inertial Measurement Unit Data. Sensors 2024, 24, 3048. https://doi.org/10.3390/s24103048
Bodrumlu T, Caliskan F. 3D Indoor Position Estimation Based on a UDU Factorization Extended Kalman Filter Structure Using Beacon Distance and Inertial Measurement Unit Data. Sensors. 2024; 24(10):3048. https://doi.org/10.3390/s24103048
Chicago/Turabian StyleBodrumlu, Tolga, and Fikret Caliskan. 2024. "3D Indoor Position Estimation Based on a UDU Factorization Extended Kalman Filter Structure Using Beacon Distance and Inertial Measurement Unit Data" Sensors 24, no. 10: 3048. https://doi.org/10.3390/s24103048
APA StyleBodrumlu, T., & Caliskan, F. (2024). 3D Indoor Position Estimation Based on a UDU Factorization Extended Kalman Filter Structure Using Beacon Distance and Inertial Measurement Unit Data. Sensors, 24(10), 3048. https://doi.org/10.3390/s24103048






