4.1. Naive Algorithm Design
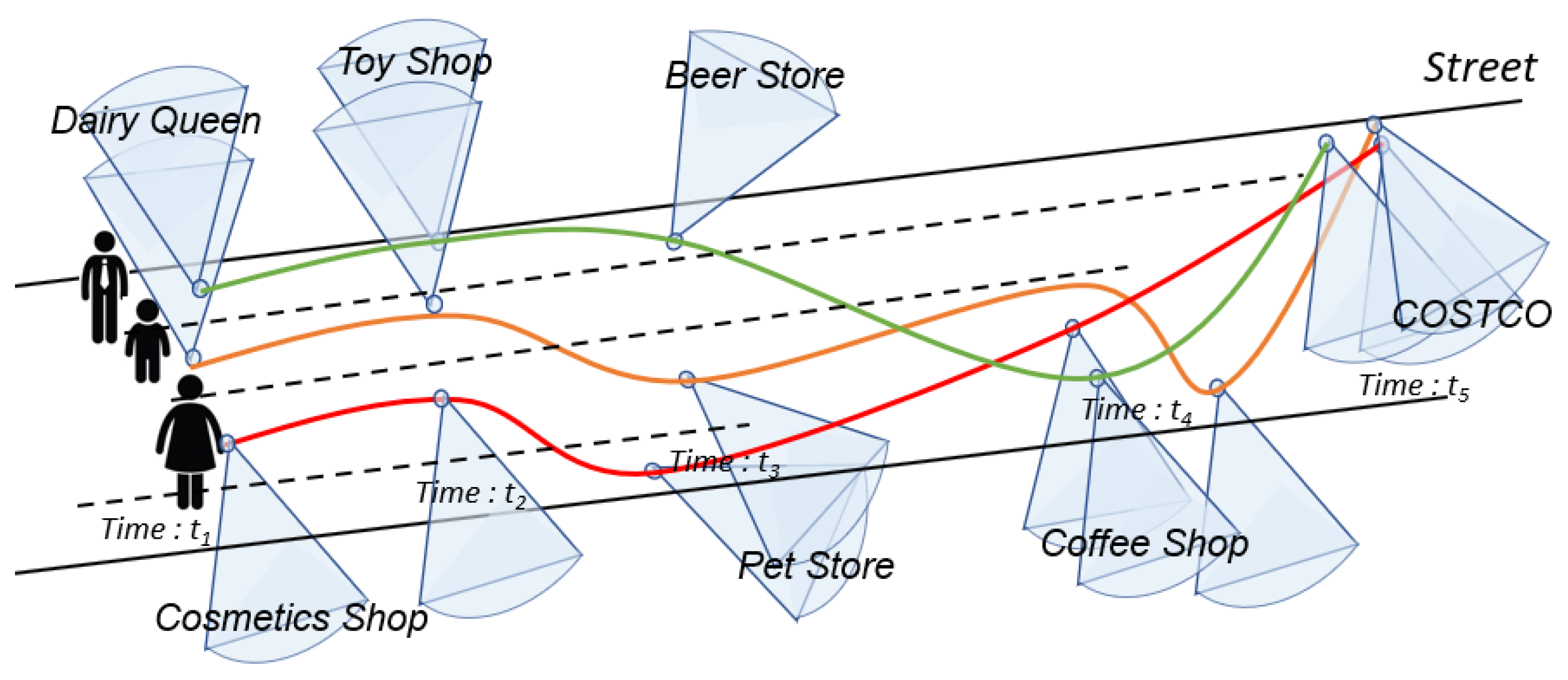
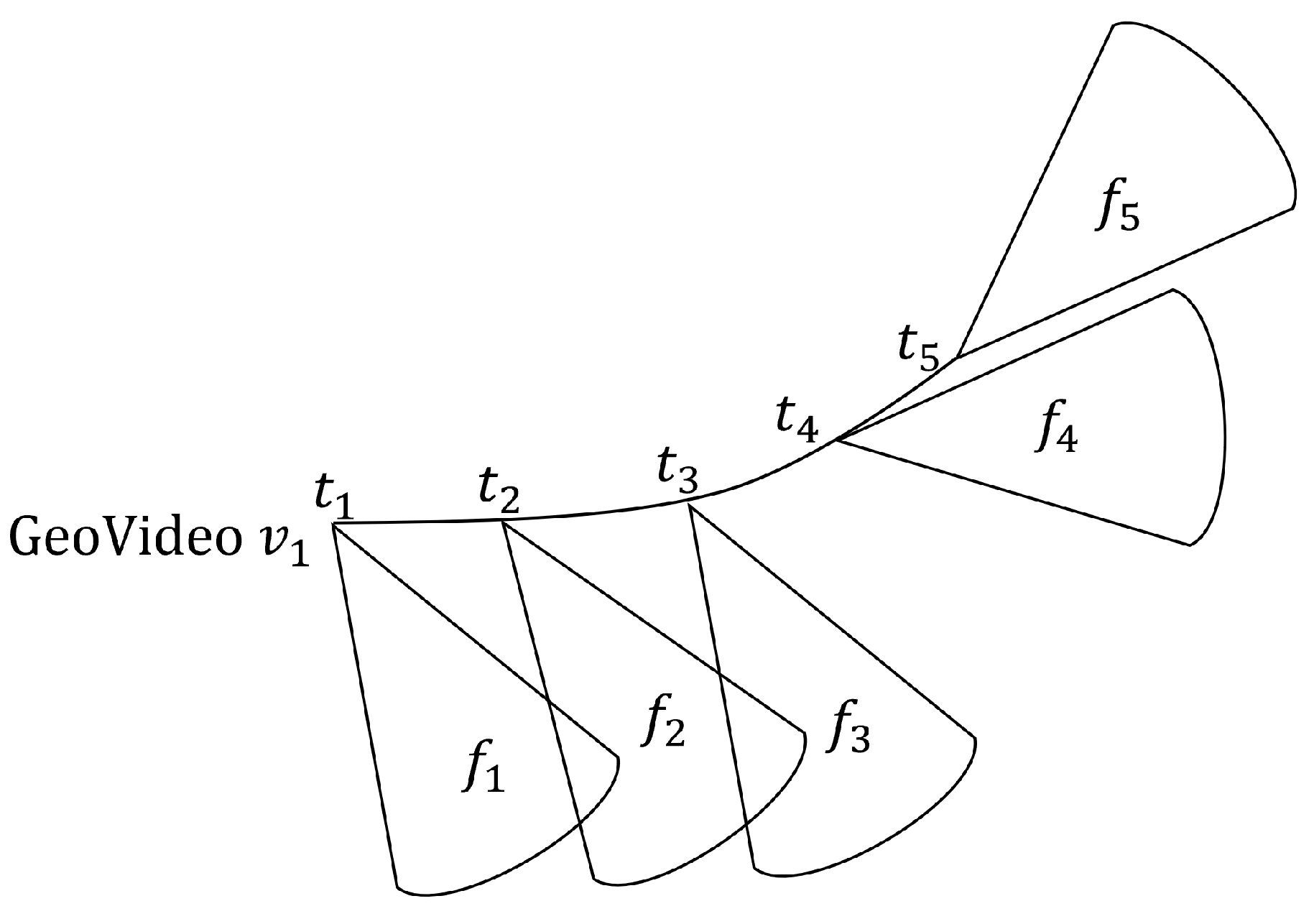
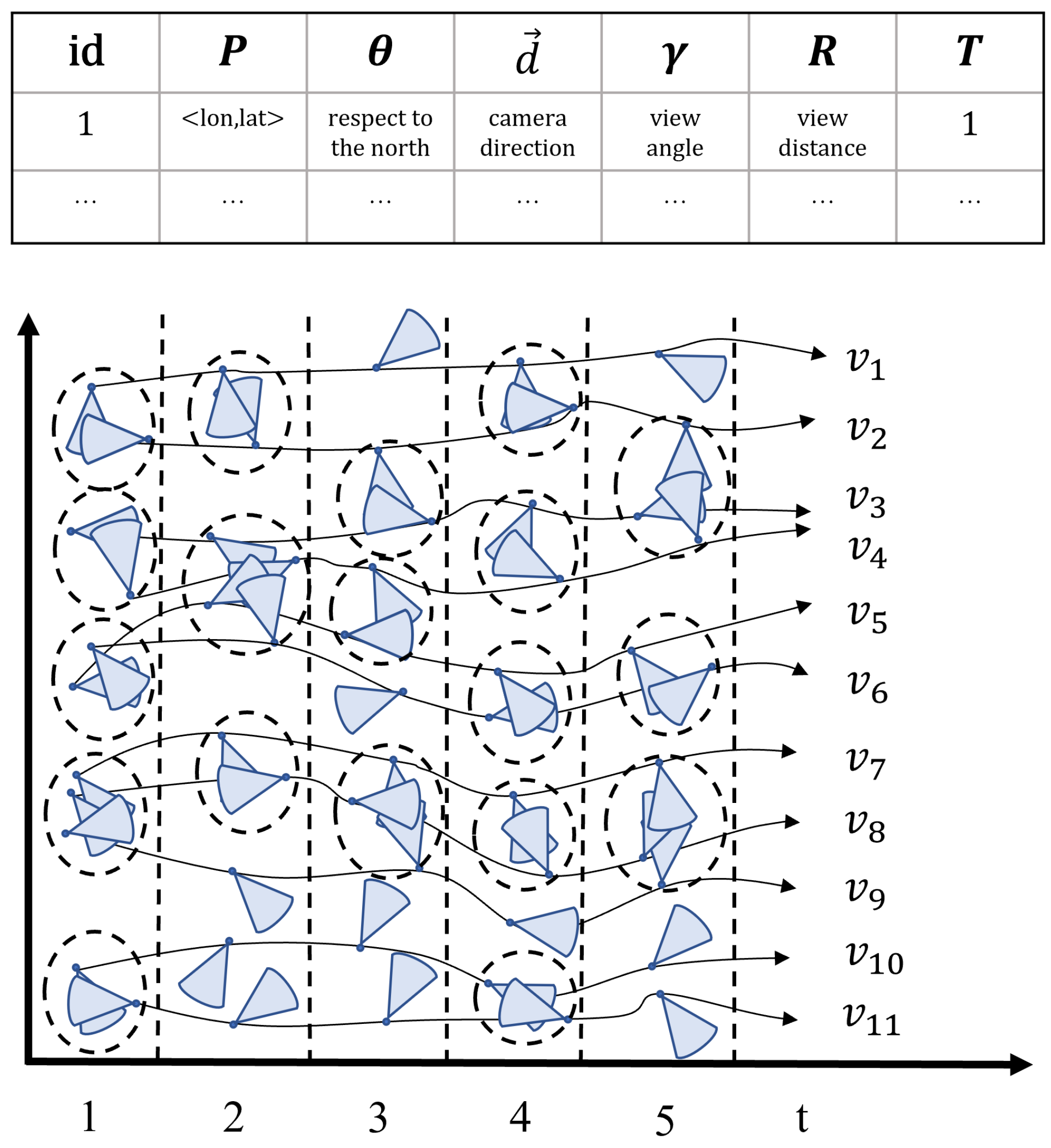
The skeleton of the homogeneous-group mining in the geographic video database VDB contains three stages. Firstly, we transform the geo-tagged video into snapshots, i.e., a snapshot at timestamp 1, a snapshot at timestamp 2,…, a snapshot at timestamp n. Secondly, we cluster the FoVs for each snapshot at each timestamp based on density clustering (FDBC). Due to limited space, we omit the algorithm in this paper.
In Algorithm 1, FoVs are arbitrarily selected from each snapshot until all FoVs have been visited. If there are at least
FoVs within a radius of
, i.e., (
), these FoVs are considered as part of the candidate cluster, and
generates a more refined cluster that satisfies the constraint. Next, the overlap between FoVs in the cluster is determined by the
function. Then, if the number of FoVs that satisfy the intersecting constraint is greater than the minimum FoV number
, they are inserted into
as candidates. Otherwise, they are marked as noise.
| Algorithm 1: FDBC(, , , ). |
![Sensors 23 04443 i001 Sensors 23 04443 i001]() |
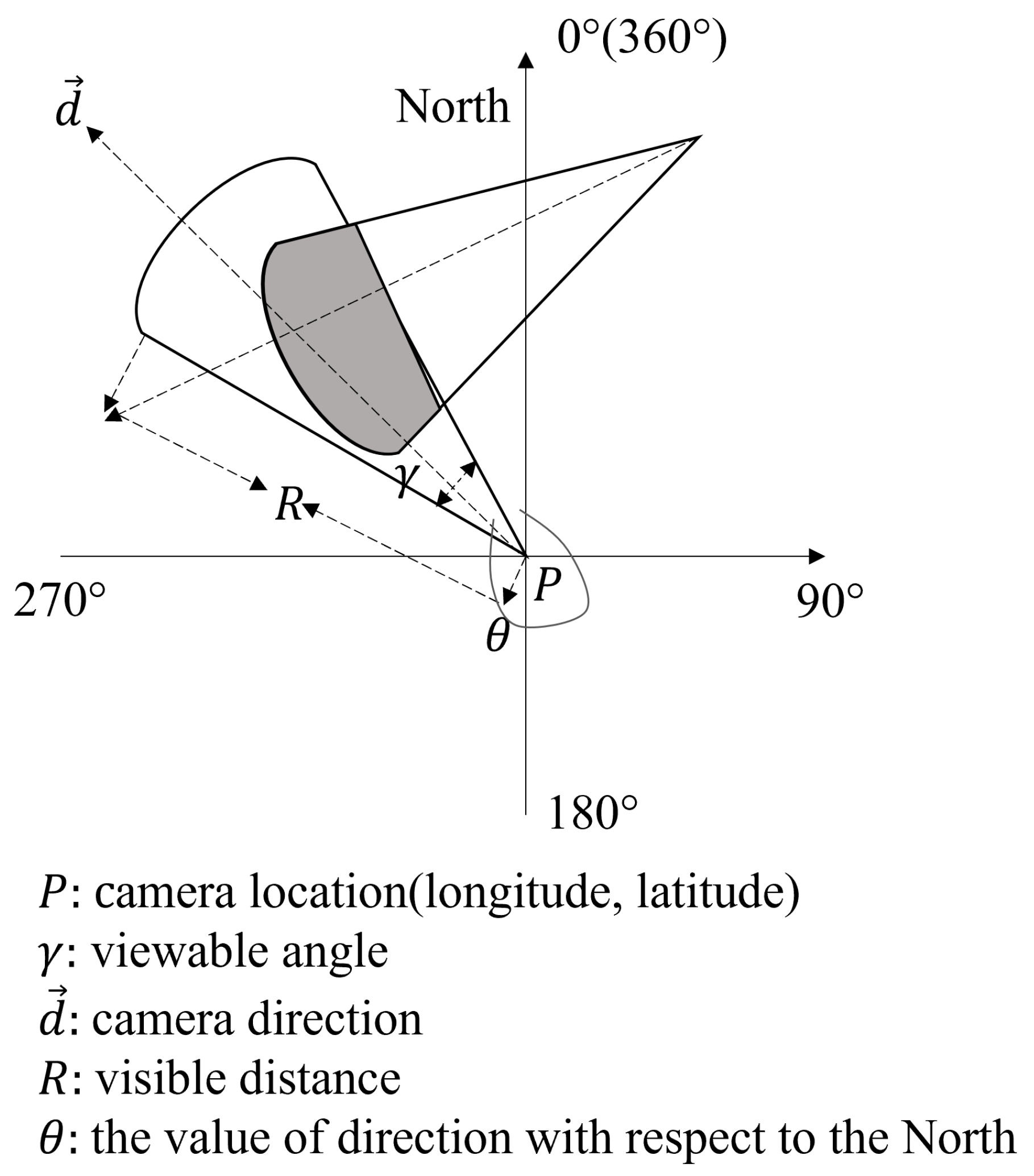
The detail for
is described as Definition 3, detecting whether a common area exists between two FoVs. We calculate the overlap area coefficient (
) after judging the distance between two FoVs. However, it is not obligatory that as long as two FoVs intersect they view the same thing. In consequence of this, we follow to the intersection area
. A result of common-area weight of no less than
(
) is stored in the list
C that is used for
. The
is depicted in Algorithm 2.
| Algorithm 2: ExpandFoVCluster(, , , , ). |
![Sensors 23 04443 i002 Sensors 23 04443 i002]() |
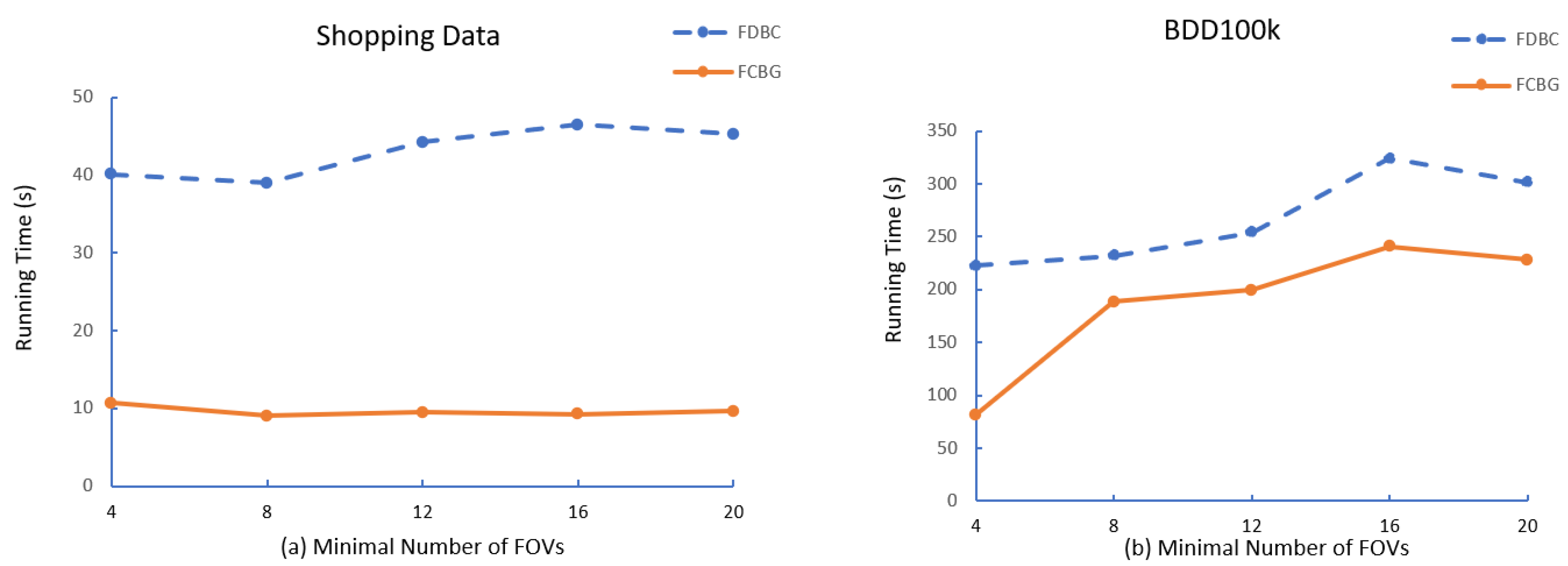
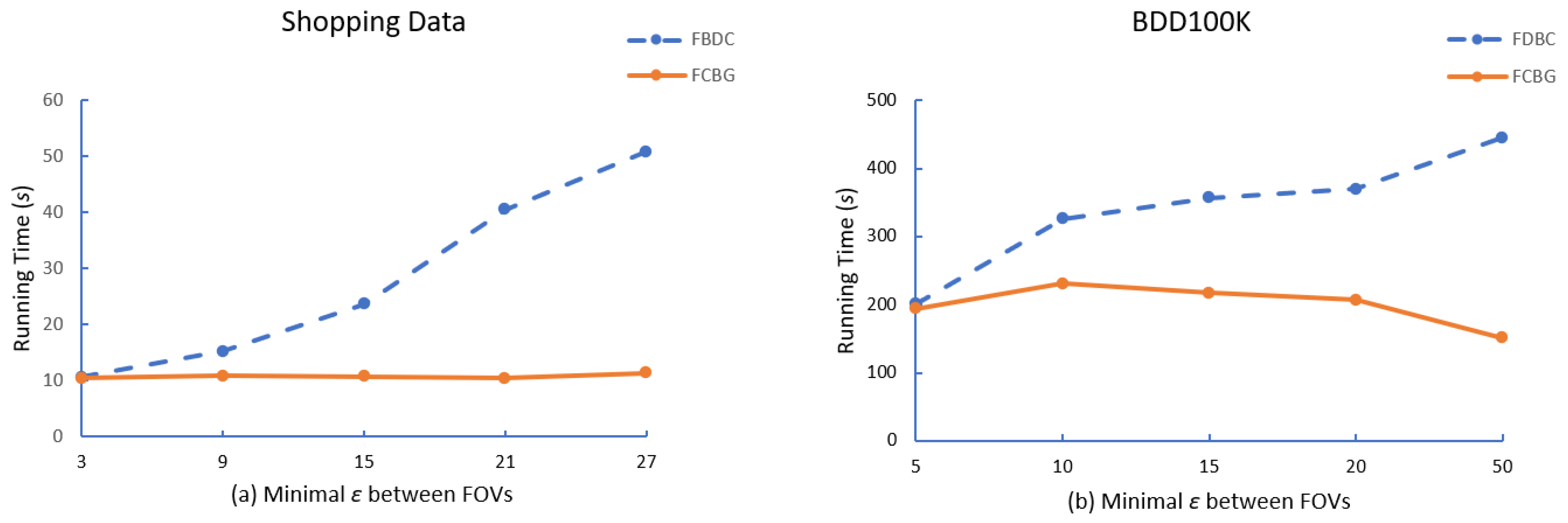
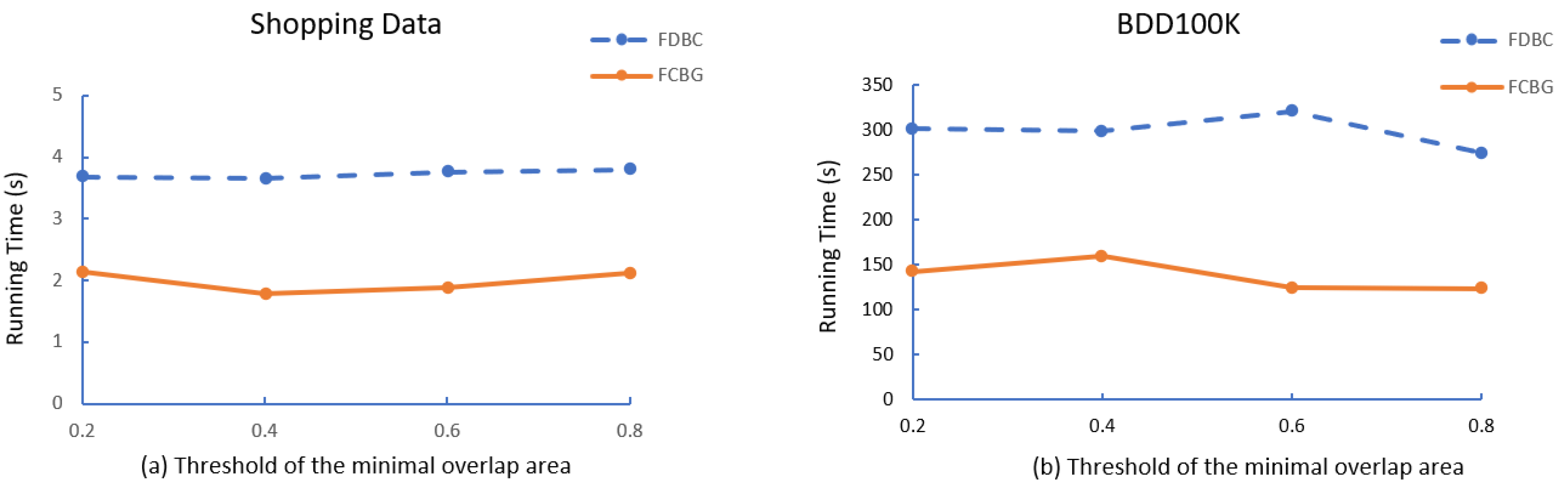
Algorithm 2 describes the expansion of the FoV cluster. For each FoV in C that has not been visited, mark it as visited and look for its neighbor . If the number in is not less than the minimum FoV number, use it as a candidate set for overlapping area calculation, and calculate the FoV afterward. If the number meets , it will be merged with the previously generated cluster, and the operation will be repeated until reaching the boundary of the cluster. ExpandFoVCluster is the working core of the algorithm and an essential operation is used for spatial query, retrieving all the FoVs belonging to a given region of the space and having a common viewable region. It can be shown that clusters are invariant with respect to the order of FoV selection in ExpandFoVCluster, and that the complexity of FDBC is the worst, where N is the number of FoVs.
Finally, we discovered groups from videos according to clusters of snapshot’s timestamps. It is described in Algorithm 3. Before that, we introduced that the conditions for grouping geo-tagged videos are view field, location, and the time the people move together. In this phase, we use constraints to judge these geo-tagged videos; whether they are a group. If geo-tagged video objects in the same cluster meet the time constraints, we regard them as a group.
In more detail, the time cost of the FDBC algorithm can be expressed as follows:
where
is the time cost of FovNeighbors,
is the time cost of ExpandFoVCluster,
is the time cost of densityoverlapArea, and
is the time cost of BoundaryFOVBelong.
The
representation is the time it takes to calculate the distance between each field of view (fov) of
and determine whether the distance is part of the adjacent fov by making sure it is within the radius
. The time required to construct the neighboring fov depends on the size of the set
in
and the radius, as shown in Equation (
8). As the radius
increases, the number of candidate fovs increases, resulting in a longer overall algorithm execution time.
where
represents the time required to calculate the neighbors associated with fov.
means the time cost to ExpandFovCluster satisfiying
and
from a dataset
by FovNeighbors. The time cost can be estimated approximately using the following equation:
where
is a set of candidates in
F, and
is the average time taken to perform ExpandFoVCluster. The number of
affects the overall running time of the algorithm.
is a selectivity rate of
.
means the time cost to do densityOverlapArea for
C with the parameter
using Equation (
4), where
is a selectivity rate of
.
means the time cost to do BoundaryFOVBelong. Each operation is performed for each element in the cluster, resulting in a time complexity of
, and the algorithm execution time is influenced by the number of fov in each cluster where
is a selectivity rate of
.
| Algorithm 3: BoundaryFoVBelong(, ). |
![Sensors 23 04443 i003 Sensors 23 04443 i003]() |
Scan clusters in the order of each snapshot with the snapshots after it, and detect the FoV belonging to the same geo-video in the cluster between snapshots. Add these FoVs into the . When the number of FoVs in is not greater than , put the timestamps of FoVs into . It is initialized using the common FoVs in clusters with a size no smaller than . After that, generate new candidates by extending. Next, for every group candidate A in , we execute the to obtain the final homogeneous groups, which is described in detail in Algorithm 4.
Definition 9 (Groups Candidates)
. Considering Definitions 5 and 6, the homogeneous groups need to satisfy the Closeness and certain time constraints. Therefore, let = ,…, be a set of the candidate set, and let = <C, T> be a candidate where is a sub-candidate of .
| Algorithm 4: MiningHomogenousGroups(, , k, s, g). |
![Sensors 23 04443 i004 Sensors 23 04443 i004]() |
In Algorithm 4, we judge the succession and connection. For succession, the most significant gap between the two time-segments is whether it is lower than g. If not, remove it. Furthermore, we remove it if the sequential time is bigger or equal to s.
Then, we judge the occurrence that the minimal number of occurrences for FoVs belongs to the same cluster in each segment; if it is less than
k, we also remove
a from
. After that, all the homogeneous groups are stored in
. As an example, a glance at
Table 2 illustrates an instance. If we set the parameters
= 2,
s = 1,
g = 2,
k = 2, and
= 0.5, then all of the groups that we would capture are shown in
Table 2.
For the groups part, we assume the number of clusters is N and the computational complexity is .
4.2. Performance Enhancement Using a Grid Index Approach
This paper proposes constructing a grid index based on area-density clustering for each snapshot. Because FoV clustering is different from point clustering, an essential condition needs to calculate the overlap area. The purpose of using the grid is to use MBR to narrow the scope of the calculation further. The details are described in the following.
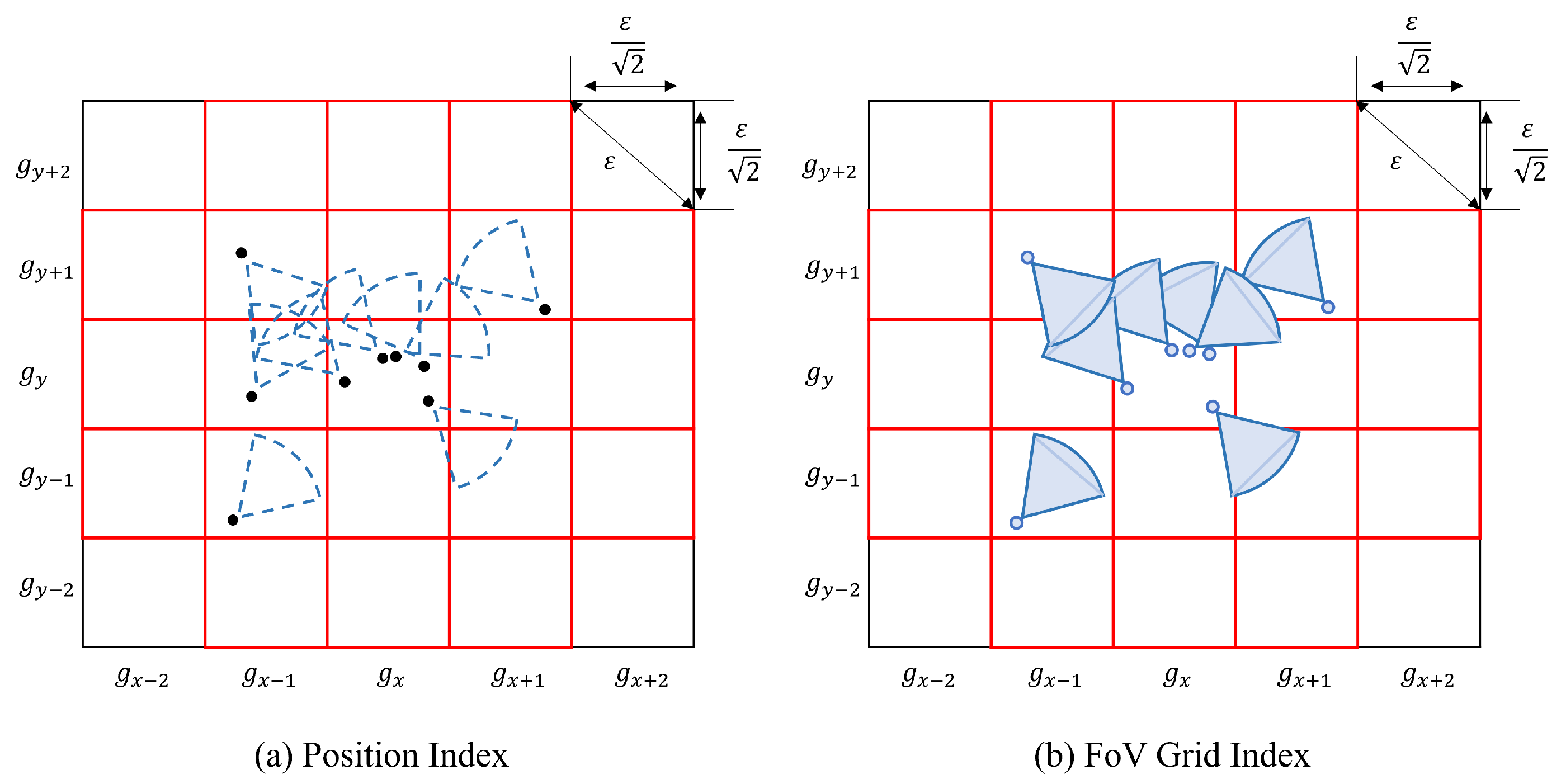
For example, if we want to find all the FoVs associated with a specific FoV, we need to compute the
. It is represented by the area in the red box in
Figure 5a. Furthermore, we can get the id of the cell that the FoV to be queried belongs to. The process is depicted in Algorithm 5. After that, we need to judge whether the number of FoVs in
is greater than the threshold
. If the quantity condition is met, we execute the second level. The second level further divides each grid in the first level into
sub-cells; it in depicted in
Figure 5b. The width
of a sub cell is as follows:
| Algorithm 5: FCBG(, , , c, ). |
![Sensors 23 04443 i005 Sensors 23 04443 i005]() |
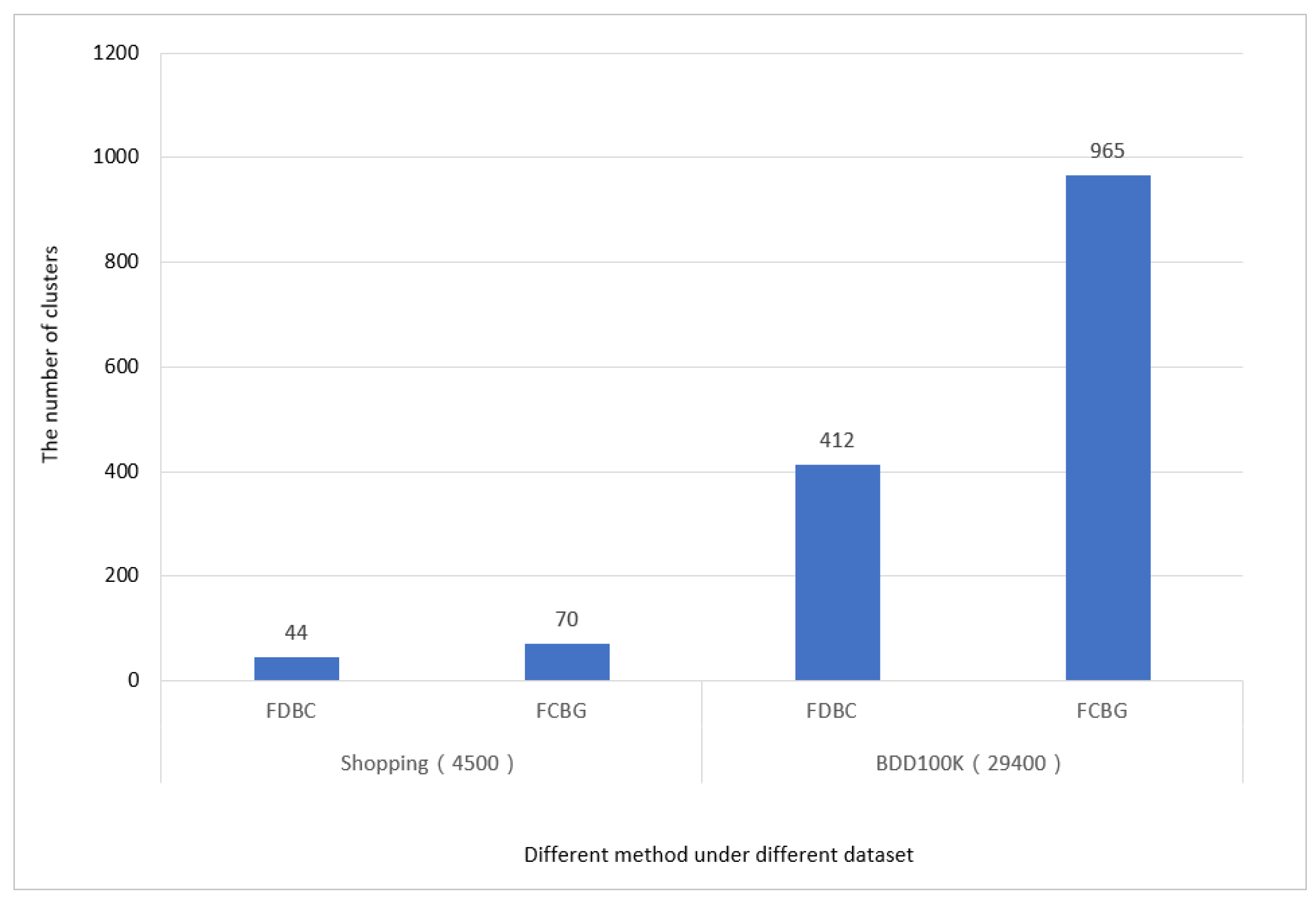
These sub-cells are used to calculate the intersection of the area between two FoVs. These FoVs will be marked as visited if they satisfy the intersection condition. Next, we need to judge the distance again. If the distance between f and is greater than the distance threshold , remove from candidate cluster C. Finally, if the number of FoVs in C is no less than , we obtain one of the clusters in a snapshot. The computational cost of FCBG is with a grid index, where N is the number FoVs in the snapshot.
In more detail, the time cost of the FDBC algorithm can be expressed as follows:
where
is the time cost of BuildFovGridIndex and calculates MBR,
is the time cost of ExpandFoVCluster, and
is the time cost of densityoverlapArea, and
is the time cost of BoundaryFOVBelong.