Investigating the Shear Strength of Granitic Gneiss Residual Soil Based on Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Overview of the Sampled Colluvial Landslides
2.1.2. Composition and Structure of GGRS
2.1.3. Parameters Considered for RSM Experimental Design
2.2. Methods
2.2.1. Direct Shear Tests
2.2.2. RSM Method
2.2.3. Analysis of Variance (ANOVA)
3. Results
3.1. Experimental Data
3.2. Modeling Shear Strength Parameters
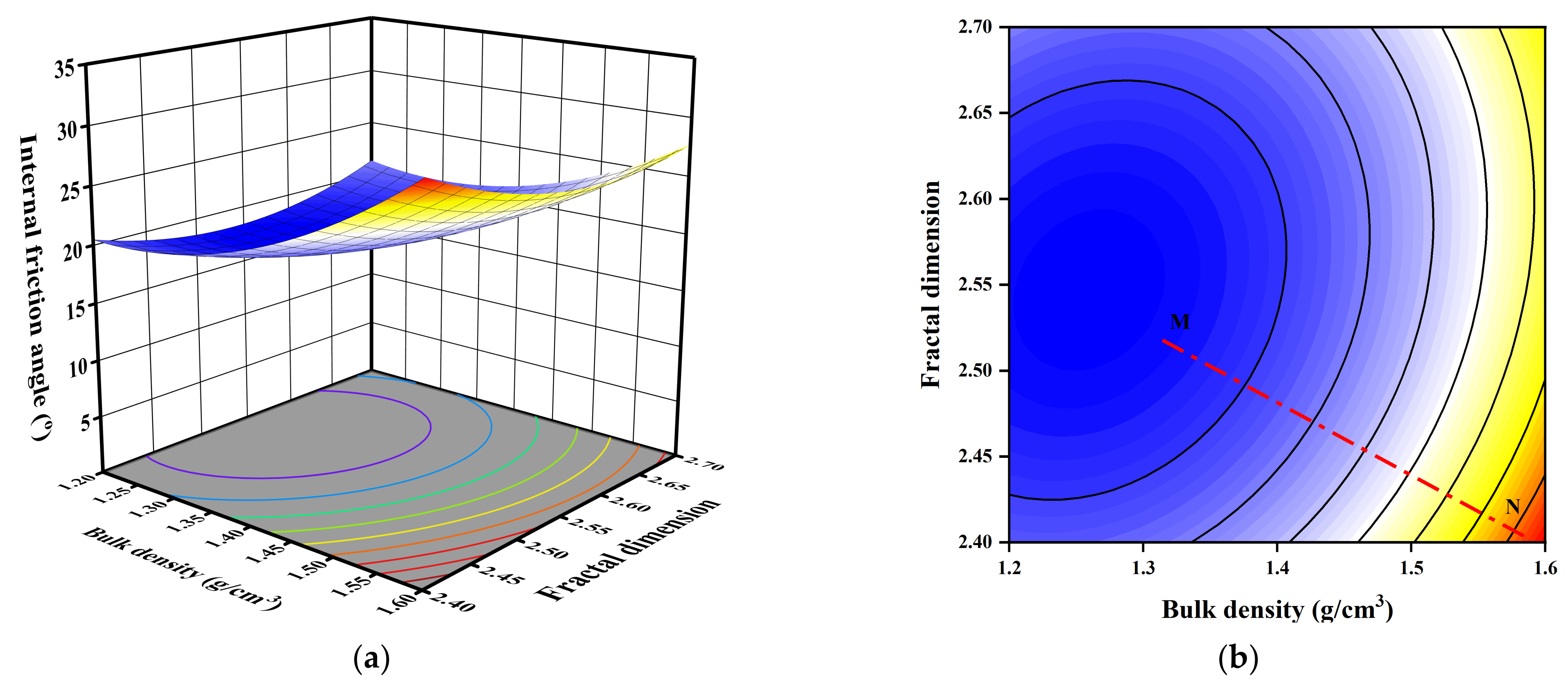
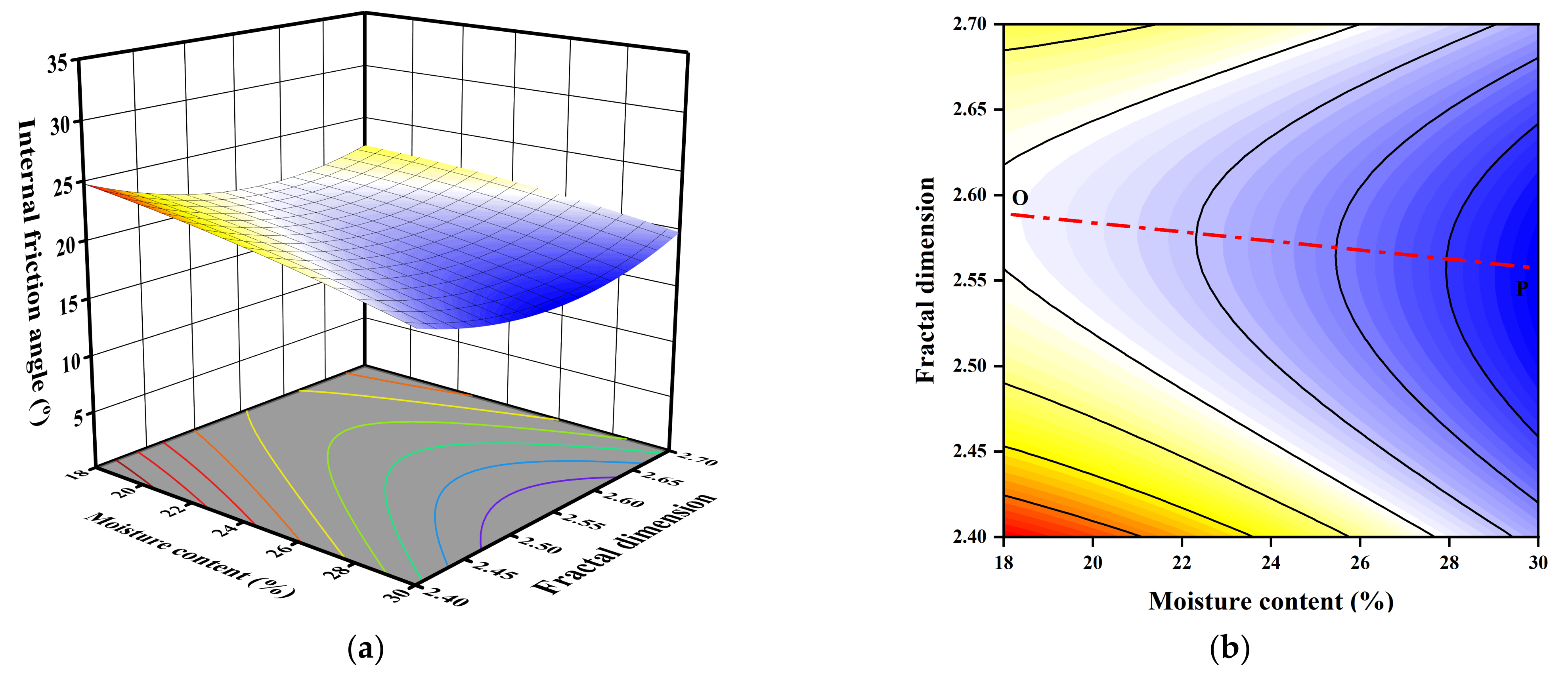
3.3. The Effect of Independent Variable and Their Interaction on the Shear Strength
3.4. Validation of the Regression Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, P.; Li, M.J. Report on Feasibility Study on Potential Geological Hazards and Risks of Cutting Slopes for Rural Housing Construction in Huanggang City, Hubei Province; Report of Investigation; The 3rd Geological Department of Hubei Provincial Geological Bureau: Huanggang, China, 2020. (In Chinese)
- Xu, Q.; Wang, W.; Li, L.; Cao, Y. Failure Mechanism of Gently Inclined Shallow Landslides Along the Soil-bedrock Interface on Ring Shear Tests. Bull. Eng. Geol. Environ. 2021, 80, 3733–3746. [Google Scholar] [CrossRef]
- Guo, H.; Xiao, Y.; Xu, L.; Sun, H.; Huang, J.; Hou, Z. Origin of allanite in gneiss and granite in the Dabie orogenic belt, Central East China. J. Asian Earth Sci. 2017, 135, 243–256. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Kong, L.; Chen, C.; Wang, G. Mechanical Response of Granite Residual Soil Subjected to Impact Loading. Int. J. Geomech. 2021, 21, 04021092. [Google Scholar] [CrossRef]
- An, R.; Kong, L.; Zhang, X.; Li, C. Effects of Dry-Wet Cycles on Three-Dimensional Pore Structure and Permeability Characteristics of Granite Residual Soil Using X-Ray Micro Computed Tomography. J. Rock. Mech. Geotech. 2022, 14, 851–860. [Google Scholar] [CrossRef]
- Ye, W.J.; Li, C.Q. The consequences of changes in the structure of loess as a result of cyclic freezing and thawing. Bull. Eng. Geol. Environ. 2019, 78, 2125–2138. [Google Scholar] [CrossRef]
- An, R.; Zhang, X.; Kong, L.; Liu, X.; Chen, C. Drying-Wetting Impacts on Granite Residual Soil: A Multi-Scale Study from Macroscopic to Microscopic Investigations. Bull. Eng. Geol. Environ. 2022, 81, 447. [Google Scholar] [CrossRef]
- Moon, S.W.; Hayashi, K.; Ku, T. Estimating Spatial Variations in Bedrock Depth and Weathering Degree in Decomposed Granite from Surface Waves. J. Geotech. Geoenviron. Eng. 2017, 143, 04017020. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, H. Experimental Study of Disintegration Mechanism for Unsaturated Granite Residual Soil. Rock Soil Mech. 2013, 34, 1668–1674. (In Chinese) [Google Scholar]
- Zhao, J.J.; Wang, S.J.; Shang, Y.J.; Yue, Z.Q. Control factors on shear strength of completely decomposed granite. Rock Soil Mech. 2005, 26, 624–628. (In Chinese) [Google Scholar] [CrossRef]
- Wu, D.; Liu, H.; Wang, C.; Xu, X.; Liu, X.; Wang, Q. The Interaction Effect of Particle Composition and Matric Suction on the Shear Strength Parameters of Unsaturated Granite Residual Soil. Arab. J. Sci. Eng. 2022, 47, 12453–12467. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, X.; Xia, J.; Miller, G.A.; Cai, C.; Guo, Z.; Hassanikhah, A. The Effect of Water Content on the Shear Strength Characteristics of Granitic Soils in South China. Soil Till Res. 2019, 187, 50–59. [Google Scholar] [CrossRef]
- Hoyos, L.R.; Velosa, C.L.; Puppala, A.J. Residual Shear Strength of Unsaturated Soils via Suction-Controlled Ring Shear Testing. Eng. Geol. 2014, 172, 1–11. [Google Scholar] [CrossRef]
- Al-Shayea, N.A. The Combined Effect of Clay and Moisture Content on the Behavior of Remolded Unsaturated Soils. Eng. Geol. 2001, 62, 319–342. [Google Scholar] [CrossRef]
- Hossain, M.A.; Yin, J.-H. Behavior of a Compacted Completely Decomposed Granite Soil from Suction Controlled Direct Shear Tests. J. Geotech. Geoenviron. 2010, 136, 189–198. [Google Scholar] [CrossRef]
- Amiri Khaboushan, E.; Emami, H.; Mosaddeghi, M.R.; Astaraei, A.R. Estimation of Unsaturated Shear Strength Parameters Using Easily-Available Soil Properties. Soil Till Res. 2018, 184, 118–127. [Google Scholar] [CrossRef]
- Jiang, Q.; Cao, M.; Wang, Y.; Wang, J.; He, Z. Estimation of Soil Shear Strength Indicators Using Soil Physical Properties of Paddy Soils in the Plastic State. Appl. Sci. 2021, 11, 5609. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, X.; Cai, C. Splash Erosion of Clay–Sand Mixtures and Its Relationship with Soil Physical Properties: The Effects of Particle Size Distribution on Soil Structure. CATENA 2015, 135, 254–262. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, F.; Yang, H.; Gao, W.; Miao, L. Orthogonal Experimental Study of Soil–Rock Mixtures under the Freeze–Thaw Cycle Environment. Int. J. Pavement Eng. 2021, 22, 1376–1388. [Google Scholar] [CrossRef]
- Ren, S.; Li, Z.Y.; Deng, G.L.; Liu, W.; Pu, W.P. Softening characteristic of gypsum rock under the action of multi-factors. Rock Soil Mech. 2018; 39, 789–796. (In Chinese) [Google Scholar]
- Lu, Y.; Cai, G.; Zhao, C. The Shear Strength of Granite Weathered Soil Under Different Hydraulic Paths. Appl. Sci. 2020, 10, 6615. [Google Scholar] [CrossRef]
- Li, J.; Zhang, P.; Hu, J.; Zhang, Y. Study of the Synergistic Effect of Induction Heating Parameters on Heating Efficiency Using Taguchi Method and Response Surface Method. Appl. Sci. 2023, 13, 555. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Vining, G.G.; Borror, C.M.; Kowalski, S.M. Response Surface Methodology: A Retrospective and Literature Survey. J. Qual. Technol. 2004, 36, 53–77. [Google Scholar] [CrossRef]
- Asadizadeh, M.; Masoumi, H.; Roshan, H.; Hedayat, A. Coupling Taguchi and Response Surface Methodologies for the Efficient Characterization of Jointed Rocks’ Mechanical Properties. Rock Mech. Rock Eng. 2019, 52, 4807–4819. [Google Scholar] [CrossRef]
- Soltani, M.; Moayedfar, R.; Vun, C.V. Using Response Surface Methodology to Assess the Performance of the Pervious Concrete Pavement. Int. J. Pavement Res. Technol. 2022, 16, 576–591. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Li, S.; Yang, L. Strength Softening Characteristics of Shale Clay Mineral Expansion. Chem. Technol. Fuels Oils 2020, 56, 300–311. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, H.; Zhan, H.; Lei, G.; Cheng, H. Investigation of Scale Effect of Numerical Unconfined Compression Strengths of Virtual Colluvial–Deluvial Soil–Rock Mixture. Int. J. Rock. Mech. Min. 2015, 77, 208–219. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, L.; Xi, X.; Nie, Z. Optimization of pulse bi-directional electrolysis in-situ synthesis of tungsten carbide by response surface methodology. Int. J. Refract. Met. Hard Mater. 2023, 111, 106063. [Google Scholar] [CrossRef]
- Babanouri, N.; Asadizadeh, M.; Hasan-Alizade, Z. Modeling Shear Behavior of Rock Joints: A Focus on Interaction of Influencing Parameters. Int. J. Rock Mech. Min. 2020, 134, 104449. [Google Scholar] [CrossRef]
- Sellke, T.; Bayarri, M.J.; Berger, J.O. Calibration of p values for testing precise null hypotheses. Am. Stat. 2001, 55, 62–71. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Chiu, A.C.F. Laboratory Study of Loose Saturated and Unsaturated Decomposed Granitic Soil. J. Geotech. Geoenviron 2003, 129, 550–559. [Google Scholar] [CrossRef]
- Li, C.; Kong, L.; An, R. Evolution of cracks in the shear bands of granite residual soil. J. Rock Mech. Geotech. Eng. 2022, 14, 1956–1966. [Google Scholar] [CrossRef]
- Kaliakin, V.N. Chapter 1—Example Problems Involving Phase Relations for Soils. In Soil Mechanics; Kaliakin, V.N., Ed.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 1–50. ISBN 978-0-12-804491-9. [Google Scholar]
- Rahai, A.; Dolati, A.; Kamel, M.E.; Babaizadeh, H. Studying the Effect of Various Parameters on Mechanical Properties of Lightweight Aggregate Concrete Using MANOVA. Mater. Struct. 2015, 48, 2353–2365. [Google Scholar] [CrossRef]
- Dong, Y.; Liao, Z.; Wang, J.; Liu, Q.; Cui, L. Potential Failure Patterns of a Large Landslide Complex in the Three Gorges Reservoir Area. Bull. Eng. Geol. Environ. 2023, 82, 41. [Google Scholar] [CrossRef]
- Zou, Z.; Luo, T.; Zhang, S.; Duan, H.; Li, S.; Wang, J.; Deng, Y.; Wang, J. A Novel Method to Evaluate the Time-Dependent Stability of Reservoir Landslides: Exemplified by Outang Landslide in the Three Gorges Reservoir. Landslides 2023. [Google Scholar] [CrossRef]



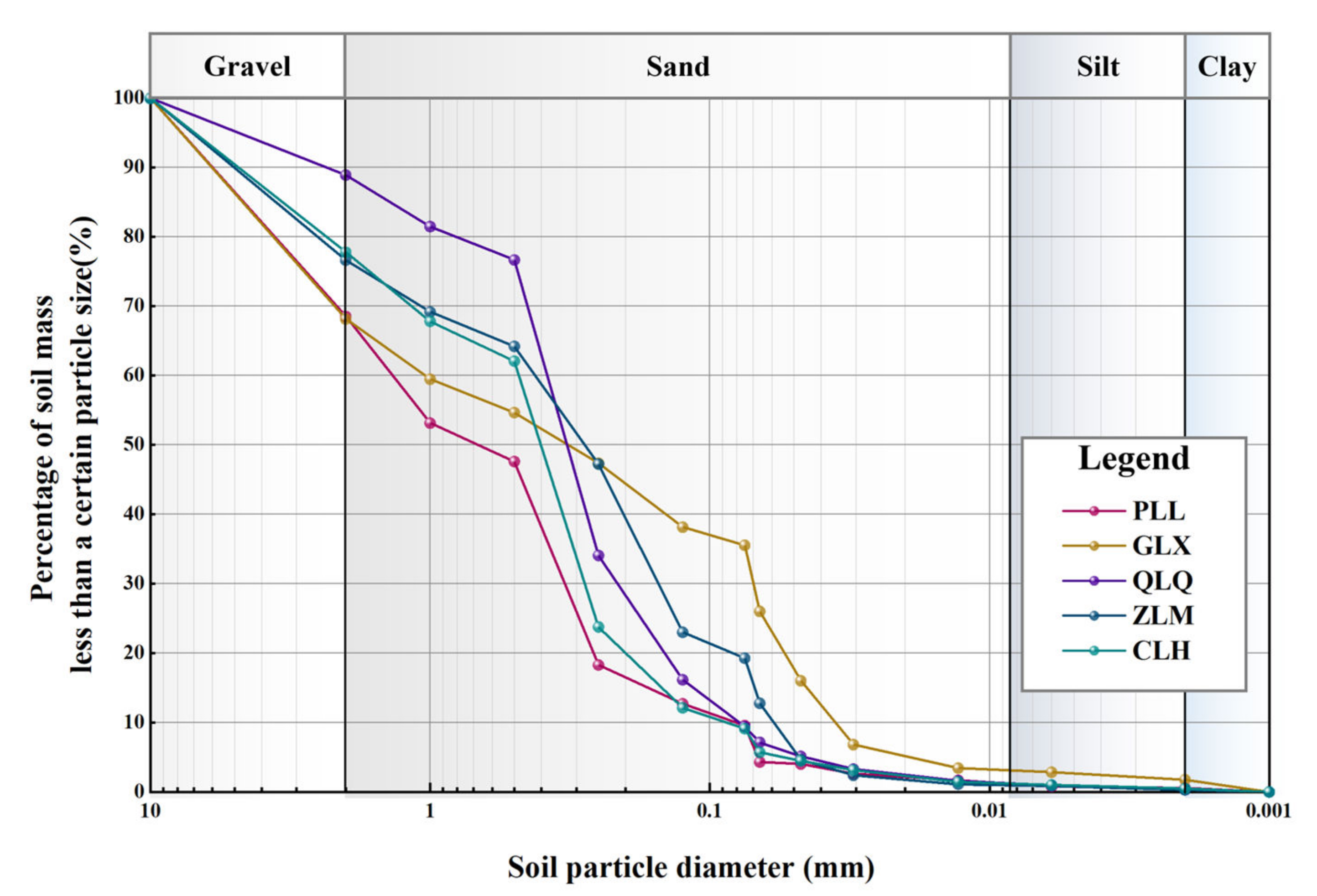







| Sample No. | Percentage of Mineral Composition (%) | ||||||
|---|---|---|---|---|---|---|---|
| Montmorillonite | Rectorite | Illite | Tremolite | Quartz | Orthoclase | Albite | |
| PLL | 37.74 | 23.54 | — | — | 21.12 | 5.75 | 11.85 |
| GLX | 65.36 | 13.9 | — | 3.1 | 10.64 | — | 7.01 |
| QLQ | 3.34 | — | 27.36 | — | 33.11 | — | 36.2 |
| ZLM | 17.92 | 33.46 | — | 12.87 | 28.54 | — | 7.22 |
| CLH | 13.64 | — | 16.15 | — | 31.79 | 10.66 | 27.76 |
| Sample No. | Percentage Content of Each Grain Group (%) | Cu | Cc | |||
|---|---|---|---|---|---|---|
| >2 mm | 0.075–2 mm | 0.002–0.075 mm | <0.002 mm | |||
| PLL | 31.49 | 58.97 | 8.99 | 0.55 | 21.822 | 1.146 |
| GLX | 31.83 | 32.65 | 33.73 | 1.79 | 19.818 | 0.077 |
| QLQ | 11.08 | 79.50 | 9.05 | 0.37 | 4.951 | 1.521 |
| ZLM | 23.37 | 57.34 | 19.01 | 0.28 | 8.036 | 0.877 |
| CLH | 22.21 | 68.66 | 8.64 | 0.49 | 6.868 | 2.594 |
| Parameters | ω/% | ρb/g · cm−3 | D |
|---|---|---|---|
| Maximum | 26.28 | 1.53 | 2.76 |
| Minimum | 23.27 | 1.20 | 2.37 |
| Mean value | 24.92 | 1.37 | 2.55 |
| Levels | ω/% | ρ/g · cm−3 | D |
|---|---|---|---|
| −1 | 18 | 1.2 | 2.4 |
| 0 | 24 | 1.4 | 2.55 |
| 1 | 30 | 1.6 | 2.7 |
| Run | ω/% | ρ/g · cm−3 | D | Response | |
|---|---|---|---|---|---|
| c/kPa | φ/° | ||||
| 1 | 24 | 1.4 | 2.55 | 11.99 | 19.99 |
| 2 | 18 | 1.2 | 2.55 | 10.53 | 17.55 |
| 3 | 18 | 1.6 | 2.55 | 17.29 | 29.82 |
| 4 | 30 | 1.4 | 2.7 | 11.98 | 19.63 |
| 5 | 24 | 1.6 | 2.4 | 16.98 | 30.33 |
| 6 | 24 | 1.2 | 2.7 | 13.29 | 22.16 |
| 7 | 18 | 1.4 | 2.7 | 13.94 | 23.23 |
| 8 | 24 | 1.2 | 2.4 | 13.25 | 22.09 |
| 9 | 30 | 1.6 | 2.55 | 15.23 | 25.39 |
| 10 | 30 | 1.2 | 2.55 | 9.95 | 15.53 |
| 11 | 24 | 1.6 | 2.7 | 15.68 | 25.52 |
| 12 | 18 | 1.4 | 2.4 | 14.56 | 24.27 |
| 13 | 30 | 1.4 | 2.4 | 12.16 | 18.96 |
| Source | Sum of Squares | Degree of Freedom | Mean Squares | F-Value | p-Value | Performance |
|---|---|---|---|---|---|---|
| Model | 61.79 | 9 | 6.87 | 6.62 | 0.0255 | significant |
| A-w | 7.84 | 1 | 7.84 | 7.57 | 0.0403 | significant |
| B-pb | 46.34 | 1 | 46.34 | 44.71 | 0.0011 | significant |
| C-D | 0.84 | 1 | 0.84 | 0.81 | 0.4103 | insignificant |
| AB | 0.33 | 1 | 0.33 | 0.31 | 0.5993 | insignificant |
| AC | 0.22 | 1 | 0.22 | 0.21 | 0.6640 | insignificant |
| BC | 0.24 | 1 | 0.24 | 0.24 | 0.6475 | insignificant |
| A2 | 8.459 × 10−3 | 1 | 8.459 × 10−3 | 8.161 × 10−3 | 0.9315 | insignificant |
| B2 | 6.60 | 1 | 6.60 | 6.37 | 0.0529 | insignificant |
| C2 | 5.87 | 1 | 5.87 | 5.67 | 0.0631 | insignificant |
| Residual Error | 5.18 | 5 | 1.04 | |||
| Total | 66.97 | 14 |
| Source | Sum of Squares | Degree of Freedom | Mean Squares | F-Value | p-Value | Performance |
|---|---|---|---|---|---|---|
| Model | 228.63 | 9 | 25.40 | 7.07 | 0.0222 | significant |
| A-w | 33.78 | 1 | 33.78 | 9.40 | 0.0279 | significant |
| B-pb | 167.30 | 1 | 167.30 | 46.53 | 0.0010 | significant |
| C-D | 3.60 | 1 | 3.60 | 1.00 | 0.3628 | insignificant |
| AB | 0.81 | 1 | 0.81 | 0.22 | 0.6558 | insignificant |
| AC | 1.78 | 1 | 1.78 | 0.50 | 0.5131 | insignificant |
| BC | 5.00 | 1 | 5.00 | 1.39 | 0.2914 | insignificant |
| A2 | 0.59 | 1 | 0.59 | 0.17 | 0.7012 | insignificant |
| B2 | 24.15 | 1 | 24.15 | 6.72 | 0.0487 | significant |
| C2 | 16.17 | 1 | 16.17 | 4.50 | 0.0874 | insignificant |
| Residual Error | 17.98 | 5 | 3.60 | |||
| Total | 246.61 | 14 |
| Test Group | w | ρb | D | Measured | Predicted | ||
|---|---|---|---|---|---|---|---|
| c | φ | c | φ | ||||
| GLX | 24.7 | 1.322 | 2.66 | 12.13 | 20.76 | 11.72 | 19.43 |
| QLQ | 13.1 | 1.617 | 2.74 | 21.25 | 29.13 | 19.26 | 30.83 |
| ZLM | 30 | 1.157 | 2.64 | 13.67 | 19.45 | 11.41 | 18.70 |
| CLH | 20.1 | 1.5 | 2.75 | 16.26 | 32.32 | 15.86 | 26.01 |
| MLW | 35.7 | 1.047 | 2.77 | 15.13 | 27.17 | 15.82 | 26.62 |
| JLM | 18.8 | 1.505 | 2.57 | 14.32 | 24.26 | 14.19 | 23.94 |
| SLC | 27.4 | 1.463 | 2.54 | 12.81 | 20.44 | 12.06 | 19.97 |
| MLK | 21.8 | 1.363 | 2.49 | 11.73 | 19.69 | 12.01 | 20.04 |
| XLB | 26.1 | 1.456 | 2.70 | 13.84 | 22.98 | 13.43 | 22.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, H.; Zhang, S.; Zhao, J.; Qin, L.; Cheng, H. Investigating the Shear Strength of Granitic Gneiss Residual Soil Based on Response Surface Methodology. Sensors 2023, 23, 4308. https://doi.org/10.3390/s23094308
Zou H, Zhang S, Zhao J, Qin L, Cheng H. Investigating the Shear Strength of Granitic Gneiss Residual Soil Based on Response Surface Methodology. Sensors. 2023; 23(9):4308. https://doi.org/10.3390/s23094308
Chicago/Turabian StyleZou, Hao, Shu Zhang, Jinqi Zhao, Liuzhi Qin, and Hao Cheng. 2023. "Investigating the Shear Strength of Granitic Gneiss Residual Soil Based on Response Surface Methodology" Sensors 23, no. 9: 4308. https://doi.org/10.3390/s23094308
APA StyleZou, H., Zhang, S., Zhao, J., Qin, L., & Cheng, H. (2023). Investigating the Shear Strength of Granitic Gneiss Residual Soil Based on Response Surface Methodology. Sensors, 23(9), 4308. https://doi.org/10.3390/s23094308






