A New Statistical Method for Determining the Clutter Covariance Matrix in Spatial–Temporal Adaptive Processing of a Radar Signal
Abstract
1. Introduction
2. Related Works
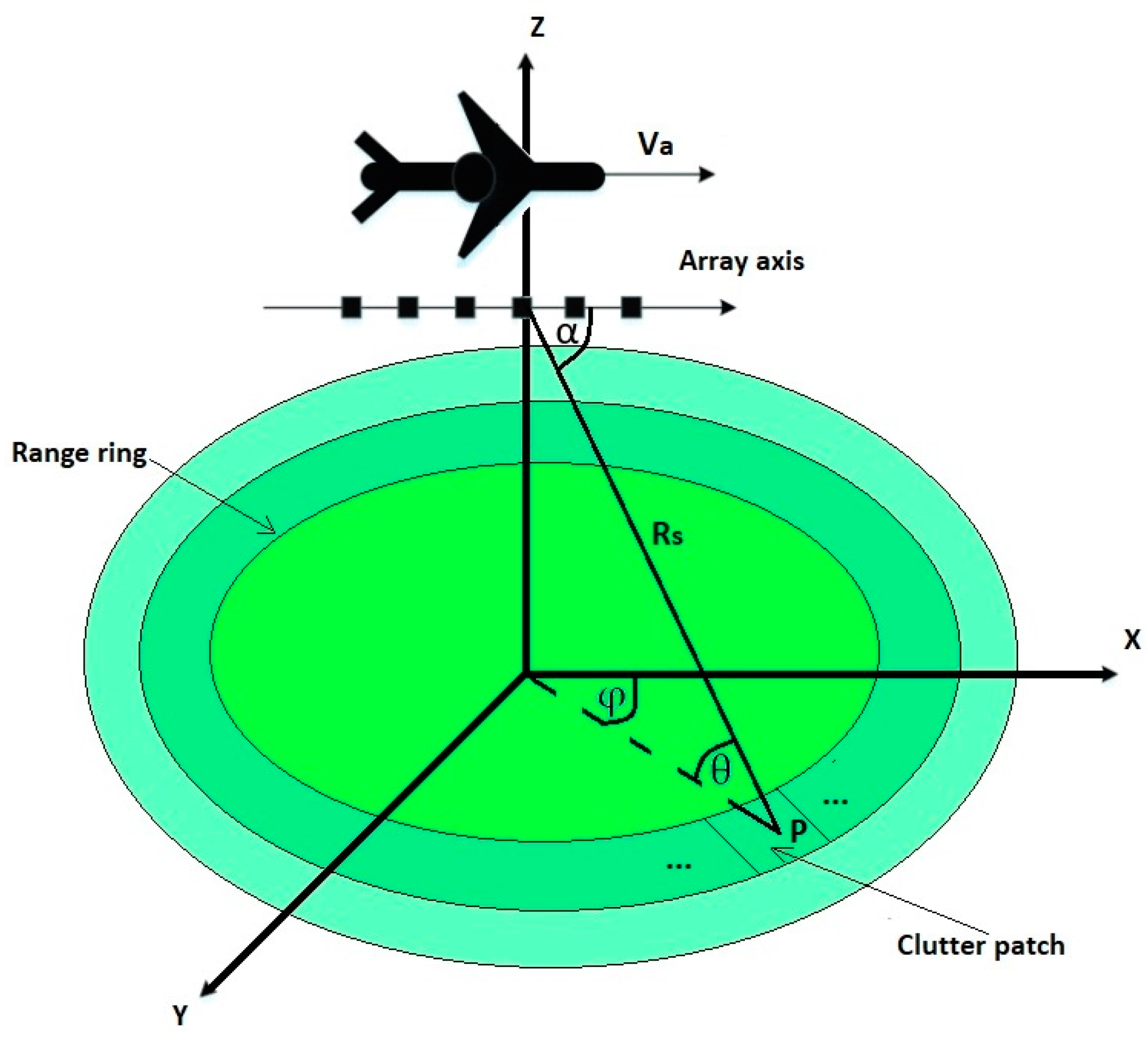
3. Signal Model
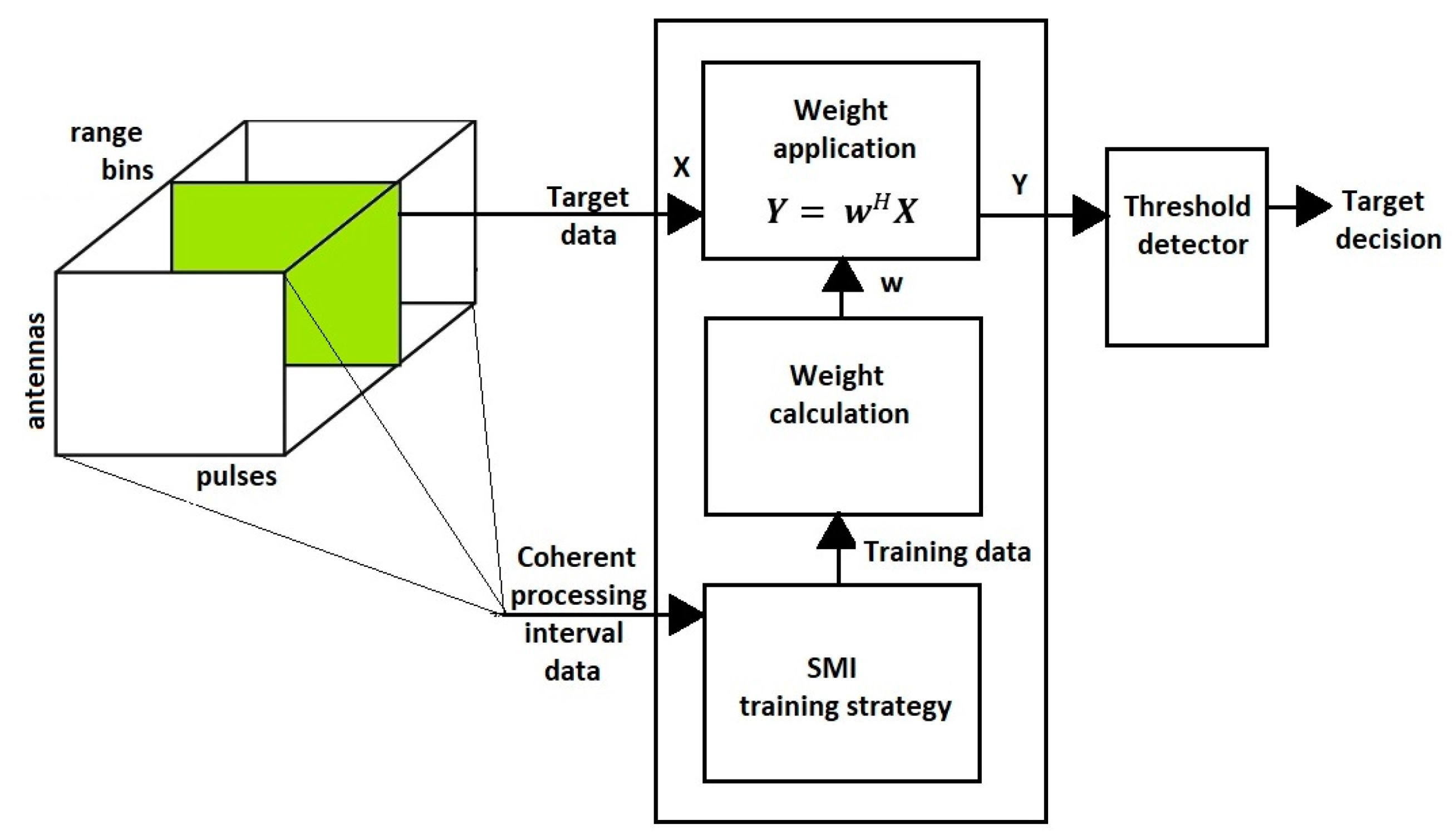
4. New Method, SMI-LU
4.1. The Common Part of Both Algorithms
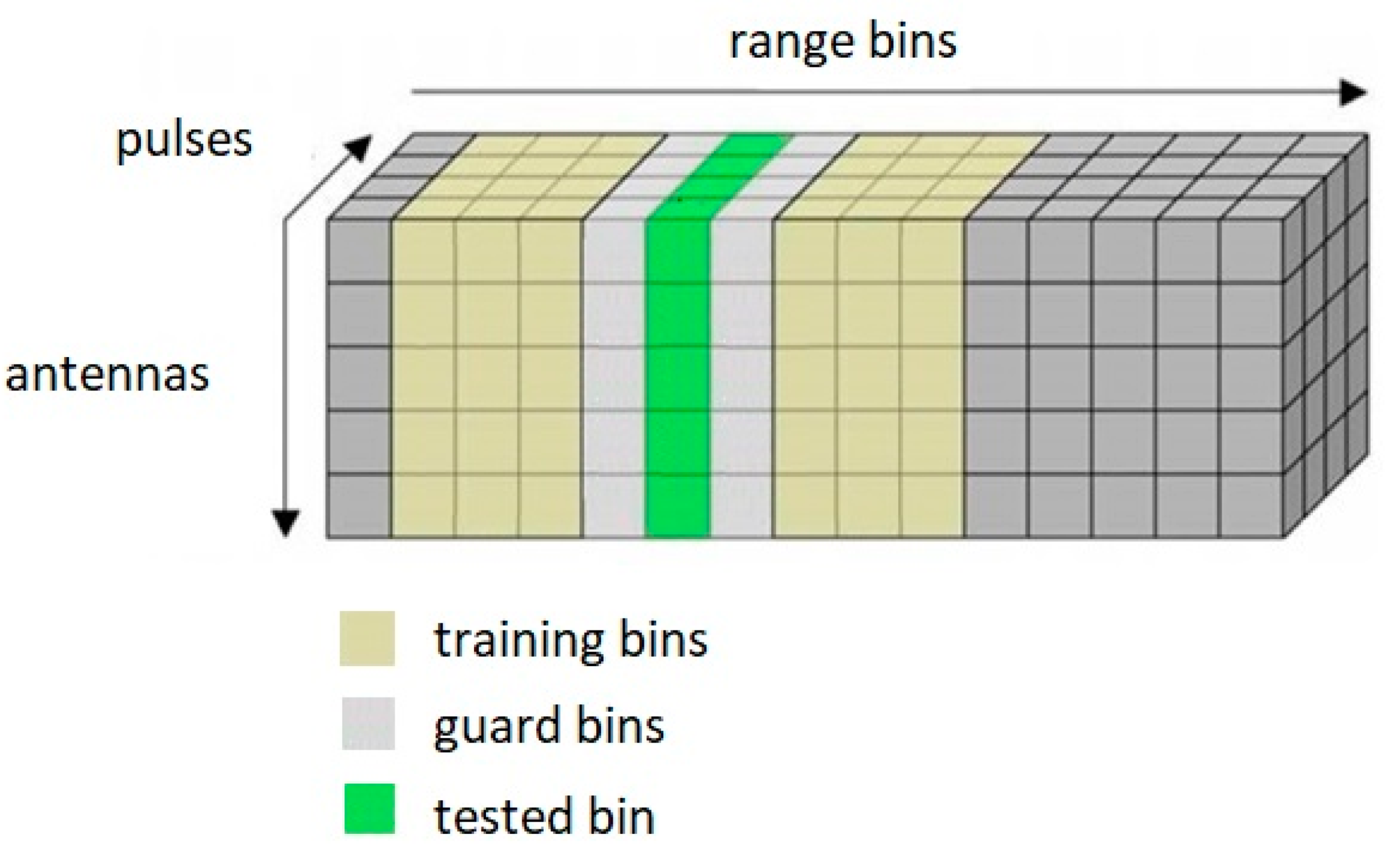
- K—number of distance bins;
- KT—number of training distance bins;
- KO—number of guard bins;
- KTARGET—distance bin under test;
- IKOP—lower index of guard bins;
- IKOZ—upper index of guard bins;
- KBEFORE—the remaining number of training bins before KTARGET;
- KAFTER—the remaining number of training bins behind KTARGET;
- KTbefore—number of training bins before KTARGET;
- KTafter—number of training bins behind KTARGET;
- IKbefore—distance training bin indexes before KTARGET;
- IKafter—distance training bin indexes behind KTARGET;
4.2. SMI-QR
4.3. SMI-LU
5. Simulation
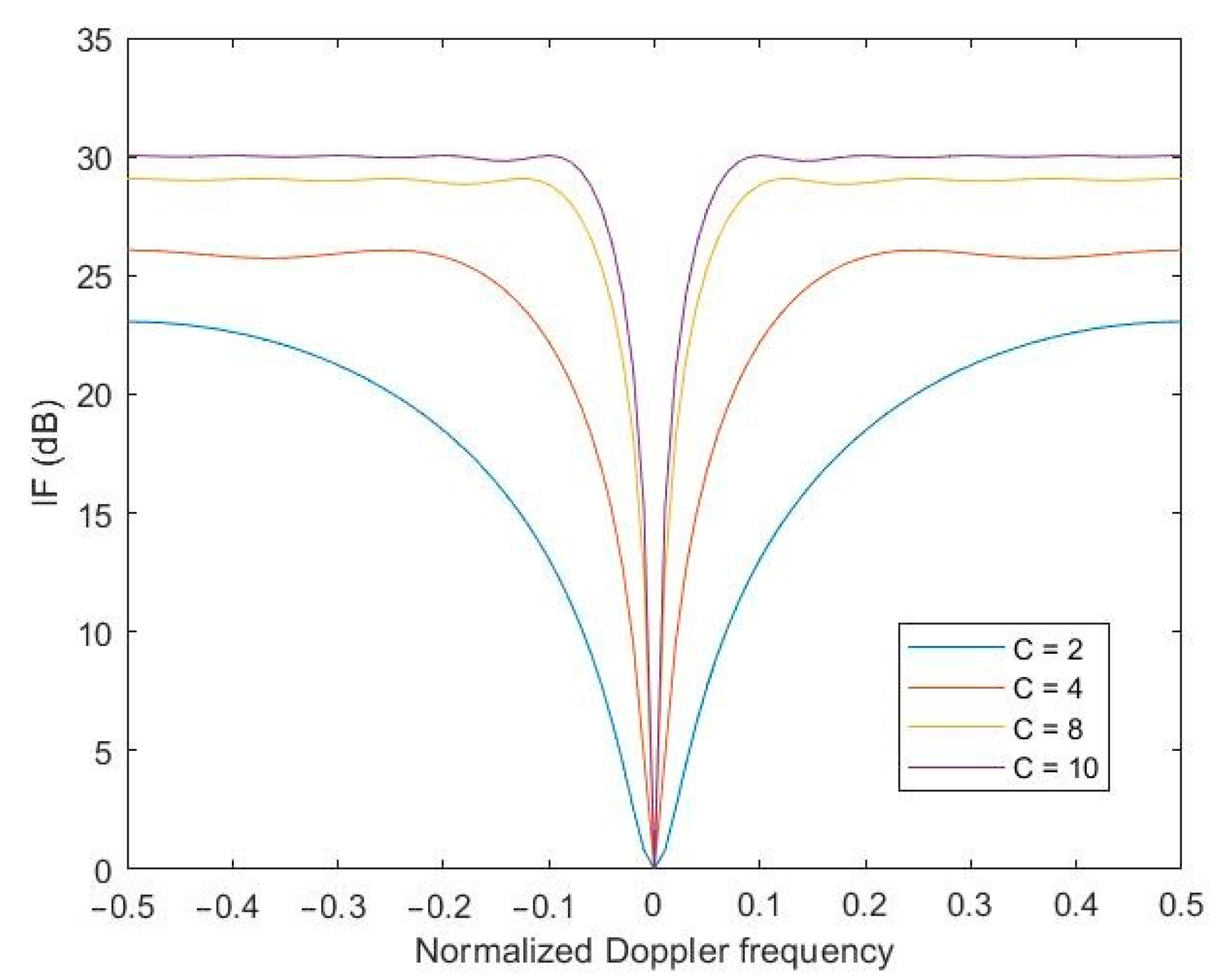
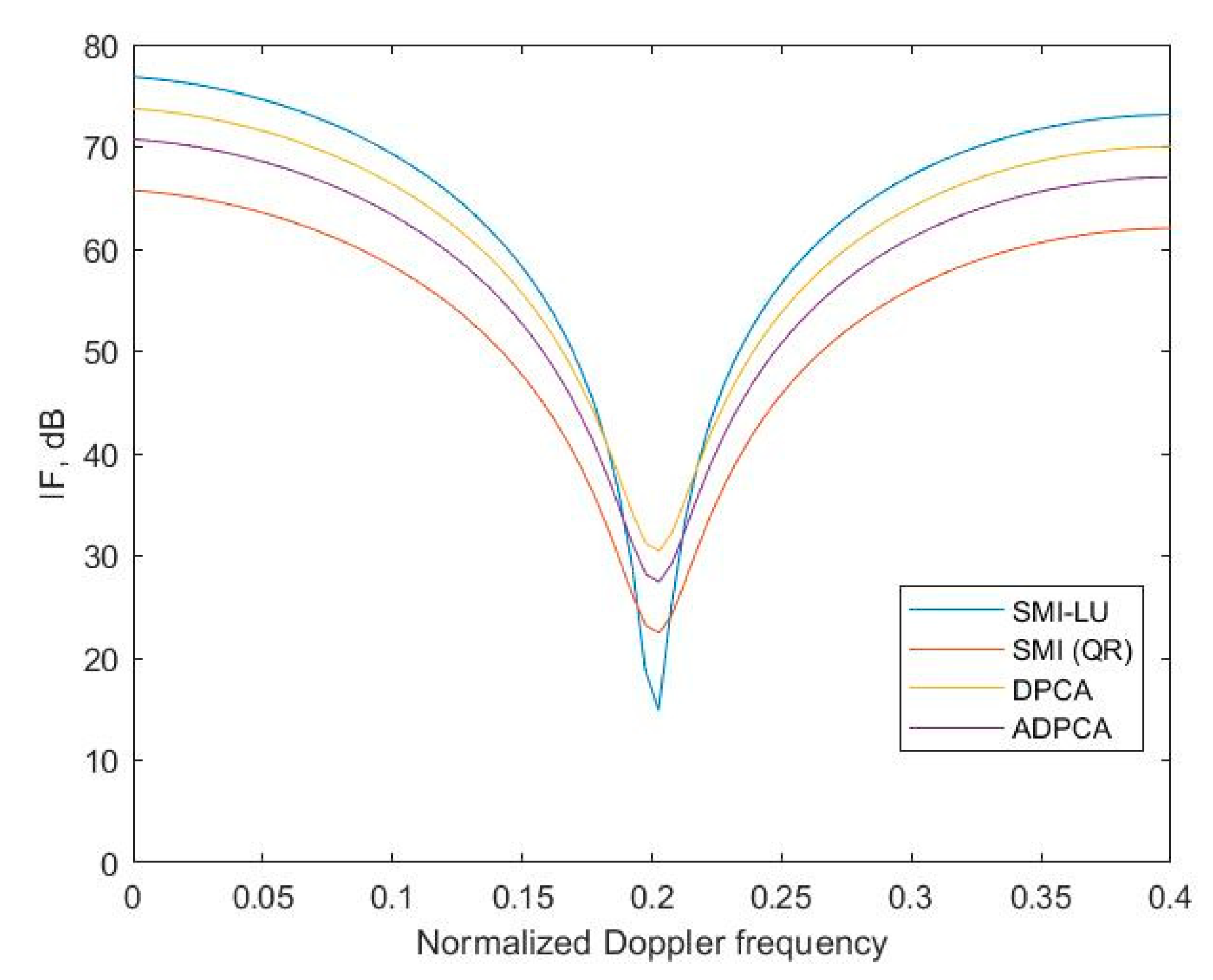
5.1. Improvement Factor
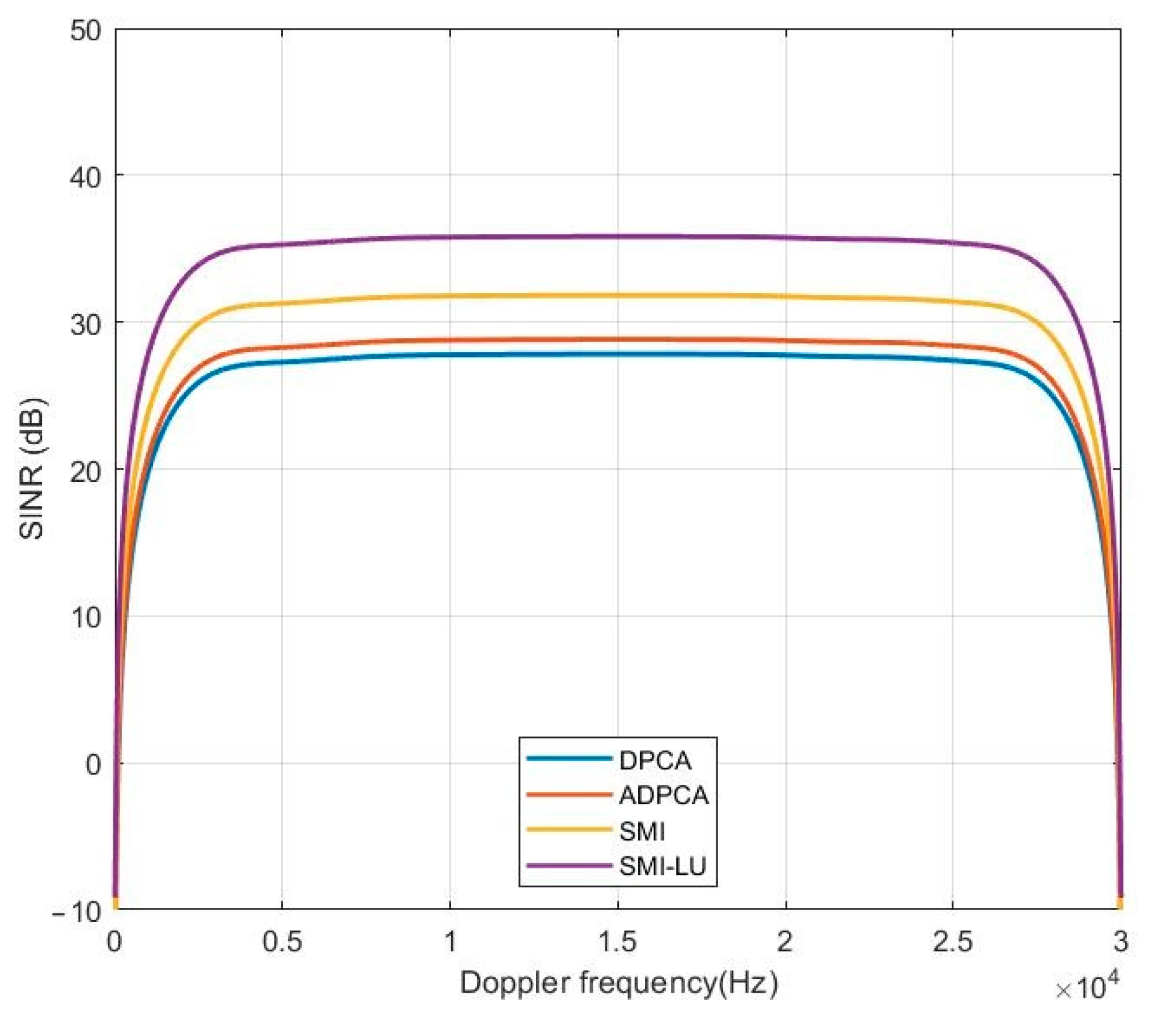
5.2. Signal-to-Interference Plus Noise Ratio
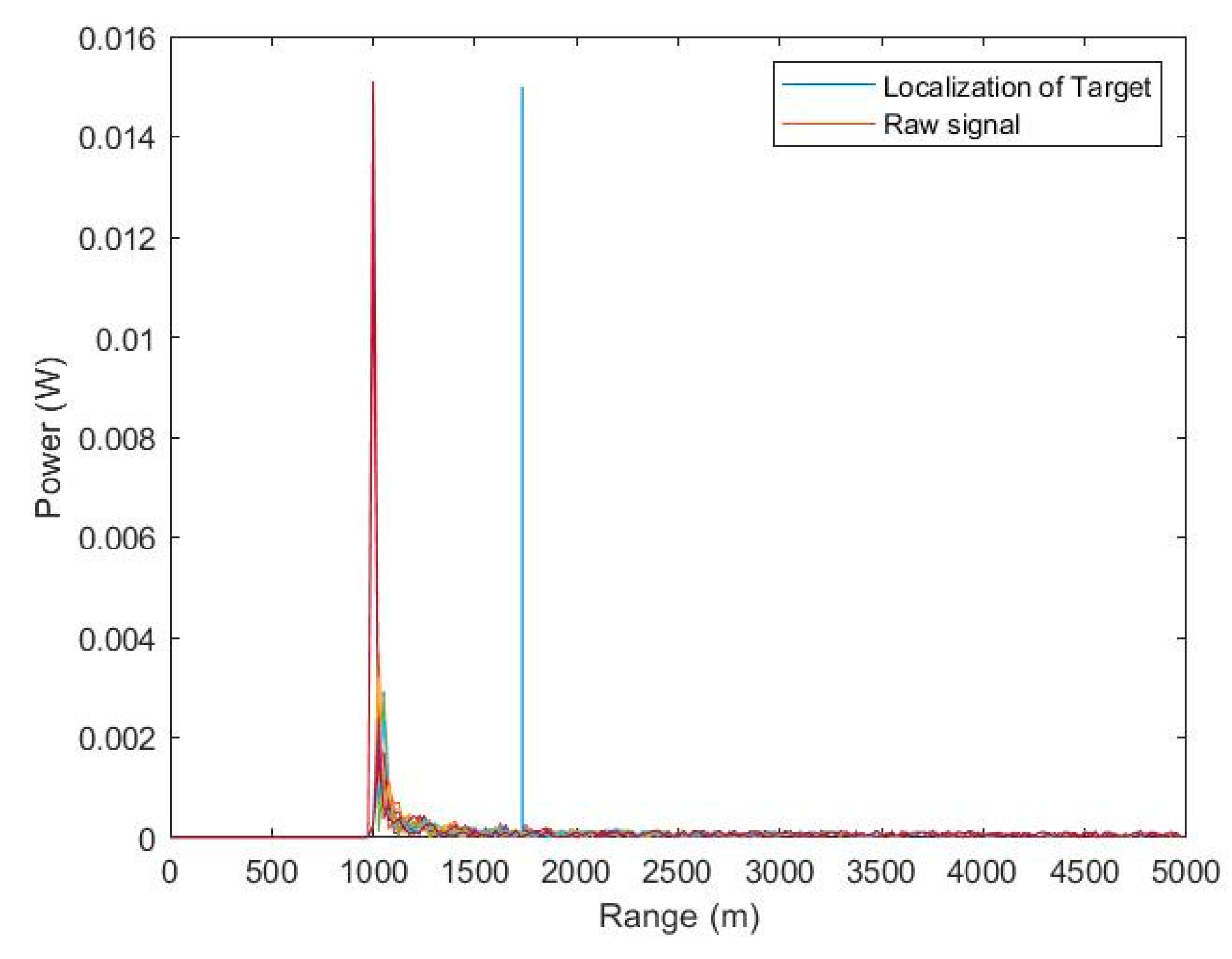
5.3. Precise Target Detection
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bużantowicz, W. A linear-quadratic stabilization system for a canard-controlled missile. In Proceedings of the 25th International Conference, Engineering Mechanics 2019, Svratka, Czech Republic, 13–16 May 2019; pp. 73–76. [Google Scholar]
- Bużantowicz, W. A sliding mode controller design for a missile autopilot system. J. Theor. Appl. Mech. 2020, 58, 169–182. [Google Scholar] [CrossRef] [PubMed]
- Bużantowicz, W. Tuning of a Linear-Quadratic Stabilization System for an Anti-Aircraft Missile. Aerospace 2021, 8, 48. [Google Scholar] [CrossRef]
- Klemm, R. Space-Time Adaptive Processing: Principles and Applications; The Institution of Electrical Engineers: London, UK, 1998. [Google Scholar]
- Burintramart, S.; Sarkar, T.K.; Zhang, Y.; Wicks, M.C. Performance comparison between statistical-basedand direct data domain STAPs. Digit. Signal Process. 2007, 17, 737–755. [Google Scholar] [CrossRef]
- Ward, J. Space-Time Adaptive Processing for Airbone Radar; Lincoln Laboratory: Lexington, MA, USA, 1998. [Google Scholar]
- Sen, S. Low-Rank Matrix Decomposition and Spatio-Temporal Sparse Recovery for STAP Radar. IEEE J. Sel. Top. Signal Process. 2015, 9, 1510–1523. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar Signal Processing; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Haimovich, A.M.; Blum, R.S.; Cimini, L.J. MIMO radar with widely separated antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO radar with colocated antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.S.; Cimini, J.; Chizhik, D.; Valenzuela, R.A. Spatial diversity in radars-models and detection performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target localization accuracy gain in MIMO radar-based systems. IEEE Trans. Inf. Theory 2010, 56, 2783–2803. [Google Scholar] [CrossRef]
- Bliss, D.W.; Forsythe, K.W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution. In Proceedings of the 37th Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 1, pp. 54–59. [Google Scholar]
- Li, J.; Stoica, P.; Xu, L.; Roberts, W. On parameter identifiability of MIMO radar. IEEE Signal Process. Lett. 2007, 14, 968–971. [Google Scholar]
- Bilik, I. Automotive MIMO radar for urban environments. In Proceedings of the IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Ender, J.H.; Klare, J. System architectures and algorithms for radar imaging by MIMO-SAR. In Proceedings of the IEEE Radar Conference (RadarConf), Pasadena, CA, USA, 4–8 May 2009; pp. 1–6. [Google Scholar]
- Lim, D.; Xu, L.; Gianelli, C.; Li, J.; Nguyen, L.; Anderson, J. Time-and frequency-domain MIMO FLGPR imaging. In Proceedings of the IEEE Radar Conference (RadarConf), Arlington, VA, USA, 10–15 May 2015; pp. 1305–1310. [Google Scholar]
- Klare, J.; Biallawons, O. Disaster management with the MIMO radar MIRA-CLE Ka: Measurements of a slowly moving wall. In Proceedings of the 10th European Conference on Synthetic Aperture Radar, VDE, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Wu, Y.; Wang, T.; Wu, J.; Duan, J. Training sample selection for space-time adaptive processing in heterogeneous environments. IEEE Geosci. Remote Sens. Lett. 2015, 12, 691–695. [Google Scholar]
- Li, H.; Bao, W.; Hu, J.; Xie, J.; Liu, R. A training samples selection method based on system identification for STAP. Signal Process. 2018, 142, 119–124. [Google Scholar] [CrossRef]
- Hu, J.; Li, J.; Li, H.; Li, K.; Liang, J. A Novel Covariance Matrix Estimation via Cyclic Characteristic for STAP. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1871–1875. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Long, T. Robust non-homogeneity detection algorithm based on prolate spheroidal wave functions for space-time adaptive processing. IET Radar Sonar Navig. 2013, 7, 47–54. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Long, T. Cross-Spectral Metric Smoothing-Based GIP for Space-Time Adaptive Processing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1388–1392. [Google Scholar]
- Yang, Z.; Li, X.; Wang, H.; Fa, R. Knowledge-aided STAP with sparse-recovery by exploiting spatiotemporal sparsity. IET Signal Process. 2016, 10, 150–161. [Google Scholar] [CrossRef]
- Ślesicka, A.; Kawalec, A. An Application of the Orthogonal Matching Pursuit Algorithm in Space-Time Adaptive Processing. Sensors 2020, 20, 3468. [Google Scholar] [CrossRef]
- Duan, K.; Wang, Z.; Xie, W.; Chen, H.; Wang, Y. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar. IET Signal Process. 2017, 11, 544–553. [Google Scholar] [CrossRef]
- Zhang, W.; An, R.; He, N.; He, Z.; Li, H. Reduced Dimension STAP Based on Sparse Recovery in Heterogeneous Clutter Environments. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 785–795. [Google Scholar] [CrossRef]
- Adve, R.S.; Hale, T.B.; Wicks, M. A Two Stage Hybrid Space-Time Adaptive Processing Algorithm. In Proceedings of the 1999 IEEE Radar Conference. Radar into the Next Millennium, Waltham, MA, USA, 22 April 1999; pp. 279–284. [Google Scholar]
- Sarkar, T.K.; Sangruji, N. An adaptive nulling system for a narrow-band signal with a look-direction constraint utilizing the conjugate gradient method. IEEE Trans. Antennas Propag. 1989, 37, 940–944. [Google Scholar] [CrossRef]
- Choi, W.; Sarkar, T.K.; Wang, H.; Mokole, E.L. Adaptive processing using real weights based on a direct data domain least squares approach. IEEE Trans. Antennas Propag. 2006, 54, 182–191. [Google Scholar] [CrossRef]
- Sun, K.; Meng, Y.; Wang, Y.; Wang, X. Direct data domain STAP using sparse representation of clutter spectrum. Signal Process. 2011, 91, 2222–2236. [Google Scholar] [CrossRef]
- Li, M.; Sun, G.; He, Z. Direct Data Domain STAP Based on Atomic Norm Minimization. In Proceedings of the 2019 IEEE Radar Conference, Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Scharf, L.L.; Friedlander, B. Matched subspace detectors. IEEE Trans. Signal Process. 1994, 42, 2146–2157. [Google Scholar] [CrossRef]
- Cristallini, D. Exploiting robust direct data domain STAP for GMTI in very high resolution SAR. In Proceedings of the IEEE RADAR 2012, Atlanta, GA, USA, 7–11 May 2012; pp. 348–353. [Google Scholar]
- Jeon, H.; Chung, Y.; Chung, W. Clutter covariance matrix estimation using weight vectors in Knowledge-aided STAP. IET Electron. Lett. 2017, 53, 560–562. [Google Scholar] [CrossRef]
- Peng, H.; Sun, Y.; Xiaopeng, Y. Robust knowledge-aided sparse recovery STAP method for non-homogeneity clutter suppression. J. Eng. 2019, 20, 6373–6376. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Y.; Meng, H. Jointly sparse recovery of multiple snapshots in STAP. In Proceedings of the 2013 IEEE Radar Conference, Ottawa, ON, Canada, 29 April–3 May 2013. [Google Scholar]
- Guo, Y.; Liao, G.; Feng, W. Sparse representation-based algorithm for airborne radar in beam-space post-Doppler reduced-dimension space-time adaptive processing. IEEE Access 2017, 5, 5896–5903. [Google Scholar] [CrossRef]
- Chen, J.; Huo, X. Theoretical results on sparse representations of multiple-measurement vectors. IEEE Trans. Signal Process. 2006, 54, 4634–4643. [Google Scholar] [CrossRef]
- Brennan, L.E.; Reed, L.S. Theory of adaptive radar. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 237–252. [Google Scholar] [CrossRef]
- Mecca, V.F.; Ramakrishnan, D.; Krolik, J.L. MIMO radar space-time adaptive processing for multipath clutter mitigation. In Proceedings of the 4th IEEE Workshop Sensor Array Multichannel Processing, Waltham, MA, USA, 12–14 July 2006; pp. 249–253. [Google Scholar]
- Guerci, J.R. Space-Time Adaptive Processing for Radar; Artech House: Norwood, MA, USA, 2003. [Google Scholar]
- Chen, C.-Y.; Vaidyanathan, P.P. MIMO radar space time adaptive processing using prolate spheroidal wave functions. IEEE Trans. Signal Process. 2008, 56, 623–635. [Google Scholar] [CrossRef]
- Forsythe, K.W.; Bliss, D.W. MIMO radar waveform constraints for GMTI. IEEE J. Sel. Top. Signal Process. 2010, 4, 21–32. [Google Scholar] [CrossRef]
- Xue, M.; Roberts, W.; Li, J.; Tan, X.; Stoica, P. MIMO radar sparse angle-doppler imaging for groundmoving target indication. In Proceedings of the IEEE Radar Conference, Arlington, VA, USA, 10–14 May 2010; pp. 553–558. [Google Scholar]
- Bergin, J.; Guerci, J.R. Mimo Radar Theory and Application; Artech House: Boston, MA, USA, 2018. [Google Scholar]
- Robey, F.C.; Coutts, S.; Weikle, D.; McHarg, J.C.; Cuomo, K. MIMO Radar Theory and Experimental Results. In Proceedings of the Conference Record of the Thirty-Eighth Asilomar Conference on, Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2004. [Google Scholar]
- Lin, Z.; Lin, M.; Champagne, B.; Zhu, W.-P.; Al-Dhahir, N. Secrecy-Energy Efficient Hybrid Beamforming for Satellite-Terrestrial Integrated Networks. IEEE Trans. Commun. 2021, 69, 6345–6360. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; de Cola, T.; Wang, J.-B.; Zhu, W.-P. Cheng J. Supporting IoT with Rate-Splitting Multiple Access in Satellite and Aerial-Integrated Networks. IEEE Internet Things J. 2021, 8, 11123–11134. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Wang, J.-B.; de Cola, T.; Wang, J. Joint Beamforming and Power Allocation for Satellite-Terrestrial Integrated Networks with Non-Orthogonal Multiple Access. IEEE J. Sel. Top. Signal Process. 2019, 13, 657–670. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Champagne, B.; Zhu, W.-P.; Al-Dhahir, N. Secure Beamforming for Cognitive Satellite Terrestrial Networks with Unknown Eavesdroppers. IEEE Syst. J. 2021, 15, 2186–2189. [Google Scholar] [CrossRef]
- Blum, R.S.; Melvin, W.L.; Wicks, M.C. An analysis of adaptive DPCA. In Proceedings of the 1996 IEEE National Radar Conference, Ann Arbor, MI, USA, 13–16 May 1996. [Google Scholar]
- Wang, H.; Cai, L. On adaptive spatial-temporal processing for airborne surveillance radar systems. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 660–669. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Radar operating frequency | 10 GHz |
| Number of transmitting antennas | 5 |
| Number of receiving antennas | 5 |
| Pulse repetition frequency | 30 kHz |
| Pulse duration | 33 µs |
| Number of pulses | 10 |
| Range | 5000 m |
| Transmitter power | 5.6 kW |
| Directional gain | 20 dB |
| Platform height | 1000 m |
| Speed of movement of the platform | [160 m/s, 160 m/s, 0] |
| Speed of movement of the target | [30 m/s, 30 m/s, 0] |
| Initial localization of the platform | [0,0,1000] |
| Initial localization of the target | [0,1000,1000] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawalec, A.; Ślesicka, A.; Ślesicki, B. A New Statistical Method for Determining the Clutter Covariance Matrix in Spatial–Temporal Adaptive Processing of a Radar Signal. Sensors 2023, 23, 4280. https://doi.org/10.3390/s23094280
Kawalec A, Ślesicka A, Ślesicki B. A New Statistical Method for Determining the Clutter Covariance Matrix in Spatial–Temporal Adaptive Processing of a Radar Signal. Sensors. 2023; 23(9):4280. https://doi.org/10.3390/s23094280
Chicago/Turabian StyleKawalec, Adam, Anna Ślesicka, and Błażej Ślesicki. 2023. "A New Statistical Method for Determining the Clutter Covariance Matrix in Spatial–Temporal Adaptive Processing of a Radar Signal" Sensors 23, no. 9: 4280. https://doi.org/10.3390/s23094280
APA StyleKawalec, A., Ślesicka, A., & Ślesicki, B. (2023). A New Statistical Method for Determining the Clutter Covariance Matrix in Spatial–Temporal Adaptive Processing of a Radar Signal. Sensors, 23(9), 4280. https://doi.org/10.3390/s23094280





