Graph Representation Learning and Its Applications: A Survey
Abstract
1. Introduction
- This paper presents a taxonomy of graph embedding models based on various algorithms and strategies.
- We provide readers with an in-depth analysis of an overview of graph embedding models with different types of graphs ranging from static to dynamic and from homogeneous to heterogeneous graphs.
- This paper presents graph transformer models, which have achieved remarkable results in a deeper understanding of graph structures in recent years.
- We cover applications of graph representation learning in various areas, from constructing graphs to applying models in specific tasks.
- We discuss the challenges and future directions of existing graph embedding models in detail.
2. Problem Description
- Directed graph: When for any , then the graph G is called an undirected graph, and G is directed graph otherwise.
- Weighted graph: is a graph in which each edge is assigned a specific weight value. Therefore, the adjacency matrix could be presented as: , where is the weight of the edge .
- Signed graph: When , the graph G is called signature/signed graph. The graph G could have all positive signed edges when for any , and G could have all negative signed edges otherwise.
- Attributed graph: A graph is an attributed graph where V, E is the set of nodes and edges, respectively, and X is the matrix of node attributes with size . Furthermore, we could also have the matrix X as the matrix of edge input attribute with size where m is the number of edges for any .
- Hyper graph: A hyper graph G could be represented as , where V denotes the set of nodes and E denotes a set of hyperedge. Each hyperedge can connect multiple nodes and is assigned a weight . The hypergraph G could be represented by an incidence matrix H size with entries if , and otherwise.
- Heterogeneous graph: A heterogeneous graph is defined as where V, and E are the set of nodes and edges, respectively, is the mapping function: , and the mapping function with , describe the set of node types and edge types, respectively, and + is the sum of the number of node types and edge types.
- Temporal dynamic graph embedding: A temporal dynamic embedding is a projection function , where and describes the collection of graph during time interval .
- Topological dynamic graph embedding: A topological dynamic graph embedding for graph for nodes is a mapping function , where .
3. Graph Representation Learning Models
3.1. Graph Kernels
- Kernels for graphs: Kernels for graphs aim to measure the similarity between graphs. The similarity between the two graphs (isomorphism) could be explained as follows: Given two undirected graphs and , and are isomorphic if they exist a bimodal mapping function such that , a and b are contiguous on if and are contiguous on .
- Kernels on graphs: To embed nodes in graphs, kernel methods refer to finding a function that maps pairs of nodes to latent space using particular similarity measures. Formally, graph kernels could be defined as: Given a graph , a function is a kernel on G if there is a mapping function such that for any node pairs .
- Coverage: The graph kernels are one of the most useful functions to measure the similarity between graph entities by performing several strategies to find a kernel in graphs. This could be seen as a generalization of the traditional statistical methods [116].
- Efficiency: Several kernel tricks have been proposed to reduce the computational cost of kernel methods on graphs [117]. Kernel tricks could reduce the number of spatial dimensions and computational complexity on substructures while still providing efficient kernels.
- Missing entities: Most kernel models could not learn node embeddings for new nodes. In the real world, graphs are dynamic, and their entities could evolve. Therefore, the graph kernels must re-learn graphs every time a new node is added, which is time-consuming and difficult to apply in practice.
- Dealing with weights: Most graph kernel models do not consider the weighted edges, which could lead to structural information loss. This could reduce the possibility of graph representation in the hidden space.
- Computational complexity: Graph kernels are an NP-hard class [109]. Although several kernel-based models aim to reduce the computational time by considering the distribution of substructures, this may increase the complexity and reduce the ability to capture the global structure.
3.2. Matrix Factorization-Based Models
- The Laplacian eigenmaps: To learn representations of a graph , these approaches first represent G as a Laplacian matrix L where and D is the degree matrix [41]. In the matrix L, the positive values depict the degree of nodes, and negative values are the weights of the edges. The matrix L could be decomposed to find the smallest number from eigenvalues which are considered node embeddings. The optimal node embedding , therefore, could be computed using an objective function:
- Node proximity matrix factorization: The objective of these models is to decompose node proximity matrix into small-sized matrices directly. In other words, the proximity of nodes in graphs will be preserved in the latent space. Formally, given a proximity matrix M, the models try to optimize the distance between two pair nodes and , which could be defined as:
| Models | Graph Types | Tasks | Loss Function |
|---|---|---|---|
| SLE [39] | Static graphs | Node classification | |
| [120] | Attributed graphs | Node classification | |
| [7] | Attributed graphs | Community detection | |
| LPP [42] | Attributed graphs | Node classification | |
| [121] | Attributed graphs | Graph reconstruction | |
| [40] | Static graphs | Node clustering | |
| GLEE [122] | Attributed graphs | Graph reconstruction, Link prediction | |
| LPP [42] | Static graphs | Node classification | |
| Grarep [15] | Static graphs | Node classification, Node clustering | |
| NECS [123] | Static graphs | Graph reconstruction, Link prediction, Node classification | |
| HOPE [5] | Static graphs | Graph reconstruction Link prediction, Node classification | |
| [124] | Static graphs | Link prediction | |
| AROPE [86] | Static graphs | Graph reconstruction, Link prediction, Node classification | |
| ProNE [43] | Static graphs | Node classification | |
| ATP [6] | Static graphs | Link prediction | |
| [125] | Static graphs | Graph partition | |
| NRL-MF [126] | Static graphs | Node classification |
| Models | Graph Types | Tasks | Loss Function |
|---|---|---|---|
| DBMM [134] | Dynamic graphs | Node classification, Node clustering | |
| [135] | Dynamic graphs | Link prediction | |
| [136] | Dynamic graphs | Link prediction | |
| LIST [137] | Dynamic graphs | Link prediction | |
| TADW [131] | Attributed graphs | Node classification | |
| PME [138] | Heterogeneous graphs | Link prediction | |
| EOE [139] | Heterogeneous graphs | Node classification | |
| [130] | Heterogeneous graphs | Link prediction | |
| ASPEM [140] | Heterogeneous graphs | Node classification, Link prediction | |
| MELL [141] | Heterogeneous graphs | Link prediction | |
| PLE [142] | Attributed graphs | Node classification |
- Training data requirement: The matrix factorization-based models do not need much data to learn embeddings. Compared to other methods, such as neural network-based models, these models bring advantages in case there is little training data.
- Coverage: Since the graphs are presented as Laplacian matrix L, or transition matrix M, then the models could capture all the proximity of the nodes in the graphs. The connection of all the pairs of nodes is observed at least once time under the matrix that makes the models could be able to handle sparsity graphs.
- Computational complexity: The matrix factorization suffers from time complexity and memory complexity for large graphs with millions of nodes. The main reason is the time it takes to decompose the matrix into a product of small-sized matrices [15].
- Missing values: Models based on matrix factorization cannot handle incomplete graphs with unseen and missing values [143,144]. When the graph data are insufficient, the matrix factorization-based models could not learn generalized vector embeddings. Therefore, we need neural network models that can generalize graphs and better predict entities in graphs.
3.3. Shallow Models
- Structure preservation: The primary concept of these approaches is to define sampling strategies that could capture the graph structure within fixed-length samples. Several sampling techniques could capture both local and global graph structures, such as random-walk sampling, role-based sampling, and edge reconstruction. The model then applies shallow neural network algorithms to learn vector embeddings in the latent space in an unsupervised learning manner. Figure 6a shows an example of a random-walk-based sampling technique in a graph from a source node to a target node .
- Proximity reconstruction: It refers to preserving a k-hop relationship between nodes in graphs. The relation between neighboring nodes in the k-hop distance should be preserved in the latent space. For instance, Figure 6b presents a 3-hop proximity from the source node .
- Unseen nodes: When there is a new node in graphs, the shallow models cannot learn embeddings for new nodes. To obtain embedding for new nodes, the models must update new patterns, for example, re-execute random-walk sampling to generate new paths for new nodes, and then the models must be re-trained to learn embeddings. The re-sampling and re-training procedures make it impractical to apply them in practice.
- Node features: Shallow models such as DeepWalk and Node2Vec mainly work suitably on homogeneous graphs and ignore information about the attributes/labels of nodes. However, in the real world, many graphs have attributes and labels that could be informative for graph representation learning. Only a few studies have investigated the attributes and labels of nodes, and edges. However, the limitations of domain knowledge when working with heterogeneous and dynamic graphs have made the model inefficient and increased the computational complexity.
- Parameter sharing: One of the problems of shallow models is that these models cannot share the parameters during the training process. From the statistical perspective, parameter sharing could reduce the computational time and the number of weight updates during the training process.
3.3.1. Structure-Preservation Models
| Models | Graph Types | Tasks | Loss Function |
|---|---|---|---|
| DeepWalk [14] | Static graphs | Node classification | |
| Node2Vec [4] | Static graphs | Node classification, Link prediction | |
| WalkLets [147] | Static graphs | Node classification | |
| Div2Vec [149] | Static graphs | Link prediction | |
| Static graphs | Node classification | ||
| Node2Vec+ [148] | Static graphs | Node classification | |
| Struct2Vec [21] | Static graphs | Node classification | |
| DiaRW [150] | Static graphs | Node classification, Link prediction | |
| Role2Vec [151] | Attributed graphs | Link prediction | |
| NERD [152] | Directed graphs | Link Prediction, Graph Reconstruction, Node classification | |
| Sub2Vec [153] | Static graphs | Community detection, graph classification | |
| Subgraph2Vec [145] | Static graphs | Graph classification, Clustering | |
| RUM [89] | Static graphs | Node classification, Graph reconstruction | |
| Gat2Vec [154] | Attributed graphs | Node classification, Link prediction | |
| ANRLBRW [155] | Attributed graphs | Node classification | |
| Gl2Vec [88] | Static graphs | Node classification |
- Generating nodes in graph : Each new node v in graph is a tuple in the original graph G. Therefore, they can map the triangle patterns of the original graph to the new graph for structure preservation.
- Generating edges of graph : Each edge of the new graph is formed from two nodes that have two edges in common in the original graph. For example, the edge denotes that we the edge in the original graph G.
- Computational complexity: Unlike kernel models and matrix factorization-based models, which require considerable computational costs, structure preservation models could learn embeddings with an efficient time. This effectiveness comes from search-based sampling strategies and the model generalizability from the training process.
- Classification tasks: Since the models aim to find structural neighbor relationships from a target node, these show power in problems involving node classification. In almost all graphs, nodes that have the same label tend to be connected at a small, fixed-length distance. This is a strength of models based on preserving structure in problems related to classification tasks.
- Transductive learning: Most models cannot learn node embeddings that have not been seen in the training data. To learn new node embeddings, the model should re-sample the graph structure and learn the new samples again which could be time-consuming.
- Missing connection problem: Many graphs have sparse connections and missing connections between nodes in the real world. However, most structure-preservation models cannot handle missing connections between nodes since the sampling strategies could not be able to capture these connections. In the case of a random-walk-based sampling strategy, for example, these models only capture graph structure when nodes are linked together.
- Parameter sharing: These models could only learn node embeddings for individual nodes and do not share parameters. The absence of sharing parameters could reduce the effectiveness of learning representation.
3.3.2. Proximity Reconstruction Models
| Models | Graph Types | Objective | Loss Function |
|---|---|---|---|
| LINE [16] | Static graphs | Node classification | |
| APP [76] | Static graphs | Link prediction | |
| PALE [77] | Static graphs | Link prediction | |
| CVLP [182] | Attributed graphs | Link prediction | |
| [183] | Static graphs | Link prediction | |
| HARP [178] | Static graphs | Node classification | |
| PTE [179] | Heterogeneous graphs | Link prediction | |
| Hin2Vec [180] | Heterogeneous graphs | Node classification, link prediction | |
| [78] | Heterogeneous graphs | Node classification | |
| [184] | Signed graphs | Link prediction | |
| [185] | Heterogeneous graphs | Node classification, Node clustering | |
| [186] | Heterogeneous graphs | Link prediction | |
| [187] | Static graphs | Node classification | |
| [188] | Heterogeneous graph | Graph reconstruction, link prediction, node classification | |
| ProbWalk [189] | Static graphs | Node classification, link prediction | |
| [190] | Static graphs | Node classification, link prediction | |
| NEWEE [191] | Static graphs | Node classification, link prediction | |
| DANE [192] | Attributed graphs | Node classification, Link prediction | |
| CENE [193] | Attributed graphs | Node classification | |
| HSCA [194] | Attributed graphs | Node classification |
- Inter-graph proximity: Proximity-based models not only explore proximity between nodes in a single graph but can also are applied for proximity reconstruction across different graphs with common nodes [183]. These methods can preserve the structural similarity of nodes in other graphs which are entirely different from other models. In the case of models based on structure-preservation strategies, these must re-learn node embeddings in other graphs.
- Proximity of nodes belonging to different clusters: In the context of clusters with different densities and sizes, proximity reconstruction-based models could capture nodes that are close to each other but in different clusters. This feature shows an advantage over structure reconstruction-based models, which tend to favor searching for neighboring nodes in the same cluster.
- Link prediction and node classification problem: Since structural identity is based on proximity between nodes, two nodes with similar neighborhoods should be close in the vector space. For instance, the LINE model considered preserving the 1st-order and 2nd-order proximity between two nodes. As a result, proximity reconstruction provides remarkable results for link prediction and node classification tasks [16,76,77].
- Weighted edges problems: Most proximity-based models do not consider the weighted edges between nodes. These models consider proximity based only on the number of connections shared without weights which could lead to structural loss.
- Capturing the whole graph structure: Proximity-based models mostly focus on 1st-order and 2nd-order proximity which cannot specify the global structure of graphs. A few models try to capture the higher-order proximity of nodes in graphs, but there is a problem with the computational complexity.
3.4. Deep Neural Network-Based Models
3.4.1. Graph Autoencoders
3.4.2. Recurrent Graph Neural Networks
- Diffusion pattern and multiple relations: RGNNs show superior learning ability when dealing with diffuse information, and they can handle multi-relational graphs where a single node has many relations. This feature is achieved due to the ability to update the states of each node in each hidden layer.
- Parameter sharing: RGNNs could share parameters across different locations, which could be able to capture the sequence node inputs. This advantage could reduce computational complexity during the training process with fewer parameters and increase the performance of the models.
3.4.3. Convolutional Graph Neural Networks
- Computational complexity: The spectral decomposition of the Laplacian matrix into matrices containing eigenvectors is time-consuming. During the training process, the dot product of the U, , and matrices also increase the training time.
- Difficulties for handling large-scale graphs: Since the number of parameters for the kernels also corresponds to the number of nodes in graphs. Therefore, spectral models could not be suitable for large-scale graphs.
- Difficulties for considering graph dynamicity: To apply convolution filters to graphs and train the model, the graph data must be transformed to the spectral domain in the form of a Laplacian matrix. Therefore, when the graph data changes, in the case of dynamic graphs, the model is not applicable to capture changes in dynamic graphs.
| Algorithm 1: GraphSAGE algorithm. The model first takes the node features as inputs. For each layer, the model aggregates the information from neighbors and then updates the hidden state of each node . |
Input: : The graph G with set of nodes V and set of edges E. : The input features of node L: The depth of hidden layers, : Differentiable aggregator functions : The set of neighbors of node . Output: : Vector representations for . 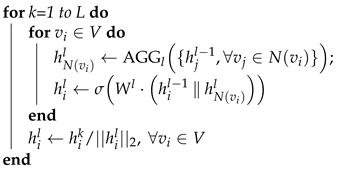 |
- A corruption function : This function aims to generate negative examples from an original graph with several changes in structure and properties.
- An encoder . The goal of function is to encode nodes into vector space so that presents vector embeddings of all nodes in graphs.
- Readout function . This function maps all embedding nodes into a single vector (supernode).
- A discriminator compares vector embeddings against the global vector of the graph by calculating a score between 0 and 1 for each vector embedding.
- Attention score: At layer l, the model takes a set of features of a node as inputs and the output . An attention score measures the importance of neighbor nodes to the target node could be computed as:where , and are trainable weights, denotes the concatenation.
- Normalization: The score then is normalized comparable across all neighbors of node using the SoftMax function:
- Aggregation: After normalization, the embeddings of node could be computed by aggregating states of neighbor nodes which could be computed as:
- Parameter sharing: Deep neural network models share weights during the training phase to reduce training time and training parameters while increasing the performance of the models. In addition, the parameter-sharing mechanism allows the model to learn multi-tasks.
- Inductive learning: The outstanding advantage of deep models over shallow models is that deep models can support inductive learning. This makes deep-learning models capable of generalizing to unseen nodes and having practical applicability.
- Over-smoothing problem: When capturing the graph structure and entity relationships, CGNNs rely on an aggregation mechanism that captures information from neighboring nodes for target nodes. This results in stacking multiple graph convolutional layers to capture higher-order graph structure. However, increasing the depth of convolution layers could lead to over-smoothing problems [252]. To overcome this drawback, models based on transformer architecture have shown several improvements compared to CGNNs using self-attention.
- The ability on disassortative graphs: Disassortative graphs are graphs where nodes with different labels tend to be linked together. However, the aggregation mechanism in GNN samples all the features of the neighboring nodes even though they have different labels. Therefore, the aggregation mechanism is the limitation and challenge of GNNs for disassortative graphs in classification tasks.
3.4.4. Graph Transformer Models
- Structural encoding-based graph transformer: These models focus on various positional encoding schemes to capture absolute and relative information about entity relationships and graph structure. Structural encoding strategies are mainly suitable for tree-like graphs since the models should capture the hierarchical relations between the target nodes and their parents as well as the interaction with other nodes of the same level.
- GNNs as an auxiliary module: GNNs bring a powerful mechanism in terms of aggregating local structural information. Therefore, several studies try integrating message-passing and GNN modules with a graph transformer encoder as an auxiliary.
- Edge channel-based attention: The graph structure could be viewed as the combination of the node and edge features and the ordered/unordered connection between them. From this perspective, we do not need GNNs as an auxiliary module. Recently, several models have been proposed to capture graph structure in depth as well as apply graph transformer architecture based on the self-attention mechanism.
3.5. Non-Euclidean Models
3.5.1. Hyperbolic Embedding Models
3.5.2. Spherical Embedding Models
3.5.3. Gaussian Embedding Models
4. Applications
4.1. Computer Vision
4.2. Natural Language Processing
4.3. Computer Security
4.4. Bioinformatics
4.5. Social Media Analysis
4.6. Recommendation Systems
4.7. Smart Cities
4.8. Computational Social Science
4.9. Digital Humanity
4.10. Semiconductor Manufacturing
4.11. Weather Forecasting
5. Evaluation Methods
5.1. Benchmark Datasets
5.2. Downstream Tasks and Evaluation Metrics
5.3. Libraries for Graph Representation Learning
6. Challenges and Future Research Directions
- Graph representation in a suitable geometric space: Euclidean space may not capture the graph structure sufficiently and lead to structural information loss.
- The trade-off between the graph structure and node features: Most graph embedding models suffer from noise from non-useful neighbor node features. This could lead to a trade-off between structure preservation and node feature representation, which can be the future research direction.
- Dynamic graphs: Many real-world graphs show dynamic behaviors representing entities’ dynamic structure and properties, bringing a potential research direction.
- Over-smoothing problem: Most GNN models suffer from this problem. The graph transformer model could only handle the over-smoothing problem in several cases.
- Disassortative graphs: Most graph representation learning models suffer from this problem. Several solutions have been proposed but have yet to fully solve to the whole extent.
- Pre-trained models: Pre-trained models could be beneficial to handle the little availability of node labels. However, a few graph embedding models have been pre-trained on specific tasks and small domains.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Open-Source Implementations
| Model | Category | URL |
|---|---|---|
| [70] | Hyperbolic space | https://github.com/facebookresearch/poincare-embeddings |
| [293] | Hyperbolic space | http://snap.stanford.edu/hgcn/ |
| [294] | Hyperbolic space | https://github.com/facebookresearch/hgnn |
| Graph2Gauss [23] | Gaussian embedding | https://github.com/abojchevski/graph2gauss |
References
- Rossi, R.A.; Ahmed, N.K. The Network Data Repository with Interactive Graph Analytics and Visualization. In Proceedings of the 29th Conference on Artificial Intelligence (AAAI 2015), Austin, TX, USA, 25–30 January 2015; AAAI Press: Austin, TX, USA, 2015; pp. 4292–4293. [Google Scholar]
- Ahmed, Z.; Zeeshan, S.; Dandekar, T. Mining biomedical images towards valuable information retrieval in biomedical and life sciences. Database J. Biol. Databases Curation 2016, 2016, baw118. [Google Scholar] [CrossRef]
- Hamilton, W.L. Graph Representation Learning. In Synthesis Lectures on Artificial Intelligence and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining (SIGKDD 2016), San Francisco, CA, USA, 13–17 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 855–864. [Google Scholar] [CrossRef]
- Ou, M.; Cui, P.; Pei, J.; Zhang, Z.; Zhu, W. Asymmetric Transitivity Preserving Graph Embedding. In Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining (ACM SIGKDD 2016), San Francisco, CA, USA, 13–17 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 1105–1114. [Google Scholar] [CrossRef]
- Sun, J.; Bandyopadhyay, B.; Bashizade, A.; Liang, J.; Sadayappan, P.; Parthasarathy, S. ATP: Directed Graph Embedding with Asymmetric Transitivity Preservation. In Proceedings of the 33th Conference on Artificial Intelligence (AAAI 2019), Honolulu, HI, USA, 27 January–1 February 2019; AAAI Press: Honolulu, HI, USA, 2019. [Google Scholar] [CrossRef]
- Cavallari, S.; Zheng, V.W.; Cai, H.; Chang, K.C.; Cambria, E. Learning Community Embedding with Community Detection and Node Embedding on Graphs. In Proceedings of the 26th Conference on Information and Knowledge Management (CIKM 2017), Singapore, 6–10 November 2017; ACM: Singapore, 2017; pp. 377–386. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Liu, W.; Pei, Y.; Wang, L.; Zha, D.; Fu, T. Dynamic Network Embedding by Semantic Evolution. In Proceedings of the International Joint Conference on Neural Networks (IJCNN 2019), Budapest, Hungary, 14–19 July 2019; IEEE: Budapest, Hungary, 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Mitrovic, S.; De Weerdt, J. Dyn2Vec: Exploiting dynamic behaviour using difference networks-based node embeddings for classification. In Proceedings of the 15th International Conference on Data Science (ICDATA 2019), Las Vegas, NV, USA, 29 July–1 August 2019; CSREA Press: Las Vegas, NV, USA, 2019; pp. 194–200. [Google Scholar]
- Lee, J.B.; Rossi, R.A.; Kim, S.; Ahmed, N.K.; Koh, E. Attention Models in Graphs: A Survey. ACM Trans. Knowl. Discov. Data 2019, 13, 62.1–62.25. [Google Scholar] [CrossRef]
- Xia, F.; Sun, K.; Yu, S.; Aziz, A.; Wan, L.; Pan, S.; Liu, H. Graph Learning: A Survey. IEEE Trans. Artif. Intell. 2021, 2, 109–127. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Y.C.; Wang, B.; Kuo, C.C. Graph representation learning: A survey. APSIPA Trans. Signal Inf. Process. 2020, 9, e15. [Google Scholar] [CrossRef]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online learning of social representations. In Proceedings of the 20th International Conference on Knowledge Discovery and Data Mining (KDD 2014), New York, NY, USA, 25–30 January 2015; ACM: New York, NY, USA, 2015; pp. 701–710. [Google Scholar] [CrossRef]
- Cao, S.; Lu, W.; Xu, Q. GraRep: Learning Graph Representations with Global Structural Information. In Proceedings of the 24th International Conference on Information and Knowledge Management (CIKM 2015), Melbourne, VIC, Australia, 19–23 October 2015; ACM: Melbourne, VIC, Australia, 2015; pp. 891–900. [Google Scholar] [CrossRef]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale Information Network Embedding. In Proceedings of the 24th International Conference on World Wide Web (WWW 2015), Florence, Italy, 18–22 May 2015; ACM: Florence, Italy, 2015; pp. 1067–1077. [Google Scholar] [CrossRef]
- Li, Y.; Tarlow, D.; Zemel, R.S. Gated Graph Sequence Neural Networks. In Proceedings of the 4th International Conference on Learning Representations (ICLR 2016), San Juan, PR, USA, 2–4 May 2016; ICLR: San Juan, PR, USA, 2016. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 5th International Conference on Learning Representations (ICLR 2017), Toulon, France, 24–26 April 2017; OpenReview.net: Toulon, France, 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. arXiv 2017, arXiv:1710.10903. [Google Scholar] [CrossRef]
- Dong, Y.; Chawla, N.V.; Swami, A. metapath2vec: Scalable Representation Learning for Heterogeneous Networks. In Proceedings of the 23rd International Conference on Knowledge Discovery and Data Mining (SIGKDD 2017), Halifax, NS, Canada, 13–17 August 2017; ACM: Halifax, NS, Canada, 2017; pp. 135–144. [Google Scholar] [CrossRef]
- Ribeiro, L.F.R.; Saverese, P.H.P.; Figueiredo, D.R. struc2vec: Learning Node Representations from Structural Identity. In Proceedings of the 23rd International Conference on Knowledge Discovery and Data Mining (KDD 2017), Halifax, NS, Canada, 13–17 August 2017; ACM: Halifax, NS, Canada, 2017; pp. 385–394. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 30th Annual Conference on Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Guyon, I., von Luxburg, U., Bengio, S., Wallach, H.M., Fergus, R., Vishwanathan, S.V.N., Garnett, R., Eds.; NeurIPS: Long Beach, CA, USA, 2017; pp. 1024–1034. [Google Scholar]
- Bojchevski, A.; Günnemann, S. Deep Gaussian Embedding of Graphs: Unsupervised Inductive Learning via Ranking. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018; OpenReview.net: Vancouver, BC, Canada, 2018. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? In Proceedings of the 7th International Conference on Learning Representations (ICLR 2019), New Orleans, LA, USA, 6–9 May 2019; OpenReview.net: New Orleans, LA, USA, 2019. [Google Scholar]
- Wang, X.; Ji, H.; Shi, C.; Wang, B.; Ye, Y.; Cui, P.; Yu, P.S. Heterogeneous Graph Attention Network. In Proceedings of the World Wide Web Conference (WWW 2019), San Francisco, CA, USA, 13–17 May 2019; ACM: San Francisco, CA, USA, 2019; pp. 2022–2032. [Google Scholar] [CrossRef]
- Velickovic, P.; Fedus, W.; Hamilton, W.L.; Liò, P.; Bengio, Y.; Hjelm, R.D. Deep Graph Infomax. In Proceedings of the 7th International Conference on Learning Representations (ICLR 2019), New Orleans, LA, USA, 6–9 May 2019; OpenReview.net: New Orleans, LA, USA, 2019. [Google Scholar]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph Neural Networks. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence (AAAI 2019), Honolulu, HI, USA, 27 January–1 February 2019; AAAI Press: Honolulu, HI, USA, 2019; pp. 3558–3565. [Google Scholar] [CrossRef]
- Chen, M.; Wei, Z.; Huang, Z.; Ding, B.; Li, Y. Simple and Deep Graph Convolutional Networks. In Proceedings of the 37th International Conference on Machine Learning (ICML 2020), Virtual Event, 13–18 July 2020; PMLR: Virtual Event, 2020; Volume 119, pp. 1725–1735. [Google Scholar]
- Dwivedi, V.P.; Bresson, X. A Generalization of Transformer Networks to Graphs. arXiv 2020, arXiv:2012.09699. [Google Scholar]
- Hussain, M.S.; Zaki, M.J.; Subramanian, D. Global Self-Attention as a Replacement for Graph Convolution. In Proceedings of the 28th Conference on Knowledge Discovery and Data Mining (KDD 2022), Washington, DC, USA, 14–18 August 2022; ACM: Washington, DC, USA, 2022; pp. 655–665. [Google Scholar] [CrossRef]
- Weisfeiler, B.; Leman, A. The reduction of a graph to canonical form and the algebra which appears therein. NTI Ser. 1968, 2, 12–16. [Google Scholar]
- Nikolentzos, G.; Siglidis, G.; Vazirgiannis, M. Graph Kernels: A Survey. J. Artif. Intell. Res. 2021, 72, 943–1027. [Google Scholar] [CrossRef]
- Shervashidze, N.; Schweitzer, P.; van Leeuwen, E.J.; Mehlhorn, K.; Borgwardt, K.M. Weisfeiler-Lehman Graph Kernels. J. Mach. Learn. Res. 2011, 12, 2539–2561. [Google Scholar]
- Morris, C.; Kersting, K.; Mutzel, P. Glocalized Weisfeiler-Lehman Graph Kernels: Global-Local Feature Maps of Graphs. In Proceedings of the International Conference on Data Mining (ICDM 2017), New Orleans, LA, USA, 18–21 November 2017; IEEE Computer Society: New Orleans, LA, USA, 2017; pp. 327–336. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Nguyen, C.H.; Mamitsuka, H. Learning Subtree Pattern Importance for Weisfeiler-Lehman Based Graph Kernels. Mach. Learn. 2021, 110, 1585–1607. [Google Scholar] [CrossRef]
- Ye, W.; Tian, H.; Chen, Q. Graph Kernels Based on Multi-scale Graph Embeddings. arXiv 2022, arXiv:2206.00979. [Google Scholar] [CrossRef]
- Orsini, F.; Frasconi, P.; Raedt, L.D. Graph Invariant Kernels. In Proceedings of the 24th International Joint Conference on Artificial Intelligence (IJCAI 2015), Buenos Aires, Argentina, 25–31 July 2015; AAAI Press: Buenos Aires, Argentina, 2015; pp. 3756–3762. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering. In Proceedings of the 14th Annual Conference on Neural Information Processing Systems (NIPS 2001), Vancouver, BC, Canada, 3–8 December 2001; Dietterich, T.G., Becker, S., Ghahramani, Z., Eds.; MIT Press: Vancouver, BC, Canada, 2001; pp. 585–591. [Google Scholar]
- Gong, C.; Tao, D.; Yang, J.; Fu, K. Signed Laplacian Embedding for Supervised Dimension Reduction. In Proceedings of the 28th Conference on Artificial Intelligence (AAAI 2014), Québec City, QC, Canada, 27–31 July 2014; AAAI Press: Québec City, QC, Canada, 2014; pp. 1847–1853. [Google Scholar]
- Allab, K.; Labiod, L.; Nadif, M. A Semi-NMF-PCA Unified Framework for Data Clustering. IEEE Trans. Knowl. Data Eng. 2017, 29, 2–16. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- He, X.; Niyogi, P. Locality Preserving Projections. In Proceedings of the 16th Neural Information Processing Systems (NIPS 2003), Vancouver and Whistler, BC, Canada, 8–13 December 2003; MIT Press: Vancouver/Whistler, BC, Canada, 2003; pp. 153–160. [Google Scholar]
- Zhang, J.; Dong, Y.; Wang, Y.; Tang, J.; Ding, M. ProNE: Fast and Scalable Network Representation Learning. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI 2019), Macao, China, 10–16 August 2019; ijcai.org: Macao, China, 2019; pp. 4278–4284. [Google Scholar] [CrossRef]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the International Joint Conference on Neural Networks (IJCNN 2005), Montreal, QC, Canada, 31 July–4 August 2005; IEEE: Montreal, QC, Canada, 2005; Volume 2, pp. 729–734. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Zhao, J.; Li, C.; Wen, Q.; Wang, Y.; Liu, Y.; Sun, H.; Xie, X.; Ye, Y. Gophormer: Ego-Graph Transformer for Node Classification. arXiv 2021, arXiv:2110.13094. [Google Scholar]
- Schmitt, M.; Ribeiro, L.F.R.; Dufter, P.; Gurevych, I.; Schütze, H. Modeling Graph Structure via Relative Position for Better Text Generation from Knowledge Graphs. arXiv 2020, arXiv:2006.09242. [Google Scholar]
- Zhang, C.; Swami, A.; Chawla, N.V. SHNE: Representation Learning for Semantic-Associated Heterogeneous Networks. In Proceedings of the 12th International Conference on Web Search and Data Mining (WSDM 2019), Melbourne, VIC, Australia, 11–15 February 2019; ACM: Melbourne, VIC, Australia, 2019; pp. 690–698. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, V.W.; Liu, Z.; Chang, K.C. Topological Recurrent Neural Network for Diffusion Prediction. In Proceedings of the International Conference on Data Mining (ICDM 2017), New Orleans, LA, USA, 18–21 November 2017; Raghavan, V., Aluru, S., Karypis, G., Miele, L., Wu, X., Eds.; IEEE Computer Society: New Orleans, LA, USA, 2017; pp. 475–484. [Google Scholar] [CrossRef]
- Wang, D.; Cui, P.; Zhu, W. Structural Deep Network Embedding. In Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining (SIGKDD 2016), San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1225–1234. [Google Scholar] [CrossRef]
- Tu, K.; Cui, P.; Wang, X.; Wang, F.; Zhu, W. Structural Deep Embedding for Hyper-Networks. In Proceedings of the 32nd Conference on Artificial Intelligence (AAAI 2018), New Orleans, LA, USA, 2–7 February 2018; AAAI Press: New Orleans, LA, USA, 2018; pp. 426–433. [Google Scholar]
- Chen, J.; Ma, T.; Xiao, C. FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018; OpenReview.net: Vancouver, BC, Canada, 2018. [Google Scholar]
- Zeng, H.; Zhou, H.; Srivastava, A.; Kannan, R.; Prasanna, V.K. GraphSAINT: Graph Sampling Based Inductive Learning Method. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020; OpenReview.net: Addis Ababa, Ethiopia, 2020. [Google Scholar]
- Jiang, H.; Cao, P.; Xu, M.; Yang, J.; Zaïane, O.R. Hi-GCN: A hierarchical graph convolution network for graph embedding learning of brain network and brain disorders prediction. Comput. Biol. Med. 2020, 127, 104096. [Google Scholar] [CrossRef]
- Li, R.; Huang, J. Learning Graph While Training: An Evolving Graph Convolutional Neural Network. arXiv 2017, arXiv:1708.04675. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. In Proceedings of the 2nd International Conference on Learning Representations (ICLR 2014), Banff, AB, Canada, 14–16 April 2014; ICLR: Banff, AB, Canada, 2014. [Google Scholar]
- Seo, M.; Lee, K.Y. A Graph Embedding Technique for Weighted Graphs Based on LSTM Autoencoders. J. Inf. Process. Syst. 2020, 16, 1407–1423. [Google Scholar] [CrossRef]
- Brody, S.; Alon, U.; Yahav, E. How Attentive are Graph Attention Networks? In Proceedings of the 10th International Conference on Learning Representations (ICLR 2022), Virtual Event, 25–29 April 2022; OpenReview.net: Virtual Event, 2022. [Google Scholar]
- Zhu, J.; Yan, Y.; Zhao, L.; Heimann, M.; Akoglu, L.; Koutra, D. Beyond Homophily in Graph Neural Networks: Current Limitations and Effective Designs. In Proceedings of the 33rd Annual Conference on Neural Information Processing Systems (NeurIPS 2020), Virtual Event, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; NeurIPS: Virtual Event, 2020. [Google Scholar]
- Suresh, S.; Budde, V.; Neville, J.; Li, P.; Ma, J. Breaking the Limit of Graph Neural Networks by Improving the Assortativity of Graphs with Local Mixing Patterns. In Proceedings of the 27th Conference on Knowledge Discovery and Data Mining (KDD 2021), Singapore, 14–18 August 2021; Zhu, F., Ooi, B.C., Miao, C., Eds.; ACM: Singapore, 2021; pp. 1541–1551. [Google Scholar] [CrossRef]
- Nguyen, D.Q.; Nguyen, T.D.; Phung, D. Universal Graph Transformer Self-Attention Networks. In Proceedings of the Companion Proceedings of the Web Conference 2022 (WWW 2022), Lyon, France, 25–29 April 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 193–196. [Google Scholar] [CrossRef]
- Zhu, J.; Li, J.; Zhu, M.; Qian, L.; Zhang, M.; Zhou, G. Modeling Graph Structure in Transformer for Better AMR-to-Text Generation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP 2019), Hong Kong, China, 3–7 November 2019; Association for Computational Linguistics: Hong Kong, China, 2019; pp. 5458–5467. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Xia, C.; Sun, L. Graph-Bert: Only Attention is Needed for Learning Graph Representations. arXiv 2020, arXiv:2001.05140. [Google Scholar]
- Shiv, V.L.; Quirk, C. Novel positional encodings to enable tree-based transformers. In Proceedings of the 32nd Annual Conference on Neural Information Processing Systems 2019 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; NeurIPS: Vancouver, BC, Canada, 2019; pp. 12058–12068. [Google Scholar]
- Wang, X.; Tu, Z.; Wang, L.; Shi, S. Self-Attention with Structural Position Representations. In Proceedings of the Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP 2019), Hong Kong, China, 3–7 November 2019; Association for Computational Linguistics: Hong Kong, China, 2019; pp. 1403–1409. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, Z.; Feng, S.; Zhong, H.; Wang, W.; Sun, Y. Masked Label Prediction: Unified Message Passing Model for Semi-Supervised Classification. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence (IJCAI 2021), Montreal, QC, Canada, 19–27 August 2021; Zhou, Z., Ed.; ijcai.org: Montreal, QC, Canada, 2021; pp. 1548–1554. [Google Scholar] [CrossRef]
- Ying, C.; Cai, T.; Luo, S.; Zheng, S.; Ke, G.; He, D.; Shen, Y.; Liu, T. Do Transformers Really Perform Badly for Graph Representation? In Proceedings of the 34th Annual Conference on Neural Information Processing Systems 2021 (NeurIPS 2021), Virtual Event, 6–14 December 2021; Ranzato, M., Beygelzimer, A., Dauphin, Y.N., Liang, P., Vaughan, J.W., Eds.; nips.cc: Virtual Event, 2021; pp. 28877–28888. [Google Scholar]
- Zhang, Y.; Wang, X.; Shi, C.; Jiang, X.; Ye, Y. Hyperbolic Graph Attention Network. IEEE Trans. Big Data 2022, 8, 1690–1701. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Shi, C.; Liu, N.; Song, G. Lorentzian Graph Convolutional Networks. In Proceedings of the The Web Conference (WWW 2021), Ljubljana, Slovenia, 19–23 April 2021; ACM/IW3C2: Ljubljana, Slovenia, 2021; pp. 1249–1261. [Google Scholar] [CrossRef]
- Nickel, M.; Kiela, D. Poincaré Embeddings for Learning Hierarchical Representations. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; nips.cc: Long Beach, CA, USA, 2017; pp. 6338–6347. [Google Scholar]
- Wang, X.; Zhang, Y.; Shi, C. Hyperbolic Heterogeneous Information Network Embedding. In Proceedings of the 33rd Conference on Artificial Intelligence (AAAI 2019), Honolulu, HI, USA, 27 January–1 February 2019; AAAI Press: Honolulu, HI, USA, 2019; pp. 5337–5344. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Variational Graph Auto-Encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Zhang, D.; Yin, J.; Zhu, X.; Zhang, C. Network Representation Learning: A Survey. IEEE Trans. Big Data 2020, 6, 3–28. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Representation Learning on Graphs: Methods and Applications. arXiv 2017, arXiv:1709.05584. [Google Scholar]
- Cai, H.; Zheng, V.W.; Chang, K.C. A Comprehensive Survey of Graph Embedding: Problems, Techniques, and Applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Y.; Liu, X.; Liu, Z.; Gao, J. Scalable Graph Embedding for Asymmetric Proximity. In Proceedings of the 31th Conference on Artificial Intelligence (AAAI 2017), San Francisco, CA, USA, 4–9 February 2017; AAAI Press: San Francisco, CA, USA, 2017; pp. 2942–2948. [Google Scholar]
- Man, T.; Shen, H.; Liu, S.; Jin, X.; Cheng, X. Predict Anchor Links across Social Networks via an Embedding Approach. In Proceedings of the 25th International Joint Conference on Artificial Intelligence (IJCAI 2016), New York, NY, USA, 9–15 July 2016; IJCAI/AAAI Press: New York, NY, USA, 2016; pp. 1823–1829. [Google Scholar]
- Gui, H.; Liu, J.; Tao, F.; Jiang, M.; Norick, B.; Han, J. Large-Scale Embedding Learning in Heterogeneous Event Data. In Proceedings of the 16th IEEE International Conference on Data Mining (ICDM 2016), Barcelona, Spain, 12–15 December 2016; IEEE Computer Society: Barcelona, Spain, 2016; pp. 907–912. [Google Scholar] [CrossRef]
- Goyal, P.; Ferrara, E. Graph embedding techniques, applications, and performance: A survey. Knowl.-Based Syst. 2018, 151, 78–94. [Google Scholar] [CrossRef]
- Casteigts, A.; Flocchini, P.; Quattrociocchi, W.; Santoro, N. Time-varying graphs and dynamic networks. Int. J. Parallel Emergent Distrib. Syst. 2012, 27, 387–408. [Google Scholar] [CrossRef]
- Li, J.; Dani, H.; Hu, X.; Tang, J.; Chang, Y.; Liu, H. Attributed Network Embedding for Learning in a Dynamic Environment. In Proceedings of the Conference on Information and Knowledge Management (CIKM 2017), Singapore, 6–10 November 2017; ACM: Singapore, 2017; pp. 387–396. [Google Scholar] [CrossRef]
- Chen, C.; Tao, Y.; Lin, H. Dynamic Network Embeddings for Network Evolution Analysis. arXiv 2019, arXiv:1906.09860. [Google Scholar]
- Shervashidze, N.; Vishwanathan, S.V.N.; Petri, T.; Mehlhorn, K.; Borgwardt, K.M. Efficient graphlet kernels for large graph comparison. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS 2009), Clearwater Beach, FL, USA, 16–18 April 2009; JMLR.org: Clearwater Beach, FL, USA, 2009; Volume 5, pp. 488–495. [Google Scholar]
- Togninalli, M.; Ghisu, M.E.; Llinares-López, F.; Rieck, B.; Borgwardt, K.M. Wasserstein Weisfeiler-Lehman Graph Kernels. In Proceedings of the 32nd Annual Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; NeurIPS: Vancouver, BC, Canada, 2019; pp. 6436–6446. [Google Scholar]
- Kang, U.; Tong, H.; Sun, J. Fast Random Walk Graph Kernel. In Proceedings of the 12th International Conference on Data Mining (ICDM 2012), Anaheim, CA, USA, 26–28 April 2012; SIAM/Omnipress: Anaheim, CA, USA, 2012; pp. 828–838. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, P.; Wang, X.; Pei, J.; Yao, X.; Zhu, W. Arbitrary-Order Proximity Preserved Network Embedding. In Proceedings of the 24th International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; ACM: London, UK, 2018; pp. 2778–2786. [Google Scholar] [CrossRef]
- Dareddy, M.R.; Das, M.; Yang, H. motif2vec: Motif Aware Node Representation Learning for Heterogeneous Networks. In Proceedings of the International Conference on Big Data (IEEE BigData), Los Angeles, CA, USA, 9–12 December 2019; IEEE: Los Angeles, CA, USA, 2019; pp. 1052–1059. [Google Scholar] [CrossRef]
- Tu, K.; Li, J.; Towsley, D.; Braines, D.; Turner, L.D. gl2vec: Learning feature representation using graphlets for directed networks. In Proceedings of the 19th International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2019), Vancouver, BC, Canada, 27–30 August 2019; ACM: Vancouver, BC, Canada, 2019; pp. 216–221. [Google Scholar] [CrossRef]
- Yu, Y.; Lu, Z.; Liu, J.; Zhao, G.; Wen, J. RUM: Network Representation Learning Using Motifs. In Proceedings of the 35th International Conference on Data Engineering (ICDE 2019), Macao, China, 8–11 April 2019; IEEE: Macao, China, 2019; pp. 1382–1393. [Google Scholar] [CrossRef]
- Hu, Q.; Lin, F.; Wang, B.; Li, C. MBRep: Motif-Based Representation Learning in Heterogeneous Networks. Expert Syst. Appl. 2022, 190, 116031. [Google Scholar] [CrossRef]
- Shao, P.; Yang, Y.; Xu, S.; Wang, C. Network Embedding via Motifs. ACM Trans. Knowl. Discov. Data 2021, 16, 44. [Google Scholar] [CrossRef]
- De Winter, S.; Decuypere, T.; Mitrović, S.; Baesens, B.; De Weerdt, J. Combining Temporal Aspects of Dynamic Networks with Node2Vec for a More Efficient Dynamic Link Prediction. In Proceedings of the International Conference on Advances in Social Networks Analysis and Mining (IEEE/ACM 2018), Barcelona, Spain, 28–31 August 2018; IEEE Press: Barcelona, Spain, 2018; pp. 1234–1241. [Google Scholar]
- Huang, X.; Song, Q.; Li, Y.; Hu, X. Graph Recurrent Networks With Attributed Random Walks. In Proceedings of the 25th International Conference on Knowledge Discovery & Data Mining (KDD 2019), Anchorage, AK, USA, 4–8 August 2019; ACM: Anchorage, AK, USA, 2019; pp. 732–740. [Google Scholar] [CrossRef]
- Sperduti, A.; Starita, A. Supervised neural networks for the classification of structures. IEEE Trans. Neural Netw. 1997, 8, 714–735. [Google Scholar] [CrossRef] [PubMed]
- Chiang, W.; Liu, X.; Si, S.; Li, Y.; Bengio, S.; Hsieh, C. Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks. In Proceedings of the 25th International Conference on Knowledge Discovery & Data Mining (KDD 2019), Anchorage, AK, USA, 4–8 August 2019; ACM: Anchorage, AK, USA, 2019; pp. 257–266. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. In Proceedings of the 29th Annual Conference on Neural Information Processing Systems (NeurIPS 2016), Barcelona, Spain, 5–10 December 2016; NeurIPS: Barcelona, Spain, 2016; pp. 3837–3845. [Google Scholar]
- Li, Q.; Han, Z.; Wu, X. Deeper Insights Into Graph Convolutional Networks for Semi-Supervised Learning. In Proceedings of the 32nd Conference on Artificial Intelligence (AAAI-18), New Orleans, LA, USA, 2–7 February 2018; McIlraith, S.A., Weinberger, K.Q., Eds.; AAAI Press: New Orleans, LA, USA, 2018; pp. 3538–3545. [Google Scholar]
- Li, G.; Xiong, C.; Thabet, A.K.; Ghanem, B. DeeperGCN: All You Need to Train Deeper GCNs. arXiv 2020, arXiv:2006.07739. [Google Scholar]
- Lin, K.; Wang, L.; Liu, Z. Mesh Graphormer. In Proceedings of the International Conference on Computer Vision (ICCV 2021), Montreal, QC, Canada, 10–17 October 2021; IEEE: Montreal, QC, Canada, 2021; pp. 12919–12928. [Google Scholar] [CrossRef]
- Rong, Y.; Bian, Y.; Xu, T.; Xie, W.; Wei, Y.; Huang, W.; Huang, J. Self-Supervised Graph Transformer on Large-Scale Molecular Data. In Proceedings of the 34th Annual Conference on Neural Information Processing Systems (NeurIPS 2020), Virtual Event, 6–12 December 2020; NeurIPS: Virtual event, 2020. [Google Scholar]
- Yao, S.; Wang, T.; Wan, X. Heterogeneous Graph Transformer for Graph-to-Sequence Learning. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (ACL 2020), Virtual Event, 5–10 July 2020; ACL: Virtual Event, 2020; pp. 7145–7154. [Google Scholar] [CrossRef]
- Nickel, M.; Kiela, D. Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry. In Proceedings of the 35th International Conference on Machine Learning (ICML 2018), Stockholm, Sweden, 10–15 July 2018; mlr.press: Stockholm, Sweden, 2018; Volume 80, pp. 3776–3785. [Google Scholar]
- Cao, Z.; Xu, Q.; Yang, Z.; Cao, X.; Huang, Q. Geometry Interaction Knowledge Graph Embeddings. In Proceedings of the 36th Conference on Artificial Intelligence (AAAI 2022), Virtual Event, 22 February–1 March 2022; AAAI Press: Virtual Event, 2022; pp. 5521–5529. [Google Scholar]
- Santos, L.D.; Piwowarski, B.; Gallinari, P. Multilabel Classification on Heterogeneous Graphs with Gaussian Embeddings. In Proceedings of the Machine Learning and Knowledge Discovery in Databases—European Conference (ECML PKDD 2016), Riva del Garda, Italy, 19–23 September 2016; Springer: Riva del Garda, Italy, 2016; Volume 9852, pp. 606–622. [Google Scholar] [CrossRef]
- Kriege, N.M. Comparing Graphs: Algorithms & Applications. Ph.D. Thesis, Technische Universität, Dortmund, Germany, 2015. [Google Scholar]
- Kondor, R.; Shervashidze, N.; Borgwardt, K.M. The graphlet spectrum. In Proceedings of the 26th Annual International Conference on Machine Learning (ICML 2009), Montreal, QC, Canada, 14–18 June 2009; ACM: Montreal, QC, Canada, 2009; Volume 382, pp. 529–536. [Google Scholar] [CrossRef]
- Feragen, A.; Kasenburg, N.; Petersen, J.; de Bruijne, M.; Borgwardt, K.M. Scalable kernels for graphs with continuous attributes. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems (NeurIPS 2013), Lake Tahoe, NV, USA, 5–8 December 2013; Burges, C.J.C., Bottou, L., Ghahramani, Z., Weinberger, K.Q., Eds.; NeurIPS: Lake Tahoe, NV, USA, 2013; pp. 216–224. [Google Scholar]
- Morris, C.; Kriege, N.M.; Kersting, K.; Mutzel, P. Faster Kernels for Graphs with Continuous Attributes via Hashing. In Proceedings of the 16th International Conference on Data Mining (ICDM 2016), Barcelona, Spain, 12–15 December 2016; IEEE Computer Society: Barcelona, Spain, 2016; pp. 1095–1100. [Google Scholar] [CrossRef]
- Borgwardt, K.M.; Kriegel, H. Shortest-Path Kernels on Graphs. In Proceedings of the 5th International Conference on Data Mining (ICDM 2005), Houston, TX, USA, 27–30 November 2005; IEEE Computer Society: Houston, TX, USA, 2005; pp. 74–81. [Google Scholar] [CrossRef]
- Kashima, H.; Tsuda, K.; Inokuchi, A. Marginalized Kernels Between Labeled Graphs. In Proceedings of the 20th International Conference Machine Learning (ICML 2003), Washington, DC, USA, 21–24 August 2003; AAAI Press: Washington, DC, USA, 2003; pp. 321–328. [Google Scholar]
- Rahman, M.; Hasan, M.A. Link Prediction in Dynamic Networks Using Graphlet. In Proceedings of the Machine Learning and Knowledge Discovery in Databases—European Conference (ECML PKDD 2016), Riva del Garda, Italy, 19–23 September 2016; Springer: Riva del Garda, Italy, 2016; Volume 9851, pp. 394–409. [Google Scholar] [CrossRef]
- Rahman, M.; Saha, T.K.; Hasan, M.A.; Xu, K.S.; Reddy, C.K. DyLink2Vec: Effective Feature Representation for Link Prediction in Dynamic Networks. arXiv 2018, arXiv:1804.05755. [Google Scholar]
- Béres, F.; Kelen, D.M.; Pálovics, R.; Benczúr, A.A. Node embeddings in dynamic graphs. Appl. Netw. Sci. 2019, 4, 64.1–64.25. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn Distances: Lightspeed Computation of Optimal Transport. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems (NeurIPS 2013), Lake Tahoe, NV, USA, 5–8 December 2013; NeurIPS: Lake Tahoe, NV, USA, 2013; pp. 2292–2300. [Google Scholar]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. ACM 1962, 5, 345. [Google Scholar] [CrossRef]
- Kriege, N.M.; Johansson, F.D.; Morris, C. A survey on graph kernels. Appl. Netw. Sci. 2020, 5, 6. [Google Scholar] [CrossRef]
- Urry, M.; Sollich, P. Random walk kernels and learning curves for Gaussian process regression on random graphs. J. Mach. Learn. Res. 2013, 14, 1801–1835. [Google Scholar]
- Bunke, H.; Irniger, C.; Neuhaus, M. Graph Matching—Challenges and Potential Solutions. In Proceedings of the 13th Image Analysis and Processing— International Conference (ICIAP 2005), Cagliari, Italy, 6–8 September 2005; Springer: Cagliari, Italy, 2005; Volume 3617, pp. 1–10. [Google Scholar] [CrossRef]
- Hofmann, T.; Buhmann, J.M. Multidimensional Scaling and Data Clustering. In Proceedings of the 7th Advances in Neural Information Processing Systems (NIPS 1994), Denver, CO, USA, 1 January 1994; Tesauro, G., Touretzky, D.S., Leen, T.K., Eds.; MIT Press: Denver, CO, USA, 1994; pp. 459–466. [Google Scholar]
- Han, Y.; Shen, Y. Partially Supervised Graph Embedding for Positive Unlabelled Feature Selection. In Proceedings of the 25th International Joint Conference on Artificial Intelligence (IJCAI 2016), New York, NY, USA, 9–15 July 2016; IJCAI/AAAI Press: New York, NY, USA, 2016; pp. 1548–1554. [Google Scholar]
- Cai, D.; He, X.; Han, J. Spectral regression: A unified subspace learning framework for content-based image retrieval. In Proceedings of the 15th International Conference on Multimedia 2007 (ICM 2007), Augsburg, Germany, 24–29 September 2007; ACM: Augsburg, Germany, 2007; pp. 403–412. [Google Scholar] [CrossRef]
- Torres, L.; Chan, K.S.; Eliassi-Rad, T. GLEE: Geometric Laplacian Eigenmap Embedding. J. Complex Netw. 2020, 8, cnaa007. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Zhang, T.; Zhang, J.; Chang, Y. Learning Network Embedding with Community Structural Information. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI 2019), Macao, China, 10–16 August 2019; ijcai.org: Macao, China, 2019; pp. 2937–2943. [Google Scholar] [CrossRef]
- Coskun, M. A high order proximity measure for linear network embedding. NiğDe öMer Halisdemir üNiversitesi MüHendislik Bilim. Derg. 2022, 11, 477–483. [Google Scholar] [CrossRef]
- Ahmed, A.; Shervashidze, N.; Narayanamurthy, S.M.; Josifovski, V.; Smola, A.J. Distributed large-scale natural graph factorization. In Proceedings of the 22nd International World Wide Web Conference (WWW 2013), Rio de Janeiro, Brazil, 13–17 May 2013; International World Wide Web Conferences Steering Committee/ACM: Rio de Janeiro, Brazil, 2013; pp. 37–48. [Google Scholar] [CrossRef]
- Lian, D.; Zhu, Z.; Zheng, K.; Ge, Y.; Xie, X.; Chen, E. Network Representation Lightening from Hashing to Quantization. IEEE Trans. Knowl. Data Eng. 2022, 35, 5119–5131. [Google Scholar] [CrossRef]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web; Technical Report 1999-66; Previous number = SIDL-WP-1999-0120; Stanford InfoLab: Stanford, CA, USA, 1999. [Google Scholar]
- Adamic, L.A.; Adar, E. Friends and neighbors on the Web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Z.; Sun, M. Representation Learning for Measuring Entity Relatedness with Rich Information. In Proceedings of the 24th International Joint Conference on Artificial Intelligence (IJCAI 2015), Buenos Aires, Argentina, 25–31 July 2015; AAAI Press: Buenos Aires, Argentina, 2015; pp. 1412–1418. [Google Scholar]
- Yang, C.; Liu, Z.; Zhao, D.; Sun, M.; Chang, E.Y. Network Representation Learning with Rich Text Information. In Proceedings of the 24th International Joint Conference on Artificial Intelligence (IJCAI 2015), Buenos Aires, Argentina, 25–31 July 2015; AAAI Press: Buenos Aires, Argentina, 2015; pp. 2111–2117. [Google Scholar]
- Yang, R.; Shi, J.; Xiao, X.; Yang, Y.; Bhowmick, S.S. Homogeneous Network Embedding for Massive Graphs via Reweighted Personalized PageRank. Proc. Vldb Endow. 2020, 13, 670–683. [Google Scholar] [CrossRef]
- Qiu, J.; Dong, Y.; Ma, H.; Li, J.; Wang, C.; Wang, K.; Tang, J. NetSMF: Large-Scale Network Embedding as Sparse Matrix Factorization. In Proceedings of the World Wide Web Conference (WWW 2019), San Francisco, CA, USA, 13–17 May 2019; ACM: New York, NY, USA, 2019; pp. 1509–1520. [Google Scholar] [CrossRef]
- Rossi, R.A.; Gallagher, B.; Neville, J.; Henderson, K. Modeling dynamic behavior in large evolving graphs. In Proceedings of the 6th International Conference on Web Search and Data Mining (WSDM 2013), Rome, Italy, 4–8 February 2013; ACM: Rome, Italy, 2013; pp. 667–676. [Google Scholar] [CrossRef]
- Yu, W.; Aggarwal, C.C.; Wang, W. Temporally Factorized Network Modeling for Evolutionary Network Analysis. In Proceedings of the 10th International Conference on Web Search and Data Mining (WSDM 2017), Cambridge, UK, 6–10 February 2017; ACM: Cambridge, UK, 2017; pp. 455–464. [Google Scholar] [CrossRef]
- Zhu, L.; Guo, D.; Yin, J.; Steeg, G.V.; Galstyan, A. Scalable Temporal Latent Space Inference for Link Prediction in Dynamic Social Networks. IEEE Trans. Knowl. Data Eng. 2016, 28, 2765–2777. [Google Scholar] [CrossRef]
- Yu, W.; Cheng, W.; Aggarwal, C.C.; Chen, H.; Wang, W. Link Prediction with Spatial and Temporal Consistency in Dynamic Networks. In Proceedings of the 26th International Joint Conference on Artificial Intelligence (IJCAI 2017), Melbourne, Australia, 19–25 August 2017; ijcai.org: Melbourne, Australia, 2017; pp. 3343–3349. [Google Scholar] [CrossRef]
- Chen, H.; Yin, H.; Wang, W.; Wang, H.; Nguyen, Q.V.H.; Li, X. PME: Projected Metric Embedding on Heterogeneous Networks for Link Prediction. In Proceedings of the 24th International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; ACM: London, UK, 2018; pp. 1177–1186. [Google Scholar] [CrossRef]
- Xu, L.; Wei, X.; Cao, J.; Yu, P.S. Embedding of Embedding (EOE): Joint Embedding for Coupled Heterogeneous Networks. In Proceedings of the 10th International Conference on Web Search and Data Mining (WSDM 2017), Cambridge, UK, 6–10 February 2017; ACM: Cambridge, UK, 2017; pp. 741–749. [Google Scholar] [CrossRef]
- Shi, Y.; Gui, H.; Zhu, Q.; Kaplan, L.M.; Han, J. AspEm: Embedding Learning by Aspects in Heterogeneous Information Networks. In Proceedings of the International Conference on Data Mining (SDM 2018), San Diego, CA, USA, 3–5 May 2018; SIAM: San Diego, CA, USA, 2018; pp. 144–152. [Google Scholar] [CrossRef]
- Matsuno, R.; Murata, T. MELL: Effective Embedding Method for Multiplex Networks. In Proceedings of the Companion Proceedings of the Web Conference 2018 (WWW 2018), Lyon, France, 23–27 April 2018; International World Wide Web Conferences Steering Committee: Geneva, Switzerland; ACM: Lyon, France, 2018; pp. 1261–1268. [Google Scholar] [CrossRef]
- Ren, X.; He, W.; Qu, M.; Voss, C.R.; Ji, H.; Han, J. Label Noise Reduction in Entity Typing by Heterogeneous Partial-Label Embedding. In Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining (KDD 2016), San Francisco, CA, USA, 13–17 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 1825–1834. [Google Scholar] [CrossRef]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D Knowledge Graph Embeddings. In Proceedings of the 32nd Conference on Artificial Intelligence (AAAI 2018), New Orleans, LA, USA, 2–7 February 2018; AAAI Press: New Orleans, LA, USA, 2018; pp. 1811–1818. [Google Scholar]
- Safavi, T.; Koutra, D. CoDEx: A Comprehensive Knowledge Graph Completion Benchmark. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP 2020), Virtual Event, 16–20 November 2020; Webber, B., Cohn, T., He, Y., Liu, Y., Eds.; ACL: Virtual Event, 2020; pp. 8328–8350. [Google Scholar] [CrossRef]
- Narayanan, A.; Chandramohan, M.; Chen, L.; Liu, Y.; Saminathan, S. subgraph2vec: Learning Distributed Representations of Rooted Sub-graphs from Large Graphs. arXiv 2016, arXiv:1606.08928. [Google Scholar]
- Wang, C.; Wang, C.; Wang, Z.; Ye, X.; Yu, P.S. Edge2vec: Edge-based Social Network Embedding. ACM Trans. Knowl. Discov. Data 2020, 14, 45.1–45.24. [Google Scholar] [CrossRef]
- Perozzi, B.; Kulkarni, V.; Chen, H.; Skiena, S. Don’t Walk, Skip!: Online Learning of Multi-scale Network Embeddings. In Proceedings of the International Conference on Advances in Social Networks Analysis and Mining 2017 (ASONAM 2017), Sydney, Australia, 31 July–3 August 2017; ACM: Sydney, Australia, 2017; pp. 258–265. [Google Scholar] [CrossRef]
- Liu, R.; Hirn, M.J.; Krishnan, A. Accurately Modeling Biased Random Walks on Weighted Graphs Using Node2vec+. arXiv 2021, arXiv:2109.08031. [Google Scholar]
- Jeong, J.; Yun, J.; Keam, H.; Park, Y.; Park, Z.; Cho, J. div2vec: Diversity-Emphasized Node Embedding. In Proceedings of the 14th Workshops on Recommendation in Complex Scenarios and the Impact of Recommender Systems co-located with 14th ACM Conference on Recommender Systems (RecSys 2020), Virtual Event, 25 September 2020; CEUR-WS.org: Virtual Event, 2020; Volume 2697. [Google Scholar]
- Zhang, Y.; Shi, Z.; Feng, D.; Zhan, X.X. Degree-Biased Random Walk for Large-Scale Network Embedding. Future Gener. Comput. Syst. 2019, 100, 198–209. [Google Scholar] [CrossRef]
- Ahmed, N.K.; Rossi, R.A.; Lee, J.B.; Willke, T.L.; Zhou, R.; Kong, X.; Eldardiry, H. Role-Based Graph Embeddings. IEEE Trans. Knowl. Data Eng. 2022, 34, 2401–2415. [Google Scholar] [CrossRef]
- Khosla, M.; Leonhardt, J.; Nejdl, W.; Anand, A. Node Representation Learning for Directed Graphs. In Proceedings of the Machine Learning and Knowledge Discovery in Databases—European Conference (ECML PKDD 2019), Dublin, Ireland, 10–14 September 2018; Springer: Würzburg, Germany, 2019; Volume 11906, pp. 395–411. [Google Scholar] [CrossRef]
- Adhikari, B.; Zhang, Y.; Ramakrishnan, N.; Prakash, B.A. Sub2Vec: Feature Learning for Subgraphs. In Proceedings of the 22nd Advances in Knowledge Discovery and Data Mining - Pacific-Asia Conference (PAKDD 2018), Melbourne, VIC, Australia, 3–6 June 2018; Springer: Melbourne, VIC, Australia, 2018; Volume 10938, pp. 170–182. [Google Scholar] [CrossRef]
- Sheikh, N.; Kefato, Z.; Montresor, A. Gat2vec: Representation Learning for Attributed Graphs. Computing 2019, 101, 187–209. [Google Scholar] [CrossRef]
- Dou, W.; Zhang, W.; Weng, Z. An Attributed Network Representation Learning Method Based on Biased Random Walk. Procedia Comput. Sci. 2020, 174, 291–298. [Google Scholar] [CrossRef]
- Narayanan, A.; Chandramohan, M.; Venkatesan, R.; Chen, L.; Liu, Y.; Jaiswal, S. graph2vec: Learning Distributed Representations of Graphs. arXiv 2017, arXiv:1707.05005. [Google Scholar]
- Yang, D.; Qu, B.; Yang, J.; Cudré-Mauroux, P. Revisiting User Mobility and Social Relationships in LBSNs: A Hypergraph Embedding Approach. In Proceedings of the The World Wide Web Conference (WWW 2019), San Francisco, CA, USA, 13–17 May 2019; ACM: San Francisco, CA, USA, 2019; pp. 2147–2157. [Google Scholar] [CrossRef]
- Zhu, Y.; Guan, Z.; Tan, S.; Liu, H.; Cai, D.; He, X. Heterogeneous hypergraph embedding for document recommendation. Neurocomputing 2016, 216, 150–162. [Google Scholar] [CrossRef]
- Hussein, R.; Yang, D.; Cudré-Mauroux, P. Are Meta-Paths Necessary?: Revisiting Heterogeneous Graph Embeddings. In Proceedings of the 27th International Conference on Information and Knowledge Management (CIKM 2018), Torino, Italy, 22–26 October 2018; ACM: Torino, Italy, 2018; pp. 437–446. [Google Scholar] [CrossRef]
- Zhang, H.; Qiu, L.; Yi, L.; Song, Y. Scalable Multiplex Network Embedding. In Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI 2018), Stockholm, Sweden, 13–19 July 2018; ijcai.org: Stockholm, Sweden, 2018; pp. 3082–3088. [Google Scholar] [CrossRef]
- Lee, S.; Park, C.; Yu, H. BHIN2vec: Balancing the Type of Relation in Heterogeneous Information Network. In Proceedings of the 28th International Conference on Information and Knowledge Management (CIKM 2019), Beijing, China, 3–7 November 2019; ACM: Beijing, China, 2019; pp. 619–628. [Google Scholar] [CrossRef]
- Li, Y.; Patra, J.C. Genome-wide inferring gene-phenotype relationship by walking on the heterogeneous network. Bioinformatics 2010, 26, 1219–1224. [Google Scholar] [CrossRef] [PubMed]
- Joodaki, M.; Ghadiri, N.; Maleki, Z.; Shahreza, M.L. A scalable random walk with restart on heterogeneous networks with Apache Spark for ranking disease-related genes through type-II fuzzy data fusion. J. Biomed. Informatics 2021, 115, 103688. [Google Scholar] [CrossRef]
- Tian, Z.; Guo, M.; Wang, C.; Xing, L.; Wang, L.; Zhang, Y. Constructing an integrated gene similarity network for the identification of disease genes. In Proceedings of the International Conference on Bioinformatics and Biomedicine (BIBM 2016), Shenzhen, China, 15–18 December 2016; IEEE Computer Society: Shenzhen, China, 2016; pp. 1663–1668. [Google Scholar] [CrossRef]
- Luo, J.; Liang, S. Prioritization of potential candidate disease genes by topological similarity of protein-protein interaction network and phenotype data. J. Biomed. Sci. 2015, 53, 229–236. [Google Scholar] [CrossRef]
- Lee, O.-J.; Jeon, H.; Jung, J.J. Learning multi-resolution representations of research patterns in bibliographic networks. J. Inf. 2021, 15, 101126. [Google Scholar] [CrossRef]
- Du, B.; Tong, H. MrMine: Multi-resolution Multi-network Embedding. In Proceedings of the 28th International Conference on Information and Knowledge Management (CIKM 2019), Beijing, China, 3–7 November 2019; ACM: Beijing, China, 2019; pp. 479–488. [Google Scholar] [CrossRef]
- Lee, O.-J.; Jung, J.J. Story embedding: Learning distributed representations of stories based on character networks. Artif. Intell. 2020, 281, 103235. [Google Scholar] [CrossRef]
- Sajjad, H.P.; Docherty, A.; Tyshetskiy, Y. Efficient Representation Learning Using Random Walks for Dynamic Graphs. arXiv 2019, arXiv:1901.01346. [Google Scholar]
- Heidari, F.; Papagelis, M. EvoNRL: Evolving Network Representation Learning Based on Random Walks. In Proceedings of the 7th International Conference on Complex Networks and Their Applications (COMPLEX NETWORKS 2018), Cambridge, UK, 11–13 December 2018; Springer: Cambridge, UK, 2018; Volume 812, pp. 457–469. [Google Scholar] [CrossRef]
- Nguyen, G.H.; Lee, J.B.; Rossi, R.A.; Ahmed, N.K.; Koh, E.; Kim, S. Continuous-Time Dynamic Network Embeddings. In Proceedings of the Companion of The Web Conference (WWW 2018), Lyon, France, 23–27 April 2018; ACM: Lyon, France, 2018; pp. 969–976. [Google Scholar] [CrossRef]
- Pandhre, S.; Mittal, H.; Gupta, M.; Balasubramanian, V.N. STwalk: Learning trajectory representations in temporal graphs. In Proceedings of the India Joint International Conference on Data Science and Management of Data (COMAD/CODS 2018), Goa, India, 11–13 January 2018; ACM: Goa, India, 2018; pp. 210–219. [Google Scholar] [CrossRef]
- Singer, U.; Guy, I.; Radinsky, K. Node Embedding over Temporal Graphs. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI 2019), Macao, China, 10–16 August 2019; ijcai.org: Macao, China, 2019; pp. 4605–4612. [Google Scholar] [CrossRef]
- Mahdavi, S.; Khoshraftar, S.; An, A. dynnode2vec: Scalable Dynamic Network Embedding. In Proceedings of the International Conference on Big Data (IEEE BigData 2018), Seattle, WA, USA, 10–13 December 2018; IEEE: Seattle, WA, USA, 2018; pp. 3762–3765. [Google Scholar] [CrossRef]
- Lin, D.; Wu, J.; Yuan, Q.; Zheng, Z. T-EDGE: Temporal WEighted MultiDiGraph Embedding for Ethereum Transaction Network Analysis. Front. Phys. 2020, 8, 204. [Google Scholar] [CrossRef]
- Lee, O.-J.; Jung, J.J.; Kim, J. Learning Hierarchical Representations of Stories by Using Multi-Layered Structures in Narrative Multimedia. Sensors 2020, 20, 1978. [Google Scholar] [CrossRef] [PubMed]
- Lee, O.-J.; Jung, J.J. Story Embedding: Learning Distributed Representations of Stories based on Character Networks (Extended Abstract). In Proceedings of the 29th International Joint Conference on Artificial Intelligence (IJCAI 2020), Yokohama, Japan, 7–15 January 2021; Bessiere, C., Ed.; ijcai.org: Yokohama, Japan, 2020; pp. 5070–5074. [Google Scholar] [CrossRef]
- Chen, H.; Perozzi, B.; Hu, Y.; Skiena, S. HARP: Hierarchical Representation Learning for Networks. In Proceedings of the 32nd Conference on Artificial Intelligence (AAAI-18), New Orleans, LA, USA, 2–7 February 2018; AAAI Press: New Orleans, LA, USA, 2018; pp. 2127–2134. [Google Scholar]
- Tang, J.; Qu, M.; Mei, Q. PTE: Predictive Text Embedding through Large-scale Heterogeneous Text Networks. In Proceedings of the 21th International Conference on Knowledge Discovery and Data Mining (SIGKDD 2015), Sydney, Australia, 10–13 August 2015; ACM: Sydney, Australia, 2015; pp. 1165–1174. [Google Scholar] [CrossRef]
- Fu, T.; Lee, W.; Lei, Z. HIN2Vec: Explore Meta-paths in Heterogeneous Information Networks for Representation Learning. In Proceedings of the Conference on Information and Knowledge Management (CIKM 2017), Singapore, 6–10 November 2017; ACM: Singapore, 2017; pp. 1797–1806. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Wei, X.; Xu, L.; Cao, B.; Yu, P.S. Cross View Link Prediction by Learning Noise-resilient Representation Consensus. In Proceedings of the 26th International Conference on World Wide Web (WWW 2017), Perth, Australia, 3–7 April 2017; ACM: Perth, Australia, 2017; pp. 1611–1619. [Google Scholar] [CrossRef]
- Liu, L.; Cheung, W.K.; Li, X.; Liao, L. Aligning Users across Social Networks Using Network Embedding. In Proceedings of the 25th International Joint Conference on Artificial Intelligence (IJCAI 2016), New York, NY, USA, 9–15 July 2016; IJCAI/AAAI Press: New York, NY, USA, 2016; pp. 1774–1780. [Google Scholar]
- Wang, S.; Tang, J.; Aggarwal, C.C.; Chang, Y.; Liu, H. Signed Network Embedding in Social Media. In Proceedings of the International Conference on Data Mining (SIAM 2017), Houston, Texas, USA, 27–29 April 2017; SIAM: Houston, TX, USA, 2017; pp. 327–335. [Google Scholar] [CrossRef]
- Huang, Z.; Mamoulis, N. Heterogeneous Information Network Embedding for Meta Path based Proximity. arXiv 2017, arXiv:1701.05291. [Google Scholar]
- Zhang, Q.; Wang, H. Not All Links Are Created Equal: An Adaptive Embedding Approach for Social Personalized Ranking. In Proceedings of the 39th International Conference on Research and Development in Information Retrieval (SIGIR 2016), Pisa, Italy, 17–21 July 2016; ACM: Pisa, Italy, 2016; pp. 917–920. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Z.; Song, G.; Fan, Y.; Du, L.; Lin, W. Tag2Vec: Learning Tag Representations in Tag Networks. In Proceedings of the World Wide Web Conference (WWW 2019), San Francisco, CA, USA, 13–17 May 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 3314–3320. [Google Scholar] [CrossRef]
- Fu, G.; Yuan, B.; Duan, Q.; Yao, X. Representation Learning for Heterogeneous Information Networks via Embedding Events. In Proceedings of the 26th International Conference (ICONIP 2019), Sydney, Australia, 12–15 December 2019; Springer: Sydney, Australia, 2019; Volume 11953, pp. 327–339. [Google Scholar] [CrossRef]
- Wu, X.; Pang, H.; Fan, Y.; Linghu, Y.; Luo, Y. ProbWalk: A random walk approach in weighted graph embedding. In Proceedings of the 10th International Conference of Information and Communication Technology (ICICT 2020), Wuhan, China, 13–15 November 2020; Elsevier Procedia: Wuhan, China, 2021; Volume 183, pp. 683–689. [Google Scholar] [CrossRef]
- Li, Q.; Cao, Z.; Zhong, J.; Li, Q. Graph Representation Learning with Encoding Edges. Neurocomputing 2019, 361, 29–39. [Google Scholar] [CrossRef]
- Li, Q.; Zhong, J.; Li, Q.; Cao, Z.; Wang, C. Enhancing Network Embedding with Implicit Clustering. In Proceedings of the 24th Database Systems for Advanced Applications (DASFAA 2019), Chiang Mai, Thailand, 22–25 April 2019; Springer: Chiang Mai, Thailand, 2019; Volume 11446, pp. 452–467. [Google Scholar] [CrossRef]
- Gao, H.; Huang, H. Deep Attributed Network Embedding. In Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI 2018), Stockholm, Sweden, 13–19 July 2018; Lang, J., Ed.; ijcai.org: Stockholm, Sweden, 2018; pp. 3364–3370. [Google Scholar] [CrossRef]
- Sun, X.; Guo, J.; Ding, X.; Liu, T. A General Framework for Content-enhanced Network Representation Learning. arXiv 2016, arXiv:1610.02906. [Google Scholar]
- Zhang, D.; Yin, J.; Zhu, X.; Zhang, C. Homophily, Structure, and Content Augmented Network Representation Learning. In Proceedings of the 16th International Conference on Data Mining (ICDM 2016), Barcelona, Spain, 12–15 December 2016; Bonchi, F., Domingo-Ferrer, J., Baeza-Yates, R., Zhou, Z., Wu, X., Eds.; IEEE Computer Society: Barcelona, Spain, 2016; pp. 609–618. [Google Scholar] [CrossRef]
- Chen, H.; Anantharam, A.R.; Skiena, S. DeepBrowse: Similarity-Based Browsing Through Large Lists (Extended Abstract). In Proceedings of the 10th International Conference on Similarity Search and Applications (SISAP 2017), Munich, Germany, 4–6 October 2017; Beecks, C., Borutta, F., Kröger, P., Seidl, T., Eds.; Springer: Munich, Germany, 2017; Volume 10609, pp. 300–314. [Google Scholar] [CrossRef]
- Cao, S.; Lu, W.; Xu, Q. Deep Neural Networks for Learning Graph Representations. In Proceedings of the 30th Conference on Artificial Intelligence (AAAI 2016), Phoenix, AZ, USA, 12–17 February 2016; Schuurmans, D., Wellman, M.P., Eds.; AAAI Press: Phoenix, AZ, USA, 2016; pp. 1145–1152. [Google Scholar]
- Shen, X.; Chung, F. Deep Network Embedding for Graph Representation Learning in Signed Networks. Trans. Cybern. 2020, 50, 1556–1568. [Google Scholar] [CrossRef]
- Goyal, P.; Kamra, N.; He, X.; Liu, Y. DynGEM: Deep Embedding Method for Dynamic Graphs. arXiv 2018, arXiv:1805.11273. [Google Scholar]
- Yu, W.; Cheng, W.; Aggarwal, C.C.; Zhang, K.; Chen, H.; Wang, W. NetWalk: A Flexible Deep Embedding Approach for Anomaly Detection in Dynamic Networks. In Proceedings of the 24th International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; ACM: London, UK, 2018; pp. 2672–2681. [Google Scholar] [CrossRef]
- Yu, Z.; Kuang, Z.; Liu, J.; Chen, H.; Zhang, J.; You, J.; Wong, H.; Han, G. Adaptive Ensembling of Semi-Supervised Clustering Solutions. IEEE Trans. Knowl. Data Eng. 2017, 29, 1577–1590. [Google Scholar] [CrossRef]
- Goyal, P.; Chhetri, S.R.; Canedo, A. dyngraph2vec: Capturing network dynamics using dynamic graph representation learning. Knowl.-Based Syst. 2020, 187, 104816. [Google Scholar] [CrossRef]
- Taheri, A.; Gimpel, K.; Berger-Wolf, T. Learning graph representations with recurrent neural network autoencoders. KDD Deep Learn. Day. Available online: https://www.kdd.org/kdd2018/files/deep-learning-day/DLDay18_paper_27.pdf (accessed on 16 April 2023).
- Khoshraftar, S.; Mahdavi, S.; An, A.; Hu, Y.; Liu, J. Dynamic Graph Embedding via LSTM History Tracking. In Proceedings of the International Conference on Data Science and Advanced Analytics (DSAA 2019), Washington, DC, USA, 5–8 October 2019; IEEE: Washington, DC, USA, 2019; pp. 119–127. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Xu, X.; Fu, C.; Zhang, D.; Zhang, Q.; Xuan, Q. E-LSTM-D: A Deep Learning Framework for Dynamic Network Link Prediction. IEEE Trans. Syst. Man Cybern. 2021, 51, 3699–3712. [Google Scholar] [CrossRef]
- Taheri, A.; Gimpel, K.; Berger-Wolf, T.Y. Sequence-to-sequence modeling for graph representation learning. Appl. Netw. Sci. 2019, 4, 68.1–68.26. [Google Scholar] [CrossRef]
- Taheri, A.; Gimpel, K.; Berger-Wolf, T.Y. Learning to Represent the Evolution of Dynamic Graphs with Recurrent Models. In Proceedings of the Companion of The World Wide Web Conference (WWW 2019), San Francisco, CA, USA, 13–17 May 2019; ACM: San Francisco, CA, USA, 2019; pp. 301–307. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, C.; Yu, L.; Zhang, X.; Chawla, N.V. Camel: Content-Aware and Meta-path Augmented Metric Learning for Author Identification. In Proceedings of the World Wide Web Conference on World Wide Web (WWW 2018), Lyon, France, 23–27 April 2018; Champin, P., Gandon, F., Lalmas, M., Ipeirotis, P.G., Eds.; ACM: Lyon, France, 2018; pp. 709–718. [Google Scholar] [CrossRef]
- Park, C.; Kim, D.; Zhu, Q.; Han, J.; Yu, H. Task-Guided Pair Embedding in Heterogeneous Network. In Proceedings of the 28th International Conference on Information and Knowledge Management (CIKM 2019), Beijing, China, 3–7 November 2019; ACM: Beijing, China, 2019; pp. 489–498. [Google Scholar] [CrossRef]
- Hu, W.; Liu, B.; Gomes, J.; Zitnik, M.; Liang, P.; Pande, V.S.; Leskovec, J. Strategies for Pre-training Graph Neural Networks. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020; OpenReview.net: Addis Ababa, Ethiopia, 2020. [Google Scholar]
- Li, R.; Wang, S.; Zhu, F.; Huang, J. Adaptive Graph Convolutional Neural Networks. In Proceedings of the 32nd Conference on Artificial Intelligence (AAAI-18), New Orleans, LA, USA, 2–7 February 2018; AAAI Press: New Orleans, LA, USA, 2018; pp. 3546–3553. [Google Scholar]
- Zhuang, C.; Ma, Q. Dual Graph Convolutional Networks for Graph-Based Semi-Supervised Classification. In Proceedings of the Conference on World Wide Web (WWW 2018), Lyon, France, 23–27 April 2018; ACM: Lyon, France, 2018; pp. 499–508. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Wu, L. Differential Privacy Preserving Spectral Graph Analysis. In Proceedings of the 17th Advances in Knowledge Discovery and Data Mining, Pacific-Asia Conference (PAKDD 2013), Gold Coast, Australia, 14–17 April 2013; Springer: Gold Coast, Australia, 2013; Volume 7819, pp. 329–340. [Google Scholar] [CrossRef]
- NT, H.; Maehara, T. Revisiting Graph Neural Networks: All We Have is Low-Pass Filters. arXiv 2019, arXiv:1905.09550. [Google Scholar]
- Wu, F.; Zhang, T.; de Souza, A.H., Jr.; Fifty, C.; Yu, T.; Weinberger, K.Q. Simplifying Graph Convolutional Networks. In Proceedings of the 36th International Conference on Machine Learning (ICML 2019), Long Beach, CA, USA, 9–15 June 2019; Chaudhuri, K., Salakhutdinov, R., Eds.; PMLR: Long Beach, CA, USA, 2019; Volume 97, pp. 6861–6871. [Google Scholar]
- Yang, Z.; Cohen, W.W.; Salakhutdinov, R. Revisiting Semi-Supervised Learning with Graph Embeddings. In Proceedings of the 33nd International Conference on Machine Learning (ICML 2016), New York City, NY, USA, 19–24 June 2016; JMLR.org: New York City, NY, USA, 2016; Volume 48, pp. 40–48. [Google Scholar]
- Levie, R.; Monti, F.; Bresson, X.; Bronstein, M.M. CayleyNets: Graph Convolutional Neural Networks with Complex Rational Spectral Filters. IEEE Trans. Signal Process. 2019, 67, 97–109. [Google Scholar] [CrossRef]
- Liu, X.; Xia, G.; Lei, F.; Zhang, Y.; Chang, S. Higher-Order Graph Convolutional Networks With Multi-Scale Neighborhood Pooling for Semi-Supervised Node Classification. IEEE Access 2021, 9, 31268–31275. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, C.; Jiang, Q.; Ma, J. Community Detection with Graph Neural Network using Markov Stability. In Proceedings of the International Conference on Artificial Intelligence in Information and Communication (ICAIIC 2022), Jeju Island, Republic of Korea, 21–24 February 2022; IEEE: Jeju Island, Republic of Korea, 2022; pp. 437–442. [Google Scholar] [CrossRef]
- Zhou, X.; Shen, Y.; Zhu, Y.; Huang, L. Predicting Multi-Step Citywide Passenger Demands Using Attention-Based Neural Networks. In Proceedings of the 11th International Conference on Web Search and Data Mining (WSDM 2018), Marina Del Rey, CA, USA, 5–9 February 2018; ACM: New York, NY, USA, 2018; pp. 736–744. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, C.; Xu, Y.; Xia, L.; Dai, P.; Bo, L.; Zhang, J.; Zheng, Y. Traffic Flow Forecasting with Spatial-Temporal Graph Diffusion Network. In Proceedings of the 35th Conference on Artificial Intelligence (AAAI 2021), Virtual Event, 2–9 February 2021; AAAI Press: Virtual Event, 2021; pp. 15008–15015. [Google Scholar]
- Zhao, Q.; Ye, Z.; Chen, C.; Wang, Y. Persistence Enhanced Graph Neural Network. In Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics (AISTATS 2020), Palermo, Italy, 26–28 August 2020; PMLR: Palermo, Italy, 2020; pp. 2896–2906. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, Australia, 6–11 August 2017; PMLR: Sydney, Australia, 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Chang, J.; Gu, J.; Wang, L.; Meng, G.; Xiang, S.; Pan, C. Structure-Aware Convolutional Neural Networks. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems 2018 (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; NeurIPS: Montréal, QC, Canada, 2018; pp. 11–20. [Google Scholar]
- Chen, J.; Zhu, J.; Song, L. Stochastic Training of Graph Convolutional Networks with Variance Reduction. In Proceedings of the 35th International Conference on Machine Learning (ICML 2018), Stockholm, Sweden, 10–15 July 2018; PMLR: Stockholm, Sweden, 2018; Volume 80, pp. 941–949. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph Convolutional Neural Networks for Web-Scale Recommender Systems. In Proceedings of the 24th International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; Guo, Y., Farooq, F., Eds.; ACM: London, UK, 2018; pp. 974–983. [Google Scholar] [CrossRef]
- Wang, H.; Lian, D.; Ge, Y. Binarized Collaborative Filtering with Distilling Graph Convolutional Networks. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI 2019), Macao, China, 10–16 August 2019; AAAI Press: Macao, China, 2019; pp. 4802–4808. [Google Scholar]
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Bachman, P.; Trischler, A.; Bengio, Y. Learning deep representations by mutual information estimation and maximization. In Proceedings of the 7th International Conference on Learning Representations (ICLR 2019), New Orleans, LA, USA, 6–9 May 2019; OpenReview.net: New Orleans, LA, USA, 2019. [Google Scholar]
- Qu, M.; Tang, J.; Shang, J.; Ren, X.; Zhang, M.; Han, J. An Attention-based Collaboration Framework for Multi-View Network Representation Learning. In Proceedings of the 26th Conference on Information and Knowledge Management (CIKM 2017), Singapore, 6–10 November 2017; ACM: Singapore, 2017; pp. 1767–1776. [Google Scholar] [CrossRef]
- Tran, D.V.; Navarin, N.; Sperduti, A. On Filter Size in Graph Convolutional Networks. In Proceedings of the Symposium Series on Computational Intelligence (SSCI 2018), Bangalore, India, 18–21 November 2018; IEEE: Bangalore, India, 2018; pp. 1534–1541. [Google Scholar] [CrossRef]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Graph Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Lo, W.W.; Layeghy, S.; Sarhan, M.; Gallagher, M.; Portmann, M. E-GraphSAGE: A Graph Neural Network based Intrusion Detection System for IoT. In Proceedings of the Network Operations and Management Symposium (NOMS 2022), Budapest, Hungary, 25–29 April 2022; IEEE: Budapest, Hungary, 2022; pp. 1–9. [Google Scholar] [CrossRef]
- Cai, T.; Luo, S.; Xu, K.; He, D.; Liu, T.; Wang, L. GraphNorm: A Principled Approach to Accelerating Graph Neural Network Training. In Proceedings of the 38th International Conference on Machine Learning (ICML 2021), Virtual Event, 18–24 July 2021; PMLR: Virtual Event, 2021; Volume 139, pp. 1204–1215. [Google Scholar]
- Le, T.; Bertolini, M.; Noé, F.; Clevert, D. Parameterized Hypercomplex Graph Neural Networks for Graph Classification. In Proceedings of the 30th Artificial Neural Networks and Machine Learning (ICANN 2021), Bratislava, Slovakia, 14–17 September 2021; Farkas, I., Masulli, P., Otte, S., Wermter, S., Eds.; Springer: Bratislava, Slovakia, 2021; Volume 12893, pp. 204–216. [Google Scholar] [CrossRef]
- Yadati, N.; Nimishakavi, M.; Yadav, P.; Nitin, V.; Louis, A.; Talukdar, P.P. HyperGCN: A New Method For Training Graph Convolutional Networks on Hypergraphs. In Proceedings of the 32nd Annual Conference on Neural Information Processing Systems 2019 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Wallach, H.M., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E.B., Garnett, R., Eds.; NeurIPS: Vancouver, BC, Canada, 2019; pp. 1509–1520. [Google Scholar]
- Zhang, W.; Liu, H.; Liu, Y.; Zhou, J.; Xiong, H. Semi-Supervised Hierarchical Recurrent Graph Neural Network for City-Wide Parking Availability Prediction. In Proceedings of the 34th Conference on Artificial Intelligence (AAAI 2020), New York, NY, USA, 7–12 February 2020; AAAI Press: New York, NY, USA, 2020; pp. 1186–1193. [Google Scholar]
- Peng, H.; Wang, H.; Du, B.; Bhuiyan, M.Z.A.; Ma, H.; Liu, J.; Wang, L.; Yang, Z.; Du, L.; Wang, S.; et al. Spatial temporal incidence dynamic graph neural networks for traffic flow forecasting. Inf. Sci. 2020, 521, 277–290. [Google Scholar] [CrossRef]
- Cheng, D.; Xiang, S.; Shang, C.; Zhang, Y.; Yang, F.; Zhang, L. Spatio-Temporal Attention-Based Neural Network for Credit Card Fraud Detection. In Proceedings of the 34th Conference on Artificial Intelligence (AAAI 2020), New York, NY, USA, 7–12 February 2020; AAAI Press: New York, NY, USA, 2020; pp. 362–369. [Google Scholar]
- Xie, Z.; Lv, W.; Huang, S.; Lu, Z.; Du, B.; Huang, R. Sequential Graph Neural Network for Urban Road Traffic Speed Prediction. IEEE Access 2020, 8, 63349–63358. [Google Scholar] [CrossRef]
- Yao, H.; Wu, F.; Ke, J.; Tang, X.; Jia, Y.; Lu, S.; Gong, P.; Ye, J.; Li, Z. Deep Multi-View Spatial-Temporal Network for Taxi Demand Prediction. In Proceedings of the 32nd Conference on Artificial Intelligence (AAAI-18), New Orleans, LA, USA, 2–7 February 2018; AAAI Press: New Orleans, LA, USA, 2018; pp. 2588–2595. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D. Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction. In Proceedings of the 31st Conference on Artificial Intelligence (AAAI 2017), San Francisco, CA, USA, 4–9 February 2017; Singh, S., Markovitch, S., Eds.; AAAI Press: San Francisco, CA, USA, 2017; pp. 1655–1661. [Google Scholar]
- Schlichtkrull, M.S.; Kipf, T.N.; Bloem, P.; van den Berg, R.; Titov, I.; Welling, M. Modeling Relational Data with Graph Convolutional Networks. In Proceedings of the 15th The Semantic Web International Conference (ESWC 2018), Heraklion, Greece, 3–7 June 2018; Springer: Heraklion, Greece, 2018; Volume 10843, pp. 593–607. [Google Scholar] [CrossRef]
- Jing, B.; Park, C.; Tong, H. HDMI: High-order Deep Multiplex Infomax. In Proceedings of the The Web Conference (WWW ’21), Ljubljana, Slovenia, 19–23 April 2021; Leskovec, J., Grobelnik, M., Najork, M., Tang, J., Zia, L., Eds.; ACM/IW3C2: Ljubljana, Slovenia, 2021; pp. 2414–2424. [Google Scholar] [CrossRef]
- Park, C.; Kim, D.; Han, J.; Yu, H. Unsupervised Attributed Multiplex Network Embedding. In Proceedings of the 34th Conference on Artificial Intelligence (AAAI 2020), New York, NY, USA, 7–12 February 2020; AAAI Press: New York, NY, USA, 2020; pp. 5371–5378. [Google Scholar]
- Wei, H.; Hu, G.; Bai, W.; Xia, S.; Pan, Z. Lifelong representation learning in dynamic attributed networks. Neurocomputing 2019, 358, 1–9. [Google Scholar] [CrossRef]
- Pareja, A.; Domeniconi, G.; Chen, J.; Ma, T.; Suzumura, T.; Kanezashi, H.; Kaler, T.; Schardl, T.B.; Leiserson, C.E. EvolveGCN: Evolving Graph Convolutional Networks for Dynamic Graphs. In Proceedings of the 34th Conference on Artificial Intelligence (AAAI 2020), New York, NY, USA, 7–12 February 2020; AAAI Press: New York, NY, USA, 2020; pp. 5363–5370. [Google Scholar]
- Sun, F.; Hoffmann, J.; Verma, V.; Tang, J. InfoGraph: Unsupervised and Semi-supervised Graph-Level Representation Learning via Mutual Information Maximization. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020; OpenReview.net: Addis Ababa, Ethiopia, 2020. [Google Scholar]
- Hu, Z.; Dong, Y.; Wang, K.; Chang, K.; Sun, Y. GPT-GNN: Generative Pre-Training of Graph Neural Networks. In Proceedings of the 26th SIGKDD Conference on Knowledge Discovery and Data Mining (KDD 2020), Virtual Event, CA, USA, 6–10 July 2020; ACM: Virtual Event, CA, USA, 2020; pp. 1857–1867. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs. SIAM J. Sci. Comput. 1998, 20, 359–392. [Google Scholar] [CrossRef]
- Zeng, H.; Zhou, H.; Srivastava, A.; Kannan, R.; Prasanna, V.K. Accurate, Efficient and Scalable Graph Embedding. In Proceedings of the International Parallel and Distributed Processing Symposium (IPDPS 2019), Rio de Janeiro, Brazil, 20–24 May 2019; IEEE: Rio de Janeiro, Brazil, 2019; pp. 462–471. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, T.; Rong, Y.; Huang, J. Adaptive Sampling Towards Fast Graph Representation Learning. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; NeurIPS: Montréal, QC, Canada, 2018; pp. 4563–4572. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; ICLR: San Diego, CA, USA, 2015. [Google Scholar]
- Zhao, L.; Akoglu, L. PairNorm: Tackling Oversmoothing in GNNs. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020; OpenReview.net: Addis Ababa, Ethiopia, 2020. [Google Scholar]
- Ma, L.; Rabbany, R.; Romero-Soriano, A. Graph Attention Networks with Positional Embeddings. In Proceedings of the 25th Advances in Knowledge Discovery and Data Mining Pacific-Asia Conference (PAKDD 2021), Virtual Event, 11–14 May 2021; Karlapalem, K., Cheng, H., Ramakrishnan, N., Agrawal, R.K., Reddy, P.K., Srivastava, J., Chakraborty, T., Eds.; Springer: Virtual Event, 2021; Volume 12712, pp. 514–527. [Google Scholar] [CrossRef]
- Huang, B.; Carley, K.M. Syntax-Aware Aspect Level Sentiment Classification with Graph Attention Networks. In Proceedings of the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP 2019), Hong Kong, China, 3–7 November 2019; Inui, K., Jiang, J., Ng, V., Wan, X., Eds.; Association for Computational Linguistics: Hong Kong, China, 2019; pp. 5468–5476. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, X.; Xie, J.; Ma, H.; King, I.; Yeung, D. GaAN: Gated Attention Networks for Learning on Large and Spatiotemporal Graphs. In Proceedings of the 34th Conference on Uncertainty in Artificial Intelligence (UAI 2018), Monterey, CA, USA, 6–10 August 2018; AUAI Press: Monterey, CA, USA, 2018; pp. 339–349. [Google Scholar]
- Haonan, L.; Huang, S.H.; Ye, T.; Xiuyan, G. Graph Star Net for Generalized Multi-Task Learning. arXiv 2019, arXiv:1906.12330. [Google Scholar]
- Abu-El-Haija, S.; Perozzi, B.; Al-Rfou, R.; Alemi, A.A. Watch Your Step: Learning Node Embeddings via Graph Attention. In Proceedings of the 31st Advances in Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; NeurIPS: Montréal, QC, Canada, 2018; pp. 9198–9208. [Google Scholar]
- Kim, D.; Oh, A. How to Find Your Friendly Neighborhood: Graph Attention Design with Self-Supervision. In Proceedings of the 9th International Conference on Learning Representations (ICLR 2021), Vienna, Austria, 3–7 May 2021; OpenReview.net: Virtual Event, 2021. [Google Scholar]
- Wang, G.; Ying, R.; Huang, J.; Leskovec, J. Improving Graph Attention Networks with Large Margin-based Constraints. arXiv 2019, arXiv:1910.11945. [Google Scholar]
- Zhu, Y.; Wang, J.; Zhang, J.; Zhang, K. Node Embedding and Classification with Adaptive Structural Fingerprint. Neurocomputing 2022, 502, 196–208. [Google Scholar] [CrossRef]
- Yang, Y.; Qiu, J.; Song, M.; Tao, D.; Wang, X. Distilling Knowledge From Graph Convolutional Networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2020), Seattle, WA, USA, 13–19 June 2020; Computer Vision Foundation/IEEE: Seattle, WA, USA, 2020; pp. 7072–7081. [Google Scholar] [CrossRef]
- Nathani, D.; Chauhan, J.; Sharma, C.; Kaul, M. Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs. In Proceedings of the 57th Conference of the Association for Computational Linguistics (ACL 2019), Florence, Italy, 28 July–2 August 2019; ACL: Florence, Italy, 2019; pp. 4710–4723. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Z.; Yang, J.; Liu, X. Deepdom: Malicious domain detection with scalable and heterogeneous graph convolutional networks. Comput. Secur. 2020, 99, 102057. [Google Scholar] [CrossRef]
- Xue, H.; Yang, L.; Rajan, V.; Jiang, W.; Wei, Y.; Lin, Y. Multiplex Bipartite Network Embedding Using Dual Hypergraph Convolutional Networks. In Proceedings of the Web Conference 2021 (WWW 2021), Ljubljana, Slovenia, 19–23 April 2021; ACM: New York, NY, USA, 2021; pp. 1649–1660. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, Z.; Liao, B.; Wu, F.; Zhuang, Y. Heterogeneous Attributed Network Embedding with Graph Convolutional Networks. In Proceedings of the 33rd Conference on Artificial Intelligence (AAAI 2019), Honolulu, HI, USA, 27 January–1 February 2019; AAAI Press: Honolulu, HI, USA, 2019; pp. 10061–10062. [Google Scholar] [CrossRef]
- Yu, P.; Fu, C.; Yu, Y.; Huang, C.; Zhao, Z.; Dong, J. Multiplex Heterogeneous Graph Convolutional Network. In Proceedings of the 28th Conference on Knowledge Discovery and Data Mining (KDD 2022), Washington, DC, USA, 14–18 August 2022; Zhang, A., Rangwala, H., Eds.; ACM: Washington, DC, USA, 2022; pp. 2377–2387. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, M.; Xie, X.; Li, W.; Guo, M. Knowledge Graph Convolutional Networks for Recommender Systems. In Proceedings of the World Wide Web Conference (WWW 2019), San Francisco, CA, USA, 13–17 May 2019; Liu, L., White, R.W., Mantrach, A., Silvestri, F., McAuley, J.J., Baeza-Yates, R., Zia, L., Eds.; ACM: San Francisco, CA, USA, 2019; pp. 3307–3313. [Google Scholar] [CrossRef]
- Mao, C.; Yao, L.; Luo, Y. MedGCN: Medication recommendation and lab test imputation via graph convolutional networks. J. Biomed. Inform. 2022, 127, 104000. [Google Scholar] [CrossRef]
- Xu, F.; Lian, J.; Han, Z.; Li, Y.; Xu, Y.; Xie, X. Relation-Aware Graph Convolutional Networks for Agent-Initiated Social E-Commerce Recommendation. In Proceedings of the 28th International Conference on Information and Knowledge Management (CIKM 2019), Beijing, China, 3–7 November 2019; Zhu, W., Tao, D., Cheng, X., Cui, P., Rundensteiner, E.A., Carmel, D., He, Q., Yu, J.X., Eds.; ACM: Beijing, China, 2019; pp. 529–538. [Google Scholar] [CrossRef]
- Wang, C.; Pan, S.; Long, G.; Zhu, X.; Jiang, J. MGAE: Marginalized Graph Autoencoder for Graph Clustering. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, CIKM 2017, Singapore, 6–10 November 2017; ACM: Singapore, 2017; pp. 889–898. [Google Scholar] [CrossRef]
- Simonovsky, M.; Komodakis, N. GraphVAE: Towards Generation of Small Graphs Using Variational Autoencoders. In Proceedings of the 27th International Conference on Artificial Neural Networks (ICANN 2018), Rhodes, Greece, 4–7 October 2018; Springer: Rhodes, Greece, 2018. [Google Scholar]
- Cao, N.D.; Kipf, T. MolGAN: An implicit generative model for small molecular graphs. arXiv 2018, arXiv:1805.11973. [Google Scholar]
- Suganuma, M.; Ozay, M.; Okatani, T. Exploiting the Potential of Standard Convolutional Autoencoders for Image Restoration by Evolutionary Search. In Proceedings of the 35th International Conference on Machine Learning (ICML 2018), Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; PMLR: Stockholm, Sweden, 2018; Volume 80, pp. 4778–4787. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations (ICLR 2014), Banff, AB, Canada, 14–16 April 2014; ICLR: Banff, AB, Canada, 2014. [Google Scholar]
- Wu, G.; Lin, S.; Shao, X.; Zhang, P.; Qiao, J. QPGCN: Graph convolutional network with a quadratic polynomial filter for overcoming over-smoothing. Appl. Intell. 2022, 53, 7216–7231. [Google Scholar] [CrossRef]
- Shi, L.; Wu, W.; Hu, W.; Zhou, J.; Chen, J.; Zheng, W.; He, L. DualGCN: An Aspect-Aware Dual Graph Convolutional Network for review-based recommender. Knowl.-Based Syst. 2022, 242, 108359. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; NeurIPS: Long Beach, CA, USA, 2017; pp. 5998–6008. [Google Scholar]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT 2019), Minneapolis, MN, USA, 2–7 June 2019; ACL: Minneapolis, MN, USA, 2019; pp. 4171–4186. [Google Scholar] [CrossRef]
- Joshi, M.; Chen, D.; Liu, Y.; Weld, D.S.; Zettlemoyer, L.; Levy, O. SpanBERT: Improving Pre-training by Representing and Predicting Spans. Trans. Assoc. Comput. Linguist. 2020, 8, 64–77. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; Gao, W. Pre-Trained Image Processing Transformer. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2021), Virtual Event, 19–25 June 2021; IEEE: Virtual Event, 2021; pp. 12299–12310. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceedings of the 9th International Conference on Learning Representations (ICLR 2021), Vienna, Austria, 3–7 May 2021; OpenReview.net: Vienna, Austria, 2021. [Google Scholar]
- Cai, D.; Lam, W. Graph Transformer for Graph-to-Sequence Learning. In Proceedings of the 34th Conference on Artificial Intelligence (AAAI 2020), New York, NY, USA, 7–12 February 2020; AAAI Press: New York, NY, USA, 2020; pp. 7464–7471. [Google Scholar]
- Jeon, H.J.; Choi, G.S.; Cho, S.Y.; Lee, H.; Ko, H.Y.; Jung, J.J.; Lee, O.-J.; Yi, M.Y. Learning contextual representations of citations via graph transformer. In Proceedings of the 2nd International Conference on Human-centered Artificial Intelligence (Computing4Human 2021), Da Nang, Vietnam, 28–29 October 2021; ceur-ws: Da Nang, Vietnam, 2021. [Google Scholar]
- Kreuzer, D.; Beaini, D.; Hamilton, W.L.; Létourneau, V.; Tossou, P. Rethinking Graph Transformers with Spectral Attention. In Proceedings of the 34th Annual Conference on Neural Information Processing Systems (NeurIPS 2021), Virtual Event, 6–14 December 2021; NeurIPS: Virtual Event, 2021; pp. 21618–21629. [Google Scholar]
- Hu, Z.; Dong, Y.; Wang, K.; Sun, Y. Heterogeneous Graph Transformer. In Proceedings of the Web Conference (WWW 2020), Taipei, Taiwan, 20–24 April 2020; ACM/IW3C2: Taipei, Taiwan, 2020; pp. 2704–2710. [Google Scholar] [CrossRef]
- Khoo, L.M.S.; Chieu, H.L.; Qian, Z.; Jiang, J. Interpretable Rumor Detection in Microblogs by Attending to User Interactions. In Proceedings of the 34th Conference on Artificial Intelligence(AAAI 2020), New York, NY, USA, 7–12 February 2020; AAAI Press: New York, NY, USA, 2020; pp. 8783–8790. [Google Scholar]
- Min, E.; Rong, Y.; Xu, T.; Bian, Y.; Luo, D.; Lin, K.; Huang, J.; Ananiadou, S.; Zhao, P. Neighbour Interaction based Click-Through Rate Prediction via Graph-masked Transformer. In Proceedings of the 45th International Conference on Research and Development in Information Retrieval (SIGIR 2022), Madrid, Spain, 11–15 July 2022; ACM: Madrid, Spain, 2022; pp. 353–362. [Google Scholar] [CrossRef]
- Shaw, P.; Uszkoreit, J.; Vaswani, A. Self-Attention with Relative Position Representations. In Proceedings of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT 2018), New Orleans, LA, USA, 1–6 June 2018; ACL: New Orleans, LA, USA, 2018; pp. 464–468. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S.; Lei, C.; Wang, G.; Tang, H.; Zhang, J.; Sun, A.; Miao, C. Pre-training Graph Transformer with Multimodal Side Information for Recommendation. In Proceedings of the Multimedia Conference (MM’21), Virtual Event, China, 20–24 October 2021; ACM: Virtual Event, China, 2021; pp. 2853–2861. [Google Scholar] [CrossRef]
- Lin, K.; Wang, L.; Liu, Z. End-to-End Human Pose and Mesh Reconstruction with Transformers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2021), Virtual Event, 19–25 June 2021; Computer Vision Foundation/IEEE: Virtual Event, 2021; pp. 1954–1963. [Google Scholar] [CrossRef]
- Makarov, I.; Kiselev, D.; Nikitinsky, N.; Subelj, L. Survey on graph embeddings and their applications to machine learning problems on graphs. PeerJ Comput. Sci. 2021, 7, e357. [Google Scholar] [CrossRef]
- Yang, M.; Zhou, M.; Li, Z.; Liu, J.; Pan, L.; Xiong, H.; King, I. Hyperbolic Graph Neural Networks: A Review of Methods and Applications. arXiv 2022, arXiv:2202.13852. [Google Scholar] [CrossRef]
- Chami, I.; Ying, Z.; Ré, C.; Leskovec, J. Hyperbolic Graph Convolutional Neural Networks. In Proceedings of the 32nd Annual Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; NeurIPS: Vancouver, BC, Canada, 2019; pp. 4869–4880. [Google Scholar]
- Liu, Q.; Nickel, M.; Kiela, D. Hyperbolic Graph Neural Networks. In Proceedings of the 32nd Annual Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; NeurIPS: Vancouver, BC, Canada, 2019; pp. 8228–8239. [Google Scholar]
- Ratcliffe, J.G.; Axler, S.; Ribet, K. Foundations of Hyperbolic Manifolds; Springer: Berlin/Heidelberg, Germany, 1994; Volume 149. [Google Scholar]
- Krioukov, D.V.; Papadopoulos, F.; Kitsak, M.; Vahdat, A.; Boguñá, M. Hyperbolic Geometry of Complex Networks. arXiv 2010, arXiv:1006.5169. [Google Scholar] [CrossRef] [PubMed]
- Defferrard, M.; Milani, M.; Gusset, F.; Perraudin, N. DeepSphere: A graph-based spherical CNN. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020; OpenReview.net: Addis Ababa, Ethiopia, 2020. [Google Scholar]
- Zhu, D.; Cui, P.; Wang, D.; Zhu, W. Deep Variational Network Embedding in Wasserstein Space. In Proceedings of the 24th International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; Guo, Y., Farooq, F., Eds.; ACM: London, UK, 2018; pp. 2827–2836. [Google Scholar] [CrossRef]
- He, S.; Liu, K.; Ji, G.; Zhao, J. Learning to Represent Knowledge Graphs with Gaussian Embedding. In Proceedings of the 24th International Conference on Information and Knowledge Management (CIKM 2015), Melbourne, VIC, Australia, 19–23 October 2015; ACM: Melbourne, VIC, Australia, 2015; pp. 623–632. [Google Scholar] [CrossRef]
- Vilnis, L.; McCallum, A. Word Representations via Gaussian Embedding. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; Bengio, Y., LeCun, Y., Eds.; ICLR: San Diego, CA, USA, 2015. [Google Scholar]
- Kampffmeyer, M.; Chen, Y.; Liang, X.; Wang, H.; Zhang, Y.; Xing, E.P. Rethinking knowledge graph propagation for zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; Computer Vision Foundation/IEEE: Long Beach, CA, USA, 2019; pp. 11487–11496. [Google Scholar]
- Zhang, T.; Zheng, W.; Cui, Z.; Li, Y. Tensor graph convolutional neural network. arXiv 2018, arXiv:1803.10071. [Google Scholar]
- Yang, L.; Zhan, X.; Chen, D.; Yan, J.; Loy, C.C.; Lin, D. Learning to Cluster Faces on an Affinity Graph. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; Computer Vision Foundation/IEEE: Long Beach, CA, USA, 2019; pp. 2298–2306. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, L.; Li, Y.; Wang, S. Linkage Based Face Clustering via Graph Convolution Network. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; Computer Vision Foundation/IEEE: Long Beach, CA, USA, 2019; pp. 1117–1125. [Google Scholar] [CrossRef]
- Narasimhan, M.; Lazebnik, S.; Schwing, A.G. Out of the Box: Reasoning with Graph Convolution Nets for Factual Visual Question Answering. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; Bengio, S., Wallach, H.M., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; NeurIPS: Montréal, QC, Canada, 2018; pp. 2659–2670. [Google Scholar]
- Cui, Z.; Xu, C.; Zheng, W.; Yang, J. Context-Dependent Diffusion Network for Visual Relationship Detection. In Proceedings of the Multimedia Conference on Multimedia Conference (MM 2018), Seoul, Republic of Korea, 22–26 October 2018; Boll, S., Lee, K.M., Luo, J., Zhu, W., Byun, H., Chen, C.W., Lienhart, R., Mei, T., Eds.; ACM: Seoul, Republic of Korea, 2018; pp. 1475–1482. [Google Scholar] [CrossRef]
- Dai, B.; Zhang, Y.; Lin, D. Detecting Visual Relationships with Deep Relational Networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; IEEE Computer Society: Honolulu, HI, USA, 2017; pp. 3298–3308. [Google Scholar] [CrossRef]
- Johnson, J.; Gupta, A.; Fei-Fei, L. Image Generation From Scene Graphs. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; Computer Vision Foundation/IEEE Computer Society: Salt Lake City, UT, USA, 2018; pp. 1219–1228. [Google Scholar] [CrossRef]
- Chen, Y.; Rohrbach, M.; Yan, Z.; Yan, S.; Feng, J.; Kalantidis, Y. Graph-Based Global Reasoning Networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; Computer Vision Foundation/IEEE: Long Beach, CA, USA, 2019; pp. 433–442. [Google Scholar] [CrossRef]
- Wang, P.; Wu, Q.; Cao, J.; Shen, C.; Gao, L.; van den Hengel, A. Neighbourhood Watch: Referring Expression Comprehension via Language-Guided Graph Attention Networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; Computer Vision Foundation/IEEE: Long Beach, CA, USA, 2019; pp. 1960–1968. [Google Scholar] [CrossRef]
- Li, M.; Chen, S.; Chen, X.; Zhang, Y.; Wang, Y.; Tian, Q. Actional-Structural Graph Convolutional Networks for Skeleton-Based Action Recognition. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; Computer Vision Foundation/IEEE: Long Beach, CA, USA, 2019; pp. 3595–3603. [Google Scholar] [CrossRef]
- Wang, X.; Gupta, A. Videos as Space-Time Region Graphs. In Proceedings of the 15th Computer Vision European Conference (ECCV 2018), Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Munich, Germany, 2018; Volume 11209, pp. 413–431. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, T.; Xu, C. Graph Convolutional Tracking. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; Computer Vision Foundation/IEEE: Long Beach, CA, USA, 2019; pp. 4649–4659. [Google Scholar] [CrossRef]
- Zhong, J.; Li, N.; Kong, W.; Liu, S.; Li, T.H.; Li, G. Graph Convolutional Label Noise Cleaner: Train a Plug-And-Play Action Classifier for Anomaly Detection. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; Computer Vision Foundation/IEEE: Long Beach, CA, USA, 2019; pp. 1237–1246. [Google Scholar] [CrossRef]
- Bastings, J.; Titov, I.; Aziz, W.; Marcheggiani, D.; Sima’an, K. Graph Convolutional Encoders for Syntax-aware Neural Machine Translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP 2017), Copenhagen, Denmark, 9–11 September 2017; Palmer, M., Hwa, R., Riedel, S., Eds.; ACL: Copenhagen, Denmark, 2017; pp. 1957–1967. [Google Scholar] [CrossRef]
- Strubell, E.; McCallum, A. Dependency Parsing with Dilated Iterated Graph CNNs. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP 2017), Copenhagen, Denmark, 9–11 September 2017; Chang, K., Chang, M., Srikumar, V., Rush, A.M., Eds.; ACL: Copenhagen, Denmark, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Vashishth, S.; Bhandari, M.; Yadav, P.; Rai, P.; Bhattacharyya, C.; Talukdar, P.P. Incorporating Syntactic and Semantic Information in Word Embeddings using Graph Convolutional Networks. In Proceedings of the 57th Conference of the Association for Computational Linguistics (ACL 2019), Florence, Italy, 28 July–2 August 2019; Korhonen, A., Traum, D.R., Màrquez, L., Eds.; ACL: Florence, Italy, 2019; pp. 3308–3318. [Google Scholar] [CrossRef]
- Kim, D.; Kim, S.; Kwak, N. Textbook Question Answering with Multi-modal Context Graph Understanding and Self-supervised Open-set Comprehension. In Proceedings of the 57th Conference of the Association for Computational Linguistics (ACL 2019), Florence, Italy, 28 July–2 August 2019; Long Papers. Korhonen, A., Traum, D.R., Màrquez, L., Eds.; ACL: Florence, Italy, 2019; Volume 1, pp. 3568–3584. [Google Scholar] [CrossRef]
- Hao, Y.; Sheng, Y.; Wang, J. A Graph Representation Learning Algorithm for Low-Order Proximity Feature Extraction to Enhance Unsupervised IDS Preprocessing. Appl. Sci. 2019, 9, 4473. [Google Scholar] [CrossRef]
- Narayanan, A.; Chandramohan, M.; Chen, L.; Liu, Y. A multi-view context-aware approach to Android malware detection and malicious code localization. Empir. Softw. Eng. 2018, 23, 1222–1274. [Google Scholar] [CrossRef]
- Nguyen, H.; Nguyen, D.; Ngo, Q.; Tran, V.; Le, V. Towards a rooted subgraph classifier for IoT botnet detection. In Proceedings of the 7th International Conference on Computer and Communications Management (ICCCM 2019), Bangkok, Thailand, 27–29 July 2019; ACM: Bangkok, Thailand, 2019; pp. 247–251. [Google Scholar] [CrossRef]
- Zitnik, M.; Agrawal, M.; Leskovec, J. Modeling polypharmacy side effects with graph convolutional networks. Bioinformatics 2018, 34, i457–i466. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhou, J.; Xu, T.; Dou, D.; Xiong, H. GeomGCL: Geometric Graph Contrastive Learning for Molecular Property Prediction. In Proceedings of the 36th Conference on Artificial Intelligence (AAAI 2022), Virtual Event, 22 February–1 March 2022; AAAI Press: Palo Alto, CA, USA, 2022; pp. 4541–4549. [Google Scholar]
- Duvenaud, D.; Maclaurin, D.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional Networks on Graphs for Learning Molecular Fingerprints. In Proceedings of the 28th Annual Conference on Neural Information Processing Systems (NeurIPS 2015), Montreal, QC, Canada, 7–12 December 2015; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; NeurIPS: Montreal, QC, Canada, 2015; pp. 2224–2232. [Google Scholar]
- Yamanishi, Y.; Araki, M.; Gutteridge, A.; Honda, W.; Kanehisa, M. Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. In Proceedings of the 16th International Conference on Intelligent Systems for Molecular Biology (ISMB 2008), Toronto, ON, Canada, 19–23 July 2008; Oxford Academic: Toronto, ON, Canada, 2008; pp. 232–240. [Google Scholar] [CrossRef]
- Cobanoglu, M.C.; Liu, C.; Hu, F.; Oltvai, Z.N.; Bahar, I. Predicting Drug-Target Interactions Using Probabilistic Matrix Factorization. J. Chem. Inf. Model. 2013, 53, 3399–3409. [Google Scholar] [CrossRef]
- Sharma, A.; Rani, R. BE-DTI’: Ensemble framework for drug target interaction prediction using dimensionality reduction and active learning. Comput. Methods Prog. Biomed. 2018, 165, 151–162. [Google Scholar] [CrossRef]
- Zheng, X.; Ding, H.; Mamitsuka, H.; Zhu, S. Collaborative matrix factorization with multiple similarities for predicting drug-target interactions. In Proceedings of the the 19th International Conference on Knowledge Discovery and Data Mining (KDD 2013), Chicago, IL, USA, 11–14 August 2013; Dhillon, I.S., Koren, Y., Ghani, R., Senator, T.E., Bradley, P., Parekh, R., He, J., Grossman, R.L., Uthurusamy, R., Eds.; ACM: Chicago, IL, USA, 2013; pp. 1025–1033. [Google Scholar] [CrossRef]
- Yamanishi, Y.; Kotera, M.; Moriya, Y.; Sawada, R.; Kanehisa, M.; Goto, S. DINIES: Drug-target interaction network inference engine based on supervised analysis. Nucleic Acids Res. 2014, 42, 39–45. [Google Scholar] [CrossRef]
- Ezzat, A.; Zhao, P.; Wu, M.; Li, X.L.; Kwoh, C.K. Drug-Target Interaction Prediction with Graph Regularized Matrix Factorization. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 646–656. [Google Scholar] [CrossRef]
- Li, X.; Yan, X.; Gu, Q.; Zhou, H.; Wu, D.; Xu, J. DeepChemStable: Chemical Stability Prediction with an Attention-Based Graph Convolution Network. J. Chem. Inf. Model. 2019, 59, 1044–1049. [Google Scholar] [CrossRef]
- Kulmanov, M.; Khan, M.A.; Hoehndorf, R. DeepGO: Predicting protein functions from sequence and interactions using a deep ontology-aware classifier. Bioinformatics 2018, 34, 660–668. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Luo, J.; Xiao, Q.; Liang, C.; Ding, P.; Cao, B. Predicting MicroRNA-Disease Associations Using Network Topological Similarity Based on DeepWalk. IEEE Access 2017, 5, 24032–24039. [Google Scholar] [CrossRef]
- Su, X.; Hu, L.; You, Z.; Hu, P.; Zhao, B. Attention-based Knowledge Graph Representation Learning for Predicting Drug-drug Interactions. Briefings Bioinform. 2022, 23, bbac140. [Google Scholar] [CrossRef]
- Çelebi, R.; Yasar, E.; Uyar, H.; Gümüs, Ö.; Dikenelli, O.; Dumontier, M. Evaluation of knowledge graph embedding approaches for drug-drug interaction prediction using Linked Open Data. In Proceedings of the 11th International Conference Semantic Web Applications and Tools for Life Sciences (SWAT4LS 2018), Antwerp, Belgium, 3–6 December 2018; Waagmeester, A., Baker, C.J.O., Splendiani, A., Beyan, O.D., Marshall, M.S., Eds.; CEUR-WS.org: Antwerp, Belgium, 2018; Volume 2275. [Google Scholar]
- Karim, M.R.; Cochez, M.; Jares, J.B.; Uddin, M.; Beyan, O.D.; Decker, S. Drug-Drug Interaction Prediction Based on Knowledge Graph Embeddings and Convolutional-LSTM Network. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics (BCB 2019), Niagara Falls, NY, USA, 7–10 September 2019; Shi, X.M., Buck, M., Ma, J., Veltri, P., Eds.; ACM: Niagara Falls, NY, USA, 2019; pp. 113–123. [Google Scholar] [CrossRef]
- Lin, X.; Quan, Z.; Wang, Z.; Ma, T.; Zeng, X. KGNN: Knowledge Graph Neural Network for Drug-Drug Interaction Prediction. In Proceedings of the 29th International Joint Conference on Artificial Intelligence (IJCAI 2020), Yokohama, Japan, 7–15 January 2021; Bessiere, C., Ed.; ijcai.org: Yokohama, Japan, 2020; pp. 2739–2745. [Google Scholar] [CrossRef]
- Zhao, T.; Hu, Y.; Valsdottir, L.R.; Zang, T.; Peng, J. Identifying drug-target interactions based on graph convolutional network and deep neural network. Briefings Bioinform. 2021, 22, 2141–2150. [Google Scholar] [CrossRef] [PubMed]
- An, Q.; Yu, L. A heterogeneous network embedding framework for predicting similarity-based drug-target interactions. Briefings Bioinform. 2021, 22, bbab275. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Y.; Guan, J.; Li, J.; Han, R.; Hao, J.; Wei, Z.; Shang, X. An end-to-end heterogeneous graph representation learning-based framework for drug-target interaction prediction. Briefings Bioinform. 2021, 22, bbaa430. [Google Scholar] [CrossRef]
- Monti, F.; Frasca, F.; Eynard, D.; Mannion, D.; Bronstein, M.M. Fake News Detection on Social Media using Geometric Deep Learning. arXiv 2019, arXiv:1902.06673. [Google Scholar]
- Benamira, A.; Devillers, B.; Lesot, E.; Ray, A.K.; Saadi, M.; Malliaros, F.D. Semi-supervised learning and graph neural networks for fake news detection. In Proceedings of the International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2019), Vancouver, BC, Canada, 27–30 August 2019; ACM: Vancouver, BC, Canada, 2019; pp. 568–569. [Google Scholar] [CrossRef]
- Nguyen, V.; Sugiyama, K.; Nakov, P.; Kan, M. FANG: Leveraging Social Context for Fake News Detection Using Graph Representation. In Proceedings of the 29th International Conference on Information and Knowledge Management (CIKM 2020), Virtual Event, Ireland, 19–23 October 2020; d’Aquin, M., Dietze, S., Hauff, C., Curry, E., Cudré-Mauroux, P., Eds.; ACM: Virtual Event, Ireland, 2020; pp. 1165–1174. [Google Scholar] [CrossRef]
- Piao, J.; Zhang, G.; Xu, F.; Chen, Z.; Li, Y. Predicting Customer Value with Social Relationships via Motif-based Graph Attention Networks. In Proceedings of the The Web Conference 2021 (WWW 2021), Ljubljana, Slovenia, 19–23 April 2021; Leskovec, J., Grobelnik, M., Najork, M., Tang, J., Zia, L., Eds.; ACM/IW3C2: Ljubljana, Slovenia, 2021; pp. 3146–3157. [Google Scholar] [CrossRef]
- Li, C.; Goldwasser, D. Encoding social information with graph convolutional networks for political perspective detection in news media. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July– 2 August 2019; ACL: Florence, Italy, 2019; pp. 2594–2604. [Google Scholar]
- Qiu, J.; Tang, J.; Ma, H.; Dong, Y.; Wang, K.; Tang, J. DeepInf: Social Influence Prediction with Deep Learning. In Proceedings of the 24th International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; Guo, Y., Farooq, F., Eds.; ACM: London, UK, 2018; pp. 2110–2119. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.M.; Volinsky, C. Matrix Factorization Techniques for Recommender Systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Gu, Q.; Zhou, J.; Ding, C.H.Q. Collaborative Filtering: Weighted Nonnegative Matrix Factorization Incorporating User and Item Graphs. In Proceedings of the International Conference on Data Mining (SDM 2010), Columbus, OH, USA, 29 April–1 May 2010; SIAM: Columbus, OH, USA, 2010; pp. 199–210. [Google Scholar] [CrossRef]
- Guo, Q.; Sun, Z.; Theng, Y. Exploiting Side Information for Recommendation. In Proceedings of the 19th International Conference (ICWE 2019), Daejeon, Republic of Korea, 11–14 June 2019; Bakaev, M., Frasincar, F., Ko, I., Eds.; Springer: Daejeon, Republic of Korea, 2019; Volume 11496, pp. 569–573. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, Q.; Yang, J.; Fang, H.; Guo, G.; Zhang, J.; Burke, R. Research commentary on recommendations with side information: A survey and research directions. Electron. Commer. Res. Appl. 2019, 37. [Google Scholar] [CrossRef]
- He, R.; Lin, C.; Wang, J.; McAuley, J.J. Sherlock: Sparse Hierarchical Embeddings for Visually-Aware One-Class Collaborative Filtering. In Proceedings of the 35th International Joint Conference on Artificial Intelligence (IJCAI 2016), New York, NY, USA, 9–15 July 2016; Kambhampati, S., Ed.; IJCAI/AAAI Press: New York, NY, USA, 2016; pp. 3740–3746. [Google Scholar]
- Zhang, Y.; Lai, G.; Zhang, M.; Zhang, Y.; Liu, Y.; Ma, S. Explicit factor models for explainable recommendation based on phrase-level sentiment analysis. In Proceedings of the 37th International Conference on Research and Development in Information Retrieval (SIGIR’14), Gold Coast, QLD, Australia, 6–11 July 2014; Geva, S., Trotman, A., Bruza, P., Clarke, C.L.A., Järvelin, K., Eds.; ACM: Gold Coast, QLD, Australia, 2014; pp. 83–92. [Google Scholar] [CrossRef]
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, Y.E.; Tang, J.; Yin, D. Graph Neural Networks for Social Recommendation. In Proceedings of the World Wide Web Conference (WWW 2019), San Francisco, CA, USA, 13–17 May 2019; Liu, L., White, R.W., Mantrach, A., Silvestri, F., McAuley, J.J., Baeza-Yates, R., Zia, L., Eds.; ACM: San Francisco, CA, USA, 2019; pp. 417–426. [Google Scholar] [CrossRef]
- Dong, X.; Yu, L.; Wu, Z.; Sun, Y.; Yuan, L.; Zhang, F. A Hybrid Collaborative Filtering Model with Deep Structure for Recommender Systems. In Proceedings of the 31st Conference on Artificial Intelligence, (AAAI 2017), San Francisco, CA, USA, 4–9 February 2017; Singh, S., Markovitch, S., Eds.; AAAI Press: San Francisco, CA, USA, 2017; pp. 1309–1315. [Google Scholar]
- Wang, X.; He, X.; Cao, Y.; Liu, M.; Chua, T. KGAT: Knowledge Graph Attention Network for Recommendation. In Proceedings of the 25th International Conference on Knowledge Discovery & Data Mining (KDD 2019), Anchorage, AK, USA, 4–8 August 2019; ACM: Anchorage, AK, USA, 2019; pp. 950–958. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T. Neural Graph Collaborative Filtering. In Proceedings of the 42nd International Conference on Research and Development in Information Retrieval (SIGIR 2019), Paris, France, 21–25 July 2019; Piwowarski, B., Chevalier, M., Gaussier, É., Maarek, Y., Nie, J., Scholer, F., Eds.; ACM: Paris, France, 2019; pp. 165–174. [Google Scholar] [CrossRef]
- van den Berg, R.; Kipf, T.N.; Welling, M. Graph Convolutional Matrix Completion. arXiv 2017, arXiv:1706.02263. [Google Scholar]
- Chai, D.; Wang, L.; Yang, Q. Bike flow prediction with multi-graph convolutional networks. In Proceedings of the 26th International Conference on Advances in Geographic Information Systems (SIGSPATIAL 2018), Seattle, WA, USA, 6–9 November 2018; Kashani, F.B., Hoel, E.G., Güting, R.H., Tamassia, R., Xiong, L., Eds.; ACM: Seattle, WA, USA, 2018; pp. 397–400. [Google Scholar] [CrossRef]
- Diehl, F.; Brunner, T.; Truong-Le, M.; Knoll, A.C. Graph Neural Networks for Modelling Traffic Participant Interaction. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV 2019), Paris, France, 9–12 June 2019; IEEE: Paris, France, 2019; pp. 695–701. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for Deep Spatial-Temporal Graph Modeling. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI 2019), Macao, China, 10–16 August 2019; Kraus, S., Ed.; ijcai.org: Macao, China, 2019; pp. 1907–1913. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting. In Proceedings of the 33rd Conference on Artificial Intelligence (AAAI 2019), Honolulu, HI, USA, 27 January–1 February 2019; AAAI Press: Honolulu, HI, USA, 2019; pp. 922–929. [Google Scholar] [CrossRef]
- Khodayar, M.; Mohammadi, S.; Khodayar, M.E.; Wang, J.; Liu, G. Convolutional Graph Autoencoder: A Generative Deep Neural Network for Probabilistic Spatio-Temporal Solar Irradiance Forecasting. IEEE Trans. Sustain. Energy 2020, 11, 571–583. [Google Scholar] [CrossRef]
- Khodayar, M.; Wang, J. Spatio-temporal graph deep neural network for short-term wind speed forecasting. IEEE Trans. Sustain. Energy 2019, 10, 670–681. [Google Scholar] [CrossRef]
- Owerko, D.; Gama, F.; Ribeiro, A. Predicting Power Outages Using Graph Neural Networks. In Proceedings of the 6th IEEE Global Conference on Signal and Information Processing (GlobalSIP 2018), Anaheim, CA, USA, 26–29 November 2018; IEEE: Anaheim, CA, USA, 2018; pp. 743–747. [Google Scholar] [CrossRef]
- Austin, A.E.; Desrosiers, T.A.; Shanahan, M.E. Directed acyclic graphs: An under-utilized tool for child maltreatment research. Child Abus. Negl. 2019, 91, 78–87. [Google Scholar] [CrossRef]
- Waller, I.; Anderson, A. Quantifying social organization and political polarization in online platforms. Nature 2021, 600, 264–268. [Google Scholar] [CrossRef]
- Kubin, E.; von Sikorski, C. The role of (social) media in political polarization: A systematic review. Ann. Int. Commun. Assoc. 2021, 45, 188–206. [Google Scholar] [CrossRef]
- Tokita, C.K.; Guess, A.M.; Tarnita, C.E. Polarized information ecosystems can reorganize social networks via information cascades. Proc. Natl. Acad. Sci. USA 2021, 118, e2102147118. [Google Scholar] [CrossRef]
- Martin, T. community2vec: Vector representations of online communities encode semantic relationships. In Proceedings of the 2nd Workshop on NLP and Computational Social Science (NLP+CSS@ACL 2017), Vancouver, BC, Canada, 3 August 2017; Hovy, D., Volkova, S., Bamman, D., Jurgens, D., O’Connor, B., Tsur, O., Dogruöz, A.S., Eds.; Association for Computational Linguistics: Vancouver, BC, Canada, 2017; pp. 27–31. [Google Scholar] [CrossRef]
- Elson, D.K.; Dames, N.; McKeown, K.R. Extracting Social Networks from Literary Fiction. In Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics (ACL 2010), Uppsala, Sweden, 11–16 July 2010; ACL: Uppsala, Sweden, 2010; pp. 138–147. [Google Scholar]
- Moretti, F. Network theory, plot analysis. New Left Rev. 2011, 2, 80–102. [Google Scholar]
- Agarwal, A.; Kotalwar, A.; Rambow, O. Automatic Extraction of Social Networks from Literary Text: A Case Study on Alice in Wonderland. In Proceedings of the 6th International Joint Conference on Natural Language Processing (IJCNLP 2013), Nagoya, Japan, 14–18 October 2013; Asian Federation of Natural Language Processing/ACL: Nagoya, Japan, 2013; pp. 1202–1208. [Google Scholar]
- Jayannavar, P.; Agarwal, A.; Ju, M.; Rambow, O. Validating Literary Theories Using Automatic Social Network Extraction. In Proceedings of the Workshop on Computational Linguistics for Literature (CLfL@NAACL-HLT 2015), Denver, CO, USA, 4 June 2015; Feldman, A., Kazantseva, A., Szpakowicz, S., Koolen, C., Eds.; The Association for Computer Linguistics: Denver, CO, USA, 2015; pp. 32–41. [Google Scholar] [CrossRef]
- Grayson, S.; Wade, K.; Meaney, G.; Greene, D. The Sense and Sensibility of Different Sliding Windows in Constructing Co-occurrence Networks from Literature. In Proceedings of the Computational History and Data-Driven Humanities International Workshop (CHDDH 2016), Dublin, Ireland, 25 May 2016; Bozic, B., Mendel-Gleason, G., Debruyne, C., O’Sullivan, D., Eds.; Springer: Dublin, Ireland, 2016; Volume 482, pp. 65–77. [Google Scholar] [CrossRef]
- Dekker, N.; Kuhn, T.; van Erp, M. Evaluating social network extraction for classic and modern fiction literature. PeerJ Prepr. 2018, 6, e27263. [Google Scholar] [CrossRef]
- Inoue, N.; Pethe, C.; Kim, A.; Skiena, S. Learning and Evaluating Character Representations in Novels. In Proceedings of the Findings of the Association for Computational Linguistics (ACL 2022), Dublin, Ireland, 22–27 May 2022; Muresan, S., Nakov, P., Villavicencio, A., Eds.; ACL: Dublin, Ireland, 2022; pp. 1008–1019. [Google Scholar] [CrossRef]
- Kounelis, A.; Vikatos, P.; Makris, C. Movie Recommendation System Based on Character Graph Embeddings. In Proceedings of the Artificial Intelligence Applications and Innovations (AIAI 2021), Crete, Greece, 25–27 June 2021; Maglogiannis, I., MacIntyre, J., Iliadis, L., Eds.; Springer: Crete, Greece, 2021; Volume 628, pp. 418–430. [Google Scholar] [CrossRef]
- Riedl, M.O. Computational Narrative Intelligence: A Human-Centered Goal for Artificial Intelligence. arXiv 2016, arXiv:1602.06484. [Google Scholar]
- Na, G.S.; Jang, S.; Lee, Y.L.; Chang, H. Tuplewise material representation based machine learning for accurate band gap prediction. J. Phys. Chem. 2020, 124, 10616–10623. [Google Scholar] [CrossRef]
- Wang, H.; Wang, K.; Yang, J.; Shen, L.; Sun, N.; Lee, H.; Han, S. GCN-RL Circuit Designer: Transferable Transistor Sizing with Graph Neural Networks and Reinforcement Learning. In Proceedings of the 57th Design Automation Conference (DAC 2020), San Francisco, CA, USA, 20–24 July 2020; IEEE: San Francisco, CA, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Y.; Madhusudan, M.; Sharma, A.K.; Xu, W.; Sapatnekar, S.S.; Harjani, R.; Hu, J. A Customized Graph Neural Network Model for Guiding Analog IC Placement. In Proceedings of the 39th International Conference On Computer Aided Design (ICCAD 2020), San Diego, CA, USA, 2–5 November 2020; IEEE: San Diego, CA, USA, 2020; pp. 135.1–135.9. [Google Scholar] [CrossRef]
- Lu, Y.; Nath, S.; Khandelwal, V.; Lim, S.K. Doomed Run Prediction in Physical Design by Exploiting Sequential Flow and Graph Learning. In Proceedings of the 40th International Conference On Computer Aided Design (ICCAD 2021), Munich, Germany, 1–4 November 2021; IEEE: Munich, Germany, 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Gallo, C.; Capozzi, V. A Wafer Bin Map “Relaxed” Clustering Algorithm for Improving Semiconductor Production Yield. Open Comput. Sci. 2020, 10, 231–245. [Google Scholar] [CrossRef]
- Ko, Y.; Fujita, H. An evidential analytics for buried information in big data samples: Case study of semiconductor manufacturing. Inf. Sci. 2019, 486, 190–203. [Google Scholar] [CrossRef]
- Mirhoseini, A.; Goldie, A.; Yazgan, M.; Jiang, J.W.; Songhori, E.M.; Wang, S.; Lee, Y.; Johnson, E.; Pathak, O.; Nazi, A.; et al. A graph placement methodology for fast chip design. Nature 2021, 594, 207–212. [Google Scholar] [CrossRef] [PubMed]
- Schulz, B.; Jacobi, C.; Gisbrecht, A.; Evangelos, A.; Chan, C.W.; Gan, B.P. Graph Representation and Embedding for Semiconductor Manufacturing Fab States. In Proceedings of the Winter Simulation Conference (WSC 2022), Singapore, 11–14 December 2022; IEEE: Singapore, 2022; pp. 3382–3393. [Google Scholar] [CrossRef]
- Jiao, X.; Li, X.; Lin, D.; Xiao, W. A Graph Neural Network based Deep Learning Predictor for Spatio-Temporal Group Solar Irradiance Forecasting. IEEE Trans. Ind. Inform. 2021, 18, 6142–6149. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. Photovoltaic power forecasting based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Lira, H.; Martí, L.; Sanchez-Pi, N. A Graph Neural Network with Spatio-Temporal Attention for Multi-Sources Time Series Data: An Application to Frost Forecast. Sensors 2022, 22, 1486. [Google Scholar] [CrossRef]
- Lin, H.; Gao, Z.; Xu, Y.; Wu, L.; Li, L.; Li, S.Z. Conditional Local Convolution for Spatio-Temporal Meteorological Forecasting. In Proceedings of the 36th Conference on Artificial Intelligence (AAAI 2022), Virtual Event, 22 February–1 March 2022; AAAI Press: Virtual Event, 2022; pp. 7470–7478. [Google Scholar]
- Jeon, H.J.; Choi, M.W.; Lee, O.-J. Day-Ahead Hourly Solar Irradiance Forecasting Based on Multi-Attributed Spatio-Temporal Graph Convolutional Network. Sensors 2022, 22, 7179. [Google Scholar] [CrossRef]
- Xiao, X.; Jin, Z.; Wang, S.; Xu, J.; Peng, Z.; Wang, R.; Shao, W.; Hui, Y. A dual-path dynamic directed graph convolutional network for air quality prediction. Sci. Total. Environ. 2022, 827, 154298. [Google Scholar] [CrossRef]
- Han, J.; Liu, H.; Zhu, H.; Xiong, H.; Dou, D. Joint Air Quality and Weather Prediction Based on Multi-Adversarial Spatiotemporal Networks. In Proceedings of the 35th Conference on Artificial Intelligence (AAAI 2021), Virtual Event, 2–9 February 2021; AAAI Press: Virtual Event, 2021; pp. 4081–4089. [Google Scholar] [CrossRef]
- Han, J.; Liu, H.; Zhu, H.; Xiong, H. Kill Two Birds with One Stone: A Multi-View Multi-Adversarial Learning Approach for Joint Air Quality and Weather Prediction. IEEE Trans. Knowl. Data Eng. 2023, 1–14. [Google Scholar] [CrossRef]
- Yano, K.; Shiina, T.; Kurata, S.; Kato, A.; Komaki, F.; Sakai, S.; Hirata, N. Graph-Partitioning Based Convolutional Neural Network for Earthquake Detection Using a Seismic Array. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020269. [Google Scholar] [CrossRef]
- van den Ende, M.P.A.; Ampuero, J.P. Automated Seismic Source Characterization Using Deep Graph Neural Networks. Geophys. Res. Lett. 2020, 47, e2020GL088690. [Google Scholar] [CrossRef]
- Zhang, X.; Reichard-Flynn, W.; Zhang, M.; Hirn, M.; Lin, Y. Spatiotemporal Graph Convolutional Networks for Earthquake Source Characterization. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024401. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Dong, J.; Sun, X.; Lima, E.; Mu, Q.; Wang, X. A CFCC-LSTM Model for Sea Surface Temperature Prediction. IEEE Geosci. Remote. Sens. Lett. 2018, 15, 207–211. [Google Scholar] [CrossRef]
- Jia, X.; Ji, Q.; Han, L.; Liu, Y.; Han, G.; Lin, X. Prediction of Sea Surface Temperature in the East China Sea Based on LSTM Neural Network. Remote. Sens. 2022, 14, 3300. [Google Scholar] [CrossRef]
- Sun, Y.; Yao, X.; Bi, X.; Huang, X.; Zhao, X.; Qiao, B. Time-Series Graph Network for Sea Surface Temperature Prediction. Big Data Res. 2021, 25, 100237. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Frery, A.C.; Ren, P. Sea Surface Temperature Prediction With Memory Graph Convolutional Networks. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Lam, R.; Sanchez-Gonzalez, A.; Willson, M.; Wirnsberger, P.; Fortunato, M.; Pritzel, A.; Ravuri, S.V.; Ewalds, T.; Alet, F.; Eaton-Rosen, Z.; et al. GraphCast: Learning skillful medium-range global weather forecasting. arXiv 2022, arXiv:2212.12794. [Google Scholar] [CrossRef]
- Shi, N.; Xu, J.; Wurster, S.W.; Guo, H.; Woodring, J.; Van Roekel, L.P.; Shen, H.W. GNN-Surrogate: A Hierarchical and Adaptive Graph Neural Network for Parameter Space Exploration of Unstructured-Mesh Ocean Simulations. IEEE Trans. Vis. Comput. Graph. 2022, 28, 2301–2313. [Google Scholar] [CrossRef]
- Cachay, S.R.; Erickson, E.; Bucker, A.F.C.; Pokropek, E.; Potosnak, W.; Bire, S.; Osei, S.; Lütjens, B. The World as a Graph: Improving El Niño Forecasts with Graph Neural Networks. arXiv 2021, arXiv:2104.05089. [Google Scholar]
- Mu, B.; Qin, B.; Yuan, S. ENSO-ASC 1.0.0: ENSO deep learning forecast model with a multivariate air–sea coupler. Geosci. Model Dev. 2021, 14, 6977–6999. [Google Scholar] [CrossRef]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Gallagher, B.; Eliassi-Rad, T. Collective Classification in Network Data. AI Mag. 2008, 29, 93–106. [Google Scholar] [CrossRef]
- Lim, K.W.; Buntine, W.L. Bibliographic Analysis with the Citation Network Topic Model. In Proceedings of the 6th Asian Conference on Machine Learning (ACML 2014), Nha Trang City, Vietnam, 26–28 November 2014; JMLR.org: Nha Trang City, Vietnam, 2014; Volume 39. [Google Scholar]
- Tang, J.; Zhang, J.; Yao, L.; Li, J.; Zhang, L.; Su, Z. ArnetMiner: Extraction and mining of academic social networks. In Proceedings of the 14th International Conference on Knowledge Discovery and Data Mining (SIGKDD 2008), Las Vegas, NV, USA, 24–27 August 2008; ACM: Las Vegas, NV, USA, 2008; pp. 990–998. [Google Scholar] [CrossRef]
- McAuley, J.J.; Leskovec, J. Learning to Discover Social Circles in Ego Networks. In Proceedings of the 26th Annual Conference on Neural Information Processing Systems (NeurIPS 2012), Lake Tahoe, NV, USA, 3–6 December 2012; NeurIPS: Lake Tahoe, NV, USA, 2012; pp. 548–556. [Google Scholar]
- Debnath, A.K.; Lopez de Compadre, R.L.; Debnath, G.; Shusterman, A.J.; Hansch, C. Structure-activity relationship of mutagenic aromatic and heteroaromatic nitro compounds. Correlation with molecular orbital energies and hydrophobicity. J. Med. Chem. 1991, 34, 786–797. [Google Scholar] [CrossRef] [PubMed]
- Borgwardt, K.M.; Ong, C.S.; Schönauer, S.; Vishwanathan, S.V.N.; Smola, A.J.; Kriegel, H. Protein function prediction via graph kernels. In Proceedings of the 13th International Conference on Intelligent Systems for Molecular Biology (ISMB 2005), Detroit, MI, USA, 25–29 June 2005; Oxford University Press: Detroit, MI, USA, 2005; pp. 47–56. [Google Scholar] [CrossRef]
- Jin, D.; Huo, C.; Liang, C.; Yang, L. Heterogeneous Graph Neural Network via Attribute Completion. In Proceedings of the Web Conference (WWW 2021), Ljubljana, Slovenia, 19–23 April 2021; Leskovec, J., Grobelnik, M., Najork, M., Tang, J., Zia, L., Eds.; ACM/IW3C2: Virtual Event, 2021; pp. 391–400. [Google Scholar] [CrossRef]
- Sun, Y.; Han, J.; Yan, X.; Yu, P.S.; Wu, T. PathSim: Meta Path-Based Top-K Similarity Search in Heterogeneous Information Networks. Proc. VLDB Endow. 2011, 4, 992–1003. [Google Scholar] [CrossRef]
- Zafarani, R.; Liu, H. Social Computing Data Repository at ASU. 2009. Available online: http://socialcomputing.asu.edu (accessed on 16 April 2023).
- Zhang, X.; Zhao, J.; LeCun, Y. Character-Level Convolutional Networks for Text Classification. arXiv 2015, arXiv:1509.01626. [Google Scholar]
- Kunegis, J. KONECT: The Koblenz network collection. In Proceedings of the 22nd International World Wide Web Conference (WWW 2013), Rio de Janeiro, Brazil, 13–17 May 2013; Carr, L., Laender, A.H.F., Lóscio, B.F., King, I., Fontoura, M., Vrandecic, D., Aroyo, L., de Oliveira, J.P.M., Lima, F., Wilde, E., Eds.; International World Wide Web Conferences Steering Committee/ACM: Rio de Janeiro, Brazil, 2013; pp. 1343–1350. [Google Scholar] [CrossRef]
- Tang, J.; Gao, H.; Liu, H. mTrust: Discerning multi-faceted trust in a connected world. In Proceedings of the 5th International Conference on Web Search and Web Data Mining (WSDM 2012), Seattle, WA, USA, 8–12 February 2012; Adar, E., Teevan, J., Agichtein, E., Maarek, Y., Eds.; ACM: Seattle, WA, USA, 2012; pp. 93–102. [Google Scholar] [CrossRef]
- Gehrke, J.; Ginsparg, P.; Kleinberg, J.M. Overview of the 2003 KDD Cup. SIGKDD Explor. 2003, 5, 149–151. [Google Scholar] [CrossRef]
- Leskovec, J.; Krevl, A. SNAP Datasets: Stanford Large Network Dataset Collection. 2014. Available online: http://snap.stanford.edu/data (accessed on 16 April 2023).
- Leskovec, J.; Lang, K.J.; Dasgupta, A.; Mahoney, M.W. Community Structure in Large Networks: Natural Cluster Sizes and the Absence of Large Well-Defined Clusters. Internet Math. 2009, 6, 29–123. [Google Scholar] [CrossRef]
- Lippmann, R.; Cunningham, R.K.; Fried, D.J.; Graf, I.; Kendall, K.R.; Webster, S.E.; Zissman, M.A. Results of the DARPA 1998 Offline Intrusion Detection Evaluation. In Proceedings of the Recent Advances in Intrusion Detection, Second International Workshop, (RAID 1999), West Lafayette, IN, USA, 7–9 September 1999; Springer: West Lafayette, IN, USA, 1999. [Google Scholar]
- Zafarani, R.; Liu, H. Users Joining Multiple Sites: Distributions and Patterns. In Proceedings of the 8th International Conference on Weblogs and Social Media (ICWSM 2014), Ann Arbor, MI, USA, 1–4 June 2014; Adar, E., Resnick, P., Choudhury, M.D., Hogan, B., Oh, A., Eds.; AAAI Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Furey, T.S.; Cristianini, N.; Duffy, N.; Bednarski, D.W.; Schummer, M.; Haussler, D. Support vector machine classification and validation of cancer tissue samples using microarray expression data. Bioinformatics 2000, 16, 906–914. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, J.; Shi, C.; Zhuang, F.; Li, J.; Wu, B. Recommendation in heterogeneous information network via dual similarity regularization. Int. J. Data Sci. Anal. 2017, 3, 35–48. [Google Scholar] [CrossRef]
- Ali, Z.; Kefalas, P.; Muhammad, K.; Ali, B.; Imran, M. Deep learning in citation recommendation models survey. Expert Syst. Appl. 2020, 162, 113790. [Google Scholar] [CrossRef]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
- Wang, M.; Zheng, D.; Ye, Z.; Gan, Q.; Li, M.; Song, X.; Zhou, J.; Ma, C.; Yu, L.; Gai, Y.; et al. Deep Graph Library: A Graph-Centric, Highly-Performant Package for Graph Neural Networks. arXiv 2019, arXiv:1909.01315. [Google Scholar]
- Cen, Y.; Hou, Z.; Wang, Y.; Chen, Q.; Luo, Y.; Yao, X.; Zeng, A.; Guo, S.; Zhang, P.; Dai, G.; et al. CogDL: An Extensive Toolkit for Deep Learning on Graphs. arXiv 2021, arXiv:2103.00959. [Google Scholar]
- Liu, M.; Luo, Y.; Wang, L.; Xie, Y.; Yuan, H.; Gui, S.; Yu, H.; Xu, Z.; Zhang, J.; Liu, Y.; et al. DIG: A Turnkey Library for Diving into Graph Deep Learning Research. J. Mach. Learn. Res. 2021, 22, 240.1–240.9. [Google Scholar]
- Zhu, Z.; Xu, S.; Tang, J.; Qu, M. GraphVite: A High-Performance CPU-GPU Hybrid System for Node Embedding. In Proceedings of the World Wide Web Conference (WWW 2019), San Francisco, CA, USA, 13–17 May 2019; Liu, L., White, R.W., Mantrach, A., Silvestri, F., McAuley, J.J., Baeza-Yates, R., Zia, L., Eds.; ACM: San Francisco, CA, USA, 2019; pp. 2494–2504. [Google Scholar] [CrossRef]
- Zhu, R.; Zhao, K.; Yang, H.; Lin, W.; Zhou, C.; Ai, B.; Li, Y.; Zhou, J. AliGraph: A comprehensive graph neural network platform. Proc. Vldb Endow. 2019, 12, 2094–2105. [Google Scholar] [CrossRef]
- Sonthalia, R.; Gilbert, A.C. Tree! I am no Tree! I am a low dimensional Hyperbolic Embedding. In Proceedings of the 33rd Annual Conference on Neural Information Processing Systems (NeurIPS 2020), Virtual Event, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; NeurIPS: Virtual Event, 2020. [Google Scholar]
- Lou, A.; Katsman, I.; Jiang, Q.; Belongie, S.; Lim, S.N.; De Sa, C. Differentiating through the FréChet Mean. In Proceedings of the 37th International Conference on Machine Learning (ICML 2020), Vienna, Austria, 13–18 July 2020; JMLR.org: Vienna, Austria, 2020. [Google Scholar]
- Shu, J.; Xi, B.; Li, Y.; Wu, F.; Kamhoua, C.A.; Ma, J. Understanding Dropout for Graph Neural Networks. In Proceedings of the Companion of The Web Conference 2022 (WWW 2022), Lyon, France, 25–29 April 2022; Laforest, F., Troncy, R., Simperl, E., Agarwal, D., Gionis, A., Herman, I., Médini, L., Eds.; ACM: Lyon, France, 2022; pp. 1128–1138. [Google Scholar] [CrossRef]
- Papp, P.A.; Martinkus, K.; Faber, L.; Wattenhofer, R. DropGNN: Random Dropouts Increase the Expressiveness of Graph Neural Networks. In Proceedings of the 34th Annual Conference on Neural Information Processing Systems 2021 (NeurIPS 2021), Virtual Event, 6–14 December 2021; Ranzato, M., Beygelzimer, A., Dauphin, Y.N., Liang, P., Vaughan, J.W., Eds.; NeurIPS: Virtual Event, 2021; pp. 21997–22009. [Google Scholar]
- Rong, Y.; Huang, W.; Xu, T.; Huang, J. DropEdge: Towards Deep Graph Convolutional Networks on Node Classification. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), Addis Ababa, Ethiopia, 26–30 April 2020; OpenReview.net: Addis Ababa, Ethiopia, 2020. [Google Scholar]
- Chien, E.; Peng, J.; Li, P.; Milenkovic, O. Adaptive Universal Generalized PageRank Graph Neural Network. In Proceedings of the 9th International Conference on Learning Representations (ICLR 2021), Vienna, Austria, 3–7 May 2021; OpenReview.net: Vienna, Austria, 2021. [Google Scholar]
- Yun, S.; Jeong, M.; Kim, R.; Kang, J.; Kim, H.J. Graph Transformer Networks. In Proceedings of the 32nd Annual Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; NeurIPS: Vancouver, BC, Canada, 2019; pp. 11960–11970. [Google Scholar]
- Yang, F.; Fan, K.; Song, D.; Lin, H. Graph-based prediction of Protein-protein interactions with attributed signed graph embedding. BMC Bioinform. 2020, 21, 1–16. [Google Scholar] [CrossRef]
- Xie, Y.; Li, S.; Yang, C.; Wong, R.C.; Han, J. When Do GNNs Work: Understanding and Improving Neighborhood Aggregation. In Proceedings of the 29th International Joint Conference on Artificial Intelligence (IJCAI 2020), Yokohama, Japan, 7–15 January 2021; Bessiere, C., Ed.; ijcai.org: Yokohama, Japan, 2020; pp. 1303–1309. [Google Scholar] [CrossRef]
- Pan, S.; Wu, J.; Zhu, X.; Zhang, C.; Wang, Y. Tri-Party Deep Network Representation. In Proceedings of the 25th International Joint Conference on Artificial Intelligence (IJCAI 2016), New York, NY, USA, 9–15 July 2016; IJCAI Press: New York, NY, USA, 2016; pp. 1895–1901. [Google Scholar]
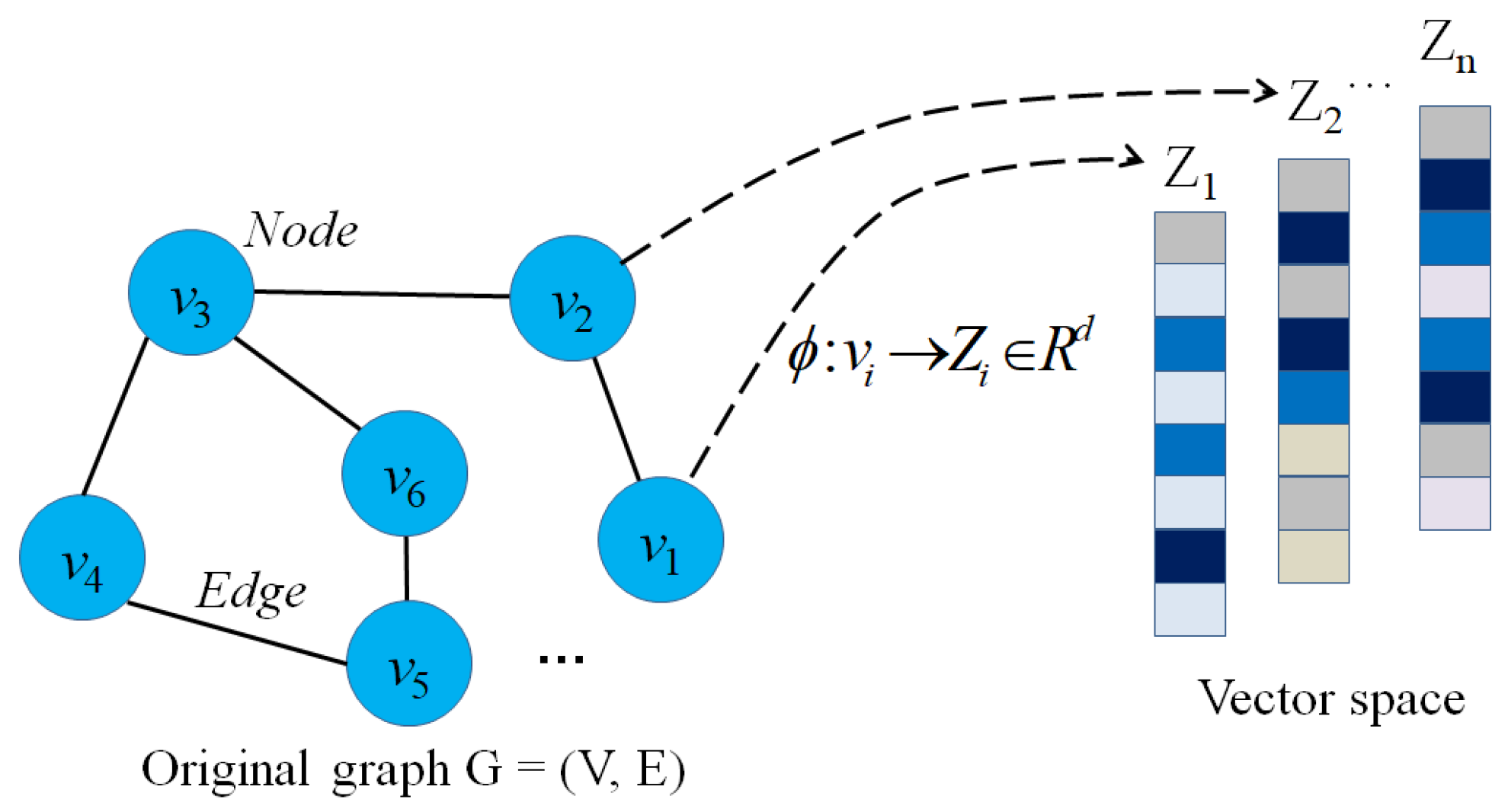
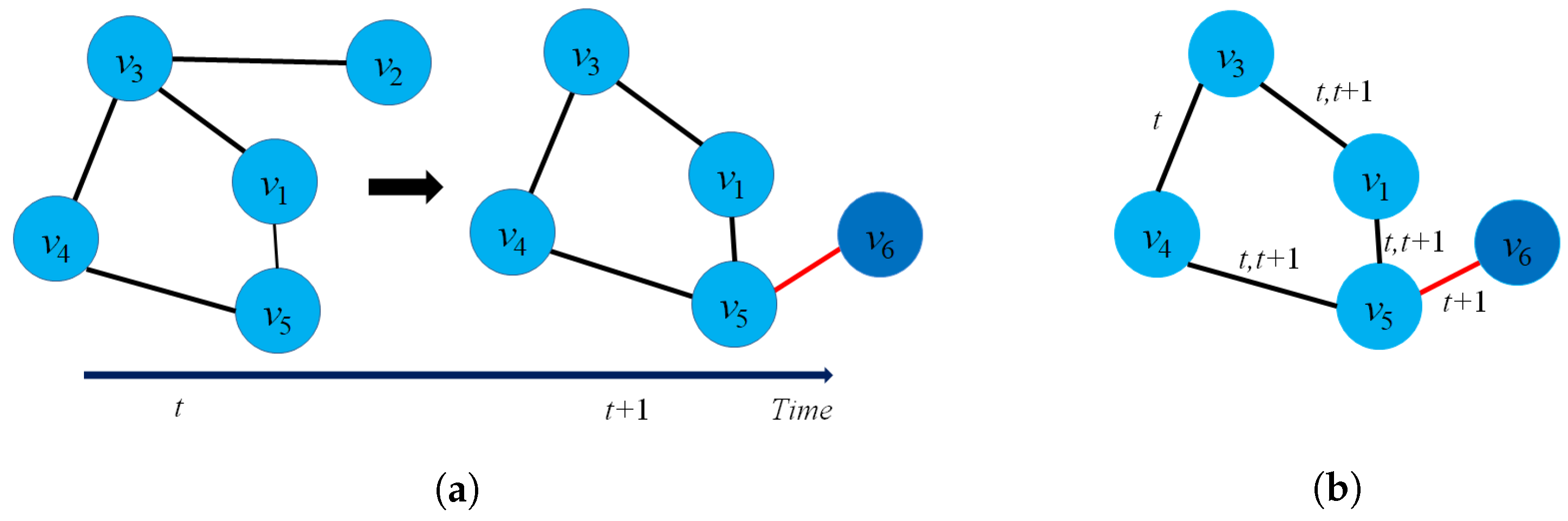
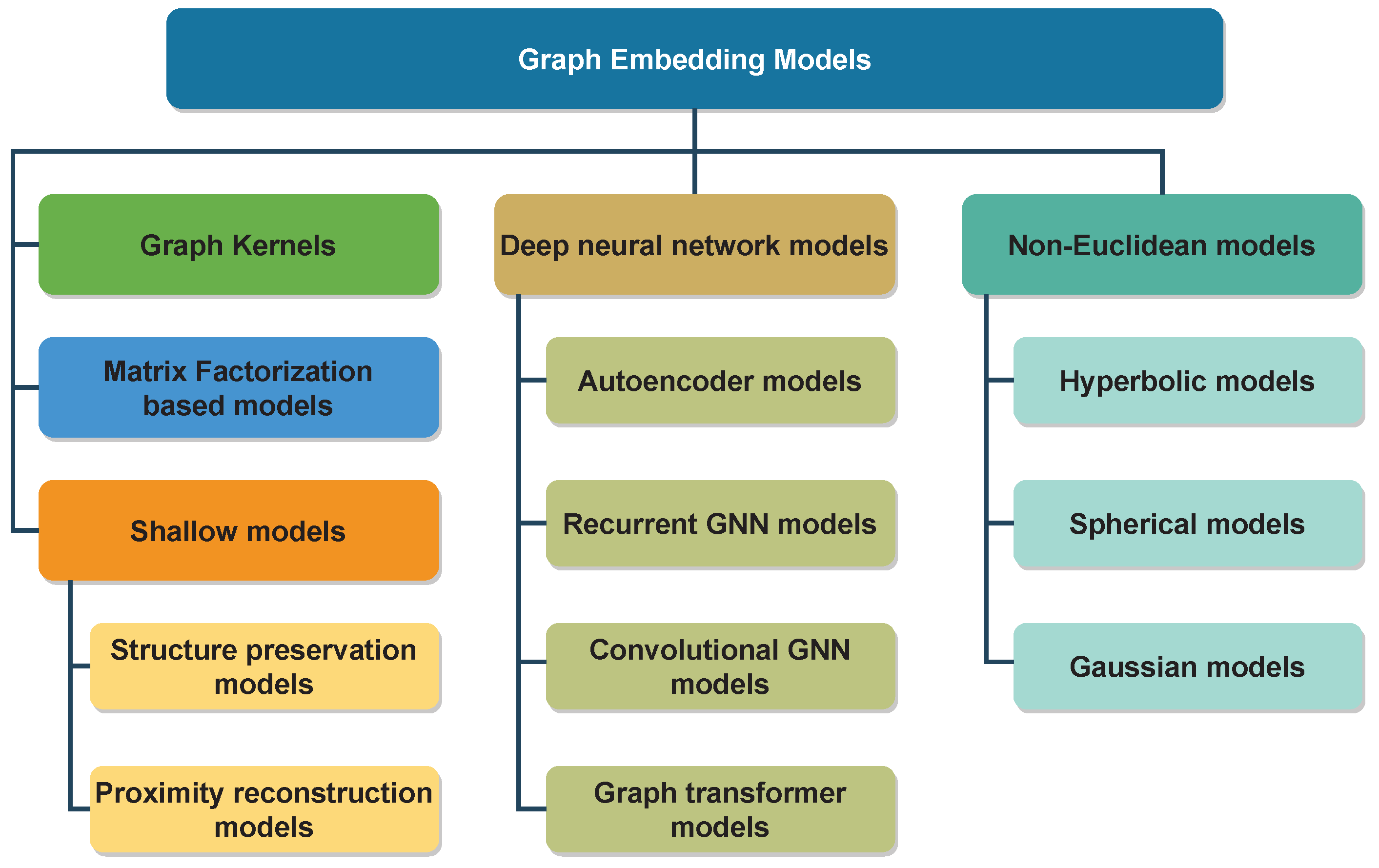
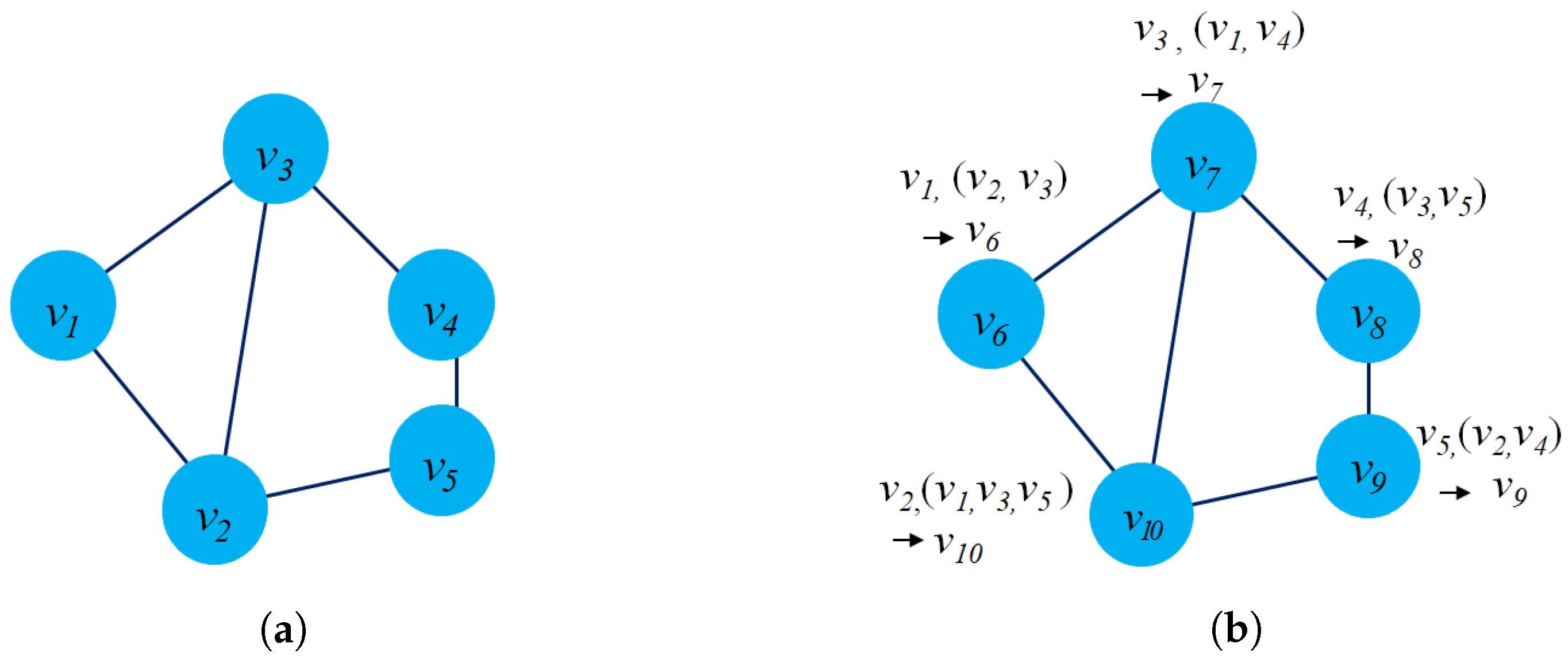
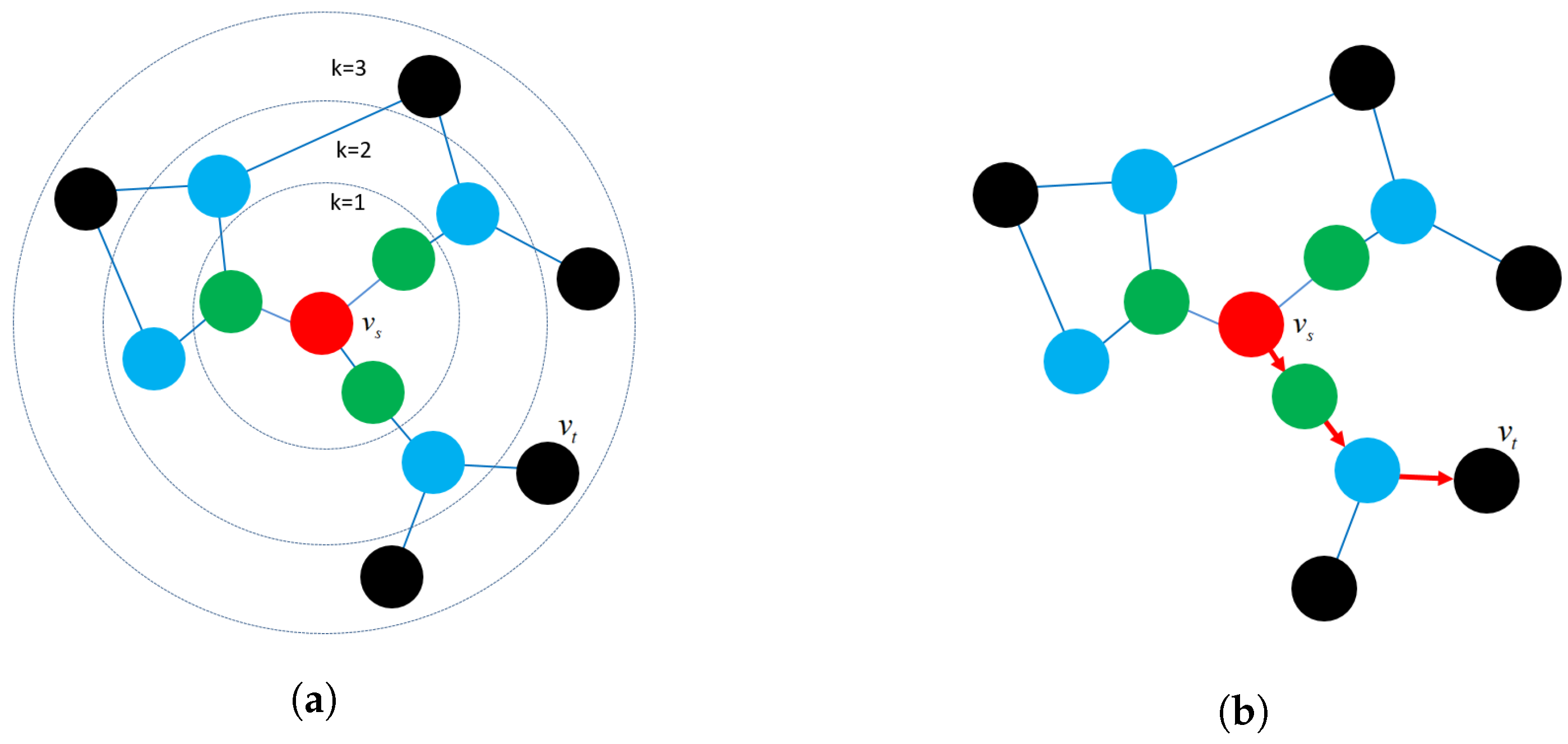
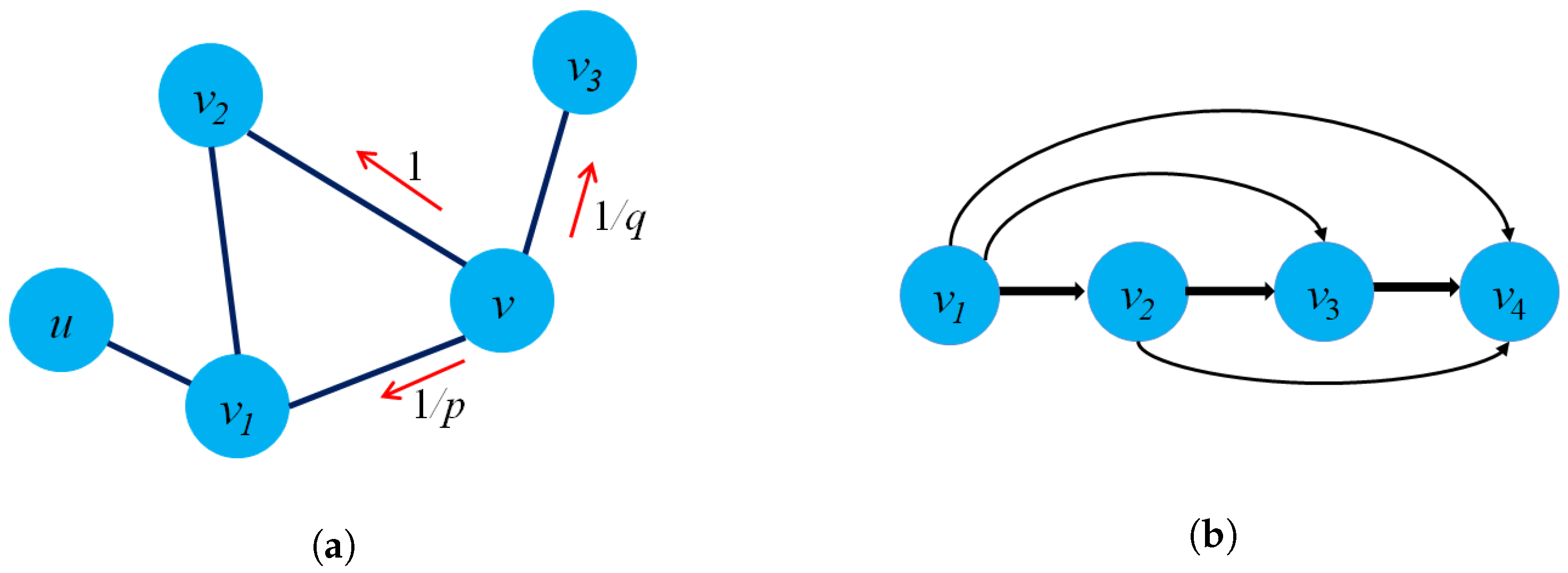
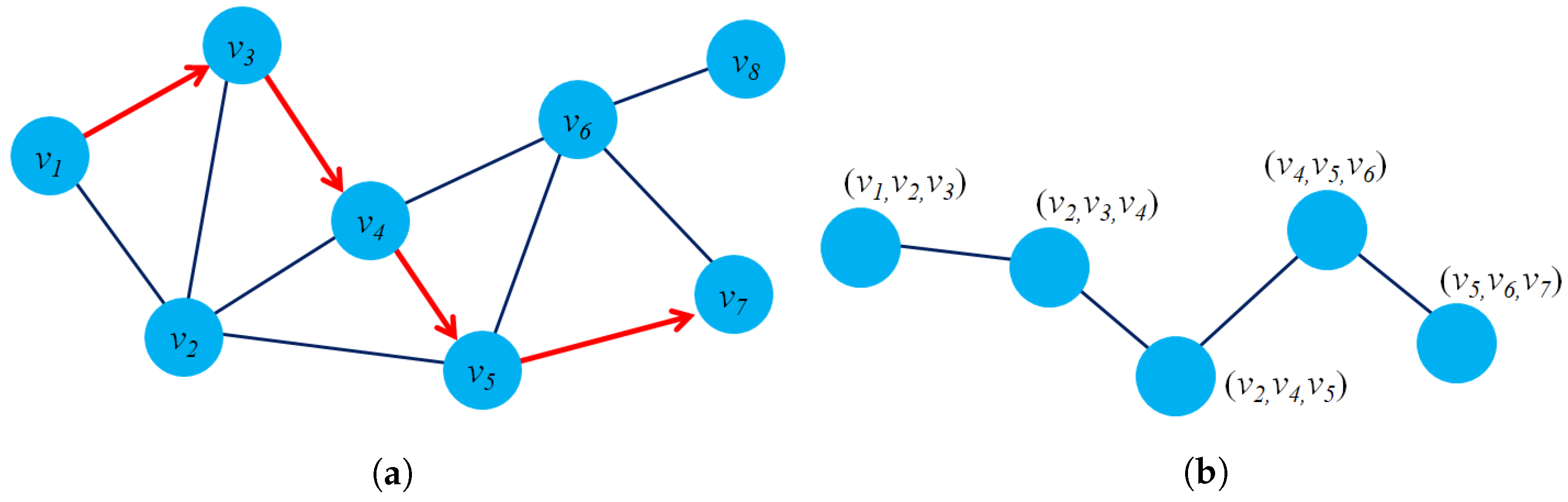
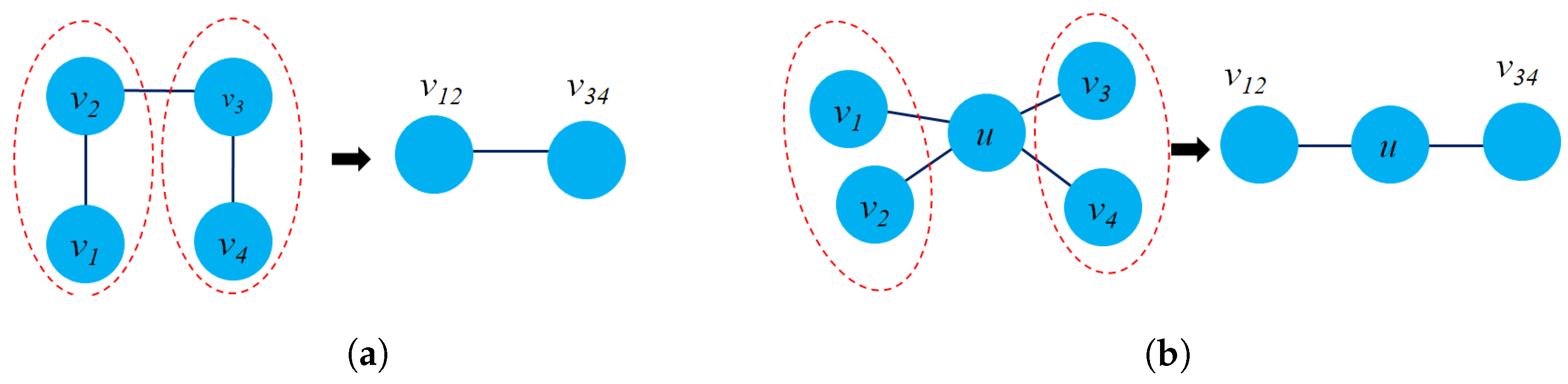


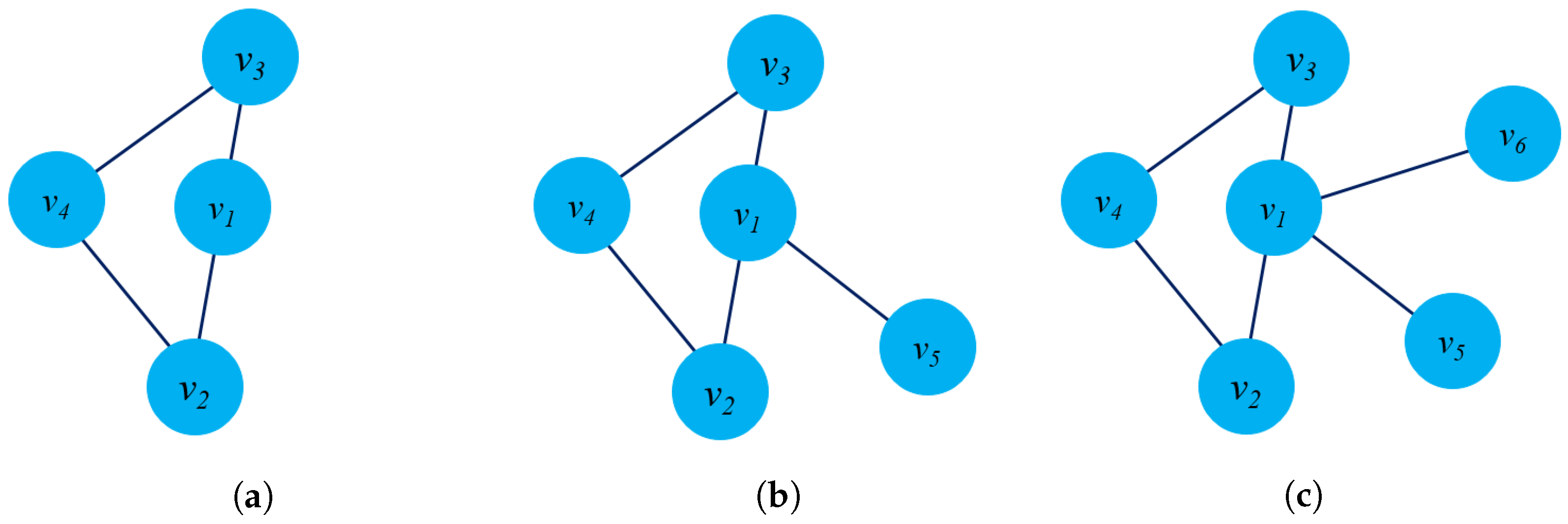
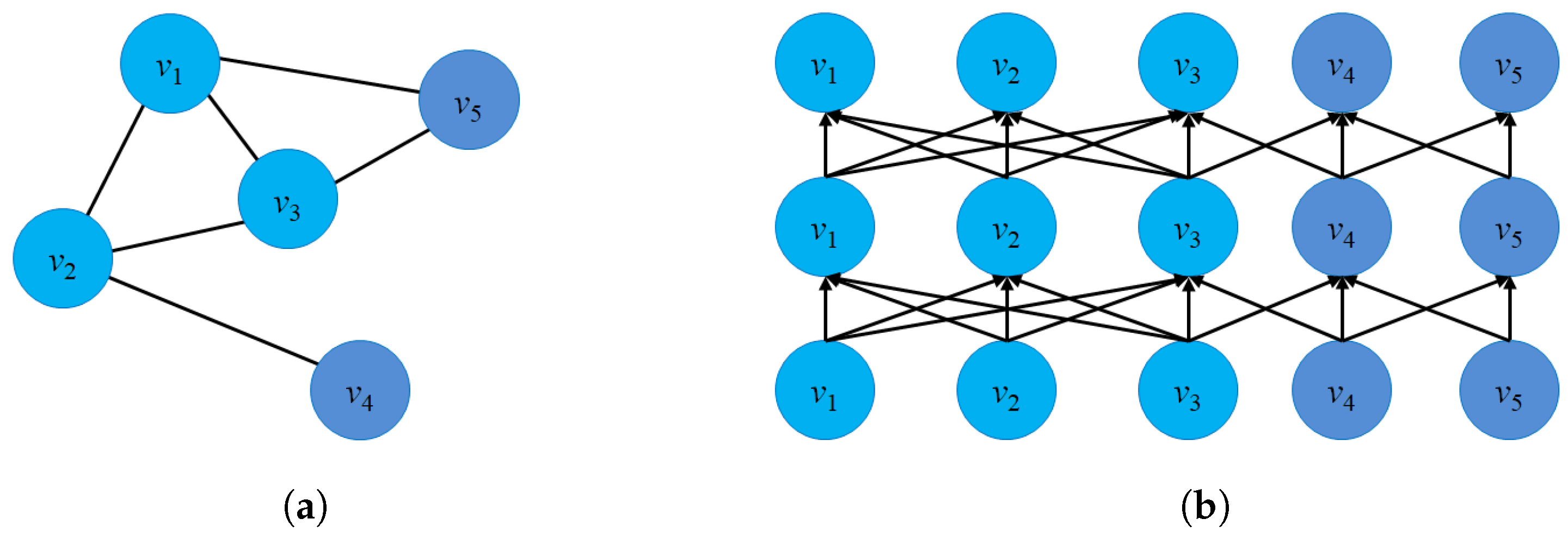
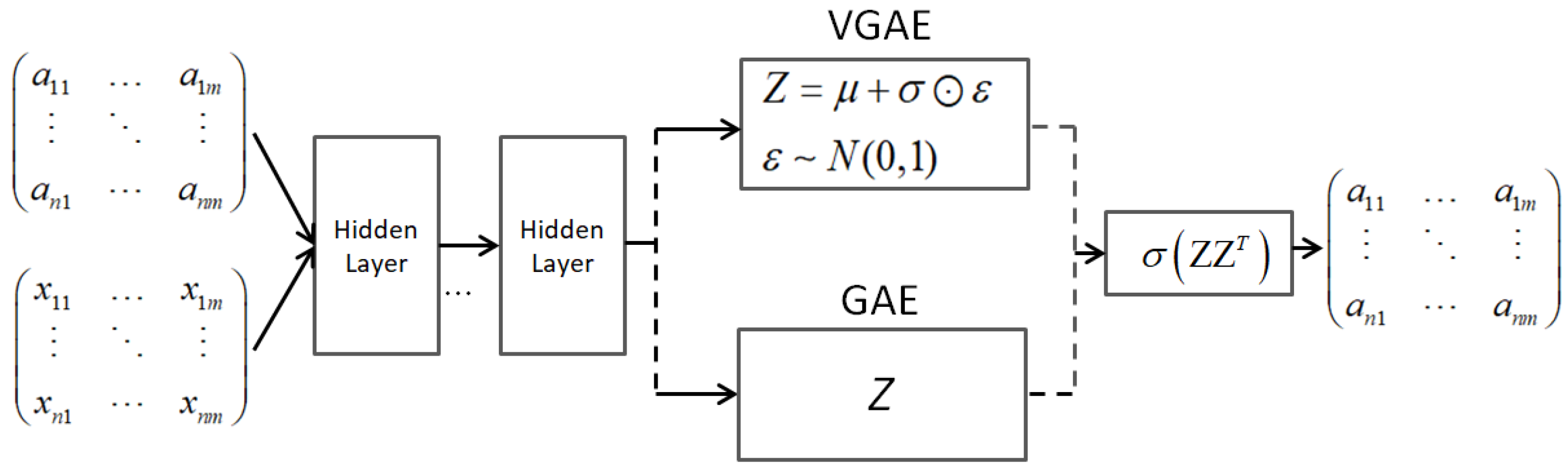
| Notations | Descriptions |
|---|---|
| V | The set of nodes in the graph G |
| E | The set of edges in graph G |
| N | The number of nodes in graph G |
| The set of edges with type t in heterogeneous graphs | |
| The node in the graph G | |
| The edge in the graph G | |
| A | The adjacency matrix of the graph G |
| X | The feature matrix of nodes in graph G |
| D | The degree matrix of nodes in graph G |
| Projection function | |
| The embedding vector of node | |
| M | The transition matrix |
| The set of neighbors of node | |
| k | The k-hop distance from a target node to other nodes |
| d | The dimension of vector in latent space |
| The label of node |
| Models | Graph Types | Tasks | Loss Function |
|---|---|---|---|
| [83] | Static graphs | Graph comparison | |
| [106] | Static graphs | Graph comparison | |
| [33] | Static graphs | Graph classification | |
| [34] | Static graphs | Graph classification | |
| [84] | Static graphs | Graph classification | |
| [35] | Static graphs | Graph classification | |
| [85] | Static graphs | Graph comparison | |
| [107] | Attributed graphs | Graph classification | |
| [37] | Attributed graphs | Graph classification | |
| [108] | Attributed graphs | Graph classification | |
| [36] | Attributed graphs | Graph classification | |
| [109] | Attributed graphs | Graph classification | |
| [110] | Attributed graphs | Graph classification | |
| GraTFEL [111] | Dynamic graphs | Graph reconstruction Link prediction | |
| [112] | Dynamic graphs | Link prediction | |
| [113] | Dynamic graphs | Link prediction |
| Models | Graph Types | Tasks | Loss Function |
|---|---|---|---|
| MBRep [90] | Hypergraphs | Link prediction | |
| Motif2Vec [87] | Heterogeneous graphs | Node classification link prediction | |
| JUST [159] | Heterogeneous graphs | Node classification Node clustering | |
| [160] | Multiplex graphs | Link prediction | |
| BHIN2Vec [161] | Heterogeneous graph | Node classification | |
| [162] | Heterogeneous graphs | Link prediction | |
| [163] | Heterogeneous graphs | Link prediction | |
| [164] | Heterogeneous graphs | Link prediction | |
| [165] | Heterogeneous graphs | Link prediction | |
| [166] | Heterogeneous graphs | Entities prediction | |
| MrMine [167] | Multiplex graphs | Graph classification | |
| [168] | Heterogeneous graph | Link prediction | |
| [169] | Dynamic graphs | Node classification | |
| [170] | Dynamic graphs | Node classification | |
| [171] | Dynamic graphs | Link prediction | |
| STWalk [172] | Dynamic graphs | Node classification | |
| [173] | Dynamic graphs | Node classification, Link prediction | |
| [174] | Dynamic graphs | Link prediction, Node classification | |
| Dyn2Vec [10] | Dynamic graphs | Node classification | |
| [92] | Dynamic graphs | Link prediction | |
| T-EDGE [175] | Dynamic graphs | Node classification | |
| LBSN2Vec [157] | Hyper graphs | Link prediction | |
| [158] | Hyper graphs | Link prediction |
| Models | Graph Types | Objective | Loss Function |
|---|---|---|---|
| SDNE [50] | Static graphs | 1st-order proximity, 2nd-order proximity | . |
| DHNE [51] | Hyper graphs | 1st-order proximity, 2nd-order proximity | . |
| DNE-SBP [197] | Signed graphs | 1st-order proximity | . |
| DynGEM [198] | Dynamic graphs | 1st-order proximity, 2nd-order proximity | . |
| NetWalk [199] | Dynamic graphs | Random walk | . |
| DNGR [196] | Static graphs | PPMI matrix | . |
| Model | Graph Type | Sampling Strategy | Loss Function |
|---|---|---|---|
| [44] | Hypergraphs | Local transition function | |
| [45] | Homogeneous graphs | Local transition function | |
| [57] | Weighted graphs | Node-weight sequences | , p(vi, vj) = SoftMax (Zj) |
| [202] | Dynamic graphs | Random walk, Shortest paths, BFS | |
| LSTM-Node2Vec [203] | Dynamic graphs | Temporal random walk | |
| E-LSTM-D [204] | Dynamic graphs | 1st-order proximity | |
| Dyngraph2Vec-AERNN [201] | Dynamic graphs | Adjacency matrix | |
| Topo-LSTM [49] | Directed graphs | Diffusion structure | |
| SHNE [48] | Heterogeneous graphs | Random walk Meta-path | |
| [17] | Directed graphs | Transition matrix | |
| GraphRNA [93] | Attributed graph | Random walk | |
| [205] | Labeled graphs | Random walks, shortest paths, and breadth-first search. | |
| [206] | Dynamic graphs | Graph reconstruction | |
| Camel [207] | Heterogeneous graphs | Link prediction | |
| TaPEm [208] | Heterogeneous graphs | Link prediction | |
| [209] | Heterogeneous graphs | Link prediction |
| Model | Graph Type | Tasks | Loss Function |
|---|---|---|---|
| [56] | Static graphs | Node classification | |
| [96] | Static graphs | Node classification | |
| [210] | Static graphs | Multi-task prediction Node classification | |
| [211] | Static graphs | Label classification | |
| GCN [18] | Knowledge graphs | Node classification | |
| EGCN [55] | Static graphs | Multi-task classification, Link prediction | |
| LNPP [212] | Static graphs | Graph Reconstruction | |
| [213] | Static graphs | Node classification | |
| [214] | Static graphs | Node classification | |
| [215] | Heterogeneous graphs | Node classification |
| Model | Graph Type | Tasks | Loss Function |
|---|---|---|---|
| HCNP [217] | Static graphs | Node classification | |
| CDMG [218] | Static graphs | Community detection | |
| [219] | Static graphs | Passenger Prediction | |
| ST-GDN [220] | Static graphs | Link prediction | |
| [221] | Static graphs | Node classification | |
| MPNNs [222] | Static graphs | Node prediction | |
| GraphSAGE [22] | Static graphs | Node classification | |
| FastGCN [52] | Static graphs | Node classification, link prediction | |
| SACNNs [223] | Static graphs | Node classification Regression tasks | |
| Cluster-GCN [95] | Static graphs | Node classification | |
| [18] | Static graphs | Node classification | |
| [224] | Static graphs | Node classification | |
| GraphSAINT [53] | Static graphs | Node classification Community prediction | |
| VGAE [72] | Static graphs | Link prediction | |
| PinSAGE [225] | Static graphs | Link prediction | |
| Hi-GCN [54] | Static graphs | Classification tasks | |
| [226] | Static graphs | Link prediction | |
| [28] | Static graph | Node classification | |
| [26] | Static graph | Node classification | |
| [227] | Static graphs | Classification tasks | |
| [228] | Static graph | Node Classification Link prediction | |
| [229] | Static graphs | Node classification Link prediction | |
| DCRNN [230] | Static graphs | Node classification | |
| PinSAGE [225] | Static graphs | Link prediction | |
| E-GraphSAGE [231] | Static graph | Edge classification | |
| GraphNorm [232] | Static graphs | Graph classification | |
| GIN [24] | Heterogeneous graphs | Node classification, Graph classification | |
| DeeperGCN [98] | Static graphs | Node property prediction, Graph property prediction | |
| PHC-GNNs [233] | Static graphs | Graph classification | |
| HGNN [27] | Hypergraphs | Node classification, Recognition tasks. | |
| HyperGCN [234] | Hypergraphs | Node classification |
| Model | Graph Type | Tasks | Loss Function |
|---|---|---|---|
| SHARE [235] | Dynamic graphs | Availability prediction | |
| Dyn-GRCNN [236] | Dynamic graphs | Traffic flow forecasting | |
| STAN [237] | Dynamic graphs | Fraud detection | |
| SeqGNN [238] | Dynamic graphs | Traffic speed prediction | |
| DMVST-Net [239] | Dynamic graphs | Taxi demand prediction | |
| ST-ResNet [240] | Dynamic graphs | Flow prediction | |
| R-GCNs [241] | Knowledge graphs | Entity classification | |
| HDMI [242] | Multiplex graphs | Node clustering, Node classification | |
| DMGI [243] | Multiplex graphs | Link Prediction, Clustering, Node classification | |
| LDANE [244] | Dynamic graphs | Graph reconstruction, Link prediction, Node classification | |
| EvolveGCN [245] | Dynamic graphs | Link prediction, Node, edge classification |
| Model | Graph Type | Tasks | Loss Function |
|---|---|---|---|
| GAT [19] | Static graphs | Node classification | |
| GATv2 [58] | Static graphs | Link prediction, Graph prediction, Node classification | |
| Gaan [255] | Static graphs | Node classification | |
| GraphStar [256] | Static graphs | Node classification, Graph classification, Link prediction | |
| HAN [25] | Heterogeneous graphs | Node classification, Node clustering | |
| [257] | Static graphs | Label-agreement prediction, Link prediction | |
| SuperGAT [258] | Static graphs | Label-agreement Link prediction | where |
| CGAT [259] | Static graphs | Node classification | |
| [260] | Static graphs | Node classification | |
| [261] | Static graphs | Node classification, Object recognition | |
| [25] | Heterogeneous graphs | Node classification, Node clustering | |
| [262] | Knowledge graphs | Relation prediction | |
| [224] | Static graphs | Node classification | |
| R-GCN [241] | Knowledge graphs | Entity classification, Link prediction | |
| DMGI [243] | Attributed multiplex graphs | Node clustering, Node classification | where |
| SHetGCN [263] | Heterogeneous graphs | Node classification | |
| DualHGCN [264] | Multiplex bipartite graphs | Node classification Link prediction | |
| HANE [265] | Heterogeneous graphs | Node classification | |
| MHGCN [266] | Multiplex heterogeneous Graph | Link prediction Node classification |
| Algorithms | Graph Types | Tasks | Loss Function |
|---|---|---|---|
| GAE [72] | Static graphs | Link prediction | |
| VGAE [72] | Static graphs | Link prediction | |
| [271] | Static graphs | Graph generation | |
| [272] | Static graphs | Graph generation | |
| MGAE [270] | Static graphs | Graph clustering | |
| [273] | Static graphs | Graph reconstruction | |
| LDANE [244] | Dynamic graphs | Graph reconstruction, Link prediction, Node classification |
| Model | Graph Type | Transformer Type | Sampling Strategy | Self-Supervised Learning |
|---|---|---|---|---|
| [64] | Tree-like graphs | Structural encoding | Dependency path BFS, DFS | Structure reconstruction |
| [65] | Tree-like graphs | Structural encoding | Dependency path | Structure reconstruction |
| [282] | Tree-like graphs | Structural encoding | SPD | Structure reconstruction |
| Graph-Bert [63] | Static graphs | Structural encoding Attention + GNN | WL and K-hop | Attribute reconstruction Structure reconstruction |
| [283] | Static graphs | Structural encoding | WL, K-hop | Structure reconstruction |
| [29] | Heterogeneous graphs | Structural encoding Edge channels | Laplacian matrix | Structure reconstruction |
| SAN [284] | Heterogeneous graphs | Structural encoding Edge channels | Laplacian matrix | Structure reconstruction |
| Grover [100] | Heterogeneous graphs | MP + Attention | k-hop | Feature prediction Motif prediction |
| Mesh Graphormer [99] | Static graphs | Attention + CGNNs | k-order proximity | Graph reconstruction |
| HGT [285] | Heterogeneous graphs | Attention+ MP | Meta-paths | Graph reconstruction |
| UGformer [61] | Heterogeneous graphs | Attention +GNN | 1st-order proximity | Graph reconstruction |
| StA-PLAN [286] | Heterogeneous graphs | Attention matrix | 1st-order proximity | Structure reconstruction |
| NI-CTR [287] | Heterogeneous graphs | Attention matrix | Subgraph sampling | Structure reconstruction |
| [101] | Heterogeneous graphs | MP + Attention | 1-hop neighbors | Structure reconstruction |
| [66] | Heterogeneous graphs | Attention + MP | Subgraph | Masked label prediction |
| Gophormer [46] | Heterogeneous graphs | Attention matrix | Ego-graph k-order proximity | Node classification |
| Graformer [47] | Knowledge graphs | Edge channels | SPD | Structure reconstruction |
| Graphormer [67] | Homogeneous graphs | Edge channels | SPD | Structure reconstruction |
| EGT [30] | Homogeneous graphs | Edge channels | SPD | Structure reconstruction |
| Models | Graph Types | Hyperbolic Models | Model Types |
|---|---|---|---|
| [70] | Homogeneous graphs | Poincaré disk | Shallow models |
| [102] | Homogeneous graphs | Lorentz model | Shallow models |
| [71] | Heterogeneous graphs | Poincaré disk | Shallow models |
| [293] | Homogeneous graphs | Poincaré disk | Convolutional GNNs |
| [294] | Homogeneous graphs | Poincaré disk, Lorentz model | GNNs |
| LGCN [69] | Homogeneous graphs | Lorentzian model | GNNs |
| [68] | Homogeneous graphs | Gyrovector model | GAT |
| Model | Graph Type | Model | Structure Preservation |
|---|---|---|---|
| VGAE [72] | Homogeneous graphs | Autoencoder-based GCNs | Random-walk sampling |
| DVNE [298] | Homogeneous graphs | Autoencoder | 1-order, 2-order proximity |
| [104] | Heterogeneous graphs | MLP | Meta-path |
| [23] | Homogeneous graphs | Autoencoder | k-order proximity |
| KG2E [299] | Knowledge graphs | Triplet score | 1-order proximity |
| Dataset | Graph Type | Category | # Nodes | # Edges |
|---|---|---|---|---|
| Cora [406] | Homogeneous graph | Citation network | 2808 | 5429 |
| Citeseer [407] | Homogeneous graph | Citation network | 3312 | 4732 |
| Reddit [22] | Homogeneous graph | Social network | 232,965 | 114,615,892 |
| PubMed [406] | Homogeneous graph | Citation network | 19,717 | 44,338 |
| Wikipedia [406] | Homogeneous graph | Webpage | 2405 | 17,981 |
| DBLP [408] | Homogeneous graph | Citation network | 781,109 | 4,191,677 |
| BlogCatalog [408] | Homogeneous graph | Social network | 10,312 | 333,983 |
| Flickr [1] | Homogeneous graph | Social network | 80,513 | 5,899,882 |
| Facebook [409] | Homogeneous graph | Social network | 4039 | 88,234 |
| PPI [22] | Homogeneous graph | Biochemical network | 56,944 | 818,716 |
| MUTAG [410] | Homogeneous graph | Biochemical network | 27,163 | 148,100 |
| PROTEIN [411] | Homogeneous graph | Biochemical network | 43,500 | 162,100 |
| Wiki | Homogeneous graph | Webpage | 4,780 | 184,81 K |
| YouTube | Homogeneous graph | Video streaming | 1,130,000 | 2,99 M |
| DBLP [412] | Heterogeneous graph | Citation network | Author (A): 4057 Paper (P): 14,328 Term (T): 7723 Venue (V): 20 | A-P: 19,645 P-T: 85,810 P-V: 14,328 |
| ACM [412] | Heterogeneous graph | Citation network | Paper (P): 4019 Author (A): 7167 Subject (S): 60 | P-P: 9615 P-A: 13,407 P-S: 4019 |
| IMDB [412] | Heterogeneous graph | Movie reviews | Movie (M): 4278 Director (D): 2081 Actor (A): 5257 | M-D: 4278 M-A: 12,828 |
| DBIS [413] | Heterogeneous graph | Citation network | Venues (V): 464 Authors (A): 5000 Publication (P): 72,902 | - |
| BlogCatalog3 [414] | Heterogeneous graph | Social network | User: 10,312 Group: 39 | 348,459 |
| Yelp [415] | Heterogeneous graph | Social media | User: 630,639 Business: 86,810 City: 10 Category: 807 | - |
| U.S. Patents [180] | Heterogeneous graph | Patent, Trademark Office | Patent: 295,145 Inventor: 293,848 Assignee: 31,805 Class: 14 | - |
| UCI [416] | Dynamic graph | Social network | 1899 | 59,835 |
| DNC [416] | Dynamic graph | Social network | 2029 | 39,264 |
| Epinions [417] | Dynamic graph | Social media | 6224 | 19496 |
| Hep-th [418] | Dynamic graph | Citation network | 34,000 | 421,000 |
| Auto Systems [419] | Dynamic graph | BGP logs | 6000 | 13,000 |
| Enron | Dynamic graph | Email network | 87,000 | 1,100,000 |
| StackOverflow [420] | Dynamic graph | Question&Answer | 14,000 | 195,000 |
| dblp [408] | Dynamic graph | Citation network | 90,000 | 749,000 |
| Darpa [421] | Dynamic graph | Computer network | 12,000 | 22,000 |
| Library | URL | Platform | Model |
|---|---|---|---|
| PyTorch Geometric (PyG) [426] | https://github.com/pyg-team/pytorch_geometric | PyTorch | Various GNN models and basic graph deep-learning operations |
| Deep Graph Library (DGL) [427] | https://github.com/dmlc/dgl | TensorFlow, PyTorch | Various GNN models and basic graph deep-learning operations |
| OpenNE | https://github.com/thunlp/OpenNE/tree/pytorch | TensorFlow, PyTorch | Shallow models: DeepWalk, Node2Vec, GAE, VGAE, LINE, TADW, SDNE, HOPE, GraRep, GCN |
| CogDL [428] | https://github.com/THUDM/cogdl | TensorFlow, PyTorch | Various GNN models |
| Dive into Graphs (DIG) [429] | https://github.com/divelab/DIG | PyTorch | Various GNN models and research-oriented studies (Graph generation, Self-supervised learning (SSL), explainability, 3D graphs, and graph out-of-distribution). |
| Graphvite [430] | https://github.com/deepgraphlearning/graphvite | Python | DeepWalk, LINE, Node2Vec, TransE, RotatE, and LargeVis. |
| GraphLearn [431] | https://github.com/alibaba/graph-learn | Python | Various GNN models, the framework can support the sampling batch graphs or offline training process. |
| Connector | https://github.com/NSLab-CUK/connector | Pytorch | Various shallow models and GNN models. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoang, V.T.; Jeon, H.-J.; You, E.-S.; Yoon, Y.; Jung, S.; Lee, O.-J. Graph Representation Learning and Its Applications: A Survey. Sensors 2023, 23, 4168. https://doi.org/10.3390/s23084168
Hoang VT, Jeon H-J, You E-S, Yoon Y, Jung S, Lee O-J. Graph Representation Learning and Its Applications: A Survey. Sensors. 2023; 23(8):4168. https://doi.org/10.3390/s23084168
Chicago/Turabian StyleHoang, Van Thuy, Hyeon-Ju Jeon, Eun-Soon You, Yoewon Yoon, Sungyeop Jung, and O-Joun Lee. 2023. "Graph Representation Learning and Its Applications: A Survey" Sensors 23, no. 8: 4168. https://doi.org/10.3390/s23084168
APA StyleHoang, V. T., Jeon, H.-J., You, E.-S., Yoon, Y., Jung, S., & Lee, O.-J. (2023). Graph Representation Learning and Its Applications: A Survey. Sensors, 23(8), 4168. https://doi.org/10.3390/s23084168






