Sparse Time-Frequency Distribution Reconstruction Using the Adaptive Compressed Sensed Area Optimized with the Multi-Objective Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Time-Frequency Signal Analysis
2.2. The Localized Rényi Entropy
2.3. Sparse Time-Frequency Distributions
2.4. The Rényi Entropy-Based TFD Reconstruction Algorithm
2.5. The Proposed Adaptive CS-AF Area Selection
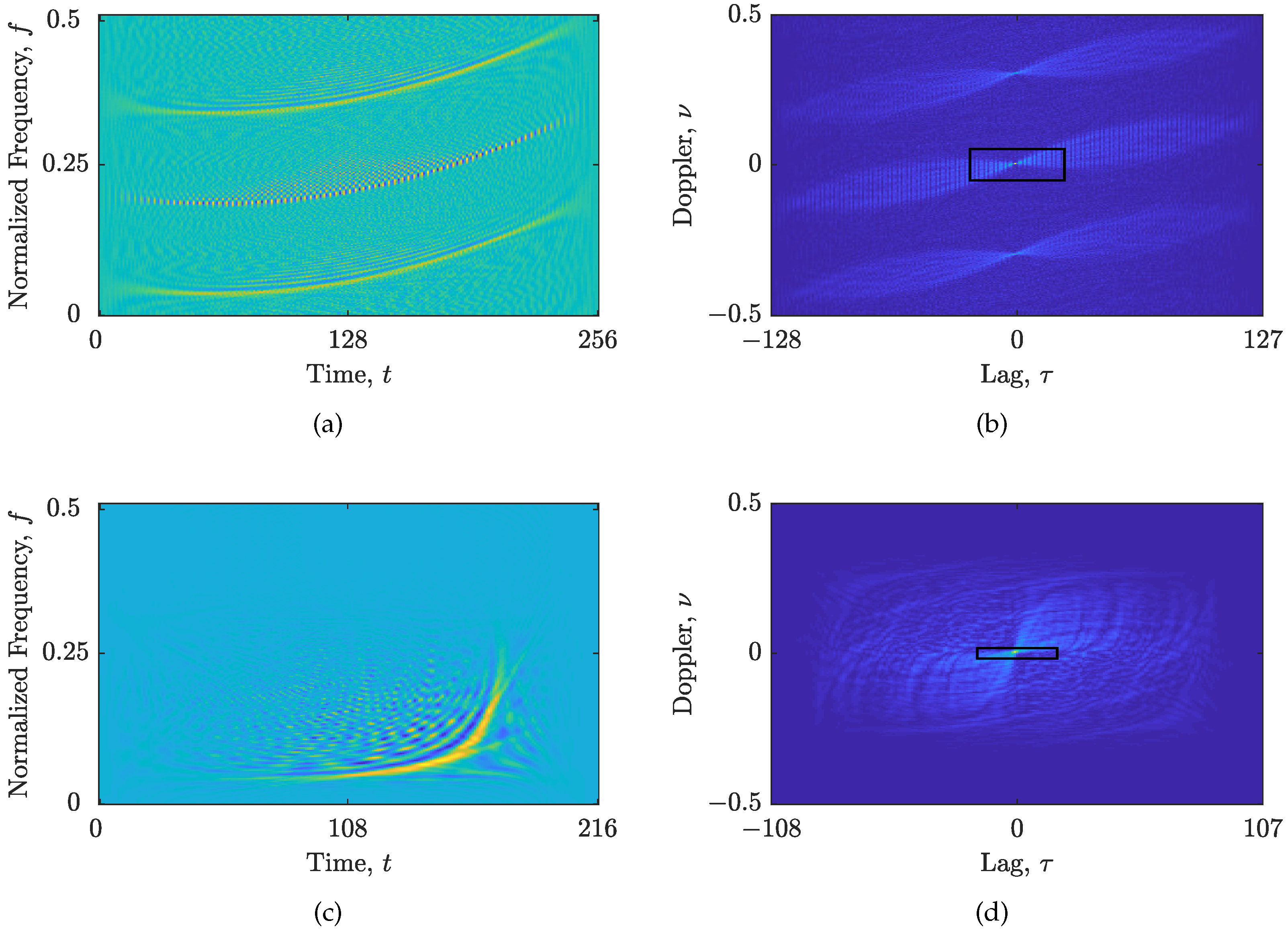
2.5.1. Ambiguity Function Thresholding
- The auto-terms are concentrated along trajectories passing through the AF origin. These trajectories follow the components’ IF law.
- The auto-term magnitude peaks at the AF origin and steadily decreases.
- The auto-terms and cross-terms may intersect in the AF.
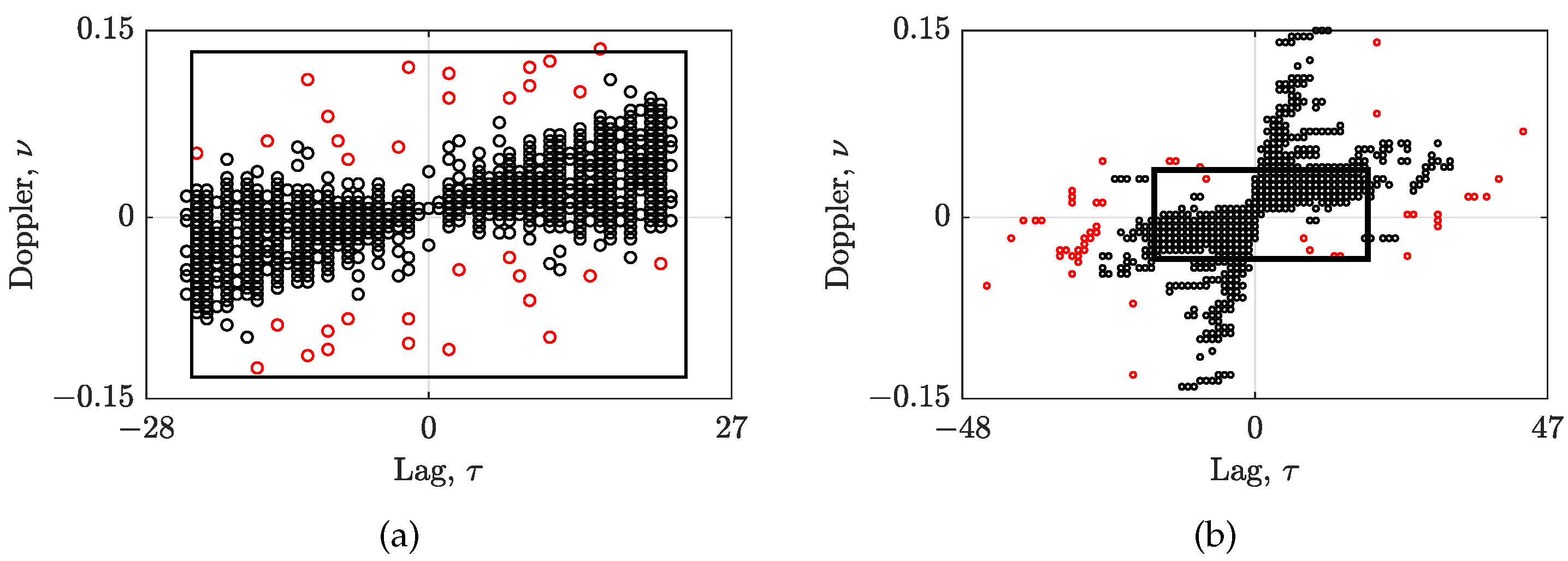
2.5.2. The Density-Based Spatial Clustering
2.6. The Proposed Objective Functions for the Multi-Objective Optimization Method
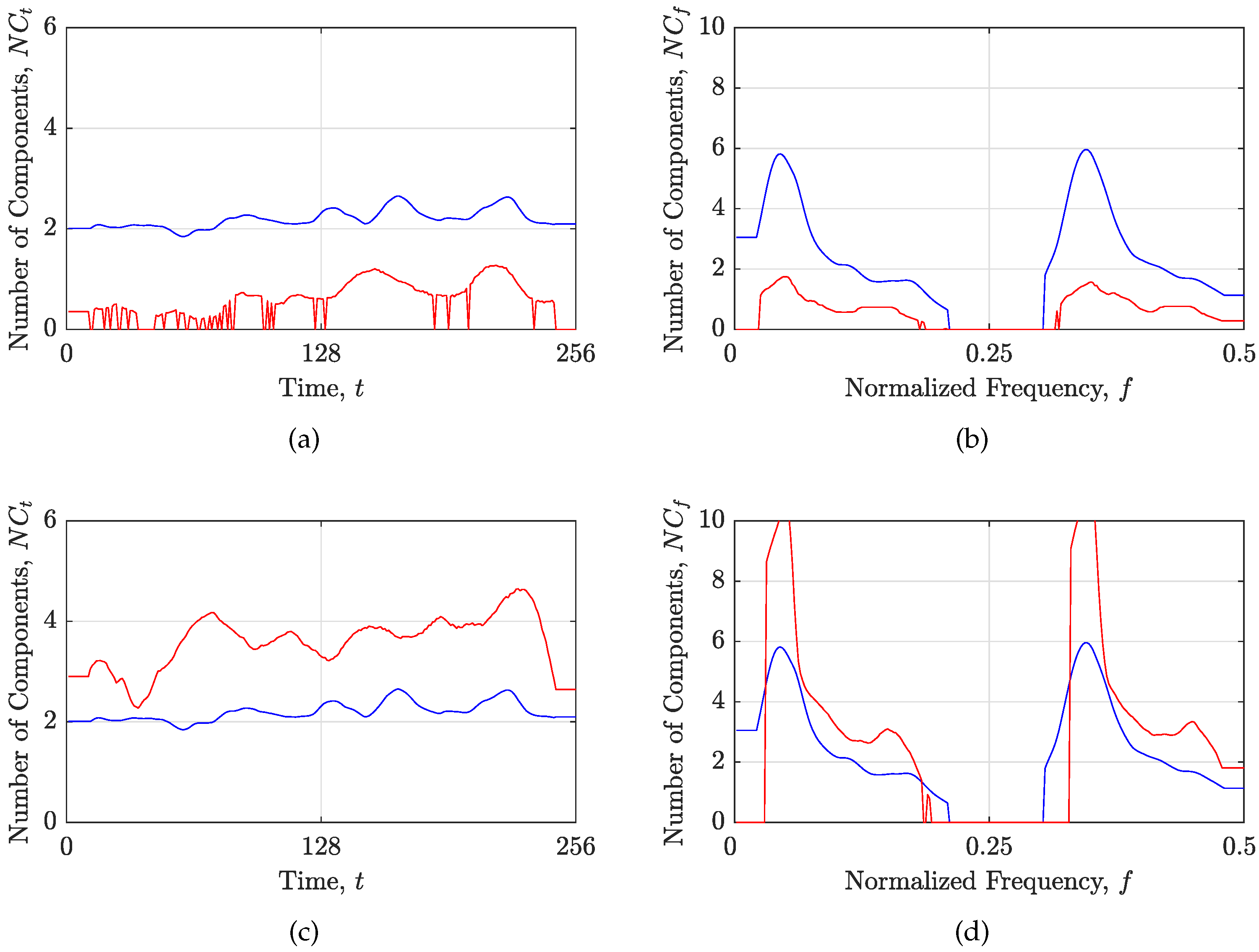
2.6.1. The Measure Based on the Localized Rényi Entropy
2.6.2. The Proposed Number of Regions with Continuously Connected Samples
2.7. The Multi-Objective Meta-Heuristic Optimization
3. Results and Discussion
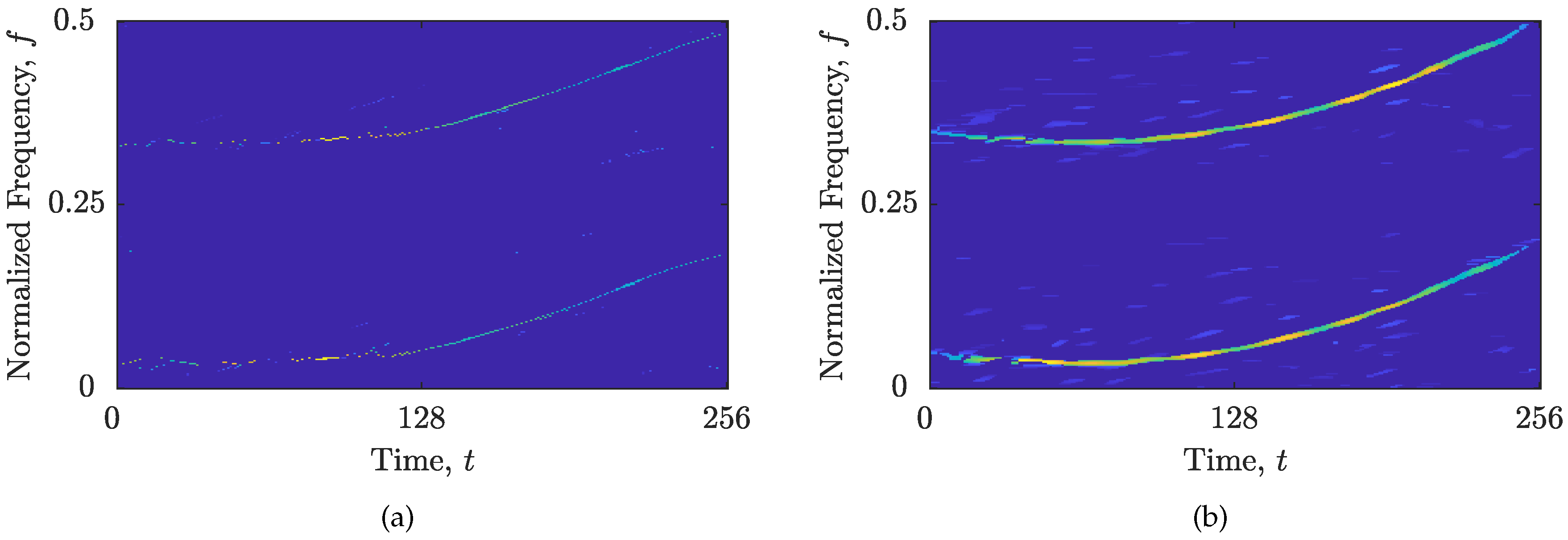
3.1. CS-AF Area Selection
3.2. The Objective Function Performance
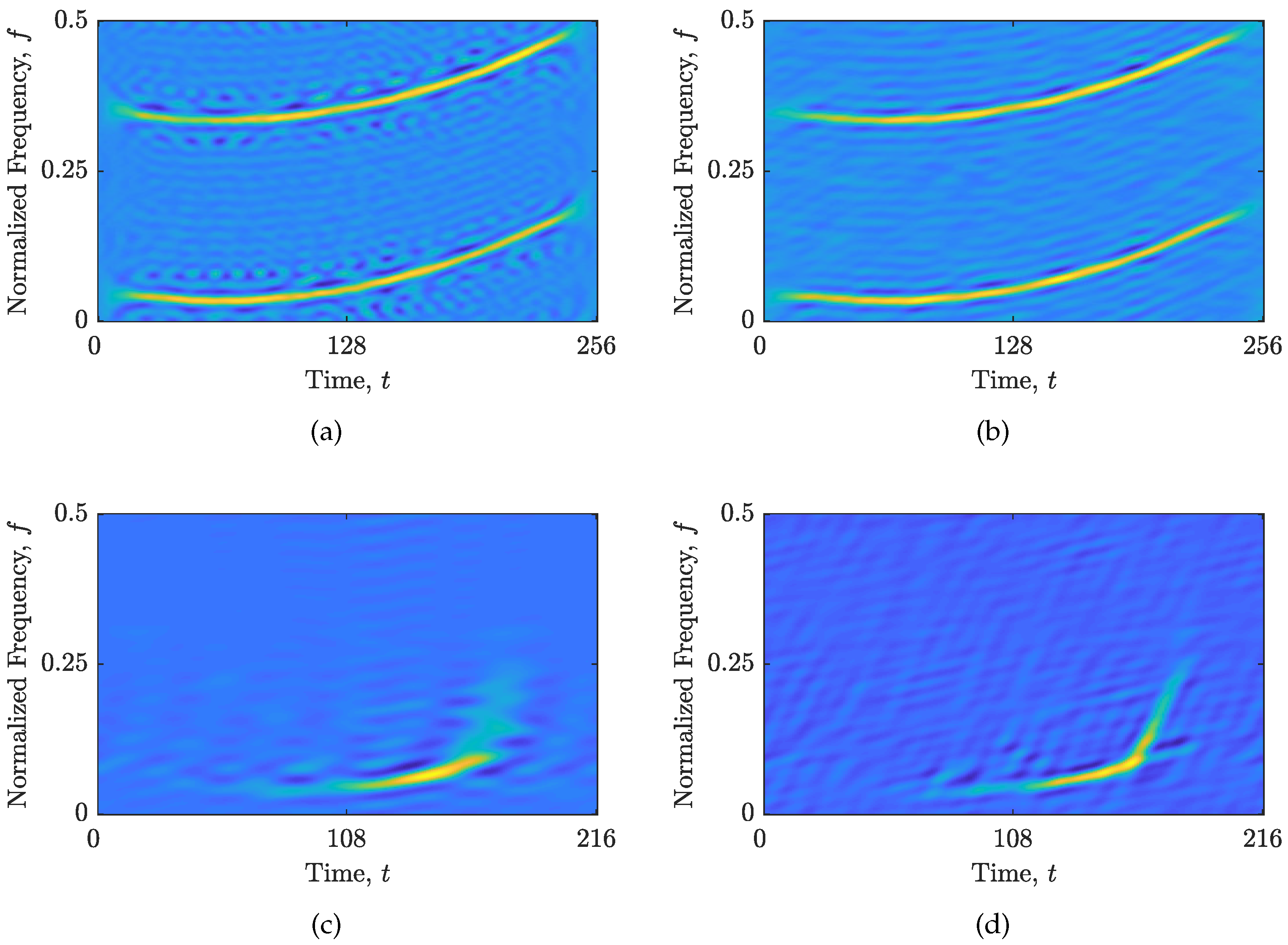
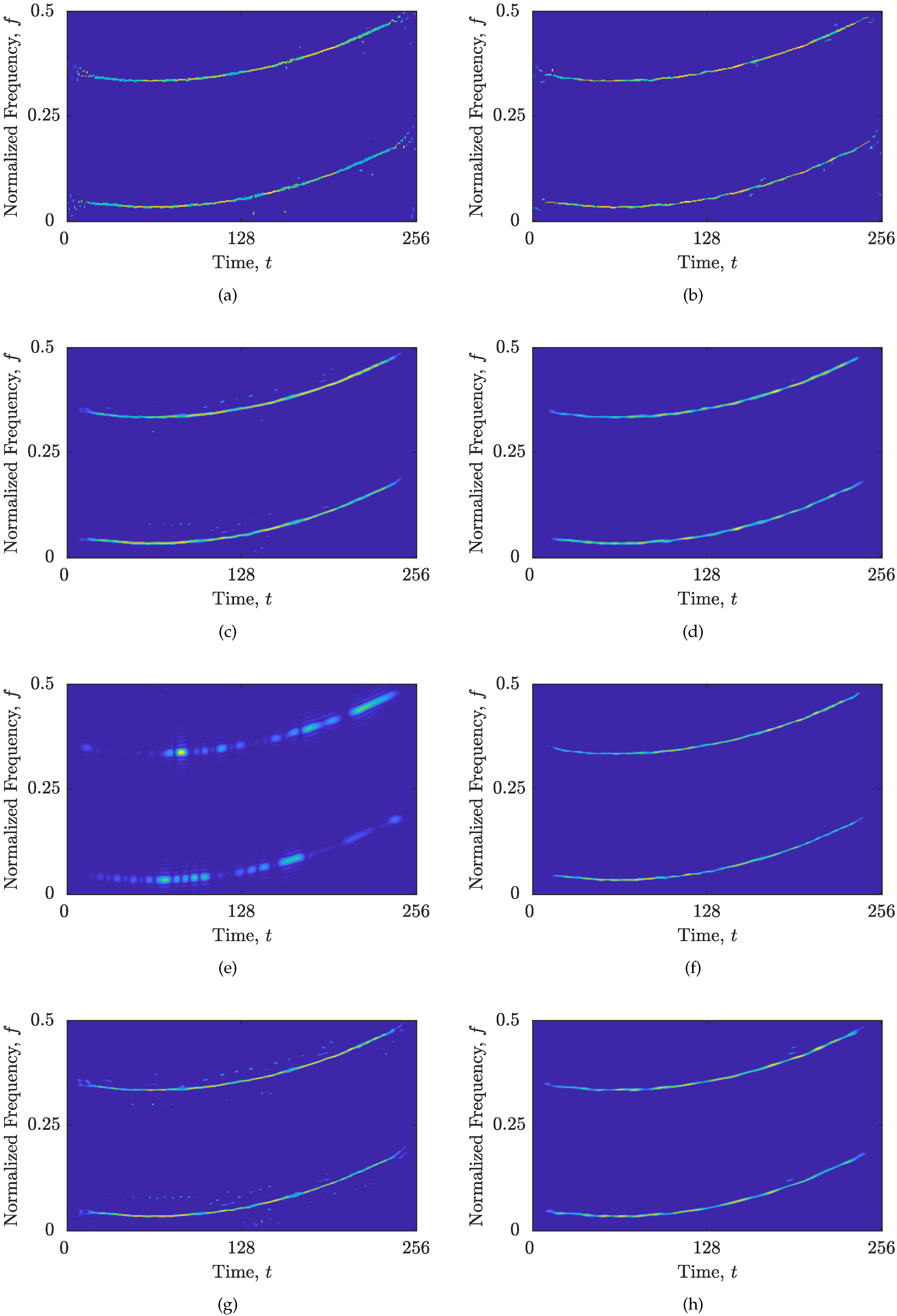
3.3. Results
3.3.1. Results for Synthetic Signal
3.3.2. Results for Real-Life Signal
3.4. Results Summary
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AF | Ambiguity function |
| AWGN | Additive white Gaussian noise |
| CS | Compressive sensing |
| DBSCAN | Density-based spatial clustering |
| EMBD | Extended modified B distribution |
| FSM | Fuzzy satisfying method |
| GDM | Gradient descent method |
| IF | Instantaneous frequency |
| LFM | Linear frequency-modulated |
| LRE | Local Rényi entropy |
| MOPSO | Multi-objective particle swarm optimization |
| MSE | Mean squared error |
| NBRE | Narrow-band Rényi entropy |
| SALSA | Split augmented Lagrangian shrinkage algorithm |
| SNR | Signal-to-noise ratio |
| SpaRSA | Sparse reconstruction by separable approximation |
| STRE | Short-term Rényi entropy |
| TF | Time-frequency |
| TFD | Time-frequency distribution |
| TwIST | Two-step iterative/shrinkage algorithm |
| WVD | Wigner–Ville distribution |
| QTFD | Quadratic time-frequency distribution |
References
- Boashash, B. Time-Frequency Signal Analysis and Processing, a Comprehensive Reference, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Stankovic, L.; Dakovic, M.; Thayaparan, T. Time-Frequency Signal Analysis with Applications; Artech House Inc.: Norwood, MA, USA, 2013. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive Sensing [Lecture Notes]. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Davenport, M.A.; Duarte, M.F.; Eldar, Y.C.; Kutyniok, G. Introduction to Compressed Sensing. In Compressed Sensing: Theory and Applications; Cambridge University Press: Cambridge, UK, 2012; pp. 1–64. [Google Scholar] [CrossRef]
- Ye, J.C. Compressed Sensing MRI: A Review From Signal Processing Perspective. BMC Biomed. Eng. 2019, 1, 8. [Google Scholar] [CrossRef] [PubMed]
- Ren, K.; Du, L.; Wang, B.; Li, Q.; Chen, J. Statistical Compressive Sensing and Feature Extraction of Time-Frequency Spectrum From Narrowband Radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 326–342. [Google Scholar] [CrossRef]
- Khobahi, S.; Soltanalian, M. Model-Based Deep Learning for One-Bit Compressive Sensing. IEEE Trans. Signal Process. 2020, 68, 5292–5307. [Google Scholar] [CrossRef]
- Mahdaoui, A.E.; Ouahabi, A.; Moulay, M.S. Image Denoising Using a Compressive Sensing Approach Based on Regularization Constraints. Sensors 2022, 22, 2199. [Google Scholar] [CrossRef]
- Zonzini, F.; Carbone, A.; Romano, F.; Zauli, M.; De Marchi, L. Machine Learning Meets Compressed Sensing in Vibration-Based Monitoring. Sensors 2022, 22, 2229. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, Y.; Song, J. Robust sparse time-frequency analysis for data missing scenarios. IET Signal Process. 2023, 17, e12184. [Google Scholar] [CrossRef]
- Stanković, L.; Orović, I.; Stanković, S.; Amin, M. Compressive Sensing Based Separation of Nonstationary and Stationary Signals Overlapping in Time-Frequency. IEEE Trans. Signal Process. 2013, 61, 4562–4572. [Google Scholar] [CrossRef]
- Stanković, L.; Stanković, S.; Orović, I.; Amin, M.G. Robust Time-Frequency Analysis Based on the L-Estimation and Compressive Sensing. IEEE Signal Process. Lett. 2013, 20, 499–502. [Google Scholar] [CrossRef]
- Volaric, I.; Sucic, V.; Stankovic, S. A Data Driven Compressive Sensing Approach for Time-Frequency Signal Enhancement. Signal Process. 2017, 141, 229–239. [Google Scholar] [CrossRef]
- Flandrin, P.; Borgnat, P. Time-Frequency Energy Distributions Meet Compressed Sensing. IEEE Trans. Signal Process. 2010, 58, 2974–2982. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, H.; Yu, L. Learning Structured Sparsity For Time-Frequency Reconstruction. In Proceedings of the ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 5398–5402. [Google Scholar] [CrossRef]
- Su, H.; Zhang, Y. Time-Frequency Analysis Based on Compressive Sensing. In Proceedings of the 2016 2nd International Conference on Cloud Computing and Internet of Things (CCIOT), Dalian, China, 22–23 October 2016; pp. 138–142. [Google Scholar] [CrossRef]
- Gholami, A. Sparse Time–Frequency Decomposition and Some Applications. IEEE Trans. Geosci. Remote. Sens. 2013, 51, 3598–3604. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Yang, J.; Li, X.; Zhang, D. A Survey of Sparse Representation: Algorithms and Applications. IEEE Access 2015, 3, 490–530. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. A New TwIST: Two-Step Iterative Shrinkage/Thresholding Algorithms for Image Restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D. Survey of Clustering Algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A Comprehensive Survey of Clustering Algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Jurdana, V.; Volaric, I.; Sucic, V. Sparse time-frequency distribution reconstruction based on the 2D Rényi entropy shrinkage algorithm. Digit. Signal Process. 2021, 118, 103225. [Google Scholar] [CrossRef]
- Stanković, L. A Measure of Some Time–Frequency Distributions Concentration. Signal Process. 2001, 81, 621–631. [Google Scholar] [CrossRef]
- Sucic, V.; Saulig, N.; Boashash, B. Estimating the number of components of a multicomponent nonstationary signal using the short-term time-frequency Rényi entropy. EURASIP J. Adv. Signal Process. 2011, 2011, 125. [Google Scholar] [CrossRef]
- Sucic, V.; Saulig, N.; Boashash, B. Analysis of Local Time-Frequency Entropy Features for Nonstationary Signal Components Time Supports Detection. Digit. Signal Process. 2014, 34, 56–66. [Google Scholar] [CrossRef]
- Jurdana, V.; Volaric, I.; Sucic, V. The Local Rényi Entropy Based Shrinkage Algorithm for Sparse TFD Reconstruction. In Proceedings of the 2020 International Conference on Broadband Communications for Next Generation Networks and Multimedia Applications (CoBCom), Graz, Austria, 12–14 July 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Flandrin, P.; Janssen, A.J.E.M.; Michel, O.J.J. Measuring Time-Frequency Information Content Using the Rényi Entropies. IEEE Trans. Inf. Theory 2001, 47, 1391–1409. [Google Scholar] [CrossRef]
- Aviyente, S.; Williams, W.J. Minimum Entropy Time-Frequency Distributions. IEEE Signal Process. Lett. 2005, 12, 37–40. [Google Scholar] [CrossRef]
- Principe, J. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer Science and Business Media: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Saulig, N.; Lerga, J.; Miličić, S.; Tomasović, Z. Block-Adaptive Renyi Entropy-Based Denoising for Non-Stationary Signals. Sensors 2022, 22, 8251. [Google Scholar] [CrossRef]
- Saulig, N.; Milanovic, Z.; Ioana, C. A local entropy-based algorithm for information content extraction from time–frequency distributions of noisy signals. Digit. Signal Process. 2017, 70, 155–165. [Google Scholar] [CrossRef]
- Volaric, I.; Sucic, V. Localized Rényi Entropy Based Sparse TFD Reconstruction. In Proceedings of the Second International Balkan Conference on Communications and Networking BalkanCom 2018 Podgorica, Montenegro, Podgorica, Montenegro, 6–8 June 2018; pp. 1–5. [Google Scholar]
- Qiu, K.; Dogandzic, A. Sparse Signal Reconstruction via ECME Hard Thresholding. IEEE Trans. Signal Process. 2012, 60, 4551–4569. [Google Scholar] [CrossRef]
- Boashash, B.; Ouelha, S. An Improved Design of High-Resolution Quadratic Time–Frequency Distributions for the Analysis of Nonstationary Multicomponent Signals Using Directional Compact Kernels. IEEE Trans. Signal Process. 2017, 65, 2701–2713. [Google Scholar] [CrossRef]
- Boashash, B.; Jawad, B.K.; Ouelha, S. Refining the Ambiguity Domain Characteristics of Non-Stationary Signals for Improved Time–Frequency Analysis: Test Case of Multidirectional and Multicomponent Piecewise LFM and HFM Signals. Digit. Signal Process. 2018, 83, 367–382. [Google Scholar] [CrossRef]
- Zhu, X.; Fujii, T. A Novel Modulation Classification Method in Cognitive Radios Based on Features Clustering of Time-Frequency. In Proceedings of the 2016 IEEE Radio and Wireless Symposium (RWS), Austin, TX, USA, 24–27 January 2016; pp. 45–47. [Google Scholar] [CrossRef]
- Paral, P.; Chatterjee, A.; Rakshit, A. Vision Sensor-Based Shoe Detection for Human Tracking in a Human–Robot Coexisting Environment: A Photometric Invariant Approach Using DBSCAN Algorithm. IEEE Sens. J. 2019, 19, 4549–4559. [Google Scholar] [CrossRef]
- Shen, J.; Hao, X.; Liang, Z.; Liu, Y.; Wang, W.; Shao, L. Real-Time Superpixel Segmentation by DBSCAN Clustering Algorithm. IEEE Trans. Image Process. 2016, 25, 5933–5942. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Suliang, M.; Jianwen, W.; Bowen, J.; Weixin, L.; Xiaowu, L. Fault Diagnosis in Gas Insulated Switchgear Based on Genetic Algorithm and Density- Based Spatial Clustering of Applications With Noise. IEEE Sens. J. 2021, 21, 965–973. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, J.; Jiang, J.; Guo, X. Robust Feature Matching Using Spatial Clustering With Heavy Outliers. IEEE Trans. Image Process. 2020, 29, 736–746. [Google Scholar] [CrossRef] [PubMed]
- Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. Density-Based Clustering in Spatial Databases: The Algorithm GDBSCAN and Its Applications. Data Min. Knowl. Discov. 1998, 2, 169–194. [Google Scholar] [CrossRef]
- Campello, R.J.G.B.; Moulavi, D.; Sander, J. Density-Based Clustering Based on Hierarchical Density Estimates. In Advances in Knowledge Discovery and Data Mining, Proceedings of the 17th Pacific-Asia Conference, PAKDD 2013, Gold Coast, Australia, 14–17 April 2013; Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–172. [Google Scholar] [CrossRef]
- Saulig, N.; Orović, I.; Sucic, V. Optimization of Quadratic Time–Frequency Distributions Using the Local Rényi Entropy Information. Signal Process. 2016, 129, 17–24. [Google Scholar] [CrossRef]
- Awal, M.A.; Boashash, B. An automatic fast optimization of Quadratic Time-frequency Distribution using the hybrid genetic algorithm. Signal Process. 2017, 131, 134–142. [Google Scholar] [CrossRef]
- Durillo, J.J.; García-Nieto, J.; Nebro, A.J.; Coello, C.A.C.; Luna, F.; Alba, E. Multi-Objective Particle Swarm Optimizers: An Experimental Comparison. In Evolutionary Multi-Criterion Optimization, Proceedings of the 5th International Conference, EMO 2009, Nantes, France, 7–10 April 2009; Ehrgott, M., Fonseca, C.M., Gandibleux, X., Hao, J.K., Sevaux, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 495–509. [Google Scholar] [CrossRef]
- Garg, H. A Hybrid PSO-GA Algorithm for Constrained Optimization Problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Lopac, N.; Jurdana, I.; Lerga, J.; Wakabayashi, N. Particle-Swarm-Optimization-Enhanced Radial-Basis-Function-Kernel-Based Adaptive Filtering Applied to Maritime Data. J. Mar. Sci. Eng. 2021, 9, 439. [Google Scholar] [CrossRef]
- Soroudi, A.; Ehsan, M.; Zareipour, H. A practical eco-environmental distribution network planning model including fuel cells and non-renewable distributed energy resources. Renew. Energy 2011, 36, 179–188. [Google Scholar] [CrossRef]
- Lopac, N.; Hržić, F.; Vuksanović, I.P.; Lerga, J. Detection of Non-Stationary GW Signals in High Noise From Cohen’s Class of Time-Frequency Representations Using Deep Learning. IEEE Access 2021, 10, 2408–2428. [Google Scholar] [CrossRef]
- Lopac, N. Detection of Gravitational-Wave Signals from Time-Frequency Distributions Using Deep Learning. Ph.D. Thesis, University of Rijeka, Faculty of Engineering, Rijeka, Croatia, 2022. [Google Scholar]
- Wright, S.J.; Nowak, R.D.; Figueiredo, M.A.T. Sparse Reconstruction by Separable Approximation. IEEE Trans. Signal Process. 2009, 57, 2479–2493. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A.T. Fast Image Recovery Using Variable Splitting and Constrained Optimization. IEEE Trans. Image Process. 2010, 19, 2345–2356. [Google Scholar] [CrossRef] [PubMed]
- Hurley, N.; Rickard, S. Comparing Measures of Sparsity. IEEE Trans. Inf. Theory 2009, 55, 4723–4741. [Google Scholar] [CrossRef]
- Lopac, N.; Lerga, J.; Cuoco, E. Gravitational-Wave Burst Signals Denoising Based on the Adaptive Modification of the Intersection of Confidence Intervals Rule. Sensors 2020, 20, 6920. [Google Scholar] [CrossRef]
- Lopac, N.; Lerga, J.; Saulig, N.; Stanković, L.; Daković, M. On Optimal Parameters for ICI-Based Adaptive Filtering Applied to the GWs in High Noise. In Proceedings of the 2021 6th International Conference on Smart and Sustainable Technologies (SpliTech), Split & Bol, Croatia, 8–11 September 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]

| Signal | ||
|---|---|---|
| RTwIST, | ||
| 39 | 397 | |
| 0.3784 | 0.1070 | |
| 0.1178 | 0.0301 | |
| 168 | 103 | |
| 0.6061 | 0.3117 | |
| 0.2649 | 0.1204 | |
| 0.8965 | 0.5133 | |
| 0.7524 | 0.4832 | |
| R | 8.299 | 10.938 |
| 0.0075 | 0.0459 | |
| 4.10 | 0.65 | |
| 0.9321 | 0.8239 | |
| Signal | ||||||||
|---|---|---|---|---|---|---|---|---|
| RTwIST [24] | TwIST [20] | SpaRSA [53] | SALSA [54] | |||||
| 2597 | 883 | 2597 | 1009 | 2597 | 1617 | 2597 | 531 | |
| 0.0179 | 0.0091 | 0.0597 | 0.0378 | 0.1029 | 0.0253 | 0.0159 | 0.0117 | |
| 0.0178 | 0.0158 | 0.0207 | 0.0187 | 0.0904 | 0.0248 | 0.0189 | 0.0199 | |
| 22 | 13 | 35 | 3 | 186 | 3 | 75 | 5 | |
| 0.1141 | 0.078 | 0.2344 | 0.1738 | 0.2866 | 0.0847 | 0.1054 | 0.0928 | |
| 0.0769 | 0.0735 | 0.0886 | 0.0792 | 0.224 | 0.091 | 0.0742 | 0.0778 | |
| 0.3192 | 0.2654 | 0.5791 | 0.6475 | 0.5833 | 0.789 | 0.6804 | 0.2983 | |
| 0.5334 | 0.6170 | 0.4897 | 0.5411 | 0.9411 | 0.6762 | 0.682 | 0.6112 | |
| R | 10.33 | 9.97 | 10.47 | 10.28 | 11.44 | 9.94 | 10.22 | 10.14 |
| 0.0269 | 0.0195 | 0.0278 | 0.0237 | 0.369 | 0.0185 | 0.0405 | 0.0431 | |
| 0.89 | 1.13 | 0.92 | 1.21 | 0.03 | 1.30 | 1.11 | 1.22 | |
| 0.8607 | 0.8781 | 0.8516 | 0.8611 | 0.6578 | 0.8771 | 0.8631 | 0.8672 | |
| * | 0.747 | 0.726 | 0.231 | 0.233 | 0.465 | 0.117 | 0.467 | 0.385 |
| Signal | ||||||||
|---|---|---|---|---|---|---|---|---|
| RTwIST [24] | TwIST [20] | SpaRSA [53] | SALSA [54] | |||||
| 525 | 441 | 525 | 505 | 525 | 505 | 525 | 456 | |
| 0.0386 | 0.0037 | 0.0404 | 0.0268 | 0.0356 | 0.0286 | 0.0155 | 0.0150 | |
| 0.0357 | 0.0093 | 0.028 | 0.0200 | 0.0245 | 0.0197 | 0.0209 | 0.0144 | |
| 9 | 10 | 4 | 2 | 4 | 4 | 7 | 7 | |
| 0.1375 | 0.0332 | 0.1221 | 0.1084 | 0.1192 | 0.1128 | 0.0733 | 0.0773 | |
| 0.1119 | 0.0510 | 0.1002 | 0.0820 | 0.0952 | 0.0807 | 0.0845 | 0.0627 | |
| 0.5148 | 0.2061 | 0.5371 | 0.5191 | 0.5212 | 0.553 | 0.4898 | 0.451 | |
| 0.5566 | 0.5092 | 0.5538 | 0.6227 | 0.5130 | 0.5747 | 0.6683 | 0.6087 | |
| R | 8.82 | 8.01 | 8.6 | 8.03 | 8.38 | 8.12 | 8.14 | 8.13 |
| 0.0134 | 0.0070 | 0.0130 | 0.0078 | 0.0109 | 0.0085 | 0.0344 | 0.0473 | |
| 2.91 | 5.22 | 4.12 | 5.53 | 4.62 | 5.23 | 5.74 | 5.61 | |
| 0.9024 | 0.9272 | 0.9075 | 0.9261 | 0.9150 | 0.9232 | 0.9230 | 0.9221 | |
| * | 0.203 | 0.331 | 0.133 | 0.250 | 0.060 | 0.050 | 0.162 | 0.137 |
| Signal , RTwIST | ||||||
|---|---|---|---|---|---|---|
| 2 dB | 6 dB | 10 dB | ||||
| 0.0320 | 0.0174 | 0.0152 | 0.0104 | 0.0102 | 0.0081 | |
| 0.0321 | 0.0211 | 0.0188 | 0.0161 | 0.0131 | 0.0112 | |
| 37 | 21 | 20 | 12 | 15 | 9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurdana, V.; Lopac, N.; Vrankic, M. Sparse Time-Frequency Distribution Reconstruction Using the Adaptive Compressed Sensed Area Optimized with the Multi-Objective Approach. Sensors 2023, 23, 4148. https://doi.org/10.3390/s23084148
Jurdana V, Lopac N, Vrankic M. Sparse Time-Frequency Distribution Reconstruction Using the Adaptive Compressed Sensed Area Optimized with the Multi-Objective Approach. Sensors. 2023; 23(8):4148. https://doi.org/10.3390/s23084148
Chicago/Turabian StyleJurdana, Vedran, Nikola Lopac, and Miroslav Vrankic. 2023. "Sparse Time-Frequency Distribution Reconstruction Using the Adaptive Compressed Sensed Area Optimized with the Multi-Objective Approach" Sensors 23, no. 8: 4148. https://doi.org/10.3390/s23084148
APA StyleJurdana, V., Lopac, N., & Vrankic, M. (2023). Sparse Time-Frequency Distribution Reconstruction Using the Adaptive Compressed Sensed Area Optimized with the Multi-Objective Approach. Sensors, 23(8), 4148. https://doi.org/10.3390/s23084148








