The Crustal Dynamics and Its Geological Explanation of the Three-Dimensional Co-Seismic Deformation Field for the 2021 Maduo MS7.4 Earthquake Based on GNSS and InSAR
Abstract
1. Introduction
2. Study Area and Data Processing
2.1. Study Area
2.2. GNSS Data Estimated the Three-Dimensional Deformation
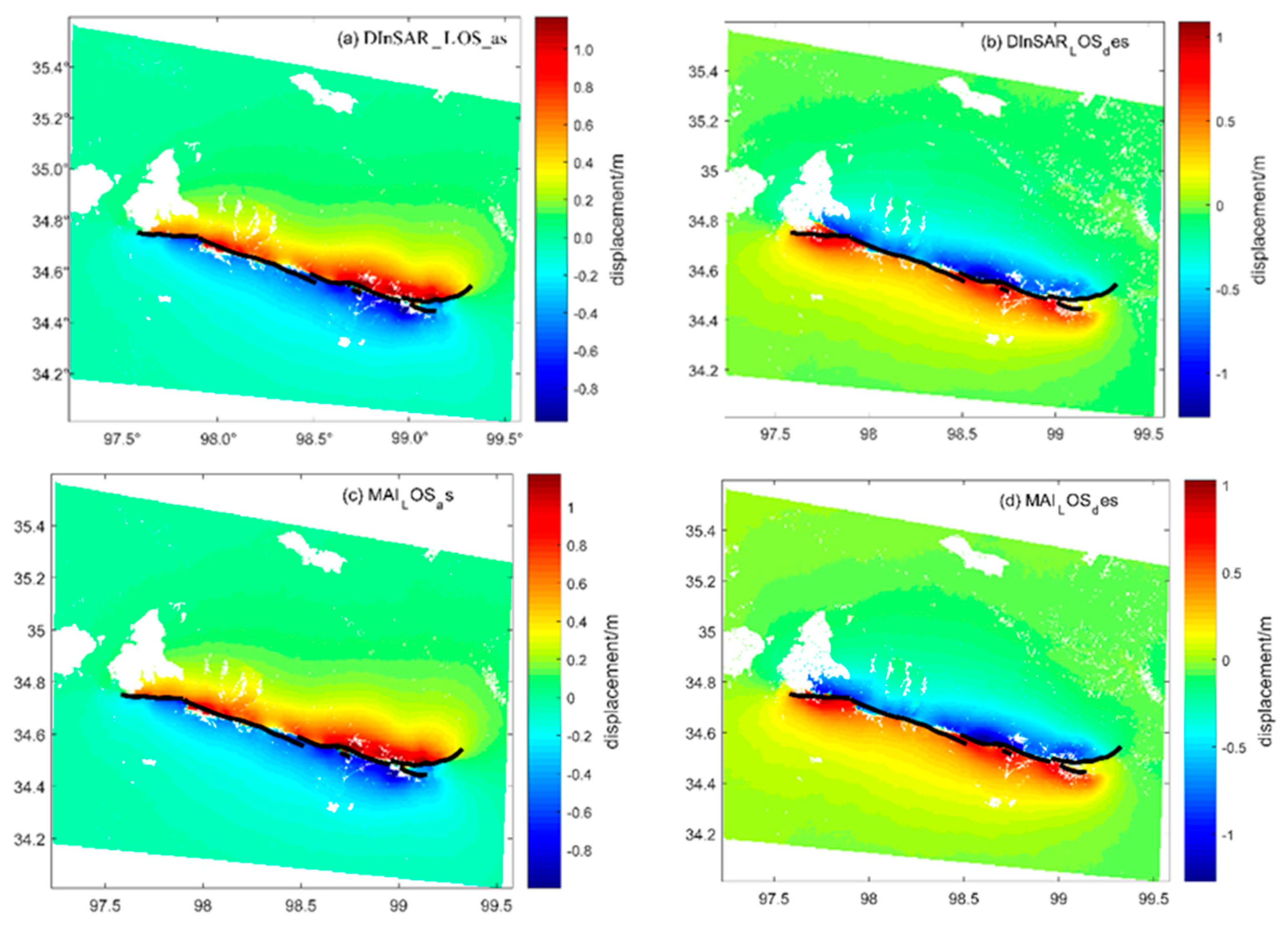
2.3. InSAR Data Estimated the One-Dimensional Deformation
3. Methodology
3.1. Multi-Source Integrating the Three-Dimensional Deformation
3.2. Adaptive Selection of the Relevant Points
3.3. Integrating Data Based on the VCE Weighting
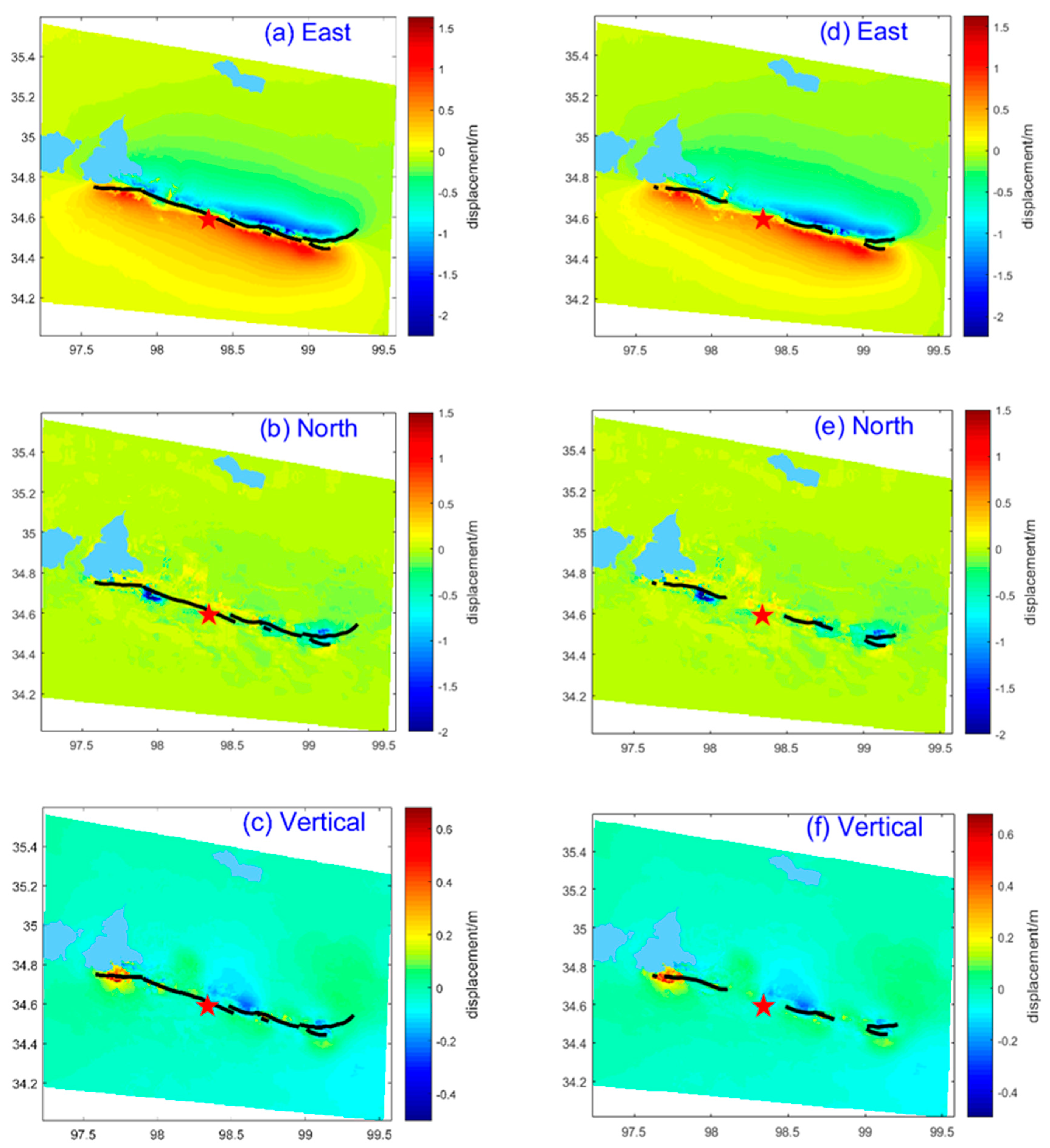
4. Results and Analysis
5. Discussion
5.1. The Integrating Mutil-Source Data
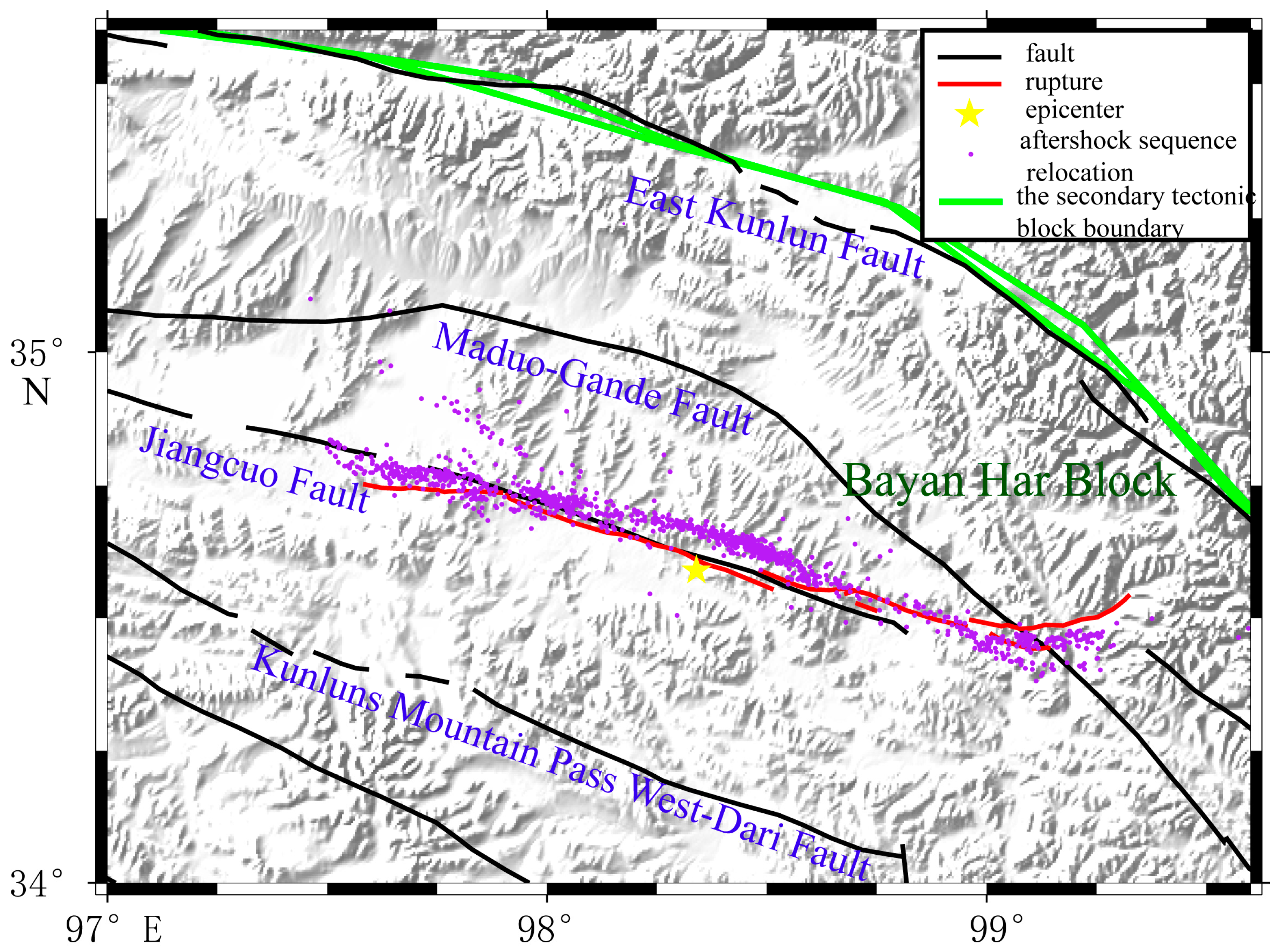
5.2. The Geodynamic Characteristic
6. Conclusions
- (1)
- The accuracy obtained by integrating GNSS and InSAR increased by 81.2% and 53.8% in the east–west direction and north–south direction, respectively. Additional constraints were helpful to obtain a high accuracy regional three-dimensional deformation field, such as increasing the GNSS stations, considering deformation correlation, removing heterogeneous points around the reference points, and the variance component estimation weighting.
- (2)
- The spatial position and the left-lateral strike-slip motion of the earthquake were consistent with those of the Jiangcuo section of the NWW strike of the Kunlun Mountain Pass–Jiangcuo fault in the south of the East Kunlun Fault. The mechanism of the left-lateral left-stepping was caused by the Riedel shear, which dominated the formation and evolution of strike-slip faults.
- (3)
- The maximum slip of the earthquake was about 4 m, which was difficult to investigate in the geological field survey due to the lack of reliable markers, and the slip was consistent with the empirical statistical results.
- (4)
- The ruptures started from the epicenter to both ends and formed bifurcations, which were rarely found in the same type of previous earthquakes that occurred in the Qinghai–Tibet Plateau.
- (5)
- The pre-existing fault controlled the vertical deformation at the north side of the near east–west surface rupture, which only dominated the east–west strike-slip. The three-dimensional deformation was consistent with the surface rupture trace. This provided direct evidence for the theoretical hypothesis that large earthquakes can not only produce a surface rupture on seismogenic faults, but also trigger pre-existing faults or new faults to produce surface ruptures or weak deformation in areas far from seismogenic faults.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, Z.S.; Ma, Z.J.; Niu, A.F.; Zhang, X.L.; Wang, S.X.; Chen, B. Approaches and Preliminary results of Crust movement researches based on the GPS in China. Earth Sci. Front. 2003, 10, 71–79. [Google Scholar]
- Guemundsson, S. Crustal Deformation Mapped by Combined GPS and InSAR; Technical University in Denmark: Kongens Lyngby, Denmark, 2000. [Google Scholar]
- Gudmundsson, S.; Sigmundsson, F. Three-Dimensional Surface Motion Maps Estimated from Combined Interferometric Synthetic Aperture Radar and GPS Data. J. Geophys. Res. 2002, 107, 2250–2264. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Tiampo, K.F.; Rundle, J.; Li, Z.H. Application of InSAR-GPS Optimization for Derivation of Fine Scale Surface Motion Maps of Southern Califotnia. IEEE Trans. Geosci. Remote Sens. 2007, 45, 512–521. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Tiampo, K.F. Analytical optimization of DInSAR and GPS dataset for derivation of three-dimensional surface motion. IEEE Geosci. Remote Sens. Lett. 2006, 3, 107–111. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Sun, Q.; Zhu, J.J.; Ding, X.L. Three-dimensional surface displacements from InSAR and GPS measurements with variance component estimation. IEEE Geosci. Remote Sens. Lett. 2012, 9, 754–758. [Google Scholar]
- Hu, J.; Li, Z.W.; Zhu, J.J.; Ding, X.L. Measuring three-dimensional surface displacements from combined InSAR and GPS data based on BFGS method. Chin. J. Geophys. 2013, 56, 117–126. [Google Scholar]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Sun, Q. Derivation of 3-D coseismic surface displacement field for the 2011 Mw9.0 Tohoku-Oki earthquake from InSAR and GPS measurements. Geophys. J. Int. 2013, 192, 573–585. [Google Scholar] [CrossRef]
- Elisabeth, S.; Stephane, D.; Jordan, B.; Laurent, P.; Laurent, M.; Joelle, N.D. Combination of INSAR and GNSS measurements for ground displacement monitoring. Procedia Technol. 2014, 16, 192–198. [Google Scholar]
- Leijen, F.J.; Samiei-Esfahany, S.; Marel, H.V.; Hanssen, R.F. A standardized approach for the integration of geodetic data for deformation analysis. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, Texas, USA, 23–28 July 2017; pp. 957–960. [Google Scholar]
- He, X.F.; Shi, G.Q.; Xiao, R.Y. Integration of GPS and InSAR for 3D Deformation Monitoring Based on Ant Colony Optimization. J. Tonfji Univ. (Nat. Sci.) 2015, 43, 1594–1600. [Google Scholar]
- Cao, H.K.; Zhao, L.H.; Zhang, Q.; Qu, W.; Nie, J.L. Ascending and Desending Orbits InSAR-GPS Data Fusion Method with Additional Systematic Parameters for Three-Dimensional Deformation Field. Ceomatics Inf. Sci. Wuhan Univ. 2018, 43, 1362–1368. [Google Scholar]
- Zhu, J.J.; Yang, Z.F.; Li, Z.W. Recent progress in retrieving and predicting mining-induced 3D displace-ments using InSAR. Acta Geod. Et Cartogr. Sin. 2019, 48, 135–144. [Google Scholar] [CrossRef]
- Béjar-Pizarro, M.; Guardiola-Albert, C.; García-Cárdenas, R.P.; Herrera, G.; Barra, A.; López Molina, A.; Tessitore, S.; Staller, A.; Ortega-Becerril, J.A.; García-García, R.P. Interpolation of GPS and Geological Data Using InSAR Deformation Maps: Method and Application to Land Subsidence in the Alto Guadalentín Aquifer (SE Spain). Remote Sens. 2016, 8, 965–981. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Guglielmino, F.; Nunnari, G.; Puglisi, G.; Spata, A. Simultaneous and Integrated Strain Tensor Estimation from Geodetic and Satellite Deformation Measurements to Obtain Three-Dimensional Displacement Maps. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1815–1826. [Google Scholar] [CrossRef]
- Guglielmino, F.; Bignami, C.; Bonforte, A.; Briole, P.; Obrizzo, F.; Puglisi, G.; Stramondo, S.; Wegmuller, U. Analysis of satellite and in situ ground deformation data integrated by the SISTEM approach: The 3 April 2010 earthquake along the Pernicana fault(Mt.Etna-Italy) case study. Earth Planet Sci. Lett. 2011, 312, 327–336. [Google Scholar] [CrossRef]
- Gugliemino, F.; Anzidei, M.; Briole, P.; Elias, P.; Puglisi, G. 3D Displacement maps of the 2009 L’Aquila earthquake (Italy) by applying the SISTEM method to GPS and DInSAR data. Terra Nova 2013, 25, 79–85. [Google Scholar] [CrossRef]
- Luo, H.P.; Chen, T. Three-Dimensional Surface Displacement Field Associated with the 25 April 2015 Gorkha, Nepal, Earthquake: Solution from Integrated InSAR and GPS Measurements with an Extended SISTEM Approach. Remote Sens. 2016, 8, 559. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Xu, C.J.; Liu, Y.; Zhao, Y.W. Three-dimensional displacement field of the 2021 Mw8.8 Maule earthquake from GPS and InSAR data with the improved ESISTEM-VCE method. Front. Earth Sci. 2022, 10, 970493. [Google Scholar] [CrossRef]
- Wang, X.; Liu, G.; Yu, B.; Dai, K.; Zhang, R.; Ma, D.; Li, Z. An integrated method based on DInSAR, MAI and displacement gradient tensor for mapping the 3D coseismic deformation field related to the 2011 Tarlay earthquake (Myanmar). Remote Sens. Environ. 2015, 170, 388–404. [Google Scholar] [CrossRef]
- Wang, Z.W. Research on resolving of three-dimensional displacement from multi-source InSAR data. Acta Geod. Cartogr. Sin. 2019, 48, 1206. [Google Scholar]
- Zhu, J.J.; Li, Z.W.; Hu, J. Research progress and methods of InSAR for deformation monitoring. Acta Geod. Cartogr. Sin. 2017, 46, 1717G1733. [Google Scholar]
- Gao, M.L.; Gong, H.L.; Chen, B.B.; Zhou, C.F.; Si, Y. Review of Three-dimensional Surface Deformation Acquisition from InSAR Measurements and Its Application. Bull. Surv. Mapp. 2017, 133, 1–4. [Google Scholar]
- Liu, J.H.; Hu, J.; Li, Z.W.; Zhu, J.J.; Sun, Q.; Gan, J. A method for measuring 3-D surface deformations with InSAR based on strain model and variance component estimation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 239–250. [Google Scholar] [CrossRef]
- Gan, J.; Hu, J.; Li, Z.W.; Yang, C.J.; Liu, J.H.; Sun, Q.; Zheng, W.J. Mapping three-dimensional co-seismic surface deformations associated with the2015 MW7.2 Murghab earthquake based on InSAR and characteristics of crustal strain. Sci. China Earth Sci. 2018, 48, 1335–1351. [Google Scholar]
- Yuan, S.; He, P.; Wen, Y.M.; Xu, C.J. Integrated InSAR and strain tensor to estimate three-dimensional coseismic displacements associated with the 2016 Mw7.0 Kumamoto earthquake. Chin. J. Geophys. 2020, 63, 1340–1356. (In Chinese) [Google Scholar]
- Hu, J.; Liu, J.; Li, Z.; Zhu, J.; Wu, L.; Sun, Q.; Wu, W. Estimating three-dimensional co-seismic deformations with the SM-VCE method based on heterogeneous SAR observations: Selection of homogeneous points and analysis of observation combinations. Remote Sens. Environ. 2021, 255, 112298. [Google Scholar] [CrossRef]
- Liu, J.H.; Hu, J.; Li, Z.W.; Zhu, J.J. Estimation of 3D coseismic deformation with InSAR: An improved SM-VCE method by window optimization. Acta Geod. Et Cartogr. Sin. 2021, 50, 1222–1239. [Google Scholar]
- Liu, J.H.; Hu, J.; Li, Z.W.; Ma, Z.; Wu, L.; Jiang, W.; Feng, G.; Zhu, J.J. Complete three-dimensional coseismic displacements due to the 2021 Maduo earthquake in Qinghai Province, China from Sentinel-1 and ALOS-2 SAR images. Sci. China Earth Sci. 2022, 65, 687–697. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. Solid Earth 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Bechor, N.B.D.; Zebker, H.A. Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 2006, 33, 275–303. [Google Scholar] [CrossRef]
- Michel, R.; Avouac, J.P.; Taboury, J. Measuring ground displacements from SAR amplitude images: Application to the landers earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar] [CrossRef]
- Grandin, R.; Klein, E.; Métois, M.; Vigny, C. 3D displacement field of the 2015 Mw8. 3 Illapel earthquake (Chile) from across- and along-track Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 2016, 43, 2552–2561. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
- Hu, J. Theory and Method of Estimating Three-Dimensional Displacement with InSAR Based on the Modern Surveying Adjustment; Central south university: Changsha, China, 2012. [Google Scholar]
- Xu, P.; Liu, Y.; Shen, Y.; Fukuda, Y. Estimability analysis of variance and covariance components. J. Geod. 2007, 81, 593–602. [Google Scholar] [CrossRef]
- Xu, P.; Shen, Y.; Fukuda, Y.; Liu, Y. Variance component estimation in linear inverse ill-posed models. J. Geod. 2006, 80, 69–81. [Google Scholar] [CrossRef]
- Cui, X.Z.; Yu, Z.C.; Tao, B.Z. Generalized Surveying Adjustment (New ER); Wuhan University Press: Wuhan, China, 2009. [Google Scholar]
- Nie, Y.; Shen, Y.; Pail, R.; Chen, Q. Efficient variance component estimation for large-scale least-squares problems in satellite geodesy. J. Geod. 2022, 96, 13. [Google Scholar] [CrossRef]
- Li, X.B.; Wang, X.Y.; Chen, Y.L. InSAR Atmospheric Delay Correction Model Integrated from Multi-Source Data Based on VCE. Remote Sens. 2022, 14, 4329. [Google Scholar] [CrossRef]
- Xu, C.J.; Deng, C.Y.; Zhou, L.X. Coseismic slip distribution inversion method based on the variance component estimation. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 37–44. [Google Scholar]
- Hua, J.; Zhao, D.Z.; Shan, X.J.; Qu, C.Y.; Zhang, Y.F.; Gong, W.Y.; Wang, Z.J.; Li, C.L.; Li, Y.C.; Zhao, L.; et al. Coseismic deformation field, slip distribution and coulomb stress disturbance of the 2021 Mw7.3 Maduo Earthquake using sentinel-1 InSAR observation. Seismol. Geol. 2021, 43, 677–691. [Google Scholar]
- Deng, Q.D.; Zhang, P.Z.; Ran, Y.K.; Yang, X.P.; Min, W.; Chen, L.C. Active tectonics and earthquake activities in China. Earth Sci. Front. 2003, 10, 66–73. [Google Scholar]
- Li, Z.M.; Li, W.Q.; Li, T.; Xu, Y.R.; Su, P.; Guo, P.; Sun, H.Y.; Ha, G.H.; Chen, G.H.; Yuan, Z.D.; et al. Seismogenic fault and coseismic surface deformation of the Maduo Ms7.4 earthquake in Qinghai, China: A quick report. Seismol. Geol. 2021, 43, 722–737. [Google Scholar]
- Wang, W.X.; Shao, Y.X.; Yao, W.Q. Rapid extraction of features and indoor reconstruction of 3D structures of Madoi Mw7.4 earthquake surface rupture based on photogrammetry method. Seismol. Geol. 2022, 44, 524–540. [Google Scholar]
- Ren, J.J.; Xu, X.W.; Zhang, G.W.; Wang, Q.X.; Zhang, Z.W.; Gai, H.L.; Kang, W.J. Co-seismic surface ruptures, slip distribution, and 3D seismogenic fault for the 2021 Mw 7.3 Maduo earthquake, central Tibetan Plateau, and its tectonic implications. Tectonophysics 2022, 827, 229275. [Google Scholar] [CrossRef]
- Li, Z.C.; Ding, K.H.; Zhang, P.; Wen, Y.M.; Zhao, L.J.; Chen, J.F. Co-seismic Deformation and Slip Distribution of 2021 Mw 7.4 Madoi Earthquake from GNSS Observation. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1489–1497. [Google Scholar]
- Wang, D.J.; Wang, D.Z.; Zhao, B.; Li, Y.; Zhao, L.J.; Wang, Y.B.; Nie, Z.S.; Qiao, X.J.; Wang, Q. 2021 Qinghai Madoi MW7.4 earthquake coseismic deformation field and fault-slip distribution using GNSS observations. Chin. J. Geophys. 2022, 65, 537–551. [Google Scholar]
- Shu, C.Z. InSAR 3D Coseismic and Postseismic Deformation of Maduo Mw7.4 and Inversion of Fault Slip Distrobution; Jilin University: Changchun, China, 2022. [Google Scholar]
- Yu, P.F.; Xiong, W.; Chen, W.; Qiao, X.J.; Wang, D.J.; Liu, G.; Zhao, B.; Nie, Z.S.; Li, Y.; Zhao, L.J.; et al. Slip model of the 2021 MS7.4 Madoi earthquake constrained by GNSS and InSAR coseismic deformation. Chin. J. Geophys. 2022, 65, 509–522. (In Chinese) [Google Scholar]
- Gao, Z.Y.; Li, Y.C.; Shan, X.J.; Zhu, C.H. Earthquake Magnitude Estimation from High-Rate GNSS Data: A Case Study of the 2021 Mw 7.3 Maduo Earthquake. Remote Sens. 2021, 13, 4478. [Google Scholar] [CrossRef]
- Yang, J.Y.; Sun, W.K.; Hong, S.Y.; Yuan, Z.Y.; Li, Y.; Chen, W.; Meng, G.j. Coseismic deformation analysis of the 2021 Qinghai Madoi M7.4 earthquake. Chin. J. Geophys. 2021, 64, 2671–2683. (In Chinese) [Google Scholar]
- Pan, J.W.; Bai, M.K.; Li, C.; Liu, F.C.; Li, H.B.; Liu, D.L.; Chevalier, M.L.; Wu, K.G.; Wang, P.; Lu, H.J.; et al. Cosesimic surface rupture and Seismogenic structure of the 2021-05-22 Maduo (Qinghai) Ms7.4 earthquake. Acta Geol. Sin. 2021, 95, 1655–1670. [Google Scholar]
- Wang, Y.B.; Li, Y.; Cai, Y.; Jiang, L.J.; Shi, H.B.; Jiang, Z.S.; Gan, W.J. Coseismic displacement and slip distribution of the 2021 May 22, Ms7.4 Madoi earthquake derived from GNSS observations. Chin. J. Geophys. 2022, 65, 523–536. [Google Scholar]
- Hu, J.; Li, Z.W.; Zhu, J.J.; Ren, X.C.; Ding, X.L. Inferring three-dimensional surface displacement field by combining SAR interferometric phase and amplitude information of scending and descending orbits. Sci. China Earth Sci. 2010, 40, 307–318. [Google Scholar]
- Zhang, Q.; Zhao, C.Y.; Ding, X.L.; Chen, Y.Q.; Wang, L.; Huang, G.W.; Yang, C.S.; Ding, X.G.; Ma, J. Research on recent characteristics of spatio temporal evolution and mechanism of Xi’an land subsidence and ground fissure by using GPS and InSAR techniques. Chin. J. Geophys. 2009, 52, 1214–1222. (In Chinese) [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Alsdorf, D. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 2. [Google Scholar] [CrossRef]
- Parsons, B.; Wright, T.; Rowe, P.; Andrews, J.; Jackson, J.; Walker, R.; Khatib, M.; Talebian, M.; Bergman, E.; Engdahl, E.R. The 1994 Sefidabeh (eastern Iran) earthquakes revisited: New evidence from satellite radar interferometry and carbonate dating about the growth of an active fold above a blind thrust fault. Geophys. J. Int. 2006, 164, 202–217. [Google Scholar] [CrossRef]
- Sudhaus, H.; Jónsson, S. Source model for the 1997 Zirkuh earthquake (MW = 7.2) in Iran derived from JERS and ERS InSAR observations. Geophys. J. Int. 2011, 185, 676–692. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, Y.; Ma, J.; Shao, R.T.; Xu, Y.F.; Hu, J. Relocation and focal mechanism solution of the 2021 Maduo, Qinghai Ms7.4 earthquake sequence. Seismol. Geol. 2021, 43, 790–805. [Google Scholar]
- Wells, D.L.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Dong, R.D.; Yao, Q.; Shi, H.Q.; Wang, Q. A Unified Model of Spatiotemporal Rupture Process for the 2001 Weast of Kunlun Mountain Pass Earthquake. Earthq. Res. China 2022, 38, 80–90. [Google Scholar]
- Wang, W.M.; He, J.K.; Wang, X.; Zhou, Y.; Hao, J.L.; Zhao, L.F.; Yao, Z.X. Rupture process models of the Yangbi and Maduo earthquakes that struck the eastern Tibetan Plateau in May 2021. Sci. Bull. 2022, 67, 466–469. [Google Scholar] [CrossRef]
- Xiong, R.W. Study on the Activity of Maduo-Gande Fault; Institute of Earthquake Forecasting, China Earthquake Administration: Beijing, China, 2010. [Google Scholar]
- Xiong, R.W.; Ren, J.W.; Zhang, J.L.; Yang, P.X.; Li, Z.M.; Hu, C.Z.; Chen, C.Y. Late quaternary active characteristics of the Gande segment in the Maduo-Gande fault zone. Earthquake 2010, 30, 65–73. [Google Scholar]
- Xiong, R.W. Late Quaternary Active Characteristics of the Maduo-Gande Fault Zone in Bayankala Block; Institute of Earthquake Forecasting, China Earthquake Administration: Beijing, China, 2013. [Google Scholar]
- Wang, W.; Fang, L.; Wu, J.; Tu, H.; Chen, L.; Lai, G.; Zhang, L. Aftershock sequence relocation of the 2021 Ms7.4 Maduo Earthquake, Qinghai, China. Sci. China Earth Sci. 2021, 64, 1371–1380. [Google Scholar] [CrossRef]
- Pertersen, M.D.; Dawson, T.E.; Chen, R.; Cao, T.Q.; Wills, C.J.; Schwartz, D.P.; Frankel, A.D. Fault displacement hazard for strike-slip faults. Bull. Seismol. Soc. Am. 2011, 101, 805–825. [Google Scholar] [CrossRef]
- Livio, F.; Serval, L.; Gurpinar, A. Locating distirbuted faulting: Contributions from InSAR imaging to probabilistic fault displacement hazard analysis (PFDHA). Quat. Int. 2016, 451, 223–233. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Li, M.F.; Meng, Y.Q.; Wu, S.X.; Cai, C.X. Research on fault activities and their seismogeological implication in Bayankala Mountain area. Res. Act. Fault. 1996, 5, 154–171. [Google Scholar]
- Yuan, Z.; Li, T.; Su, P.; Sun, H.; Ha, G.; Guo, P.; Chen, G.; Jobe, J.T. Large surface rupture gaps and low surface fault slip of the 2021 Mw 7.4 Maduo earthquake along a low-activity strike-slip fault, Tibetan Plateau. Geophys. Res. Lett. 2022, 49, e2021GL096874. [Google Scholar] [CrossRef]
- Song, X.H.; Wang, S.J.; Pan, S.Z.; Song, J.J. Deep seismotectonic environment of the 2021 Madoi Ms7.4 earthquake. Seismol. Geol. 2021, 43, 757–770. [Google Scholar]
- Deng, Q.D.; Cheng, S.P.; Ma, J.; Du, P. Seismic activities and earthquake potential in the Tibetan plateau. Chin. J. Geophys. 2014, 57, 2025–2042. [Google Scholar]
- Li, C.J. Lithospheric Deformation Characteristics and Related Mechanisms in SE Tibetan Plateau; Institute of Geology, China Earthquake Administration: Beijing, China, 2021. [Google Scholar]
- Yuan, J.Y.; Wang, Y.L.; Zhan, B.L.; Yuan, X.M.; Wu, X.Y.; Ma, J.J. Comprehensive investigation and analysis of liquefaction damage caused by the Ms7.4 Maduo earthquake in 2021 on the Tibetan Plateau, China. Soil Dyn. Earthq. Eng. 2022, 155, 107191. [Google Scholar] [CrossRef]
- Yao, W.Q.; Wang, Z.J.; Liu, J.; Liu, X.L.; Han, F.L.; Shao, Y.X.; Wang, W.X.; Xu, J.; Qin, K.X.; Gao, Y.P.; et al. Discussion on coseismic surface rupture length of the 2021 Mw7.4 Madoi earthquake, Qinghai, China. Seismol. Geol. 2022, 44, 541–559. [Google Scholar]
- Lv, M.M.; Chang, L.J.; Lu, L.Y.; Liu, J.D.; Wu, P.P.; Guo, H.L.; Cao, X.L.; Ding, Z.F. Focal mechanism solutions of the aftershocks of the 2021 Qinghai Madoi MS7.4 earthquake and its seismogenic structure characteristics. Chin. J. Geophys. 2022, 65, 1991–2005. (In Chinese) [Google Scholar]
- Xiao, L.H.; Zheng, R.; Zou, R. Co-seismic Slip Distribution of THE 2021 Mw7.4 Maduo, Qinghai Earthquake Estimated from InSAR and GPS Measurements. J. Earth Sci. 2022, 33, 885–891. [Google Scholar] [CrossRef]
- Deng, W.Z.; Liu, J.; Yang, Z.G.; Sun, L.; Zhang, X.M. Preliminary analysis for rupture process of the May 22th, 2021, Madoi (Qinghai) Ms7.4 earthquake. Seismol. Geol. 2022, 44, 1059–1070. [Google Scholar]
- Zhan, Y.; Liang, M.J.; Sun, X.Y.; Huang, F.P.; Zhao, L.Q.; Gong, Y.; Han, J.; Li, C.X.; Zhang, P.Z.; Zhang, H.P. Deep structure and seismogenic pattern of the 2021.5.22 Madoi (Qing hai) Ms7.4 earthquake. Chin. J. Geophys. 2021, 64, 2232–2252. [Google Scholar]
- Han, L.F.; Liu, J.; Yao, W.Q. Detailed mapping of the surface rupture near the epicenter segment of the 2021 Madoi MW7.4 earthquake and discussion on distributed rupture in the step-over. Seismol. Geol. 2022, 44, 484–505. [Google Scholar]
- Xie, W.B.; Hu, J.W.; Zuo, X.Q.; Zhang, Y.M.; Liu, Y.Z. Analysis of 3D deformation field caused by Yushu Mw7. 1 earthquake based on InSAR technology. Geotech. Investig. Surv. 2019, 5, 45–52. [Google Scholar]
- Sylvester, A.G. Strike-slip faults. Geol. Soc. Am. Bull. 1988, 100, 1666–1703. [Google Scholar] [CrossRef]
- Li, H.B.; Pan, J.W.; Lin, A.; Sun, Z.M.; Liu, D.L.; Zhang, J.J.; Li, C.L.; Liu, K.; Chevalier, M.L.; Yun, K.; et al. Coseismic surface ruptures associated with the 2014 MW 6.9 yutian earthquake on the Altyn Tagh fault, Tibetan Plateau. Bull. Seismol. Soc. Am. 2016, 106, 595–608. [Google Scholar] [CrossRef]
- Ren, J.J.; Zhang, Z.W.; Gai, H.L.; Kang, W.J. Typical Riedel shear structures of the coseismic surface rupture zone produced by the 2021 MW 7.3 Maduo earthquake, Qinghai, China, and the implications for seismic hazards in the block interior. Nat. Hazards Res. 2021, 1, 145–152. [Google Scholar] [CrossRef]
- Earthquake Agency of Xinjiang Uygur Autonomous Region. The Fuyun Earthquake Fault Zone; Seismological Press: Beijing, China, 1985. [Google Scholar]
- Xu, Z.G.; Liang, S.S.; Zhang, G.W.; Liang, J.H.; Zou, L.Y.; Li, X.M.; Chen, Y.H. Analysis of seismogenic structure of Madoi, Qinghai MS7.4 earthquake on May 22, 2021. Chin. J. Geophys. 2021, 64, 2657–2670. (In Chinese) [Google Scholar]
- Jin, Z.; Fialko, Y. Coseismic and early postseismic deformation due to the 2021 M7.4 Maduo (China) earthquake. Geophys. Res. Lett. 2021, 48, e2021GL095213. [Google Scholar] [CrossRef]
- He, L.J.; Feng, G.C.; Wu, X.X.; Lu, H.; Xu, W.B.; Wang, Y.D.; Liu, J.H.; Hu, J.; Li, Z.W. Coseismic and early postseismic slip models of the 2021 Mw 7.4 Maduo earthquake (Western China) estimated by space-based geodetic data. Geophys. Res. Lett. 2021, 48, e2021GL095860. [Google Scholar] [CrossRef]
- Chen, K.J.; Avouac, J.P.; Geng, J.H.; Liang, C.R.; Zhang, Z.G.; Li, Z.C.; Zhang, S.P. The 2021 Mw7.4 Madoi earthquake: An archetype bilateral slip-pulse rupture arrested at a splay fault. Geophys. Res. Lett. 2022, 49, e2021GL095243. [Google Scholar]
- Zhao, D.; Qu, C.; Chen, H.; Shan, X.; Song, X.; Gong, W. Tectonic and geometric control on fault kinematics of the 2021 Mw7.3 Maduo (China) earthquake inferred from interseismic, coseismic, and postseismic InSAR observations. Geophys. Res. Lett. 2021, 48, e2021GL095417. [Google Scholar] [CrossRef]
- Pan, J.W.; Li, H.B.; Chevalier, M.L.; Tapponnier, P.; Bai, M.K.; Li, C.; Liu, F.C.; Liu, D.L.; Wu, K.G.; Wang, P.; et al. Co-seismic rupture of the 2021, Mw7.4 Maduo earthquake (northern Tibet): Short-cutting of the kunlun fault big bend. Earth Planet. Sci. Lett. 2022, 594, 117703. [Google Scholar] [CrossRef]
- Shao, Y.X.; Liu, Z.J.; Gao, Y.P.; Wang, W.X.; Yao, W.Q.; Han, F.L.; Liu, Z.J.; Zou, X.B.; Wang, Y.; Li, Y.S.; et al. Co-seismic displacement measurement and distributed deformation characterization: A case of 2021 Mw7.4 Madoi earthquake. Seismol. Geol. 2022, 44, 506–523. [Google Scholar]
- Liu, X.L.; Xia, T.; Liu, J. Distributed characteristics of the surface deformation associated with the 2021 MW7.4 Madoi earthquake, Qinghai, China. Seismol. Geol. 2022, 44, 461–483. [Google Scholar]
- Chen, H.; Qu, C.Y.; Zhao, D.Z.; Ma, C.; Shan, X.J. Rupture kinematics and coseismic slip model of the 2021 Mw7.3 Maduo (China) earthquake: Implications for the seismic hazard of the kunlun fault. Remote Sens. 2021, 13, 3327. [Google Scholar] [CrossRef]
- Zheng, A.; Yu, X.W.; Qian, J.Q.; Liu, X.G.; Zhang, W.B.; Chen, X.F.; Xu, W.B. Cascading rupture process of the 2021 Maduo, China earthquake revealed by the joint inversion of seismic and geodetic data. Tectonophysics 2023, 849, 229732. [Google Scholar] [CrossRef]
- Zhu, M.; Chen, F.L.; Fu, B.H.; Chen, W.K.; Qiao, Y.F.; Shi, P.L.; Zhou, W.; Lin, H.; Liao, Y.A.; Gao, S. Earthquake-induced risk assessment of cultural heritage based on InSAR and seismic intensity: A case study of Zhalang temple affected by the 2021 Mw 7.4 Maduo (China) earthquake. Int. J. Disaster Risk Reduct. 2023, 84, 103482. [Google Scholar] [CrossRef]



| Orbit | Acquisition Date of the Master Image | Acquisition Date of the Slave Image | Imaging Mode | Wavelength /cm | Revisit Period /d |
|---|---|---|---|---|---|
| Ascending (T99) | 20 May 2021 (Sentinel-1A) | 26 May 2021 (Sentinel-1B) | IW | 5.6 | 6 |
| Descending (T106) | 20 May 2021 (Sentinel-1A) | 26 May 2021 (Sentinel-1B) | IW | 5.6 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chen, Y.; Wang, X.; Xiong, R. The Crustal Dynamics and Its Geological Explanation of the Three-Dimensional Co-Seismic Deformation Field for the 2021 Maduo MS7.4 Earthquake Based on GNSS and InSAR. Sensors 2023, 23, 3793. https://doi.org/10.3390/s23083793
Li X, Chen Y, Wang X, Xiong R. The Crustal Dynamics and Its Geological Explanation of the Three-Dimensional Co-Seismic Deformation Field for the 2021 Maduo MS7.4 Earthquake Based on GNSS and InSAR. Sensors. 2023; 23(8):3793. https://doi.org/10.3390/s23083793
Chicago/Turabian StyleLi, Xiaobo, Yanling Chen, Xiaoya Wang, and Renwei Xiong. 2023. "The Crustal Dynamics and Its Geological Explanation of the Three-Dimensional Co-Seismic Deformation Field for the 2021 Maduo MS7.4 Earthquake Based on GNSS and InSAR" Sensors 23, no. 8: 3793. https://doi.org/10.3390/s23083793
APA StyleLi, X., Chen, Y., Wang, X., & Xiong, R. (2023). The Crustal Dynamics and Its Geological Explanation of the Three-Dimensional Co-Seismic Deformation Field for the 2021 Maduo MS7.4 Earthquake Based on GNSS and InSAR. Sensors, 23(8), 3793. https://doi.org/10.3390/s23083793







