Backscattering Analysis at ATR on Rough Surfaces by Ground-Based Polarimetric Radar Using Coherent Decomposition
Abstract
1. Introduction
1.1. Problem and Tasks
- Select an object decomposition theorem for feature space design and test an acceptable scattering mechanism after calibration
- Conduct data calibration considering the effect of rough ground surface on object recognition
- Explore supervised learning as an ATR tool for polarimetric radar.
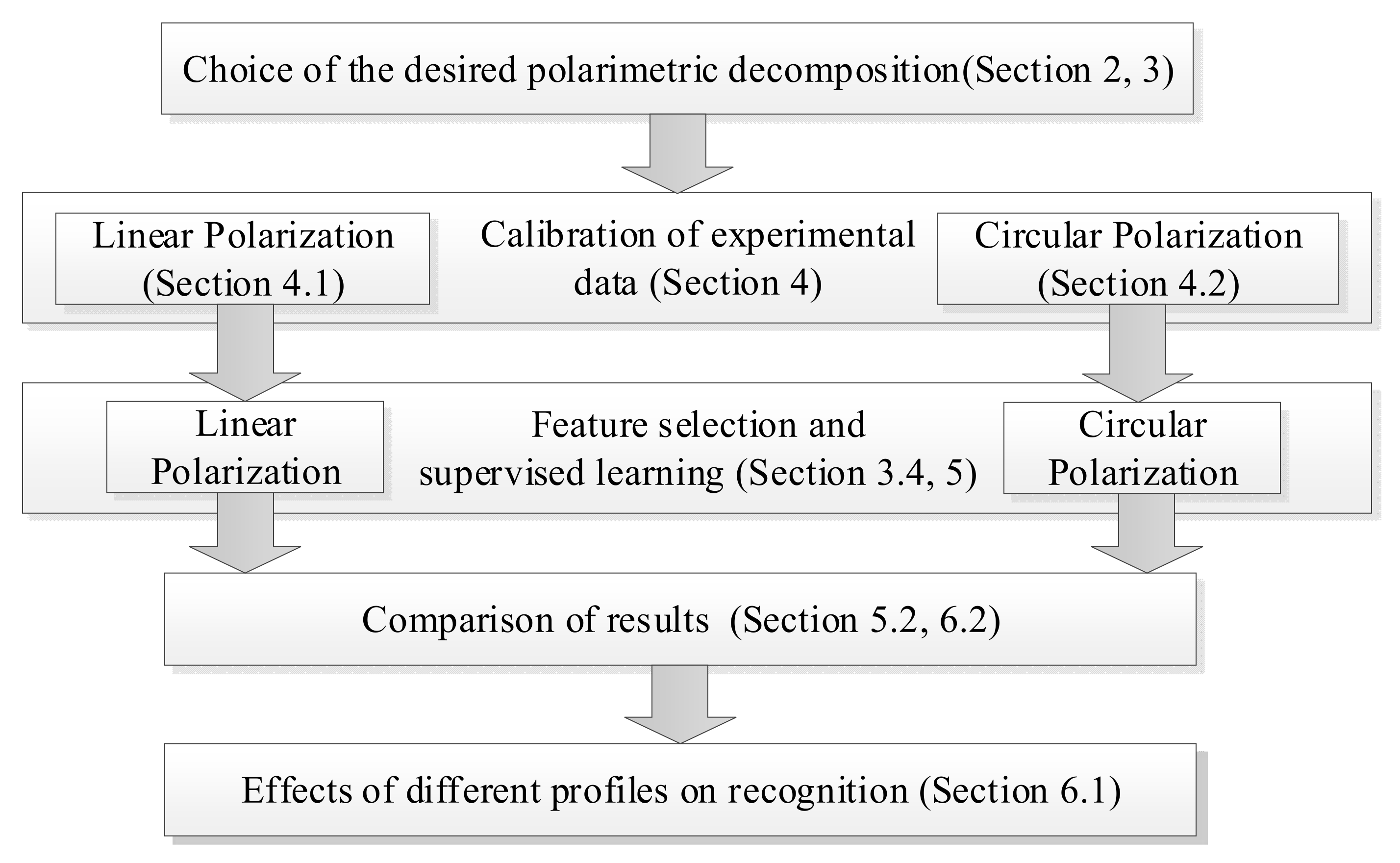
1.2. Structure of the Article
2. Theoretical Part
2.1. Assumptions
- Kennaugh matrix dichotomy (Kennaugh–Huynen scattering matrix)
- Decomposition of the covariance matrix (Freeman and Durden)
- Coherent scattering matrix decomposition (Pauli, Krogager, Cameron).
- The transmitted electromagnetic wave is a plane monochromatic wave with constant frequency, amplitude, and initial phase in time.
- In the propagation of a polarized wave, there are additive and multiplicative interferences.
- Polarimetric radar generates a signal with strict linear (vertical and horizontal) and strict circular (right and left) polarization.
- The classification procedure involves obtaining labeled data on detected objects; hence it is a supervised learning task.
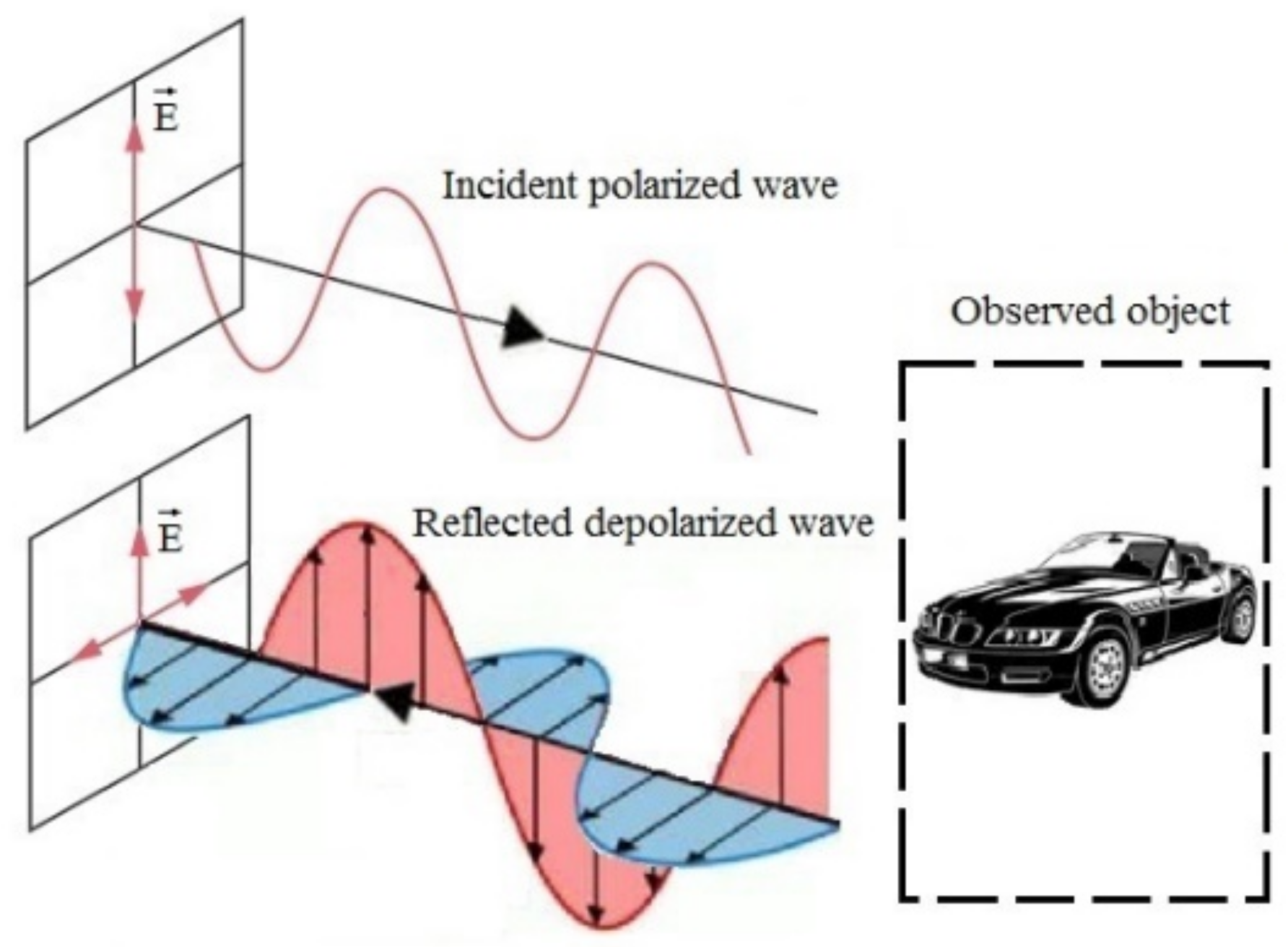
2.2. Polarized Wave Model
- The Jones calculus. This is a mathematical description of a fully polarized wave in which the Jones vectors and linear elements of the Jones matrix (Equation (1)) determine the polarization:where are amplitudes and phases of the transmitted and received signals, respectively, along the axis; are amplitudes and phases of the transmitted and received signals, respectively, along the axis; are complex reflection coefficients expressing the direct transformations of the incidental wave; and are complex reflection coefficients expressing the cross-transformations of the incidental wave.
- Mueller calculus. A mathematical description of arbitrarily polarized scattering is given by the Stokes vector, which is expressed as follows:where denotes the Stokes vector of scattering waves, and denotes the Stokes vector of an incidental wave; and is the Muller matrix, which characterizes the scattering properties of the object.
- The Mueller calculus has only a phenomenological interpretation and is not related to the electromagnetic theory, whereas the Jones calculus derives directly from this theory.
- The Jones calculus allows for the absolute phase, while the Mueller calculus does not consider the phase at all.
- The elements of the Jones matrix correspond to the radiation amplitude, while the elements of the Muller matrix are related to the scattering intensity.
3. Polarimetric Decomposition of Feature Space
3.1. Pauli Decomposition
3.2. Krogager Decomposition
3.3. Cameron Decomposition
3.4. Assessment of Feature Space for the Learning Algorithm
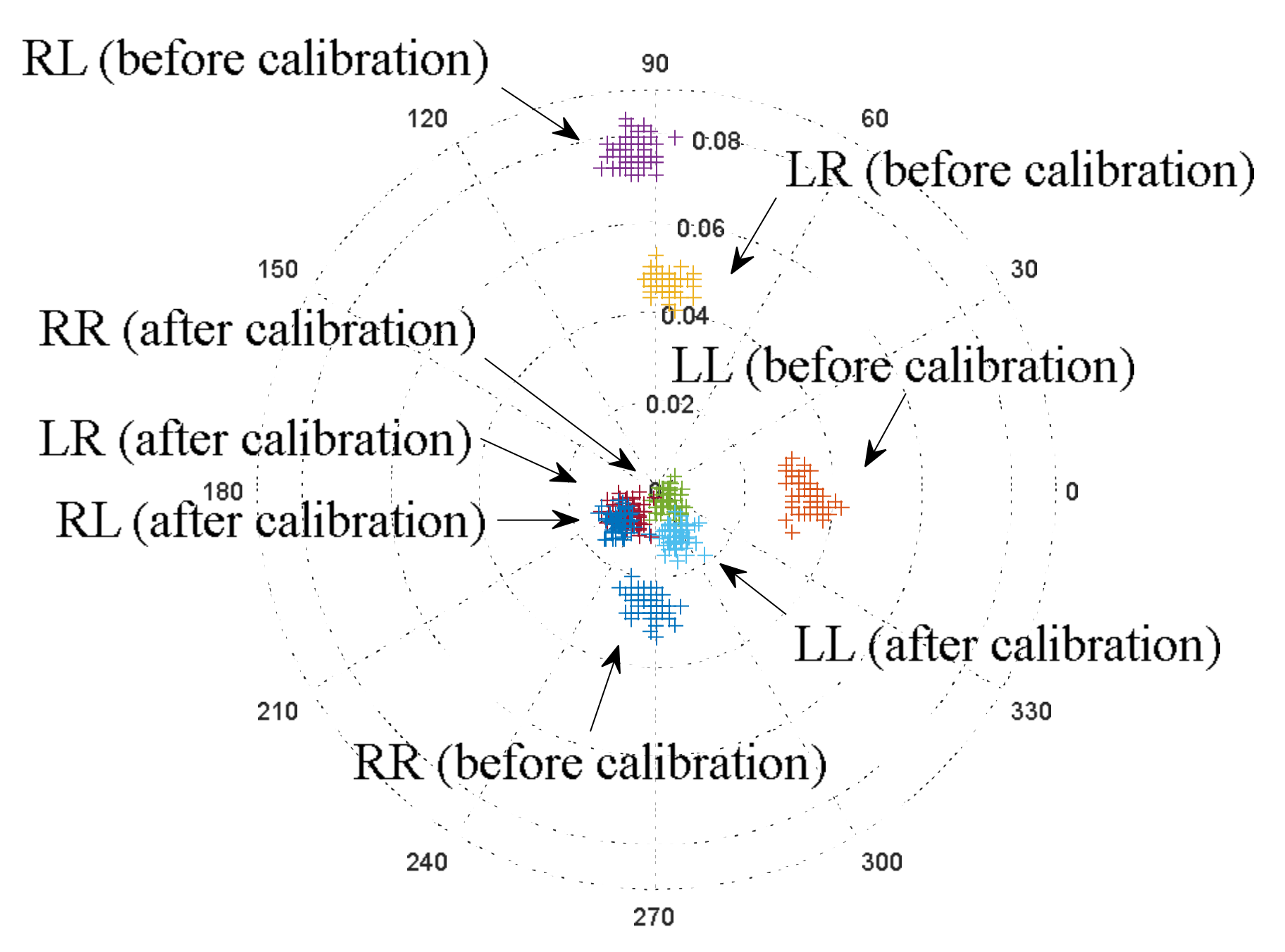
4. Data and Calibration
- Linear polarization (vertical and horizontal plane)
- Circular polarization (right and left rotation).
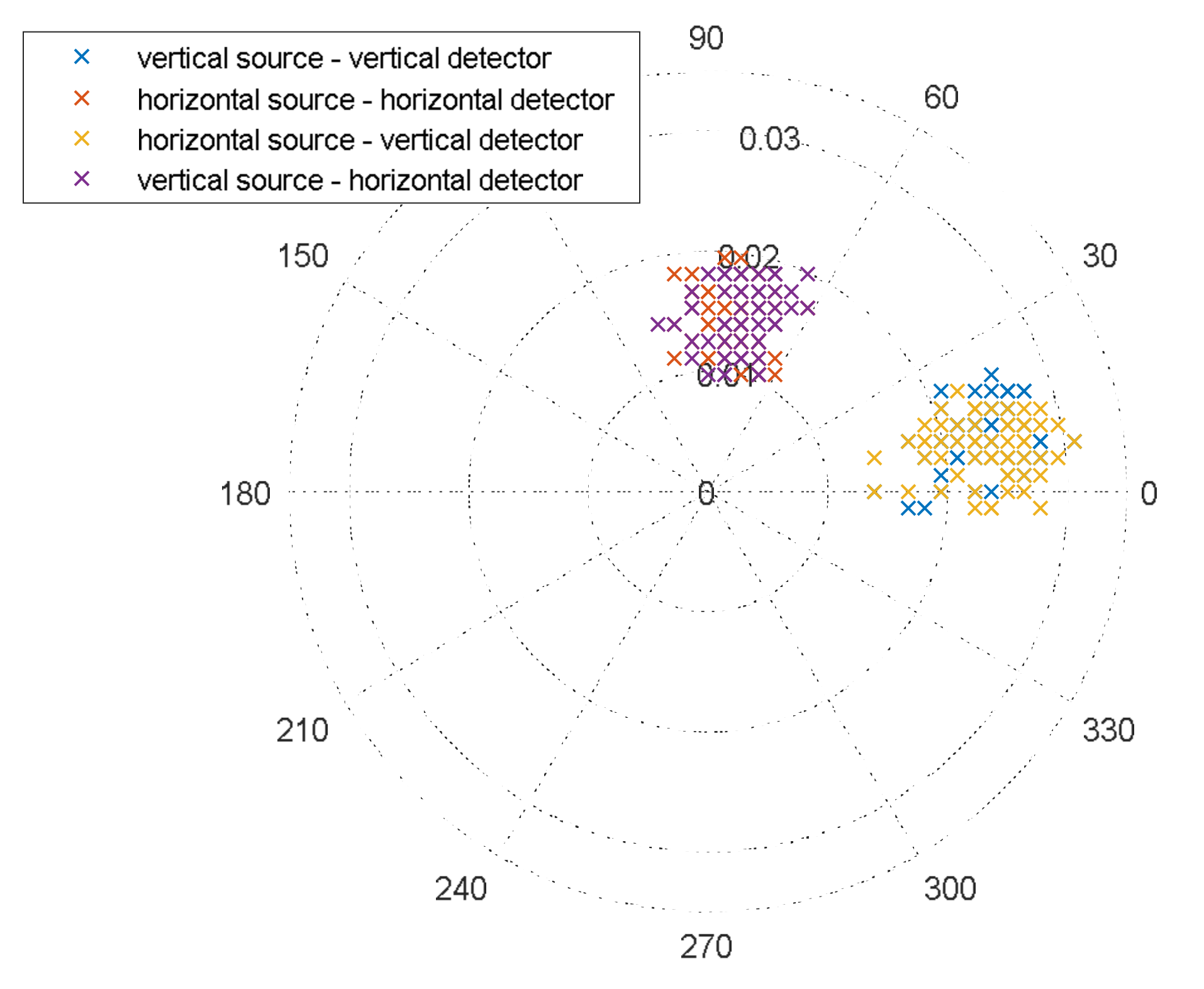
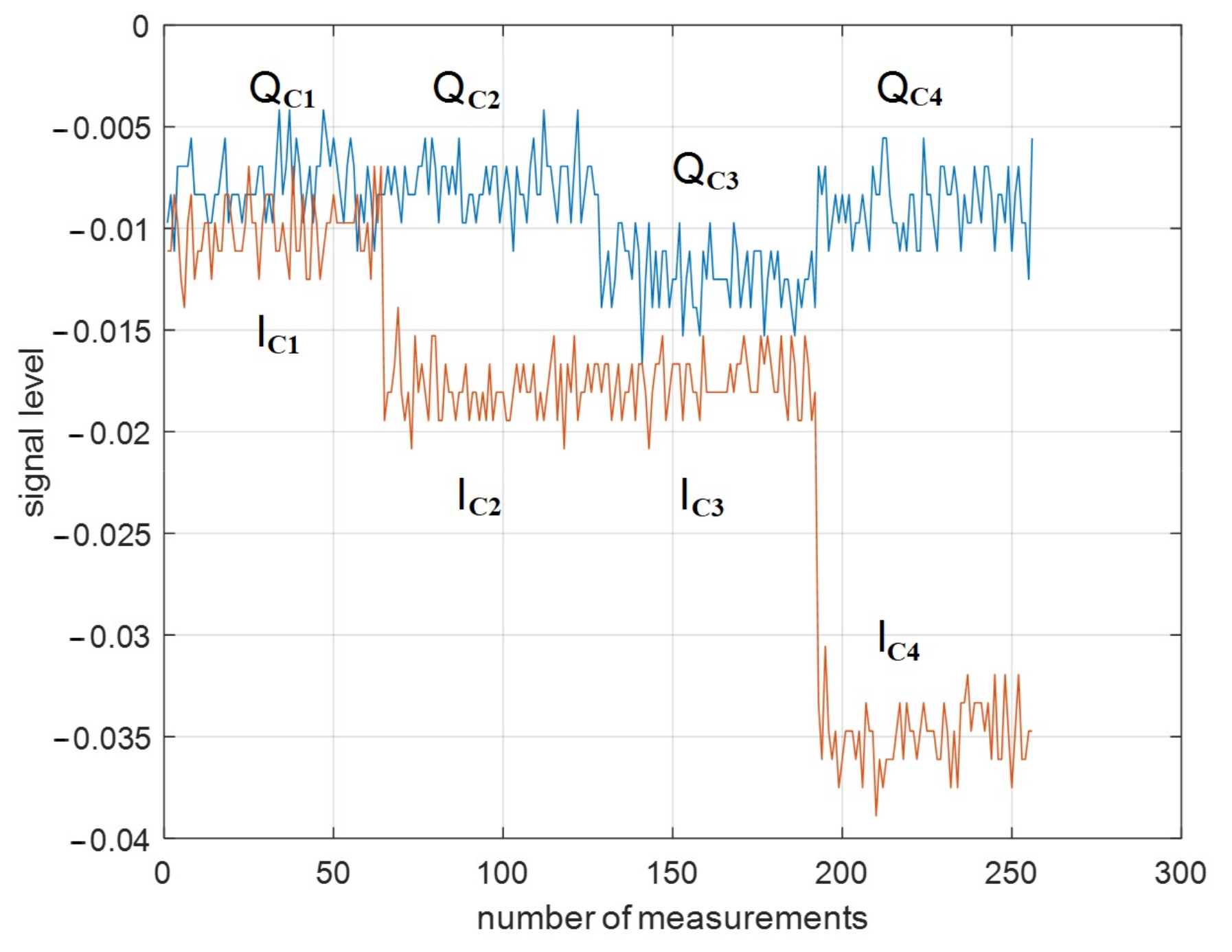
4.1. Linear Polarization Data
4.2. Circular Polarization Data
5. Supervised Learning for Polarimetric Recognition
5.1. Modeling Polarimetric Recognition
5.2. Comparison with Similar Methods
6. Results and Discussion
6.1. Influence of Different Target Profiles and Weather Conditions
6.2. Estimation of Binary Classifiers
7. Conclusions
Funding
Conflicts of Interest
Appendix A. The Coefficients Chart Depending on the Profile (Truck)


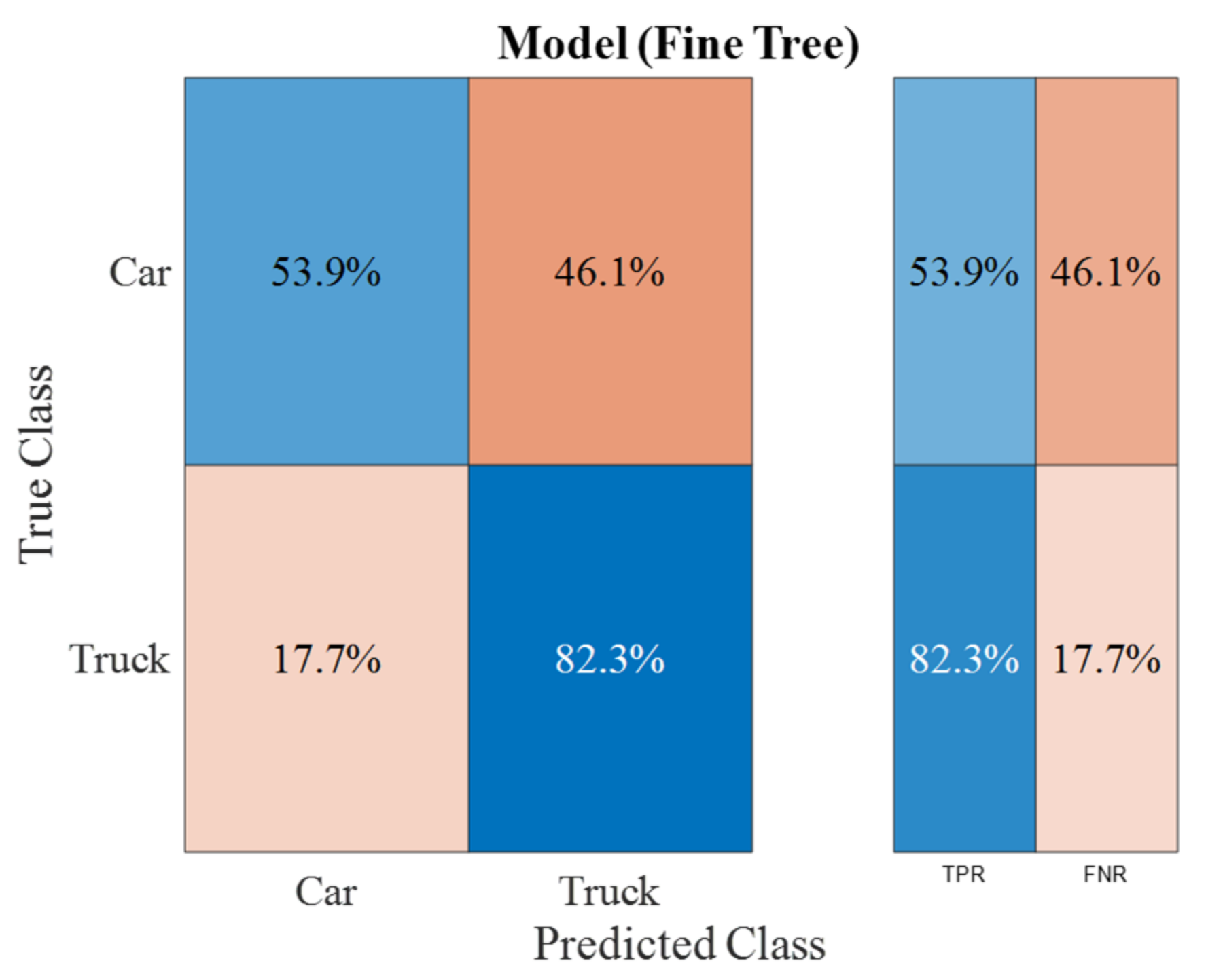
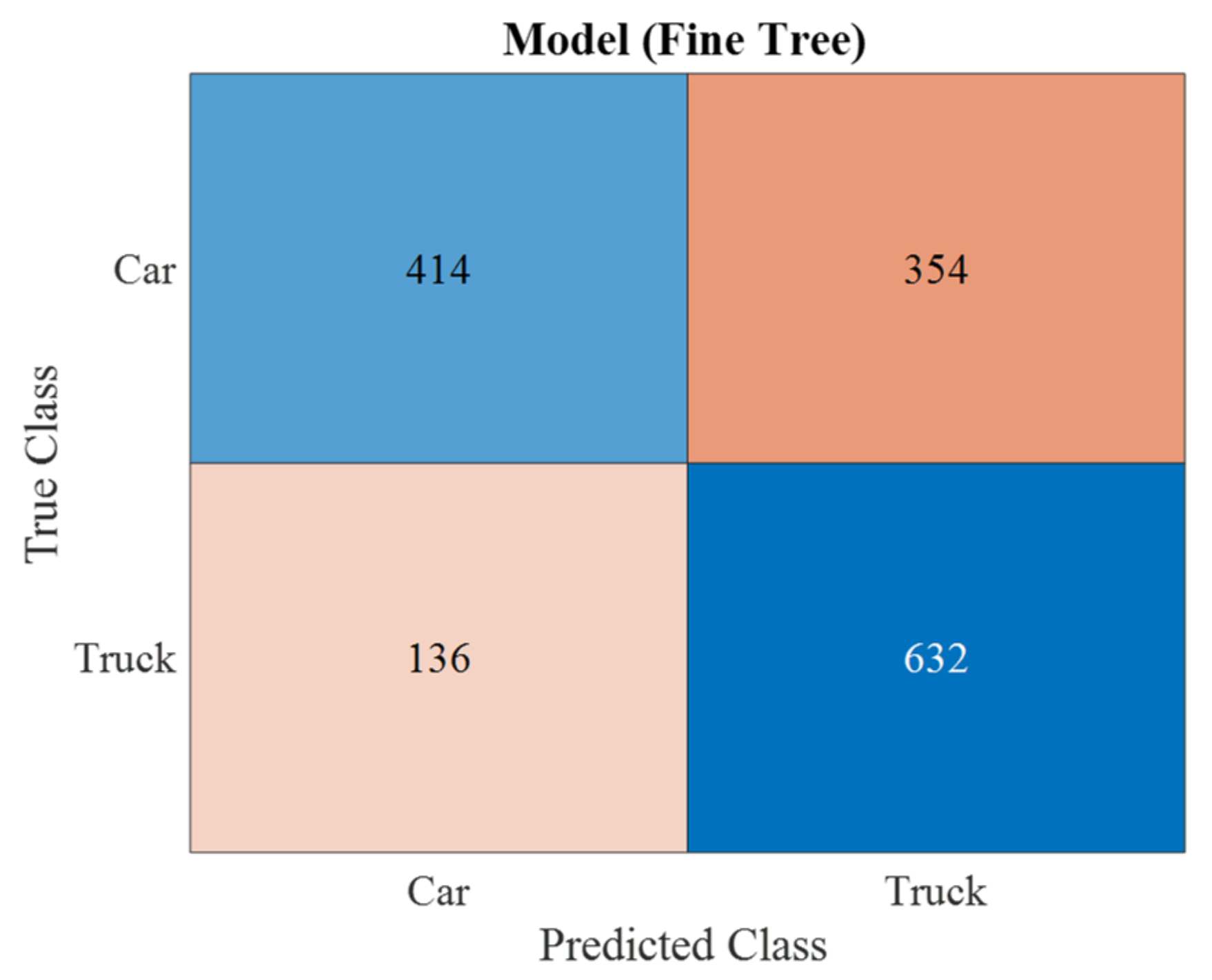
Appendix B. Confusion Matrix of the True Positive Rate of Classification

References
- Visentin, T. Polarimetric Radar for Automotive Applications. Ph.D. Thesis, Karlsruhe Technology Institute, Karlsruhe, Germany, 2019. [Google Scholar]
- He, Y.; Yang, J. Polarization Estimation with a Single Vector Sensor for Radar Detection. Remote Sens. 2022, 14, 1137. [Google Scholar] [CrossRef]
- Yang, F.; Gao, W.; Xu, B.; Yang, J. Multi-Frequency Polarimetric SAR Classification Based on Riemannian Manifold and Simultaneous Sparse Representation. Remote Sens. 2015, 7, 8469–8488. [Google Scholar] [CrossRef]
- Li, Y.; Quan, S.; Xiang, D.; Wang, W.; Hu, C.; Liu, Y.; Wang, X. Ship Recognition from Chaff Clouds with Sophisticated Polarimetric Decomposition. Remote Sens. 2020, 12, 1813. [Google Scholar] [CrossRef]
- Huynen, J.R. Phenomenological Theory of Radar Targets. Ph.D. Thesis, Technical University, Delft, The Netherlands, 1970. [Google Scholar]
- Kennaugh, E. Polarization Properties of Radar Reflection. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 1952. [Google Scholar]
- Mott, H. Polarization in Antennas and Radar; Wiley: Hoboken, NJ, USA, 1986; 297p. [Google Scholar]
- Kvasnov, A.V.; Shkodyrev, V.P.; Arsenyev, D.G. Method of recognition the radar emitting sources based on the naive bayesian classifier. WSEAS Trans. Systems Control 2019, 14, 112–120. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications. Optical Science and Engineering; CRC Press: Boca Raton, FL, USA, 2009; 400p. [Google Scholar]
- Richards, J.A. Remote Sensing with Imaging Radar; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; 361p. [Google Scholar]
- Kozlov, A.; Logvin, A.; Sarychev, V.; Shatrakov, Y.; Zavalishin, I. Introduction to the Theory of Radiopolarimetric Navigation Systems; Springer Aerospace Technology: Singapore, 2020; 365p. [Google Scholar]
- Cloude, S.R. Polarization: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009; 453p. [Google Scholar]
- Ryzhkov, A.V.; Zrnic, D.S. Radar Polarimetry for Weather Observations; Springer: Cham, Switzerland, 2019; 497p. [Google Scholar]
- Rico-Ramirez, M.A.; Cluckie, I.D. Classification of Ground Clutter and Anomalous Propagation Using Dual-Polarization Weather Radar. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1892–1904. [Google Scholar] [CrossRef]
- Da Silveira, R.B.; Holt, A.R. An automatic identification of clutter and anomalous propagation in polarization-diversity weather radar data using neural networks. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1777–1788. [Google Scholar] [CrossRef]
- Torvik, B.; Olsen, K.E.; Griffiths, H. Classification of Birds and UAVs Based on Radar Polarimetry. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1305–1309. [Google Scholar] [CrossRef]
- Zrnic, D.S.; Ryzhkov, A.V. Observations of insects and birds with a polarimetric radar. IEEE Trans. Geosci. Remote Sens. 1998, 36, 661–668. [Google Scholar] [CrossRef]
- Deep, Y.; Held, P.P.; Ram, S.; Dagmar Steinhauser, D.; Gupta, A.; Gruson, F.; Koch, A.; Roy, A. Polarimetric Radar Cross-Sections of Pedestrians at Automotive Radar Frequencies. IET Radar, Sonar & Navigation. arXiv 2020, arXiv:1910.13706. [Google Scholar]
- Visentin, T.; Hasch, J.; Zwick, T. Analysis of Multipath and DOA Detection Using a Fully Polarimetric Automotive Radar. In Proceedings of the 2017 European Radar Conference (EURAD), Nuremberg, Germany, 8–13 October 2017; pp. 45–48. [Google Scholar]
- Vassilev, V. Road Surface Recognition at Mm-Wavelengths Using a Polarimetric Radar. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6985–6990. [Google Scholar] [CrossRef]
- Guo, X.; Yin, J.; Li, K.; Yang, J.; Shao, Y. Scattering Intensity Analysis and Classification of Two Types of Rice Based on Multi-Temporal and Multi-Mode Simulated Compact Polarimetric SAR Data. Remote Sens. 2022, 14, 1644. [Google Scholar] [CrossRef]
- Sadjadi, F. Improved target classification using optimum polarimetric SAR signatures. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 38–49. [Google Scholar] [CrossRef]
- Zebker, H.A.; Van Zyl, J.J. Imaging radar polarimetry: A review. Proc. IEEE 1991, 79, 1583–1606. [Google Scholar] [CrossRef]
- Shui, P.; Xu, S.; Liu, H. Range-Spread Target Detection using Consecutive HRRPs. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 647–665. [Google Scholar] [CrossRef]
- Jacobs, S.P.; O’Sullivan, J.A. Automatic target recognition using sequences of high resolution radar range-profiles. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 364–381. [Google Scholar] [CrossRef]
- Visentin, T.; Sagainov, A.; Hasch, J.; Zwick, T. Classification of Objects in Polarimetric Radar Images Using CNNs at 77 GHz. In Proceedings of the 2017 IEEE Asia Pacific Microwave Conference (APMC), Kuala Lumpar, Malaysia, 13–16 November 2017; pp. 356–359. [Google Scholar]
- Tatarinov, V.N.; Tatarinov, S.V.; van Genderen, P. Principles of utilization of polarization invariant parameters for classification and recognition of distributed radar objects: Part I. Simplest model of a distributed object. In Proceedings of the 2011 Tyrrhenian International Workshop on Digital Communications—Enhanced Surveillance of Aircraft and Vehicles, Capri, Italy, 12–14 September 2011; pp. 79–82. [Google Scholar]
- Sadjadi, F. Technique for Selection of Optimum Polarimetric Angles in Radar Signature Classification. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 459–463. [Google Scholar]
- Wang, J.; Liu, Z.; Ran, L.; Xie, R. Feature Extraction Method for DCP HRRP-Based Radar Target Recognition via m−χ Decomposition and Sparsity-Preserving Discriminant Correlation Analysis. IEEE Sens. J. 2020, 20, 4321–4332. [Google Scholar] [CrossRef]
- Touzi, R. Target Scattering Decomposition in Terms of Roll-Invariant Target Parameters. IEEE Trans. Geosci. Remote Sens. 2007, 45, 73–84. [Google Scholar] [CrossRef]
- Cameron, W.L.; Rais, H. Polarization Scatter Feature Metric Space. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3638–3647. [Google Scholar] [CrossRef]
- Berizzi, F.; Martorella, M.; Capria, A.; Paladini, R.; Calugi, D. H/α Polarimetric Features for Man-Made Target Classification. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar]
- Long, T.; Zhang, L.; Li, Y.; Wang, Y. Geometrical Structure Classification of Target HRRP Scattering Centers Based on Dual Polarimetric H/alpha Features. IEEE Access 2019, 7, 141679–141688. [Google Scholar] [CrossRef]
- Kawalec, A.; Owczarek, R.; Dudczyk, J. Karhunen-Loeve Transformation in Radar Signal Features Processing. In Proceedings of the 2006 International Conference on Microwaves, Radar & Wireless Communications, Krakow, Poland, 22–24 May 2006; pp. 1168–1171. [Google Scholar]
- Lin, J.; Guo, Y.; Li, W.; Zhang, Y.; Chen, Z. Polarimetric Calibration Based on Lexicographic-Basis Decomposition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1149–1152. [Google Scholar] [CrossRef]
- Choudhary, V.; Rönnow, D.; Jansson, M. A Singular Value Decomposition Based Approach for Classifying Concealed Objects in Short Range Polarimetric Radar Imaging. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium—Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019; pp. 4109–4115. [Google Scholar]
- Wang, S.; Feng, W.; Sato, M. Polarimetric Calibration for a Ground-based Synthetic Aperture Radar System. In Proceedings of the 2019 Photonics & Electromagnetics Research Symposium—Fall (PIERS—Fall), Xiamen, China, 17–20 December 2019; pp. 632–639. [Google Scholar]
- Sarabandi, K.; Ulaby, F.T.; Tassoudji, M.A. Calibration of polarimetric radar systems with good polarization isolation. IEEE Trans. Geosci. Remote Sens. 1990, 28, 70–75. [Google Scholar] [CrossRef]
- Kvasnov, A.V. Methodology of classification and recognition of the radar emission sources based on Bayesian programming. IET Radar Sonar Navig. 2020, 14, 1175–1182. [Google Scholar] [CrossRef]
- Kvasnov, A.V. Method of Classification of Fixed Ground Objects by Radar Images with the Use of Artificial Neural Networks. In Proceedings of the International Conference on Cyber-Physical Systems and Control (CPS&C’2019), Saint Petersburg, Russia, 10–12 June 2019; pp. 608–616. [Google Scholar]
- Kvasnov, A.V.; Shkodyrev, V.P. A classification technique of civil objects by artificial neural networks using estimation of entropy on synthetic aperture radar images. J. Sens. Sens. Syst. 2021, 10, 127–134. [Google Scholar] [CrossRef]
- Aldhubaib, F.; Shuley, N.V. Radar Target Recognition Based on Modified Characteristic Polarization States. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1921–1933. [Google Scholar] [CrossRef]
- Jafari, M.; Maghsoudi, Y.; Valadan Zoej, M.J. A New Method for Land Cover Characterization and Classification of Polarimetric SAR Data Using Polarimetric Signatures. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3595–3607. [Google Scholar] [CrossRef]
- Visentin, T.; Hasch, J.; Zwick, T. Polarimetric RCS Measurements of Selected Two-Wheeled Vehicles for Automotive Radar. In Proceedings of the 2017 European Radar Conference (EURAD), Nuremberg, Germany, 11–13 October 2017; pp. 53–56. [Google Scholar]
- Chicco, D.; Jurman, G. The advantages of the Matthew’s correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]
- Kvasnov, A.V.; Nikitin, N.A.; Shkodyrev, V.P. Experience in Design of Artificial Neural Network for Object Detection on Monochromatic Images. In System Analysis in Engineering and Control; Springer: Cham, Switzerland, 2022; Volume 442, pp. 424–430. [Google Scholar]
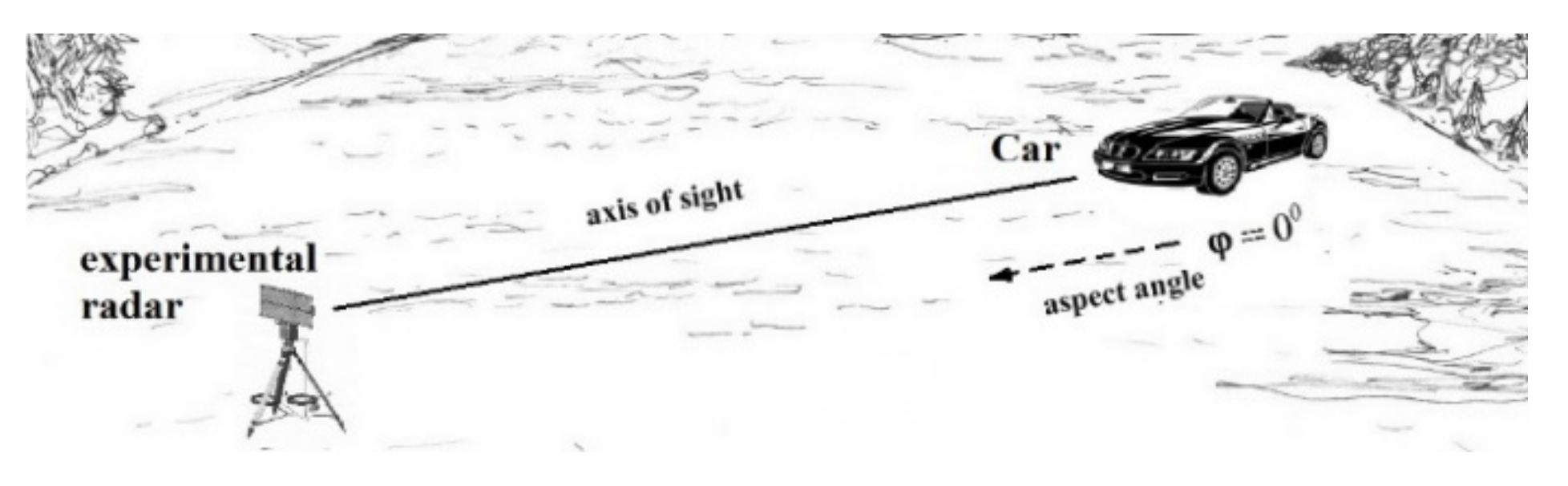






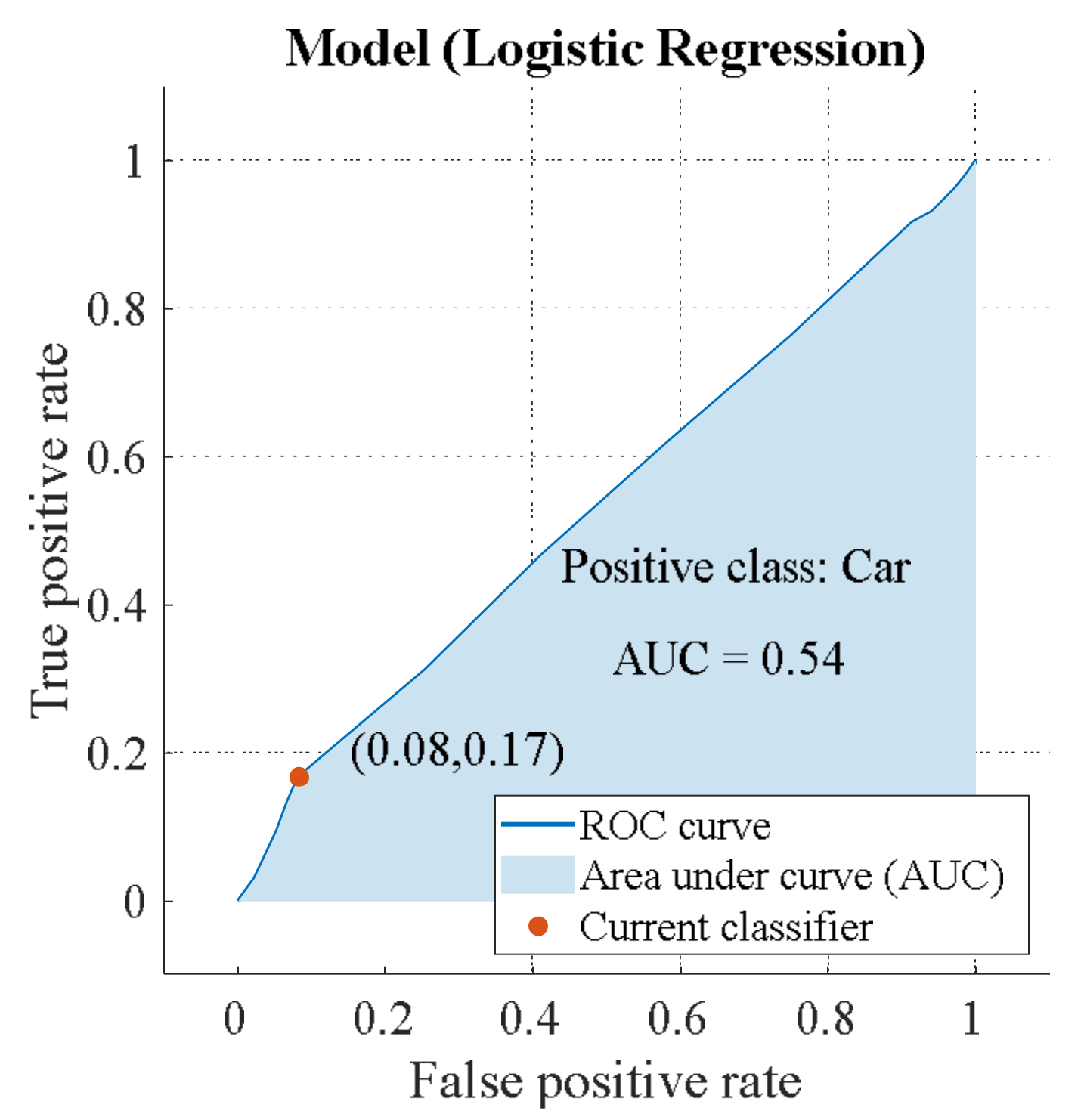
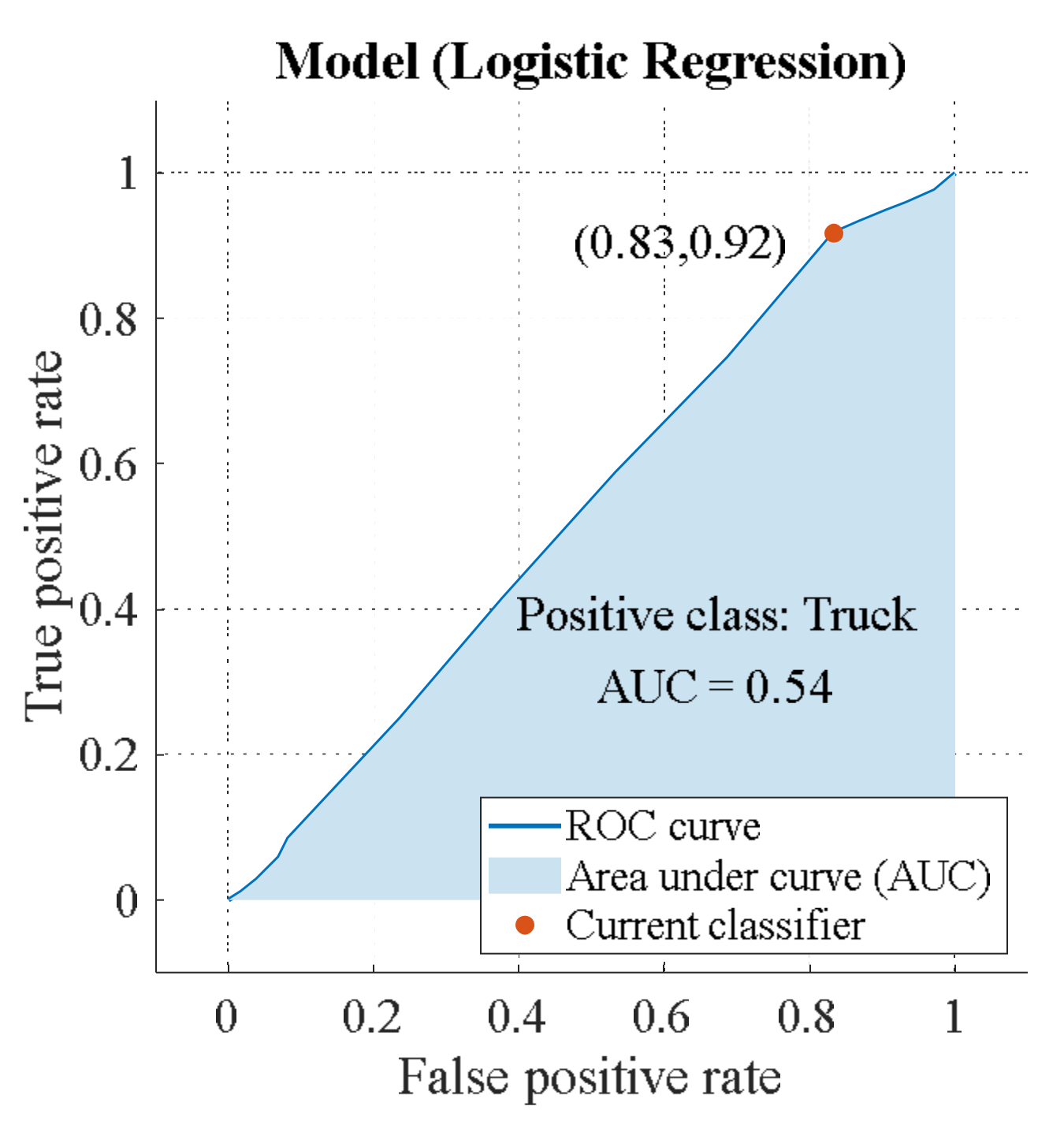
| Parameter | Value |
|---|---|
| Distance to target | 150 m |
| Sight angle | flat |
| Angles of profile | 360° (periodicity 15°) |
| Radar resolution (range) | 0.5 m |
| Radar resolution (azimuth) | 1.8° |
| Time registration | 10 ms |
| Type of Polarization | F1 Score | MCC |
|---|---|---|
| Linear (Car) | 0.6282 | 0.3775 |
| Linear (Truck) | 0.7206 | 0.3775 |
| Circular (Car) | 0.2667 | 0.1260 |
| Circular (Truck) | 0.6667 | 0.1260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kvasnov, A.V. Backscattering Analysis at ATR on Rough Surfaces by Ground-Based Polarimetric Radar Using Coherent Decomposition. Sensors 2023, 23, 3614. https://doi.org/10.3390/s23073614
Kvasnov AV. Backscattering Analysis at ATR on Rough Surfaces by Ground-Based Polarimetric Radar Using Coherent Decomposition. Sensors. 2023; 23(7):3614. https://doi.org/10.3390/s23073614
Chicago/Turabian StyleKvasnov, Anton V. 2023. "Backscattering Analysis at ATR on Rough Surfaces by Ground-Based Polarimetric Radar Using Coherent Decomposition" Sensors 23, no. 7: 3614. https://doi.org/10.3390/s23073614
APA StyleKvasnov, A. V. (2023). Backscattering Analysis at ATR on Rough Surfaces by Ground-Based Polarimetric Radar Using Coherent Decomposition. Sensors, 23(7), 3614. https://doi.org/10.3390/s23073614






