DiffNILM: A Novel Framework for Non-Intrusive Load Monitoring Based on the Conditional Diffusion Model
Abstract
1. Introduction
- DiffNILM is the first NILM framework adopting the diffusion model. Specifically, We engineer the conditional diffusion model to address the NILM task, where the total active power and embedded time tags are fed to the model as conditional input, and the appliance power waveform is generated step-by-step from Gaussian noise.
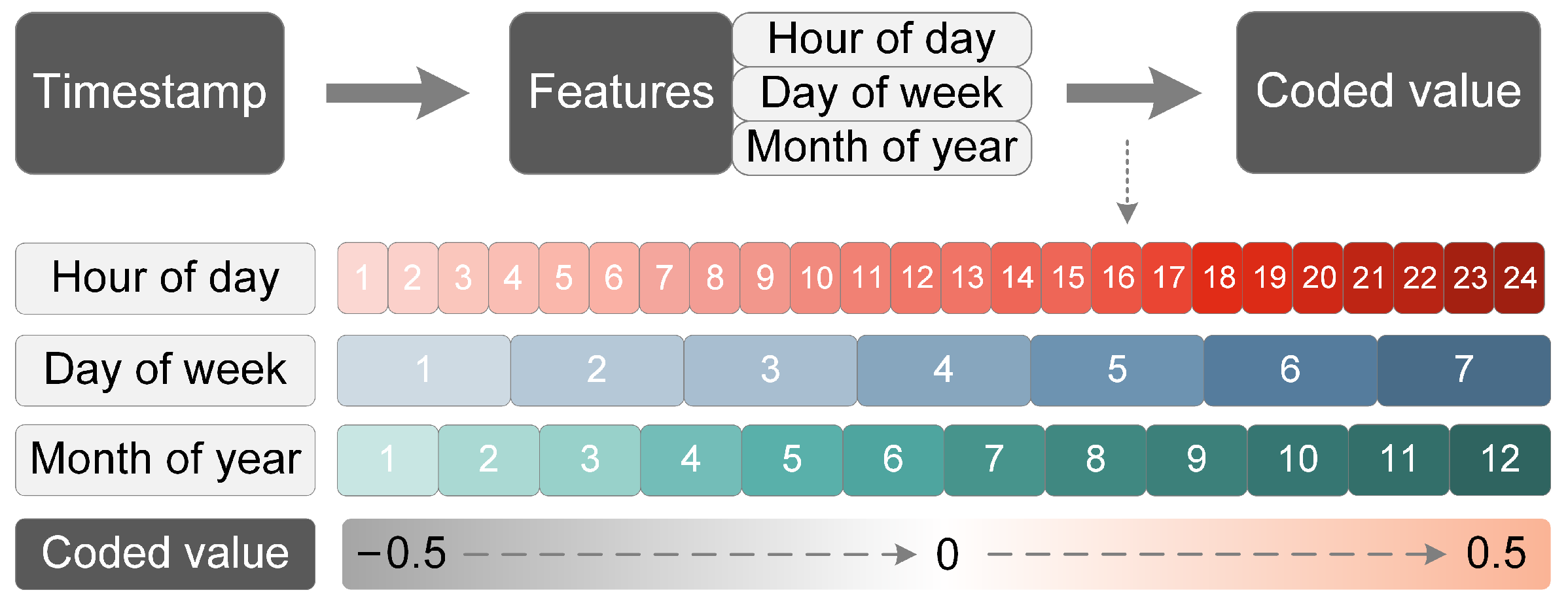
- We propose an encoding method for multi-scale temporal features that takes into account the regularity of power consumption behaviors.
- We implement and evaluate the proposed method on two public datasets, REDD and UKDALE. Empirical results demonstrate that DiffNILM outperforms previous models, as evidenced by both classification metrics and regression metrics.
2. Related Works
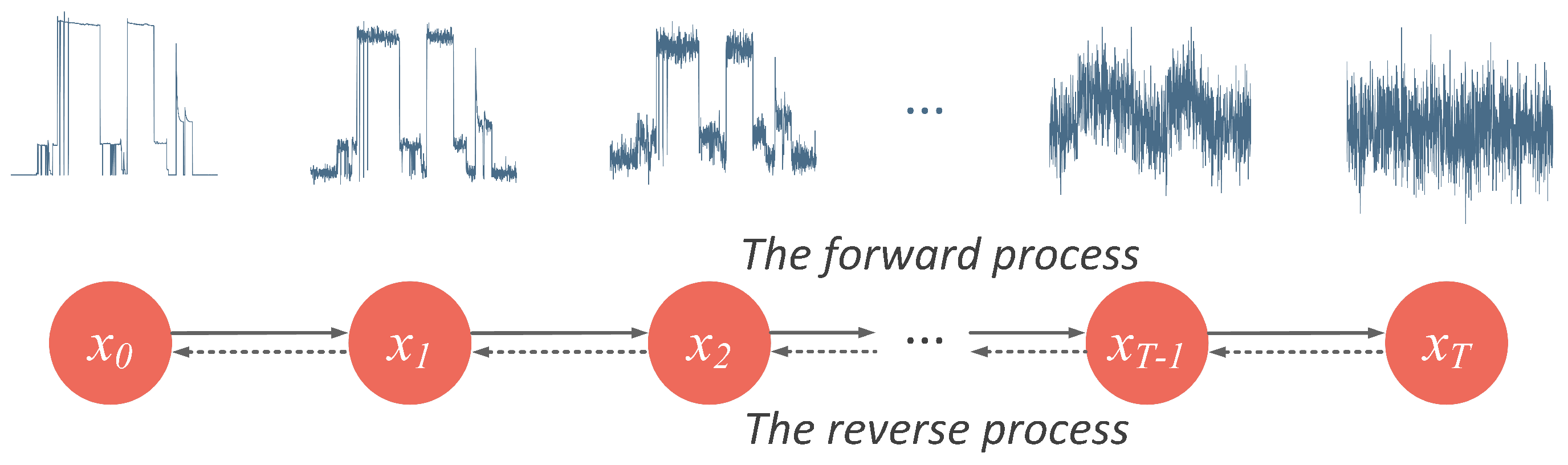
3. Denoising Diffusion Probabilistic Models
3.1. The Forward Process
3.2. The Reverse Process
3.3. Training a Diffusion Model
4. Design
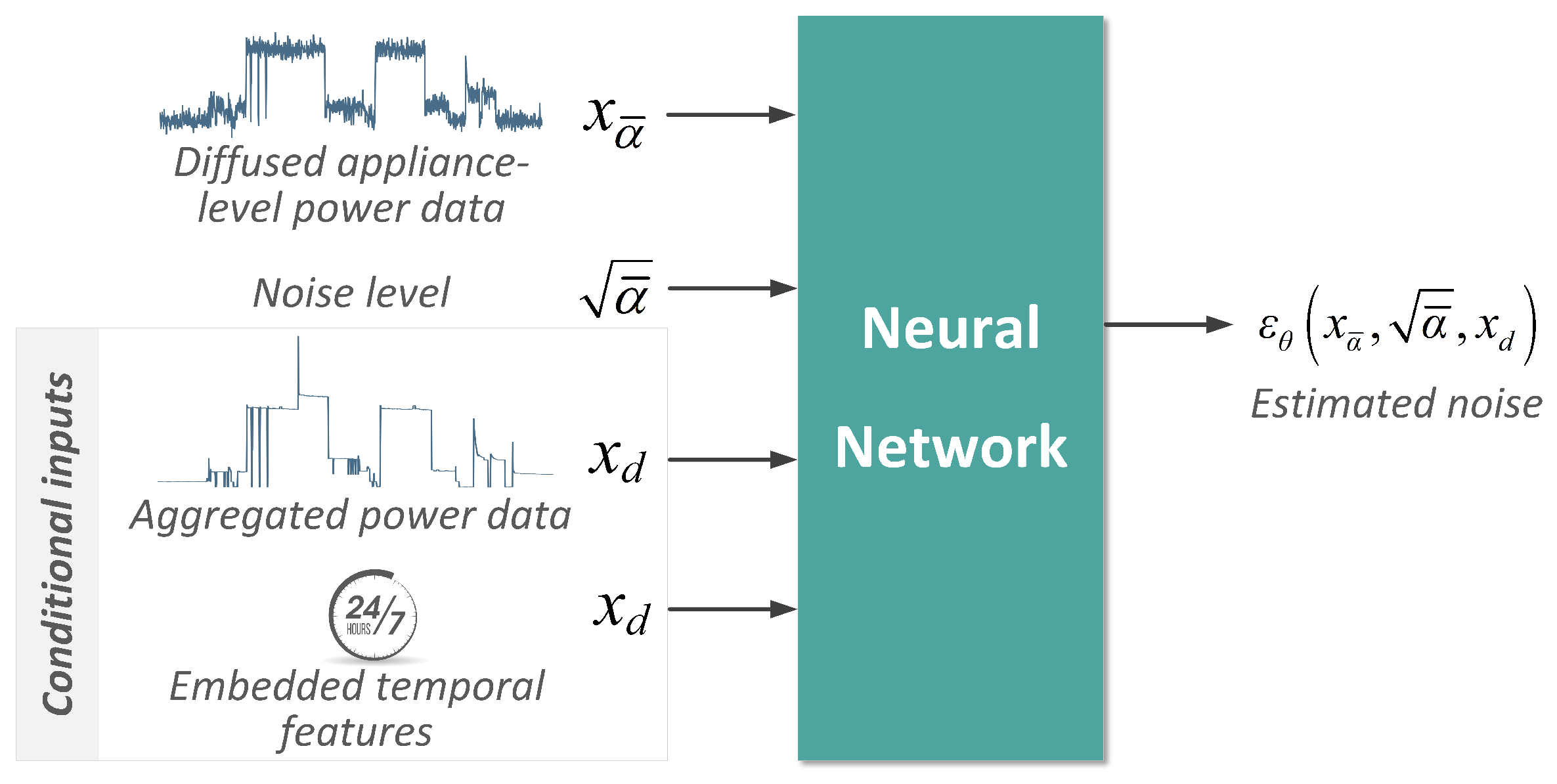
4.1. Conditional Diffusion Model as Appliance-Level Data Generator
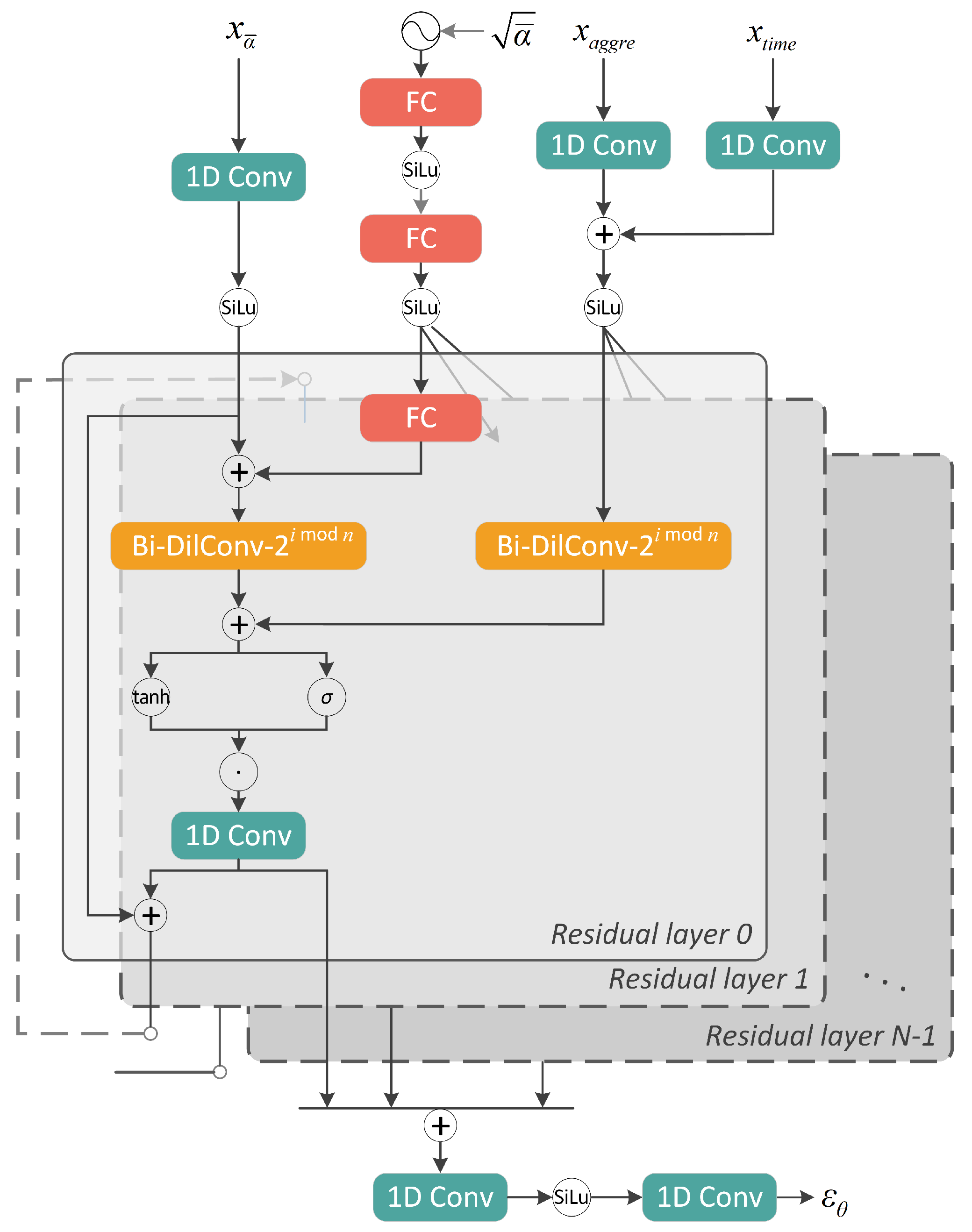
4.2. Network Architecture
4.3. Training and Sampling Procedures
| Algorithm 1: Training. |
|
1: repeat 2: 3: 4: 5: 6: Take gradient descent step on 7: until converged |
| Algorithm 2: Sampling. |
|
1: 2: for do 3: 4: 5: 6: 7: end for 8: return |
5. Experiments
5.1. Dataset
- Step 1: Merge the data of split-phase mains meter. Two-phase power supply is commonly-used in North American households, so, for REDD, we calculated the sum of each mains meter to obtain the actual aggregated power data.
- Step 2: Resample the power data at a fixed interval of 6 s.
- Step 3: Fill data gaps shorter than 3 min by forward-filling, and fill those longer than 3 min with zeros.
- Step 4: Attach status labels to the datasets. An appliance is classified as being in an ‘on’ state at a particular time point and assigned a status label of 1, provided that its power consumption falls within the acceptable ‘on’ power range and its operation time exceeds the minimum duration specified in Table 1. Otherwise, a status label of 0 is assigned.
- Step 5: Standardize the power data according to Formula (14) to enhance the accuracy of the model and convergence speed.
5.2. Evaluation Metrics
5.2.1. Classification Metrics
5.2.2. Regression Metrics
5.3. Implementation Details
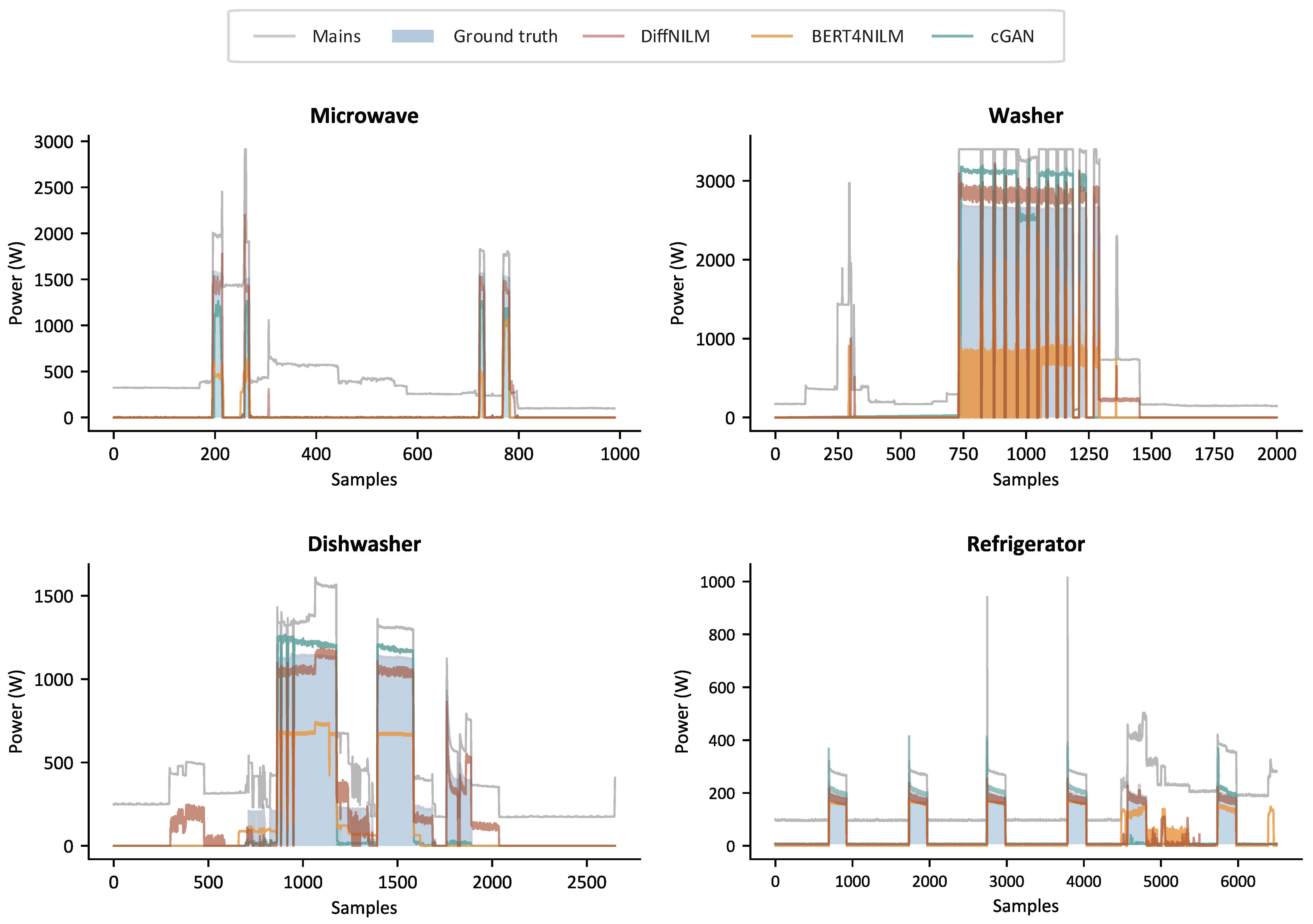
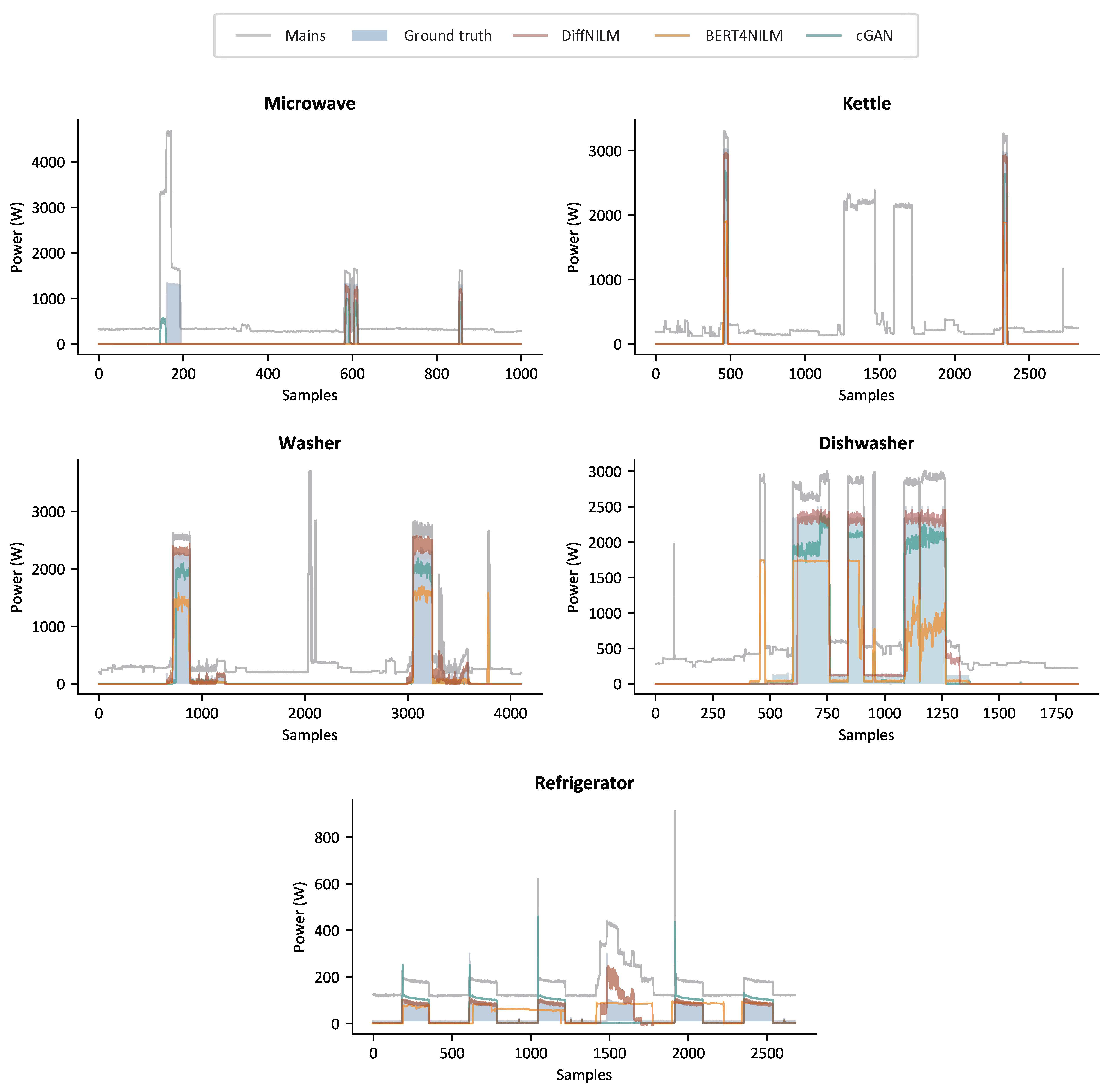
5.4. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Sehwag, V.; Hazirbas, C.; Gordo, A.; Ozgenel, F.; Canton, C. Generating High Fidelity Data from Low-density Regions using Diffusion Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11492–11501. [Google Scholar]
- Wolleb, J.; Sandkühler, R.; Bieder, F.; Valmaggia, P.; Cattin, P.C. Diffusion Models for Implicit Image Segmentation Ensembles. arXiv 2021, arXiv:2112.03145. [Google Scholar]
- Kong, Z.; Ping, W.; Huang, J.; Zhao, K.; Catanzaro, B. Diffwave: A versatile diffusion model for audio synthesis. arXiv 2020, arXiv:2009.09761. [Google Scholar]
- Luo, S.; Hu, W. Diffusion probabilistic models for 3d point cloud generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–20 June 2021; pp. 2837–2845. [Google Scholar]
- Hart, G.W. Nonintrusive appliance load monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar] [CrossRef]
- Mukaroh, A.; Le, T.T.H.; Kim, H. Background load denoising across complex load based on generative adversarial network to enhance load identification. Sensors 2020, 20, 5674. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Kim, H. Household appliance classification using lower odd-numbered harmonics and the bagging decision tree. IEEE Access 2020, 8, 55937–55952. [Google Scholar]
- Gillis, J.M.; Alshareef, S.M.; Morsi, W.G. Nonintrusive load monitoring using wavelet design and machine learning. IEEE Trans. Smart Grid 2015, 7, 320–328. [Google Scholar] [CrossRef]
- Heo, S.; Kim, H. Toward load identification based on the Hilbert transform and sequence to sequence long short-term memory. IEEE Trans. Smart Grid 2021, 12, 3252–3264. [Google Scholar]
- Wang, A.L.; Chen, B.X.; Wang, C.G.; Hua, D. Non-intrusive load monitoring algorithm based on features of V–I trajectory. Electr. Power Syst. Res. 2018, 157, 134–144. [Google Scholar] [CrossRef]
- Hassan, T.; Javed, F.; Arshad, N. An empirical investigation of VI trajectory based load signatures for non-intrusive load monitoring. IEEE Trans. Smart Grid 2013, 5, 870–878. [Google Scholar] [CrossRef]
- Kolter, J.Z.; Johnson, M.J. REDD: A public data set for energy disaggregation research. In Proceedings of the Workshop on Data Mining Applications in Sustainability (SIGKDD), San Diego, CA, USA, 21 August 2011; Volume 25, pp. 59–62. [Google Scholar]
- Kim, H.; Marwah, M.; Arlitt, M.; Lyon, G.; Han, J. Unsupervised disaggregation of low frequency power measurements. In Proceedings of the 2011 SIAM International Conference on Data Mining, Mesa, AZ, USA, 28–30 April 2011; pp. 747–758. [Google Scholar]
- Kolter, J.Z.; Jaakkola, T. Approximate inference in additive factorial hmms with application to energy disaggregation. In Proceedings of the Artificial Intelligence and Statistics, La Palma, Spain, 21–23 April 2012; pp. 1472–1482. [Google Scholar]
- Mao, Y.; Dong, K.; Zhao, J. Non-intrusive load decomposition technology based on CRF model. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 3909–3915. [Google Scholar]
- Gong, F.; Han, N.; Zhou, Y.; Chen, S.; Li, D.; Tian, S. A svm optimized by particle swarm optimization approach to load disaggregation in non-intrusive load monitoring in smart homes. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; pp. 1793–1797. [Google Scholar]
- Piga, D.; Cominola, A.; Giuliani, M.; Castelletti, A.; Rizzoli, A.E. Sparse optimization for automated energy end use disaggregation. IEEE Trans. Control Syst. Technol. 2015, 24, 1044–1051. [Google Scholar] [CrossRef]
- Kelly, J.; Knottenbelt, W. Neural nilm: Deep neural networks applied to energy disaggregation. In Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments, Seoul, Republic of Korea, 4–5 November 2015; pp. 55–64. [Google Scholar]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Xia, M.; Wang, K.; Song, W.; Chen, C.; Li, Y. Non-intrusive load disaggregation based on composite deep long short-term memory network. Expert Syst. Appl. 2020, 160, 113669. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1995; Volume 3361, p. 1995. [Google Scholar]
- Zhang, C.; Zhong, M.; Wang, Z.; Goddard, N.; Sutton, C. Sequence-to-point learning with neural networks for non-intrusive load monitoring. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- He, D.; Lin, W.; Liu, N.; Harley, R.G.; Habetler, T.G. Incorporating non-intrusive load monitoring into building level demand response. IEEE Trans. Smart Grid 2013, 4, 1870–1877. [Google Scholar]
- Athanasiadis, C.L.; Papadopoulos, T.A.; Doukas, D.I. Real-time non-intrusive load monitoring: A light-weight and scalable approach. Energy Build. 2021, 253, 111523. [Google Scholar] [CrossRef]
- Makonin, S.; Popowich, F.; Bajić, I.V.; Gill, B.; Bartram, L. Exploiting HMM sparsity to perform online real-time nonintrusive load monitoring. IEEE Trans. Smart Grid 2015, 7, 2575–2585. [Google Scholar] [CrossRef]
- Rafiq, H.; Zhang, H.; Li, H.; Ochani, M.K. Regularized LSTM based deep learning model: First step towards real-time non-intrusive load monitoring. In Proceedings of the 2018 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–15 August 2018; pp. 234–239. [Google Scholar]
- Krystalakos, O.; Nalmpantis, C.; Vrakas, D. Sliding window approach for online energy disaggregation using artificial neural networks. In Proceedings of the 10th Hellenic Conference on Artificial Intelligence, Patras, Greece, 9–12 July 2018; pp. 1–6. [Google Scholar]
- Hu, M.; Tao, S.; Fan, H.; Li, X.; Sun, Y.; Sun, J. Non-intrusive load monitoring for residential appliances with ultra-sparse sample and real-time computation. Sensors 2021, 21, 5366. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Yue, Z.; Witzig, C.R.; Jorde, D.; Jacobsen, H.A. Bert4nilm: A bidirectional transformer model for non-intrusive load monitoring. In Proceedings of the 5th International Workshop on Non-Intrusive Load Monitoring, Virtual, 18 November 2020; pp. 89–93. [Google Scholar]
- Sykiotis, S.; Kaselimi, M.; Doulamis, A.; Doulamis, N. Electricity: An efficient transformer for non-intrusive load monitoring. Sensors 2022, 22, 2926. [Google Scholar] [CrossRef]
- Bejarano, G.; DeFazio, D.; Ramesh, A. Deep latent generative models for energy disaggregation. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 850–857. [Google Scholar]
- Langevin, A.; Carbonneau, M.A.; Cheriet, M.; Gagnon, G. Energy disaggregation using variational autoencoders. Energy Build. 2022, 254, 111623. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, K.; Shen, Z.; Cai, X.; Jia, Z. Sequence-to-subsequence learning with conditional gan for power disaggregation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3202–3206. [Google Scholar]
- Kaselimi, M.; Doulamis, N.; Voulodimos, A.; Doulamis, A.; Protopapadakis, E. EnerGAN++: A generative adversarial gated recurrent network for robust energy disaggregation. IEEE Open J. Signal Process. 2020, 2, 1–16. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February 22–1 March 2022; Volume 35, pp. 11106–11115. [Google Scholar]
- Lee, J.; Han, S. Nu-wave: A diffusion probabilistic model for neural audio upsampling. arXiv 2021, arXiv:2104.02321. [Google Scholar]
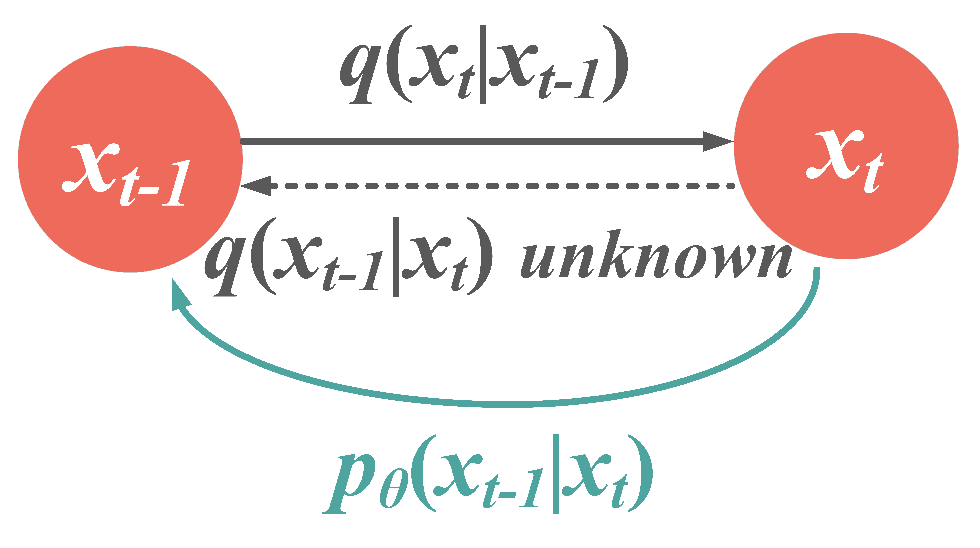

| Appliance | Reasonable ‘on’ Power Range (W) | Minimum Duration of Operation (s) |
|---|---|---|
| Microwave | 200∼1800 | 12 |
| Washer | 40∼3500 | 1800 |
| Dish washer | 50∼1200 | 1800 |
| Refrigerator | 50∼400 | 60 |
| Symbol | Description | Value |
|---|---|---|
| L | Length of the input and output power sequences | 480 |
| T | Maximum diffusion step | 1000 |
| Noise schedule | ||
| Inference step | 8 | |
| Inference noise schedule | ||
| N | Number of residual layers | 30 |
| C | Number of residual channels | 128 |
| n | Length of the dilation cycle | 10 |
| Appliance | Model | Accuracy ↑ | F1-Score ↑ | MAE ↓ | MRE ↓ |
|---|---|---|---|---|---|
| Bi-LSTM | 0.989 | 0.604 | 17.39 | 0.058 | |
| CNN | 0.986 | 0.378 | 18.59 | 0.060 | |
| Microwave | BERT4NILM | 0.989 | 0.476 | 17.58 | 0.057 |
| cGAN | 0.989 | 0.415 | 18.15 | 0.058 | |
| DiffNILM | 0.989 | 0.430 | 17.13 | 0.057 | |
| Bi-LSTM | 0.989 | 0.125 | 35.73 | 0.020 | |
| CNN | 0.970 | 0.274 | 36.12 | 0.042 | |
| Washer | BERT4NILM | 0.991 | 0.559 | 34.96 | 0.022 |
| cGAN | 0.990 | 0.478 | 29.67 | 0.025 | |
| DiffNILM | 0.988 | 0.569 | 26.44 | 0.019 | |
| Bi-LSTM | 0.956 | 0.421 | 25.25 | 0.056 | |
| CNN | 0.953 | 0.298 | 25.29 | 0.053 | |
| Dish washer | BERT4NILM | 0.969 | 0.523 | 20.49 | 0.039 |
| cGAN | 0.951 | 0.295 | 24.80 | 0.055 | |
| DiffNILM | 0.971 | 0.593 | 18.16 | 0.037 | |
| Bi-LSTM | 0.789 | 0.709 | 44.82 | 0.841 | |
| CNN | 0.796 | 0.689 | 35.69 | 0.822 | |
| Refrigerator | BERT4NILM | 0.841 | 0.756 | 32.35 | 0.806 |
| cGAN | 0.811 | 0.732 | 33.83 | 0.820 | |
| DiffNILM | 0.868 | 0.794 | 33.58 | 0.808 | |
| Bi-LSTM | 0.931 | 0.465 | 30.80 | 0.244 | |
| CNN | 0.926 | 0.410 | 28.92 | 0.244 | |
| Average | BERT4NILM | 0.948 | 0.579 | 26.35 | 0.231 |
| cGAN | 0.935 | 0.498 | 26.70 | 0.240 | |
| DiffNILM | 0.954 | 0.597 | 23.70 | 0.230 |
| Appliance | Model | Accuracy ↑ | F1-Score ↑ | MAE ↓ | MRE ↓ |
|---|---|---|---|---|---|
| Bi-LSTM | 0.995 | 0.060 | 6.55 | 0.014 | |
| CNN | 0.995 | 0.341 | 6.36 | 0.014 | |
| Microwave | BERT4NILM | 0.995 | 0.014 | 6.57 | 0.014 |
| cGAN | 0.996 | 0.474 | 5.98 | 0.012 | |
| DiffNILM | 0.996 | 0.501 | 4.54 | 0.012 | |
| Bi-LSTM | 0.938 | 0.150 | 15.66 | 0.067 | |
| CNN | 0.913 | 0.173 | 11.90 | 0.094 | |
| Washer | BERT4NILM | 0.966 | 0.325 | 6.98 | 0.040 |
| cGAN | 0.959 | 0.376 | 10.84 | 0.062 | |
| DiffNILM | 0.986 | 0.390 | 5.74 | 0.058 | |
| Bi-LSTM | 0.976 | 0.605 | 36.36 | 0.033 | |
| CNN | 0.947 | 0.560 | 25.45 | 0.069 | |
| Dish washer | BERT4NILM | 0.966 | 0.667 | 16.18 | 0.049 |
| cGAN | 0.961 | 0.646 | 13.89 | 0.042 | |
| DiffNILM | 0.980 | 0.662 | 19.58 | 0.030 | |
| Bi-LSTM | 0.573 | 0.174 | 43.74 | 0.956 | |
| CNN | 0.772 | 0.718 | 29.29 | 0.758 | |
| Refrigerator | BERT4NILM | 0.813 | 0.766 | 25.47 | 0.732 |
| cGAN | 0.818 | 0.801 | 25.11 | 0.730 | |
| DiffNILM | 0.857 | 0.816 | 22.82 | 0.699 | |
| Bi-LSTM | 0.994 | 0.531 | 21.26 | 0.007 | |
| CNN | 0.997 | 0.850 | 9.64 | 0.003 | |
| Kettle | BERT4NILM | 0.998 | 0.907 | 6.82 | 0.002 |
| cGAN | 0.998 | 0.911 | 7.09 | 0.002 | |
| DiffNILM | 0.999 | 0.918 | 4.59 | 0.002 | |
| Bi-LSTM | 0.875 | 0.229 | 21.80 | 0.261 | |
| CNN | 0.919 | 0.521 | 14.28 | 0.261 | |
| Average | BERT4NILM | 0.943 | 0.503 | 11.47 | 0.194 |
| cGAN | 0.946 | 0.642 | 14.58 | 0.170 | |
| DiffNILM | 0.964 | 0.657 | 11.45 | 0.164 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Dong, K.; Zhao, J. DiffNILM: A Novel Framework for Non-Intrusive Load Monitoring Based on the Conditional Diffusion Model. Sensors 2023, 23, 3540. https://doi.org/10.3390/s23073540
Sun R, Dong K, Zhao J. DiffNILM: A Novel Framework for Non-Intrusive Load Monitoring Based on the Conditional Diffusion Model. Sensors. 2023; 23(7):3540. https://doi.org/10.3390/s23073540
Chicago/Turabian StyleSun, Ruichen, Kun Dong, and Jianfeng Zhao. 2023. "DiffNILM: A Novel Framework for Non-Intrusive Load Monitoring Based on the Conditional Diffusion Model" Sensors 23, no. 7: 3540. https://doi.org/10.3390/s23073540
APA StyleSun, R., Dong, K., & Zhao, J. (2023). DiffNILM: A Novel Framework for Non-Intrusive Load Monitoring Based on the Conditional Diffusion Model. Sensors, 23(7), 3540. https://doi.org/10.3390/s23073540






