Stiffness Considerations for a MEMS-Based Weighing Cell
Abstract
1. Introduction
2. Material and Methods
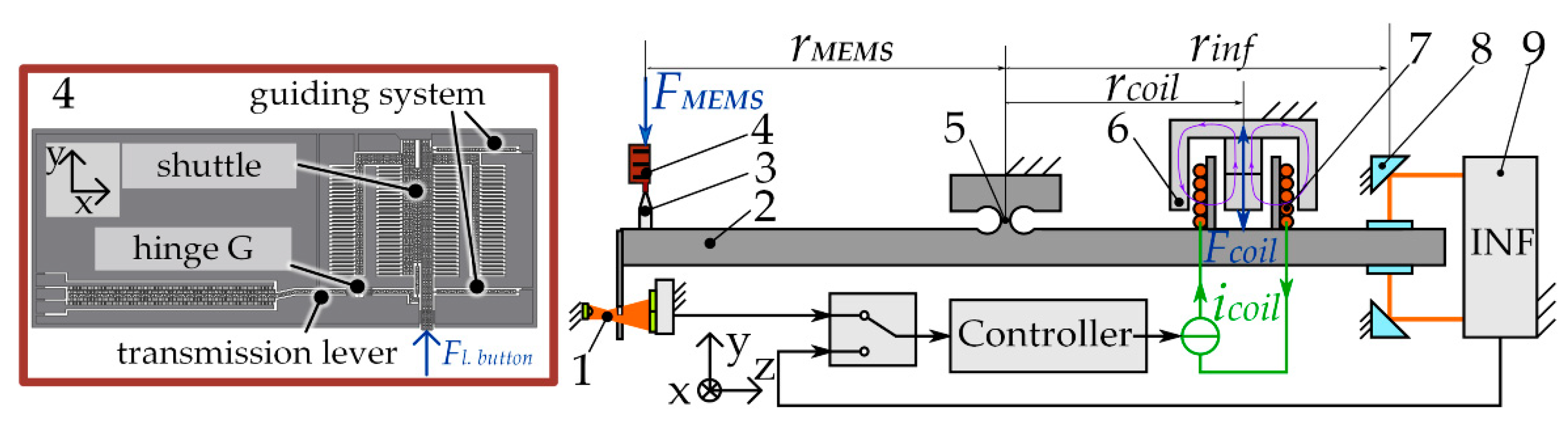
2.1. Stiffness of the MEMS-Based Weighing Cell
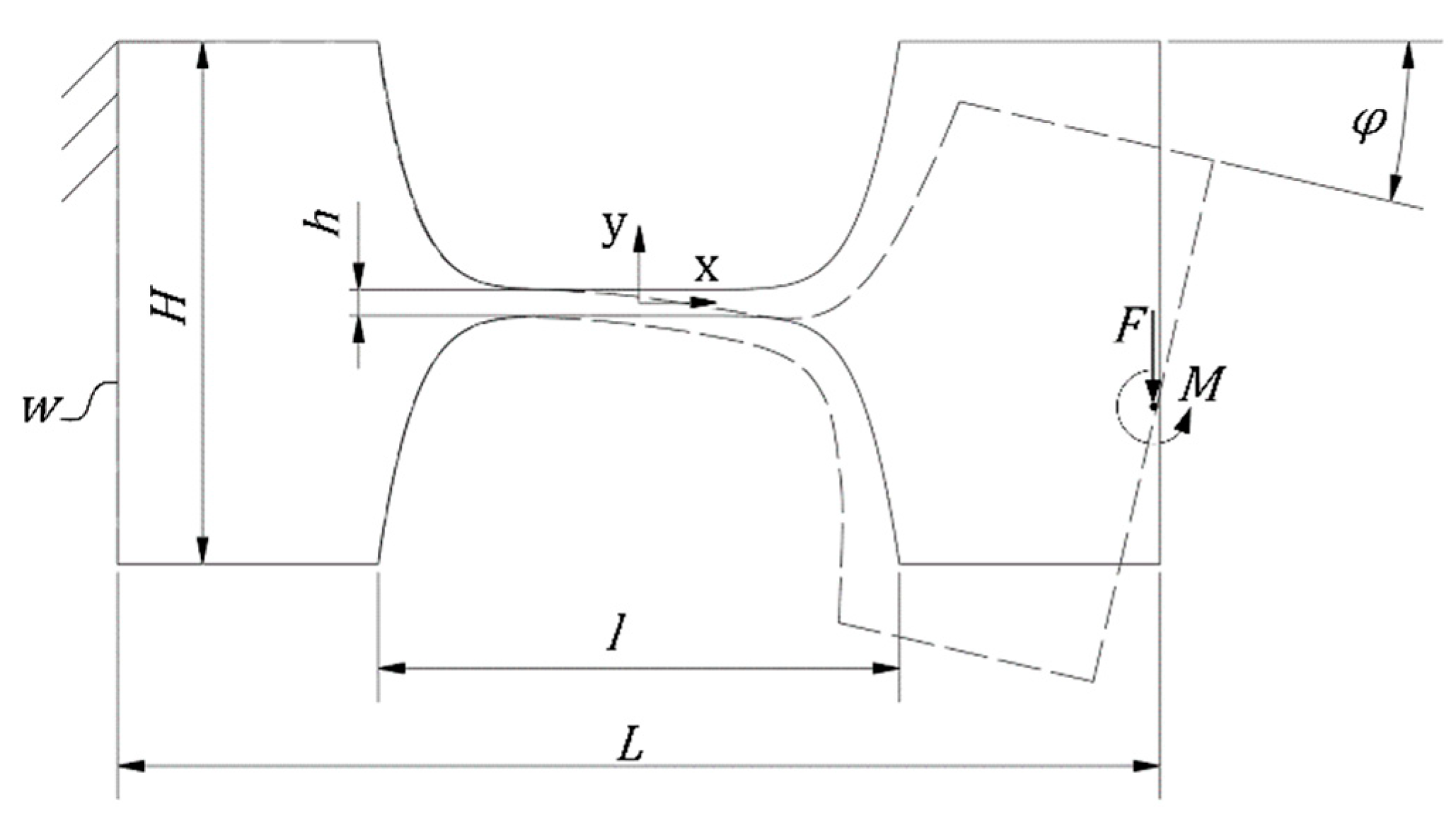
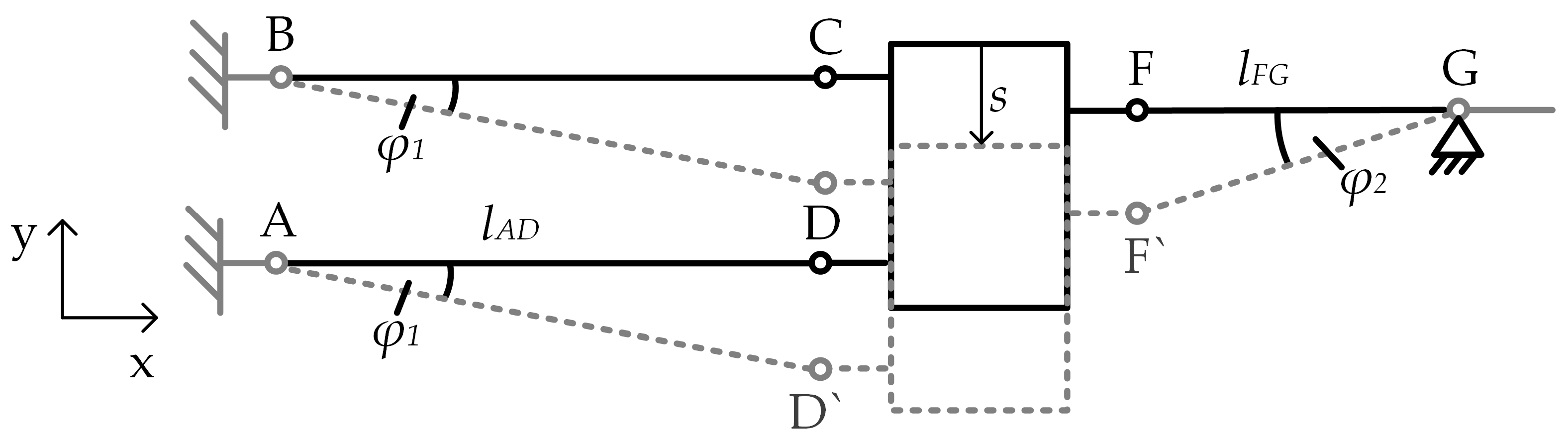
2.1.1. Analytical Stiffness Calculation
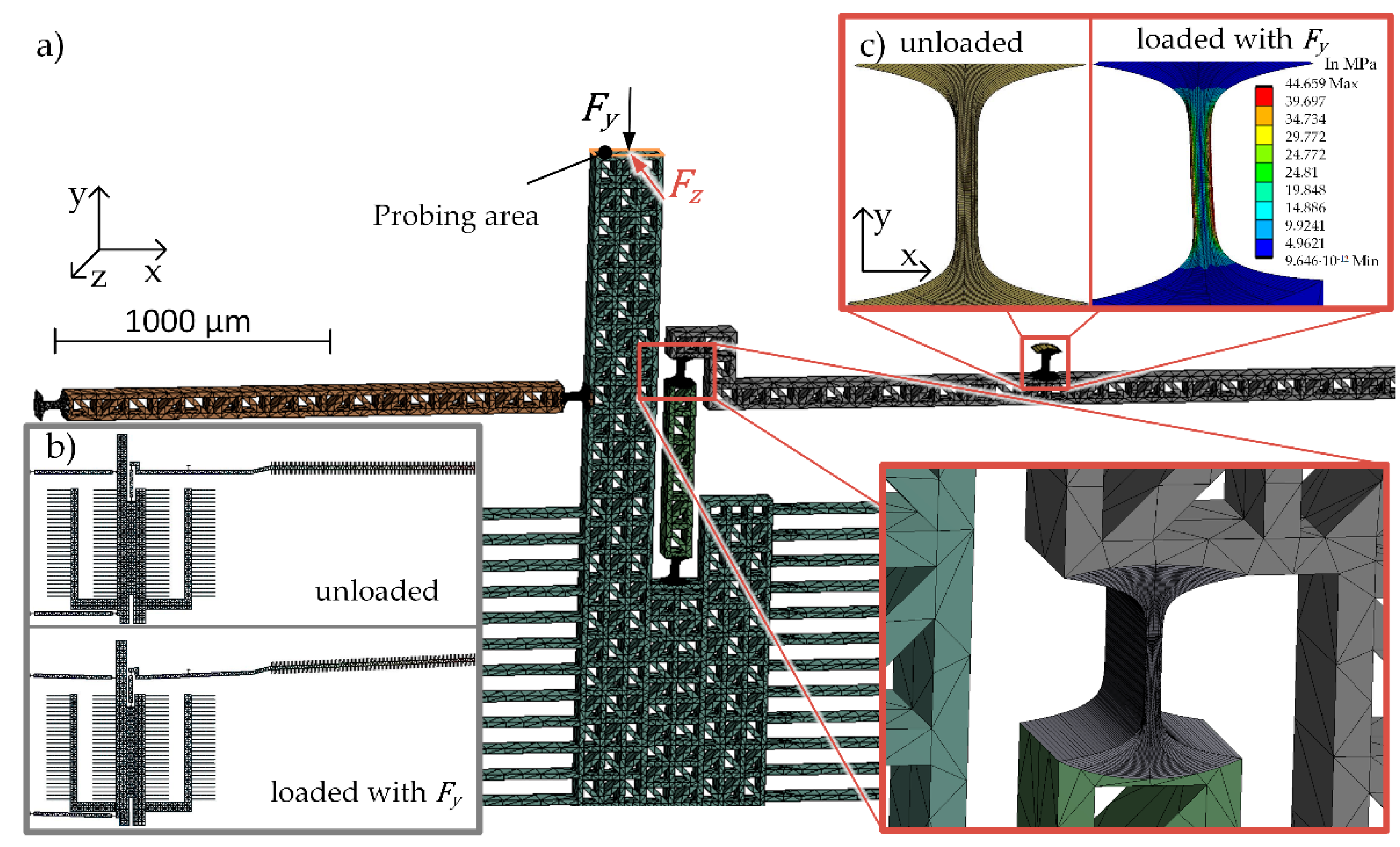
2.1.2. Numerical Stiffness Calculation
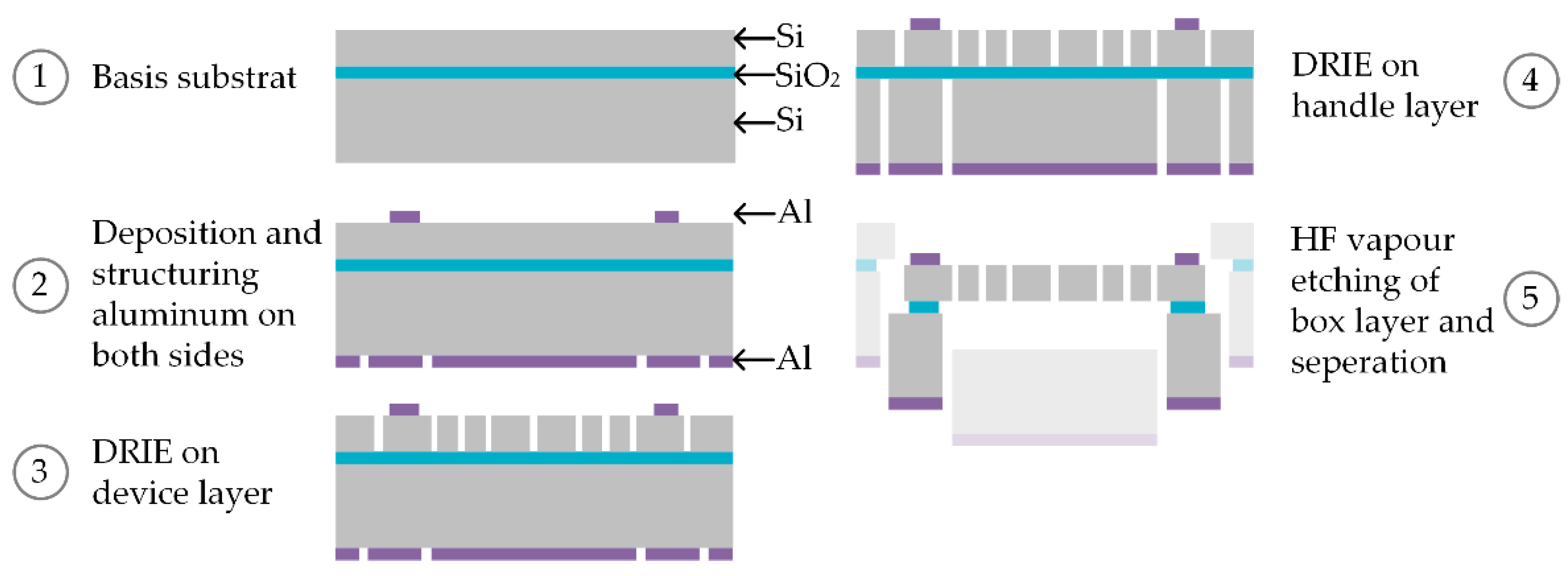
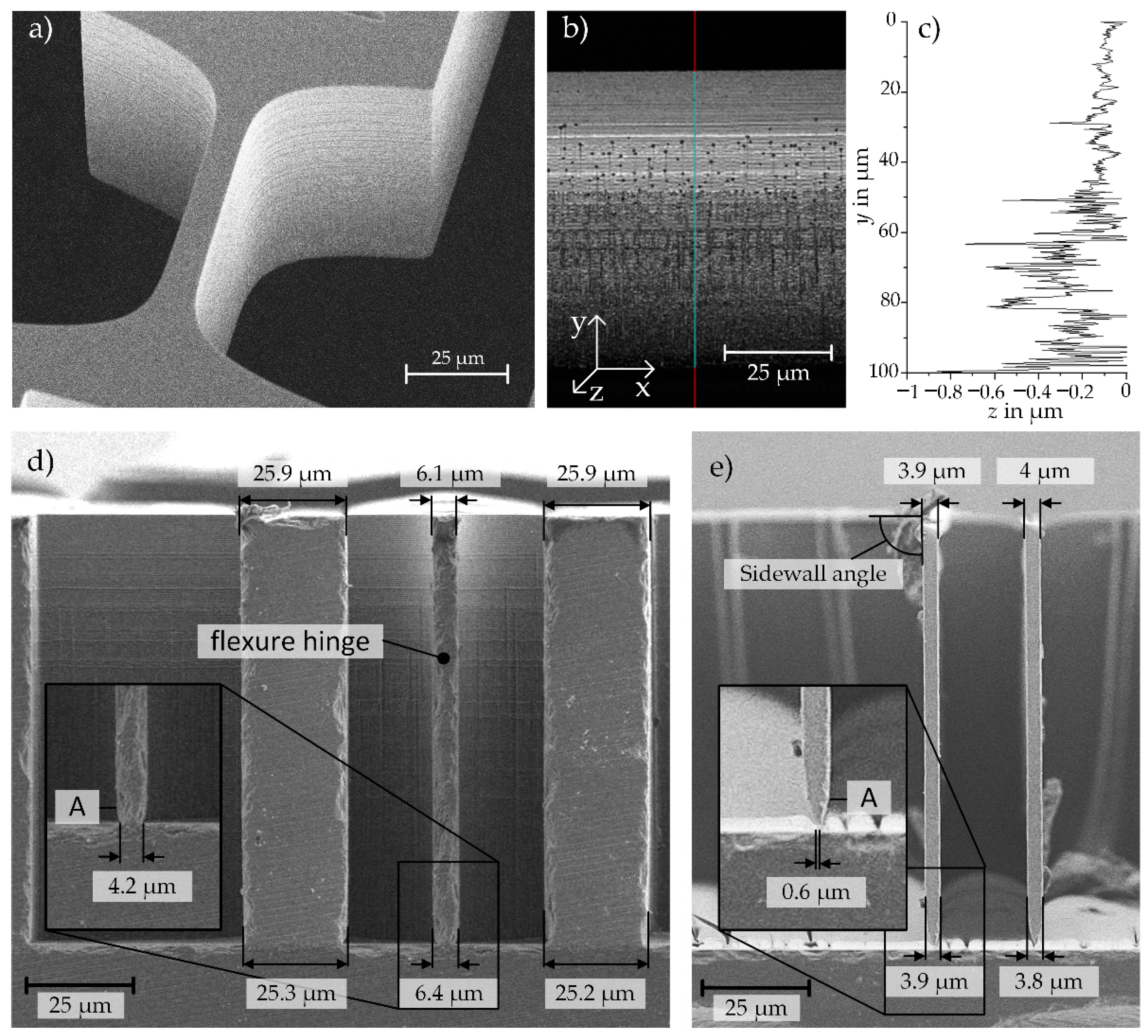
2.2. Microfabrication of MEMS-Based Weighing Cells
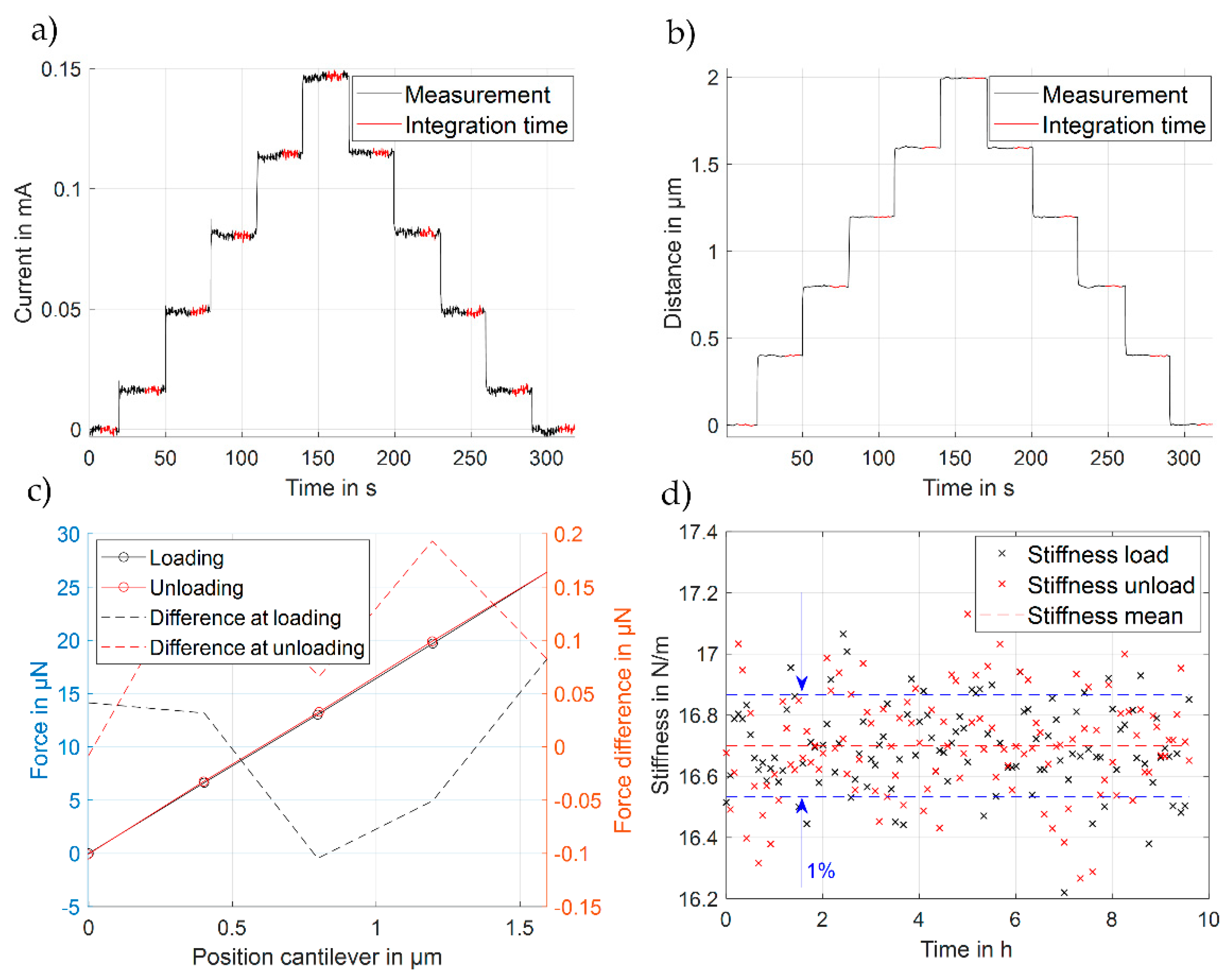
2.3. Experimental Determination of the System Stiffness
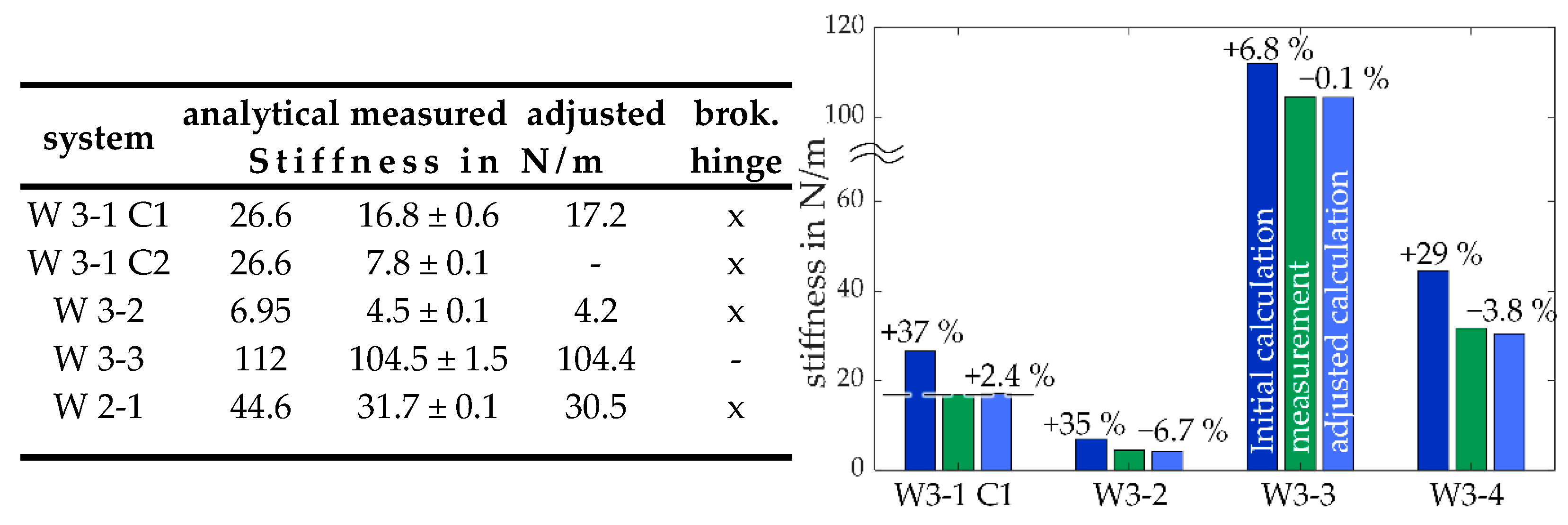
3. Results and Discussion
3.1. Theoretical Stiffnesses Evaluation
3.2. Analysis of the Influences of Fabrication Tolerances on the System Stiffness
3.2.1. Measured Influencing Geometry Parameters
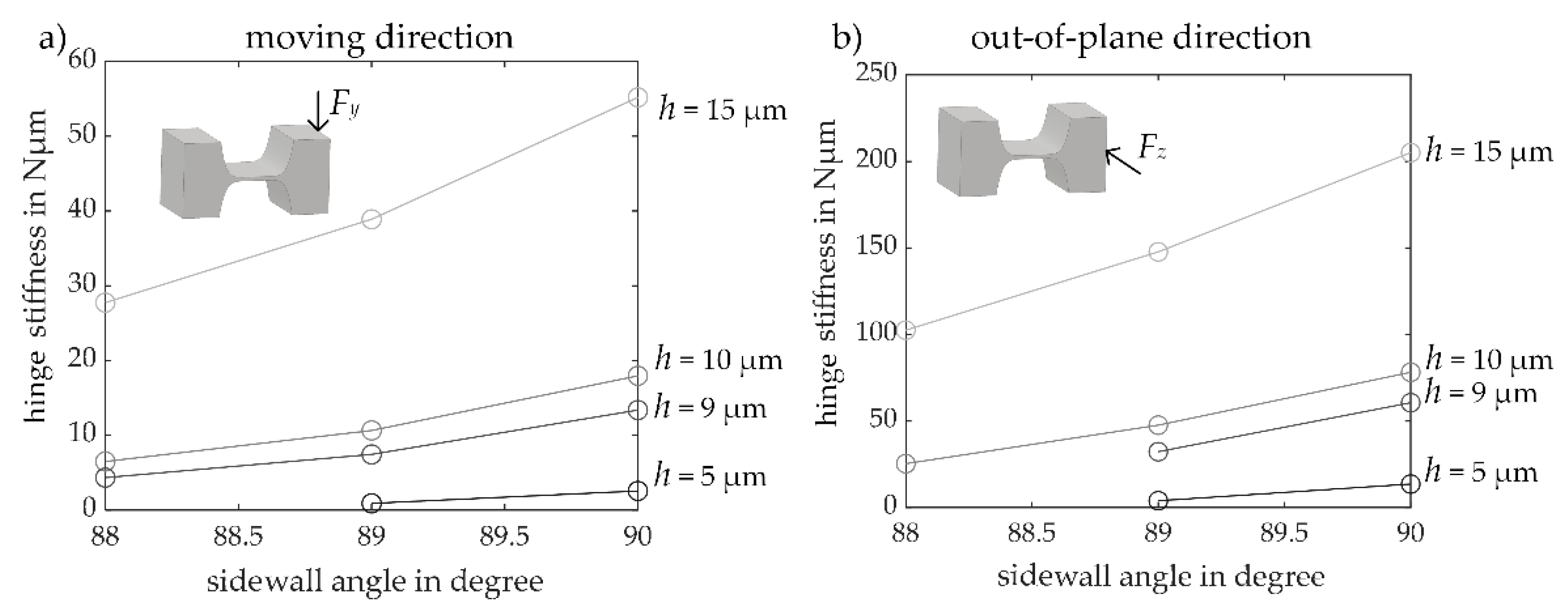
3.2.2. Sidewall Angle Influence on the Stiffness
3.3. Experimental Investigation of the System Stiffness
3.4. Discussion of the Theoretical and Experimental Results
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- López, D.; Decca, R.S.; Fischbach, E.; Krause, D.E. MEMS-Based Force Sensor: Design and Applications. Bell Labs Tech. J. 2005, 10, 61–80. [Google Scholar] [CrossRef]
- Bao, G.; Suresh, S. Cell and molecular mechanics of biological materials. Nat. Mater. 2003, 2, 715–725. [Google Scholar] [CrossRef] [PubMed]
- Enachescu, M.; Schleef, D.; Ogletree, D.F.; Salmeron, M. Integration of point-contact microscopy and atomic-force microscopy: Application to characterization of graphite/Pt (111). Phys. Rev. B 1999, 60, 16913–16919. [Google Scholar] [CrossRef]
- Binnig, G.; Quate, C.F.; Gerber, C.H. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Dufrêne, Y. Towards nanomicrobiology using atomic force microscopy. Nat. Rev. Microbiol. 2008, 6, 674–680. [Google Scholar] [CrossRef] [PubMed]
- Darnieder, M.; Pabst, M.; Wenig, R.; Zentner, L.; Theska, R.; Fröhlich, T. Static behavior of weighing cells. J. Sens. Sens. Syst. 2018, 7, 587–600. [Google Scholar] [CrossRef]
- Diethold, C.; Hilbrunner, F. Force Measurement of Low Forces in Combination with High Dead Loads by the Use of Electromagnetic Force Compensation. Meas. Sci. Technol. 2012, 23, 074017. [Google Scholar] [CrossRef]
- Yamakawa, Y.; Yamazaki, T.; Tamura, J.; Tanaka, O. Dynamic behaviors of a checkweigher with electromagnetic force compensation. In Proceedings of the XIX IMEKO World Congress Fundamental and Applied Metrology, Lisbon, Portugal, 6−11 September 2009. [Google Scholar]
- Kim, M.-S.; Choi, J.-H.; Kim, J.-H.; Park, Y.K. SI-traceable determination of spring constants of various atomic force microscope cantilevers with a small uncertainty of 1%. Meas. Sci. Technol. 2007, 18, 3351. [Google Scholar] [CrossRef]
- Coskun, M.B.; Moore, S.; Moheimani, S.O.R.; Neild, A.; Alan, T. Zero displacement microelectromechanical force sensor using feedback control. Appl. Phys. Lett. 2014, 104, 153502. [Google Scholar] [CrossRef]
- Joyce, S.A.; Houston, J.E. A new force sensor incorporating force-feedback control for interfacial force microscopy. Rev. Sci. Instrum. 1991, 62, 710–715. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.; Li, Y. Investigation on Surface Forces Measurement Using Force- Balanced MEMS Sensor. In Proceedings of the 2006 1st IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Zhuhai, China, 18–21 January 2006; pp. 784–787. [Google Scholar] [CrossRef]
- Maroufi, M.; Alemansour, H.; Coskun, M.B.; Moheimani, S.O.R. An adjustable-stiffness MEMS force sensor: Design, characterization, and control. Mechatronics 2018, 56, 198–210. [Google Scholar] [CrossRef]
- Moore, S.I.; Coskun, M.B.; Alan, T.; Neild, A.; Moheimani, S.O.R. Feedback-Controlled MEMS Force Sensor for Characterization of Microcantilevers. J. Microelectromech. Syst. 2015, 24, 1092–1101. [Google Scholar] [CrossRef]
- Nastro, A.; Ferrari, M.; Ferrari, V. Double-Actuator Position-Feedback Mechanism for Adjustable Sensitivity in Electrostatic-Capacitive MEMS Force Sensors. Sens. Actuators A. Phys. 2020, 312, 112–127. [Google Scholar] [CrossRef]
- Shen, Y.; Winder, E.; Xi, N.; Pomeroy, C.A.; Wejinya, U.C. Closed-Loop Optimal Control-Enabled Piezoelectric Microforce Sensors. IEEE/ASME Trans. Mechatron. 2006, 11, 420–427. [Google Scholar] [CrossRef]
- Wedrich, K.; Darnieder, M.; Vierzigmann, E.; Barth, A.; Theska, R.; Strehle, S. Conceptual design of a microscale balance based on force compensation. Mech. Mach. Sci. 2020, 96, 103–114. [Google Scholar] [CrossRef]
- Henning, S.; Linß, S.; Zentner, L. detasFLEX—A computational design tool for the analysis of various notch flexure hinges based on non-linear modeling. Mech. Sci. 2018, 9, 389–404. [Google Scholar] [CrossRef]
- Sari, I.; Zeimpekis, I.; Kraft, M. A dicing free SOI process for MEMS devices. Microelectron. Eng. 2012, 95, 121–129. [Google Scholar] [CrossRef]
- Diethold, C.; Kühnel, M.; Hilbrunner, F.; Fröhlich, T.; Manske, E. Determination of force to displacement curves using a nanopositioning system based on electromagnetic force compensated balances. Measurement 2014, 51, 343–348. [Google Scholar] [CrossRef]
- Cherkasova, V.; Fröhlich, T. Capacitive Calibration Capabilities in an EMFC Balance. In Proceedings of the IMEKO TC3, T5, TC16 and TC22 International Conference, Cavtat, Dubrovnik, 11–13 October 2022. [Google Scholar]
- Dannberg, O. Entwicklung Eines Prüfstandes zur Rückführbaren Kalibrierung von Cantilevern. Doctoral Dissertation, Technische Universität Ilmenau, Ilmenau, Germany, 2020. [Google Scholar]
- Xu, T.; Tao, Z.; Li, H.; Tan, X.; Li, H. Effects of deep reactive ion etching parameters on etching rate and surface morphology in extremely deep silicon etch process with high aspect ratio. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]



| System | Hinge Size in µm | Lever Size in µm | Dir. | Stiff. Single Hinge in Nµm | Analytical Solution in N/m | Numerical Solution in N/m | Deviation in% | Stiffness Ratio |
|---|---|---|---|---|---|---|---|---|
| W 3-1 C1/C2 | h = 9 l = 100 | lAD = 2000 lFG = 1400 | −y | 13.18 | 26.6 | 27.6 | 3.8 | 5.1 |
| −z | - | 139.7 | - | |||||
| W 3-2 | h = 7 l = 200 | lAD = 2000 lFG = 1400 | −y | 3.27 | 6.95 | 7.2 | 3.6 | 10.8 |
| −z | - | 78 | - | |||||
| W 3-3 | h = 15 l = 100 | lAD = 2000 lFG = 1400 | −y | 55.46 | 112 | 111.95 | 0.04 | 1.8 |
| −z | - | 200.4 | - | |||||
| W 2-1 | h = 9 l = 100 | lAD = 1700 lFG = 1000 | −y | 13.18 | 44.6 | 45.5 | 2.0 | 4.2 |
| −z | - | 192.3 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wedrich, K.; Cherkasova, V.; Platl, V.; Fröhlich, T.; Strehle, S. Stiffness Considerations for a MEMS-Based Weighing Cell. Sensors 2023, 23, 3342. https://doi.org/10.3390/s23063342
Wedrich K, Cherkasova V, Platl V, Fröhlich T, Strehle S. Stiffness Considerations for a MEMS-Based Weighing Cell. Sensors. 2023; 23(6):3342. https://doi.org/10.3390/s23063342
Chicago/Turabian StyleWedrich, Karin, Valeriya Cherkasova, Vivien Platl, Thomas Fröhlich, and Steffen Strehle. 2023. "Stiffness Considerations for a MEMS-Based Weighing Cell" Sensors 23, no. 6: 3342. https://doi.org/10.3390/s23063342
APA StyleWedrich, K., Cherkasova, V., Platl, V., Fröhlich, T., & Strehle, S. (2023). Stiffness Considerations for a MEMS-Based Weighing Cell. Sensors, 23(6), 3342. https://doi.org/10.3390/s23063342








