Structure and Technological Parameters’ Effect on MISFET-Based Hydrogen Sensors’ Characteristics
Abstract
1. Introduction
2. Materials and Methods
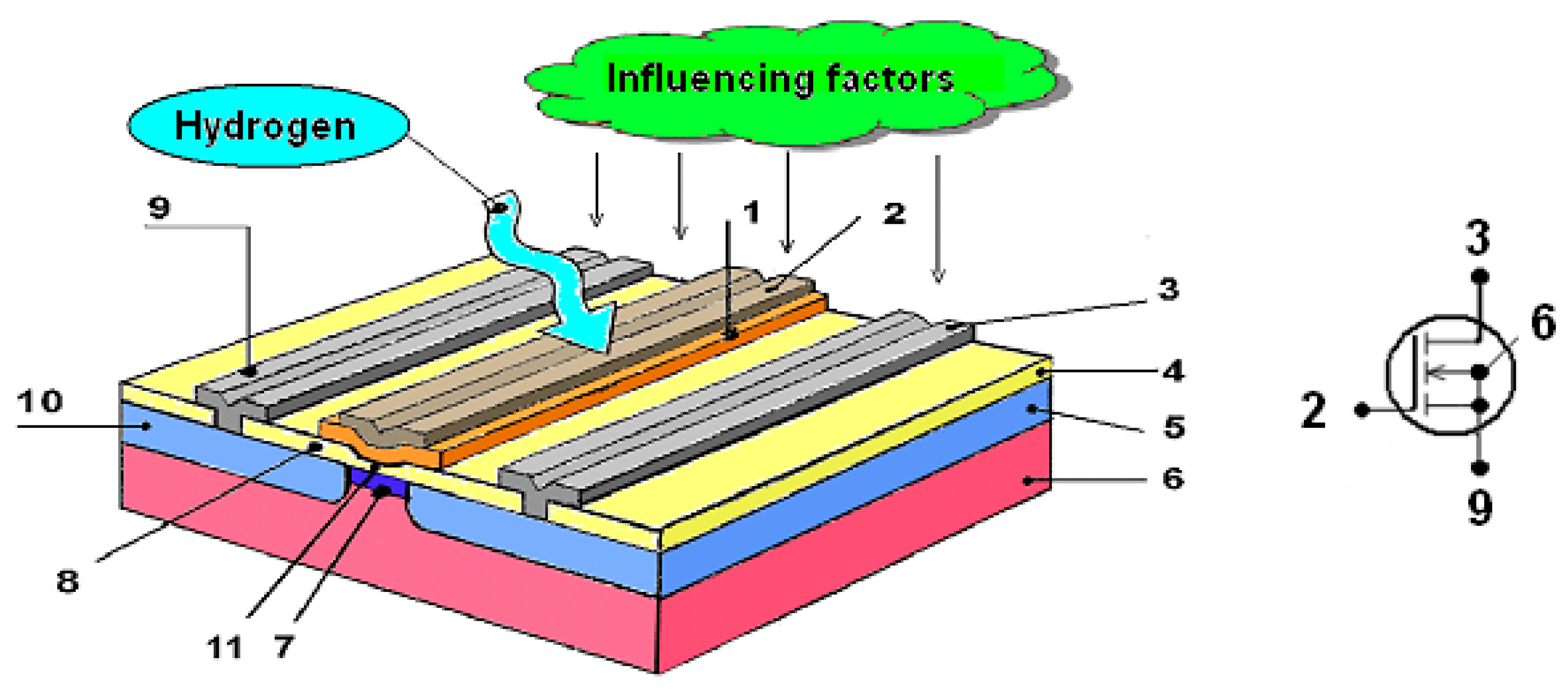
2.1. Initial Structure and Technological Parameters of TSE
2.2. Metrological Characteristics of TSE
3. Results
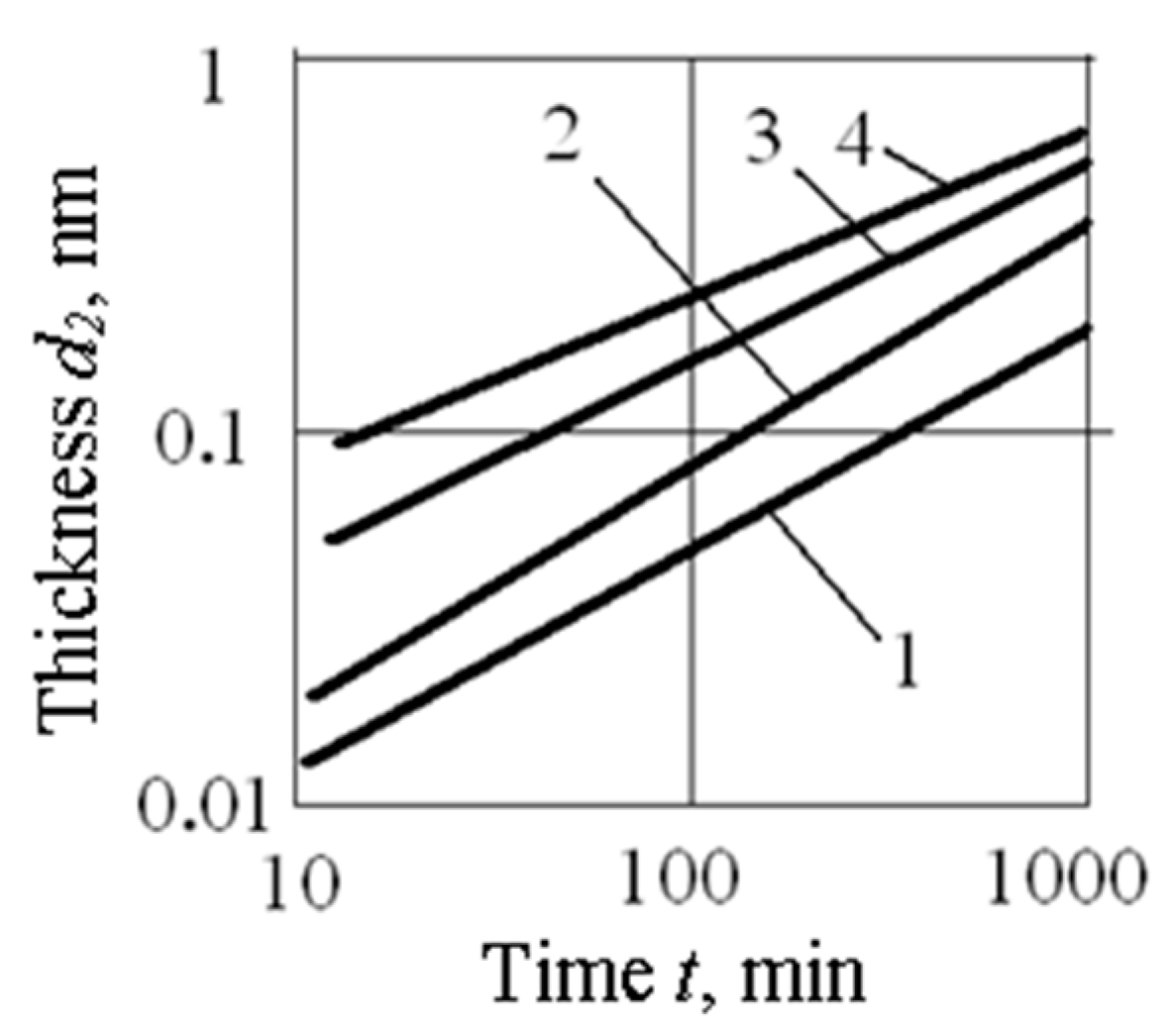
3.1. Influence of Film Manufacturing Technology and Thicknesses on the Components of the Conversion Function
3.2. Influence of Material’s Parameters and Topological Dimensions of Elements on Conversion Function Components
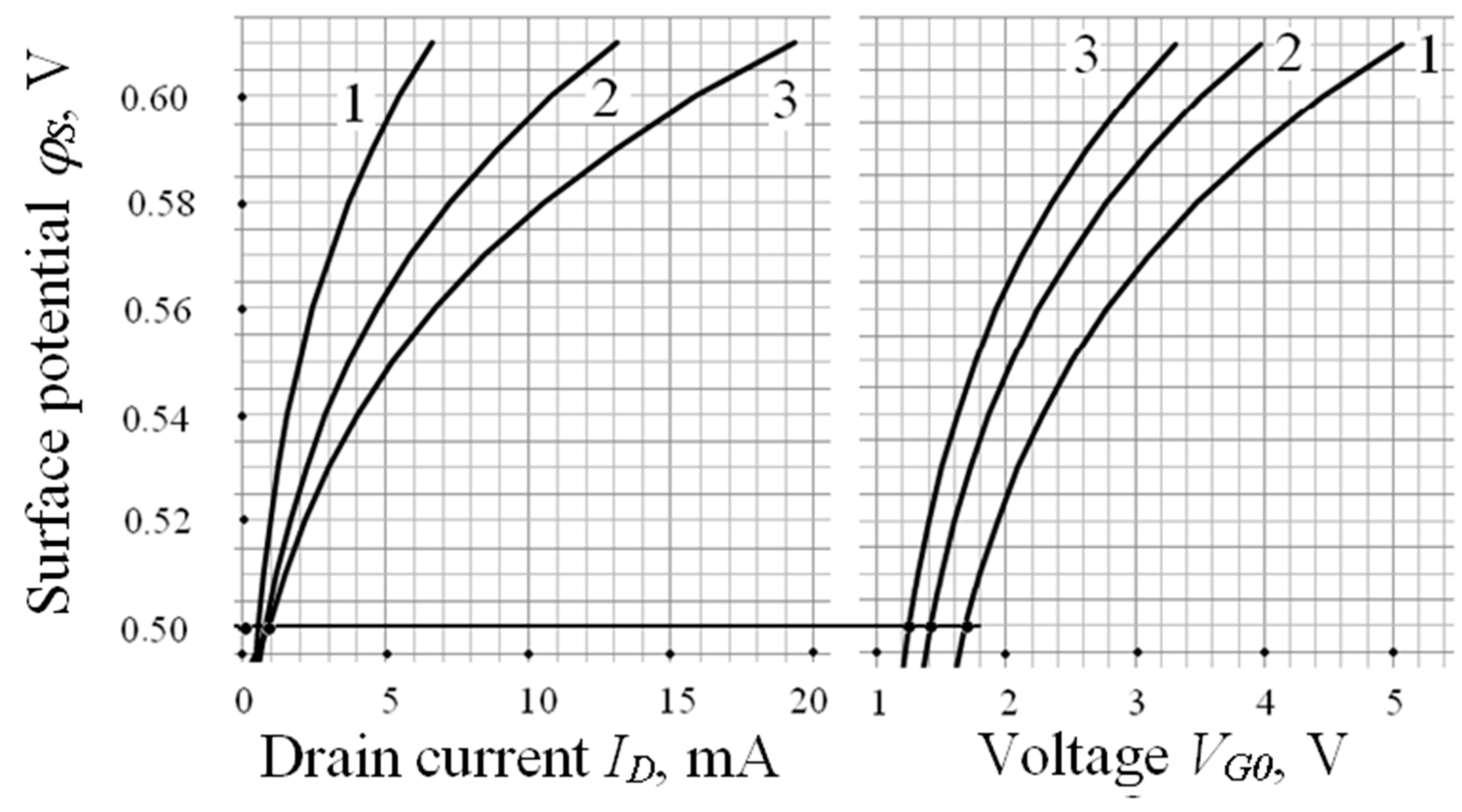
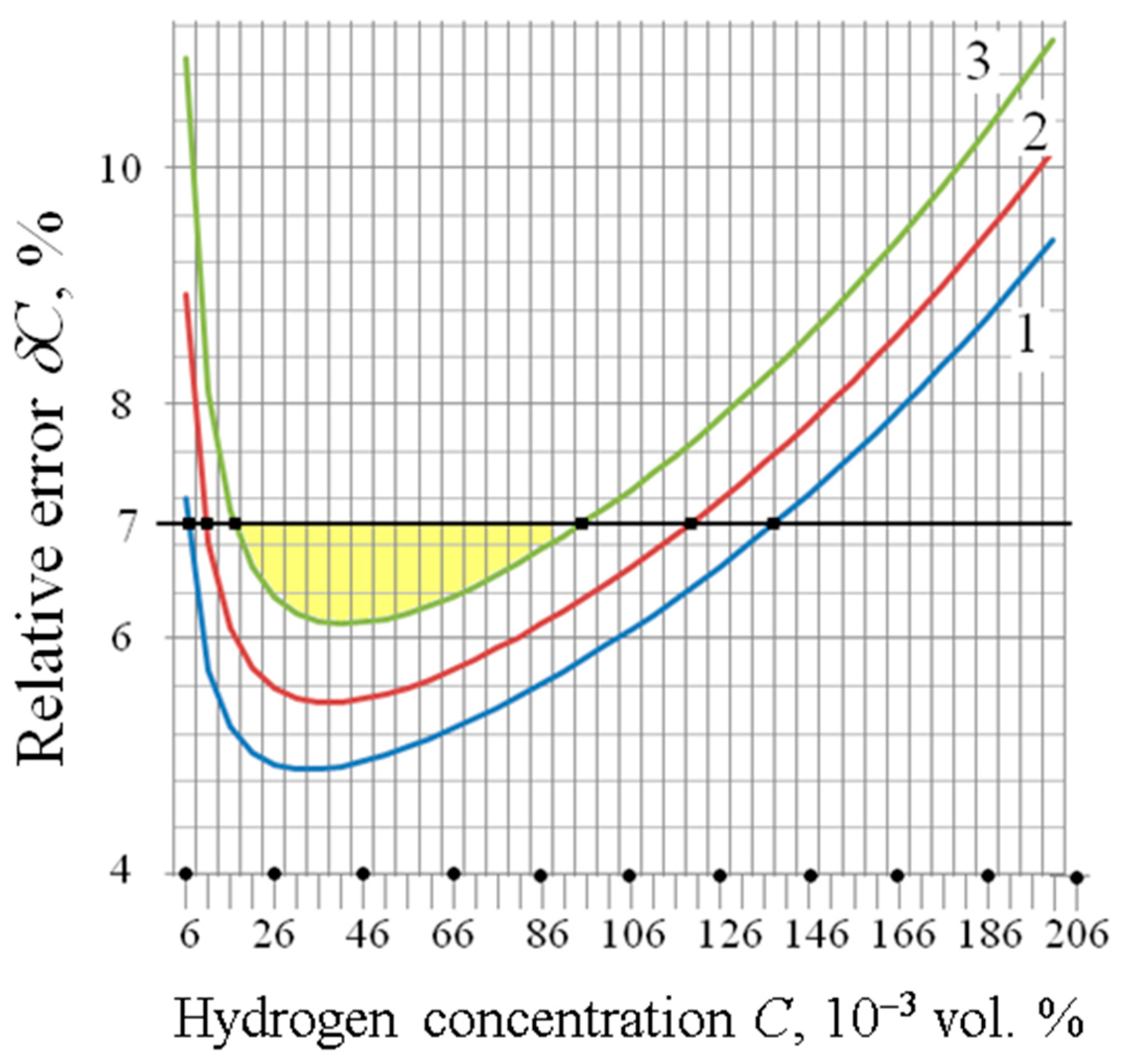
3.3. Influence of Specific Capacity on the Main Metrological Characteristics of TSE
4. Discussion
- All the considered STPs of the TSE (pk in Table 2) affect the components of the conversion function on which the main metrological characteristics depend.
- The deposition technology and thickness of the metal film dm can affect the conversion function components ΔQte(C) and Δφms(C) on which the sensor’s hydrogen sensitivity and the response time depend. A quantitative analysis of the effect of the Pd films technological characteristics on TSE hydrogen sensitivity requires special experimental studies. In the investigated TSE, the Pd film has a porous structure. Therefore, it can be assumed that the hydrogen sensitivity and response time will be independent of dm and of its deviations Δdm from the nominal values of dmn.
- The values of VG0 and ΔVG0 depend on NA, C0 and the given electrical parameters ID and VD. With the growth of ID and VD, the error ΔVG0 decreases. As a result of the calibration of the measuring device, the zero error is determined by the error ΔVG0 or the instrumental error of the voltage measurement ΔV (in the examples considered, ΔV is 1 mV).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hübert, T.; Boon-Brett, L.; Black, G. Banach, U. Hydrogen sensors—A review. Sens. Actuators B 2011, 157, 329–352. [Google Scholar] [CrossRef]
- Hong, S.; Wu, M.; Hong, Y.; Jeong, Y.; Jung, G.; Shin, W.; Park, J.; Kim, D.; Jang, D.; Lee, J.H. FET-type gas sensors: A review. Sens. Actuators B 2020, 330, 129240. [Google Scholar] [CrossRef]
- Tejaswini, S.; Paresh, K. Work Function-Based MOS Hydrogen Sensor and its Functionality: A Review. Adv. Mater. Interfaces 2021, 8, 2100649. [Google Scholar]
- Lundström, I.; Shivaraman, S.; Svensson, C.; Lundkvist, L. A hydrogen-sensitive MOS field-effect transistor. Appl. Phys. Lett. 1975, 26, 55–57. [Google Scholar] [CrossRef]
- Lundström, I. Hydrogen sensitive MOS-structures, Part I: Principles and applications. Sens. Actuators 1981, 1, 423–426. [Google Scholar] [CrossRef]
- Lundström, I.; Armgarth, M.; Spetz, A.; Winquist, F. Gas sensors based on catalytic metal-gate field-effect devices. Sens. Actuators 1986, 3–4, 399–421. [Google Scholar] [CrossRef]
- Spetz, A.; Helmersson, U.; Enquist, F.; Armgarth, M.; Lundström, I. Structure and ammonia sensitivity of thin platinum or iridium gates in metal–oxide–silicon capacitors. Thin Solid Film. 1989, 177, 77–93. [Google Scholar] [CrossRef]
- Lundström, I.; Sundgren, H.; Winquist, F.; Eriksson, M.; Krants-Rülcker, C.; Lloyd-Spets, A. Twenty-five years of field effect gas sensor research in Linköping. Sens. Actuators B Chem. 2007, 121, 247–262. [Google Scholar] [CrossRef]
- Lin, K.W.; Cheng, C.C.; Cheng, S.Y.; Yu, K.H.; Wang, C.K.; Chuang, H.M.; Liu, W.C. A novel Pd/oxide/GaAs metal–insulator–semiconductor field-effect transistor (MISFET) hydrogen sensor. Semicond. Sci. Technol. 2001, 16, 997–1001. [Google Scholar] [CrossRef]
- Andersson, M.; Pearce, R.; Lloyd-Spetz, A. New generation SiC based field effect transistor gas sensors. Sens. Actuators B Chem. 2013, 179, 95–106. [Google Scholar] [CrossRef]
- Kalinina, L.; Litvinov, A.; Nikolaev, I.; Samotaev, N. MIS-Field Effect Sensors for low concentration of H2S for enviromental monitoring. Procedia Eng. 2010, 5, 1216–1219. [Google Scholar] [CrossRef]
- Yaqoob, U.; Younis, M.I. Chemical Gas Sensors: Recent Developments, Challenges, and the Potential of Machine Learning—A Review. Sensors 2021, 21, 2877. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q.; Cao, Y.Q.; Arulraj, D.; Liu, C.; Wu, D.; Li, W.M.; Li, A.D. Resistive-Type Hydrogen Sensors Based on Zinc Oxide Nanostructures. J. Electrochem. Soc. 2020, 167, 067528. [Google Scholar] [CrossRef]
- Podlepetsky, B.; Nikiforova, M.; Kovalenko, A. Chip temperature influence on characteristics of MISFET hydrogen sensors. Sens. Actuators B 2018, 254, 1200–1205. [Google Scholar] [CrossRef]
- Podlepetsky, B.; Kovalenko, A.; Samotaev, N. Influence of electrical modes on performance of MISFET hydrogen sensors. Sens. Actuators B 2017, 248, 1017–1022. [Google Scholar] [CrossRef]
- Podlepetsky, B. Effect of irradiation on hydrogen sensors based on MISFET. Sens. Actuators B 2017, 238, 1207–1213. [Google Scholar] [CrossRef]
- Gurlo, A.; Clarke, D. High-Sensitivity Hydrogen Detection: Hydrogen-Induced Swelling of Multiple Cracked Palladium Films on Compliant Substrates. Angew. Chem. Int. Ed. 2011, 50, 10130–10132. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, M.; Lundström, I.; Ekedahl, L.-G. A model of the Temkin isotherm behaviour for hydrogen adsorption at Pd–SiO2 interfaces. J. Appl. Phys. 1997, 82, 3143–3146. [Google Scholar] [CrossRef]
- Fogelberg, J.; Eriksson, M.; Dannetun, H.; Petersson, L.-G. Kinetic modeling of hydrogen adsorption/absorption in thin films on hydrogen-sensitive field-effect devices: Observation of large hydrogen-induced dipoles at the Pd–SiO2 interface. J. Appl. Phys. 1995, 78, 988–996. [Google Scholar] [CrossRef]
- Irokawa, Y.; Usami, M. First-Principles Studies of Hydrogen Absorption at Pd-SiO2 Interfaces. Sensors 2015, 15, 14757–14765. [Google Scholar] [CrossRef]
- Podlepetsky, B.I.; Kovalenko, A.V. Errors of Integrated Hydrogen Sensors based on FETs with Structure Pd-(Ag)–Ta2o5–Sio2–si. J. Electrochem. Soc. 2020, 167, 167524. [Google Scholar] [CrossRef]
- Li, X.; Le Thai, M.; Dutta, R.K.; Qiao, S.; Chandran, G.T.; Penner, R.M. Sub-6 nm Palladium Nanoparticles For Faster, More Sensitive H2 Detection Using Carbon Nanotube Ropes. ACS Sens. 2017, 2, 282. [Google Scholar] [CrossRef]
- Penner, R. A Nose for Hydrogen Gas: Fast, Sensitive H2 Sensors using Electrodeposited Nanomaterials. Acc. Chem. Res. 2017, 50, 1902–1910. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Yun, J.; Gao, M.; Kim, H.; Cho, M.; Park, I. Nanoporous Silicon Thin Film-Based Hydrogen Sensor Using Metal-Assisted Chemical Etching with Annealed Palladium Nanoparticles. ACS Appl. Mater. Interfaces 2020, 12, 43614–43623. [Google Scholar] [CrossRef] [PubMed]
- Shin, W.; Hong, S.; Jung, G.; Jeong, Y.; Park, J.; Kim, D.; Lee, J.H. Improved signal-to-noise-ratio of FET-type gas sensors using body bias control and embedded micro-heater. Sens. Actuators B 2021, 329, 129166. [Google Scholar] [CrossRef]
- Guo, S.Y.; Hou, P.X.; Zhang, F.; Liu, C.; Cheng, H.M. Gas Sensors Based on Single-Wall Carbon Nanotubes. Molecules 2022, 27, 5381. [Google Scholar] [CrossRef]
- Usagava, T.; Takeyasu, K.; Fukutani, K. Hydrogen-Induced Dipoles and Sensing Principles of Pt-Ti-O gate Si-MISFET Hydrogen Gas Sensors. Procedia Eng. 2014, 87, 1015–1018. [Google Scholar] [CrossRef]
- Usagava, T.; Daugherty, D. Semiconductor Gas Sensor. U.S. Patent 20160097731A1, 7 April 2016. [Google Scholar]
- Sharma, B.; Sharma, A.; Kim, J. Recent advances on H2 sensor technologies based on MOX and FET devices: A review. Sens. Actuators B 2018, 262, 758–770. [Google Scholar] [CrossRef]
- Kumar, A.; Zhao, Y.; Mohammadi, M.M.; Liu, J. Palladium Nanosheet-Based Dual Gas Sensors for Sensitive Room-Temperature Hydrogen and Carbon Monoxide Detection. ACS Sens. 2022, 7, 225–234. [Google Scholar] [CrossRef]
- Saxena, P.; Shukla, P. A Review on Gas Sensor Technology and Its Applications. In Computational and Experimental Methods in Mechanical Engineering; Smart Innovation, Systems and Technologies; Rao, V.V., Kumaraswamy, A., Kalra, S., Saxena, A., Eds.; Springer: Singapore, 2022; p. 239. [Google Scholar]
- Available online: http://ece723.tripod.com/lec04.pdf.p.20 (accessed on 15 February 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual authors and contributors and not of MDPI and/or the editors. MDPI and/or the editors disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
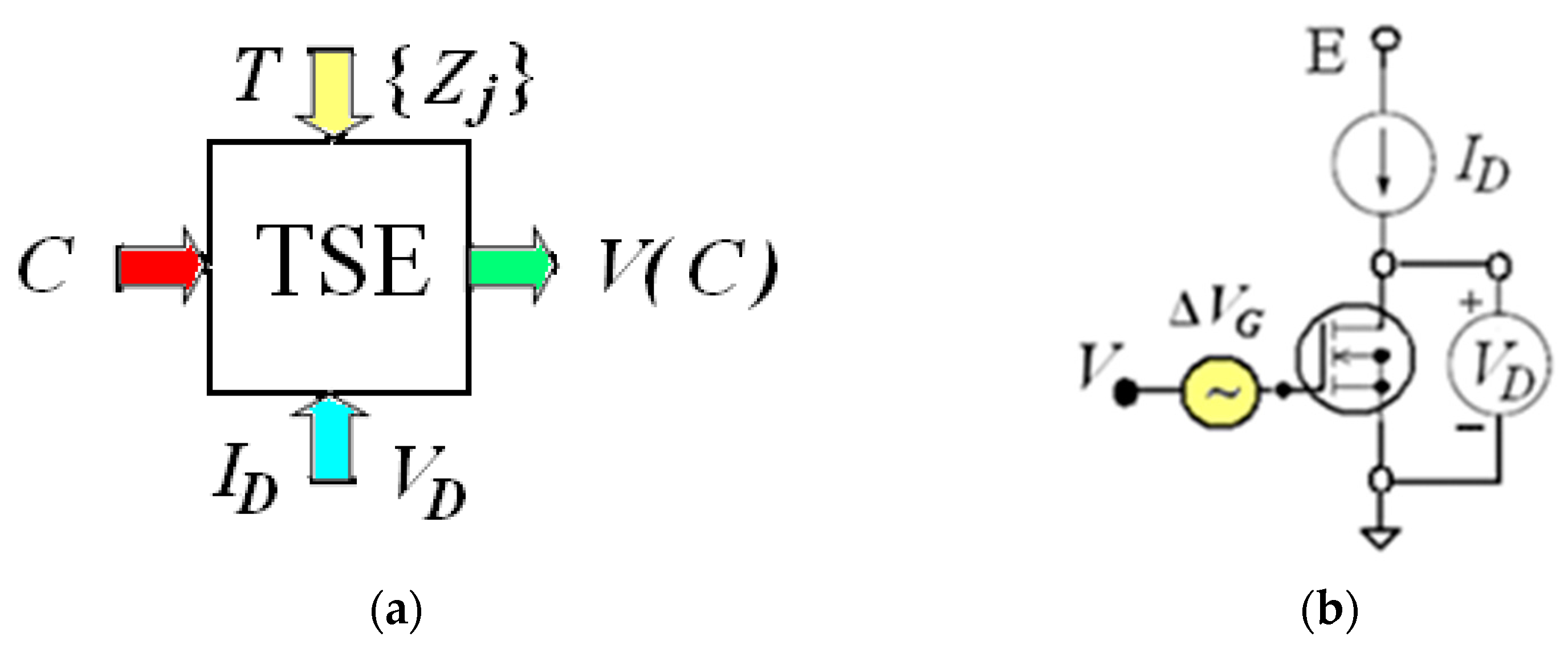

| Symbols | Parameters | Values |
|---|---|---|
| Parameters of semiconductor and dielectric materials | ||
| ε1, ε2 and ε3 | relative permittivity of Ta2O5, SiO2 and Si | 25, 4 and 12 |
| NA | concentration of acceptors in Si | 5 × 1015 cm−3 |
| µn | electron mobility in the channel | 200 cm2/(V∙s) |
| Dimensions of structural elements | ||
| L and w | channel length and width | 10 μm and 3.2 mm |
| d1 and d2 | thicknesses of Ta2O5 and SiO2 | 90 nm and 80 nm |
| dm | thickness of the gate metal film | 70 nm |
| Constants and derived parameters | ||
| ε0 | dielectric constant of vacuum | 8.85 × 10−12 F/m |
| k | Boltzmann constant | 1.38 × 10−23 J/K |
| q | electron charge | 1.6 × 10−19 Cl |
| d | thickness of the gate dielectric is (d1 + d2) | 170 nm |
| ε | effective permittivity of the dielectric layer is (dε1ε2)/(ε1d2 + ε2d1) | 7.1 |
| C0 | specific capacity of the dielectric (ε0ε)/d | 37 nF/cm2 |
| a | charge parameter in Si is (2q ε0∙ε3∙NA)1/2/C0 | 1.18 V1/2 |
| b | specific steepness is (µnw C0)/L | 2 mA/V2 |
| Physical and electrical parameters | ||
| φms | output work difference potential Pd– Si | φms0 = 85 mV |
| T | chip temperature | 400 K |
| φT | thermal potential (kT/q) at 400 K | 33 mV |
| φgb | the potential of the band gap in Si | 1.08 V |
| φs0 | the potential of acceptors’ level is φT ln(NA/ni) at 400 K | 0.21 V |
| φs | surface potential is [φ(SiO2 − Si) − φF] | 0.2…0.8 V |
| Qte and Qss | charge densities in the dielectric and in SiO2 − Si interface | (5…100) nKl/cm2 |
| ID | drain current | (2…300) μA |
| VD | voltage between the drain and the source | (0.1…0.5) V |
| VG | voltage between the gate and the substrate | (1…3) V |
| Qte and Qss | charge densities in the dielectric and in SiO2 − Si interface | (5…100) nCl/cm2 |
| ID | drain current | (2…300) μA |
| VD | voltage between the drain and the source | (0.1…0.5) V |
| VG | voltage between the gate and the substrate | (1…3) V |
| k | STP | Components of TSE Models | |
|---|---|---|---|
| 1 | film production technologies | Pd | ΔQte (C); Δφms(C); φms0 |
| 2 | Ta2O5 | ΔQte(C); C0; b | |
| 3 | SiO2 | Qte0; Qss; C0; b | |
| 4 | film thicknesses | Pd (dM) | ΔQte (C); Δφms(C) |
| 5 | Ta2O5 (d1) | ΔQte(C); Qte0; C0; b | |
| 6 | SiO2 (d2) | Qte0; C0; b | |
| 7 | acceptor concentration | (NA) | a; φs0; Qss |
| 8 | channel length | (L) | b |
| 9 | channel width | (w) | |
| 10 | electron mobility in the channel | (µn) | |
| 11 | relative dielectric permittivity | Ta2O5 (ε1) | a; b; C0 |
| 12 | SiO2 (ε2) | ||
| 13 | Si (ε3) | ||
| Parameters → | δC0, % | a, V | δa, % | w/L Is 0.003 | w/L Is 0.006 | ||||
|---|---|---|---|---|---|---|---|---|---|
| ↓ C0, nF/cm2 | b, mA/V2 | δb, % | ΔVG0, mV | b, mA/V2 | δb, % | ΔVG0, mV | |||
| 30 | 2.1 | 1.37 | 3.1 | 1.62 | 7.3 | 6 | 3.24 | 7.0 | 3 |
| 40 | 3.6 | 1.02 | 4.6 | 2.16 | 8.8 | 4.6 | 4.32 | 8.5 | 2.3 |
| 50 | 5.5 | 0.82 | 6.5 | 2.70 | 10.4 | 3.7 | 5.4 | 10.1 | 1.8 |
| MC → | VG0, V | ΔVm, V | kC, 1/(vol.%) | Sdmax, V/(vol.%) | δCmin, % | Cth, ppm | C1, ppm | C2, ppm | Cmax, ppm |
|---|---|---|---|---|---|---|---|---|---|
| ↓ C0, nF/cm2 | |||||||||
| 30 | 1.55 | 0.61 | 8 | 4.88 | 4.9 | 2.0 | 50 | 1410 | 8016 |
| 40 | 1.52 | 0.42 | 3.36 | 5.5 | 2.9 | 90 | 1210 | 7550 | |
| 50 | 1.48 | 0.32 | 2.56 | 6.1 | 3.9 | 160 | 960 | 7210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podlepetsky, B.; Samotaev, N.; Etrekova, M.; Litvinov, A. Structure and Technological Parameters’ Effect on MISFET-Based Hydrogen Sensors’ Characteristics. Sensors 2023, 23, 3273. https://doi.org/10.3390/s23063273
Podlepetsky B, Samotaev N, Etrekova M, Litvinov A. Structure and Technological Parameters’ Effect on MISFET-Based Hydrogen Sensors’ Characteristics. Sensors. 2023; 23(6):3273. https://doi.org/10.3390/s23063273
Chicago/Turabian StylePodlepetsky, Boris, Nikolay Samotaev, Maya Etrekova, and Artur Litvinov. 2023. "Structure and Technological Parameters’ Effect on MISFET-Based Hydrogen Sensors’ Characteristics" Sensors 23, no. 6: 3273. https://doi.org/10.3390/s23063273
APA StylePodlepetsky, B., Samotaev, N., Etrekova, M., & Litvinov, A. (2023). Structure and Technological Parameters’ Effect on MISFET-Based Hydrogen Sensors’ Characteristics. Sensors, 23(6), 3273. https://doi.org/10.3390/s23063273






