Sieve Search Centroiding Algorithm for Star Sensors
Abstract
1. Introduction
2. Sieve Search Algorithm
2.1. Characteristics of PSF Gray Value Distribution
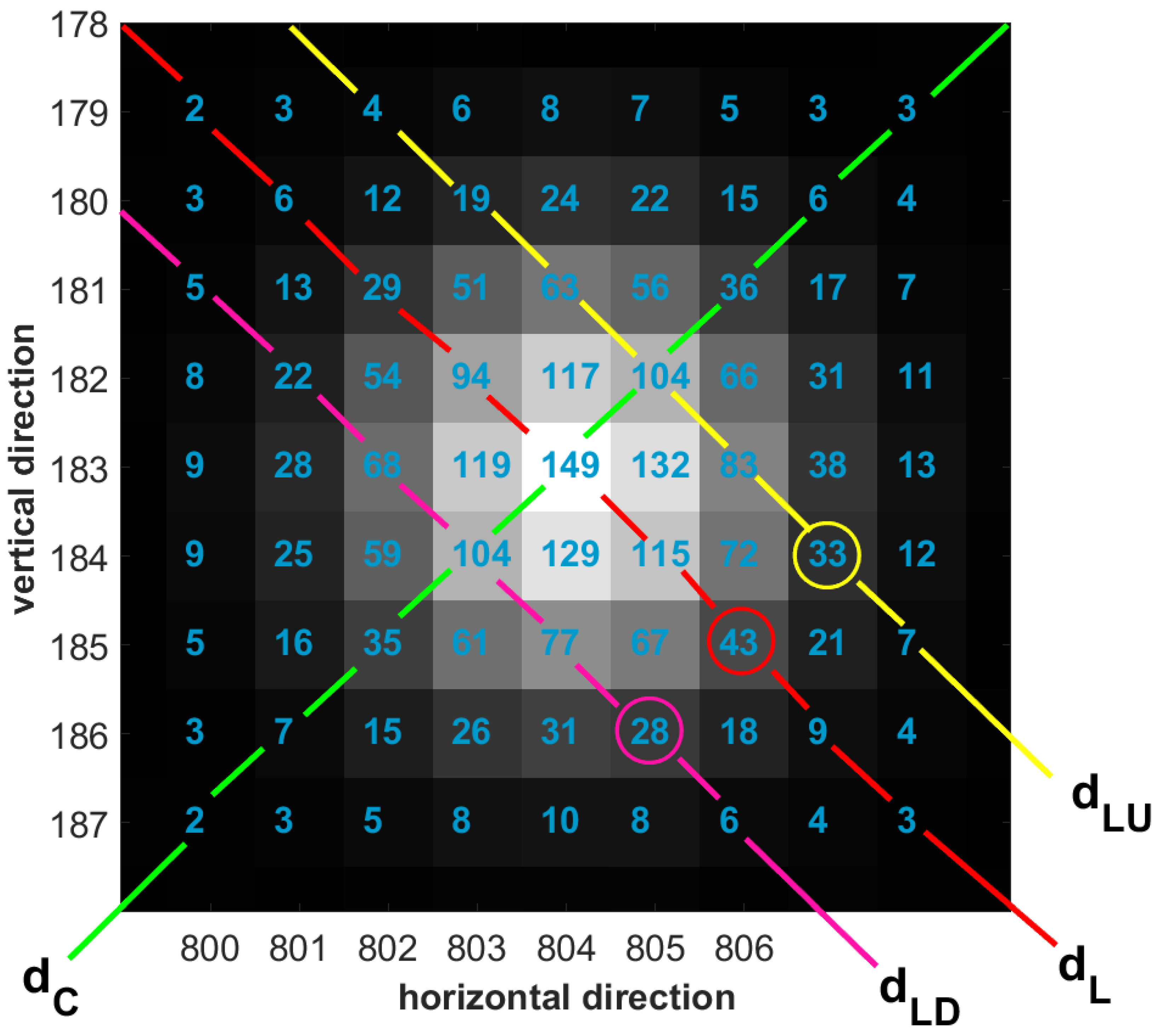
- the ROI matrix is nearly symmetric. For an ROI matrix, let represent the n-element vector, consisting of gray values in the pixels along the leading diagonal . The off-diagonals and are a pixels apart from . The gray value vectors corresponding to and are and , respectively. It can be observed that the value of the elements in and are almost similar, where . In Figure 3, the off-diagonals and are two pixels apart from . The grey value vectors , , and . The values of elements in and are found to be comparable, where . In other words, the pixels along the off-diagonals, equidistant from a diagonal element on both sides of the principal diagonals, have comparable gray value accumulation.
- as we transverse along the pixels at the same radial distance from the brightest pixel, the magnitude increases as we move closer to the principal diagonal pixels. Here, magnitude is referred to the gray value of the pixel. Let represent the gray value of a pixel , along , at some radial distance from the most illuminated pixel in the ROI. At the same radial distance, in the neighborhood of , the gray value of the pixels along and are and , respectively. Then, is marginally greater than and . In Figure 3, the brightest pixel has an accumulated gray value of 149. Among the pixels at the same radial distance from it, the gray value at the pixel along the principal diagonal is marginally greater than that along the off-diagonal pixels .
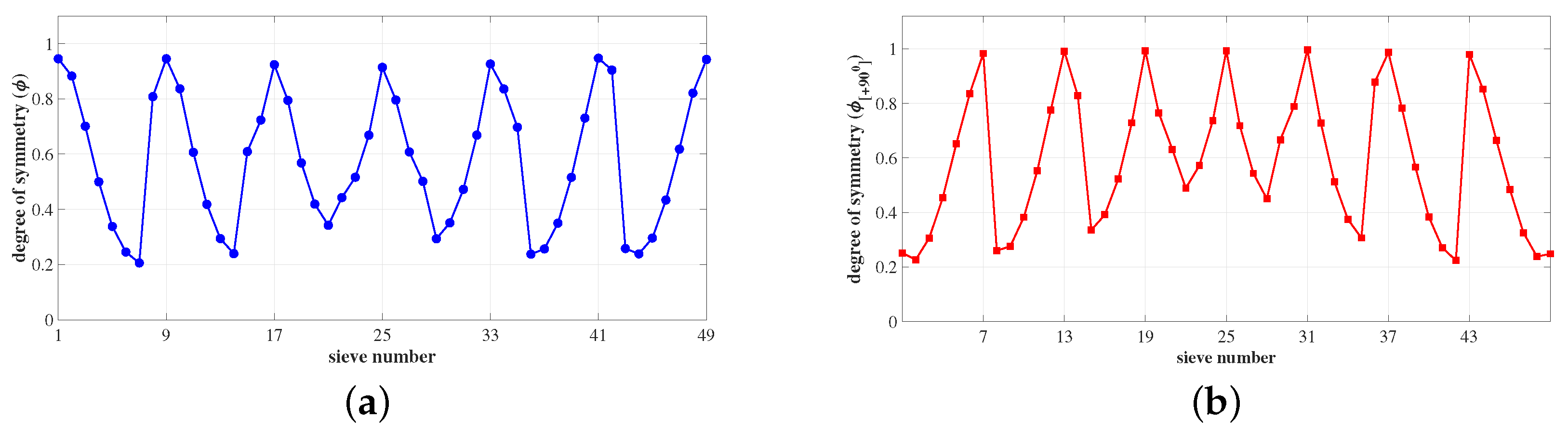
2.2. Sieve Segmentation and Symmetry
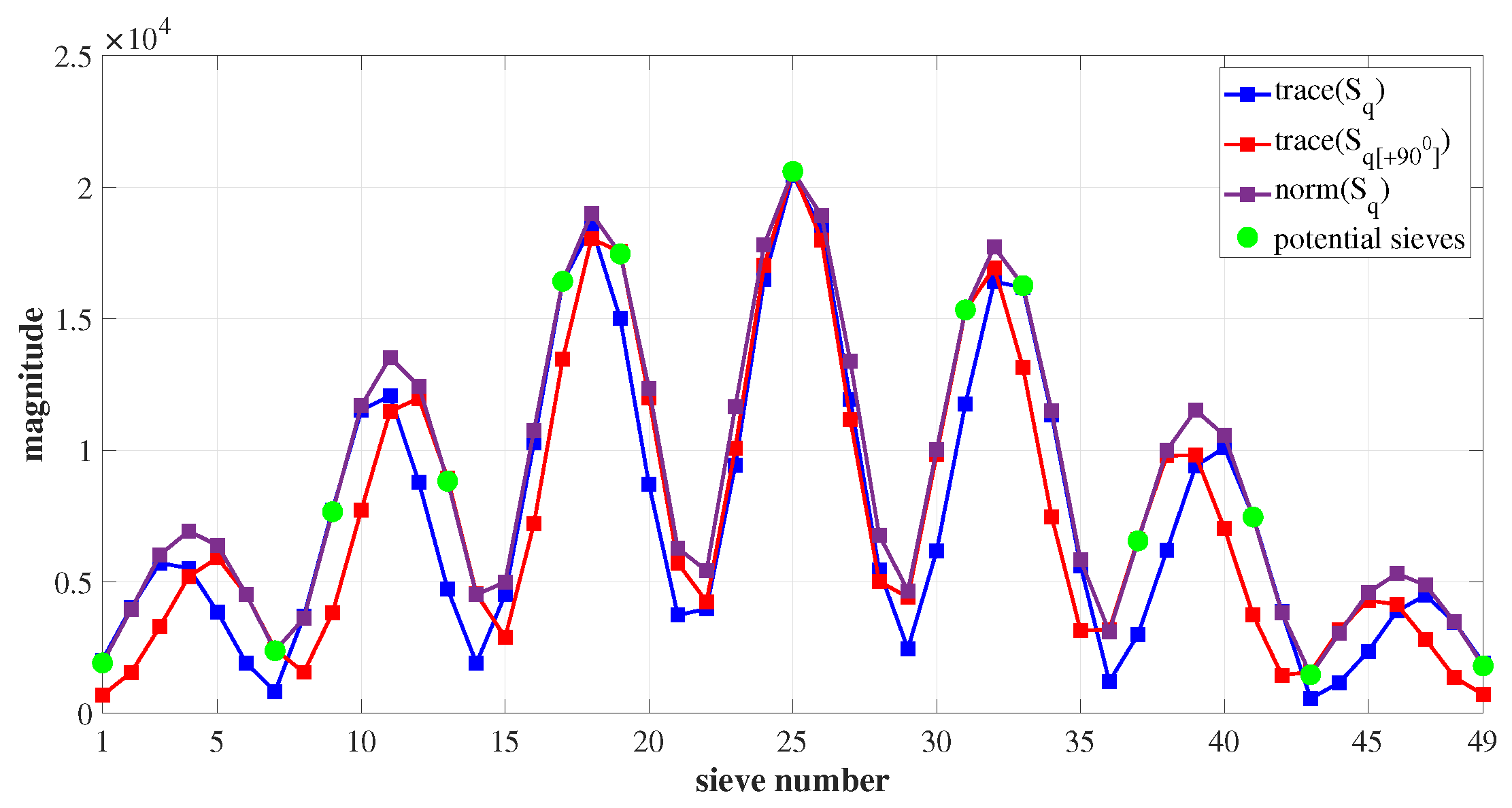
2.3. Characteristics of Sieve Magnitude
2.4. Centroiding Based on Sieve Search Algorithm
- (i)
- An ROI of size not less than pixel window is created around the star image spot. The accumulated gray value distribution inside the ROI is used to populate the elements of the corresponding ROI matrix.
- (ii)
- The ROI matrix is segregated into square sub-matrices called sieves. The degree of symmetry and magnitude of each sieve in the ROI is evaluated and stored as and , respectively, where . The sieves are rotated by clockwise. The corresponding and are determined.
- (iii)
- (iv)
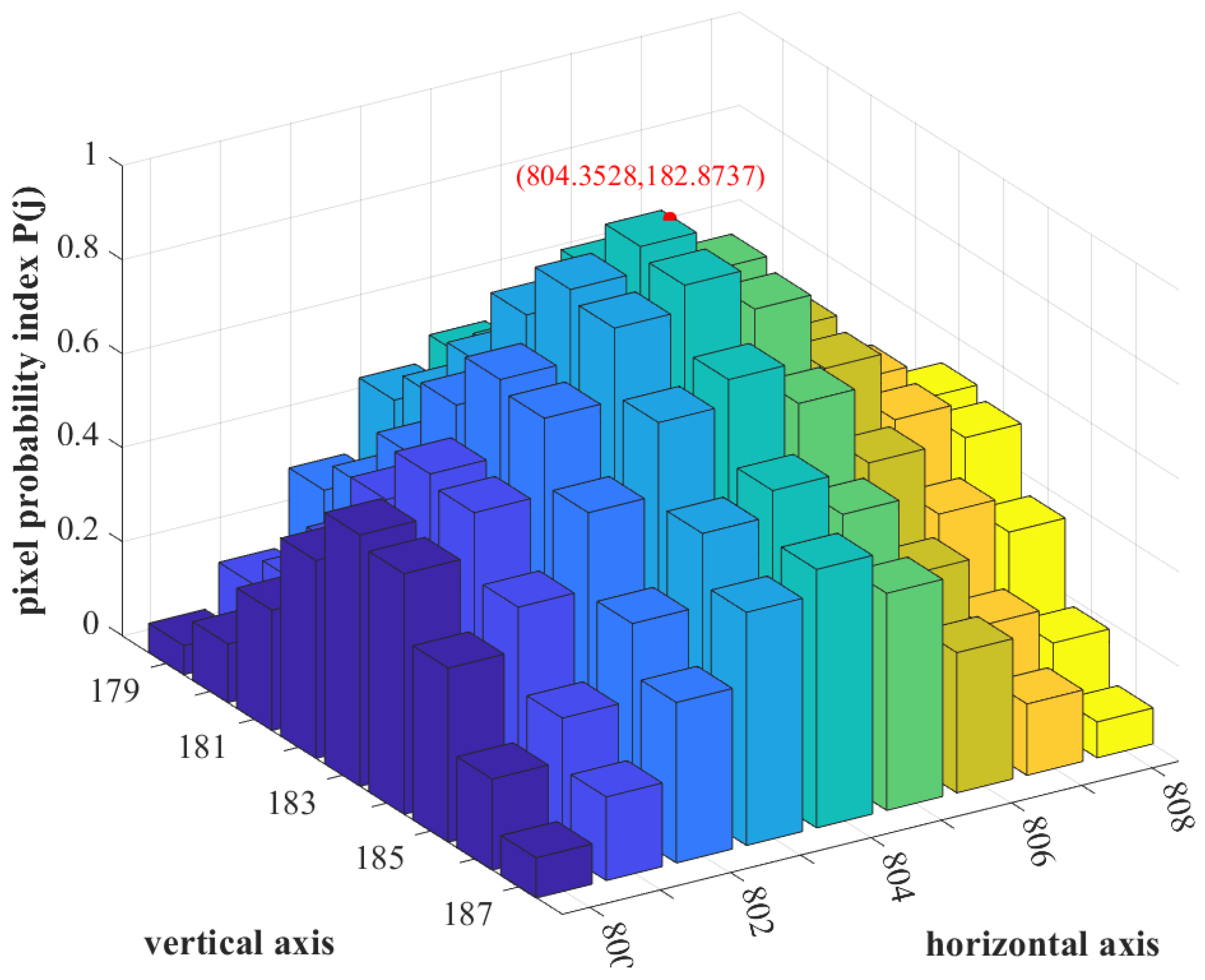
- For every sieve in the ROI, the value of its degree of symmetry–magnitude product is associated with each pixel contained in it. Consequently, for a pixel j, the value of , resulting from the various sieves it constitutes, adds up, given by,where U is a set formed by the sieves that contain pixel j. As is depicted in Figure 7, the probability of each pixel in the ROI possessing the centroid of the image spot, referred to as the pixel probability index , is given by,
- (v)
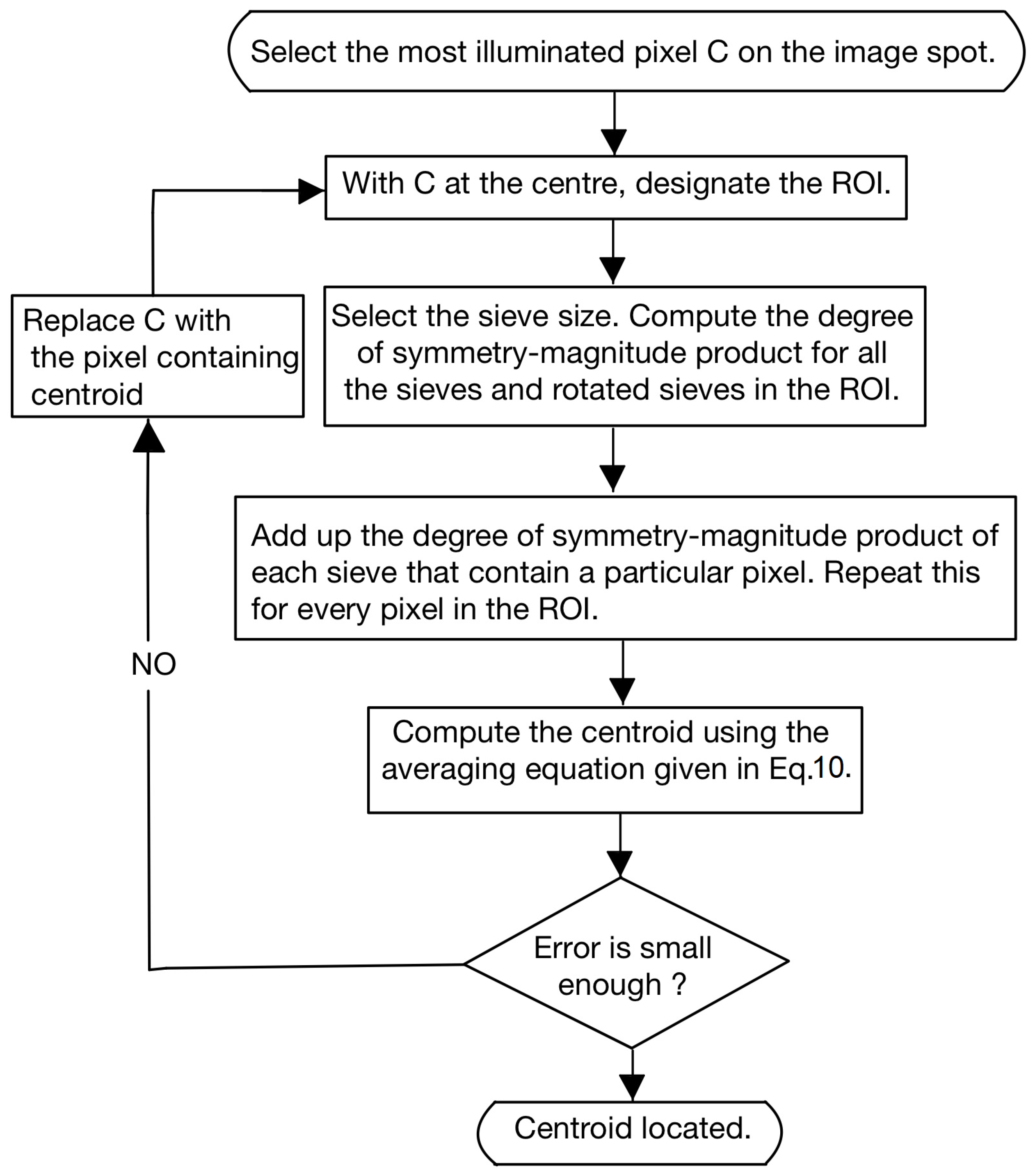
- Let and correspond to the horizontal and vertical coordinates of pixel j. The value of the centroid is computed as,where W is a set formed by the pixels in the star spot. A flowchart explaining the working of the SSA is given in Figure 8.
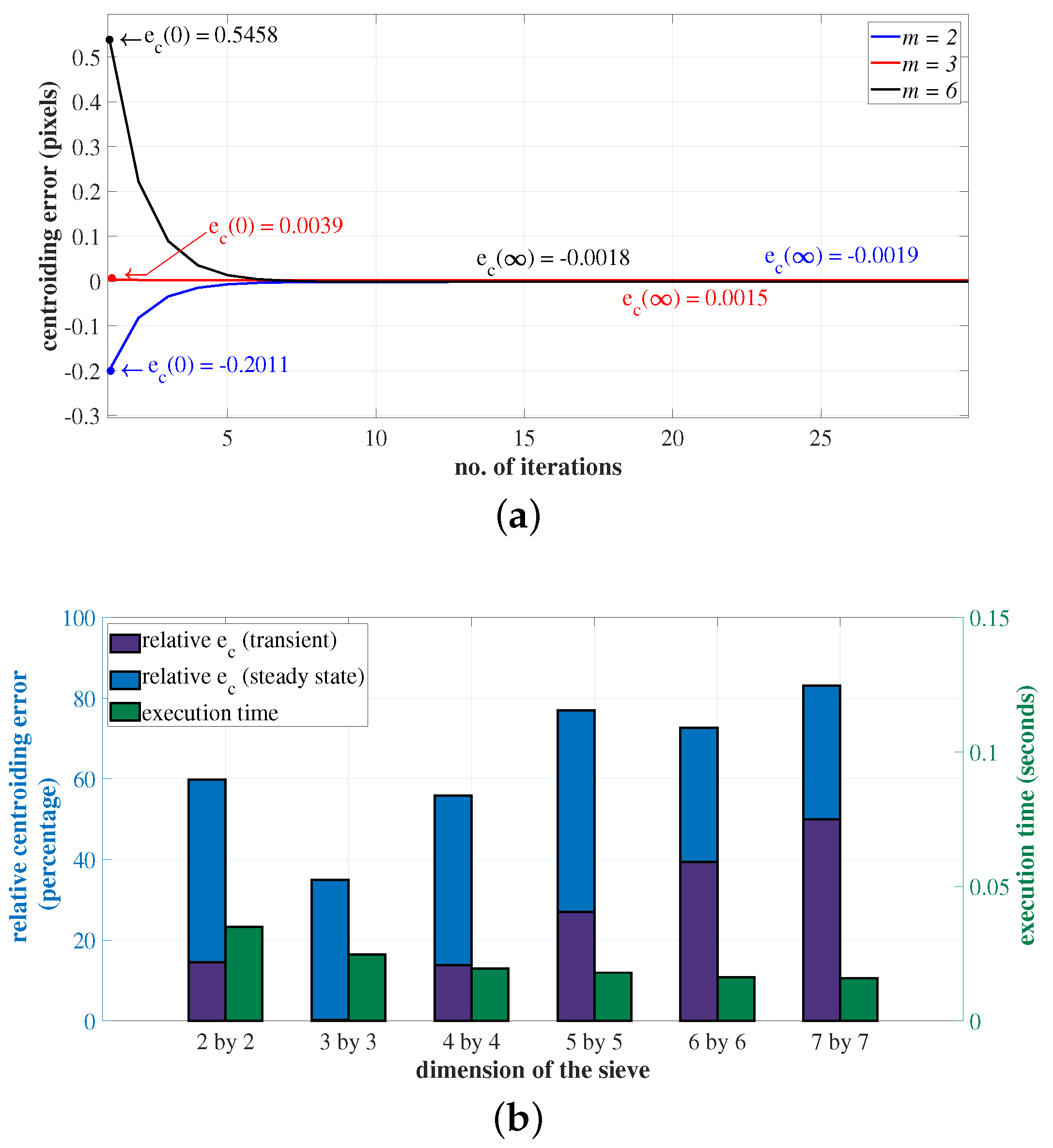
2.5. Optimal Sieve Size
3. Materials and Methods
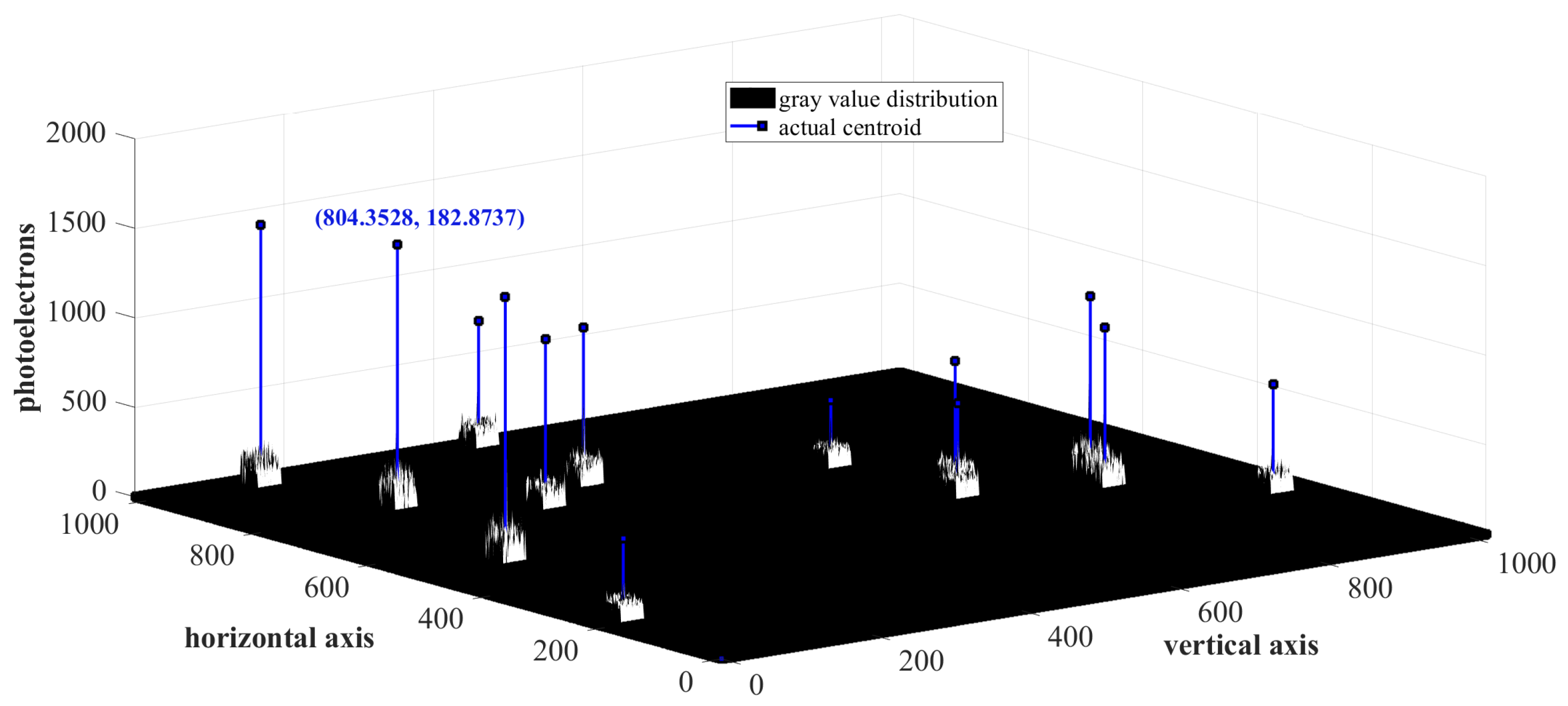
3.1. Simulation of Star Images
3.2. Simulation of Noise Process
3.3. Selection of Attributes
- the radius of the Gaussian spread in both directions, .
- the size of the star image pixel window was .
- the average level of noise corresponding to a star image spot was restricted to 7% of the accumulated gray value in the most illuminated pixel of that star image.
3.4. Particulars of Experiments
4. Results and Analysis
4.1. Sensitivity of Centroiding Accuracy to Various Parameters
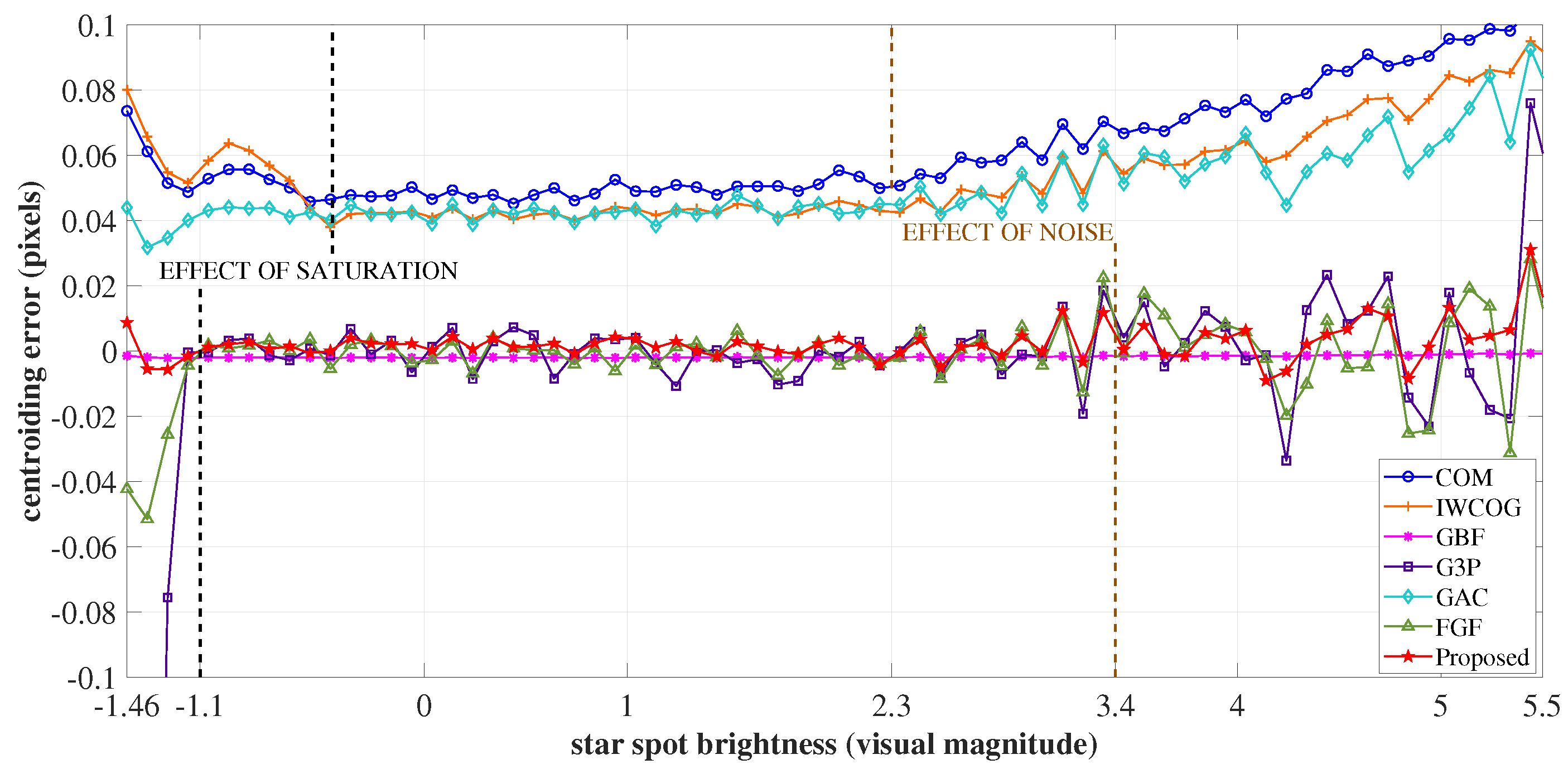
4.1.1. Brightness
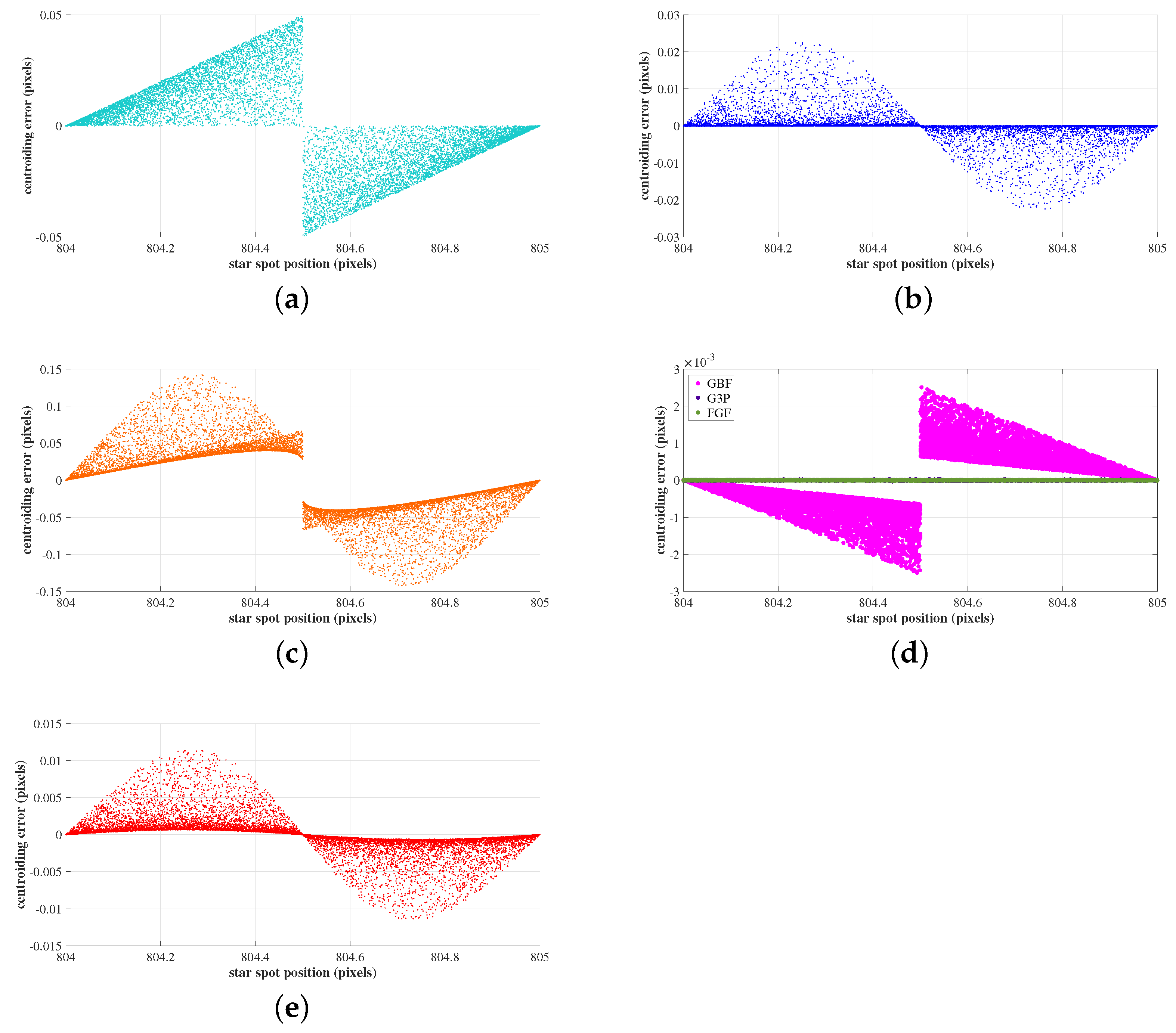
4.1.2. Location of Star Spot Inside a Pixel
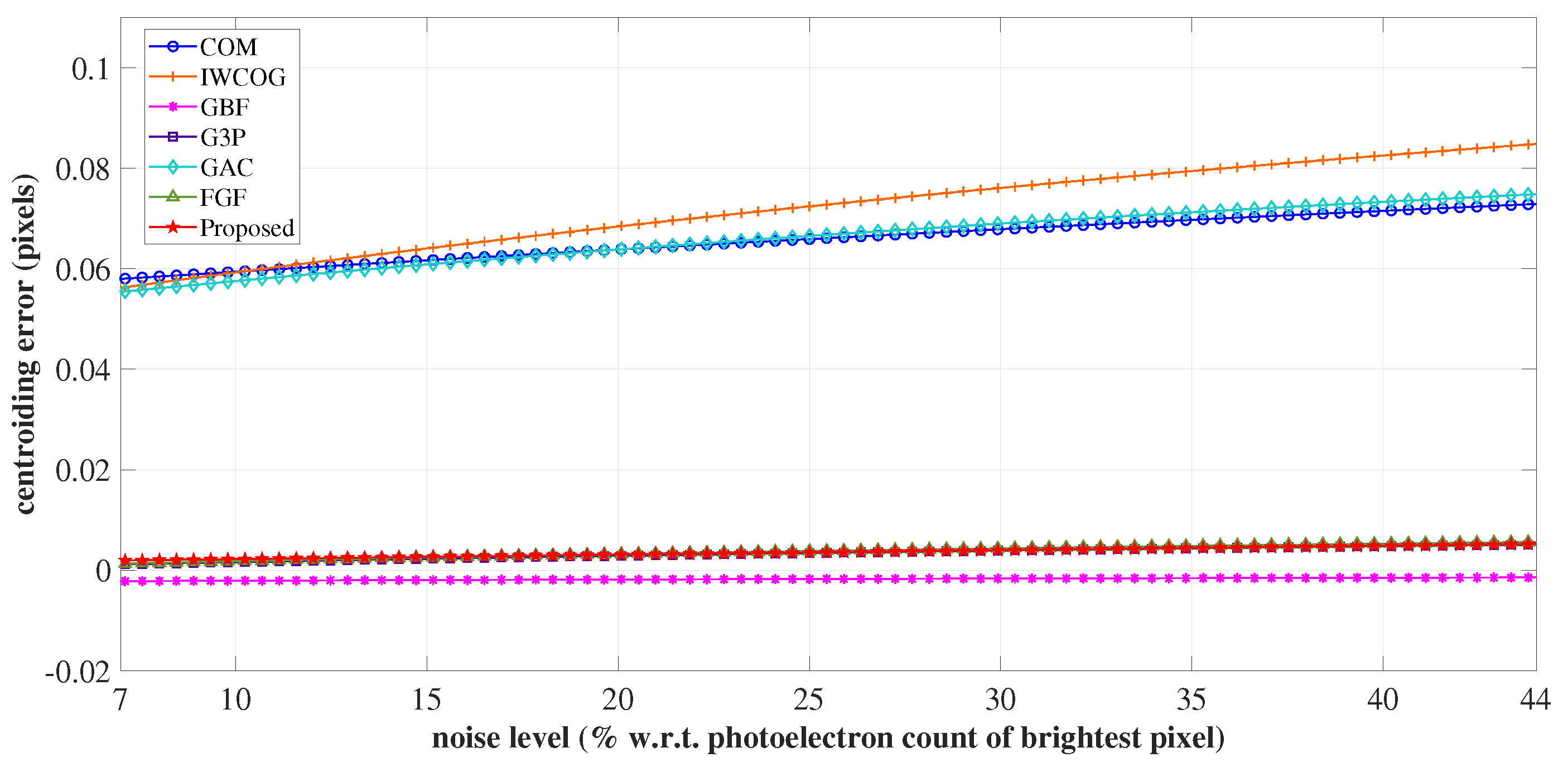
4.1.3. Noise Floor
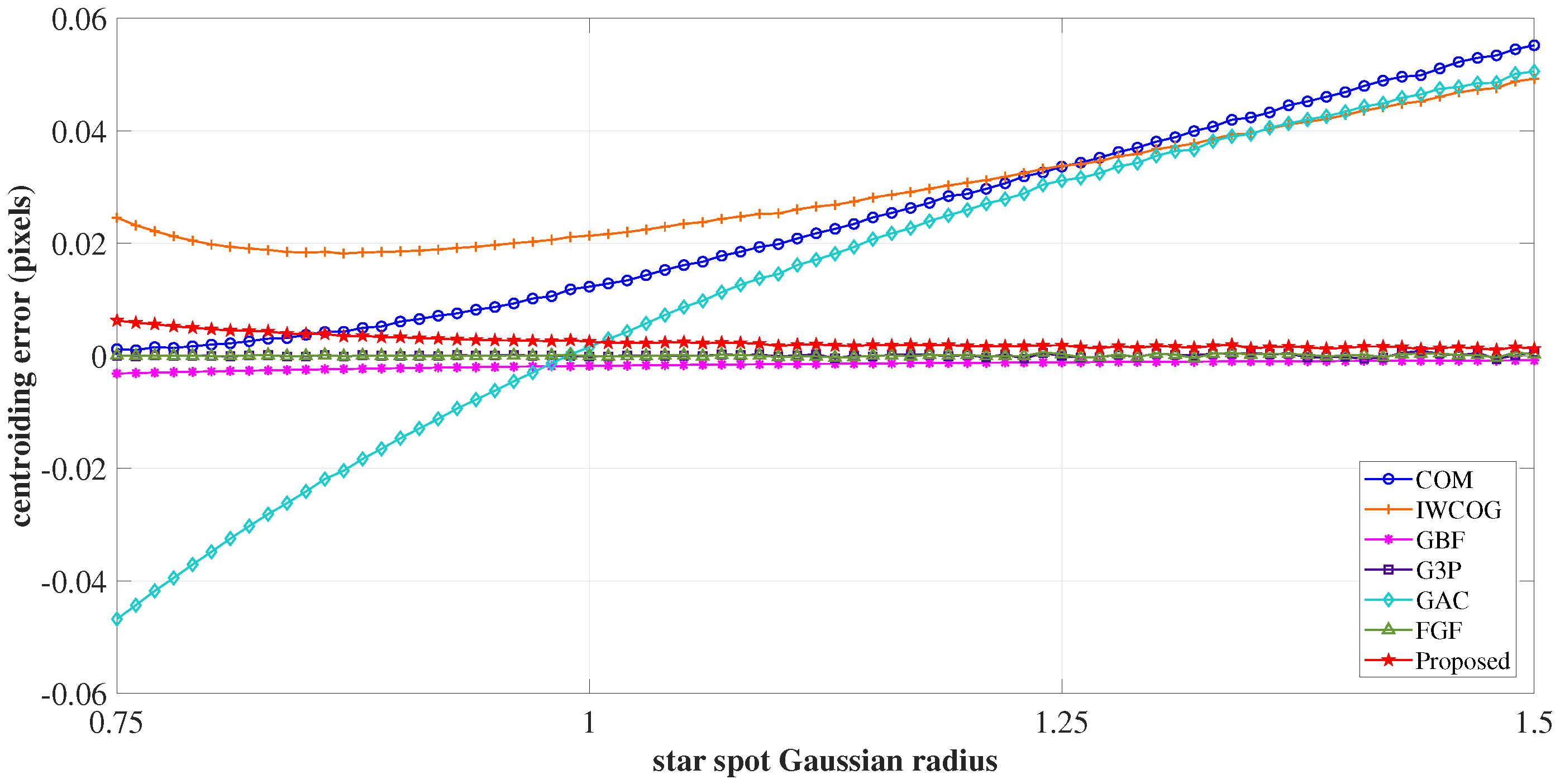
4.1.4. Gaussian Spread
4.2. Special Cases: Performance Evaluation
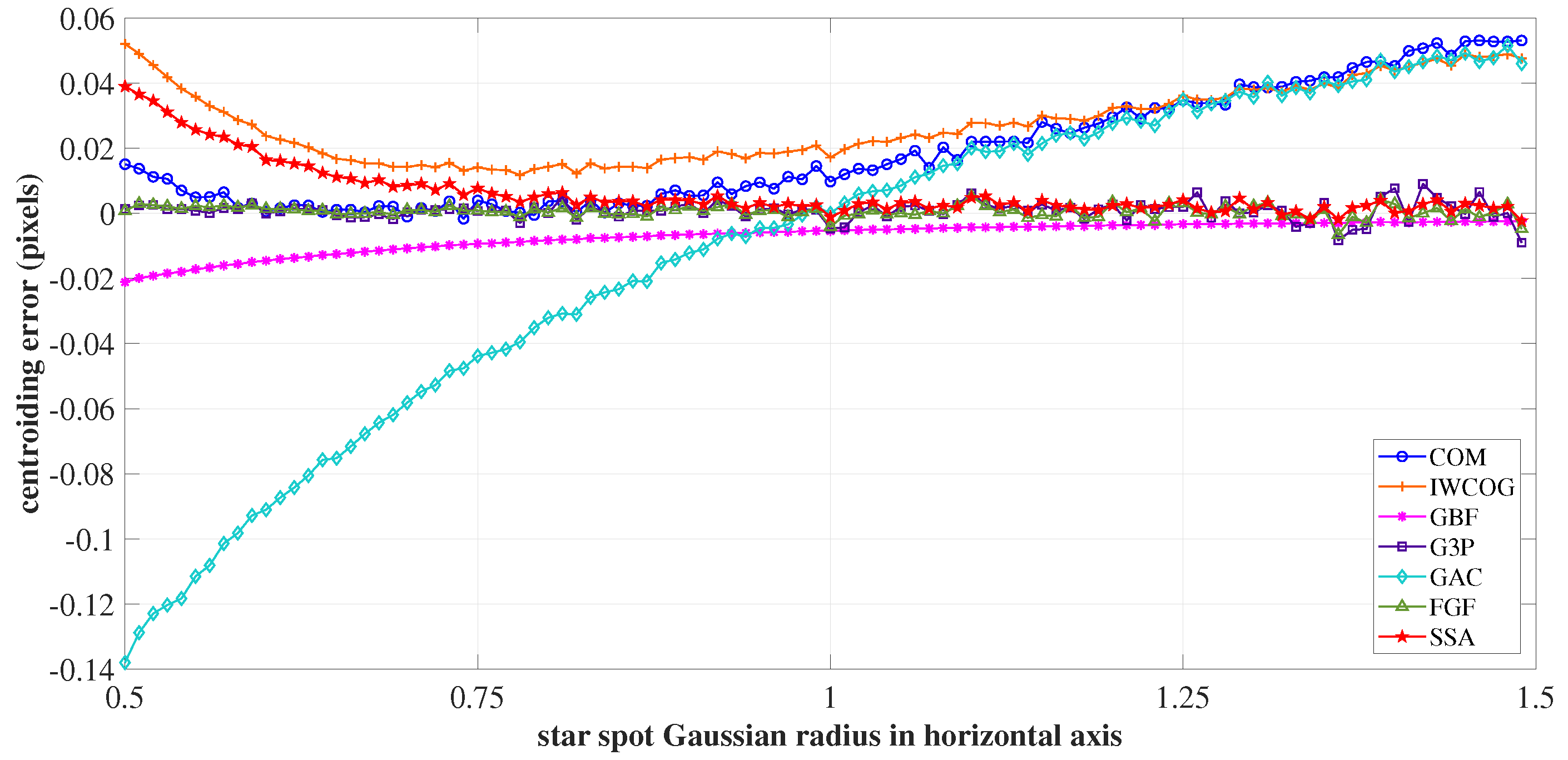
4.2.1. Non-Uniform PSF
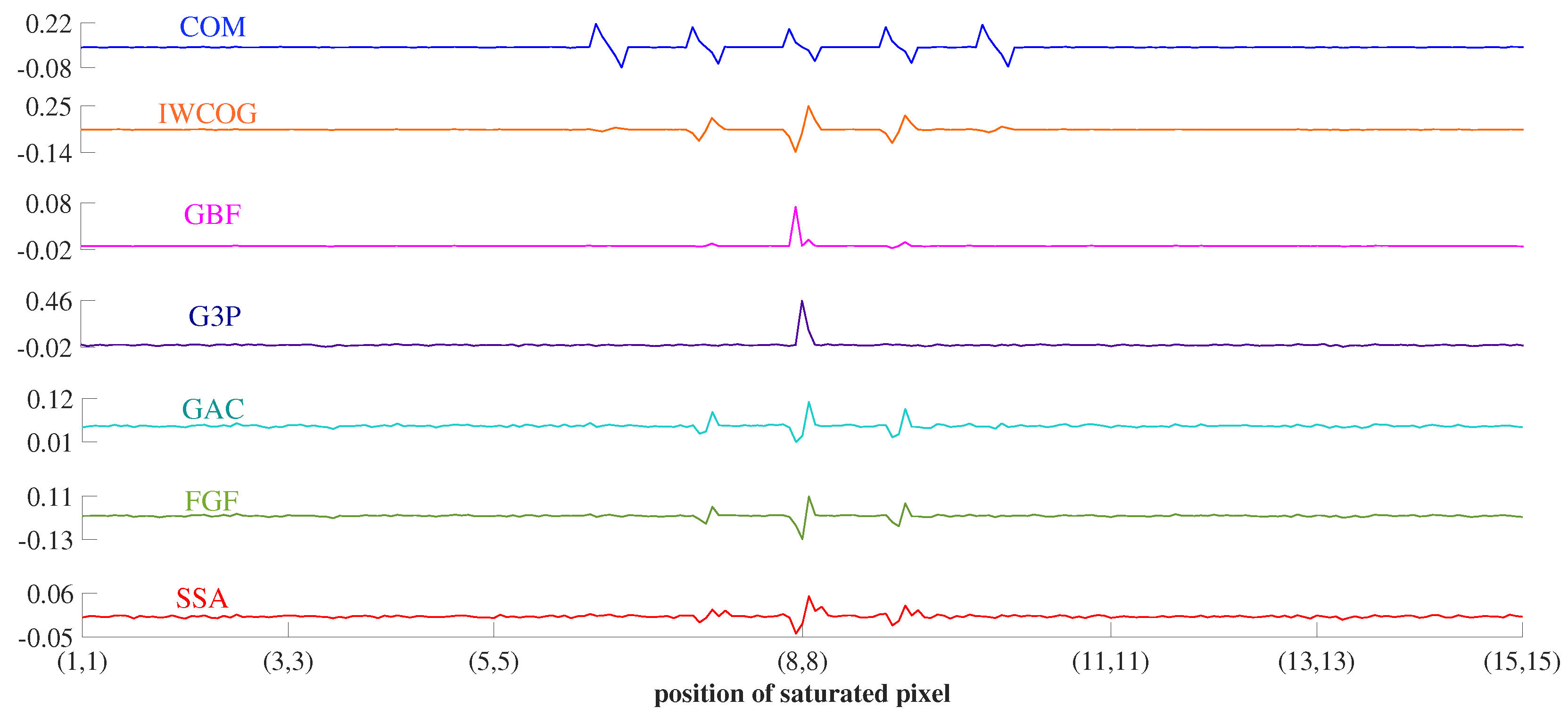
4.2.2. Stuck Pixel Noise
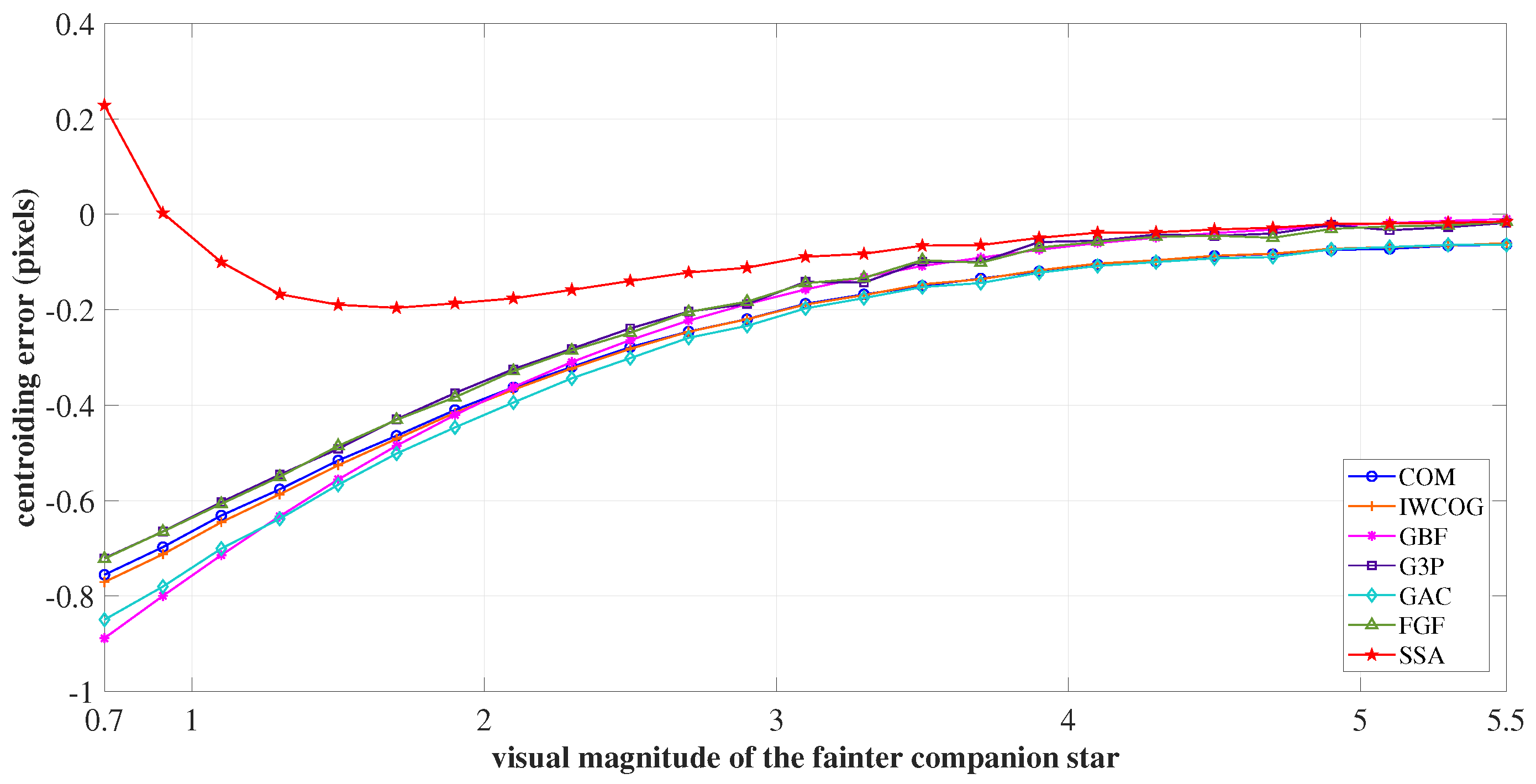
4.2.3. Optical-Double Stars
4.3. Execution Time
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fallon, L., III. Star sensors. In Spacecraft Attitude Determination and Control; Wertz, J.R., Ed.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1978; p. 186. ISBN 978-94-009-9907-7. [Google Scholar]
- Liebe, C.C. Accuracy performance of star trackers—A tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Samaan, M.A. Toward Faster and More Accurate Star Sensors Using Recursive Centroiding and Star Identification. Ph.D. Thesis, Texas A&M University, Austin, TX, USA, 2003. [Google Scholar]
- Wang, H.; Xu, E.; Li, Z.; Jingjin, L.; Quin, T. Gaussian analytic centroiding method of star image of star tracker. Adv. Space Res. 2015, 56, 2196–2205. [Google Scholar] [CrossRef]
- Huffman, K.M.; Sedwick, R.J.; Stafford, J.; Pavaerill, J.; Seng, W. Designing star trackers to meet micro-satellite requirements. In Proceedings of the International Conference on Space Operations (SpaceOps2006), Rome, Italy, 19–23 June 2006; pp. 1–29. [Google Scholar] [CrossRef]
- Baker, K.L.; Moallem, M.M. Iteratively weighted centroiding for Shack- Hartmann wave-front sensors. Opt. Express 2007, 15, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Shortis, M.; Clarke, T.; Short, T. A Comparison of some techniques for the subpixel location of discrete target images. SPIE Videometrics III 1994, 2350, 239–250. [Google Scholar] [CrossRef]
- Sheppard, C.J.R. Microscopy overview. In Encyclopedia of Modern Optics; Guenther, R.D., Steel, D.G., Bayvel, L., Eds.; Elsevier: Oxford, UK, 2004; pp. 61–68. ISBN 978-0-12-369395-2. [Google Scholar]
- Schowengerdt, R.A. Sensor models. In Remote Sensing; Schowengerdt, R.A., Ed.; Academic Press: Cambridge, MA, USA, 2007; Chapter 3; pp. 75–126. ISBN 978-0-12-369407-2. [Google Scholar]
- Airy, G.B. On the diffraction of an object-glass with circular aperture. Trans. Cambridge Philos. Soc. 1835, 5, 283–291. [Google Scholar]
- Katake, A.B. Modeling, Image Processing and Attitude Estimation of High Speed Star Sensors. Ph.D. Thesis, Texas A&M University, Austin, TX, USA, 2006. [Google Scholar]
- Zhang, B.; Zerubia, J.; Olivo-Marin, J. Gaussian approximations of fluorescence microscope point-spread function models. Appl. Opt. 2007, 46, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Mortari, D.; Bruccoleri, C.; La Rosa, S.; Junkins, J.L. CCD Data Processing Improvements for star Cameras. In Proceedings of the International Conference on Dynamics and Control of System and Structures in Space, Denver, CO, USA, 22–25 April 2002. [Google Scholar]
- Tremsin, A.S.; Vallerga, J.V.; Siegmund, O.H.W.; Hull, J.S. Centroiding algorithms and spatial resolution of photon counting detectors with cross strip anodes. Proc. SPIE 2003, 5164, 1–12. [Google Scholar] [CrossRef]
- Yang, J.; Liang, B.; Zhang, T.; Song, J. A novel systematic error compensation algorithm based on least squares support vector regression for star sensor image centroid estimation. Sensors 2011, 11, 7341–7363. [Google Scholar] [CrossRef]
- Wei, X.; Xu, J.; Li, J. S-curve centroiding error correction for star sensor. Acta Astronaut. 2014, 99, 231–241. [Google Scholar] [CrossRef]
- Delabie, T.; Schutter, J.D.; Vandenbussche, B. An Accurate and efficient Gaussian fit centroiding algorithm for star trackers. J. Astronaut. 2014, 61, 60–84. [Google Scholar] [CrossRef]
- Wan, X.; Wang, G.; Wei, X.; Li, J.; Zhang, G. Star centroiding based on fast Gaussian fitting for star sensors. Sensors 2018, 18, 2836. [Google Scholar] [CrossRef]
- Fialho, M.A.A.; Mortari, D. Theoretical limits of star sensor accuracy. Sensors 2019, 19, 5355. [Google Scholar] [CrossRef] [PubMed]
- Asadnezhad, M.; Eslamimajd, A.; Hajghassem, H. Optical system design of star sensor and stray light analysis. J. Eur. Opt. Soc. 2018, 14, 1–11. [Google Scholar] [CrossRef]
- Wei, X.; Wen, D.; Song, Z.; Xi, J.; Zhang, W.; Liu, G.; Li, Z. A systematic error compensation method based on an optimized extreme learning machine for star sensor image centroid estimation. Appl. Sci. 2019, 9, 4751. [Google Scholar] [CrossRef]
- Pong, C.M.; Smith, M.W. Camera modeling, centroiding performance, and geometric camera calibration on ASTERIA. In Proceedings of the IEEE Aerospace Conference 2019, Big Sky, MT, USA, 2–9 March 2019; pp. 1–17. [Google Scholar] [CrossRef]
- Wei, X.; Tan, W.; Li, J.; Zhang, G. Exposure time optimization for highly dynamic star trackers. Sensors 2014, 14, 4914–4931. [Google Scholar] [CrossRef]
- Di1, P.; Qi1, Z.; Weizhi, Q.; Bing, L.; Pingchuan, R. Star spot centroid extraction method in high dynamic condition based on difference hash algorithm. In Proceedings of the 12th Asia Conference on Mechanical and Aerospace Engineering (ACMAE 2021), Nanjing, China, 29–31 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, G.; Wei, X. Improving star centroiding accuracy in stray light base on background estimation. In Proceedings of the IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON 2018), Vancouver, ON, Canada, 1–3 November 2018; pp. 513–518. [Google Scholar] [CrossRef]
- He, Y.; Wang, H.; Feng, L.; You, S.; Lu, J.; Jiang, W. Centroid extraction algorithm based on grey-gradient for autonomous star sensor. Optik 2019, 194, 162932. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J.; Zhang, G.; Lu, Y. Accurate and robust synchronous extraction algorithm for star centroid and nearby celestial body edge. IEEE Access 2019, 7, 126742–126752. [Google Scholar] [CrossRef]
- Samed, A.L.; Karagoz, I.; Dogan, A. An Improved star detection algorithm using a combination of statistical and morphological image processing techniques. In Proceedings of the IEEE Applied Imagery Pattern Recognition Workshop (AIPR 2018), Washington, DC, USA, 9–11 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, H.; Xie, J.; Tang, X.; Jia, D.; Sun, G. Stellar map centroid positioning based on dark channel denoising and feasibility of jitter detection on ZiYuan3 satellite platform. J. Appl. Rem. Sens. 2021, 15, 016519. [Google Scholar] [CrossRef]
- Lu, K.; Liu, E.; Zhao, R.; Zhang, H.; Tian, H. Star sensor denoising algorithm based on edge protection. Sensors 2021, 21, 5255. [Google Scholar] [CrossRef]
- Mu, Z.; Wang, J.; He, X.; Wei, Z.; He, J.; Zhang, L.; Lv, Y.; He, D. Restoration method of a blurred star image for a star sensor under dynamic conditions. Sensors 2019, 19, 4127. [Google Scholar] [CrossRef]
- Erlank, A.O. Development of cubeStar: A cubeSat-Compatible Star Tracker. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2013. [Google Scholar]
- Ofodile, I.; Kutt, J.; Kivastik, J.; Nigol, M.K.; Parelo, A.; Ilbis, E.; Ehrpais, H.; Slavinskis, A. ESTCube-2 attitude determination and control: Step towards interplanetary cubeSats. In Proceedings of the IEEE Aerospace Conference 2019, Big Sky, MT, USA, 2–9 March 2019; pp. 1–12. [Google Scholar] [CrossRef]
- Kopacz, J.R.; Herschitz, R.; Roney, J. Small satellites an overview and assessment. Acta Astronaut. 2020, 170, 93–105. [Google Scholar] [CrossRef]
- Qian, X.; Yu, H.; Chen, S. A global-shutter centroiding measurement CMOS image sensor with star region SNR improvement for star trackers. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 1555–1562. [Google Scholar] [CrossRef]
- Bao, J.; Zhan, H.; Sun, T.; Fu, S.; Xing, F.; You, Z. A window-adaptive centroiding method based on energy iteration for spot target localization. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Piotrowski, L.; Batsch, T.; Czyrkowski, H.; Cwiok, M.; Dabrowski, R.; Kasprowicz, G.; Majcher, A.; Majczyna, A.; Małek, K.; Mankiewicz, L.; et al. PSF modelling for very wide-field CCD astronomy. Astron. Astrophys. 2013, 551, 1–15. [Google Scholar] [CrossRef]
- Bodewig, E. Measures of the magnitude of a matrix. In Matrix Calculus; Bodewig, E., Ed.; Elsevier: Amsterdam, The Netherlands, 1959; p. 43. ISBN 978-1-4832-3214-0. [Google Scholar]
- STAR 1000 Detailed Specification; APS-FF-DU-03-004; Fillfactory Image Sensors: Belgium. 2006. Available online: https://escies.org/download/webDocumentFile?id=62275 (accessed on 22 February 2023).
- Rabie, T. Adaptive hybrid mean and median filtering of high-ISO long-exposure sensor noise for digital photography. J. Electron. Imaging 2004, 13, 264–277. [Google Scholar] [CrossRef]
- Buchheim, R.K. CCD Double Star Observations at Altimira Observatory: Spring 2008. J. Double Star Obs. 2008, 3, 103–110. [Google Scholar]
- Buchheim, R.K. CCD Measurements of Visual Double Stars. In Proceedings of the 27th Annual Symposium on Telescope Science, Big Bear Lake, CA, USA, 20–22 May 2008; pp. 13–23. [Google Scholar]




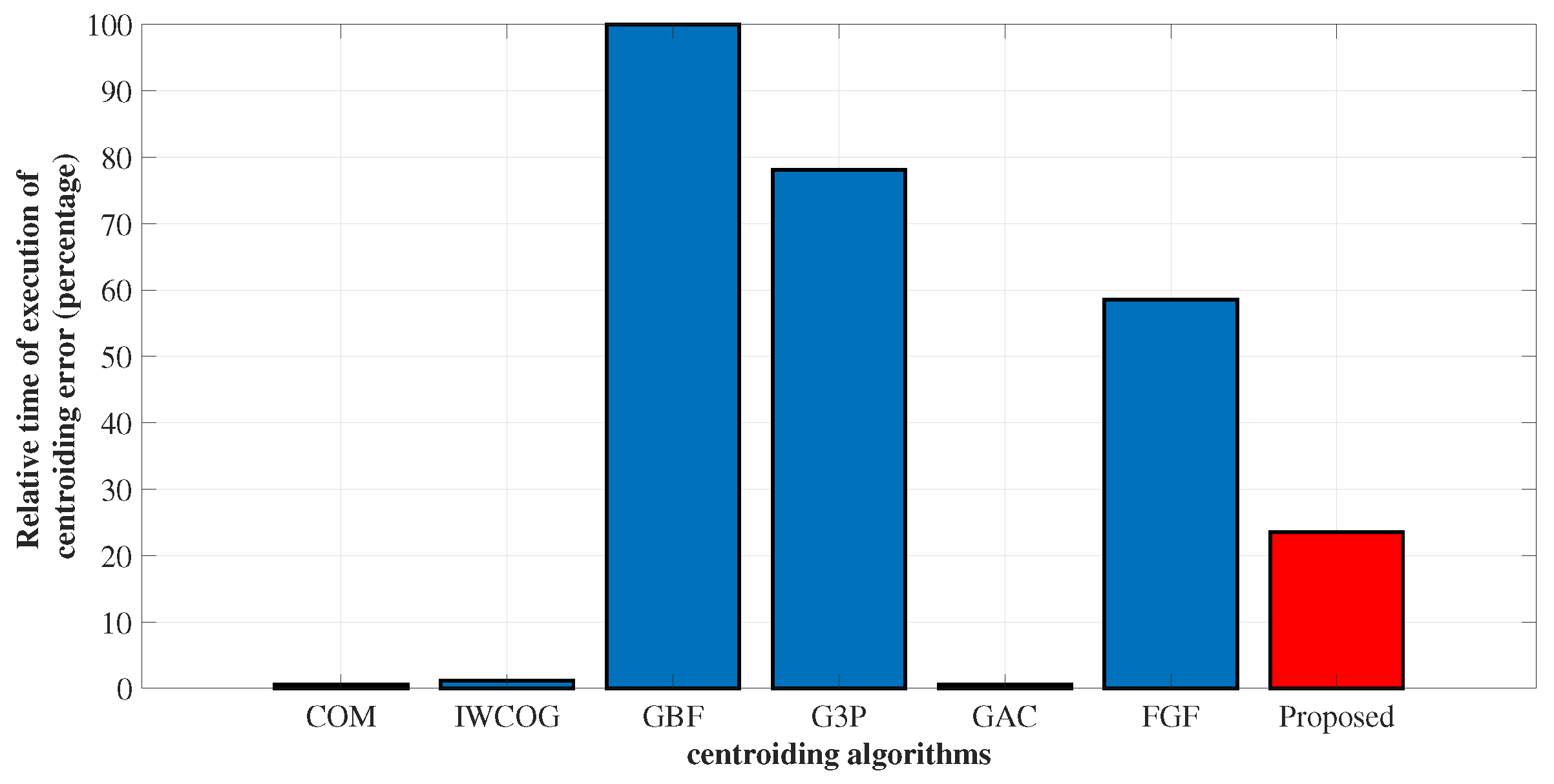
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karaparambil, V.C.; Manjarekar, N.S.; Singru, P.M. Sieve Search Centroiding Algorithm for Star Sensors. Sensors 2023, 23, 3222. https://doi.org/10.3390/s23063222
Karaparambil VC, Manjarekar NS, Singru PM. Sieve Search Centroiding Algorithm for Star Sensors. Sensors. 2023; 23(6):3222. https://doi.org/10.3390/s23063222
Chicago/Turabian StyleKaraparambil, Vivek Chandran, Narayan Suresh Manjarekar, and Pravin Madanrao Singru. 2023. "Sieve Search Centroiding Algorithm for Star Sensors" Sensors 23, no. 6: 3222. https://doi.org/10.3390/s23063222
APA StyleKaraparambil, V. C., Manjarekar, N. S., & Singru, P. M. (2023). Sieve Search Centroiding Algorithm for Star Sensors. Sensors, 23(6), 3222. https://doi.org/10.3390/s23063222





