Designing a Geodesic Faceted Acoustical Volumetric Array Using a Novel Analytical Method
Abstract
1. Introduction
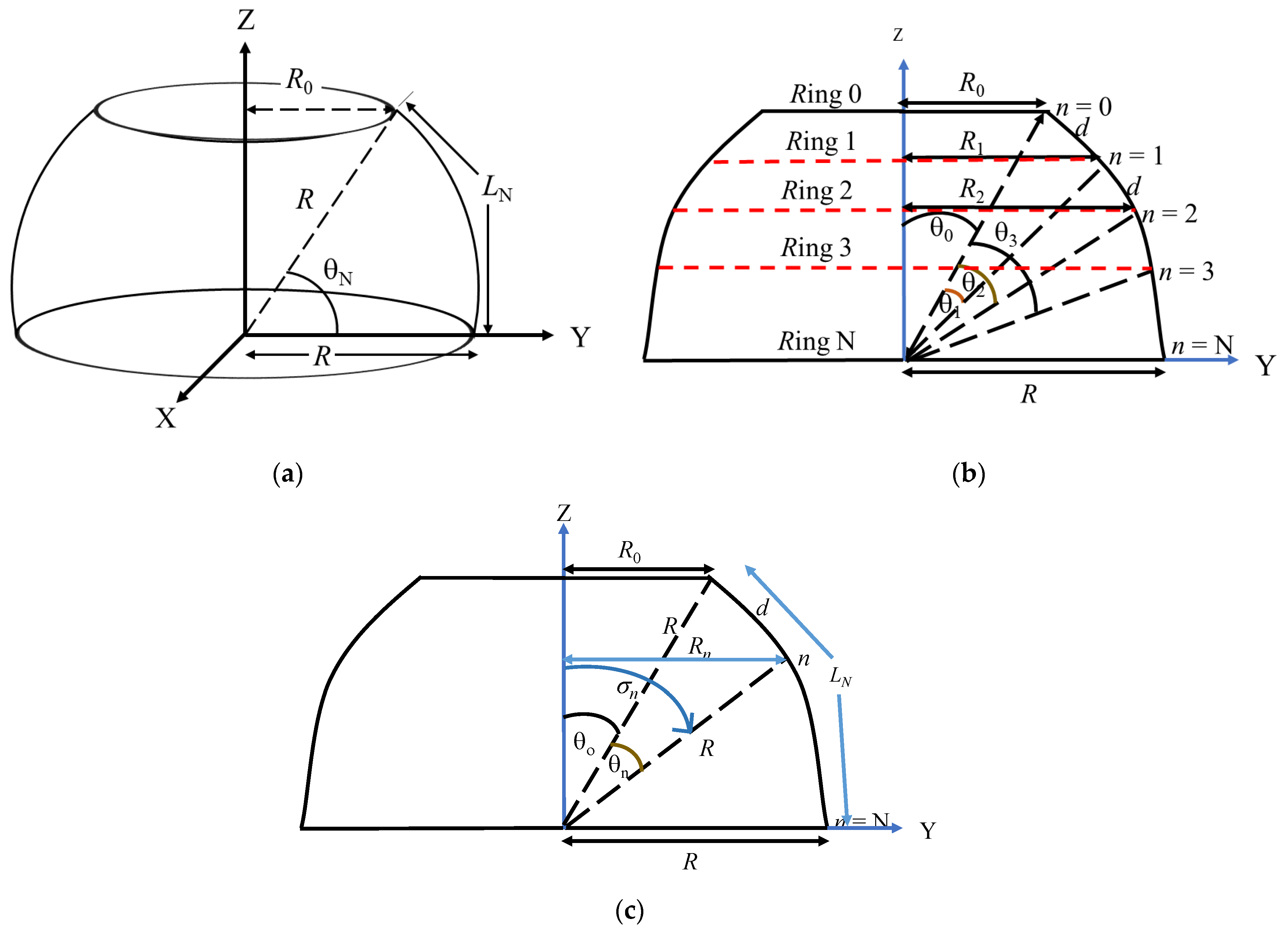
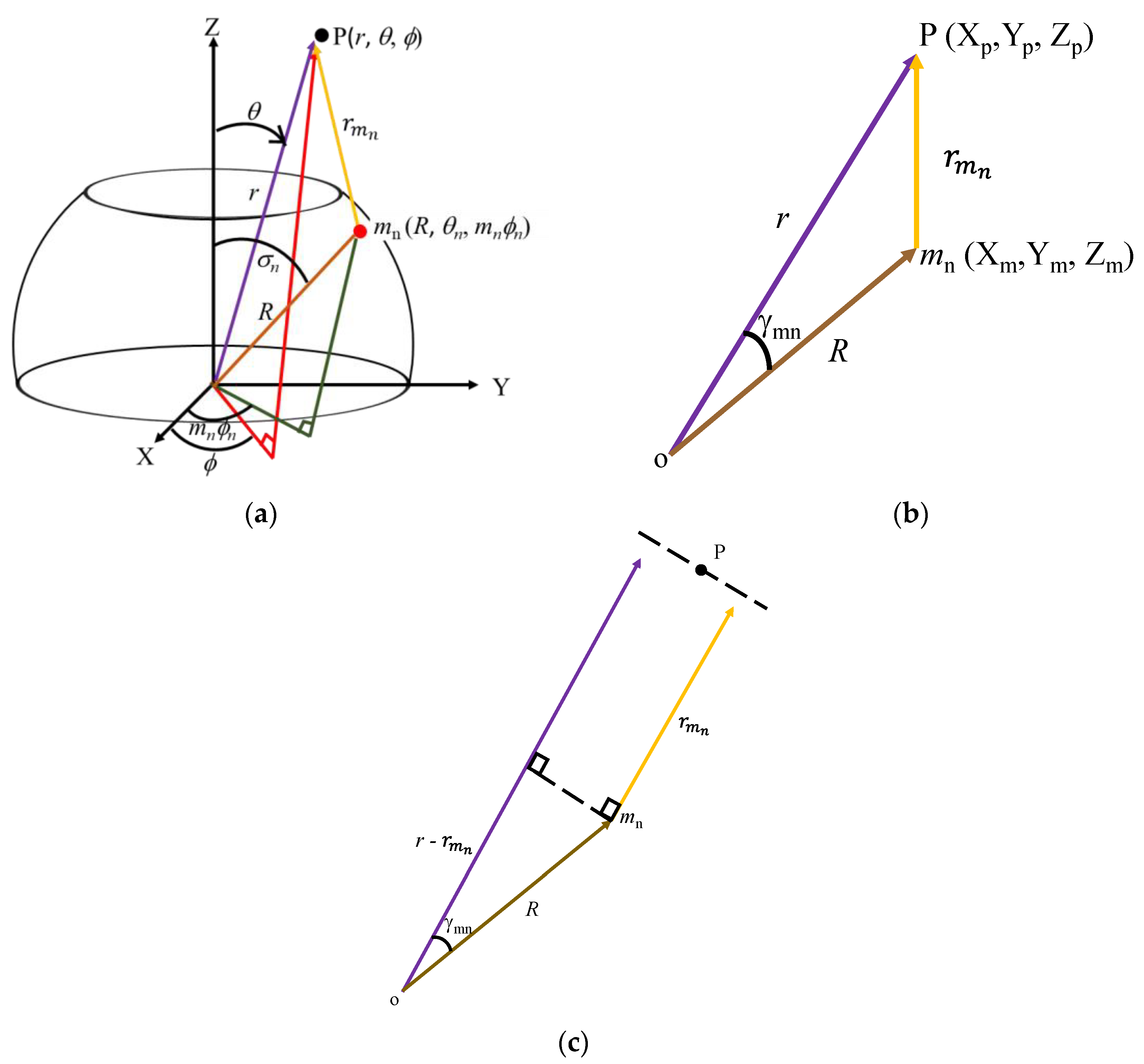
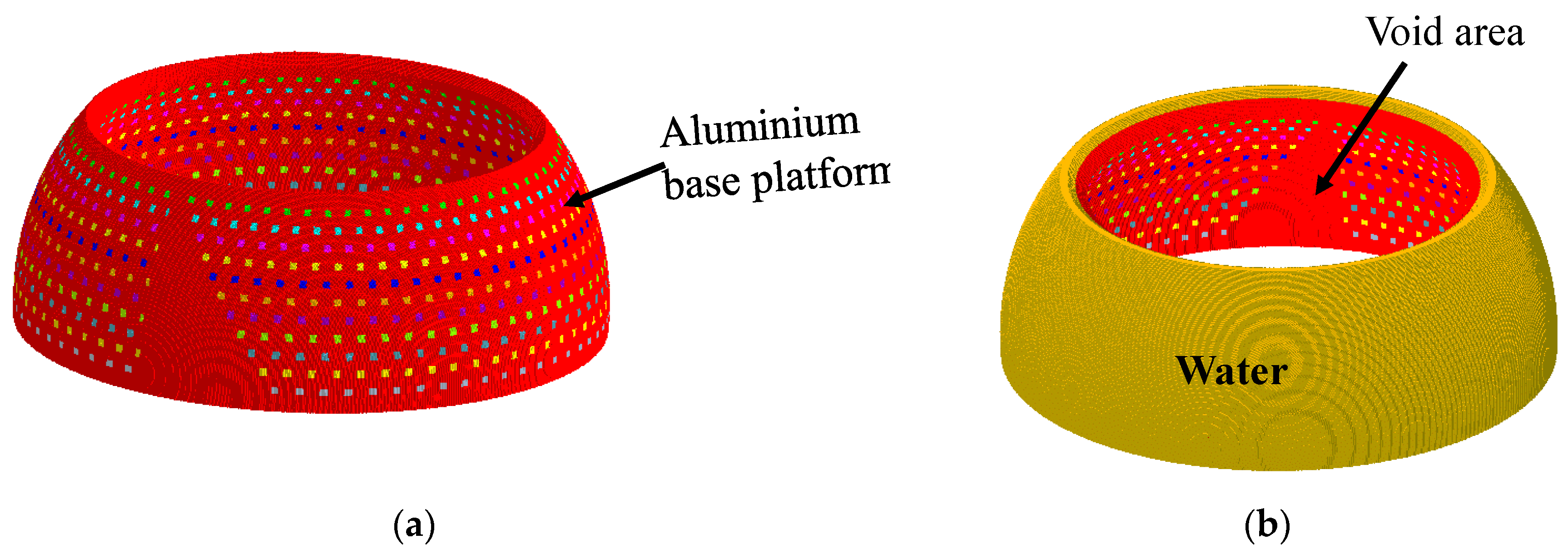
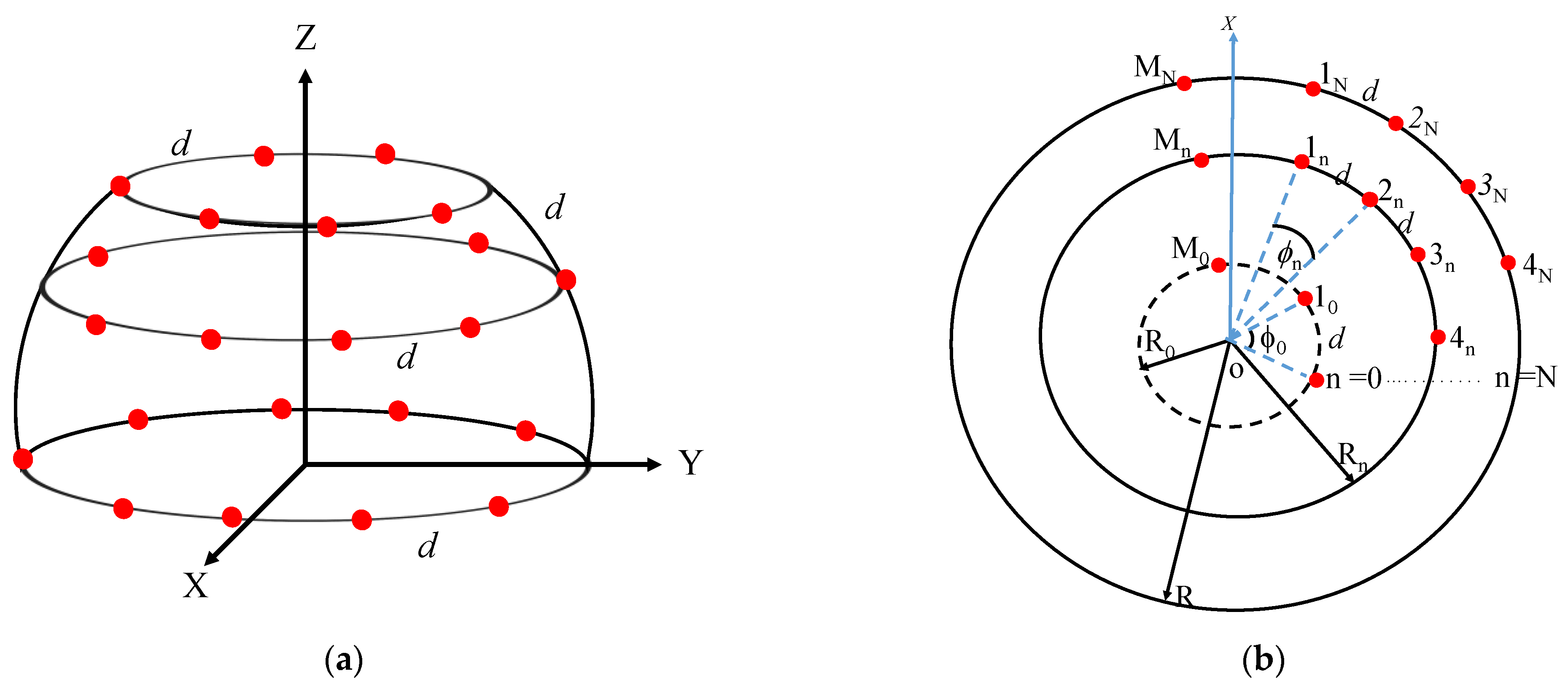
2. Geometry of the Hosting Platform
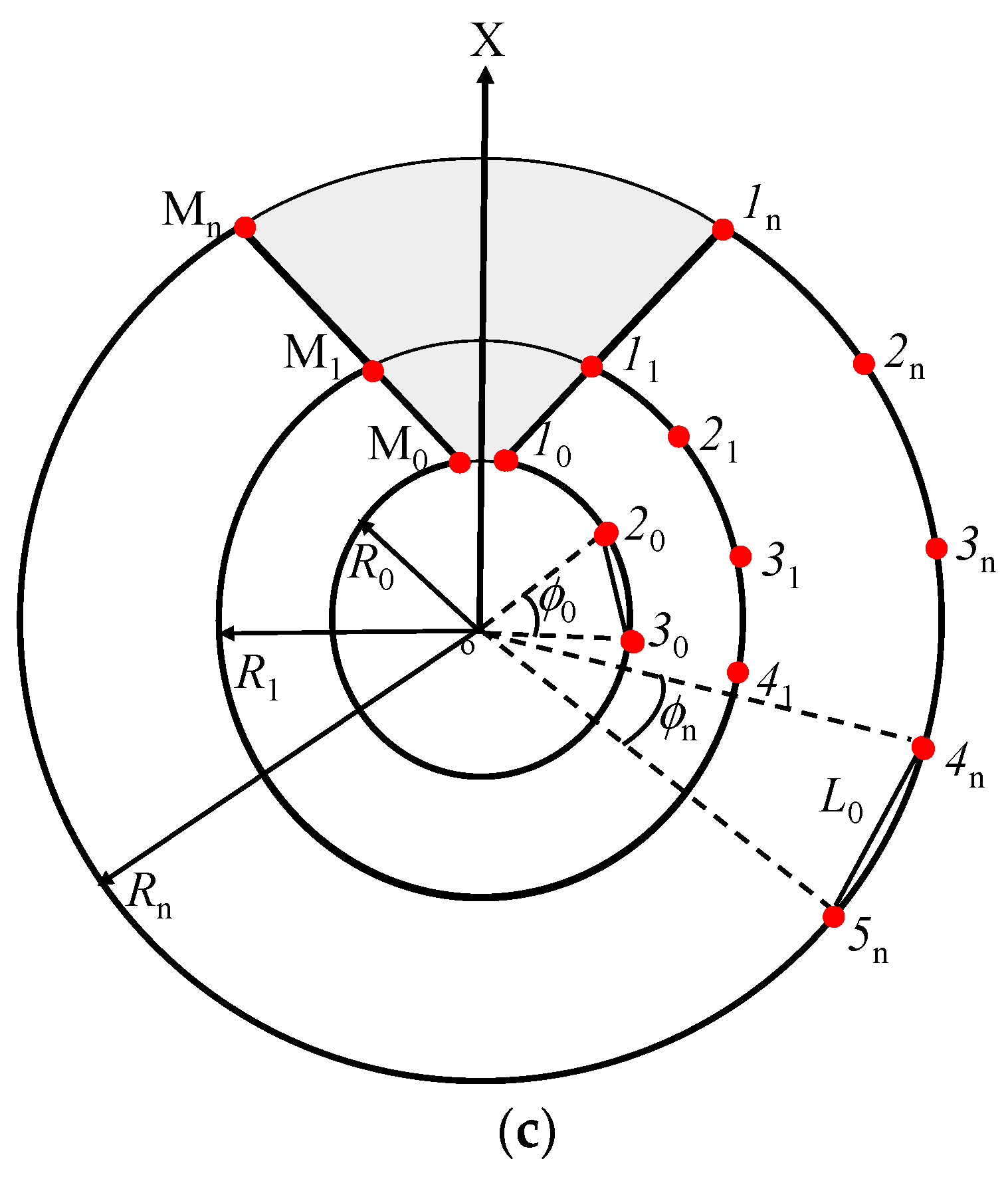
2.1. Geometrical Analysis of the Geodesic Faceted Array
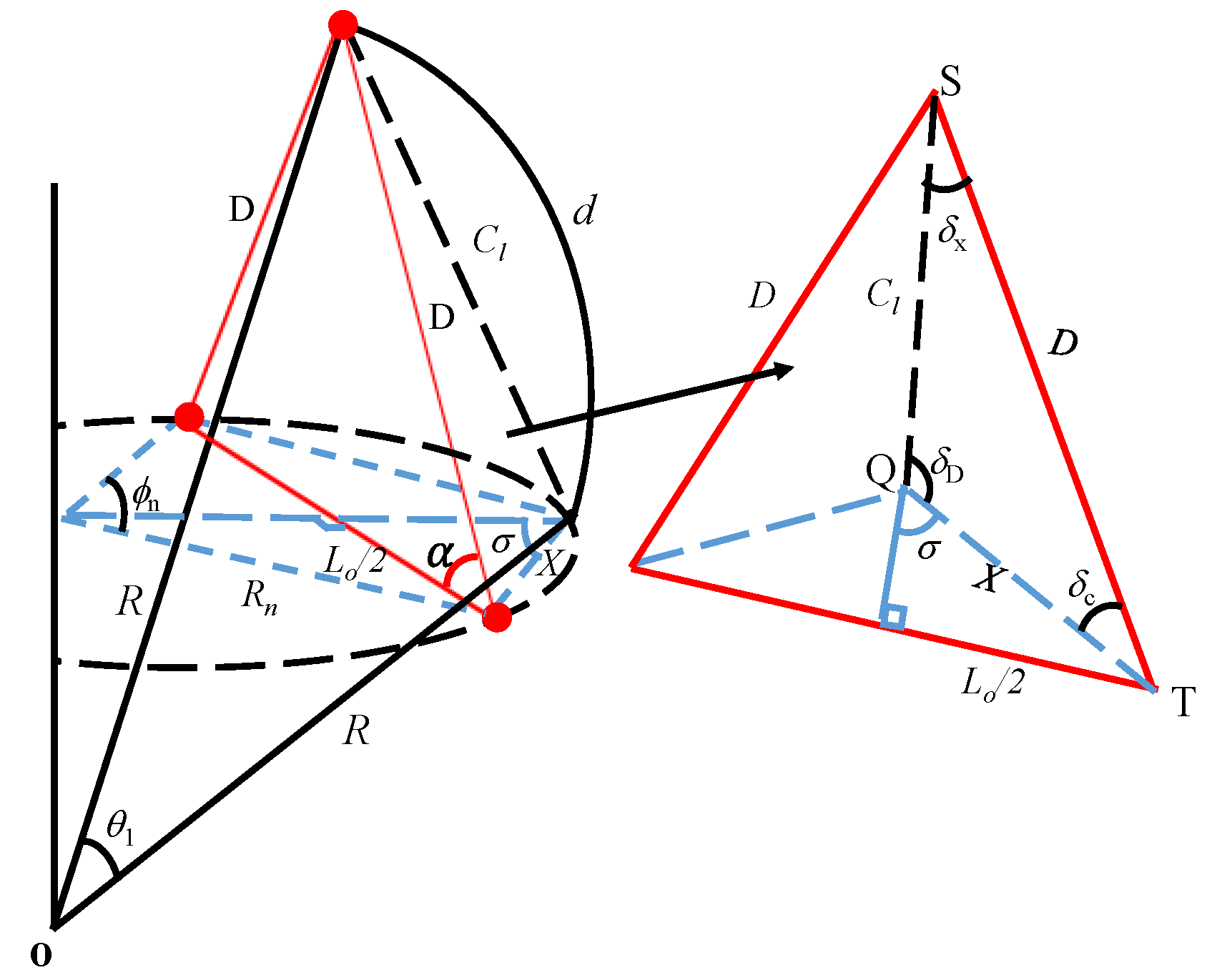
2.2. Characteristic Equations of the Geodesic Faceted Array
2.3. Derivation of the Directional Factor of the Array
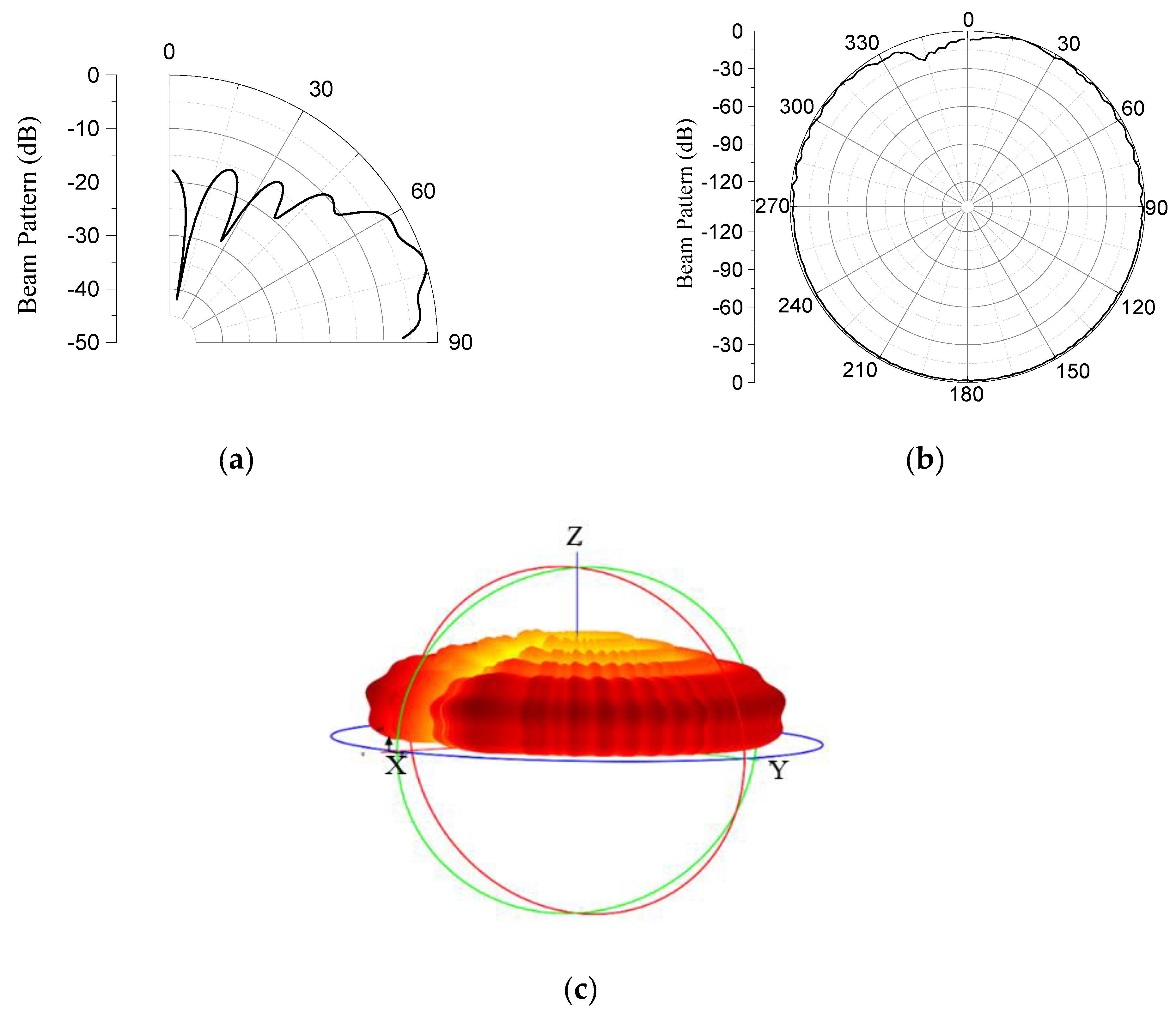
3. Design of the Geodesic Faceted Array
Subject to: 19° ≤ BW ≤ 21°
SLL ≤ −8 dB
Elevation ripple level (ERL) ≤ 3 dB
Azimuth ripple level (ARL) ≤ 3 dB
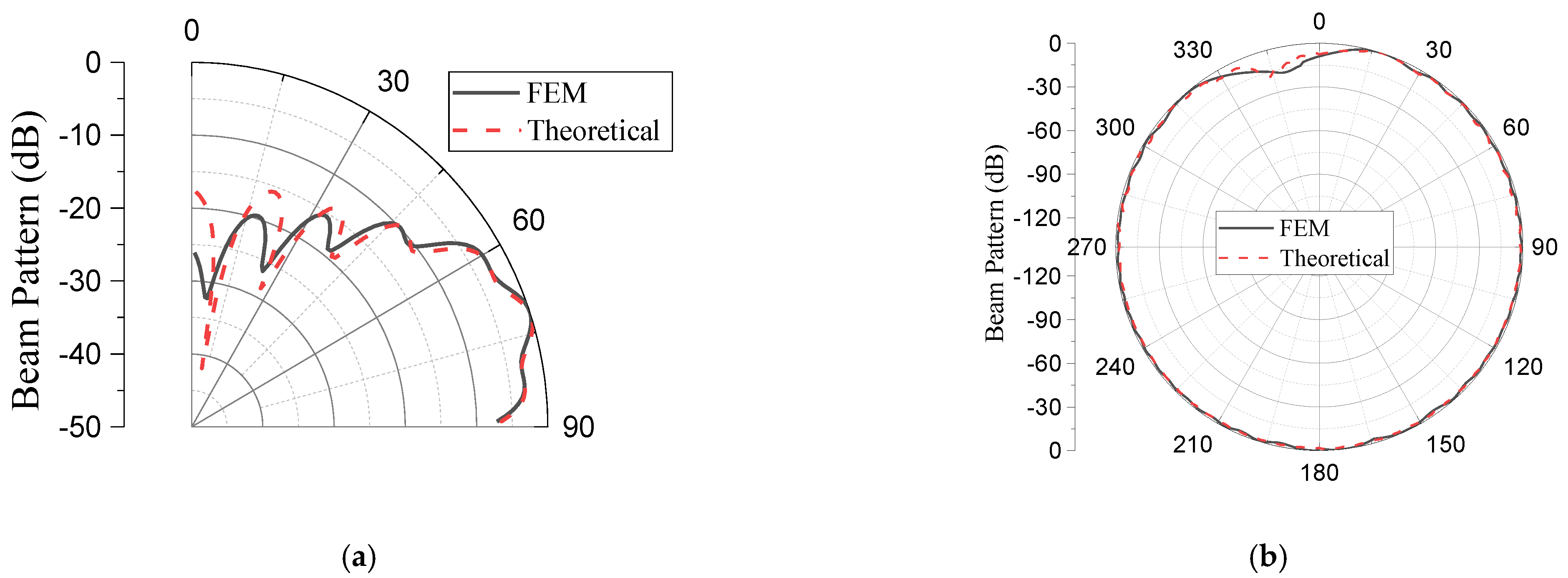
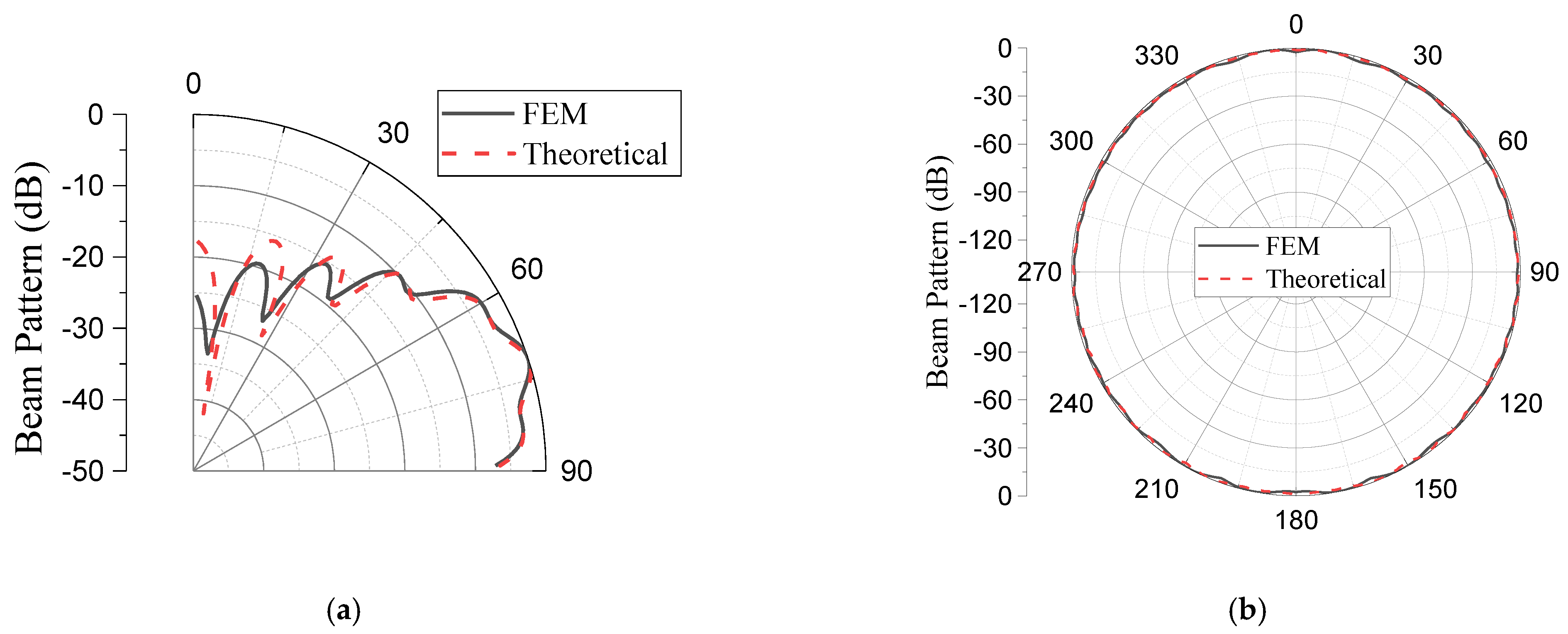
4. Validation of the GFA Design Using the Finite Element Method
5. Comparison with a Conventional Spherical Array
Subject to: 19° ≤ BW ≤ 21°
SLL ≤ −9.4 dB
Elevation Ripple level (ERL) ≤ 2.9 dB
Azimuth Ripple level (ARL) ≤ 2.9 dB
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Josefsson, L.; Persson, P. Conformal array antenna theory and design. In IEEE Press Series on Electromagnetic Wave Theory; El-Hawary, M.E., Ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2006; pp. 1,182,354–355,437. [Google Scholar]
- Munno, F. Conformal array geometry for hemispherical coverage. Electronics 2021, 10, 903. [Google Scholar] [CrossRef]
- Park, J.; Lim, H.J.; Trinh-Van, S.; Park, D.; Jung, Y.K.; Lim, D.; Hwang, K.C. Derivation of a universally valid array factor of a conformal arrays based on phase compensation and genetic learning particle swarm optimization. Appl. Sci. 2022, 12, 6501. [Google Scholar] [CrossRef]
- Baee, R.K.; Forooraghi, K.; Chamaani, S. Conformal array pattern synthesis using a hybrid WARP/2LB-MOPSO algorithm. Int. J. Antennas Propag. 2012, 2012, 202906. [Google Scholar]
- Tomasic, B.; Turtle, J.; Liu, S. Spherical arrays-design considerations. In Proceedings of the 2005 18th International Conference on Applied Electromagnetics and Communications, Dubrovnik, Croatia, 12–14 October 2005. [Google Scholar]
- Wong, K.T.; Morris, Z.N.; Nnonyelu, C.J. Rules-of-thumb to design a uniform spherical array for direction finding—Its Cramér–Rao bounds’ nonlinear dependence on the number of sensors. J. Acoust. Soc. Am. 2019, 145, 714–723. [Google Scholar] [CrossRef]
- Yang, Y.; Chu, Z.; Shen, L.; Xu, Z. Functional delay and sum beamforming for three-dimensional acoustic source identification with solid spherical arrays. J. Sound Vib. 2016, 373, 340–359. [Google Scholar] [CrossRef]
- Huang, D. Theory and numerical simulation for a design of broadband constant beam pattern transducer. J. Acoust. Soc. Am. 2017, 142, 421–427. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Qin, L.; Zhong, C.; Hao, S. Spherical-omnidirectional piezoelectric composite transducer for high- frequency underwater acoustics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2021, 68, 1791–1796. [Google Scholar] [CrossRef]
- Nagaoka, R.; Tabata, T.; Takagi, R.; Yoshizawa, S.; Umemura, S.I.; Saijo, Y. Development of real-time 3-D photoacoustic imaging system employing spherically curved array transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2017, 64, 1223–1233. [Google Scholar] [CrossRef]
- Yang, B.; Shi, S.; Yang, D. Acoustic source localization using the open spherical microphone array in the low-frequency range. MATEC Web Conf. 2019, 283, 04001. [Google Scholar] [CrossRef]
- Radivojević, V.M.; Rupčić, S.; Grgić, K. Radiation pattern optimisation of an antenna array on the spherical surface by using a varying number of optimisation parameters. IET Microw. Antennas Propag. 2017, 11, 1846–1853. [Google Scholar] [CrossRef]
- Hayashi, E.; Kanno, N.; Shintate, R.; Ishii, T.; Nagaoka, R.; Saijo, Y. 3D ultrasound imaging by synthetic transmit aperture beamforming using a spherically curved array transducer. Jpn. J. Appl. Phys. 2022, 61, SG1034. [Google Scholar] [CrossRef]
- Sadeghpour, S.; Meyers, S.; Kruth, J.P.; Vleugels, J.; Kraft, M.; Puers, R. Resonating shell: A spherical-omnidirectional ultrasound transducer for underwater sensor networks. Sensors 2019, 19, 757. [Google Scholar] [CrossRef] [PubMed]
- Saqib, N.U.; Khan, I.A. hybrid antenna array design for 3-D direction of arrival estimation. PLoS ONE 2015, 10, e0118914. [Google Scholar] [CrossRef] [PubMed]
- Huong, N.T. Beamforming phased array antenna toward indoor positioning applications. In Advance Radio Frequency Antennas for Modern Communication and Medical Systems; Sabban, A., Ed.; IntechOpen Limited: London, UK, 2020; p. 42. [Google Scholar]
- Tomasic, B.; Turtle, J.; Liu, S.; Schmier, R.; Bharj, S.; Oleski, P. The geodesic dome phased array antenna for satellite control and communication-subarray design, development and demonstration. In Proceedings of the IEEE International Symposium on Phased Array Systems and Technology, Boston, MA, USA, 14–17 October 2003; pp. 411–416. [Google Scholar]
- Goossens, R.; Bogaert, I.; Rogier, H. Phase-mode processing for spherical antenna arrays with a finite number of antenna elements and including mutual coupling. IEEE Trans. Antennas Propag. 2009, 57, 3783–3790. [Google Scholar] [CrossRef]
- Daher, E.B. Analysis and Design of Nonuniform Arrays for Direction Finding. Ph.D. Thesis, Villanova University, Villanova, PA, USA, 2016. [Google Scholar]
- Du, C.; Leclere, Q.; Li, B. Design and Evaluation of Open Spherical Microphone Arrays. In Proceedings of the 24th International Congress on Sound Vibration, London, UK, 23–37 July 2017. [Google Scholar]
- Dianfei, P.; Yanshan, B.; Naiping, C. Hemispherical Coverage Array Antenna and Performance Analysis. Wirel. Pers. Commun. 2015, 80, 1193–1201. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, P.; Zhuang, Z.; Wei, J.; Liu, X.; Wang, H.; Li, L. Design of a Spherical Conformal Phased Array Antenna Based on the Truncated Icosahedron. In Proceedings of the 2020 IEEE Radar Conference, Florence, Italy, 21–25 September 2020. [Google Scholar]
- Grech, C.; Azzopardi, M.A.; Buttigieg, V. Circular Lattice Design for UHF Geodesic Dome Phased Array Antenna with Reduced Footprint. In Proceedings of the 2020 International Symposium on Antennas and Propagation, Osaka, Japan, 25–28 January 2021. [Google Scholar]
- Qiu, Z.; Habeshaw, R.; Fortine, J.; Huang, Z.; Démoré, C.; Cochran, S. New piezocrystal material in the development of a 96-element array transducer for MR-guided focused ultrasound surgery. AIP Conf. Proc. 2012, 1503, 282–287. [Google Scholar]
- Sim, M.J.; Hong, C.; Jeong, W.B. Hybrid equivalent circuit/finite element/boundary element modeling for effective analysis of an acoustic transducer array with flexible surrounding structures. Appl. Sci. 2021, 11, 2702. [Google Scholar] [CrossRef]
- Pelham, T.G.; Hilton, G.; Mellios, E.; Lewis, R. Conformal antenna array design using aperture synthesis and on-platform modeling. IEEE Access 2021, 9, 60880–60890. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Plummer, J.C. Multistart algorithms for seeking feasibility. Comput. Oper. Res. 2008, 35, 1379–1393. [Google Scholar] [CrossRef]
- De Witte, E. Design and Development of Spherical Array Antennas. Ph.D. Thesis, University College, London, UK, 2007. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; John Wiley & Sons Inc: New York, NY, USA, 2000; p. 195. [Google Scholar]
- Kim, H.; Roh, Y. Analysis of the radiation pattern of conformal array transducers. J. Acoust. Soc. Korea 2010, 29, 431–438. [Google Scholar]
- Koukouvinos, C. Orthogonal 2k and 3k factorial designs constructed using sequences with zero autocorrelation. Stat. Probab. Lett. 1996, 28, 59–63. [Google Scholar] [CrossRef]
- Yusuf, T.A.; Pyo, S.; Roh, Y. A novel versatile approach for underwater conformal volumetric array design. Sensors 2021, 21, 3591. [Google Scholar] [CrossRef]
- Gerlotto, F.; Georgakarakos, S.; Eriksen, P.K. The application of multibeam sonar technology for quantitative estimates of fish density in shallow water acoustic surveys. Aquat. Living Resour. 2000, 13, 385–393. [Google Scholar] [CrossRef]
- Baron, V.; Finez, A.; Bouley, S.; Fayet, F.; Mars, J.I.; Nicolas, B. Hydrophone array optimization, conception, and validation for localization of acoustic sources in deep-sea mining. IEEE J. Ocean. Eng. 2021, 46, 555–563. [Google Scholar] [CrossRef]
- Nishimura, C.E. Fundamentals of Acoustic Backscatter Imagery; Naval Research Laboratory: Washington, DC, USA, 1997. [Google Scholar]

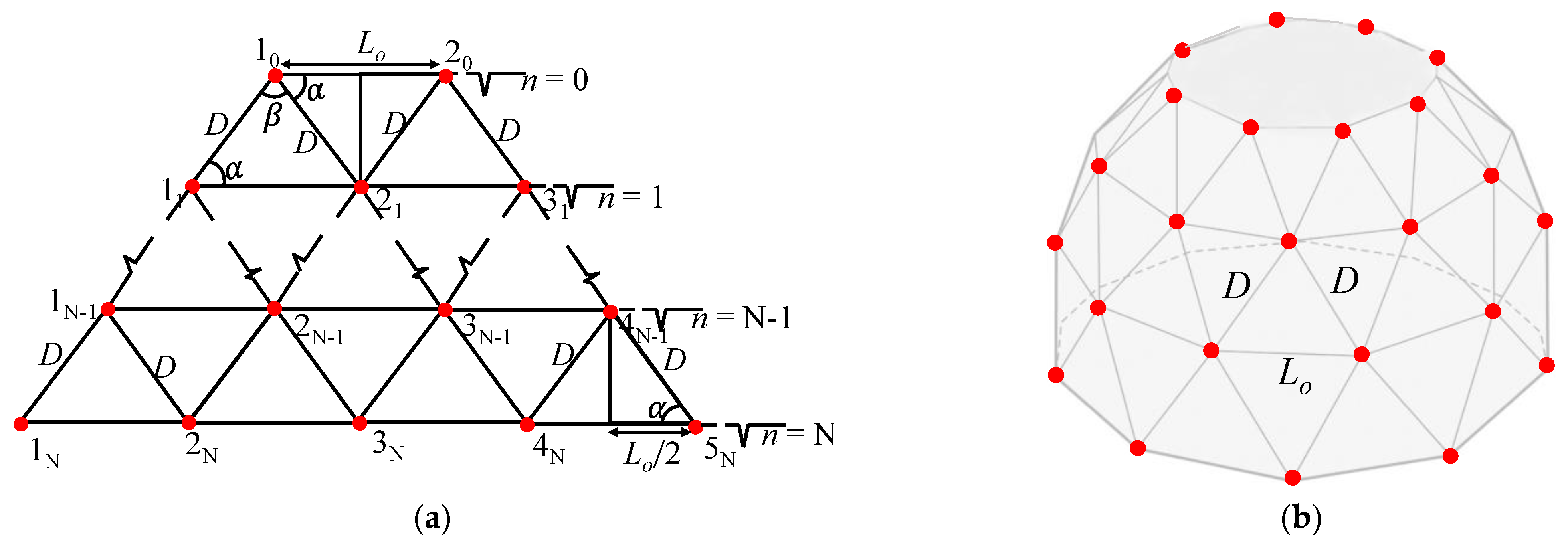




| Parameter | Specification | |
|---|---|---|
| Size of the platform | Radius, R | 800 mm |
| Arc angle, θN | 35° | |
| Performance requirements | Elevation half-power (−3 dB) Beamwidth (BW) | 20° [33] |
| Elevation side lobe level (SLL) | ≤−8 dB [34] | |
| Ripple level | ≤3 dB | |
| Center frequency | 16 kHz [35] |
| Geometrical Parameter | Lower Bound | Basic | Upper Bound |
|---|---|---|---|
| N | 7 | 9 | 11 |
| a (mm) | 9 | 12 | 15 |
| α (o) | 59 | 60 | 61 |
| co | 0.58 | 0.60 | 0.62 |
| Geometrical parameter | N | 10 |
| a (mm) | 10.0 | |
| α (o) | 61.0 | |
| co | 0.6 | |
| Performance output | BW (o) | 20.6 |
| SLL (dB) | −9.4 | |
| ERL (dB) | 2.9 | |
| ARL (dB) | 2.9 |
| Methods | Performance Outputs | |||
|---|---|---|---|---|
| BW (°) | SLL (dB) | ERL (dB) | ARL (dB) | |
| Theoretical | 20.6 | −9.4 | 2.9 | 2.9 |
| FEM | 20.5 | −9.9 | 2.9 | 3.0 |
| Design Variable | Lower Bound | Basic | Upper Bound |
|---|---|---|---|
| N | 7 | 9 | 11 |
| a (mm) | 9 | 12 | 15 |
| Design variable | N | 10 |
| a (mm) | 10.0 | |
| Performance output | BW (°) | 20.6 |
| SLL (dB) | −9.4 | |
| ERL (dB) | 2.9 | |
| ARL (dB) | 2.8 |
| Methods | Performance Outputs | |||
|---|---|---|---|---|
| BW (°) | SLL (dB) | ERL (dB) | ARL (dB) | |
| Theoretical | 20.6 | −9.4 | 2.9 | 2.8 |
| FEM | 20.6 | −9.9 | 2.9 | 2.9 |
| Model | Structural Parameters | Performance Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R (mm) | θN (o) | N | a (mm) | BW (o) | SLL (dB) | ERL (dB) | ARL (dB) | NE | % Element Reduction | |
| Spherical | 800 | 35 | 10 | 10 | 20.6 | −9.4 | 2.9 | 2.8 | 1054 | -- |
| Geodesic | 800 | 35 | 10 | 10 | 20.6 | −9.4 | 2.9 | 2.9 | 880 | 16.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yusuf, T.A.; Roh, Y. Designing a Geodesic Faceted Acoustical Volumetric Array Using a Novel Analytical Method. Sensors 2023, 23, 3173. https://doi.org/10.3390/s23063173
Yusuf TA, Roh Y. Designing a Geodesic Faceted Acoustical Volumetric Array Using a Novel Analytical Method. Sensors. 2023; 23(6):3173. https://doi.org/10.3390/s23063173
Chicago/Turabian StyleYusuf, Taofeek Ayotunde, and Yongrae Roh. 2023. "Designing a Geodesic Faceted Acoustical Volumetric Array Using a Novel Analytical Method" Sensors 23, no. 6: 3173. https://doi.org/10.3390/s23063173
APA StyleYusuf, T. A., & Roh, Y. (2023). Designing a Geodesic Faceted Acoustical Volumetric Array Using a Novel Analytical Method. Sensors, 23(6), 3173. https://doi.org/10.3390/s23063173






