Trunk Velocity Changes in Response to Physical Perturbations Are Potential Indicators of Gait Stability
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
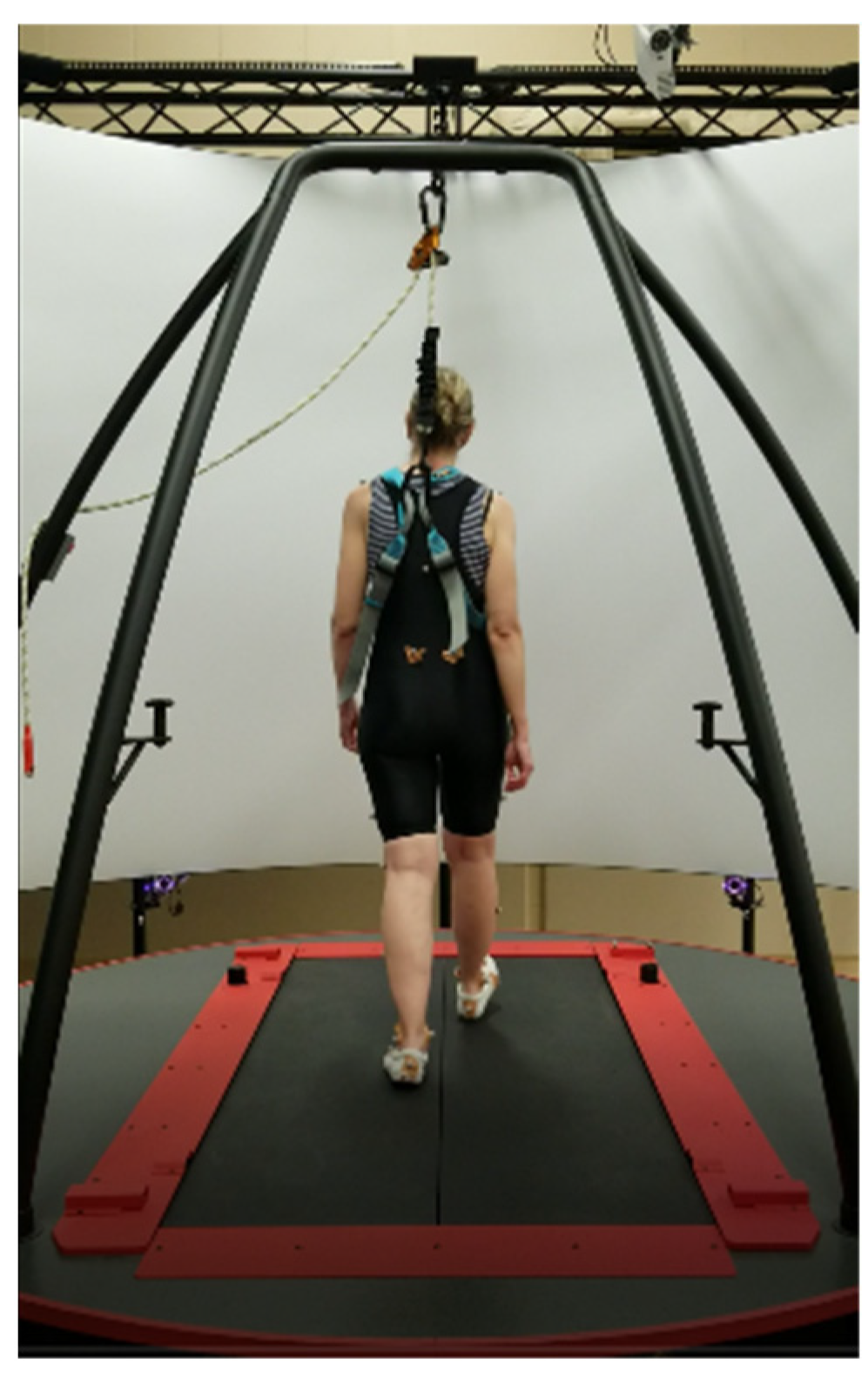
2.2. Setup
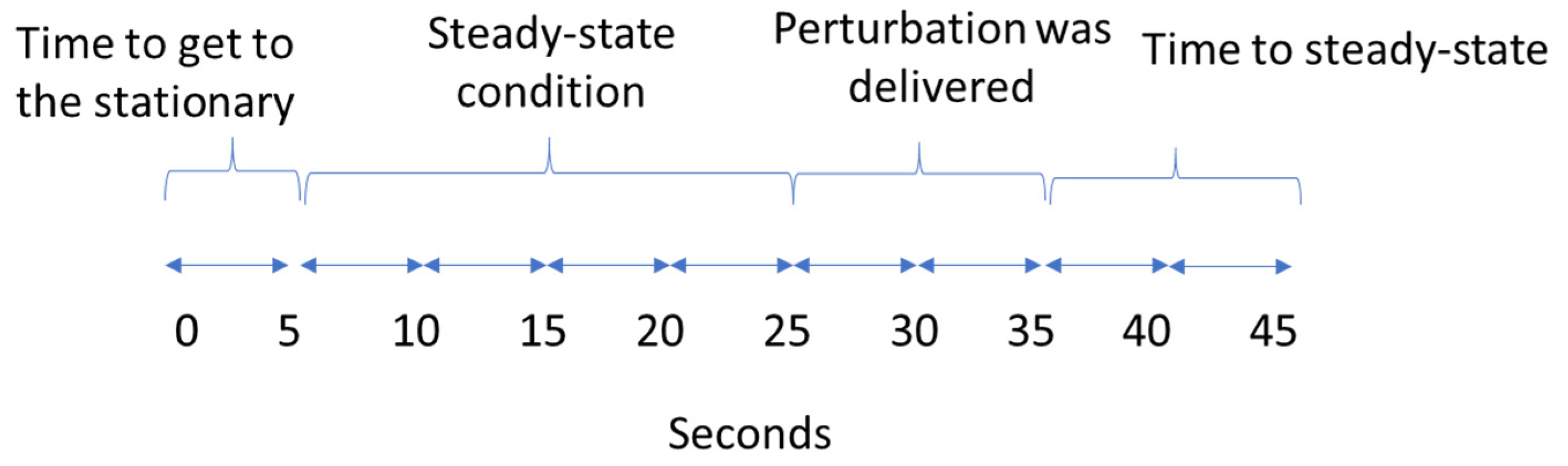
2.3. Procedures
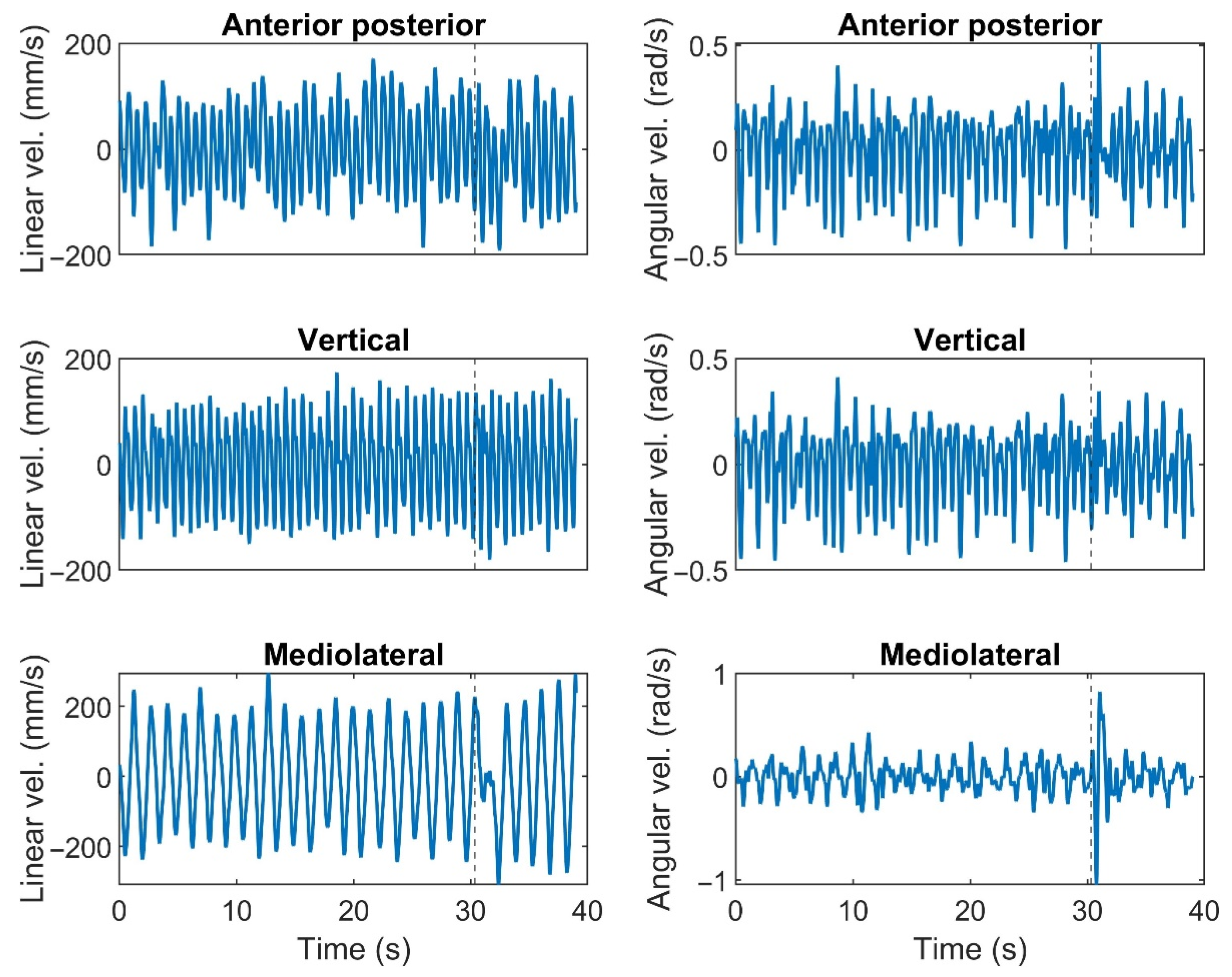
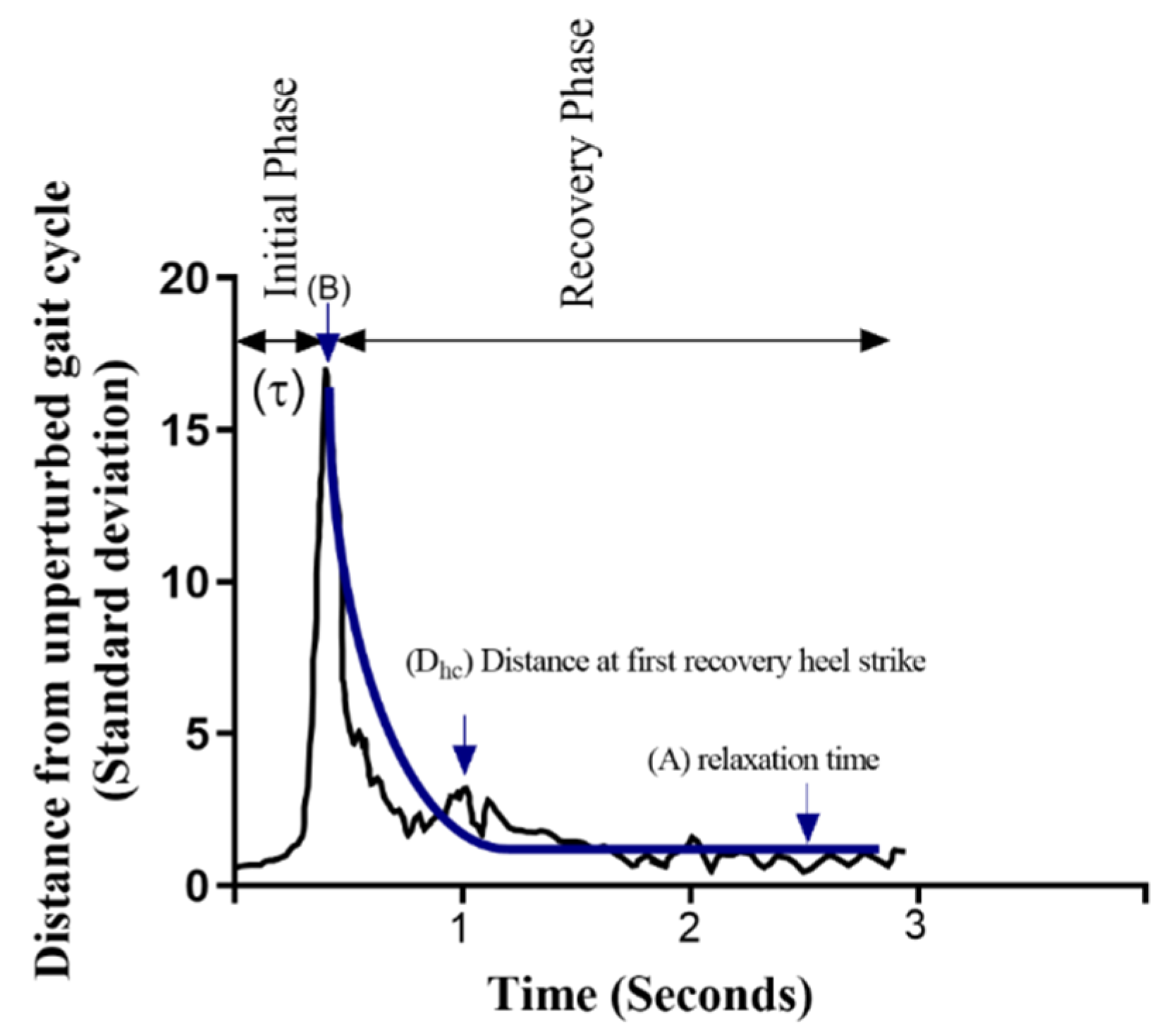
2.4. Data Processing and Analysis
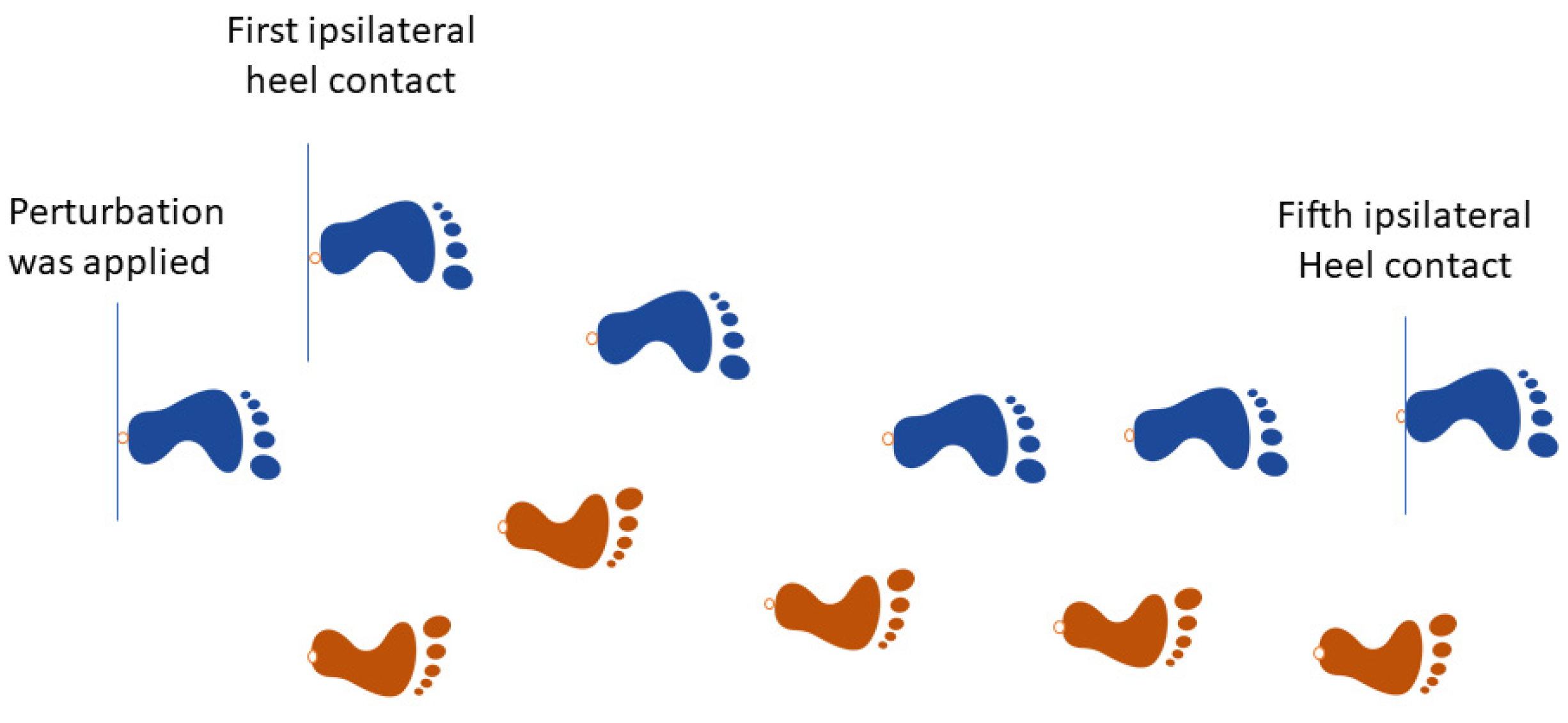
2.4.1. Trunk’s Response
2.4.2. Stability Metric
2.5. Statistics
3. Results
3.1. Association of Trunk Responses with MOS Measures (Effect of Speed)
3.2. Association of Trunk Responses with MOS Measures (Effects of Magnitude)
4. Discussion
4.1. Effects of Speed
4.2. Effects of Magnitude
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berry, S.D.; Miller, R.R. Falls: Epidemiology, pathophysiology, and relationship to fracture. Curr. Osteoporos. Rep. 2008, 6, 149–154. [Google Scholar] [CrossRef]
- Madehkhaksar, F.; Klenk, J.; Sczuka, K.; Gordt, K.; Melzer, I.; Schwenk, M. The effects of unexpected mechanical perturbations during treadmill walking on spatiotemporal gait parameters, and the dynamic stability measures by which to quantify postural response. PLoS ONE 2018, 13, e0195902. [Google Scholar] [CrossRef]
- O’Connor, S.M.; Kuo, A.D. Direction-dependent control of balance during walking and standing. J. Neurophysiol. 2009, 102, 1411–1419. [Google Scholar] [CrossRef]
- McIntosh, E.I.; Zettel, J.L.; Vallis, L.A. Stepping responses in young and older adults following a perturbation to the support surface during gait. J. Mot. Behav. 2017, 49, 288–298. [Google Scholar] [CrossRef]
- Brough, L.G.; Klute, G.K.; Neptune, R.R. Biomechanical response to mediolateral foot-placement perturbations during walking. J. Biomech. 2021, 116, 110213. [Google Scholar] [CrossRef]
- Bruijn, S.M.; Meijer, O.G.; Beek, P.J.; van Dieen, J.H. Assessing the stability of human locomotion: A review of current measures. J. R. Soc. Interface 2013, 10, 20120999. [Google Scholar] [PubMed]
- Bruijn, S.M.; Meijer, O.G.; Beek, P.J.; Van Dieen, J.H. The effects of arm swing on human gait stability. J. Exp. Biol. 2010, 213, 3945–3952. [Google Scholar]
- Gerards, M.H.; Meijer, K.; Karamanidis, K.; Grevendonk, L.; Hoeks, J.; Lenssen, A.F.; McCrum, C. Adaptability to balance perturbations during walking as a potential marker of falls history in older adults. Front. Sport. Act. Living 2021, 3. [Google Scholar]
- Hendrik, R.; Tyler, F.; John, J.J. Strategies for the control of balance during locomotion. Kinesiol. Rev. 2018, 7, 18–25. [Google Scholar] [CrossRef]
- Forbes, P.A.; Vlutters, M.; Dakin, C.J.; van der Kooij, H.; Blouin, J.-S.; Schouten, A.C. Rapid limb-specific modulation of vestibular contributions to ankle muscle activity during locomotion. J. Physiol. 2017, 595, 2175–2195. [Google Scholar] [CrossRef] [PubMed]
- Shirota, C.; Simon, A.M.; Rouse, E.J.; Kuiken, T.A. The effect of perturbation onset timing and length on tripping recovery strategies. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 7833–7836. [Google Scholar] [CrossRef]
- Fallahtafti, F.; Curtze, C.; Samson, K.; Yentes, J.M. Chronic obstructive pulmonary disease patients increase medio-lateral stability and limit changes in antero-posterior stability to curb energy expenditure. Gait Posture 2020, 75, 142–148. [Google Scholar] [CrossRef]
- Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. Effects of walking speed on gait biomechanics in healthy participants: A systematic review and meta-analysis. Syst. Rev. 2019, 8, 153. [Google Scholar] [CrossRef]
- Donker, S.F.; Beek, P.J. Interlimb coordination in prosthetic walking: Effects of asymmetry and walking velocity. Acta Psychol. 2002, 110, 265–288. [Google Scholar] [CrossRef] [PubMed]
- Suptitz, F.; Karamanidis, K.; Moreno Catala, M.; Bruggemann, G.P. Symmetry and reproducibility of the components of dynamic stability in young adults at different walking velocities on the treadmill. J. Electromyogr. Kinesiol. 2012, 22, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Dingwell, J.B.; Marin, L.C. Kinematic variability and local dynamic stability of upper body motions when walking at different speeds. J. Biomech. 2006, 39, 444–452. [Google Scholar] [CrossRef] [PubMed]
- MacKinnon, C.D.; Winter, D.A. Control of whole body balance in the frontal plane during human walking. J. Biomech. 1993, 26, 633–644. [Google Scholar] [CrossRef]
- Crenshaw, J.R.; Rosenblatt, N.J.; Hurt, C.P.; Grabiner, M.D. The discriminant capabilities of stability measures, trunk kinematics, and step kinematics in classifying successful and failed compensatory stepping responses by young adults. J. Biomech. 2012, 45, 129–133. [Google Scholar] [CrossRef]
- Hof, A.L. The ‘extrapolated center of mass’ concept suggests a simple control of balance in walking. Hum. Mov. Sci. 2008, 27, 112–125. [Google Scholar] [CrossRef]
- Hof, A.L.; Gazendam, M.G.; Sinke, W.E. The condition for dynamic stability. J. Biomech. 2005, 38, 1–8. [Google Scholar] [CrossRef]
- van den Bogert, A.J.; Geijtenbeek, T.; Even-Zohar, O.; Steenbrink, F.; Hardin, E.C. A real-time system for biomechanical analysis of human movement and muscle function. Med. Biol. Eng. Comput. 2013, 51, 1069–1077. [Google Scholar] [CrossRef]
- Post, A.A.; Peper, C.E.; Daffertshofer, A.; Beek, P.J. Relative phase dynamics in perturbed interlimb coordination: Stability and stochasticity. Biol. Cybern. 2000, 83, 443–459. [Google Scholar] [CrossRef]
- Roeles, S.; Rowe, P.J.; Bruijn, S.M.; Childs, C.R.; Tarfali, G.D.; Steenbrink, F.; Pijnappels, M. Gait stability in response to platform, belt, and sensory perturbations in young and older adults. Med. Biol. Eng. Comput. 2018, 56, 2325–2335. [Google Scholar] [CrossRef] [PubMed]
- Vlutters, M.; Van Asseldonk, E.H.F.; van der Kooij, H. Foot placement modulation diminishes for perturbations near foot contact. Front. Bioeng. Biotechnol. 2018, 6, 48. [Google Scholar] [CrossRef]
- Kaya, B.K.; Krebs, D.E.; Riley, P.O. Dynamic stability in elders: Momentum control in locomotor ADL. J. Gerontol. Ser. A 1998, 53, M126–M134. [Google Scholar] [CrossRef]
- Hof, A.L.; Vermerris, S.M.; Gjaltema, W.A. Balance responses to lateral perturbations in human treadmill walking. J. Exp. Biol. 2010, 213, 2655–2664. [Google Scholar] [CrossRef] [PubMed]
- Hof, A.L.; Duysens, J. Responses of human hip abductor muscles to lateral balance perturbations during walking. Exp. Brain Res. 2013, 230, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, J.; Thorstensson, A.; Halbertsma, J. Changes in leg movements and muscle activity with speed of locomotion and mode of progression in humans. Acta Physiol. Scand. 1985, 123, 457–475. [Google Scholar] [CrossRef]
- Kavanagh, J.J. Lower trunk motion and speed-dependence during walking. J. Neuroeng. Rehabil. 2009, 6, 9. [Google Scholar] [CrossRef] [PubMed]
- Vlutters, M.; van Asseldonk, E.H.F.; van der Kooij, H. Lower extremity joint-level responses to pelvis perturbation during human walking. Sci. Rep. 2018, 8, 14621. [Google Scholar] [CrossRef]
- Vlutters, M.; van Asseldonk, E.H.F.; van der Kooij, H. Reduced center of pressure modulation elicits foot placement adjustments, but no additional trunk motion during anteroposterior-perturbed walking. J. Biomech. 2018, 68, 93–98. [Google Scholar] [CrossRef] [PubMed]


| Small (2.5 cm) | Medium (5 cm) | Large (7.5 cm) | |
|---|---|---|---|
| Slow Speed (−40% preferred) | Condition #2 | ||
| Preferred Speed | Condition #1 | Condition #3 | Condition #5 |
| Fast Speed (+40% preferred) | Condition #4 |
| Age (Years) | Body Mass (kg) | Height (cm) | Preferred Walking Speed (m/s) |
|---|---|---|---|
| 24.26 (3.67) | 67.71 (10.57) | 174.48 (10.37) | 1.22 (0.06) |
| Covariates and Interactions | Dependent Variables | |||||||
|---|---|---|---|---|---|---|---|---|
| B | D_hc | β | ||||||
| F | sig | F | sig | F | sig | F | sig | |
| MOS1 | 2.010 | 0.164 | 1.222 | 0.275 | 6.043 | 0.018 * | 0.044 | 0.834 |
| MOS1 × speed | 0.035 | 0.966 | 0.545 | 0.584 | 0.412 | 0.665 | 1.634 | 0.207 |
| MOS mean | 2.387 | 0.130 | 11.747 | 0.001 * | 9.465 | 0.004 * | 0.223 | 0.639 |
| MOS mean × speed | 0.009 | 0.991 | 0.260 | 0.772 | 1.163 | 0.322 | 0.819 | 0.448 |
| MOS variability | 4.425 | 0.041 * | 1.666 | 0.204 | 0.778 | 0.383 | 0.018 | 0.895 |
| MOS variability × speed | 0.218 | 0.805 | 0.324 | 0.725 | 0.438 | 0.648 | 0.717 | 0.494 |
| Dependent | Factors and Covariates | Speed (Levels) | Estimated | Std. Error | T | Sig | 95% Confidence Interval | |
|---|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | |||||||
| MOS variability | - | 0.031 | 0.022161 | - | - | −0.0135 | 0.075951 | |
| Speed | Fast | 0.657 | 0.512 | 1.283 | 0.206 | −0.376 | 1.690 | |
| Slow | 0.521 | 0.504 | 1.035 | 0.306 | −0.495 | 1.538 | ||
| MOS variability × speed | Fast | −0.015 | 0.025 | −0.616 | 0.541 | −0.065 | 0.035 | |
| Slow | −0.016 | 0.027 | −0.612 | 0.544 | −0.071 | 0.038 | ||
| B | MOS mean | 0.306 | 0.139 | 2.199 | - | 0.025 | 0.587 | |
| Speed | Fast | −6.049 | 9.293 | −0.651 | 0.519 | −24.804 | 12.705 | |
| Slow | 3.852 | 9.139 | 0.421 | 0.676 | −14.592 | 22.297 | ||
| MOS mean × speed | Fast | −0.125 | 0.175 | −0.714 | 0.479 | −0.478 | 0.228 | |
| Slow | −0.063 | 0.184 | −0.342 | 0.734 | −0.435 | 0.309 | ||
| D_hc | MOS1 | - | −0.026 | 0.047 | - | - | −0.122 | 0.069 |
| MOS mean | - | 0.041 | 0.051 | - | - | −0.061 | 0.143 | |
| Speed | Fast | −1.201 | 3.389 | −0.354 | 0.725 | −8.039 | 5.638 | |
| Slow | 3.594 | 3.333 | 1.079 | 0.287 | −3.131 | 10.320 | ||
| MOS1 × speed | Fast | −0.050 | 0.057 | −0.881 | 0.384 | −0.164 | 0.065 | |
| Slow | −0.027 | 0.055 | −0.487 | 0.629 | −0.137 | 0.084 | ||
| MOS mean × speed | Fast | 0.090 | 0.064 | 1.414 | 0.165 | −0.038 | 0.219 | |
| Slow | 0.026 | 0.067 | 0.390 | 0.698 | −0.109 | 0.162 | ||
| β | Speed | Fast | −0.006 | 0.053 | −0.128 | 0.899 | −0.115 | 0.101 |
| Slow | 0.003 | 0.052 | 0.072 | 0.943 | −0.103 | 0.110 | ||
| Covariates & Interactions | Dependent Variables | |||||||
|---|---|---|---|---|---|---|---|---|
| B | D_hc | β | ||||||
| F | sig | F | sig | F | sig | F | sig | |
| MOS1 | 3.451 | 0.070 | 2.395 | 0.129 | 2.329 | 0.134 | 0.729 | 0.398 |
| MOS1 × magnitude | 1.262 | 0.294 | 0.283 | 0.755 | 0.277 | 0.759 | 0.103 | 0.902 |
| MOS mean | 3.233 | 0.079 | 9.042 | 0.004 * | 2.201 | 0.145 | 0.031 | 0.862 |
| MOS mean × magnitude | 0.598 | 0.555 | 0.534 | 0.590 | 0.088 | 0.916 | 0.147 | 0.864 |
| MOS variability | 5.803 | 0.020 * | 1.846 | 0.182 | 0.129 | 0.721 | 0.345 | 0.560 |
| MOS variability × magnitude | 0.389 | 0.680 | 0.375 | 0.690 | 0.249 | 0.781 | 0.057 | 0.945 |
| Dependent | Factors and Covariates | Magnitude (Levels) | Estimated | Std. Error | T | Sig | 95% Confidence Interval | |
|---|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | |||||||
| MOS variability | - | 0.031 | 0.0208 | - | - | −0.011 | 0.073 | |
| Magnitude | Small | 0.452 | 0.528 | 0.855 | 0.397 | −0.614 | 1.518 | |
| Large | 0.117 | 0.485 | 0.241 | 0.811 | −0.863 | 1.097 | ||
| MOS variability × magnitude | Small | 0.012 | 0.031 | 0.381 | 0.705 | −0.050 | 0.074 | |
| Large | −0.015 | 0.030 | −0.520 | 0.606 | −0.075 | 0.044 | ||
| B | MOS mean | - | 0.306 | 0.114 | - | - | 0.075 | 0.536 |
| Magnitude | Small | −4.076 | 8.367 | −0.487 | 0.629 | −20.961 | 12.808 | |
| Large | 2.021 | 7.691 | 0.263 | 0.794 | −13.499 | 17.542 | ||
| MOS mean × magnitude | Small | −0.133 | 0.167 | −0.804 | 0.426 | −0.470 | 0.202 | |
| Large | −0.159 | 0.168 | −0.949 | 0.348 | −0.499 | 0.179 | ||
| D_hc | Magnitude | Small | −0.857 | 4.325 | −0.198 | 0.844 | −9.586 | 7.871 |
| Large | 4.852 | 3.976 | 1.220 | 0.229 | −3.171 | 12.876 | ||
| β | Magnitude | Small | 0.057 | 0.068 | 0.833 | 0.409 | −0.081 | 0.195 |
| Large | −0.021 | 0.063 | −0.330 | 0.743 | −0.148 | 0.106 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fallahtafti, F.; Bruijn, S.; Mohammadzadeh Gonabadi, A.; Sangtarashan, M.; Boron, J.B.; Curtze, C.; Siu, K.-C.; Myers, S.A.; Yentes, J. Trunk Velocity Changes in Response to Physical Perturbations Are Potential Indicators of Gait Stability. Sensors 2023, 23, 2833. https://doi.org/10.3390/s23052833
Fallahtafti F, Bruijn S, Mohammadzadeh Gonabadi A, Sangtarashan M, Boron JB, Curtze C, Siu K-C, Myers SA, Yentes J. Trunk Velocity Changes in Response to Physical Perturbations Are Potential Indicators of Gait Stability. Sensors. 2023; 23(5):2833. https://doi.org/10.3390/s23052833
Chicago/Turabian StyleFallahtafti, Farahnaz, Sjoerd Bruijn, Arash Mohammadzadeh Gonabadi, Mohammad Sangtarashan, Julie Blaskewicz Boron, Carolin Curtze, Ka-Chun Siu, Sara A. Myers, and Jennifer Yentes. 2023. "Trunk Velocity Changes in Response to Physical Perturbations Are Potential Indicators of Gait Stability" Sensors 23, no. 5: 2833. https://doi.org/10.3390/s23052833
APA StyleFallahtafti, F., Bruijn, S., Mohammadzadeh Gonabadi, A., Sangtarashan, M., Boron, J. B., Curtze, C., Siu, K.-C., Myers, S. A., & Yentes, J. (2023). Trunk Velocity Changes in Response to Physical Perturbations Are Potential Indicators of Gait Stability. Sensors, 23(5), 2833. https://doi.org/10.3390/s23052833









