Evapotranspiration in Semi-Arid Climate: Remote Sensing vs. Soil Water Simulation
Abstract
1. Introduction
2. Materials and Methods
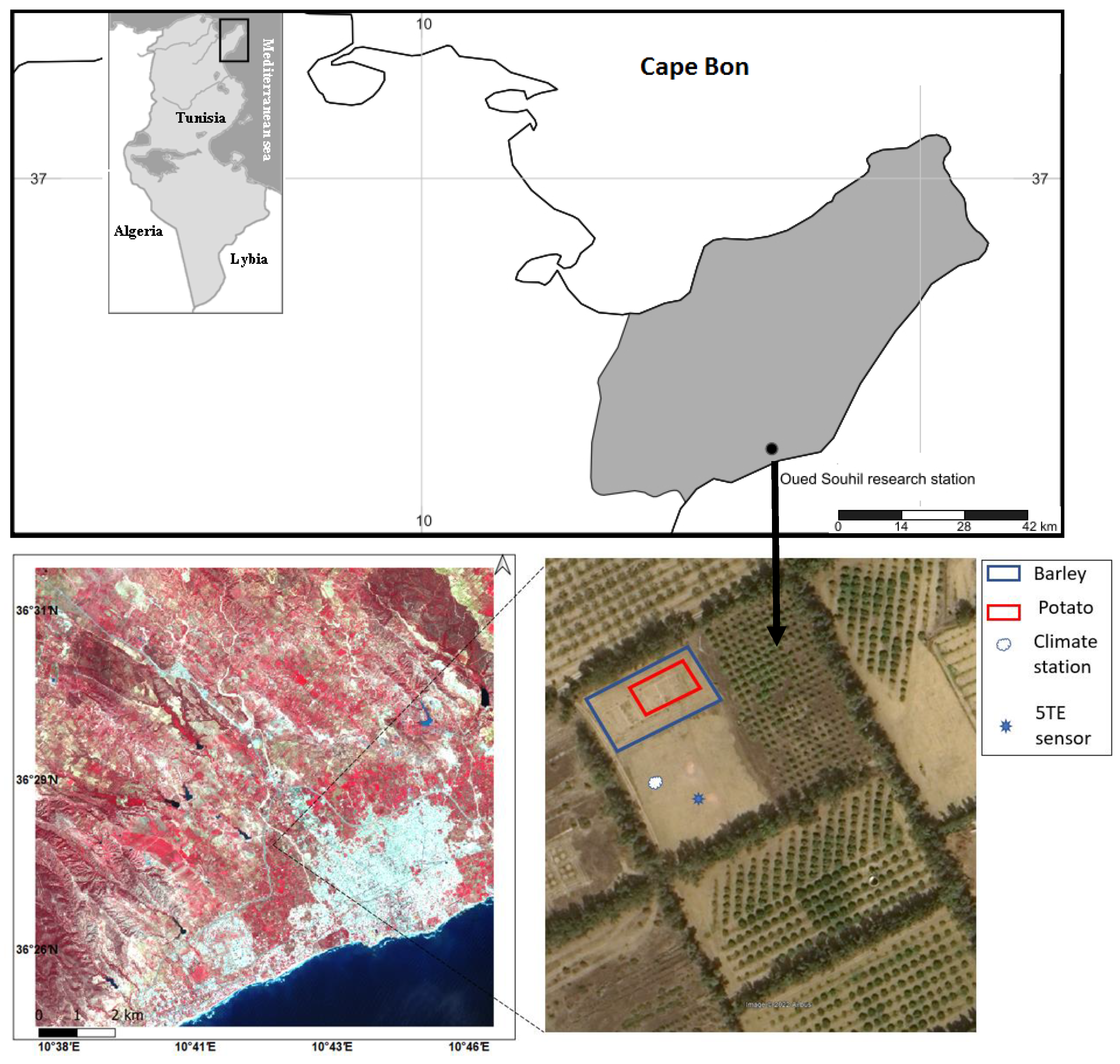
2.1. Study Area and Data Collection
2.1.1. Crop Water Need
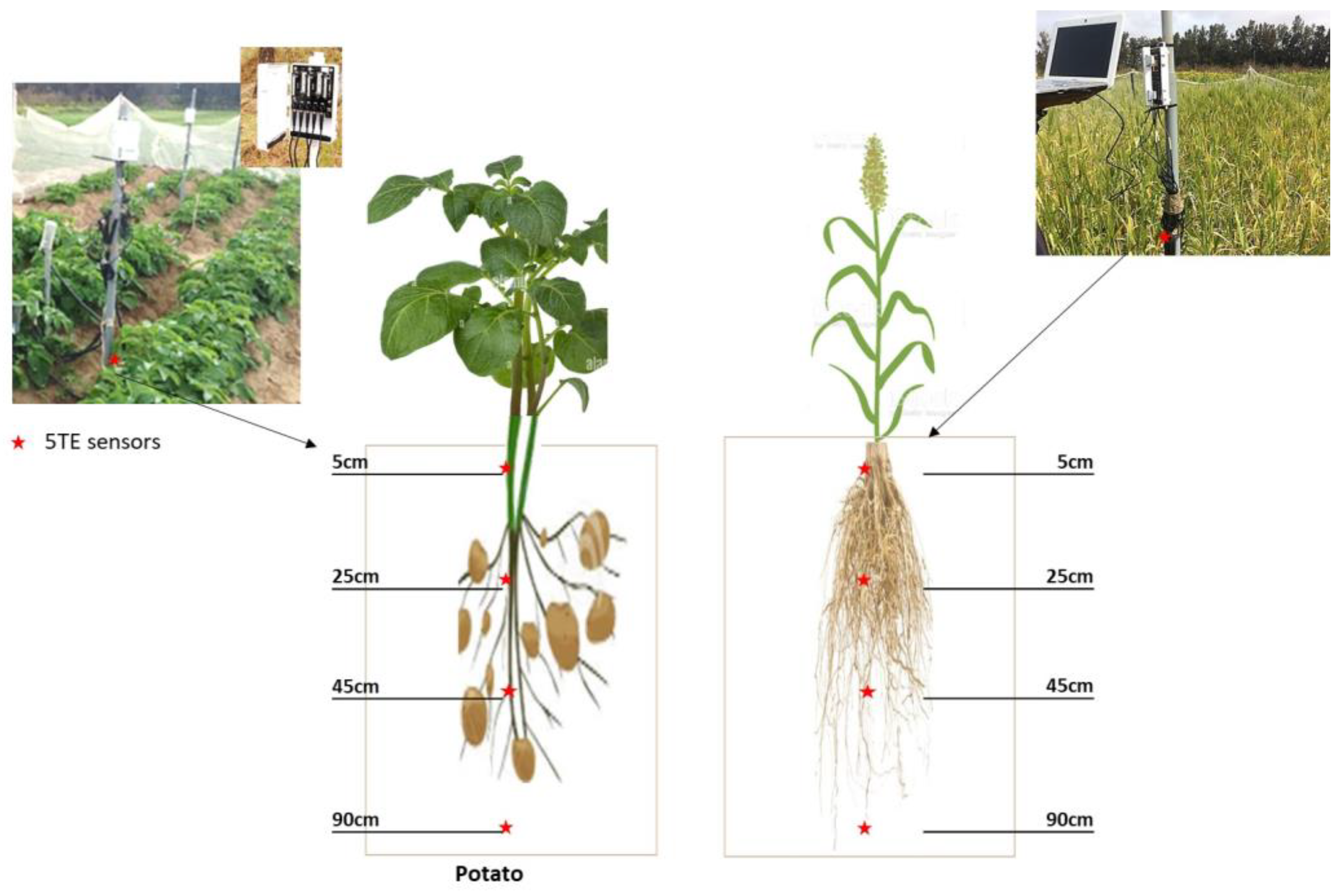
2.1.2. Soil Water Content Monitoring
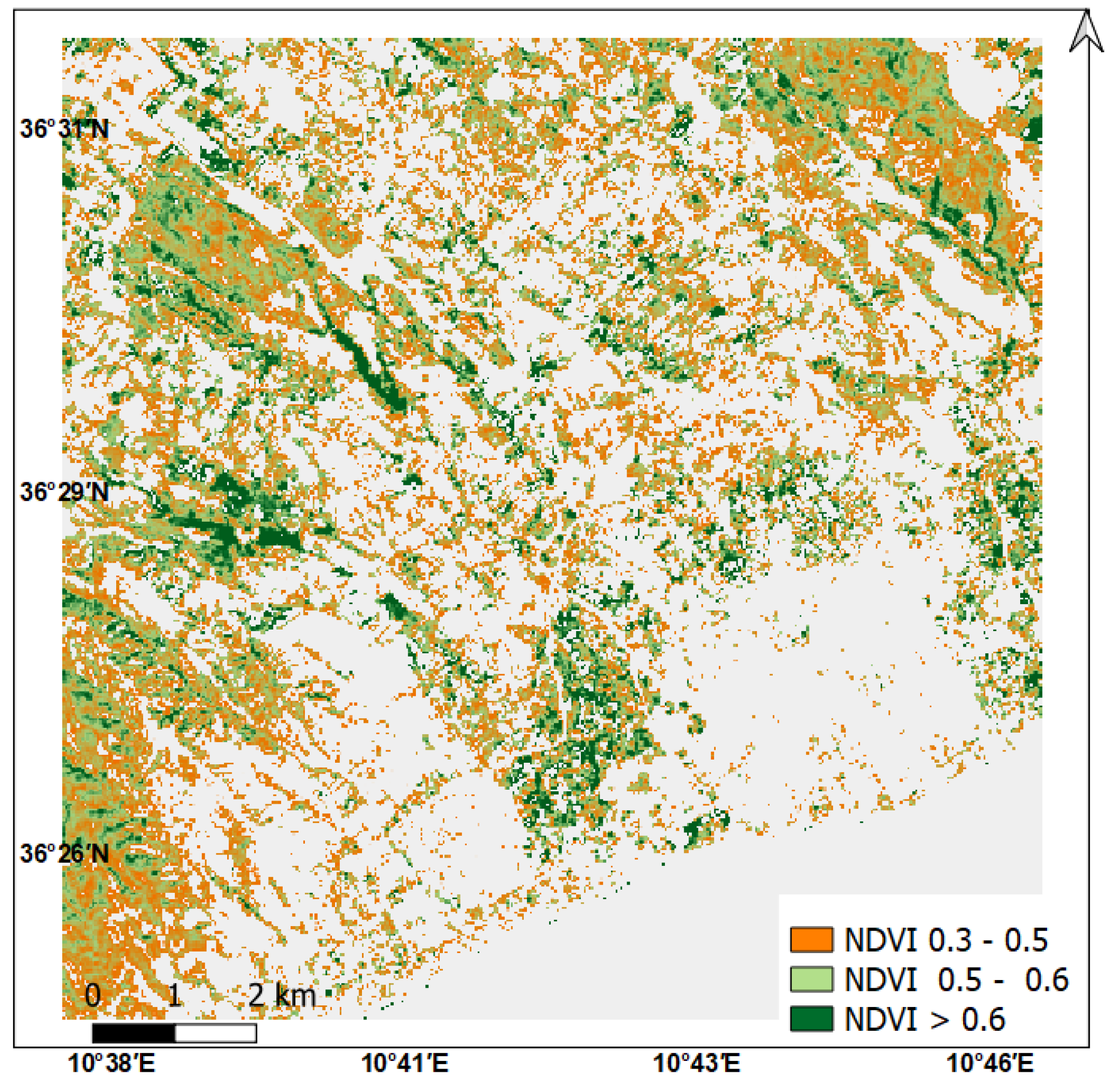
2.1.3. Earth Observation Data
2.2. ETa Estimation Approaches
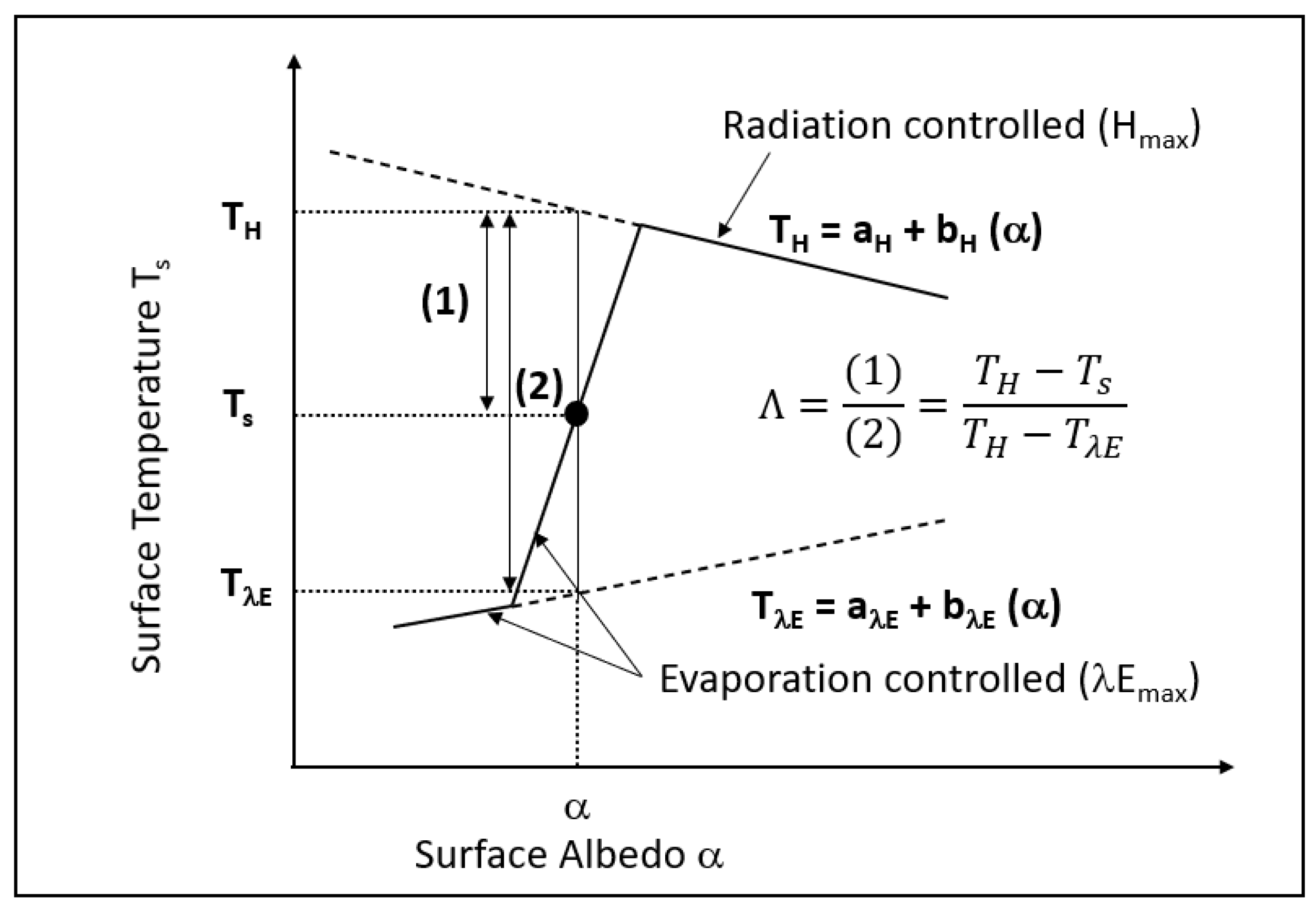
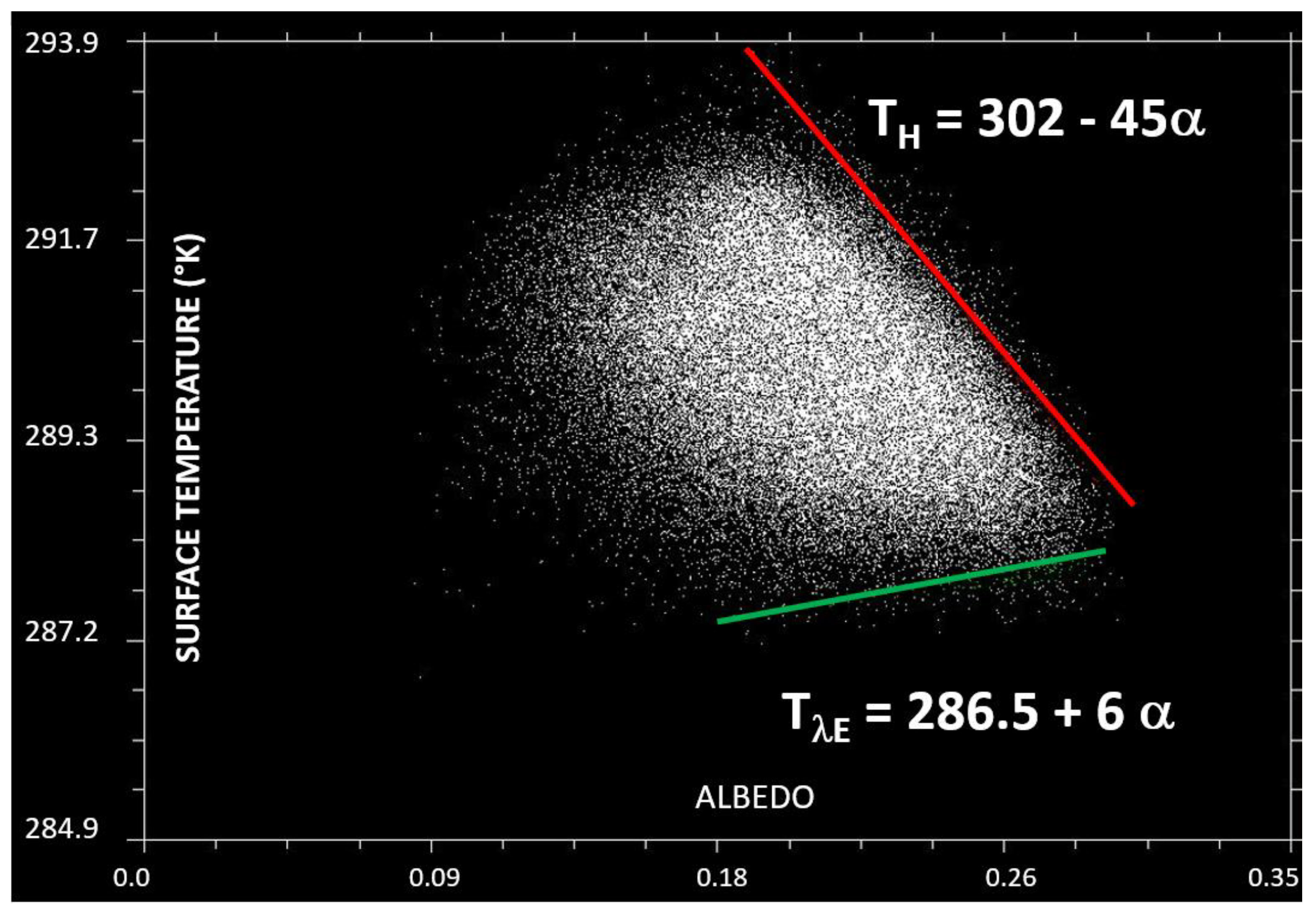
2.2.1. ETa by S-SEBI
- -
- For saturated soil, such as irrigated areas, the temperature is almost constant at low Ts because available energy is used for evaporation. At higher reflectance, Ts increases because of decreasing ETa due to less soil moisture. This is the “evaporation controlled” state corresponding to the dry edge of the scatter
- -
- At an inflexion threshold reflectance, the surface temperature decreases with increasing reflectance because no more evaporation can take place. This is the “radiation controlled” state corresponding to the wet edge of the scatter.
2.2.2. ETa by HYDRUS-1D Transient State Model
Modelling Approach
Boundary, and Initial Conditions
Root Water Uptake and Root Depth
3. Results and Discussion
3.1. Energetic Fluxes Assessment by S-SEBI
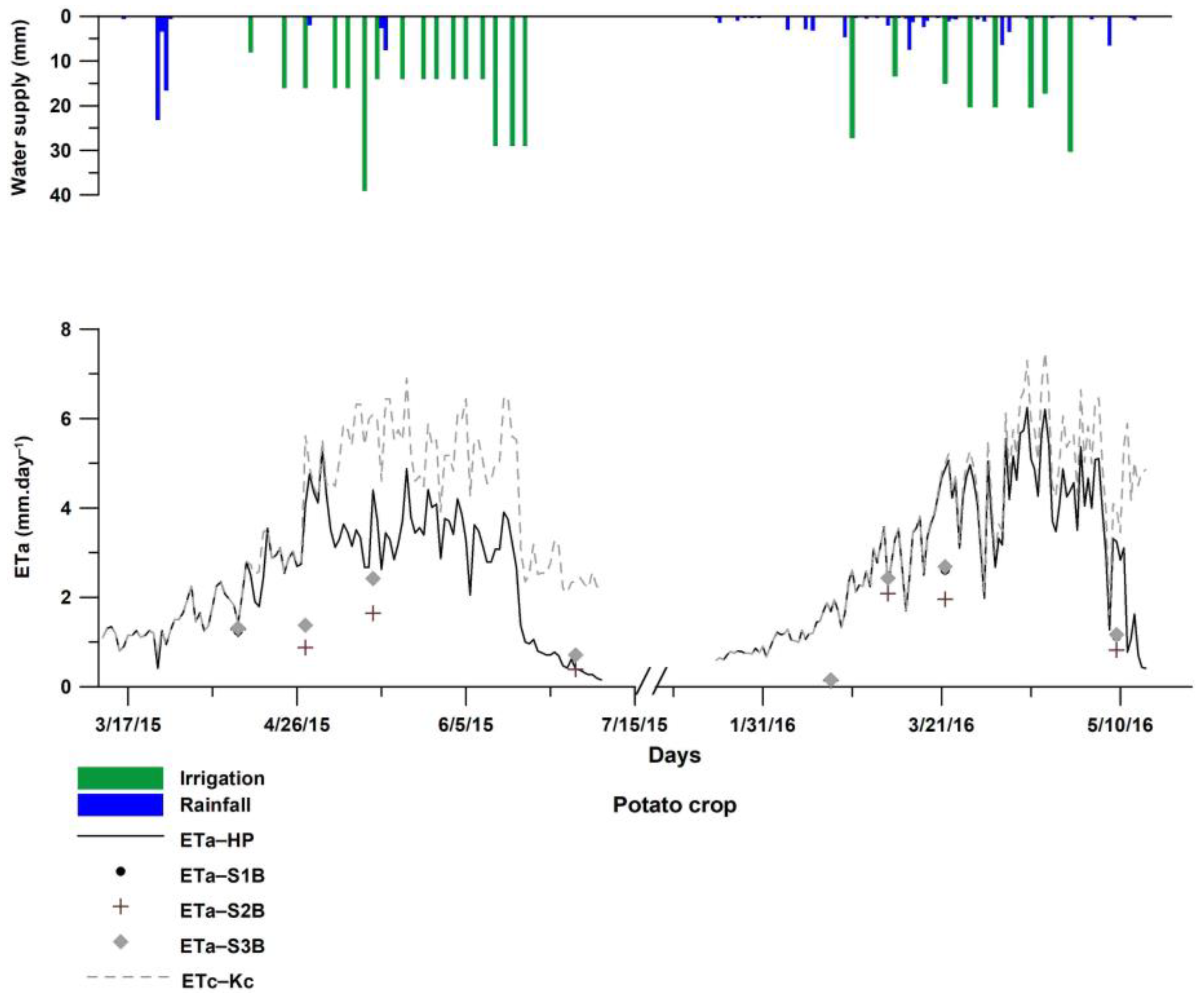
3.2. ETa Results for Irrigated Potato
3.2.1. ETa Estimated by HYDRUS-1D
3.2.2. ETa Estimated by S-SEBI
3.3. ETa Results for Rainfed Barley
3.3.1. ETa Estimated by HYDRUS-1D
3.3.2. ETa Estimated by S-SEBI
4. Conclusions and Future Perspectives
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perry, C.; Steduto, P.; Karajeh, F. Does improved irrigation technology save water. In A Review of the Evidence; FAO: Rome, Italy, 2017. [Google Scholar]
- Tarabella, A. Food Products Evolution: Innovation Drivers and Market Trends; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Topp, G.C.; Davis, J.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Slama, F.; Zemni, N.; Bouksila, F.; De Mascellis, R.; Bouhlila, R. Modelling the impact on root water uptake and solute return flow of different drip irrigation regimes with brackish water. Water 2019, 11, 425. [Google Scholar] [CrossRef]
- Zemni, N.; Bouksila, F.; Persson, M.; Slama, F.; Berndtsson, R.; Bouhlila, R. Laboratory calibration and field validation of soil water content and salinity measurements using the 5TE sensor. Sensors 2019, 19, 5272. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A Coupled Remote Sensing and Simplified Surface Energy Balance Approach to Estimate Actual Evapotranspiration from Irrigated Fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
- Kustas, W.P.; Daughtry, C.S. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. For. Meteorol. 1990, 49, 205–223. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Roerink, G.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Acharya, B.; Sharma, V. Comparison of satellite driven surface energy balance models in estimating crop evapotranspiration in semi-arid to arid inter-mountain region. Remote Sens. 2021, 13, 1822. [Google Scholar] [CrossRef]
- Chirouze, J.; Boulet, G.; Jarlan, L.; Fieuzal, R.; Rodriguez, J.; Ezzahar, J.; Er-Raki, S.; Bigeard, G.; Merlin, O.; Garatuza-Payan, J. Intercomparison of four remote-sensing-based energy balance methods to retrieve surface evapotranspiration and water stress of irrigated fields in semi-arid climate. Hydrol. Earth Syst. Sci. 2014, 18, 1165–1188. [Google Scholar] [CrossRef]
- Le Page, M.; Toumi, J.; Khabba, S.; Hagolle, O.; Tavernier, A.; Kharrou, M.H.; Er-Raki, S.; Huc, M.; Kasbani, M.; Moutamanni, A.E. A life-size and near real-time test of irrigation scheduling with a sentinel-2 like time series (SPOT4-Take5) in Morocco. Remote Sens. 2014, 6, 11182–11203. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, C.M.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating evapotranspiration of an apple orchard using a remote sensing-based soil water balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef]
- Pereira, L.; Paredes, P.; Jovanovic, N. Soil water balance models for determining crop water and irrigation requirements and irrigation scheduling focusing on the FAO56 method and the dual Kc approach. Agric. Water Manag. 2020, 241, 106357. [Google Scholar] [CrossRef]
- Bai, Y.; Li, X.; Zhou, S.; Yang, X.; Yu, K.; Wang, M.; Liu, S.; Wang, P.; Wu, X.; Wang, X. Quantifying plant transpiration and canopy conductance using eddy flux data: An underlying water use efficiency method. Agric. For. Meteorol. 2019, 271, 375–384. [Google Scholar] [CrossRef]
- Effendi, I. Evapotranspiration in Dry Climate Area: Comparing Remote Sensing Techniques with Unsaturated Zone Water Flow Simulation; University of Twente: Enschede, The Netherlands, 2012. [Google Scholar]
- Galleguillos, M.; Jacob, F.; Prévot, L.; French, A.; Lagacherie, P. Comparison of two temperature differencing methods to estimate daily evapotranspiration over a Mediterranean vineyard watershed from ASTER data. Remote Sens. Environ. 2011, 115, 1326–1340. [Google Scholar] [CrossRef]
- Er-Raki, S.; Ezzahar, J.; Merlin, O.; Amazirh, A.; Hssaine, B.A.; Kharrou, M.H.; Khabba, S.; Chehbouni, A. Performance of the HYDRUS-1D model for water balance components assessment of irrigated winter wheat under different water managements in semi-arid region of Morocco. Agric. Water Manag. 2021, 244, 106546. [Google Scholar] [CrossRef]
- Tu, A.; Xie, S.; Mo, M.; Song, Y.; Li, Y. Water budget components estimation for a mature citrus orchard of southern China based on HYDRUS-1D model. Agric. Water Manag. 2021, 243, 106426. [Google Scholar] [CrossRef]
- Zemni, N.; Slama, F.; Bouksila, F.; Bouhlila, R. Simulating and monitoring water flow, salinity distribution and yield production under buried diffuser irrigation for date palm tree in Saharan Jemna oasis (North Africa). Agric. Ecosyst. Environ. 2022, 325, 107772. [Google Scholar] [CrossRef]
- Richards, L.A. Diagnosis and Improvement of Saline and Alkali Soils; Agricultural Handbook 60; U.S. Department of Agriculture: Washington, DC, USA, 1954. [Google Scholar]
- Monteith, J.L. Evaporation and environment in the State and Movement of Water in Living Organisms. In Proceedings of the Symposia of the Society for Experimental Biology; No. 19; Cambridge University Press: Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef]
- Hilhorst, M.A. A pore water conductivity sensor. Soil Sci. Soc. Am. J. 2000, 64, 1922–1925. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.; Anderson, G.; Acharya, P.; Robertson, D.; Chetwynd, J.; Adler-Golden, S. MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- Menenti, M.; Choudhury, B. Parameterization of land surface evapotranspiration using a location dependent potential evapotranspiration and surface temperature range. In Proceedings of the International symposium on Exchange Processes at the Land Surface of a Range of Space and Time Scales, Yokohama, Japan, 19–21 July 1993; Volume 212, pp. 561–568. [Google Scholar]
- Choudhury, B.; Reginato, R.; Idso, S. An analysis of infrared temperature observations over wheat and calculation of latent heat flux. Agric. For. Meteorol. 1986, 37, 75–88. [Google Scholar] [CrossRef]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Sugita, M.; Brutsaert, W. Daily evaporation over a region from lower boundary layer profiles measured with radiosondes. Water Resour. Res. 1991, 27, 747–752. [Google Scholar] [CrossRef]
- Ogée, J.; Lamaud, E.; Brunet, Y.; Berbigier, P.; Bonnefond, J.-M. A long-term study of soil heat flux under a forest canopy. Agric. For. Meteorol. 2001, 106, 173–186. [Google Scholar] [CrossRef]
- Choudhury, B.J. Relationships between vegetation indices, radiation absorption, and net photosynthesis evaluated by a sensitivity analysis. Remote Sens. Environ. 1987, 22, 209–233. [Google Scholar] [CrossRef]
- Santanello, J.A., Jr.; Friedl, M.A. Diurnal covariation in soil heat flux and net radiation. J. Appl. Meteorol. 2003, 42, 851–862. [Google Scholar] [CrossRef]
- Cellier, P.; Richard, G.; Robin, P. Partition of sensible heat fluxes into bare soil and the atmosphere. Agric. For. Meteorol. 1996, 82, 245–265. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Clothier, B.; Clawson, K.; Pinter Jr, P.; Moran, M.; Reginato, R.; Jackson, R. Estimation of soil heat flux from net radiation during the growth of alfalfa. Agric. For. Meteorol. 1986, 37, 319–329. [Google Scholar] [CrossRef]
- Daughtry, C.; Kustas, W.P.; Moran, M.; Pinter Jr, P.; Jackson, R.; Brown, P.; Nichols, W.; Gay, L. Spectral estimates of net radiation and soil heat flux. Remote Sens. Environ. 1990, 32, 111–124. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Sobrino, J.; Gómez, M.; Jiménez-Muñoz, J.; Olioso, A.; Chehbouni, G. A simple algorithm to estimate evapotranspiration from DAIS data: Application to the DAISEX campaigns. J. Hydrol. 2005, 315, 117–125. [Google Scholar] [CrossRef]
- Jackson, R.D.; Hatfield, J.L.; Reginato, R.; Idso, S.; Pinter Jr, P. Estimation of daily evapotranspiration from one time-of-day measurements. Agric. Water Manag. 1983, 7, 351–362. [Google Scholar] [CrossRef]
- Colaizzi, P.; Evett, S.; Howell, T.; Tolk, J. Comparison of five models to scale daily evapotranspiration from one-time-of-day measurements. Trans. ASABE 2006, 49, 1409–1417. [Google Scholar] [CrossRef]
- Fikadu, T.; Teferi, E.; Dubale, B.; Gusha, B.; Mantel, S.K.; Tanner, J.; Palmer, C.G.; Woldu, Z.; Alamirew, T.; Zeleke, G. Implications of Watershed Management Practices on Water Availability Using Hydrus-1D Model in the Aba Gerima Watershed, Upper Blue Nile Basin, Ethiopia. Water 2022, 14, 3095. [Google Scholar] [CrossRef]
- Selim, T.; Bouksila, F.; Berndtsson, R.; Persson, M. Soil water and salinity distribution under different treatments of drip irrigation. Soil Sci. Soc. Am. J. 2013, 77, 1144–1156. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.; Kolinska-Malinka, K.; Zaradny, H. Simulation of field water uptake by plants using a soil water dependent root extraction function. J. Hydrol. 1976, 31, 13–26. [Google Scholar] [CrossRef]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Nasr, Z.; Zairi, A.; Ben Nouna, B.; Ouslati, T. Détermination de la consommation en eau journalière par bilan d’énergie des cultures annuelles (blé et pomme de terre). Evolution avec la biomasse et application au pilotage des ir-rigations. In Proceedings of the Actes du séminaire Economie de l’eau en Irrigation, Hammamet, Tunisie, 14–16 November 2000; pp. 114–125. [Google Scholar]
- Afrasiabian, Y.; Noory, H.; Mokhtari, A.; Nikoo, M.R.; Pourshakouri, F.; Haghighatmehr, P. Effects of spatial, temporal, and spectral resolutions on the estimation of wheat and barley leaf area index using multi-and hyper-spectral data (case study: Karaj, Iran). Precis. Agric. 2021, 22, 660–688. [Google Scholar] [CrossRef]
- Boukari, M. Modelling of Biophysical Variables of Rainfed Crops in Lebna Catchment by SENTINEL2 for Water Productivity Estimation; University of Tunis El Manar: Tunis, Tunisia, 2017. [Google Scholar]
- Difonzo, F.V.; Masciopinto, C.; Vurro, M.; Berardi, M. Shooting the Numerical Solution of Moisture Flow Equation with Root Water Uptake Models: A Python Tool. Water Resour. Manag. 2021, 35, 2553–2567. [Google Scholar] [CrossRef]
- Maas, E.V.; Hoffman, G.J. Crop salt tolerance—Current assessment. J. Irrig. Drain. Div. 1977, 103, 115–134. [Google Scholar] [CrossRef]
- Duchemin, B.; Hadria, R.; Erraki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.; Kharrou, M. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Barnes, E.M.; Kimball, B.A. Estimating cotton evapotranspiration crop coefficients with a multispectral vegetation index. Irrig. Sci. 2003, 22, 95–104. [Google Scholar] [CrossRef]
- Schapendonk, A.; Spitters, C.; Groot, P. Effects of water stress on photosynthesis and chlorophyll fluorescence of five potato cultivars. Potato Res. 1989, 32, 17–32. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, N.; Pan, F.; Pan, X.; Wang, X.; Yang, P. Adjusting Sowing Dates Improved Potato Adaptation to Climate Change in Semiarid Region, China. Sustainability 2017, 9, 615. [Google Scholar] [CrossRef]
- Han, X.; Wei, Z.; Zhang, B.; Li, Y.; Du, T.; Chen, H. Crop evapotranspiration prediction by considering dynamic change of crop coefficient and the precipitation effect in back-propagation neural network model. J. Hydrol. 2021, 596, 126104. [Google Scholar] [CrossRef]
- Allen, M.F. Water dynamics of mycorrhizas in arid soils. In Fungi in Biogeochemical Cycles; Gadd, G.M., Ed.; Cambridge University Press: Cambridge, UK, 2006; pp. 74–97. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef]
- Ghazouani, H.; Capodici, F.; Ciraolo, G.; Maltese, A.; Rallo, G.; Provenzano, G. Potential of thermal images and simulation models to assess water and salt stress: Application to potato crop in central Tunisia. Chem. Eng. Trans. 2017, 58, 709–714. [Google Scholar]
- Garcia-Santos, V.; Niclòs, R.; Valor, E. Evapotranspiration Retrieval Using S-SEBI Model with Landsat-8 Split-Window Land Surface Temperature Products over Two European Agricultural Crops. Remote Sens. 2022, 14, 2723. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Souza da Rocha, N.; Skoković, D.; Suélen Käfer, P.; López-Urrea, R.; Jiménez-Muñoz, J.C.; Alves Rolim, S.B. Evapotranspiration Estimation with the S-SEBI Method from Landsat 8 Data against Lysimeter Measurements at the Barrax Site, Spain. Remote Sens. 2021, 13, 3686. [Google Scholar] [CrossRef]
- Jackson, R.D. Canopy temperature and crop water stress. In Advances in Irrigation; Elsevier: Amsterdam, The Netherlands, 1982; Volume 1, pp. 43–85. [Google Scholar] [CrossRef]
- Cucho-Padin, G.; Rinza, J.; Ninanya, J.; Loayza, H.; Quiroz, R.; Ramírez, D.A. Development of an open-source thermal image processing software for improving irrigation management in potato crops (Solanum tuberosum L.). Sensors 2020, 20, 472. [Google Scholar] [CrossRef] [PubMed]
- Wen, W.; Timmermans, J.; Chen, Q.; van Bodegom, P.M. Monitoring the combined effects of drought and salinity stress on crops using remote sensing in the Netherlands. Hydrol. Earth Syst. Sci. 2022, 26, 4537–4552. [Google Scholar] [CrossRef]
- Bisquert, M.; Sánchez, J.M.; López-Urrea, R.; Caselles, V. Estimating high resolution evapotranspiration from disaggregated thermal images. Remote Sens. Environ. 2016, 187, 423–433. [Google Scholar] [CrossRef]
- Mokhtari, A.; Noory, H.; Pourshakouri, F.; Haghighatmehr, P.; Afrasiabian, Y.; Razavi, M.; Fereydooni, F.; Sadeghi Naeni, A. Calculating potential evapotranspiration and single crop coefficient based on energy balance equation using Landsat 8 and Sentinel-2. ISPRS J. Photogramm. Remote Sens. 2019, 154, 231–245. [Google Scholar] [CrossRef]
- Dos Santos, R.A.; Mantovani, E.C.; Fernandes-Filho, E.I.; Filgueiras, R.; Lourenço, R.D.S.; Bufon, V.B.; Neale, C.M.U. Modeling Actual Evapotranspiration with MSI-Sentinel Images and Machine Learning Algorithms. Atmosphere 2022, 13, 1518. [Google Scholar] [CrossRef]
- Bufon, V.B.; Lascano, R.J.; Bednarz, C.; Booker, J.D.; Gitz, D.C. Soil water content on drip irrigated cotton: Comparison of measured and simulated values obtained with the Hydrus 2-D model. Irrig. Sci. 2012, 30, 259–273. [Google Scholar] [CrossRef]
- Pardo, J.; Domínguez, A.; Léllis, B.; Montoya, F.; Tarjuelo, J.; Martínez-Romero, A. Effect of the optimized regulated deficit irrigation methodology on quality, profitability and sustainability of barley in water scarce areas. Agric. Water Manag. 2022, 266, 107573. [Google Scholar] [CrossRef]
- Merlin, O. An original interpretation of the wet edge of the surface temperature–albedo space to estimate crop evapotranspiration (SEB-1S), and its validation over an irrigated area in northwestern Mexico. Hydrol. Earth Syst. Sci. 2013, 17, 3623–3637. [Google Scholar] [CrossRef]
- Rockström, J.; Falkenmark, M. Semiarid Crop Production from a Hydrological Perspective: Gap between Potential and Actual Yields. Crit. Rev. Plant Sci. 2000, 19, 319–346. [Google Scholar] [CrossRef]




| Soil Depth (m) | Clay (%) (d < 2 μm) | Silt (%) (2 ≤ d < 50 μm) | Sand (%) (50 ≤ μm d < 2 mm) | Bulk Density (g·cm−3) |
|---|---|---|---|---|
| 0–0.2 | 4 | 25 | 70 | 1.41 |
| 0.2–0.4 | 15 | 11 | 73 | 1.52 |
| 0.4–0.6 | 16 | 12 | 71 | 1.69 |
| 0.6–0.8 | 19 | 11 | 70 | 1.73 |
| 0.8–1.0 | 17 | 11 | 70 | 1.81 |
| Season | 1 | 2 | 3 | |
|---|---|---|---|---|
| Crop | Potato: 11 March 2015 to 7 July 2015 | Potato: 18 January 2016 to 17 May 2016 | Barley: 18 October 2016 to 20 June 2017 | |
| Irrigation (mm) | 336 | 170 | 0 | |
| Rainfall (mm) | 20 | 70 | 291 | |
| ET0 (mm) | 439 | 321 | ||
| Kc | Kc-ini | 0.5 | 0.5 | 0.3 |
| Kc-mid | 1.15 | 1.15 | 1.15 | |
| Kc-end | 0.75 | 0.75 | 0.25 |
| Depth (m) | Θr (m3·m−3) | θs (m3·m−3) | α (m−1) | n (−) | Ks (m·day−1) |
|---|---|---|---|---|---|
| 0–0.2 | 0.036 | 0.3938 | 3.32 | 1.69 | 2 |
| 0.2–0.4 | 0.0555 | 0.3947 | 4 | 1.60 | 1 |
| 0.4–0.6 | 0.0515 | 0.3571 | 3.14 | 1.50 | 0.28 |
| 0.6–0.8 | 0.051 | 0.3416 | 4 | 1.23 | 0.125 |
| 0.8–1.0 | 0.0507 | 0.3388 | 1 | 1.40 | 0.68 |
| Model | ETc Estimation | Earth Observation | Meteo | Soil/ Irrigation/ | Scenario |
|---|---|---|---|---|---|
| S-SEBI | Ts, ρ, α, NDVI Evaporative fraction Λ Soil fluxG0: Clothier (1986) [36] Daughtry et al. (1990) [37] Bastianssen et al. (1998) [38] Sobrino et al. (2005) [39] Sensible heat flux H Latent heat flux λE | Landsat 8 OLI TOA: Top of Atmosphere B2 [0.45–0.51 μm] (wb = 0.293) B3 [0.53–0.59 μm] (wb = 0.274) B4 [0.64–0.67 μm] (wb = 0.233) B5 [0.85–0.88 μm] (wb = 0.156) B6 [1.57–1.65 μm] (wb = 0.033) B7 [2.11–2.29 μm] (wb = 0.011) B10 [10.60–11.19 μm] B11 [11.50–12.51 μm] B2 to B7: 30 m res. B10 to B11: 100 m res. Sentinel 2 MSI TOC: Top of Canopy B4 [0.65–0.68μm] (10 m res.) B8 [0.78–0.90μm] (10 m res.) | Daily (Ta, Rg) | S1P1, S2P1, S3P1 S1P2, S2P2, S3P2 S1B, S2B, S3B | |
| FAO-Kc | Kc Allan (1998) [6] ET0 Penman-Monteith, (1965) [23] | Daily (Ta, Rg, air humidity, wind speed) | FP1, FP2, FB | ||
| HYDRUS-1D | ET0 Penman-Monteith, (1965) [23] LAI potato Nasr et al. (2002) [48] LAI barley Afrasiabian et al. (2020) [49] LAI barley NDVI Sentinel 2 Boukari (2017) [50] Evaporation E Transpiration T | Precipitation | θ ECp Irrigation doses ECw Soil texture Soil hydraulic properties Crop parameters Feddes et al. (1974) [46] | HP1, HP2 H1B, H2B |
| RMSE [W·m−2] Scenario | G0–CLO S1 | G0–BAS S2 | G0–SOB S3 | λE–CLO S1 | λE–BAS S2 | λE–SOB S3 |
|---|---|---|---|---|---|---|
| Potato (8 dates) | 25.09 | 117.51 | 19.42 | 9.29 | 41.99 | 7.62 |
| Barley (7 dates) | 27.36 | 113.70 | 36.75 | 7.72 | 25.31 | 9.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakroun, H.; Zemni, N.; Benhmid, A.; Dellaly, V.; Slama, F.; Bouksila, F.; Berndtsson, R. Evapotranspiration in Semi-Arid Climate: Remote Sensing vs. Soil Water Simulation. Sensors 2023, 23, 2823. https://doi.org/10.3390/s23052823
Chakroun H, Zemni N, Benhmid A, Dellaly V, Slama F, Bouksila F, Berndtsson R. Evapotranspiration in Semi-Arid Climate: Remote Sensing vs. Soil Water Simulation. Sensors. 2023; 23(5):2823. https://doi.org/10.3390/s23052823
Chicago/Turabian StyleChakroun, Hedia, Nessrine Zemni, Ali Benhmid, Vetiya Dellaly, Fairouz Slama, Fethi Bouksila, and Ronny Berndtsson. 2023. "Evapotranspiration in Semi-Arid Climate: Remote Sensing vs. Soil Water Simulation" Sensors 23, no. 5: 2823. https://doi.org/10.3390/s23052823
APA StyleChakroun, H., Zemni, N., Benhmid, A., Dellaly, V., Slama, F., Bouksila, F., & Berndtsson, R. (2023). Evapotranspiration in Semi-Arid Climate: Remote Sensing vs. Soil Water Simulation. Sensors, 23(5), 2823. https://doi.org/10.3390/s23052823








