Distributed Relative Localization Algorithms for Multi-Robot Networks: A Survey
Abstract
1. Introduction
- This work summarizes the distributed multi-robot network relative localization methods and classifies various methods according to their design methodologies and types of measurements. A detailed introduction is presented for each type of distributed relative localization algorithm. The advantages and limitations of each type of distributed relative localization algorithm are analyzed and compared.
- Key problems in distributed localization algorithms, namely local subnetwork organization, communication efficiency, and the robustness of distributed localization, are investigated.
- The popular simulation experiment platforms are investigated, and the characteristics of each platform are analyzed from different aspects, which can be a reference for researchers conducting simulation experiments.
2. Related Reviews
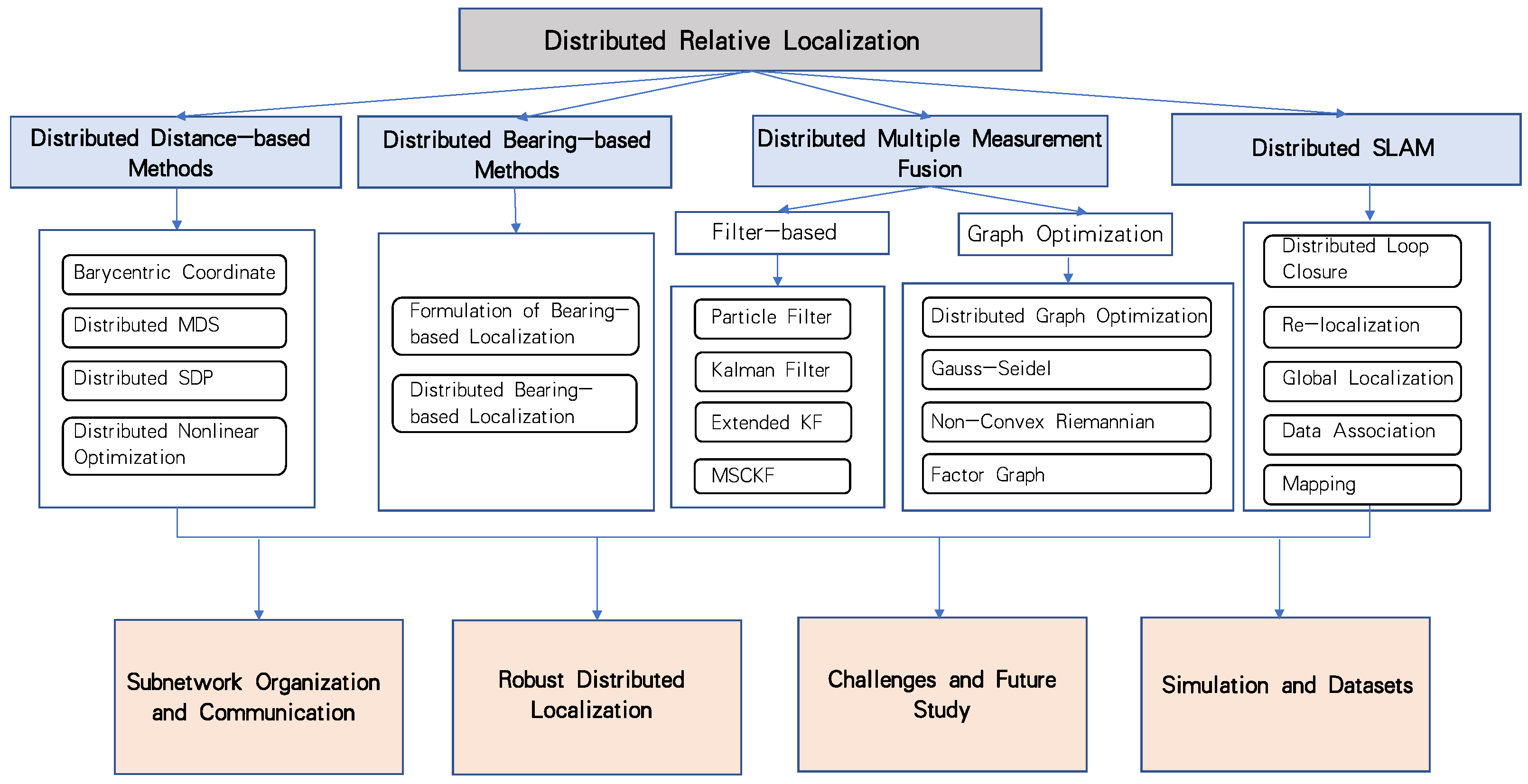
3. Distance-Based Distributed Relative Localization Methods
- Barycentric coordinate-based methods, which present a linear representation of the localization problem and derive naturally distributed iterative algorithms running at distributed nodes that can guarantee converging to the correct states under specific conditions.
- Distributed algorithms developed from their centralized versions, which include: (i) distributed multi-dimensional scaling (MDS), (ii) distributed semi-definite programming (SDP), and (iii) distributed nonlinear optimization.
3.1. Barycentric Coordinate-Based Algorithms
3.1.1. Formulation of Barycentric Distributed Localization
3.1.2. Dealing with Convex Hull Constraints and Noises
3.1.3. Communication Problems for Barycentric Distributed Localization
3.2. Distributed Algorithms Transformed from Centralized Algorithms
3.2.1. Distributed Multi-Dimensional Scaling
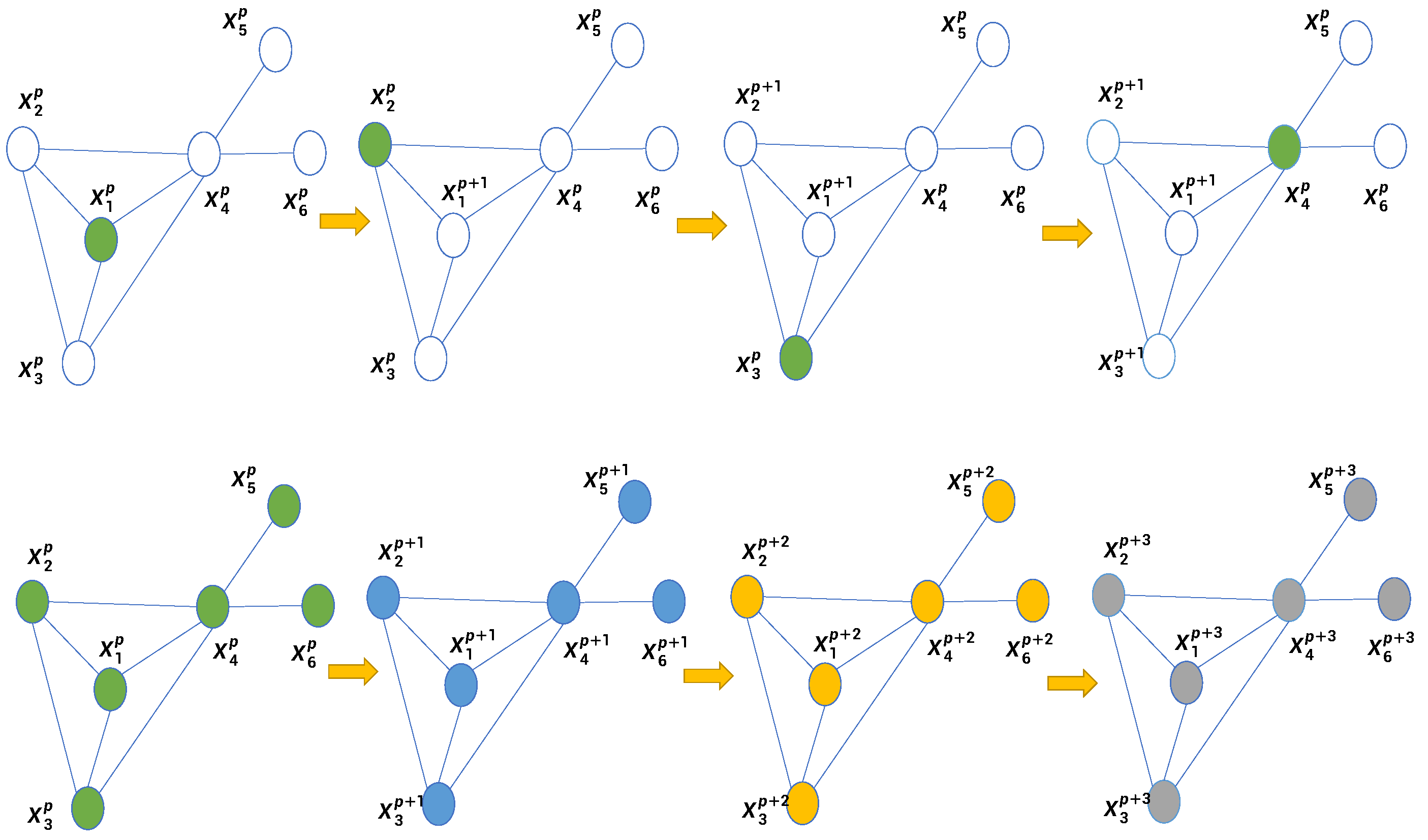
- Step 1: Divide the network into sub-networks (clusters). In the cluster, pairwise distances are needed.In distributed systems, each agent in the network runs the division algorithm individually and asynchronously without centralized control and scheduling. Generally, we can divide the network according to the characteristics of the graph nodes. The simplest way is to divide the nodes according to their degree centrality [9,33]. First, for each node i in the network, construct the set consisting of all the direct neighbors of node i. Then, update by for . Search the largest cardinality group in the network and set it as a cluster. Repeat the process in the last part of the network until the network is divided.
- Step 2: Perform the MDS-based algorithm in each cluster to calculate the relative coordinates. This step constructs the accurate local graph.We can conduct the classic MDS method to calculate the relative coordinates in the cluster. While to reduce the computational complexity, the improved MDS, MDS-MAP [34], is deployed in many papers [26,33,35]. The MDS-MAP algorithm uses the Floyd algorithm in each cluster to fill in the missing range measurements, thus, reducing the range error caused by too many hops.However, the method does not address the problem of errors in the measurement itself. When the measurement error is significant, the matrix in the MDS algorithm may not be able to perform the eigenvalue decomposition. The operations on linear equations and matrix decomposition in MDS are susceptible to measurement errors. In paper [26], the authors use singular value decomposition instead of eigenvalue decomposition to deal with the connection matrix and compute the relative coordinates matrix Z. Then, a more accurate matrix Z is obtained by minimizing , where B can be derived from the matrix composed of the square of the distances.
- Step 3: Merge all the local graphs into a global network based on the common nodes in each local graph. This is a key step in the algorithm, especially for large networks [36,37].The traditional method uses the overlapping edges between subgraphs for merging [38], but this method is prone to ambiguity. Kim et al. [35] add a distance constraint to the splicing process, i.e., they choose the network that does not generate new edges as the result.In fact, the uniqueness of subgraph merging can be determined: Two individual maps can be uniquely merged in m-dimensional space if and only if at least common nodes exist. Dan et al. [33] propose that merging remains unique when the number of common nodes is less than m+1; however, some specific edges exist. Based on these conditions, they design corresponding merging strategies that guarantee uniqueness.
3.3. Distributed Semi Definite Programming
3.4. Distributed Nonlinear Optimization
4. Bearing-Based Distributed Relative Localization Methods
4.1. Formulation of Bearing-Based Localization
4.2. Distributed Bearing-Based Localization
5. Multiple Measurement Fusion
5.1. Filter-Based Multi-Sensor Fusion and Localization
5.1.1. Particle Filter and Relative Localization
5.1.2. Formulation of Kalman-Filter-Based Localization
5.1.3. Distributed Kalman-Filter-Based Relative Localization
5.2. Distributed Graph-Optimization-Based Multi-Sensor Fusion and Localization
5.2.1. The Formulation of Distributed Graph Optimization
5.2.2. Algorithms for Distributed Graph Optimization
5.3. Other Solvers for Distributed Graph Optimization
- (1)
- Gauss–Seidel Algorithm
- (2)
- Non-Convex Riemannian Optimization
- (3)
- Factor Graph Optimization
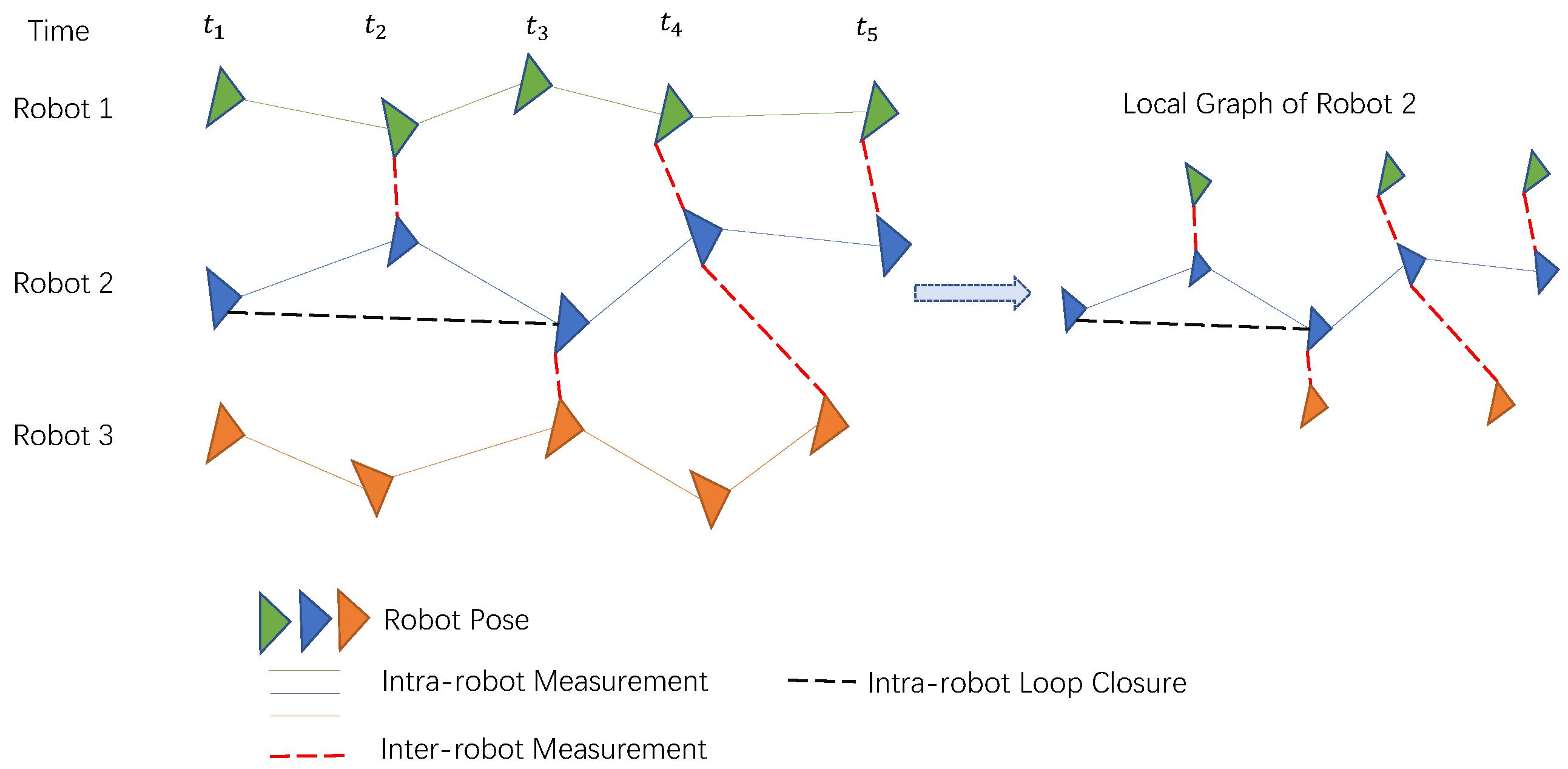
6. Distributed Simultaneous Localization and Mapping
6.1. Distributed SLAM Algorithms
6.1.1. Distributed Loop Closures
6.1.2. Relocalization and Global Localization
6.1.3. Data Association
6.2. Distributed Mapping-Oriented Algorithms
7. Local Subnetwork Organization and Communication
7.1. Local Subnetwork Organization
7.2. Communication Efficiency
8. Robust Distributed Localization
8.1. Initialization
8.2. Measurement Noises
9. Challenges and Future Study on Distributed Localization
9.1. Dynamic Topology
9.2. Scalability
9.3. Distributed Active Localization
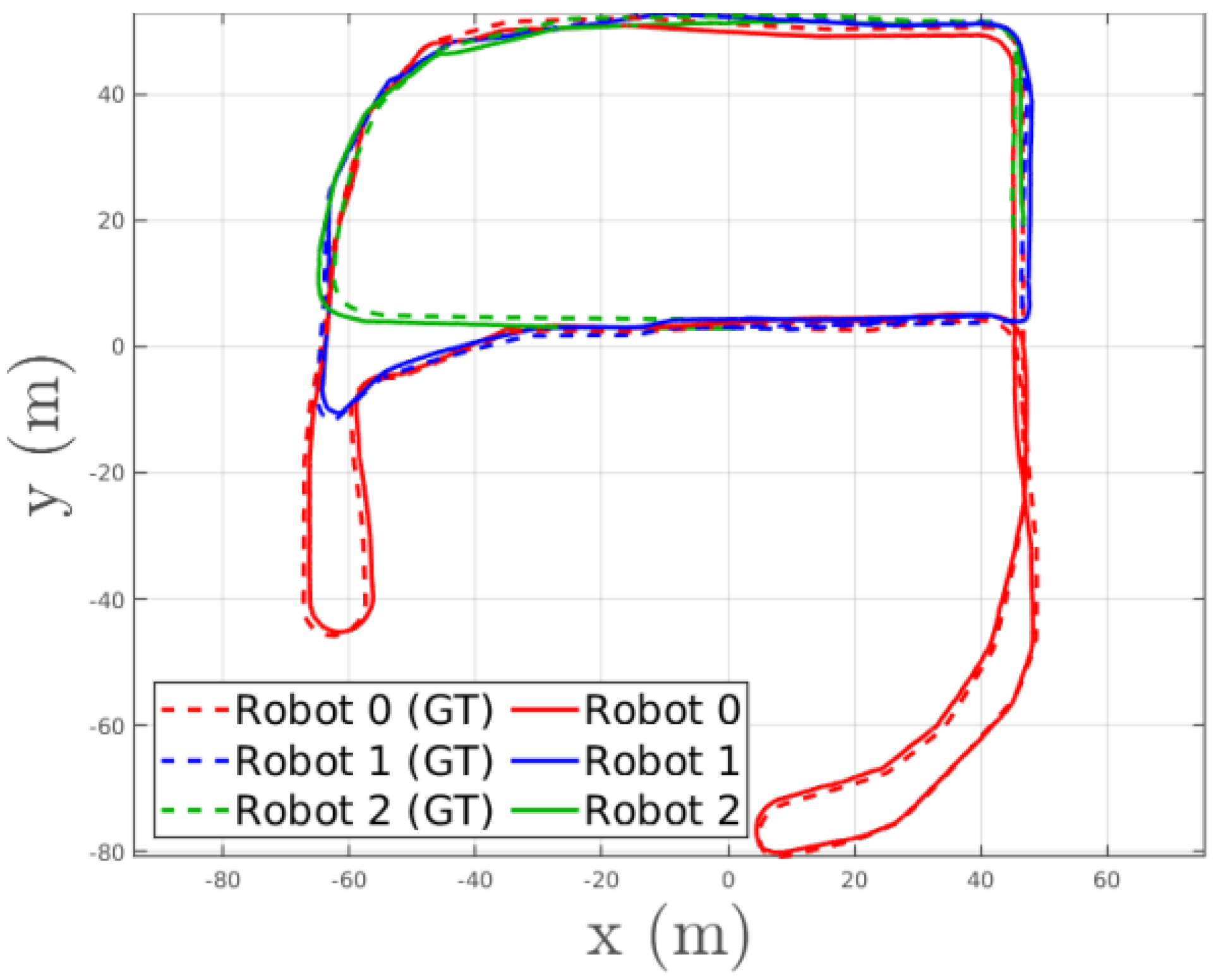
10. Simulation Platforms and Datasets
- Open source. The open source experimental platform allows researchers to change the details of the simulation according to their experimental needs, such as the model of the robot, the type and parameters of the sensors, and the communication mode. The open source platform has better scalability.
- Supported OS. Windows, Linux, and Mac are the most popular operating systems on the market. Robots or other edge devices may run on any of these operating systems. Therefore, a simulation platform adapted to these operating system is closer to the real world.
- ROS supported. Robot Operating System (ROS) [130] is one of the most popular robot software frameworks. The simulation platform can provide data sources and operational feedback for ROS to simulate real-world experiments.
- Model. The model of the simulation object is the most critical part of the experiment. The model here includes not only the physical appearance but also sensors, communication modules, and computing power.
- Scene quality. The robot’s ability to perceive and operate on the environment is basic. Therefore, the quality of the environment should be as close to reality as possible and also simulate the noise in the environment.
- Distributed capabilities. Simulation experiments are usually executed on a single machine; however, the multi-robot distributed localization algorithm is designed to be executed on multiple robots in a distributed manner. This is also important for the implementation of distributed simulation.
11. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gautam, A.; Mohan, S. A review of research in multi-robot systems. In Proceedings of the 2012 IEEE seventh International Conference on Industrial and Information Systems (ICIIS), Chennai, India, 6–9 August 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–5. [Google Scholar]
- Halder, S.; Ghosal, A. A survey on mobility-assisted localization techniques in wireless sensor networks. J. Netw. Comput. Appl. 2016, 60, 82–94. [Google Scholar] [CrossRef]
- Goel, S.; Kealy, A.; Gikas, V.; Retscher, G.; Toth, C.; Brzezinska, D.G.; Lohani, B. Cooperative localization of unmanned aerial vehicles using GNSS, MEMS inertial, and UWB sensors. J. Surv. Eng. 2017, 143, 04017007. [Google Scholar] [CrossRef]
- Miwa, M.; Ushiroda, T. Precision Flight Drones with RTK-GNSS. J. Robot. Mechatron. 2021, 33, 371–378. [Google Scholar] [CrossRef]
- Stempfhuber, W.; Buchholz, M. A precise, low-cost RTK GNSS system for UAV applications. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Zurich, Switzerland, 14–16 September 2011. [Google Scholar]
- Bulusu, N.; Heidemann, J.; Estrin, D. GPS-less low-cost outdoor localization for very small devices. IEEE Pers. Commun. 2000, 7, 28–34. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Zaini, A.H.; Guo, K.; Xie, L. An ultra-wideband-based multi-UAV localization system in GPS-denied environments. In Proceedings of the 2016 International Micro Air Vehicles Conference, Beijing, China, 17–21 October 2016; Volume 6, pp. 1–15. [Google Scholar]
- Shang, Y.; Ruml, W.; Zhang, Y.; Fromherz, M.P. Localization from mere connectivity. In Proceedings of the Fourth ACM International Symposium on Mobile Ad Hoc Networking & Computing, Annapolis, MD, USA, 1–3 June 2003; pp. 201–212. [Google Scholar]
- Chen, R.; Yang, B.; Zhang, W. Distributed and collaborative localization for swarming UAVs. IEEE Internet Things J. 2020, 8, 5062–5074. [Google Scholar] [CrossRef]
- Cunningham, A.; Indelman, V.; Dellaert, F. DDF-SAM 2.0: Consistent distributed smoothing and mapping. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 5220–5227. [Google Scholar]
- Cheng, B.H.; Hudson, R.E.; Lorenzelli, F.; Vandenberghe, L.; Yao, K. Distributed gauss-newton method for node loclaization in wireless sensor networks. In Proceedings of the IEEE sixth Workshop on Signal Processing Advances in Wireless Communications, New York, NY, USA, 5–8 June 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 915–919. [Google Scholar]
- Tian, Y.; Koppel, A.; Bedi, A.S.; How, J.P. Asynchronous and parallel distributed pose graph optimization. IEEE Robot. Autom. Lett. 2020, 5, 5819–5826. [Google Scholar] [CrossRef]
- Ping, H.; Wang, Y.; Shen, X.; Li, D.; Chen, W. On Node Localizability Identification in Barycentric Linear Localization. ACM Trans. Sens. Netw. (TOSN) 2022, 19, 1–26. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, H.; Xie, L. Survey on localization systems and algorithms for unmanned systems. Unmanned Syst. 2021, 9, 129–163. [Google Scholar] [CrossRef]
- Çaşka, S.; Gayretli, A. A survey of uav/ugv collaborative systems. CIE44&IMSS 2014, 14, 453–463. [Google Scholar]
- Chowdhury, T.J.; Elkin, C.; Devabhaktuni, V.; Rawat, D.B.; Oluoch, J. Advances on localization techniques for wireless sensor networks: A survey. Comput. Netw. 2016, 110, 284–305. [Google Scholar] [CrossRef]
- Khelifi, F.; Bradai, A.; Benslimane, A.; Rawat, P.; Atri, M. A survey of localization systems in internet of things. Mob. Netw. Appl. 2019, 24, 761–785. [Google Scholar] [CrossRef]
- Shule, W.; Almansa, C.M.; Queralta, J.P.; Zou, Z.; Westerlund, T. Uwb-based localization for multi-uav systems and collaborative heterogeneous multi-robot systems. Procedia Comput. Sci. 2020, 175, 357–364. [Google Scholar] [CrossRef]
- Tian-Yuan, S.; Yong-Cai, W.; De-Ying, L. A Survey and Evaluation of Graph Realization Algorithms. Acta Autom. Sin. 2020, 46, 613–630. [Google Scholar]
- Gupta, A.; Fernando, X. Simultaneous Localization and Mapping (SLAM) and Data Fusion in Unmanned Aerial Vehicles: Recent Advances and Challenges. Drones 2022, 6, 85. [Google Scholar] [CrossRef]
- Couturier, A.; Akhloufi, M.A. A review on absolute visual localization for UAV. Robot. Auton. Syst. 2021, 135, 103666. [Google Scholar] [CrossRef]
- Kuriakose, J.; Joshi, S.; Vikram Raju, R.; Kilaru, A. A review on localization in wireless sensor networks. In Proceedings of the Advances in Signal Processing and Intelligent Recognition Systems, Trivandrum, India, 13–15 March 2014; pp. 599–610. [Google Scholar]
- Khan, U.A.; Kar, S.; Moura, J.M. Linear theory for self-localization: Convexity, barycentric coordinates, and cayley–menger determinants. IEEE Access 2015, 3, 1326–1339. [Google Scholar] [CrossRef]
- Khan, U.A.; Kar, S.; Moura, J.M. Distributed sensor localization in random environments using minimal number of anchor nodes. IEEE Trans. Signal Process. 2009, 57, 2000–2016. [Google Scholar] [CrossRef]
- Sippl, M.J.; Scheraga, H.A. Cayley-Menger coordinates. Proc. Natl. Acad. Sci. USA 1986, 83, 2283–2287. [Google Scholar] [CrossRef]
- Han, T.; Lin, Z.; Zheng, R.; Han, Z.; Zhang, H. A barycentric coordinate based approach to three-dimensional distributed localization for wireless sensor networks. In Proceedings of the 2017 13th IEEE International Conference on Control & Automation (ICCA), Ohrid, Macedonia, 3–6 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 600–605. [Google Scholar]
- Diao, Y.; Lin, Z.; Fu, M. A barycentric coordinate based distributed localization algorithm for sensor networks. IEEE Trans. Signal Process. 2014, 62, 4760–4771. [Google Scholar] [CrossRef]
- Huang, X.; Tian, Y.; Wang, B. A distributed localization algorithm based on barycentric coordinate with communication delays and package loss. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 8119–8124. [Google Scholar]
- Xia, Y.; Yu, C.; He, C. An Exploratory Distributed Localization Algorithm Based on 3D Barycentric Coordinates. IEEE Trans. Signal Inf. Process. Over Netw. 2022, 8, 702–712. [Google Scholar] [CrossRef]
- Cao, K.; Han, Z.; Lin, Z.; Xie, L. Bearing-only distributed localization: A unified barycentric approach. Automatica 2021, 133, 109834. [Google Scholar] [CrossRef]
- Ping, H.; Wang, Y.; Li, D.; Chen, W. Understanding Node Localizability in Barycentric Linear Localization. IEEE/ACM Trans. Netw. 2022, 1–16. [Google Scholar] [CrossRef]
- Torgerson, W.S. Multidimensional scaling: I. Theory and method. Psychometrika 1952, 17, 401–419. [Google Scholar] [CrossRef]
- Jia, D.; Li, W.; Wang, P.; Feng, X.; Li, H.; Jiao, Z. An advanced distributed MDS-MAP localization algorithm with improved merging strategy. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1980–1985. [Google Scholar]
- Shang, Y.; Ruml, W. Improved MDS-based localization. In Proceedings of the IEEE INFOCOM 2004, Hong Kong, China, 7–11 March 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 4, pp. 2640–2651. [Google Scholar]
- Kim, E.; Woo, S.; Kim, C.; Kim, K. Lamsm: Localization algorithm with merging segmented maps for underwater sensor networks. In Proceedings of the International Conference on Embedded and Ubiquitous Computing, Taipei, Taiwan, 1–4 December 2007; Springer: Cham, Switzerland, 2007; pp. 445–454. [Google Scholar]
- Sun, T.; Wang, Y..; Li, D.; Gu, Z.; Xu, J. WCS: Weighted Component Stitching for Sparse Network Localization. IEEE/ACM Trans. Netw. 2018, 26, 2242–2253. [Google Scholar] [CrossRef]
- Sun, T.; Wang, Y.; Li, D.; Chen, W.; Gu, Z. Robust component-based network localization with noisy range measurements. In Proceedings of the International Conference on Computer Communication and Networks (Icccn), Hangzhou, China, 30 July 2018–2 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–9. [Google Scholar]
- Shon, M.; Jo, M.; Choo, H. An interactive cluster-based MDS localization scheme for multimedia information in wireless sensor networks. Comput. Commun. 2012, 35, 1921–1929. [Google Scholar] [CrossRef]
- Biswas, P.; Lian, T.C.; Wang, T.C.; Ye, Y. Semidefinite programming based algorithms for sensor network localization. ACM Trans. Sens. Netw. (TOSN) 2006, 2, 188–220. [Google Scholar] [CrossRef]
- Kim, S.; Kojima, M.; Waki, H. Exploiting sparsity in SDP relaxation for sensor network localization. SIAM J. Optim. 2009, 20, 192–215. [Google Scholar] [CrossRef]
- Li, S.; Wang, X.; Zhao, S.; Wang, J.; Li, L. Local semidefinite programming-based node localization system for wireless sensor network applications. IEEE Syst. J. 2013, 8, 879–888. [Google Scholar] [CrossRef]
- Biswas, P.; Toh, K.C.; Ye, Y. A distributed SDP approach for large-scale noisy anchor-free graph realization with applications to molecular conformation. SIAM J. Sci. Comput. 2008, 30, 1251–1277. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Wang, J.; Shen, Y. Distributed 3D relative localization of UAVs. IEEE Trans. Veh. Technol. 2020, 69, 11756–11770. [Google Scholar] [CrossRef]
- Cornejo, A.; Nagpal, R. Distributed range-based relative localization of robot swarms. In Proceedings of the Algorithmic Foundations of Robotics XI: Selected Contributions of the Eleventh International Workshop on the Algorithmic Foundations of Robotics, Istanbul, Turkey, 3–5 August 2014; Springer: Cham, Switzerland, 2015; pp. 91–107. [Google Scholar]
- Mensing, C.; Plass, S. Positioning algorithms for cellular networks using TDOA. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 4, p. IV. [Google Scholar]
- Bejar, B.; Belanovic, P.; Zazo, S. Distributed Gauss–Newton method for localization in Ad-Hoc networks. In Proceedings of the 2010 Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1452–1454. [Google Scholar]
- Priyantha, N.B.; Balakrishnan, H.; Demaine, E.; Teller, S. Anchor-free distributed localization in sensor networks. In Proceedings of the first International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 5–7 November 2003; pp. 340–341. [Google Scholar]
- Medidi, M.; Slaaen, R.A.; Zhou, Y.; Mallery, C.J.; Medidi, S. Scalable localization in wireless sensor networks. In Proceedings of the High Performance Computing-HiPC 2006: 13th International Conference, Bangalore, India, 18–21 December 2006; Springer: Cham, Switzerland, 2006; pp. 522–533. [Google Scholar]
- Leonardos, S.; Daniilidis, K.; Tron, R. Distributed 3-D bearing-only orientation localization. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1834–1841. [Google Scholar]
- Costa, J.A.; Patwari, N.; Hero, A.O. Distributed Weighted-Multidimensional Scaling for Node Localization in Sensor Networks. ACM Trans. Sen. Netw. 2006, 2, 39–64. [Google Scholar] [CrossRef]
- Deng, H.; Fu, Q.; Quan, Q.; Yang, K.; Cai, K.Y. Indoor multi-camera-based testbed for 3-D tracking and control of UAVs. IEEE Trans. Instrum. Meas. 2019, 69, 3139–3156. [Google Scholar] [CrossRef]
- Zhang, Z. Determining the epipolar geometry and its uncertainty: A review. Int. J. Comput. Vis. 1998, 27, 161–195. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, X.; Yang, Y.; Yang, Y. Distributed Cooperative Localization Based on Bearing-Only Sensors. IEEE Sensors J. 2021, 21, 23645–23657. [Google Scholar] [CrossRef]
- Fang, X.; Li, X.; Xie, L. Angle-displacement rigidity theory with application to distributed network localization. IEEE Trans. Autom. Control. 2020, 66, 2574–2587. [Google Scholar] [CrossRef]
- Schiano, F.; Giordano, P.R. Bearing rigidity maintenance for formations of quadrotor UAVs. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1467–1474. [Google Scholar]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and sensor fusion technology in autonomous vehicles: A review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef]
- Thrun, S. Probabilistic robotics. Commun. ACM 2002, 45, 52–57. [Google Scholar] [CrossRef]
- Gustafsson, F. Particle filter theory and practice with positioning applications. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 53–82. [Google Scholar] [CrossRef]
- Wen, C.Y.; Hsiao, Y.C. Decentralized anchor-free localization for wireless ad hoc sensor networks. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2777–2785. [Google Scholar]
- Luo, Q.; Liu, C.; Yan, X.; Shao, Y.; Yang, K.; Wang, C.; Zhou, Z. A Distributed Localization Method for Wireless Sensor Networks Based on Anchor Node Optimal Selection and Particle Filter. Sensors 2022, 22, 1003. [Google Scholar] [CrossRef]
- Piniés, P.; Tardós, J.D. Scalable SLAM building conditionally independent local maps. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 3466–3471. [Google Scholar]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef]
- Mourikis, A.I.; Roumeliotis, S.I. A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation. In Proceedings of the ICRA, Rome, Italy, 10–14 April 2007; Volume 2, p. 6. [Google Scholar]
- Hu, J.S.; Chen, M.Y. A sliding-window visual-IMU odometer based on tri-focal tensor geometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3963–3968. [Google Scholar]
- Guo, C.X.; Kottas, D.G.; DuToit, R.; Ahmed, A.; Li, R.; Roumeliotis, S.I. Efficient Visual-Inertial Navigation using a Rolling-Shutter Camera with Inaccurate Timestamps. In Proceedings of the Robotics: Science and Systems, Virtually, 12–16 July 2014. [Google Scholar]
- Roumeliotis, S.I.; Bekey, G.A. Distributed multirobot localization. IEEE Trans. Robot. Autom. 2002, 18, 781–795. [Google Scholar] [CrossRef]
- Geneva, P.; Eckenhoff, K.; Lee, W.; Yang, Y.; Huang, G. Openvins: A research platform for visual-inertial estimation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4666–4672. [Google Scholar]
- Melnyk, I.V.; Hesch, J.A.; Roumeliotis, S.I. Cooperative vision-aided inertial navigation using overlapping views. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 936–943. [Google Scholar]
- Zhu, P.; Yang, Y.; Ren, W.; Huang, G. Cooperative visual-inertial odometry. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 13135–13141. [Google Scholar]
- Jia, S.; Jiao, Y.; Zhang, Z.; Xiong, R.; Wang, Y. Fej-viro: A consistent first-estimate jacobian visual-inertial-ranging odometry. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1336–1343. [Google Scholar]
- Chenchana, B.; Labbani-Igbida, O.; Renault, S.; Boria, S. Range-based collaborative MSCKF localization. In Proceedings of the 2018 25th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Stuttgart, Germany, 20–22 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Grisetti, G.; Kümmerle, R.; Strasdat, H.; Konolige, K. g2o: A general framework for (hyper) graph optimization. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 11 March 2011; pp. 9–13. [Google Scholar]
- Agarwal, S.; Mierle, K. Ceres Solver: Tutorial & Reference; Google Inc.: Mountain View, CA, USA, 2012; Volume 2, p. 8. [Google Scholar]
- Dellaert, F. Factor Graphs and GTSAM: A Hands-On Introduction; Technical report; Georgia Institute of Technology: Atlanta, GA, USA, 2012. [Google Scholar]
- Rosen, D.M.; Carlone, L.; Bandeira, A.S.; Leonard, J.J. SE-Sync: A certifiably correct algorithm for synchronization over the special Euclidean group. The Int. J. Robot. Res. 2019, 38, 95–125. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5135–5142. [Google Scholar]
- Xu, H.; Wang, L.; Zhang, Y.; Qiu, K.; Shen, S. Decentralized visual-inertial-UWB fusion for relative state estimation of aerial swarm. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 8776–8782. [Google Scholar]
- Calafiore, G.C.; Carlone, L.; Wei, M. Distributed optimization techniques for range localization in networked systems. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2221–2226. [Google Scholar]
- Xu, H.; Zhang, Y.; Zhou, B.; Wang, L.; Yao, X.; Meng, G.; Shen, S. Omni-Swarm: A Decentralized Omnidirectional Visual–Inertial–UWB State Estimation System for Aerial Swarms. IEEE Trans. Robot. 2022, 38, 3374–3394. [Google Scholar] [CrossRef]
- Molina Martel, F.; Sidorenko, J.; Bodensteiner, C.; Arens, M.; Hugentobler, U. Unique 4-DOF relative pose estimation with six distances for UWB/V-SLAM-based devices. Sensors 2019, 19, 4366. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Giorgi, G.; Lee, Y.H.; Günther, C. Enhancing accuracy in visual slam by tightly coupling sparse ranging measurements between two rovers. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 440–446. [Google Scholar]
- Nguyen, T.H.; Nguyen, T.M.; Xie, L. Flexible and Resource-Efficient Multi-Robot Collaborative Visual-Inertial-Range Localization. IEEE Robot. Autom. Lett. 2021, 7, 928–935. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.M.; Xie, L. Range-focused fusion of camera-IMU-UWB for accurate and drift-reduced localization. IEEE Robot. Autom. Lett. 2021, 6, 1678–1685. [Google Scholar] [CrossRef]
- Boroson, E.R.; Hewitt, R.; Ayanian, N.; de la Croix, J.P. Inter-robot range measurements in pose graph optimization. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4806–4813. [Google Scholar]
- Sünderhauf, N.; Protzel, P. Switchable constraints for robust pose graph SLAM. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1879–1884. [Google Scholar]
- Choudhary, S.; Carlone, L.; Nieto, C.; Rogers, J.; Christensen, H.I.; Dellaert, F. Distributed trajectory estimation with privacy and communication constraints: A two-stage distributed gauss-seidel approach. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 5261–5268. [Google Scholar]
- Tian, Y.; Khosoussi, K.; Rosen, D.M.; How, J.P. Distributed certifiably correct pose-graph optimization. IEEE Trans. Robot. 2021, 37, 2137–2156. [Google Scholar] [CrossRef]
- Kaess, M.; Ranganathan, A.; Dellaert, F. iSAM: Incremental smoothing and mapping. IEEE Trans. Robot. 2008, 24, 1365–1378. [Google Scholar] [CrossRef]
- Kaess, M.; Johannsson, H.; Roberts, R.; Ila, V.; Leonard, J.J.; Dellaert, F. iSAM2: Incremental smoothing and mapping using the Bayes tree. Int. J. Robot. Res. 2012, 31, 216–235. [Google Scholar] [CrossRef]
- Cunningham, A.; Paluri, M.; Dellaert, F. DDF-SAM: Fully distributed SLAM using constrained factor graphs. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3025–3030. [Google Scholar]
- Macario Barros, A.; Michel, M.; Moline, Y.; Corre, G.; Carrel, F. A comprehensive survey of visual slam algorithms. Robotics 2022, 11, 24. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar odometry and mapping in real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014; Volume 2, pp. 1–9. [Google Scholar]
- Xie, Y.; Zhang, Y.; Chen, L.; Cheng, H.; Tu, W.; Cao, D.; Li, Q. RDC-SLAM: A real-time distributed cooperative SLAM system based on 3D LiDAR. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14721–14730. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, F. R 3 LIVE: A Robust, Real-time, RGB-colored, LiDAR-Inertial-Visual tightly-coupled state Estimation and mapping package. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 10672–10678. [Google Scholar]
- Lajoie, P.Y.; Ramtoula, B.; Wu, F.; Beltrame, G. Towards collaborative simultaneous localization and mapping: A survey of the current research landscape. arXiv 2021, arXiv:2108.08325. [Google Scholar] [CrossRef]
- Badalkhani, S.; Havangi, R.; Farshad, M. Multi-Robot SLAM in Dynamic Environments with Parallel Maps. Int. J. Humanoid Robot. 2021, 18, 2150011. [Google Scholar] [CrossRef]
- Egodagamage, R.; Tuceryan, M. Distributed monocular visual SLAM as a basis for a collaborative augmented reality framework. Comput. Graph. 2018, 71, 113–123. [Google Scholar] [CrossRef]
- Schmuck, P.; Chli, M. CCM-SLAM: Robust and efficient centralized collaborative monocular simultaneous localization and mapping for robotic teams. J. Field Robot. 2019, 36, 763–781. [Google Scholar] [CrossRef]
- Ouyang, M.; Shi, X.; Wang, Y.; Tian, Y.; Shen, Y.; Wang, D.; Wang, P.; Cao, Z. A Collaborative Visual SLAM Framework for Service Robots. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8679–8685. [Google Scholar]
- Zhao, Y.; Ma, X.; Ye, Y. A Multi-Robot Collaborative Monocular SLAM Based on Semi-Direct Method. In Proceedings of the 2022 Prognostics and Health Management Conference (PHM-2022 London), London, UK, 27–29 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 473–477. [Google Scholar]
- Gao, L.; Battistelli, G.; Chisci, L. Random-finite-set-based distributed multirobot SLAM. IEEE Trans. Robot. 2020, 36, 1758–1777. [Google Scholar] [CrossRef]
- Gouveia, B.D.; Portugal, D.; Silva, D.C.; Marques, L. Computation sharing in distributed robotic systems: A case study on slam. IEEE Trans. Autom. Sci. Eng. 2014, 12, 410–422. [Google Scholar] [CrossRef]
- Zou, D.; Tan, P.; Yu, W. Collaborative visual SLAM for multiple agents: A brief survey. Virtual Real. Intell. Hardw. 2019, 1, 461–482. [Google Scholar] [CrossRef]
- Cieslewski, T.; Choudhary, S.; Scaramuzza, D. Data-efficient decentralized visual SLAM. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2466–2473. [Google Scholar]
- Arandjelovic, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN architecture for weakly supervised place recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 5297–5307. [Google Scholar]
- Lajoie, P.Y.; Ramtoula, B.; Chang, Y.; Carlone, L.; Beltrame, G. DOOR-SLAM: Distributed, online, and outlier resilient SLAM for robotic teams. IEEE Robot. Autom. Lett. 2020, 5, 1656–1663. [Google Scholar] [CrossRef]
- Mangelson, J.G.; Dominic, D.; Eustice, R.M.; Vasudevan, R. Pairwise consistent measurement set maximization for robust multi-robot map merging. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2916–2923. [Google Scholar]
- Huang, Y.; Shan, T.; Chen, F.; Englot, B. DiSCo-SLAM: Distributed scan context-enabled multi-robot lidar slam with two-stage global-local graph optimization. IEEE Robot. Autom. Lett. 2021, 7, 1150–1157. [Google Scholar] [CrossRef]
- Kim, G.; Kim, A. Scan context: Egocentric spatial descriptor for place recognition within 3D point cloud map. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4802–4809. [Google Scholar]
- Pham, V.C.; Juang, J.C. A multi-robot, cooperative, and active slam algorithm for exploration. Int. J. Innov. Comput. Inf. Control. 2013, 9, 2567–2583. [Google Scholar]
- Gálvez-López, D.; Tardos, J.D. Bags of binary words for fast place recognition in image sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Xiong, J.; Cheong, J.W.; Ding, Y.; Xiong, Z.; Dempster, A.G. Efficient Distributed Particle Filter for Robust Range-Only SLAM. IEEE Internet Things J. 2022, 9, 21932–21945. [Google Scholar] [CrossRef]
- Chellali, R. A distributed multi robot SLAM system for environment learning. In Proceedings of the 2013 IEEE Workshop on Robotic Intelligence in Informationally Structured Space (RiiSS), Singapore, 16–19 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 82–88. [Google Scholar]
- Deutsch, I.; Liu, M.; Siegwart, R. A framework for multi-robot pose graph SLAM. In Proceedings of the 2016 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Angkor Wat, Cambodia, 6–10 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 567–572. [Google Scholar]
- Choudhary, S.; Carlone, L.; Nieto, C.; Rogers, J.; Liu, Z.; Christensen, H.I.; Dellaert, F. Multi robot object-based slam. In Proceedings of the 2016 International Symposium on Experimental Robotics, Nagasaki, Japan, 3–8 October 2016; Springer: Cham, Switzerland, 2017; pp. 729–741. [Google Scholar]
- Choudhary, S.; Carlone, L.; Nieto, C.; Rogers, J.; Christensen, H.I.; Dellaert, F. Distributed mapping with privacy and communication constraints: Lightweight algorithms and object-based models. Int. J. Robot. Res. 2017, 36, 1286–1311. [Google Scholar] [CrossRef]
- Chang, Y.; Tian, Y.; How, J.P.; Carlone, L. Kimera-Multi: A system for distributed multi-robot metric-semantic simultaneous localization and mapping. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 11210–11218. [Google Scholar]
- Rosinol, A.; Abate, M.; Chang, Y.; Carlone, L. Kimera: An open-source library for real-time metric-semantic localization and mapping. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1689–1696. [Google Scholar]
- Karrer, M.; Chli, M. Distributed variable-baseline stereo SLAM from two UAVs. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 82–88. [Google Scholar]
- Tian, Y.; Chang, Y.; Arias, F.H.; Nieto-Granda, C.; How, J.P.; Carlone, L. Kimera-multi: Robust, distributed, dense metric-semantic SLAM for multi-robot systems. IEEE Trans. Robot. 2022, 38, 2022–2038. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, W.; Cai, W.; Zhu, W.; Shen, T.; Shu, F.; Wang, J. Communication-Efficient Coordinated RSS-Based Distributed Passive Localization via Drone Cluster. IEEE Trans. Veh. Technol. 2021, 71, 1072–1076. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Bai, X.; Li, D. Communication Efficient, Distributed Relative State Estimation in UAV Networks. IEEE J. Sel. Areas Commun. 2023, 1. [Google Scholar] [CrossRef]
- Liang, J.; Liu, Z.; Zhou, Z.; Xu, Y. Communication-efficient Federated Indoor Localization with Layerwise Swapping Training-Fed Avg. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2022, E105, 1493–1502. [Google Scholar] [CrossRef]
- Mou, Z.; Gao, F.; Liu, J.; Wu, Q. Resilient UAV swarm communications with graph convolutional neural network. IEEE J. Sel. Areas Commun. 2021, 40, 393–411. [Google Scholar] [CrossRef]
- Shell, D.A.; Mataric, M.J. On foraging strategies for large-scale multi-robot systems. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 2717–2723. [Google Scholar]
- Pham, V.C.; Juang, J.C. An improved active SLAM algorithm for multi-robot exploration. In Proceedings of the SICE Annual Conference 2011, Tokyo, Japan, 13–18 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1660–1665. [Google Scholar]
- Gottipati, S.K.; Seo, K.; Bhatt, D.; Mai, V.; Murthy, K.; Paull, L. Deep active localization. IEEE Robot. Autom. Lett. 2019, 4, 4394–4401. [Google Scholar] [CrossRef]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–13 May 2009; Volume 3, p. 5. [Google Scholar]
- Shah, S.; Dey, D.; Lovett, C.; Kapoor, A. Airsim: High-fidelity visual and physical simulation for autonomous vehicles. In Springer Proceedings in Advanced Robotics; Springer: Cham, Switzerland, 2018; pp. 621–635. [Google Scholar]
- OpenSourceRoboticsFoundation. Gazebo. Available online: https://bitbucket.org/osrf/gazebo/src/master/ (accessed on 30 December 2022).
- Dai, X.; Ke, C.; Quan, Q.; Cai, K.Y. RFlySim: Automatic test platform for UAV autopilot systems with FPGA-based hardware-in-the-loop simulations. Aerosp. Sci. Technol. 2021, 114, 106727. [Google Scholar] [CrossRef]
- PIXHAWK. jMAVSim. Available online: https://github.com/PX4/jMAVSim (accessed on 30 December 2022).
- LAAS; ONERA. Morse. Available online: https://github.com/morse-simulator/morse (accessed on 30 December 2022).
- Berndt, J. FightGear. Available online: https://www.flightgear.org (accessed on 30 December 2022).
- Meyer, A. XPlane. Available online: https://www.x-plane.com (accessed on 30 December 2022).
- Levy, S.D. HackflightSim. Available online: https://github.com/simondlevy/HackflightSim (accessed on 30 December 2022).
| Survey | Date | Focus | Multi-Robot Localization | Distributed Methods | Challenges & Trend | Experiment Platform |
|---|---|---|---|---|---|---|
| [15] | 2014 | Collaboration systems | Yes | Few | No | No |
| [16] | 2016 | Localization | Yes | Few | Yes | No |
| [17] | 2019 | Localization, IoT | Yes | Medium | Yes | No |
| [18] | 2020 | Localization, UWB | Yes | Few | No | No |
| [14] | 2021 | Localization, single robot | No | No | Yes | No |
| [21] | 2021 | Localization, single robot | No | No | Yes | No |
| [20] | 2022 | SLAM | Yes | Few | Yes | No |
| Our work | 2022 | Distributed relative localization | Yes | Most | Yes | Yes |
| Algorithm Category | Paper | Anchor Number | Characteristics |
|---|---|---|---|
| Barycentric Coordinate-Based | [24,27,29] | ≥3 | Slow convergence speed; Sensitive to noise; Topology may be limited to convex hull. |
| Distributed MDS | [9,33,50] | ≥0 | Dense network; Sensitive to noise. |
| Distributed SDP | [41,43,49] | ≥0 | Dense network; Sensitive to noise; High convergence speed. |
| Nonlinear Optimization | [11,46] | ≥s | Tolerate to sparsity in some extend; High convergence speed; General model. |
| Solution | Year | Method | Sensors | Characteristics |
|---|---|---|---|---|
| Graph optimization | 2020 | Xu et al. [78] | Camera, IMU, UWB | Involing range measurement. Decentralized scheme. |
| 2022 | Omni-swarm [80] | Fisheye-camera, IMU, UWB | Omni-directional. | |
| 2022 | Nguyen et al. [83] | Camera, IMU, UWB | Range-focused fusion. | |
| Filter | 2018 | Chenchana et al. [71] | Camera, IMU, UWB | Involving range measurement |
| 2021 | DISC-VIO [69] | Camera, IMU | Using MSCKF. Only simulation experiment. | |
| Factor graph | 2013 | DDF-sam [10] | Camera, IMU, GPS | Factor graph. Anti-factor. |
| Gauss–Seidel | 2016 | Choudhary et al. [87] | LIDAR, IMU, wheel odometry | Two-stage distributed Gauss–Seidel approach. |
| Year | Method | Sensors (Frontend) | Backend | Characteristics |
|---|---|---|---|---|
| 2017 | Choudhary et al. [118] | LIDAR, IMU, wheel odometry | Gauss–Seidel | Object-based model |
| 2018 | Cieslewski et al. [106] | Camera | Gauss–Seidel | Data efficient. |
| 2020 | DOOR-SLAM [108] | Camera | Graph optimization | Outlier rejection. Communication Efficiency. |
| 2021 | Karrer et al. [121] | Camera, IMU, UWB | Filter | Invole range measurement |
| 2022 | Kimera-multi [122] | Camera, IMU | Graph optimization | Semantic map. Outlier Rejection. |
| Platform | Open Source | Supported OS | ROS Supported | Model | Scene Quality | Distributed Capabilities |
|---|---|---|---|---|---|---|
| AirSim [131] | ✓ | Win, Linux | ✓ | Car, Quadrotor | High | |
| Gazebo [132] | ✓ | Linux, MacOS | ✓ | Robot, Quadrotor | Middle | |
| RflySim [133] | ✓ | Win | ✓ | Car, Quadrotor, Fixed-wing | High | ✓ |
| Jmavsim [134] | ✓ | Win, Linux, MacOS | ✓ | Quadrotor | Low | |
| Morse [135] | ✓ | Linux | ✓ | Robot, Quadrotor | Middle | |
| FightGear [136] | ✓ | Win, Linux, MacOS | Quadrotor, Fixed-wing | Low | ||
| XPlane [137] | ✓ | Win, Linux | Fixed-wing | High | ||
| HackFlightSim [138] | ✓ | Win, Linux | ✓ | Fixed-wing, Multirotor | Middle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wang, Y.; Li, D.; Zhao, Q. Distributed Relative Localization Algorithms for Multi-Robot Networks: A Survey. Sensors 2023, 23, 2399. https://doi.org/10.3390/s23052399
Wang S, Wang Y, Li D, Zhao Q. Distributed Relative Localization Algorithms for Multi-Robot Networks: A Survey. Sensors. 2023; 23(5):2399. https://doi.org/10.3390/s23052399
Chicago/Turabian StyleWang, Shuo, Yongcai Wang, Deying Li, and Qianchuan Zhao. 2023. "Distributed Relative Localization Algorithms for Multi-Robot Networks: A Survey" Sensors 23, no. 5: 2399. https://doi.org/10.3390/s23052399
APA StyleWang, S., Wang, Y., Li, D., & Zhao, Q. (2023). Distributed Relative Localization Algorithms for Multi-Robot Networks: A Survey. Sensors, 23(5), 2399. https://doi.org/10.3390/s23052399







