Online Calibration Study of Non-Contact Current Sensors for Three-Phase Four-Wire Power Cables
Abstract
1. Introduction
2. Self-Calibration Theory and Simulation
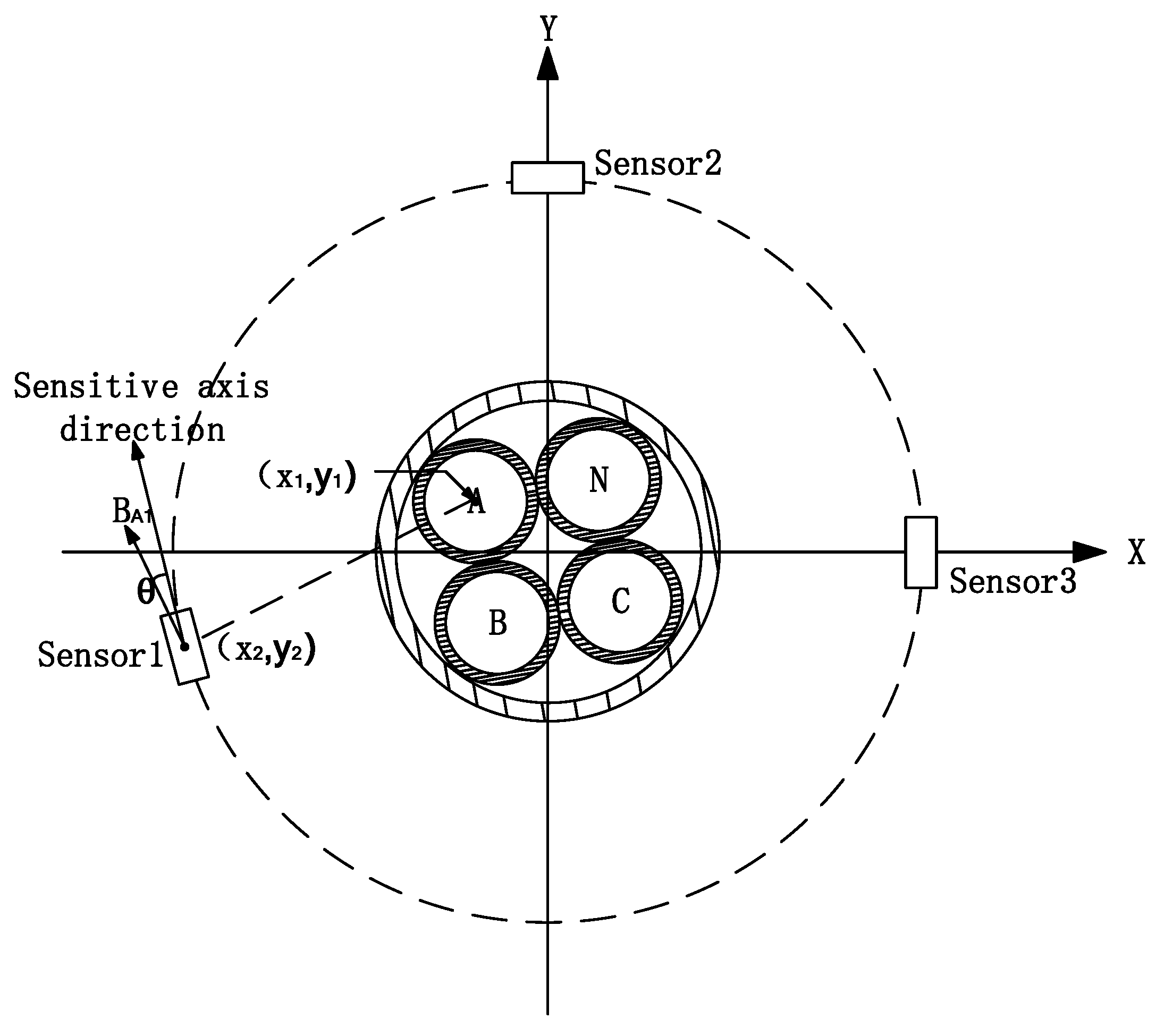
2.1. Multi-Core Cable Measurement Principle
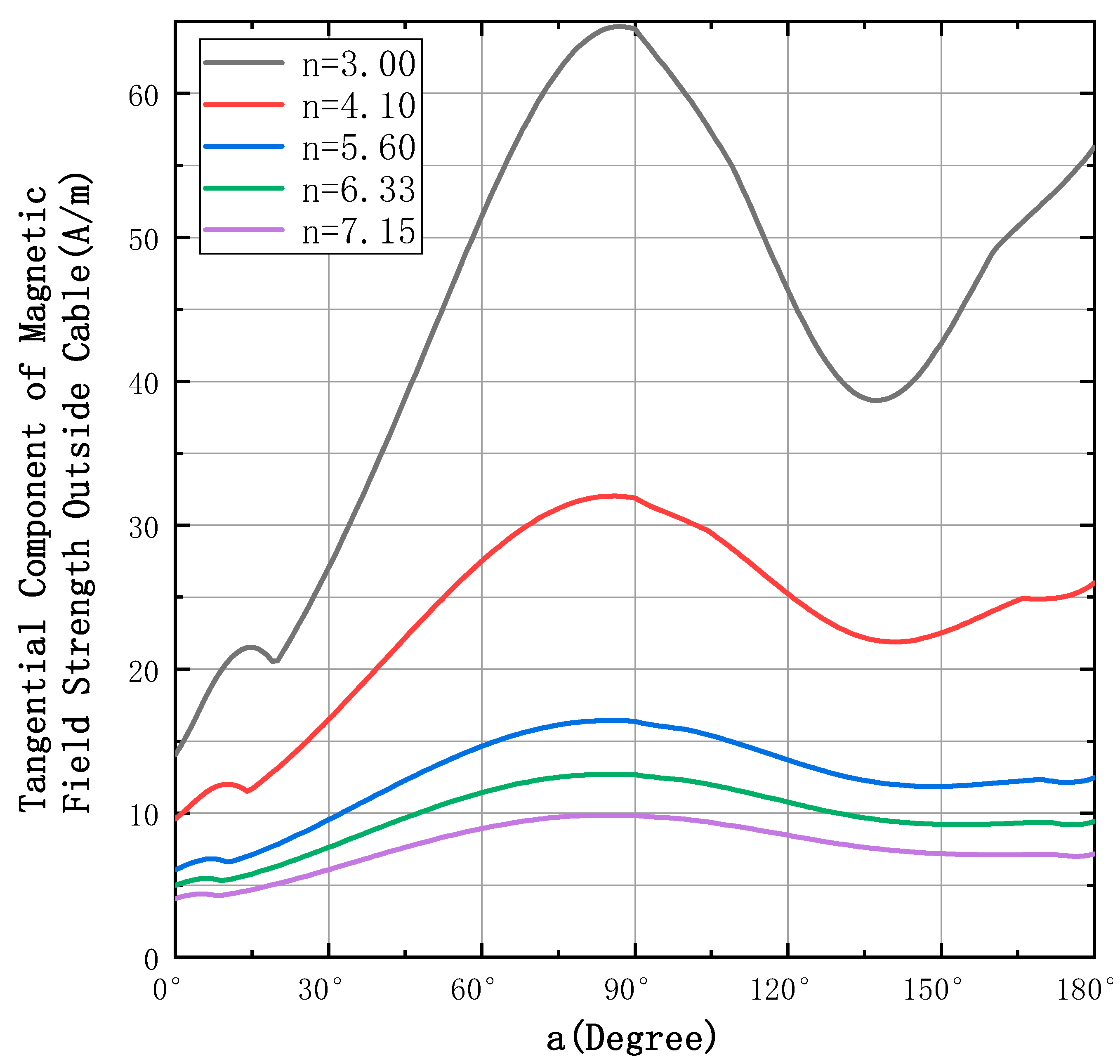
2.2. Tangential Component of Magnetic Field Strength Outside Cable
3. Calibration Scheme and Sensor Array Design
3.1. Calibration Scheme Design
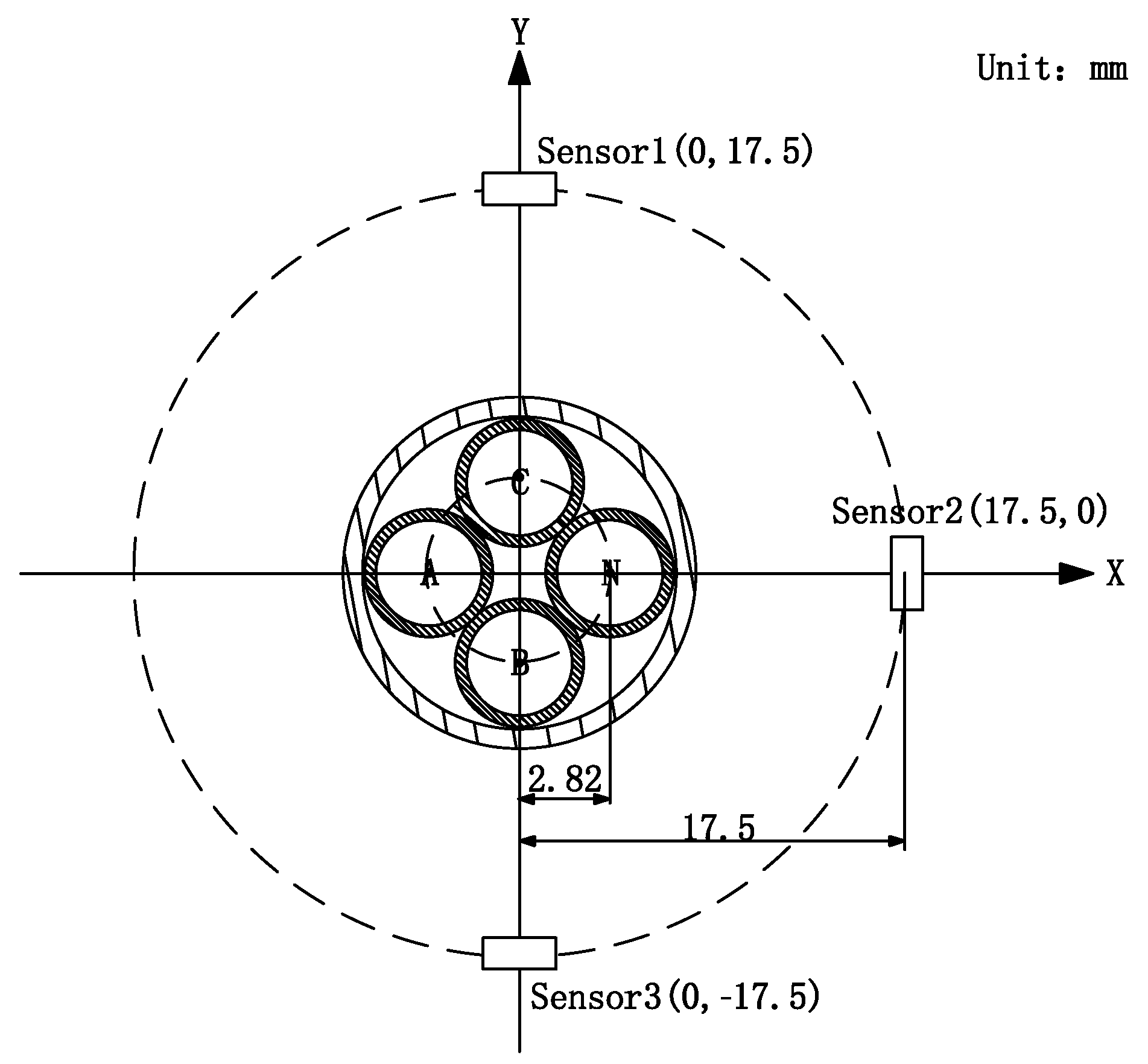
3.2. Sensor Array Design
3.3. Auxiliary Centering Device
4. Experimental Verification and Analysis
4.1. Magnetic Field Strength Distribution Experiment in the Tangential Direction
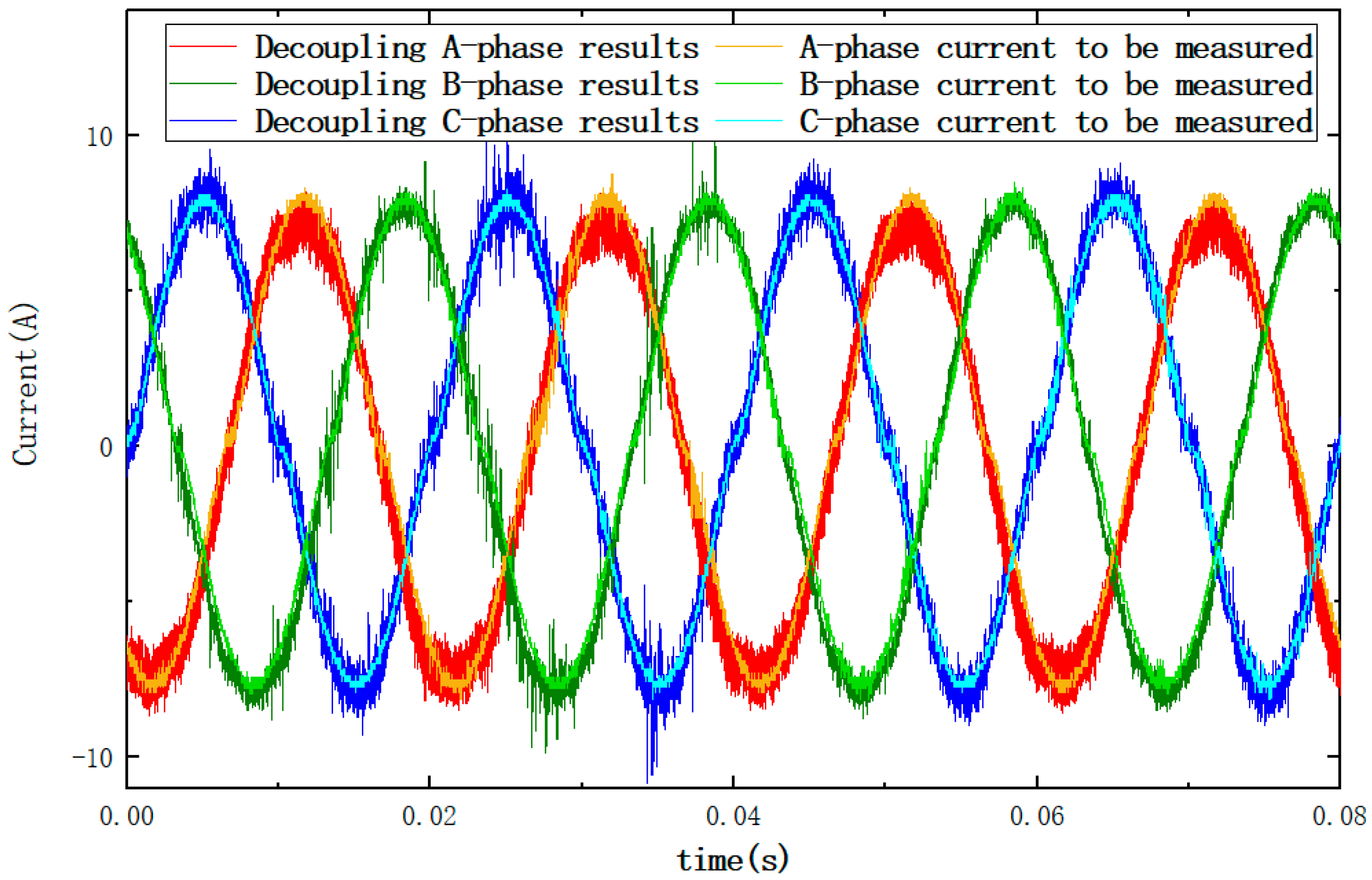
4.2. Experiment of Current Reconstruction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, S.Y.; Song, S.F.; Li, L.X.; Shen, J. Survey on Smart Grid Technology. Power Syst. Technol. 2009, 33, 1–7. [Google Scholar]
- Zhang, P.; Li, F.; Bhatt, N. Next-Generation Monitoring Analysis and Control for the Future Smart Control Center. IEEE Trans. Smart Gmart Grid 2010, 1, 186–192. [Google Scholar] [CrossRef]
- Li, F.; Qiao, W.; Sun, H.; Wang, J.; Xia, Y.; Xu, Z.; Zhang, P. Smart Transmisson Grid: Vision and Framework. IEEE Trans. Smart Grid 2010, 2, 168–177. [Google Scholar] [CrossRef]
- Yang, Q.; Sun, S.P.; Sima, W.X.; He, Y.X.; Luo, M.D. Progress of Advanced Voltage/Current Sensing Techniques for Smart Grid. High Volt. Eng. 2019, 45, 349–367. [Google Scholar]
- Li, L.C.; Zhang, Y.J.; Chen, X.Z.; Cai, Z.X.; Han, Y.X.; Yang, P. Models for the integration of smart grids and energy networks and their development prospects. Autom. Electr. Power Syst. 2016, 40, 1–9. [Google Scholar]
- Boyer, W.; Mcbride, S. Study of Security Attributes of Smart Grid Systems—Current Cyber Security Issues. In Office of Scientific Technical Information Technical Reports; Idaho National Lab. (INL): Idaho Falls, ID, USA, 2009. [Google Scholar]
- Shaojie, G. Study on Current Fault Detection Mechansim for a Three-Phase Five-Wire Cable; Jilin University: Changchun, China, 2022. [Google Scholar]
- Lenz, J.; Edelstein, A.S. Magnetic Sensors and Their Application. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Selva, K.T.; Forsberg, O.A.; Merkoulova, D.; Ghasemifard, F.; Taylor, N.; Norgren, M. Non-contact Current Measurement in Power Transmission Lines. Procedia Technol. 2015, 21, 498–506. [Google Scholar] [CrossRef]
- Kirkham, H. Current Measurement methods for the smart gird. IEEE Power Energy Soc. Gen. Meet. 2009, 6, 26–30. [Google Scholar]
- Ziegler, S.; Woodward, R.C.; Lu, C.; Borle, L.J. Current Sensing Techniques: A Review. IEEE Sens. J. 2009, 4, 354–376. [Google Scholar] [CrossRef]
- Guo, W.; Zhou, S.L.; Wang, L.; Pei, H.; Zhang, C.; Li, C.H. Design and application of power cable condition online monitoring system. High Volt. Eng. 2019, 45, 3459–3466. [Google Scholar]
- Sun, T.X. Three-core cable self-energy extraction method and its application in thermal state monitoring. High Volt. Appar. 2019, 55, 215–220. [Google Scholar]
- Ma, G.M.; Wang, S.H.; Qin, W.Q.; Zhang, B.; Zhang, J.Z.; Chen, C. Research and Prospect of Optical Fiber Sensing of Transmission Line Operation Status. High Volt. Eng. 2022, 48, 3032–3047. [Google Scholar]
- Mohamed, E.; Amr, I.; Abd-Elhady, M. A Proposed Non-Invasive Rogowski Coil Designfor Measuring 3-Phase Currents Througha 3-Core Cable. IEEE Sens. J. 2021, 21, 593–599. [Google Scholar]
- Sun, X.; Poon, K.C.; Ghan, G.; Sum, C.L.; Lee, W.K.; Jiang, L.J.; Philip, W.T.P. Operation-State Monitoring and Energization-Status Identification for Underground Power Cables by Magnetic Field Sensing. IEEE Sens. J. 2013, 13, 4527–4533. [Google Scholar] [CrossRef]
- Yanling, Y.; Shisong, L.; Dong, J.; Songling, H.; Wei, Z. Measuring method for phase current of symmetrical three-core power cable based on magnetic sensors. CHINA Meas. Test 2016, 42, 29–32+72. [Google Scholar]
- Hou, Y.P. Research on Piezoelectric Beam Current Sensor for Three-Phase Four-Wire Conductors; Jilin University: Changchun, China, 2019. [Google Scholar]
- Gao, P. Power System Current Measurement Using Sensor Array Techniques; University of Alberta: Edmonton, AB, Canada, 2018. [Google Scholar]
- Donnal, J.S.; Leeb, S.B. Noncontact Power Meter. IEEE Sens. J. 2015, 15, 1161–1169. [Google Scholar] [CrossRef]
- Donnal, J. MIT-Home NILM-A Comprehensive Energy Monitoring Toolkit; Massachusetts Institute of Technology: Cambridge, MA, USA, 2014. [Google Scholar]
- Donnal, J.S.; Lindahl, P.; Lawrence, D.; Zachar, R.; Leeb, S. Untangling Non-Contact Power Monitoring Puzzles. IEEE Sens. J. 2017, 17, 3542–3550. [Google Scholar] [CrossRef]







| Extreme Point | n = 3 | n = 4.1 | n = 5.6 | n = 6.33 | n = 7.15 |
|---|---|---|---|---|---|
| First minimum point | 0° | 0° | 0° | 0° | 0° |
| First maximum point | 16° | 13° | 8° | 7° | 6° |
| Second minimum point | 21° | 15° | 12° | 11° | 9° |
| Second maximum point | 89° | 88° | 86° | 85° | 86° |
| Third minimum point | 139° | 142° | 149° | 152° | 162° |
| Third maximum point | \ | 167° | 170° | 172° | 173° |
| Fourth minimum point | \ | 172° | 177° | 179° | 179° |
| Fourth maximum point | 180° | 180° | 180° | 180° | 180° |
| Simulation of Magnetic Field Strength Distribution Law | |
|---|---|
| Rule one | the minimum value occurs at a = 0°, the position directly opposite the N phase. |
| Rule two | the maximum value occurs in the interval of a ∈ [−90°, −85°) ∪ (85°, 90°]. |
| Rule three | a ∈ [0°, 180°] or a ∈ [180°, 360°] there are four extreme value points and four minimal value points in the interval. |
| Rule four | the positions of phases B and C are in the monotonic interval. |
| Minimum Point | |
|---|---|
| First minimum point | a = 0° |
| First maximum point | |
| Second minimum point | Between the second and third maximum values |
| Second maximum point | Between the third and fourth maximum values |
| Maximum Point | |
| Third minimum point | Between the first and second minimum values |
| Third maximum point | a∈ [−90°, −85°) ∪ (85°, 90°] |
| Fourth minimum point | |
| Fourth maximum point | a = 180° |
| Experimental Apparatus | Introduction |
|---|---|
| Three-phase current source | WuXi Electronic Technology Co., Ltd. ANZ13-3KVA-1000 Hz, maximum output current 6 A |
| Three-phase four-wire power cable | 4 × 6 mm2, GB/T5013.4-2008 |
| Oscilloscope | Tektronix MDO3024 |
| Three-phase resistor | 10 ± 0.5 Ω |
| Auxiliary centering device | Photosensitive resin 3D printing, molding size tolerance ±0.2 mm |
| Fluxgate chip DRV425RTJT | TEXAS INSTRUMENTS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, P.; Zhang, W.; Yang, L.; Zhang, W.; Yu, H.; Huang, R.; Zhu, J.; Liu, X. Online Calibration Study of Non-Contact Current Sensors for Three-Phase Four-Wire Power Cables. Sensors 2023, 23, 2391. https://doi.org/10.3390/s23052391
Yan P, Zhang W, Yang L, Zhang W, Yu H, Huang R, Zhu J, Liu X. Online Calibration Study of Non-Contact Current Sensors for Three-Phase Four-Wire Power Cables. Sensors. 2023; 23(5):2391. https://doi.org/10.3390/s23052391
Chicago/Turabian StyleYan, Peiwu, Wenbin Zhang, Le Yang, Wenying Zhang, Hao Yu, Rujin Huang, Junyu Zhu, and Xi Liu. 2023. "Online Calibration Study of Non-Contact Current Sensors for Three-Phase Four-Wire Power Cables" Sensors 23, no. 5: 2391. https://doi.org/10.3390/s23052391
APA StyleYan, P., Zhang, W., Yang, L., Zhang, W., Yu, H., Huang, R., Zhu, J., & Liu, X. (2023). Online Calibration Study of Non-Contact Current Sensors for Three-Phase Four-Wire Power Cables. Sensors, 23(5), 2391. https://doi.org/10.3390/s23052391






