On the Feasibility of Monitoring Power Transformer’s Winding Vibration and Temperature along with Moisture in Oil Using Optical Sensors
Abstract
1. Introduction
- Insufficient drying at the manufacturing site;
- Exposure to humid air during site installation/commissioning or maintenance;
- Aging of the cellulose produces water;
- Leaking gaskets;
- Malfunction of the dehydrating breather;
- etc.
2. Materials and Methods
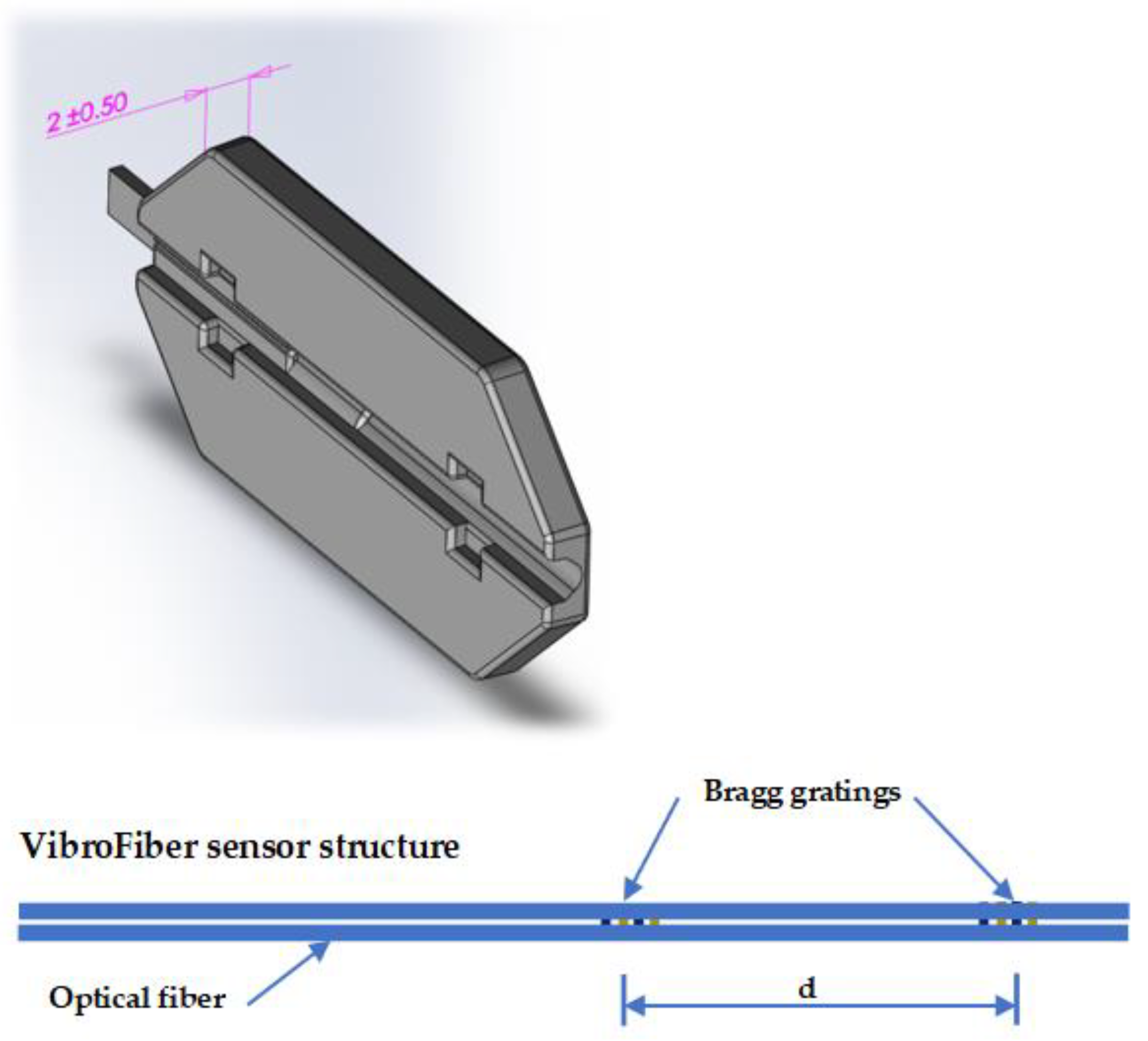
2.1. Fiber Bragg Grating (FBG) Vibration Model
2.2. Fiber Bragg Grating (FBG) Temperature Model
2.3. Fiber Bragg Grating (FBG) Moisture Model
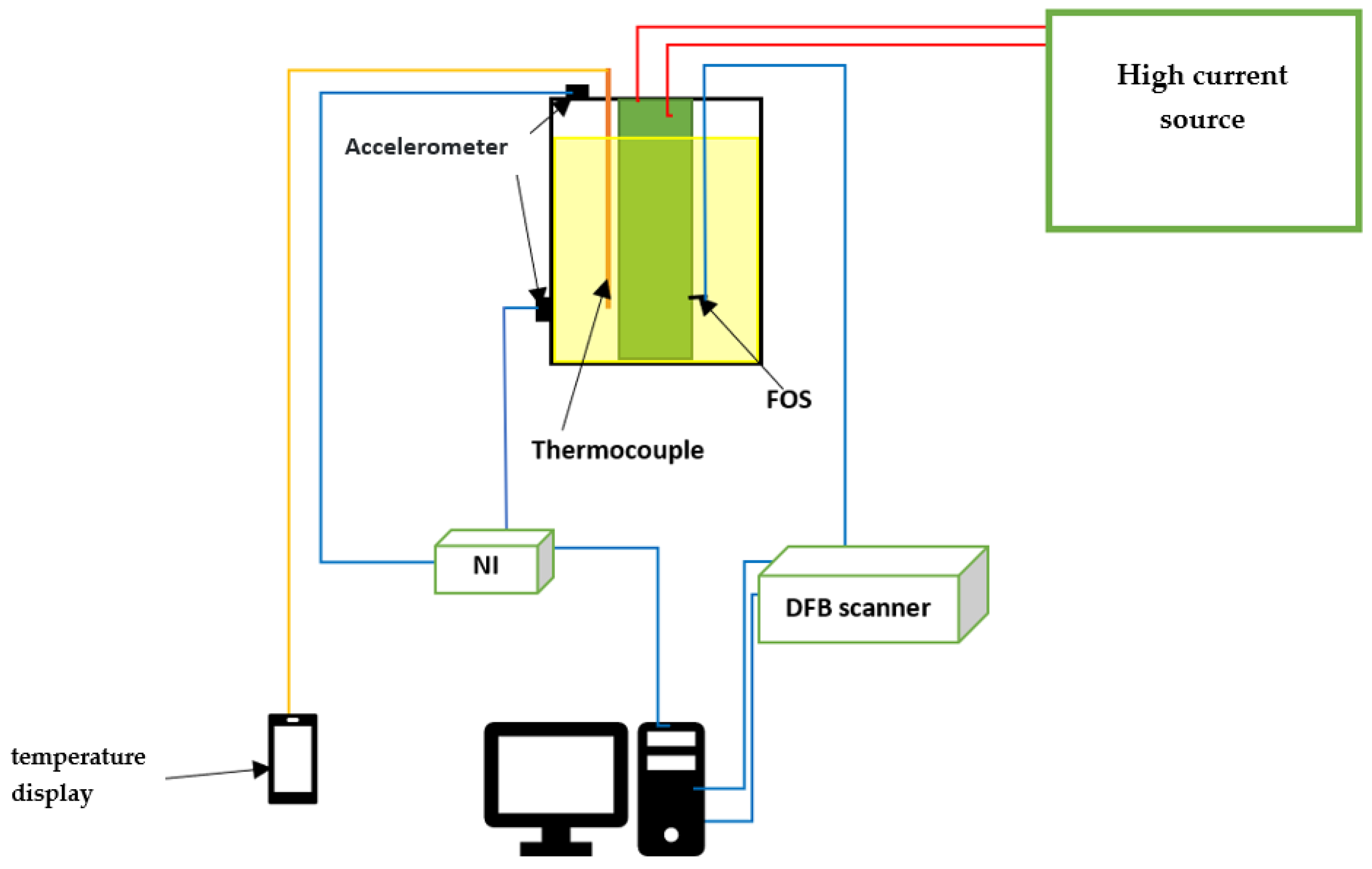
3. Laboratory Setup
4. Results and Discussion
4.1. Load-Dependent Vibrations
4.2. Temperature Monitoring with the Sensor
4.3. Moisture in Oil Assessment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, F.H.; Xu, J.; Jin, Z.J.; Gui, S.S. Experimental Research of Vibration Sweep Frequency Response Analysis to Detect the Winding Deformation of Power Transformer. In IEEE PES T&D 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Hu, C.; Wang, P.; Youn, B.D.; Lee, W.-R.; Yoon, J.T. Copula-Based Statistical Health Grade System Against Mechanical Faults of Power Transformers. IEEE Trans. Power Deliv. 2012, 27, 1809–1819. [Google Scholar] [CrossRef]
- Garcia, B.; Burgos, J.C.; Alonso, A.M. Transformer tank vibration modeling as a method of detecting winding deformations-part I: Theoretical foundation. IEEE Trans. Power Deliv. 2006, 21, 157–163. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Ma, Y.; He, L.; Ma, H.; Wu, J. Mechanical Fault Diagnosis of Transformer Based on Vibration Signal Spectrum Centroid. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanging, China, 20–23 September 2020; pp. 1–5. [Google Scholar]
- Bartoletti, C.; Desiderio, M.; Carlo, D.D.; Fazio, G.; Muzi, F.; Sacerdoti, G.; Salvatori, F. Vibro-acoustic techniques to diagnose power transformers. IEEE Trans. Power Deliv. 2004, 19, 221–229. [Google Scholar] [CrossRef]
- Murugan, R.; Ramasamy, R. Understanding the power transformer component failures for health index-based maintenance planning in electric utilities. Eng. Fail. Anal. 2019, 96, 274–288. [Google Scholar] [CrossRef]
- Hong Kaixing, P.Z. Vibration model of power transformer under short-circuit condition. In Proceedings of the 2009 International Conference on Electrical Machines and Systems, Incheon, Republic of Korea, 10–13 October 2009. [Google Scholar]
- Kuhn, G.G.; Sousa, K.M.; Martelli, C.; Bavastri, C.A.; Silva, J.C.C.d. Embedded FBG Sensors in Carbon Fiber for Vibration and Temperature Measurement in Power Transformer Iron Core. IEEE Sens. J. 2020, 20, 13403–13410. [Google Scholar] [CrossRef]
- Hong, K.; Huang, H.; Fu, Y.; Zhou, J. A vibration measurement system for health monitoring of power transformers. Measurement 2016, 93, 135–147. [Google Scholar] [CrossRef]
- Duan, X.; Zhao, T.; Liu, J.; Zhang, L.; Zou, L. Analysis of Winding Vibration Characteristics of Power Transformers Based on the Finite-Element Method. Energies 2018, 11, 2404. [Google Scholar] [CrossRef]
- Zhou, H.; Hong, K.; Huang, H.; Zhou, J. Transformer winding fault detection by vibration analysis methods. Appl. Acoust. 2016, 114, 136–146. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, N.; Du, J.; Han, F.; Wang, H. A Novel Approach to Investigate the Core Vibration in Power Transformers. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Suassuna de Andrade Ferreira, R.; Picher, P.; Ezzaidi, H.; Fofana, I. A Machine-Learning Approach to Identify the Influence of Temperature on FRA Measurements. Energies 2021, 14, 5718. [Google Scholar] [CrossRef]
- Kennedy, G.; McGrail, A.; Lapworth, J. Using Cross-Correlation Coefficients to Analyze Transformer Sweep Frequency Response Analysis (SFRA) Traces. In Proceedings of the IEEE PES PowerAfrica 2007 Conference and Exposition Johannesburg, Johannesburg, South Africa, 16–20 July 2007. [Google Scholar]
- Dawood, K.; Alboyaci, B.; Cinar, M.A.; Sonmez, O. A New method for the Calculation of Leakage Reactance in Power Transformers. J. Electr. Eng. Technol. 2017, 12, 1883–1890. [Google Scholar] [CrossRef]
- Kung, P.; Idsinga, R.; Fu, J.B.; Durand, H.V.; Yang, C.S.; Comanici, M.I. Online detection of windings distortion in power transformers by direct vibration measurement using a thin fiber optics sensor. In Proceedings of the 2016 IEEE Electrical Insulation Conference (EIC), Montreal, QC, Canada, 19–22 June 2016; pp. 576–578. [Google Scholar]
- Arakelian, V.G.; Fofana, I. Water in Oil-Filled High-Voltage Equipment Part I: States, Solubility, and Equilibrium in Insulating Materials. IEEE Electr. Insul. Mag. 2007, 23, 15–27. [Google Scholar] [CrossRef]
- Arakelian, V.; Fofana, I. Water in Oil-Filled High-Voltage Equipment Part II: Water Content as Physicochemical Tools for Insulation Condition Diagnostic. IEEE Electr. Insul. Mag. 2007, 23, 15–24. [Google Scholar] [CrossRef]
- Boudaden, J.; Steinmaßl, M.; Endres, H.-E.; Drost, A.; Eisele, I.; Kutter, C.; Müller-Buschbaum, P. Polyimide-Based Capacitive Humidity Sensor. Sensors 2018, 18, 1516. [Google Scholar] [CrossRef] [PubMed]
- Martin, D.; Saha, T.; Perkasa, C.; Lelekakis, N.; Gradnik, T. Fundamental concepts of using water activity probes to assess transformer insulation water content. IEEE Electr. Insul. Mag. 2016, 32, 9–16. [Google Scholar] [CrossRef]
- Ansari, M.A.; Martin, D.; Saha, T.K. Advanced Online Moisture Measurements in Transformer Insulation Using Optical Sensors. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1803–1810. [Google Scholar] [CrossRef]
- Lin, Y.; Gong, Y.; Wu, Y.; Wu, H. Polyimide-coated fiber Bragg grating for relative humidity sensing. Photonic Sens. 2015, 5, 60–66. [Google Scholar] [CrossRef]
- Fofana, I. 50 years in the development of insulating liquids. IEEE Electr. Insul. Mag. 2013, 29, 13–25. [Google Scholar] [CrossRef]
- Sékongo, B.; Brettschneider, S.; Rao, U.M.; Fofana, I.; Jabbari, M.; Picher, P.; Yeo, Z. Pre-Breakdown and Breakdown Behavior of Synthetic and Natural Ester Liquids under AC Stress. Energies 2022, 15, 167. [Google Scholar] [CrossRef]
- Sékongo, B.; Rao, U.M.; Fofana, I.; Jabbari, M.; Akre, S.; Yeo, Z. Temperature dependence of the pre-breakdown and breakdown phenomena in natural esters under AC stress. IET Sci. Meas. Technol. 2020, 14, 762–769. [Google Scholar] [CrossRef]
- Yao, K.; Lin, Q.; Jiang, Z.; Zhao, N.; Tian, B.; Shi, P.; Peng, G.-D. Modeling and Analysis of a Combined Stress-Vibration Fiber Bragg Grating Sensor. Sensors 2018, 18, 743. [Google Scholar] [CrossRef] [PubMed]
- Kung, P. Generator Insulation-Aging On-Line Monitoring Technique Based on Fiber Optic Detecting Technology. In Simulation and Modelling of Electrical Insulation Weaknesses in Electrical Equipment; Intechopen: London, UK, 2018. [Google Scholar] [CrossRef]
- Habel, J.; Boilard, T.; Frenière, J.-S.; Trépanier, F.; Bernier, M. Femtosecond FBG Written through the Coating for Sensing Applications. Sensors 2017, 17, 2519. [Google Scholar] [CrossRef] [PubMed]
- Akre, S.; Vahid, B.; Peter, K.; Issouf, F. Assessing Water Content and Vibration from Dynamic Measurement in Transformer. In Proceedings of the CIGRE Canada Conference, Montreal, QC, Canada, 16–19 September 2019; Volume CIGRE-177. [Google Scholar]
- CIGRE. Moisture Measurement and Assessment in Transformer Insulation—Evaluation of Chemical Methods and Moisture Capacitive Sensors; Brochure, no. 741; CIGRÉ: Paris, France, 2018. [Google Scholar]
- Buck, A.L. New Equations for Computing Vapor Pressure and Enhancement Factor. J. Appl. Meteorol. Climatol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Beltle, M.; Tenbohlen, S. Usability of vibration measurement for power transformer diagnosis and monitoring. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23–27 September 2012; pp. 281–284. [Google Scholar]
- Fofana, I.; Borsi, H.; Gockenbach, E. Fundamental investigations on some transformer liquids under various outdoor conditions. IEEE Trans. Dielectr. Electr. Insul. 2001, 8, 1040–1047. [Google Scholar] [CrossRef]














Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akre, S.; Fofana, I.; Yéo, Z.; Brettschneider, S.; Kung, P.; Sékongo, B. On the Feasibility of Monitoring Power Transformer’s Winding Vibration and Temperature along with Moisture in Oil Using Optical Sensors. Sensors 2023, 23, 2310. https://doi.org/10.3390/s23042310
Akre S, Fofana I, Yéo Z, Brettschneider S, Kung P, Sékongo B. On the Feasibility of Monitoring Power Transformer’s Winding Vibration and Temperature along with Moisture in Oil Using Optical Sensors. Sensors. 2023; 23(4):2310. https://doi.org/10.3390/s23042310
Chicago/Turabian StyleAkre, Simplice, Issouf Fofana, Zié Yéo, Stephan Brettschneider, Peter Kung, and Bekibenan Sékongo. 2023. "On the Feasibility of Monitoring Power Transformer’s Winding Vibration and Temperature along with Moisture in Oil Using Optical Sensors" Sensors 23, no. 4: 2310. https://doi.org/10.3390/s23042310
APA StyleAkre, S., Fofana, I., Yéo, Z., Brettschneider, S., Kung, P., & Sékongo, B. (2023). On the Feasibility of Monitoring Power Transformer’s Winding Vibration and Temperature along with Moisture in Oil Using Optical Sensors. Sensors, 23(4), 2310. https://doi.org/10.3390/s23042310










