Testing Thermostatic Bath End-Scale Stability for Calibration Performance with a Multiple-Sensor Ensemble Using ARIMA, Temporal Stochastics and a Quantum Walker Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Aspects in the Methodological Developments
2.1.1. The Statistical Time Series Screening Assisted by ARIMA Modeling
2.1.2. Time Series Mode Screening Using a Quantum Walker
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
2.2. The Case Study for Testing Temperature Stability with a Sensor Ensemble
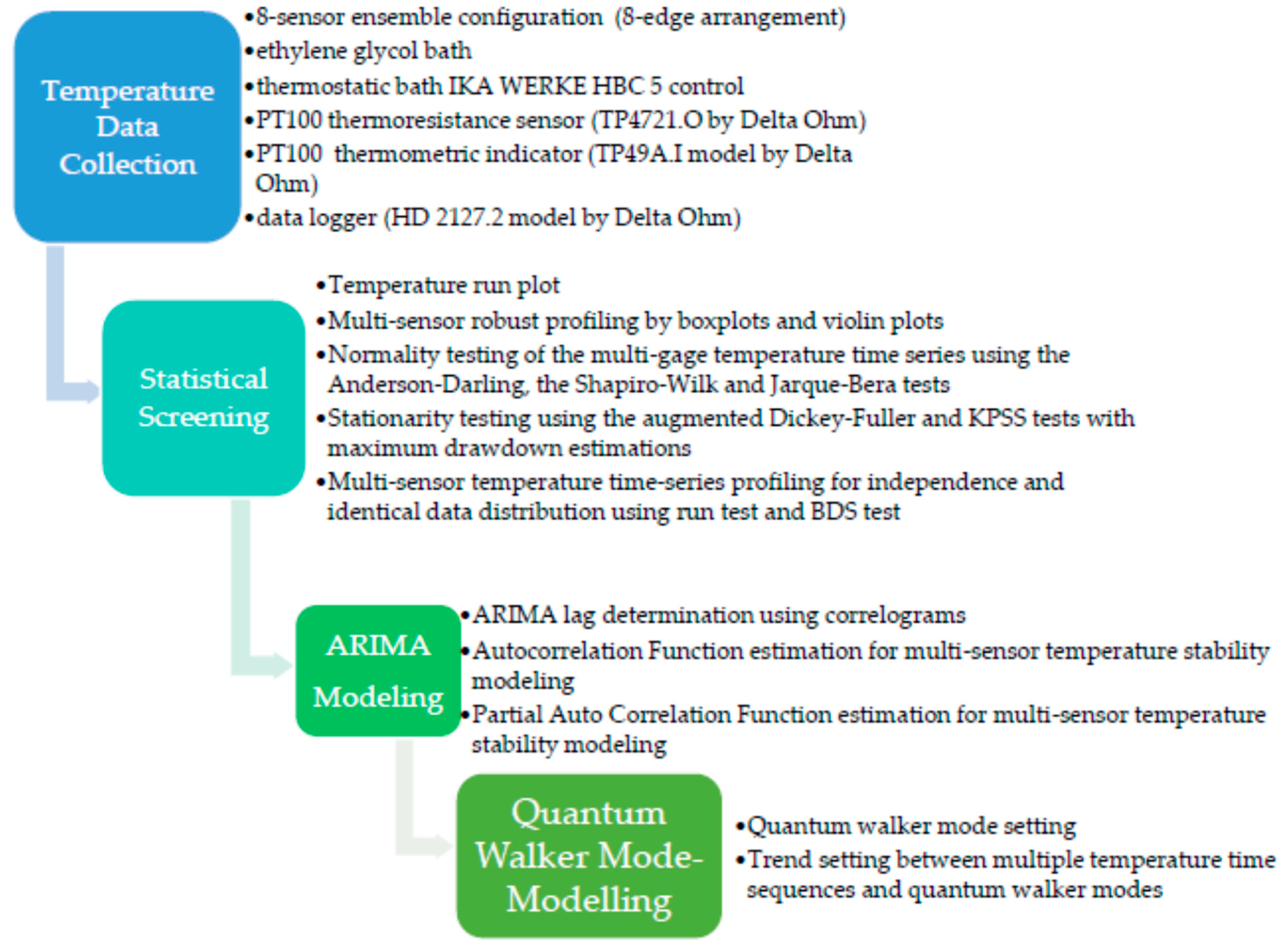
2.3. The Methodological Outline
- (1)
- Determine the type of physical measurements that must be performed in the calibration gage limits.
- (2)
- Select the appropriate testing medium.
- (3)
- Determine a convenient size for the sensor ensemble and spatially arrange them in the testing medium.
- (4)
- Collect and record the data streaks from each sensor unit in the ensemble.
- (5)
- (6)
- (7)
- (8)
- (9)
- Assess the ARIMA modeling results of the individual temperature data streaks by considering the lags of the stationarized series (AR terms) and the lags of the forecast errors (MA terms) [28].
- (10)
- Evaluate the significance of the AR and MA coefficients.
- (11)
- Index the individual time series modes using a continuous-time quantum random walk algorithm and check for proper model fitting by testing the behavior of the residuals on a Q-Q plot.
- (12)
- Retain and compare the characteristic number of modes among the individual temperature data streaks. Finally, inspect the selected cut of modes for similarities among different time series and test the time sequences according to the Akaike information criterion [70].
2.4. Computational Aids
3. Results
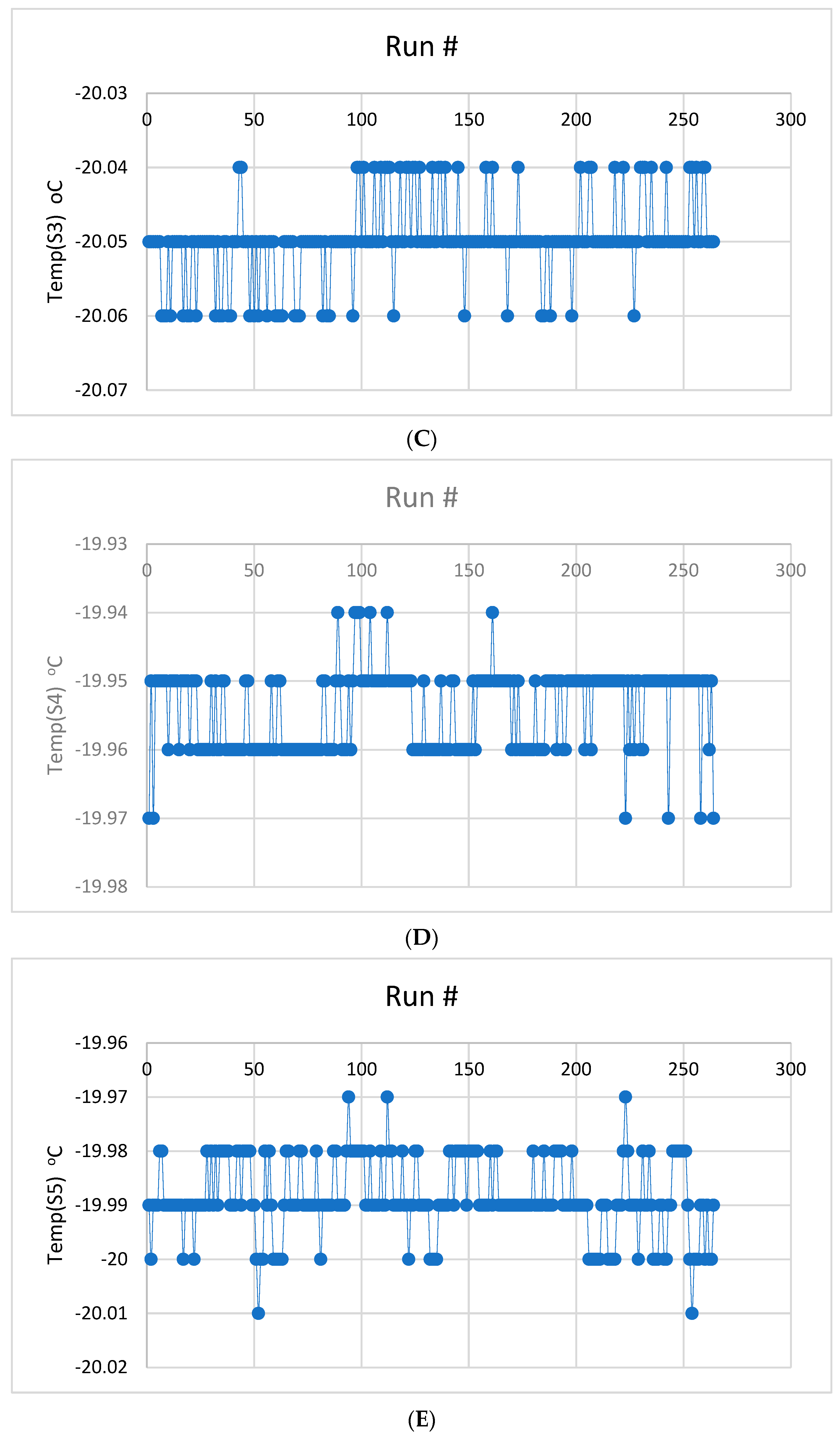
3.1. Statistical Analysis of the Sensor Ensemble Time Series Data
3.1.1. Basic Inferential Testing of the Sensor Ensemble Temperature Data Streaks
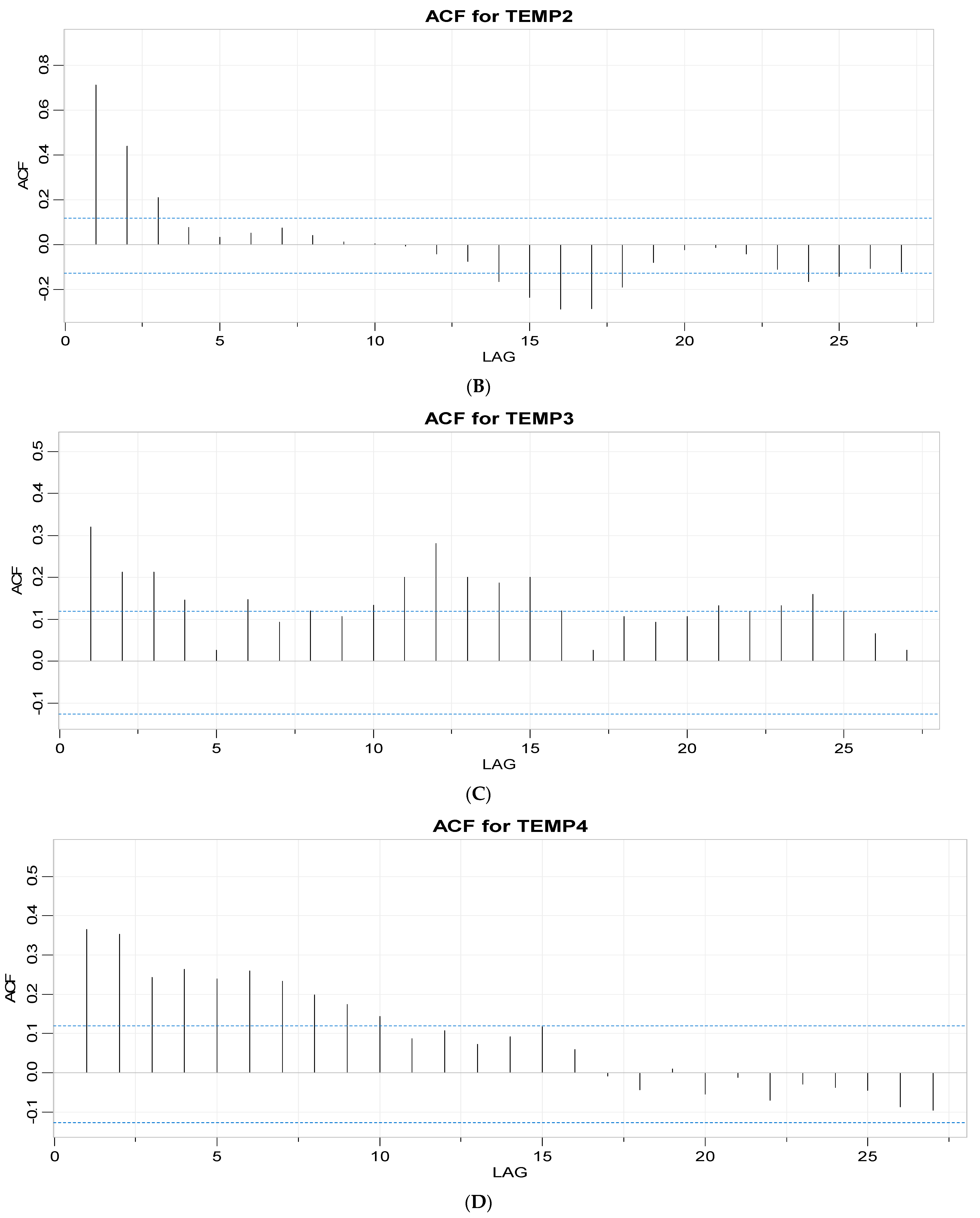
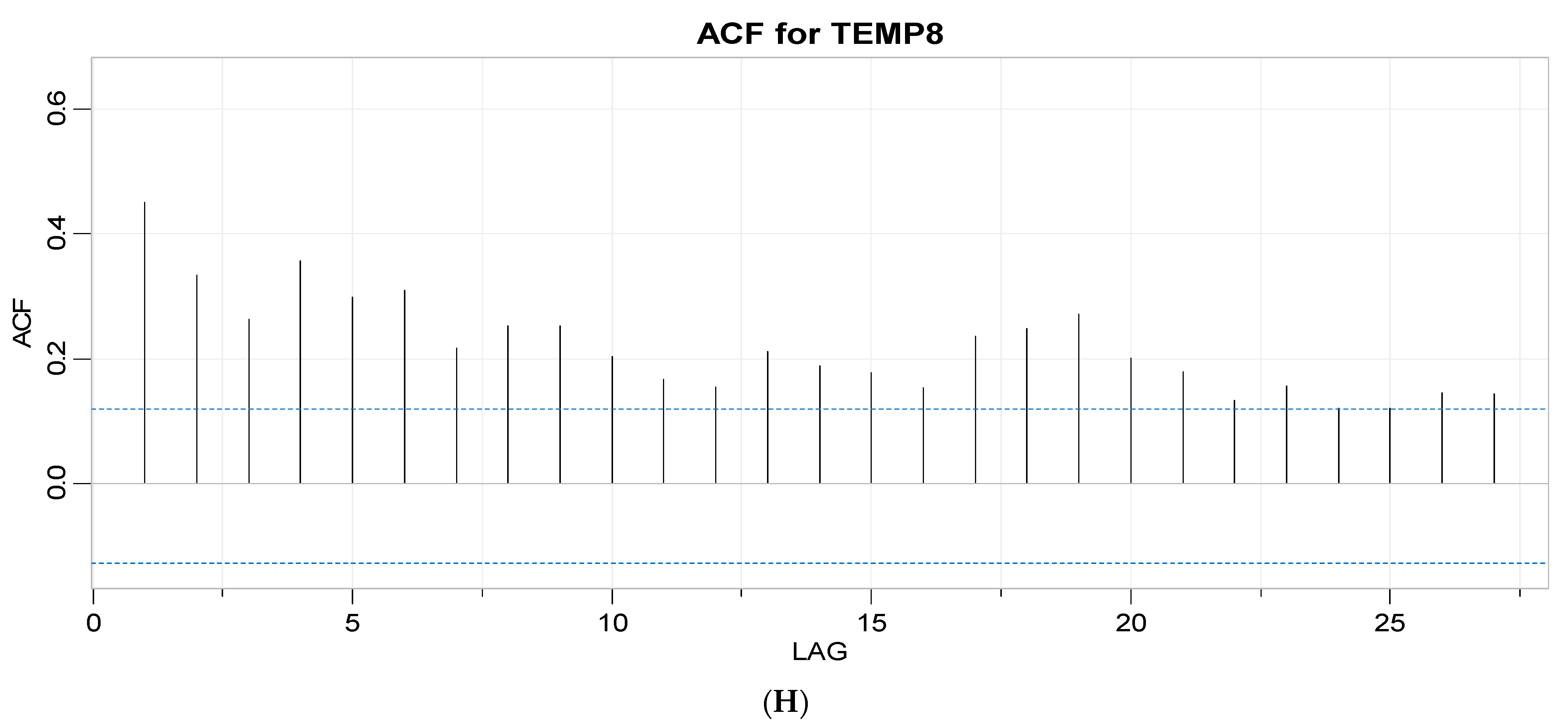
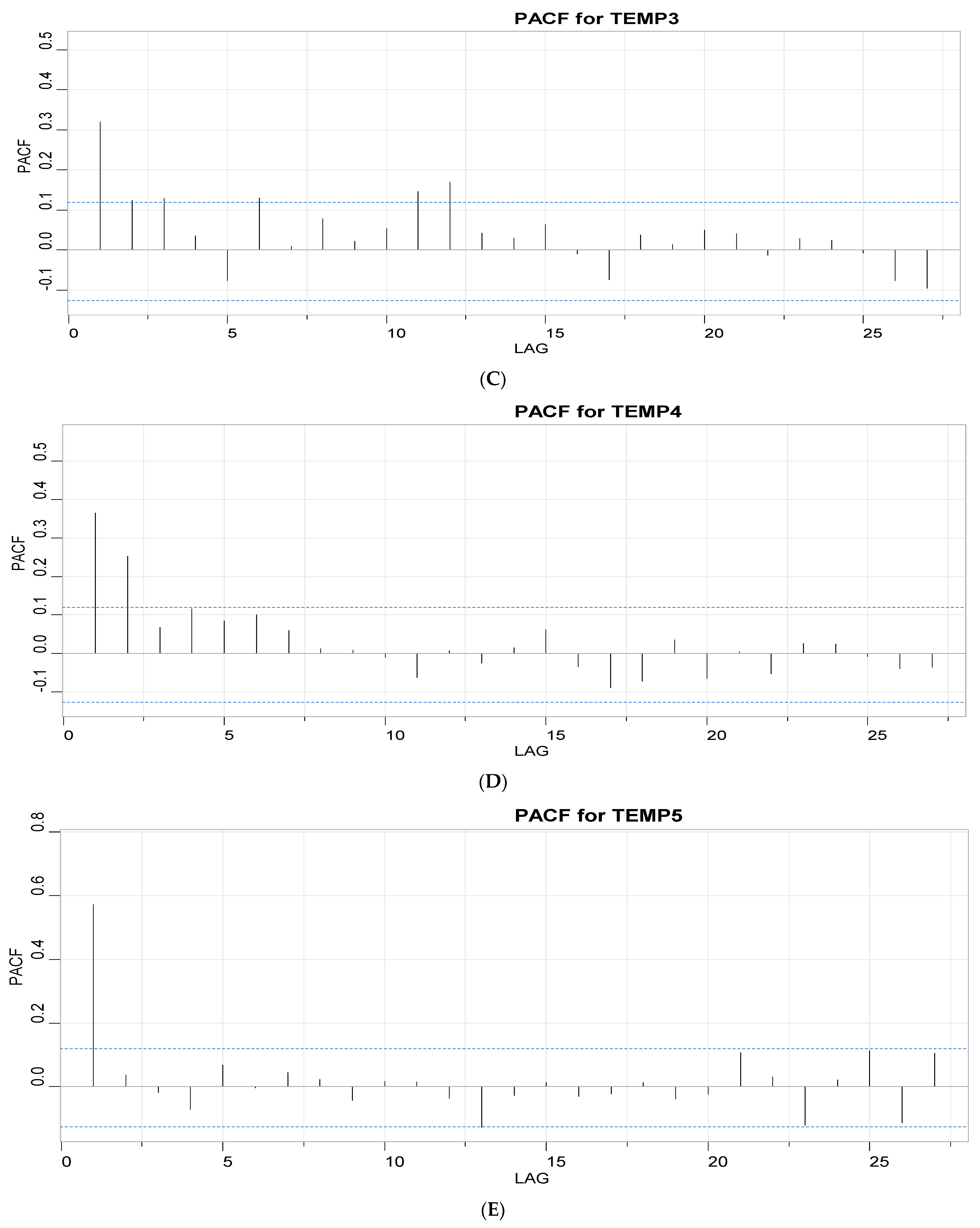
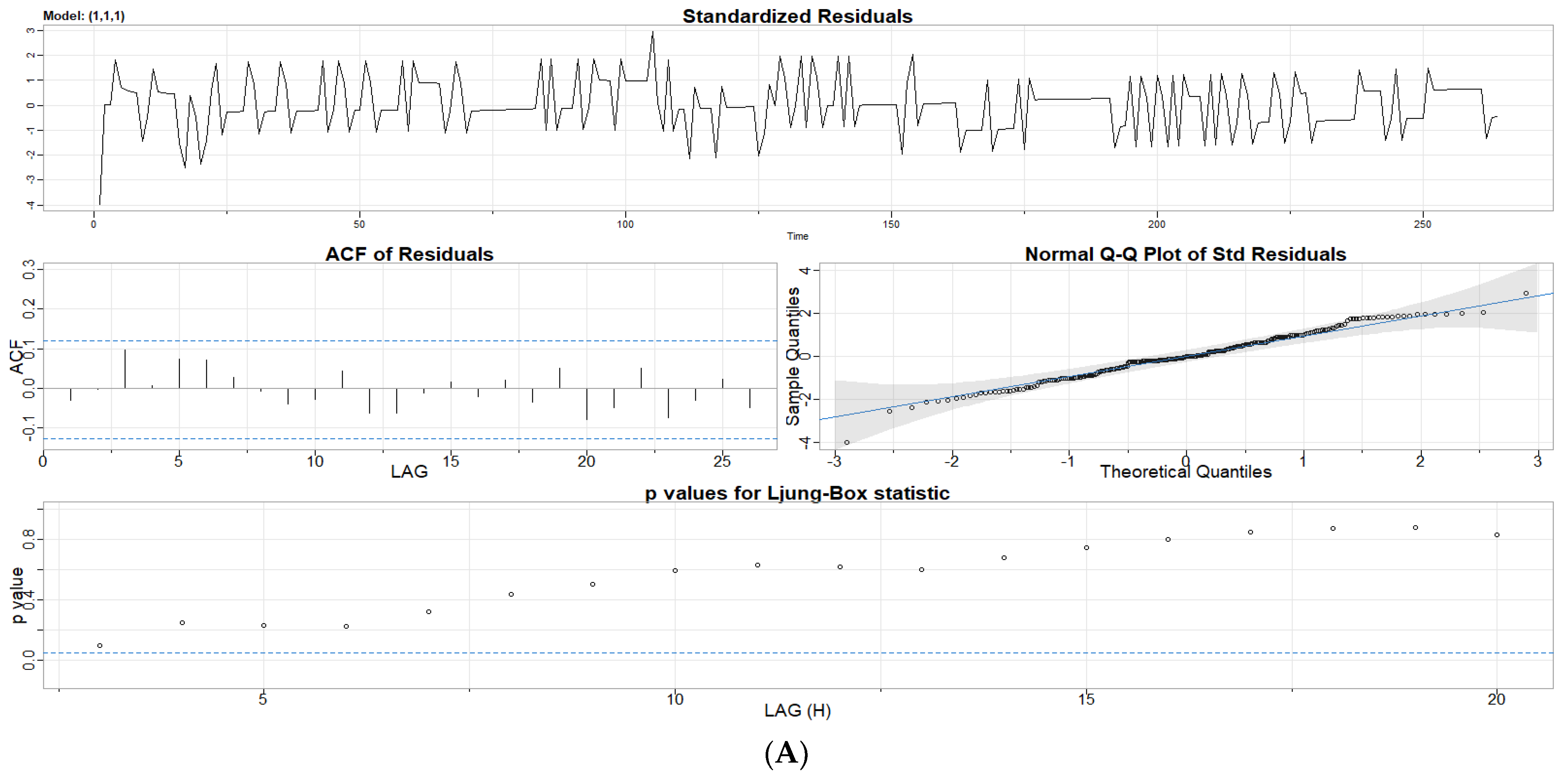
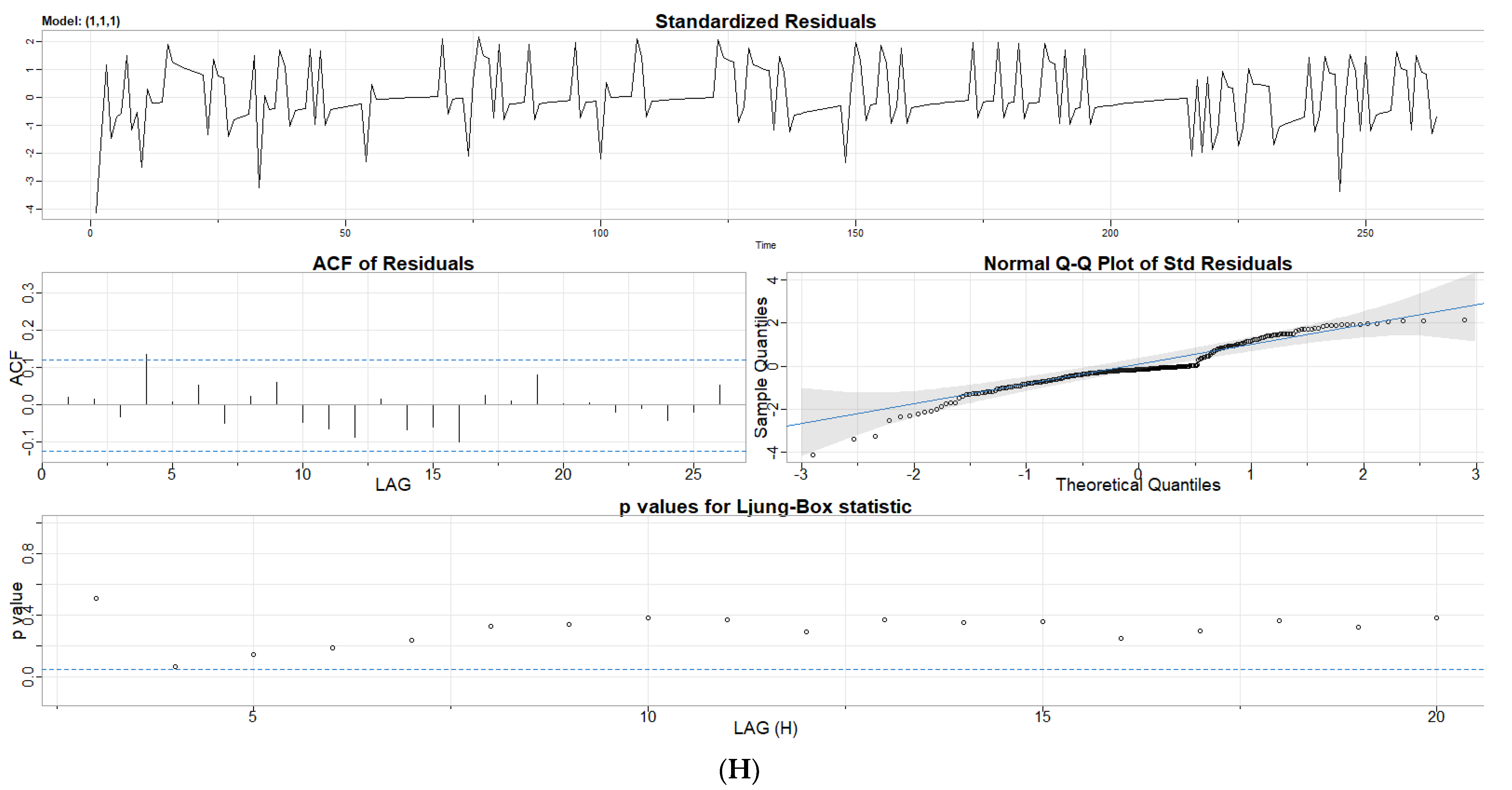
3.1.2. Autoregression and Moving Average Parameter Screening
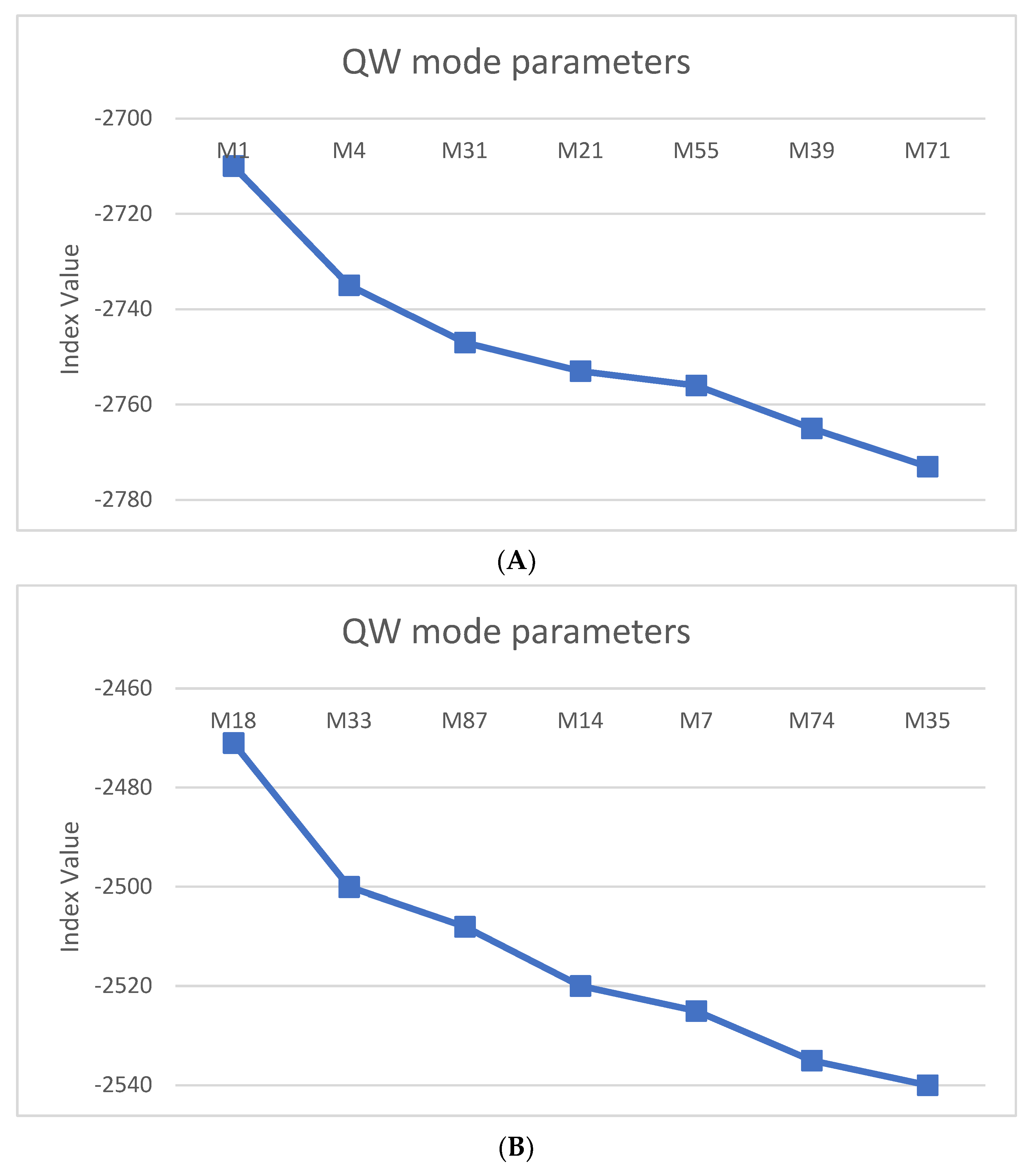
3.2. Time Series Mode Screening Using Continuous Time Quantum Random Walks
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Beier, G.; Niehoff, S.; Xue, B. More Sustainability in Industry through Industrial Internet of Things? Appl. Sci. 2018, 8, 219. [Google Scholar] [CrossRef]
- Salam, A. Internet of Things for Sustainable Community Development; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development; Department of Economic and Social Affairs, United Nations: New York, NY, USA, 2015; Available online: https://sdgs.un.org/2030agenda (accessed on 14 September 2022).
- Kumar, S.; Tiwari, P.; Zymbler, M. Internet of Things is a revolutionary approach for future technology enhancement: A review. J. Big Data 2019, 6, 111. [Google Scholar] [CrossRef]
- Oke, A.E.; Arowoiya, V.A. Evaluation of internet of things (IoT) application areas for sustainable construction. Smart Sustain. Built Environ. 2021, 10, 387–402. [Google Scholar] [CrossRef]
- Hassoun, A.; Aït-Kaddour, A.; Abu-Mahfouz, A.M.; Rathod, N.B.; Bader, F.; Barba, F.J.; Biancolillo, A.; Cropotova, J.; Galanakis, C.M.; Jambrak, A.R.; et al. The fourth industrial revolution in the food industry—Part I: Industry 4.0 technologies. Crit. Rev. Food Sci. Nutr. 2022. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Singh, R.P.; Rab, S.; Suman, R. Significance of sensors for industry 4.0: Roles, capabilities, and applications. Sens. Int. 2021, 2, 100110. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Rab, S.; Singh, R.P.; Suman, R. Sensors for daily life: A review. Sens. Int. 2021, 2, 100121. [Google Scholar] [CrossRef]
- Schütze, A.; Helwig, N.; Schneider, T. Sensors 4.0—Smart sensors and measurement technology enable Industry 4.0. J. Sens. Sens. Syst. 2018, 7, 359–371. [Google Scholar] [CrossRef]
- Ramírez-Moreno, M.A.; Keshtkar, S.; Padilla-Reyes, D.A.; Ramos-López, E.; García-Martínez, M.; Hernández-Luna, M.C.; Mogro, A.E.; Mahlknecht, J.; Huertas, J.I.; Peimbert-García, R.E.; et al. Sensors for Sustainable Smart Cities: A Review. Appl. Sci. 2021, 11, 8198. [Google Scholar] [CrossRef]
- Khatua, P.K.; Ramachandaramurthy, V.K.; Kasinathan, P.; Yong, J.Y.; Pasupuleti, J.; Rajagopalan, A. Application and assessment of internet of things toward the sustainability of energy systems: Challenges and issues. Sustain. Cities Soc. 2020, 53, 101957. [Google Scholar] [CrossRef]
- Kumar, T.; Srinivasan, R.; Mani, M. An Emergy-based Approach to Evaluate the Effectiveness of Integrating IoT-based Sensing Systems into Smart Buildings. Sustain. Energy Technol. Assess. 2022, 52, 102225. [Google Scholar] [CrossRef]
- Aivazidou, E.; Banias, G.; Lampridi, M.; Vasileiadis, G.; Anagnostis, A.; Papageorgiou, E.; Bochtis, D. Smart Technologies for Sustainable Water Management: An Urban Analysis. Sustainability 2021, 13, 13940. [Google Scholar] [CrossRef]
- Palermo, S.A.; Maiolo, M.; Brusco, A.C.; Turco, M.; Pirouz, B.; Greco, E.; Spezzano, G.; Piro, P. Smart Technologies for Water Resource Management: An Overview. Sensors 2022, 22, 6225. [Google Scholar] [CrossRef]
- Glória, A.; Cardoso, J.; Sebastião, P. Sustainable Irrigation System for Farming Supported by Machine Learning and Real-Time Sensor Data. Sensors 2021, 21, 3079. [Google Scholar] [CrossRef]
- Al-Kahtani, M.S.; Khan, F.; Taekeun, W. Application of Internet of Things and Sensors in Healthcare. Sensors 2022, 22, 5738. [Google Scholar] [CrossRef]
- Saini, J.; Dutta, M.; Marques, G. Sensors for indoor air quality monitoring and assessment through Internet of Things: A systematic review. Environ. Monit. Assess. 2021, 193, 66. [Google Scholar] [CrossRef]
- Potyrailo, R. Multivariable Sensors for Ubiquitous Monitoring of Gases in the Era of Internet of Things and Industrial Internet. Chem. Rev. 2016, 116, 11877–11923. [Google Scholar] [CrossRef]
- Lutz, E.; Carteri Coradi, P. Applications of new technologies for monitoring and predicting grains quality stored: Sensors, Internet of Things, and Artificial Intelligence. Measurement 2022, 188, 110609. [Google Scholar] [CrossRef]
- Jamshed, M.A.; Ali, K.; Abbasi, Q.H.; Imran, M.A.; Ur-Rehman, M. Challenges, Applications, and Future of Wireless Sensors in Internet of Things: A Review. IEEE Sens. J. 2022, 22, 5482–5494. [Google Scholar] [CrossRef]
- Childs, P.R.; Greenwood, J.R.; Long, C.A. Review of temperature measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. [Google Scholar] [CrossRef]
- Rai, V.K. Temperature sensors and optical sensors. Appl. Phys. B 2007, 88, 297–303. [Google Scholar]
- Bucher, J.L. The Quality Calibration Handbook: Developing and Managing a Calibration Program; ASQ Quality Press: Milwaukee, WI, USA, 2006. [Google Scholar]
- Durivage, M.A. Practical Attribute and Variable Measurement System Analysis (MSA): A Guide for Conducting Gage R&R Studies and Test Method Validations; ASQ Quality Press: Milwaukee, WI, USA, 2015. [Google Scholar]
- Shewhart, W.A. Statistical Method from the Viewpoint of Quality Control; Dover: Mineola, NY, USA, 2012. [Google Scholar]
- Deming, D.E. Statistical Adjustment of Data; Dover: Mineola, NY, USA, 2011. [Google Scholar]
- Juran, J.M.; Defeo, J.A. Juran’s Quality Handbook: The Complete Guide to Performance Excellence; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis; Prentice-Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Wellek, S. A critical evaluation of the current “p-value controversy”. Biom. J. 2017, 5, 854–872. [Google Scholar] [CrossRef] [PubMed]
- Johnson, V.E. Evidence from marginally significantly t statistics. Am. Stat. 2019, 73, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a world beyond “p < 0.05”. Am. Stat. 2019, 73, 1–19. [Google Scholar]
- Matthews, R.A. Moving towards the post p < 0.05 era via the analysis of credibility. Am. Stat. 2019, 73, 202–212. [Google Scholar]
- Calin-Jageman, R.J.; Cumming, G. The new statistics for better science: Ask how much, how uncertain, and what else is known. Am. Stat. 2019, 73, 271–280. [Google Scholar] [CrossRef]
- Hubbard, R.; Haig, B.D.; Parsa, R.A. The limited role of formal statistical inference in scientific inference. Am. Stat. 2019, 73, 91–98. [Google Scholar] [CrossRef]
- Poincare, H. Science and Method; Thomas Nelson and Sons: London, UK, 2014. [Google Scholar]
- Popper, K. The Logic of Scientific Discovery; Taylor & Francis e-Library: London, UK, 2005. [Google Scholar]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915–928. [Google Scholar] [CrossRef]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Ambainis, A. Quantum walks and their algorithmic applications. Int. J. Quantum Inf. 2003, 1, 507–518. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Kadian, K.; Garhwal, S.; Kumar, A. Quantum walk and its application domains: A systematic review. Comput. Sci. Rev. 2021, 41, 100419. [Google Scholar] [CrossRef]
- Kendon, V. A random walk approach to quantum algorithms. Philos. Trans. R. Soc. A 2006, 364, 3407–3422. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Shikano, Y.; Chisaki, K.; Segawa, E.; Konno, N. Emergence of randomness and arrow of time in quantum walks. Phys. Rev. A 2010, 81, 062129. [Google Scholar] [CrossRef]
- Shenvi, N.; Kempe, J.; Whaley, K.B. A quantum random walk search algorithm. Phys. Rev. A 2003, 67, 052307. [Google Scholar] [CrossRef]
- Apers, S.; Gilyen, A.; Jeffery, S. A unified framework of quantum walk search. arXiv 2019, arXiv:1912.04233. [Google Scholar]
- Gudder, S.P. Quantum Probability; Academic Press Inc.: San Diego, CA, USA, 1988. [Google Scholar]
- Chisaki, K.; Konno, N.; Segawa, E.; Shikano, Y. Crossovers induced by discrete-time quantum walks. Quantum Inf. Comput. 2011, 11, 741–760. [Google Scholar] [CrossRef]
- Bjerre-Nielsen, A.; Kassarnig, V.; Dreyer Lassen, D.; Lehmann, S. Task-specific information outperforms surveillance-style big data in predictive analytics. Proc. Natl. Acad. Sci. USA 2021, 118, e2020258118. [Google Scholar] [CrossRef]
- Ihaka, R.; Gentleman, R. R: A Language for Data Analysis and Graphics. J. Comput. Graph. Stat. 1996, 5, 299–314. [Google Scholar]
- Giorgi, F.M.; Ceraolo, C.; Mercatelli, D. The R Language: An Engine for Bioinformatics and Data Science. Life 2022, 12, 648. [Google Scholar] [CrossRef]
- R Core Team. R (Version 4.1.3): A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 10 March 2022).
- Stewart Lowndes, J.S.; Best, B.D.; Scarborough, C.; Afflerbach, J.C.; Frazier, M.R.; O’Hara, C.C.; Jiang, N.; Halpern, B.S. Our path to better science in less time using open data science tools. Nat. Ecol. Evol. 2017, 1, 0160. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Kamal, A.; Dhakal, P.; Javaid, A.Y.; Devabhaktuni, V.K.; Kaur, D.; Zaientz, J.; Marinier, R. Recent Advances and Challenges in Uncertainty Visualization: A Survey. J. Vis. 2021, 24, 861–890. [Google Scholar] [CrossRef]
- Thrun, M.C.; Gehlert, T.; Ultsch, A. Analyzing the fine structure of distributions. PLoS ONE 2020, 15, e0238835. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, A.; Cassemiro, K.N.; Potocek, V.; Gabris, A.; Jex, I.; Silberhorn, C. Decoherence and disorder in quantum walks: From ballistic spread to localization. Phys. Rev. Lett. 2011, 106, 180403. [Google Scholar] [CrossRef]
- Valeli, T. A Comparative SPC Study to Calibrate Thermostatic Bath Using Two Methods. Master’s Thesis, Advanced and Industrial Manufacturing Systems, Kingston University, London, UK, 2022. [Google Scholar]
- Zeng, Q.; Chen, L.; Xie, M.; Fu, Y.; Zhou, Z. Calibration of thermostatic bath used on electronic thermometer verification. Appl. Mech. Mater. 2014, 635–637, 819–823. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley Publishing: Reading, MA, USA, 1977. [Google Scholar]
- Hintze, J.L.; Nelson, R.D. Violin plots: A box plot-Density trace synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar]
- Anderson, T.W.; Darling, D.A. A test of goodness-of-fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. As analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Jarque, C.M.; Bera, A.K. Efficient tests for normality, homoscedasticity, and serial independence of regression residuals. Econ. Lett. 1980, 6, 255–259. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root. J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Wald, A.; Wolfowitz, J. On a test whether two samples are from the same population. Ann. Math. Statist. 1940, 11, 147–162. [Google Scholar] [CrossRef]
- Brock, W.; Dechert, D.; Scheinkman, J. A Test for Independence Based on the Correlation Dimension; Economics Working Paper SSRI-8702; University of Wisconsin: Madison, WI, USA, 1987. [Google Scholar]
- Brock, W.A.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Ljung, G.M.; Box, G.E. On the measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]












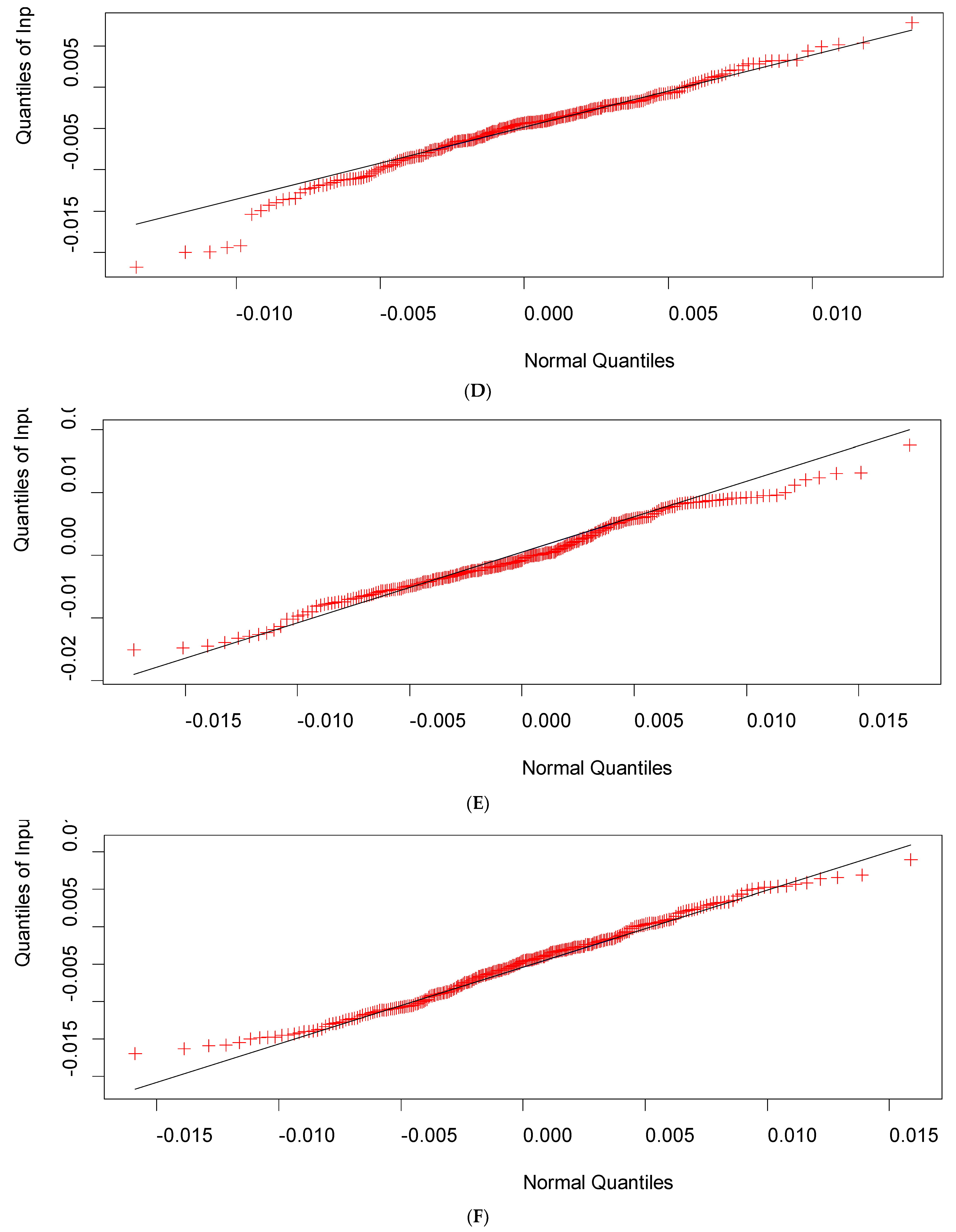

| AD-Test 1 | SW-Test 2 | JB-Test 3 | |
|---|---|---|---|
| Sensor Time Series ID # | An (p-Value) | W (p-Value) | X2 (p-Value) |
| 1 | 53,183 (p < 0.001) | 0.797 (p < 0.001) | 1.77 (0.411) |
| 2 | 53,774 (p < 0.001) | 0.908 (p < 0.001) | 1.73 (0.420) |
| 3 | 53,822 (p < 0.001) | 0.711 (p < 0.001) | 2.97 (0.226) |
| 4 | 53,313 (p < 0.001) | 0.753 (p < 0.001) | 3.65 (0.161) |
| 5 | 53,491 (p < 0.001) | 0.828 (p < 0.001) | 0.64 (0.727) |
| 6 | 53,617 (p < 0.001) | 0.792 (p < 0.001) | 1.14 (0.565) |
| 7 | 53,633 (p < 0.001) | 0.799 (p < 0.001) | 6.50 (0.039) |
| 8 | 53,446 (p < 0.001) | 0.741 (p < 0.001) | 3.62 (0.164) |
| Augmented Dickey-Fuller Test | KPSS Test | Maximum Drawdown (°C) | |
|---|---|---|---|
| Sensor Time Series ID # | DF (p-Value) | KPSS (p-Value) | |
| 1 | −4.510 (p < 0.01) | 1.209 (p < 0.01) | 0.03 |
| 2 | −4.572 (p < 0.01) | 0.027 (p > 0.1) | 0.05 |
| 3 | −5.376 (p < 0.01) | 0.739 (p < 0.01) | 0.02 |
| 4 | −3.419 (p = 0.052) | 0.302 (p > 0.1) | 0.03 |
| 5 | −4.874 (p < 0.01) | 0.252 (p > 0.1) | 0.04 |
| 6 | −6.819 (p < 0.01) | 0.368 (p = 0.091) | 0.03 |
| 7 | −7.031 (p < 0.01) | 0.981 (p < 0.01) | 0.03 |
| 8 | −4.146 (p < 0.01) | 0.807 (p < 0.01) | 0.03 |
| Runs Test | BDS Test | ||||
|---|---|---|---|---|---|
| Temperature Sensor ID # | Median (°C) | Runs | p-Value | Epsilon Values | p-Value |
| 1 | −19.93 | 47 | p < 0.001 | 0.003 | p < 0.001 |
| 0.007 | p < 0.001 | ||||
| 0.010 | p < 0.001 | ||||
| 0.013 | p < 0.001 | ||||
| 2 | −20.04 | 35 | p < 0.001 | 0.005 | p < 0.001 |
| 0.010 | p < 0.001 | ||||
| 0.015 | p < 0.001 | ||||
| 0.020 | p < 0.001 | ||||
| 3 | −20.05 | 55 | p = 0.004 | 0.003 | p = 0.334 |
| 0.005 | p = 0.334 | ||||
| 0.008 | p = 0.334 | ||||
| 0.011 | p < 0.001 | ||||
| 4 | −19.95 | 11 | p = 0.009 | 0.003 | p < 0.001 |
| 0.006 | p < 0.001 | ||||
| 0.009 | p < 0.001 | ||||
| 0.012 | p < 0.001 | ||||
| 5 | −19.99 | 65 | p < 0.001 | 0.004 | p < 0.001 |
| 0.007 | p < 0.001 | ||||
| 0.011 | p < 0.001 | ||||
| 0.014 | p < 0.001 | ||||
| 6 | −20.01 | 31 | p < 0.001 | 0.003 | p < 0.001 |
| 0.006 | p < 0.001 | ||||
| 0.010 | p < 0.001 | ||||
| 0.013 | p < 0.001 | ||||
| 7 | −20.02 | 78 | p < 0.001 | 0.003 | p < 0.001 |
| 0.007 | p < 0.001 | ||||
| 0.010 | p < 0.001 | ||||
| 0.013 | p < 0.001 | ||||
| 8 | −19.98 | 54 | p < 0.001 | 0.003 | p < 0.001 |
| 0.006 | p < 0.001 | ||||
| 0.009 | p < 0.001 | ||||
| 0.011 | p < 0.001 |
| AR Coefficient Statistics | MA Coefficient Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Temperature Sensor ID # | Estimate | Standard Error | t-Value | p-Value | Estimate | Standard Error | t-Value | p-Value | AIC | BIC |
| 1 | 0.431 | 0.056 | 7.692 | p < 0.001 | −1.000 | 0.019 | −52.025 | p < 0.001 | −7.70 | −7.64 |
| 2 | 0.643 | 0.061 | 10.477 | p < 0.001 | 0.145 | 0.074 | 1.956 | p = 0.052 | −7.10 | −7.04 |
| 3 | 0.183 | 0.067 | 2.746 | p = 0.007 | −0.944 | 0.025 | −37.962 | p < 0.001 | −7.75 | −7.70 |
| 4 | 0.897 | 0.046 | 19.437 | p < 0.001 | −0.663 | 0.080 | −8.346 | p < 0.001 | −7.65 | −7.60 |
| 5 | 0.567 | 0.051 | 11.086 | p < 0.001 | −1.000 | 0.014 | −69.782 | p < 0.001 | −7.44 | −7.39 |
| 6 | 1.455 −0.718 | 0.092 0.081 | 15.757 −8.851 | p < 0.001 p < 0.001 | −0.967 0.361 | 0.118 0.120 | −8.173 3.002 | p < 0.001 p = 0.003 | −7.65 | −7.57 |
| 7 | 0.465 | 0.055 | 8.482 | p < 0.001 | −1.000 | 0.0102 | −97.811 | p < 0.001 | −7.47 | −7.41 |
| 8 | 0.242 | 0.070 | 3.461 | p < 0.001 | −0.930 | 0.030 | −30.737 | p < 0.001 | −7.79 | −7.74 |
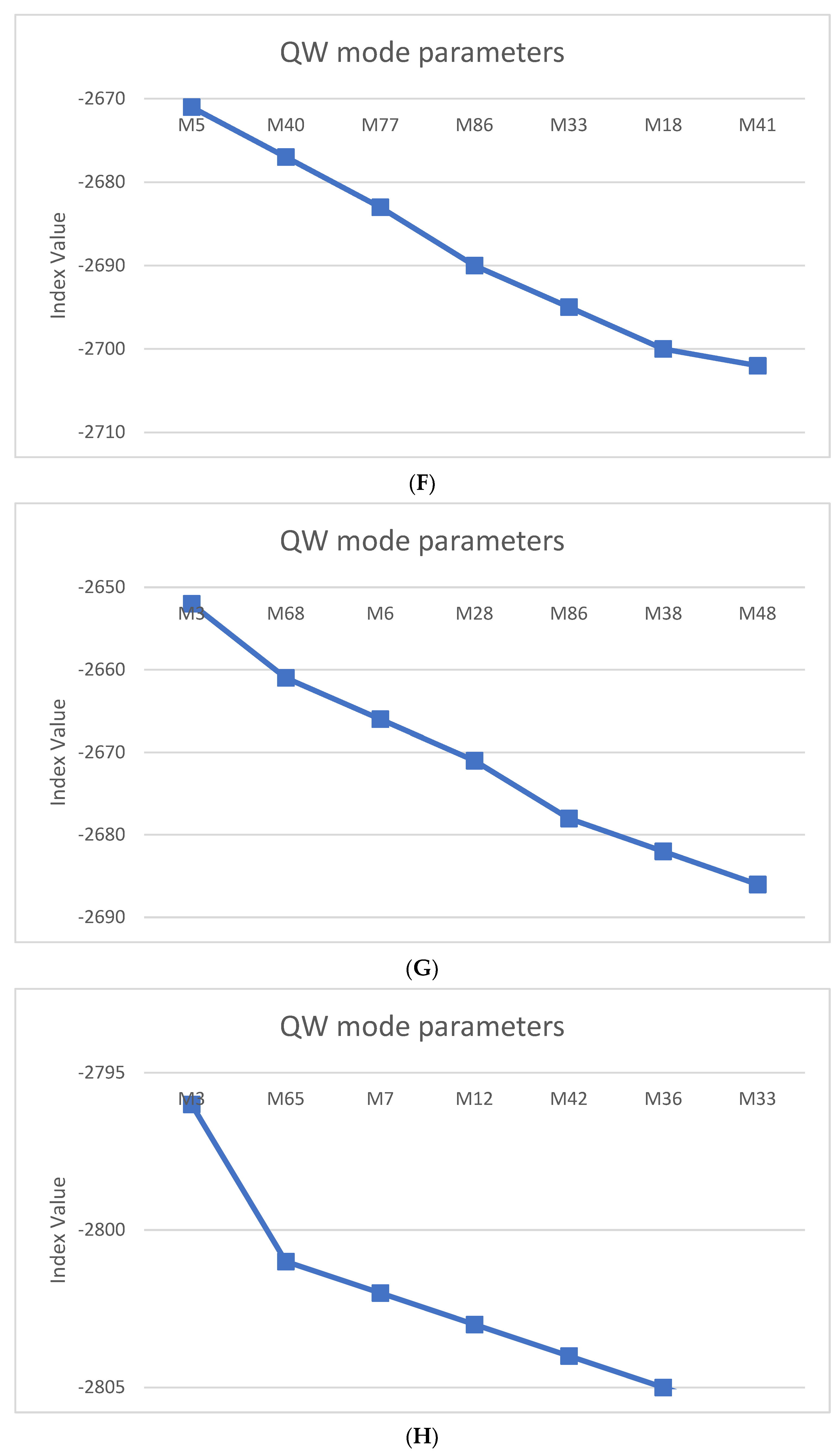
| Temperature Sensor ID | Retained no. of Modes | Leading Mode Sequences | AIC |
|---|---|---|---|
| 1 | 14 | 3-4-31-21-55-39-71 | 1725 |
| 2 | 22 | 18-33-87-14-7-74-35 | 1691 |
| 3 | 9 | 6-60-3-5-91-88-82 | 1850 |
| 4 | 7 | 7-4-19-10-30-21-47 | 1858 |
| 5 | 11 | 18-3-13-23-78-41-81 | 1780 |
| 6 | 10 | 5-40-77-86-33-18-41 | 1806 |
| 7 | 13 | 3-68-6-28-86-38-48 | 1749 |
| 8 | 11 | 3-65-7-12-42-36-33 | 1796 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Besseris, G. Testing Thermostatic Bath End-Scale Stability for Calibration Performance with a Multiple-Sensor Ensemble Using ARIMA, Temporal Stochastics and a Quantum Walker Algorithm. Sensors 2023, 23, 2267. https://doi.org/10.3390/s23042267
Besseris G. Testing Thermostatic Bath End-Scale Stability for Calibration Performance with a Multiple-Sensor Ensemble Using ARIMA, Temporal Stochastics and a Quantum Walker Algorithm. Sensors. 2023; 23(4):2267. https://doi.org/10.3390/s23042267
Chicago/Turabian StyleBesseris, George. 2023. "Testing Thermostatic Bath End-Scale Stability for Calibration Performance with a Multiple-Sensor Ensemble Using ARIMA, Temporal Stochastics and a Quantum Walker Algorithm" Sensors 23, no. 4: 2267. https://doi.org/10.3390/s23042267
APA StyleBesseris, G. (2023). Testing Thermostatic Bath End-Scale Stability for Calibration Performance with a Multiple-Sensor Ensemble Using ARIMA, Temporal Stochastics and a Quantum Walker Algorithm. Sensors, 23(4), 2267. https://doi.org/10.3390/s23042267




