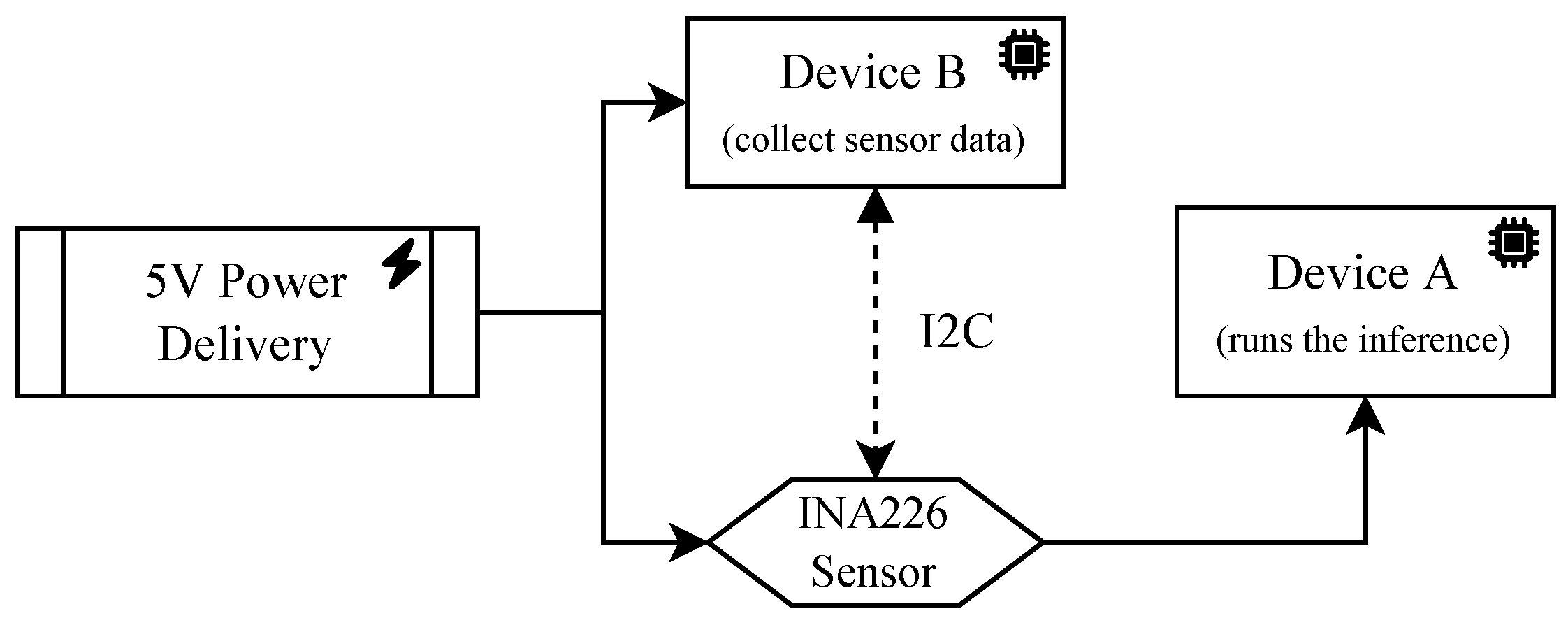
The measurements were taken by using, in conjunction, two devices and a voltage/current sensor (
Figure 4). The first device (Device A) is the one in which the inference is run. We used a Raspberry Pi 3 and the Google Coral DevBoard. The second device (Device B), a Raspberry Pi 3, is connected via I2C protocol to a voltage/current sensor breakout board based on the Texas Instruments INA226. The current flowing to Device A passes through the sensor, which measures the voltage and current at the same time. The sensor has a sampling rate that is approximately near to 2000 Hz. Therefore, it allows for capturing the power behavior even for neural networks with FPS greater than 30 fps (standard real-time threshold value). In this particular case, we estimate to have
samples for every frame. We remark that the sampling rate is not constant, but it depends on the CPU activity.
The tests presented in this section are based on 100 sessions of 25 s in which we loaded each image from persistent storage and 100 sessions of 40 s where the entire dataset was loaded in RAM before starting the inference. Device B started recording the current and voltage measurements, and in parallel, the inference was started on Device A for the given amount of seconds.
6.1. Current and Voltage Footprint
The purpose of this section is to study the current and voltage traces of the inference process. We selected, as a test, the model which uses MobileNetV3
as encoder and TDSConv2D as decoder (see the model with
in
Table 6). This was selected because the model in question has a low inference frame rate, thus allowing to clearly highlight its energy behavior during the inference of every frame. We ran two experiments in the first (
Figure 5); we only performed the inference for 20 s, while in the second (
Figure 6), we first loaded the entire dataset in RAM and then we performed the inference process.
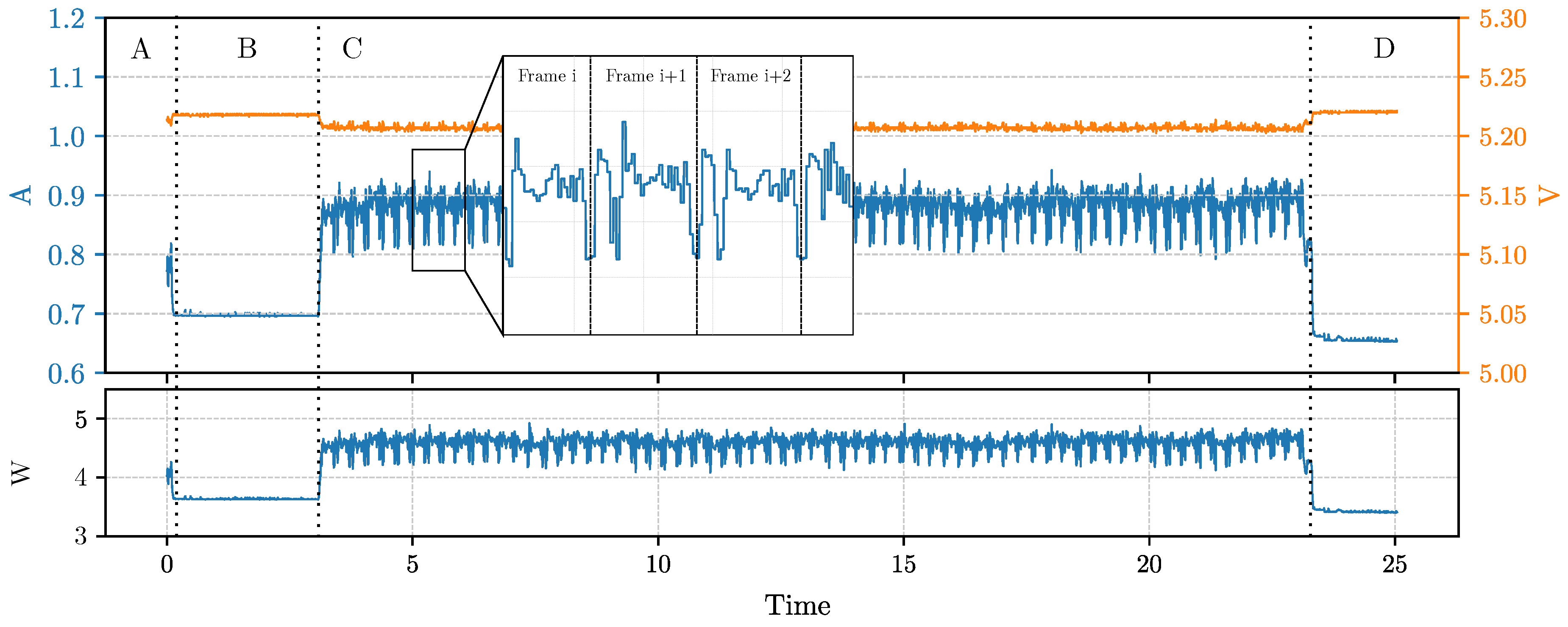
Figure 5 shows the traces of current (in blue) and voltages (in orange) during the entire test. We can easily distinguish from the graph the main phases of the procedure. Phase A comprehends the start of the test routine, while in phase B, we executed a process sleep of 3 s (we used the Python function
time.sleep() in order to highlight in the charts when the inference process started); then, the C phase regards the inference, and finally, in the D phase, the device returns to the idle state. What we can observe is that, first of all, the sleep phase has an instant current absorption of 700 mA, which is slightly higher than the idle phase in which we have 680 mA. Then, during the inference, we can easily distinguish each analyzed frame. This is because the model runs at about 4.60 FPS. Every frame inference begins with a current drop of about 100 mA on average due to the passage to the next frame and the tensor allocation for the inference. The instant power consumption during the inference is, on average, 4.589 W.
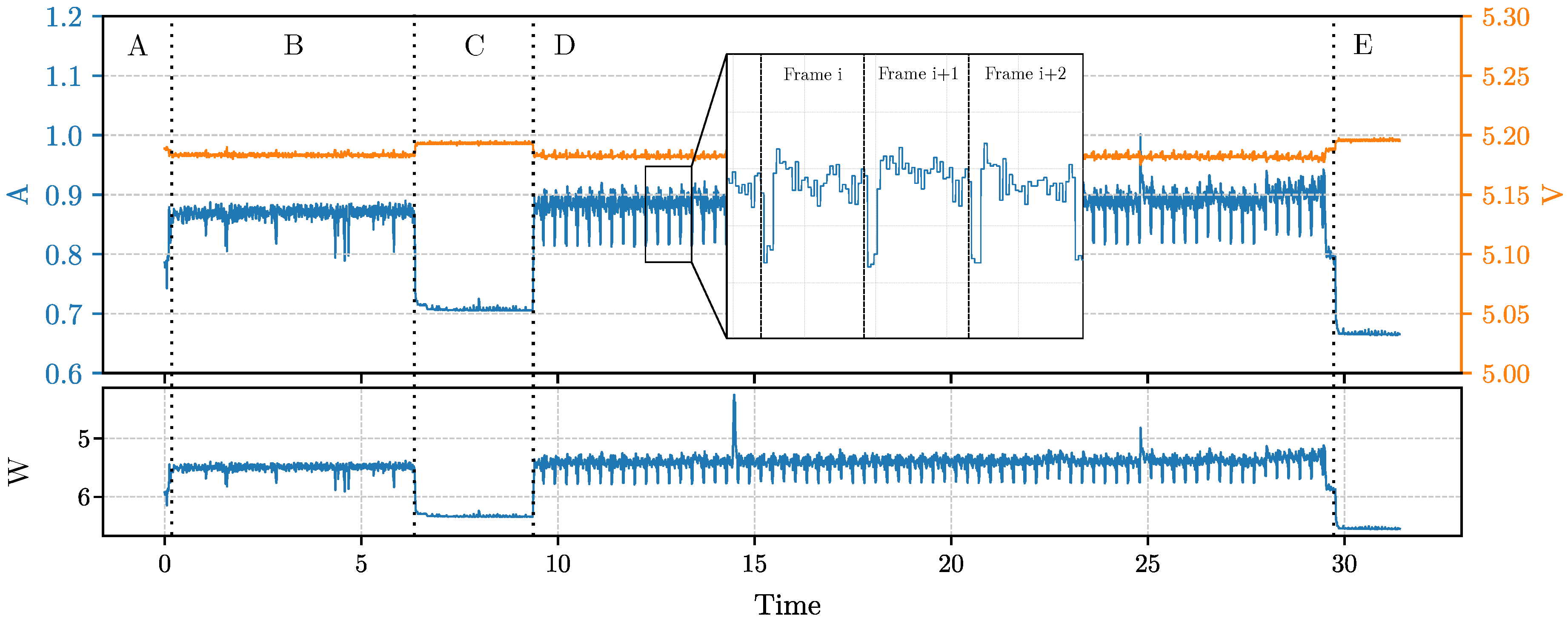
Moreover, in
Figure 6 we report the result of the same test while keeping the dataset entirely loaded in RAM during phase B. In this second test, the loading of the dataset in memory requires about 5.6 s (phase B); then, the script executes the sleep for 3 s (phase C) and the inference (phase D) for 20 s. Finally, the system goes idle in phase E. What we can observe from the traces is that the dataset load does not interfere with the actual power consumption of the inference. What can be noticed is that having the image already loaded in RAM, which can be the case of an image that is retrieved from a camera sensor, makes the power trace during inference more stable. This is because loading images from persistent storage is slow and requires a certain amount of waiting time, depending on the size of the image.
6.2. Models Inference Energy Consumption
In our setup, the model inference is a CPU-bound task, and it does not require interaction with storage or network, at least when the images to be processed are already loaded in RAM. Moreover, the classic inference with a model is not distributed, and it is a single-threaded operation. This means that during the inference, one CPU core will be used at one hundred percent of its time, independently from the model that it is used. However, different CPU operations have different energy consumptions. For example, the energy required for memory access depends on the type of data read or written [
37]. Motivated by this idea, we studied which is the energy impact of the inference in every float32 model that we considered in this paper, assuming that images are directly loaded from RAM, which is the typical usage scenario when, for example, a camera is attached to the device.
For performing the energy assessment of the models, we conducted a series of 100 tests per model as the one presented in
Figure 6. For each test
k s.t.
and for each model
i s.t.
, we then computed the total energy consumption during the inference by using Equation (
4), called
. From there, the energy consumed per second is actually the average power requirement during the inference, for
, which is the duration of the experiment, can be defined as:
We will omit the time
t since it is fixed for every test. The average power requirement for the inference of model
i is the average among all tests, and then:
Table 6 shows the
sorted for every model. We also reported the confidence interval based on the Student’s t-distribution with a
p-value of 0.05. However, to give statistical significance to the mean value of the power, we conducted the ANOVA test with 34 degrees of freedom, that is, the number of models. The test, with a
p-value
, reports a significance of <0.001, F-Value
and
. This proves that some of the means are effectively different from others.
To clearly understand which means are statistically acceptable as different, we conducted a Student’s
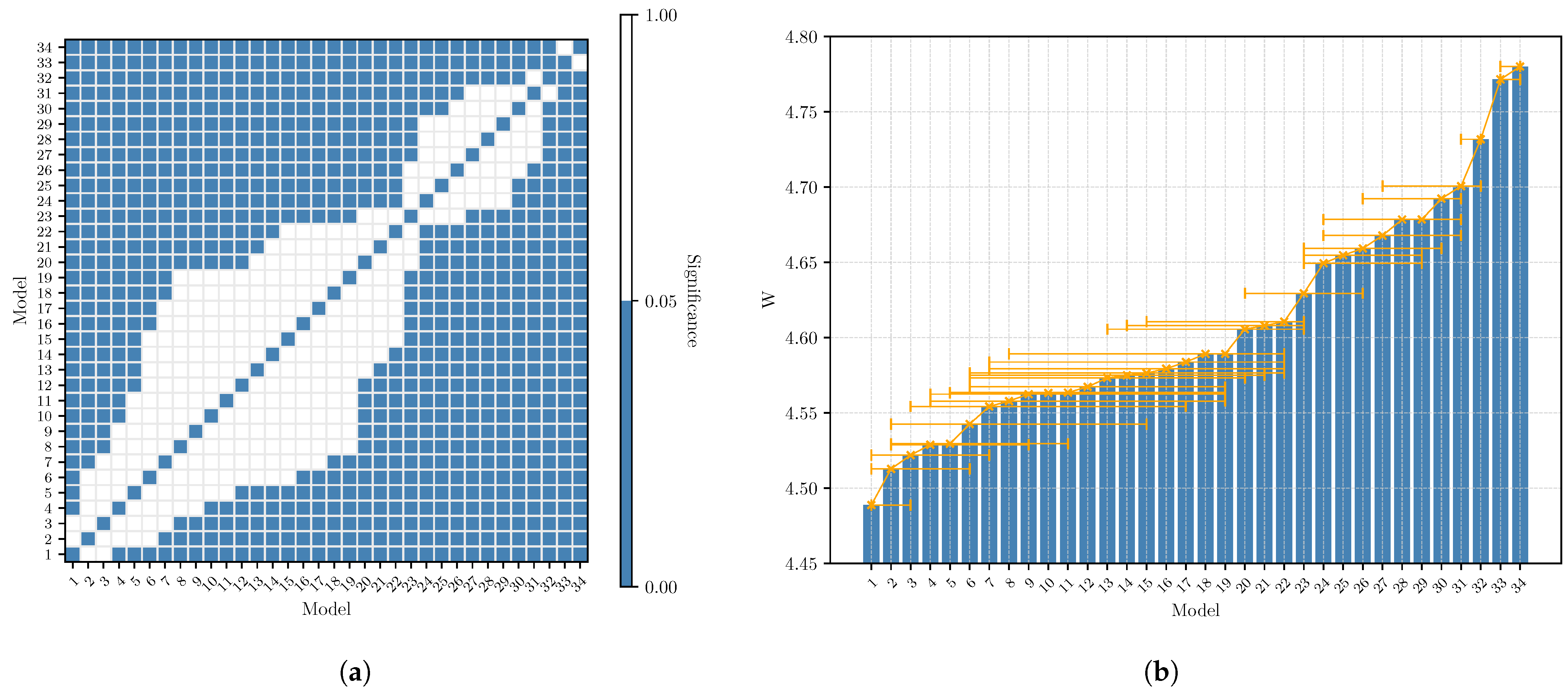
t-test between each possible model. The result of the test is shown in
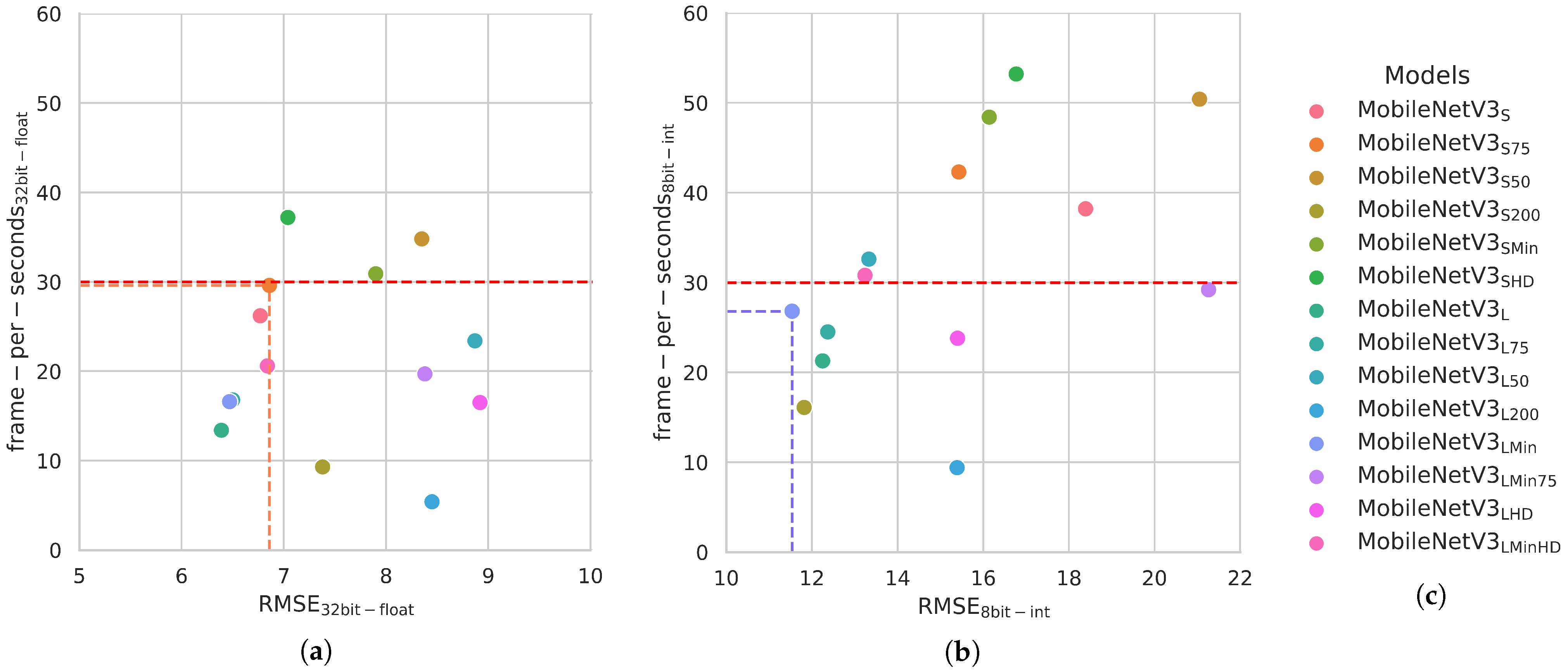
Figure 7, in particular,
Figure 7a shows the significance of the
t-test between each possible combination of two models, while
Figure 7b report also the
value for each model. What we can observe, also with the model data in
Table 6, is that the power requirement for the inference is different only between specific models. In particular, we can notice how models which are based on the most energy-demanding architectures are both based on the “NNConv5” decoder, which is the only one based on 5 × 5 convolutional blocks, while the other has a 3 × 3 one.
We can conclude the energy assessment by giving some considerations about the results listed in
Table 7. The first result is that the energy required for the inference (
) is not dependent on the inference time (that is
) or on the floating-point operations (FLOPs), which the model requires. Actually, the Pearson correlation test reports a correlation of
(sign.
,
p-value
) between the models’ FLOPs and the
and
(sign.
,
p-value
) between the FPS and the
. This suggests a weak correlation between the variables, in particular, a positive one for the FLOPs since a higher number of operations reduce the number of processed frame per second, therefore, it increases the time of CPU dedicated to the inference instead of preparing the model for the next frame. This also explains the negative correlation between
and the FPS and the fact that the Pearson correlation between FPS and FLOPs is strong and negative (i.e.,
, sign.
,
p-value
). The weak correlation between the power consumed (
) and the complexity of the model (FLOPs or FPS) is instead justified by the fact that what changes among the models is the type of operations that are carried out. Indeed, for example, models with
and
have a comparable complexity of about 470 M FLOPs; however, the models
differ by
. This is because the model with
, dealing with images of a bigger size, has to perform a higher number of memory access (and therefore a higher probability of cache miss) in which the CPU waits for the data to be retrieved and does not do any computation.
Finally, the results in
Table 6 are sorted in terms of the mean
. In particular, we can observe that the first model (model with
) allows for saving about 6.48% of energy during the inference with respect to the last one (model with
). Instead, regarding the proposed models in
Section 3, they are mapped to model with
(Mob.NetV3
), which represents the best trade-off between fps and RMSE, and the model with
(Mob.NetV3
), which targets the 8-bit architecture. Since the energy assessment only targets the 32-bit architecture, we can observe that model
also offers a relatively low energy consumption, which is 4.7% lower than the model with
.