Improved Spread Spectrum Aloha Protocol and Beam-Hopping Approach for Return Channel in Satellite Internet of Things
Abstract
:1. Introduction
- An ISSA random access protocol has been proposed to improve the access capacity. The preamble is introduced in each beam-hopping slot that is used to accommodate the head of users’ burst signal. The capacity analysis and numerical simulation are conducted for this protocol and the results indicate that performance of the ISSA protocol outperforms the conventional ones.
- Give the mathematical model and analysis of beam scheduling in beam-hopping satellite IoT systems. Firstly, the influencing factors have been analyzed, and a mathematical optimization model based on linear programming has been presented. Secondly, the performance analysis indicates the potential of beam-hopping in satellite IoT systems.
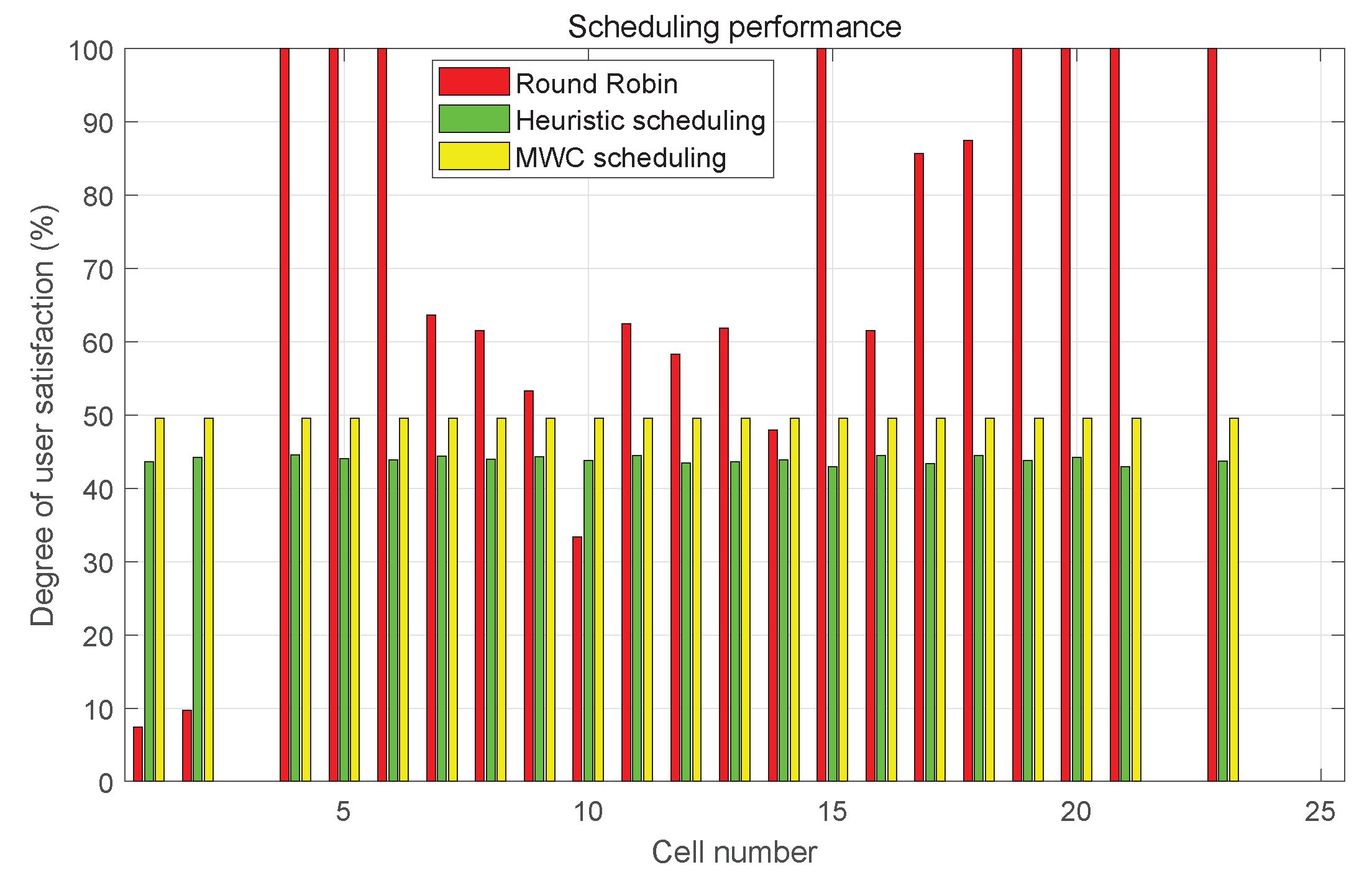
- Two novel beam scheduling algorithms have been presented. To deal with the nonuniform user/traffic distribution in beam-hopping satellite systems, a heuristic beam scheduling algorithm with low complexity is given, and Maximum-Weighted Clique (MWC) beam scheduling algorithm is proposed to improve the system capacity further. Simulation results indicate that the throughput is improved greatly.
2. System Model and Protocol Design
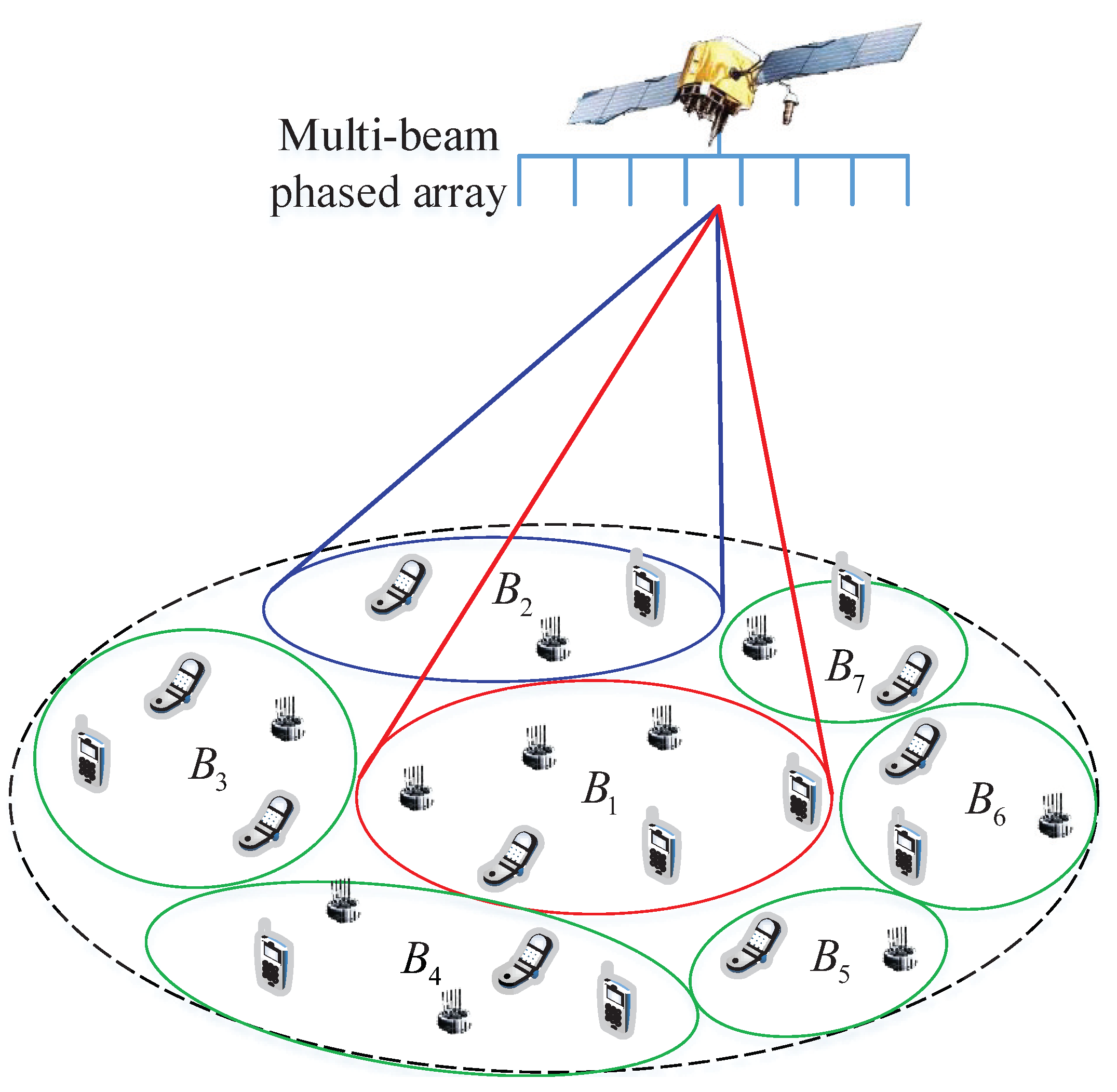
2.1. System Model
2.2. Protocol Design
3. Beam-Hopping Scheduling Algorithm
3.1. Considerations on Beam Scheduling
3.1.1. Beam-Hopping Approaches
- Full scheme. All beams employ the full frequency band allocated to the satellite, and the beams working in the same slot have to be apart sufficiently from each other to avoid or diminish the co-channel interference.
- Reuse scheme. This scheme divides the whole frequency band into several mutually disjoint sub-bands so that different beams are able to use different sub-bands to illuminate adjacent cells simultaneously.
- Hybrid scheme. This scheme is a hybrid of the full and reuse schemes. A beam can employ full or sub-bands, and the beams working simultaneously cannot employ the same frequency, even only partially overlap, unless there is sufficient spatial isolation among them.
3.1.2. Signal Model
3.1.3. Interference Avoiding
3.2. Optimization of Beam Scheduling
3.3. Heuristic Scheduling Algorithm
- Distribution of STs or traffic. The cells cover more STs or traffic will be allocated more slots.
- Inter-beam interference. The angle between any two beams’ pointing with frequency overlap must be larger than the beam width or a setting angle.
- Fairness of STs. The slot allocation for all cells is proportional to the number of STs or traffic contained in.
- Delay requirement. Beam-hopping satellite communication system provides Real-Time (RT) service (call, video call, etc.) and non-RT service (data, picture, video, etc.). RT service is sensitive to delay, which is an important criterion. Generally speaking, the target of scheduling strategy is maximizing the throughput for NRT data and minimizing the delay for RT data.
- Channel condition. The coverage area of a satellite is large and different cells may characterized as different channel condition for diverse path losses and weather conditions. Better channel conditions bring higher transmission capacity. The cell where the footprint is located has the largest channel capacity under the same condition due to the minimum path loss.
| Algorithm 1 Heuristic Beam Scheduling Algorithm |
|
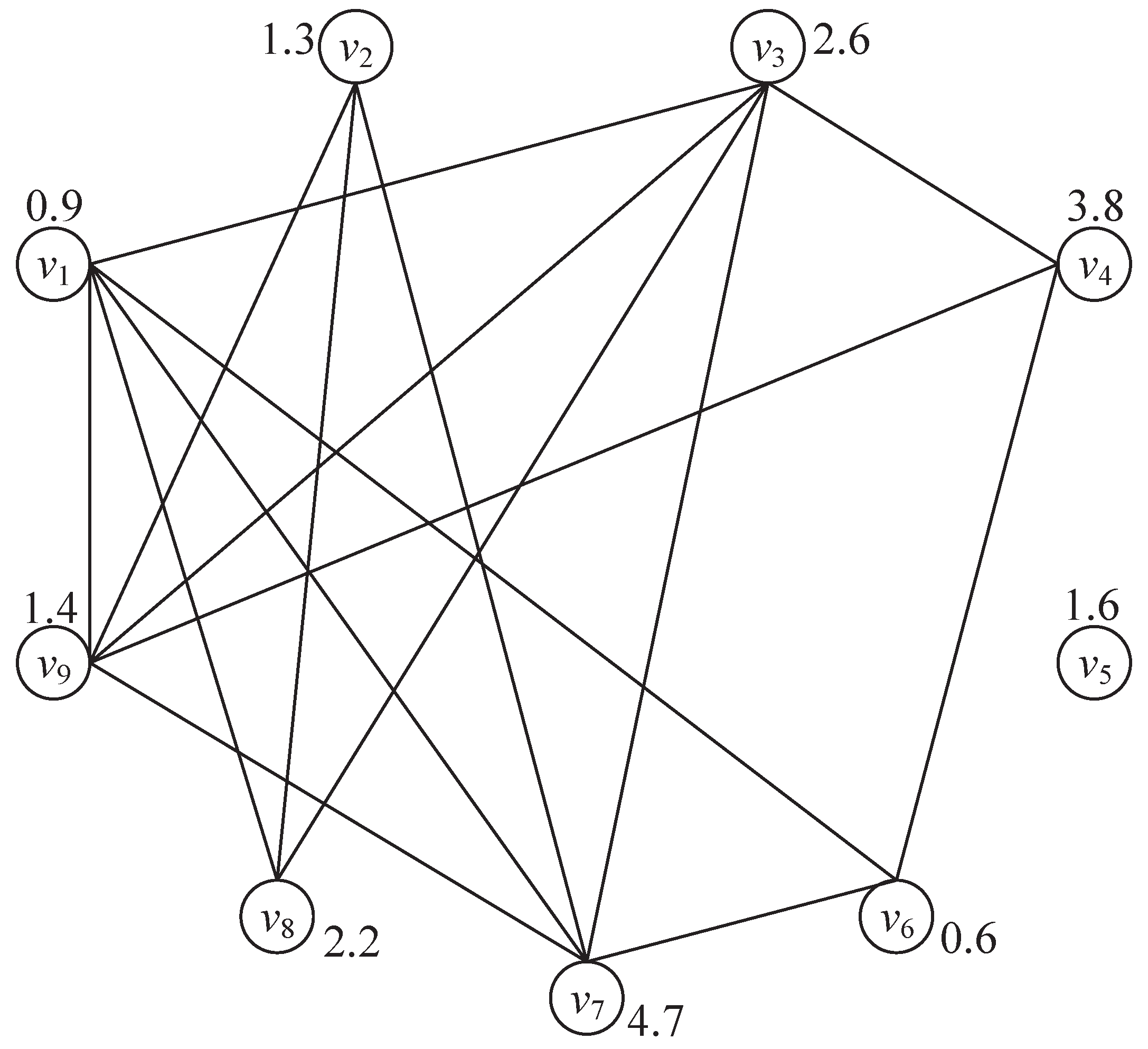
3.4. Maximum-Weighted Clique Scheduling Algorithm
- Cells and are not adjacent.
- .
| Algorithm 2 Maximum-Weighted Clique Beam Scheduling Algorithm. |
|
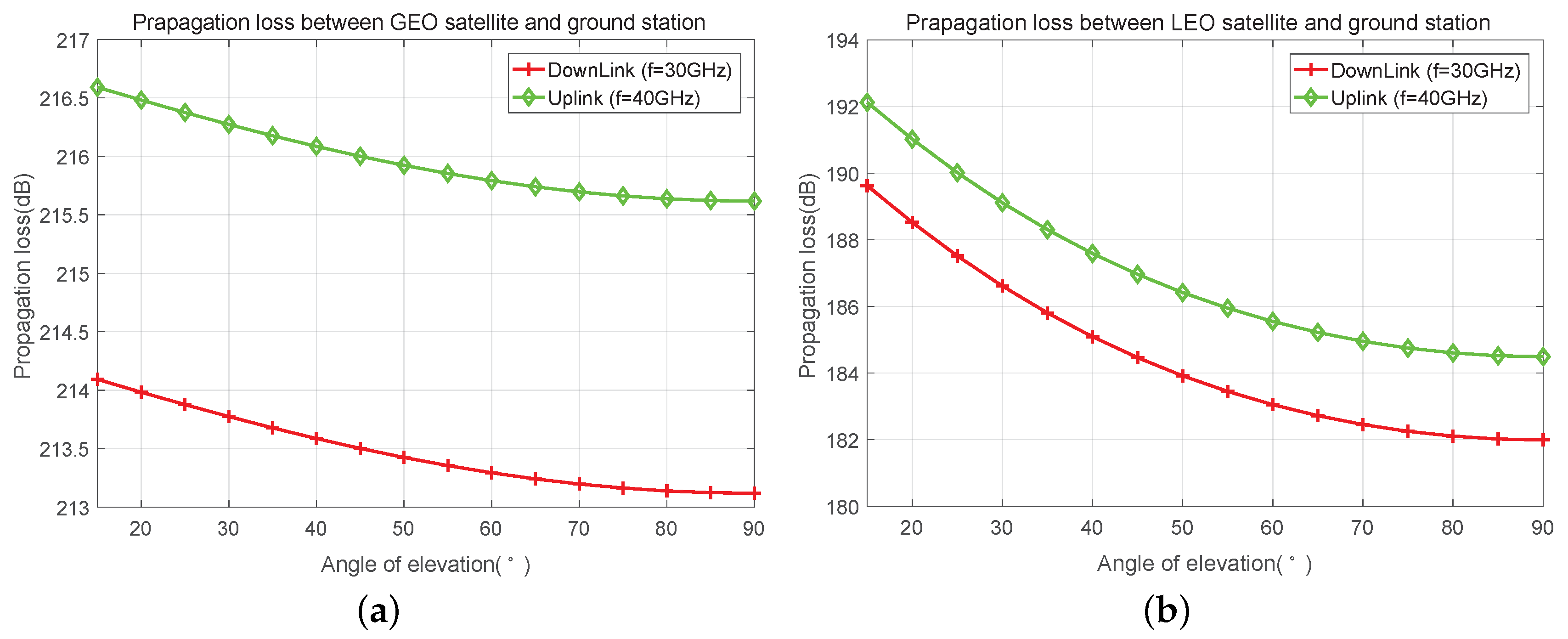
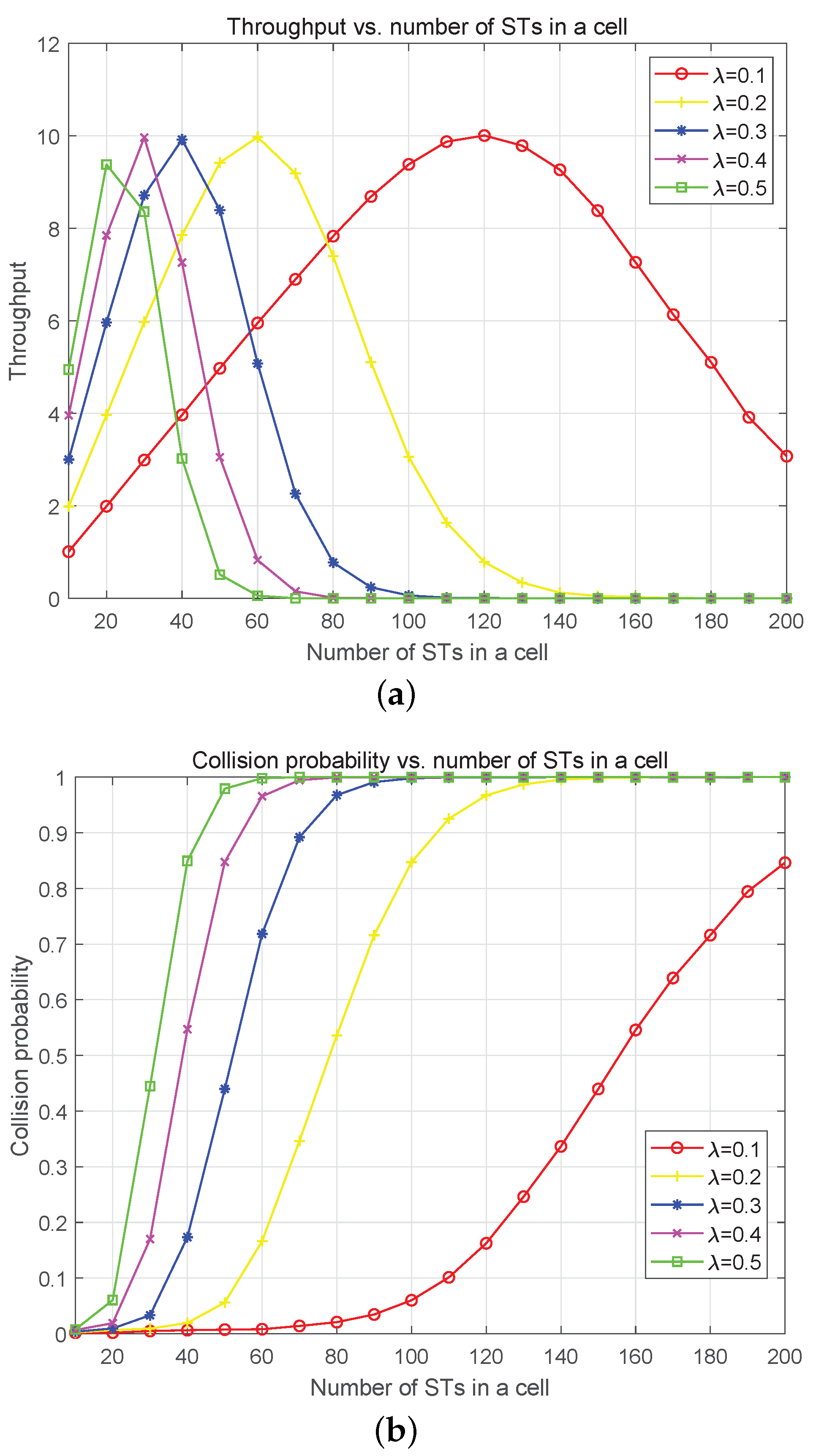
4. Performance Analysis
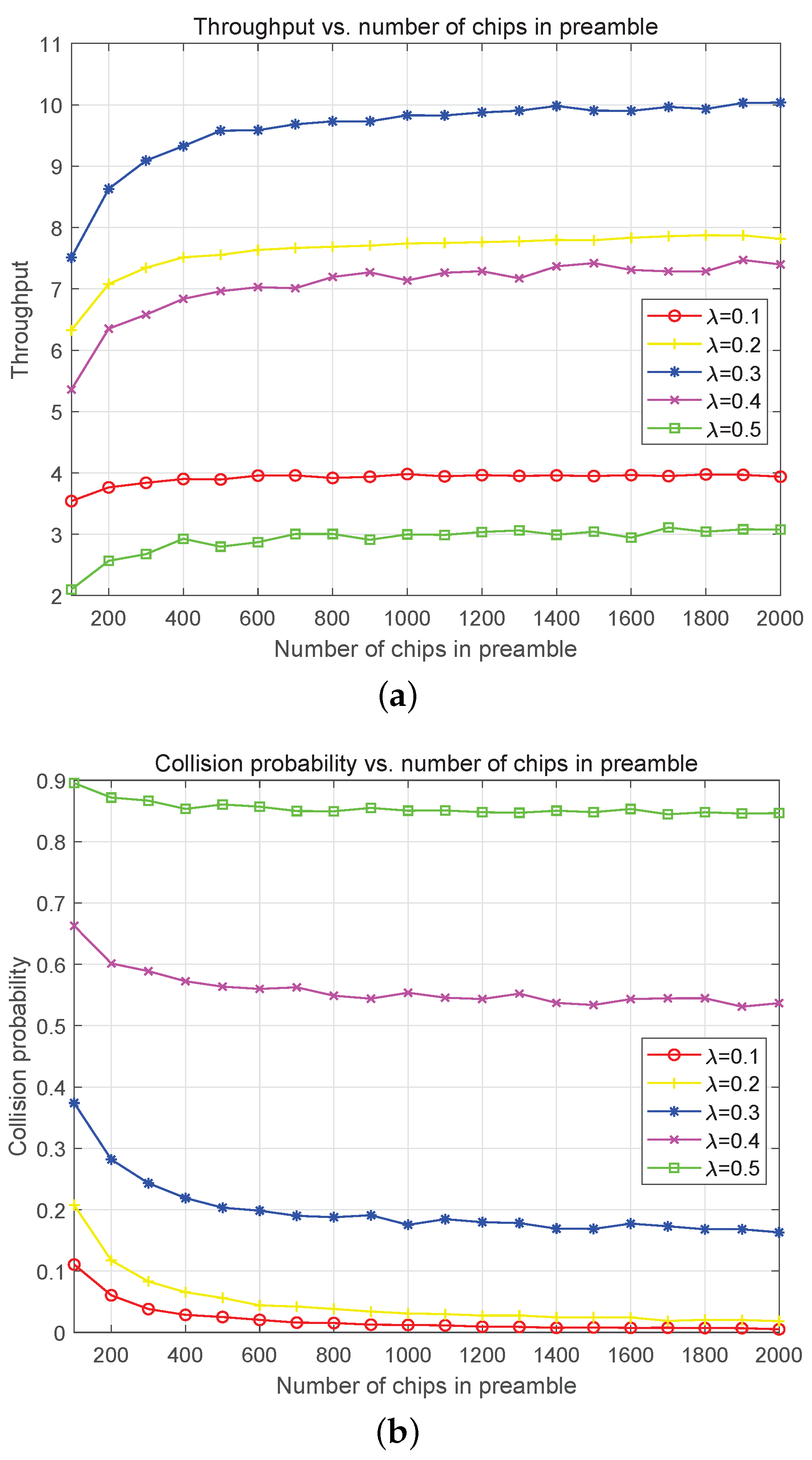
5. Simulation Results
6. Remarks
- Doppler shift. In LEO constellation, the rapid movement of LEO satellite relative to the ground results in a large and changed Doppler shift, also includes the change of delay and propagation loss. This has a huge and unfavorable influence on the time and frequency synchronization between satellite and terrestrial users and the power control. To deal with this problem, the prediction of satellite position and velocity based on ephemeris and telemetered data will play an import and key role. The related scheme has been verified on-orbit in the Chinese Global Broadband Multimedia Beta satellite, whose orbital altitude is 950 km. The result indicate that our scheme works well and the Doppler shift has been reduced to 10∼200 Hz with frequency.
- LEO satellite constellation. In our designed beam-hopping satellite system, the beam-hopping interval is at the millisecond level and the beam-hopping cycle is at the second level. While the visible time of LEO satellite is about minutes to tens of minutes, which is much longer than beam-hopping interval and beam-hopping cycle. Through the calculation of the azimuth and elevation, the largest changes in a beam-hopping interval are below 0.5° when the orbital altitude is 1000 km, which has little effect on the performance. The beam pointing does not need to be adjusted within a beam-hopping interval. In addition, the division of service areas ensure that the satellite can cover STs even at the edge of the service area in LEO constellation. In addition, the division of service areas has been discussed in our authorized patent. However, if the orbital altitude is 500 km or even lower or the designed beam-hopping interval is long, the change of azimuth and elevation will be large and bring greater difficulties to the system design.
- Geostationary surface (GeoSurf) constellation. GeoSurf constellation has been proposed in [27] to ease the system design. With GeoSurf constellation, steering antennas will not be needed, and the tropospheric propagation fading is minimized both for the stationary fading due to water vapor and oxygen, and for rain attenuation. While, the Doppler shift is largely minimized for the connected satellite and would always be viewed almost at the local zenith. Furthermore, the footprint of a single satellite is always the same, therefore making the design easier. The main problem is the large number of satellites crowding the polar region, resulting in serious system self-interference. However, it can be eased by changing the orbital inclination and turning off some satellite loads at high latitudes. In [28], the authors give the evaluation results on both the output of a direct channel and the interference coming from the orthogonal channel in a GeoSurf satellite constellation.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Notations
| Abbreviations | |
| AWGN | Additional Gaussian White Noise |
| BER | Bit Error Rate |
| BH | Beam-Hopping |
| BQP | Binary Quadratic Programming |
| CDMA | Code Division Multiple Access |
| CRDSA | Contention Resolution Diversity Slotted Aloha |
| CSA | Coded Slotted Aloha |
| DLL | Double-Loop Learning |
| DSA | Diversity Slotted Aloha |
| ECEF | Earth-Centered Earth-Fixed |
| E-SSA | Enhanced-SSA |
| FBHCA | Flexible Beam-Hopping Control Algorithm |
| FEC | Forward Error Code |
| GA | Genetic Algorithm |
| GEO | Geostationary Earth Orbit |
| IRSA | Irregular Repetition Slotted Aloha |
| IoT | Internet of Things |
| ISSA | Improved Spread Spectrum Aloha |
| LEO | Low Earth Orbit |
| MADRL | Multi-Agents Deep Reinforcement Learning |
| maxUSWG | maximal User Service Weight Gain |
| MPMM | Multiplier Penalty and Majorization Minimization |
| MWC | Maximum Weighted Clique |
| NOMA | Non-Orthogonal Multiple Access |
| NRT | non-RT |
| Probability Density Function | |
| QoS | Quality of Service |
| QPSK | Quadrature Phase Shift Keying |
| RA | Random Access |
| RT | Real-Time |
| SA | Slotted Aloha |
| SDP | Semi-Definition Programming |
| SIC | Successive Interference Cancellation |
| SINR | Signal to Interference plus Noise Ratio |
| SS | Spread Spectrum |
| SSA | Spread Spectrum Aloha |
| ST | Satellite Terminal |
| TDMA | Time Division Multiple Access |
| Notations | |
| Set of edges in auxiliary graph | |
| Auxiliary graph | |
| Set used to store the beam-hopping pattern | |
| Set of slots | |
| Set of beams | |
| Set of cells | |
| Set of all adjacent vertices for | |
| Set used to store the proportion of online STs | |
| Clique in the auxiliary graph | |
| Maximum weighted clique | |
| Clique set based on auxiliary graph | |
| Set used to store the number of allocated slots to each cell | |
| Cell set used to store the vertices in auxiliary graph | |
| Weight set used to store the weights of all cells’ or vertices’ | |
| Beam angle set | |
| A | Channel gain matrix |
| B | Beam bandwidth |
| Number of online STs in cell k | |
| Receiving antenna gain matrix | |
| Transmitting antenna gain matrix | |
| Gain of phased array antenna with off-axis angle | |
| Backward channel gain matrix at slot i | |
| I | Number of slots in a BH cycle |
| J | Number of beams |
| K | Number of cells |
| M | Number of chips in preamble |
| N | Number of phased array elements |
| Power of white Gaussian noise | |
| Number of chips in preamble | |
| Transmitting power matrix at slot i | |
| If cell k still needs service at slot i, ; Otherwise, | |
| S | Throughput expressed in packets/users per beam-hopping slot |
| T | Number of STs in a cell whose signal arrived at satellite in a BH cycle |
| Maximum throughput in a parameter setting | |
| X | Beam occupancy condition |
| Transmitting antenna gain from cell k using beam j | |
| Receiving antenna gain at satellite on beam j | |
| Backward link gain from ST in cell k to on-board receiver using beam j | |
| Total transmitting power in cell k using beam j | |
| Packet recovery probability | |
| Vertex in auxiliary graph used to represent cell k | |
| Weight of cell k or vertex | |
| Illuminating state, if beam j illuminate cell k at slot i, ; Otherwise, | |
| The illuminating state of cell k using beam j | |
| SNIR of receiving signal at on-board receiver from cell k using beam j at slot i | |
| Channel gain of beam j over backward link | |
| Receiving SNR before hybrided at satellite | |
| Receiving SNR after hybrided at satellite | |
| Spectrum Spread factor | |
| Antenna efficiency | |
| Off-axis angle of phased array antenna | |
| Angle of interference avoidance threshold | |
| Angle between two beams illuminate cell and | |
| Angle between two beams illuminate cell and at slot i | |
| Poisson arrival rate | |
| Beam-hopping cycle denoted as the number of slots | |
| Minimum number of slots allocated to a cell in a BH cycle |
References
- Peyravi, H. Medium Access Control Protocols Performance in Satellite Communications. IEEE Commun. Mag. 1999, 37, 62–71. [Google Scholar] [CrossRef]
- Choudhury, G.; Rappaport, S. Diversity ALOHA-A Random Access Scheme for Satellite Communications. IEEE Trans. Commun. 1983, 31, 450–457. [Google Scholar] [CrossRef]
- Casini, E.; Gaudenzi, R.D.; Herrero, O.D.R. Contention Resolution Diversity Slotted ALOHA (CRDSA): An Enhanced Random Access Scheme for Satellite Access Packet Networks. IEEE Trans. Wirel. Commun. 2007, 6, 1408–1417. [Google Scholar] [CrossRef]
- Liva, G. Graph-Based Analysis and Optimization of Contention Resolution Diversity Slotted ALOHA. IEEE Trans. Commun. 2007, 59, 477–487. [Google Scholar] [CrossRef]
- Paolini, E.; Liva, G.; Chiani, M. Coded Slotted ALOHA: A Graph-Based Method for Uncoordinated Multiple Access. IEEE Trans. Inform. Theory 2015, 61, 6815–6832. [Google Scholar] [CrossRef]
- Abramson, N. Multiple Access in Wireless Digital Networks. Proc. IEEE 1994, 82, 1360–1370. [Google Scholar] [CrossRef]
- Pateros, C. Novel Direct Sequence Spread Spectrum Multiple Access Technique. In Proceedings of the MILCOM 2000, Los Angeles, CA, USA, 22–25 October 2000; pp. 564–568. [Google Scholar]
- Herrero, O.D.R.; Gaudenzi, R.D. High Efficiency Satellite Multiple Access Scheme for Machine-to-Machine Communications. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2961–2989. [Google Scholar] [CrossRef]
- Li, Y.T.; Luo, Z.Q.; Zhou, W.Y.; Zhu, J.K. Benefits Analysis of Beam Hopping in Satellite Mobile System with Unevenly Distributed Traffics. China Commun. 2021, 18, 11–23. [Google Scholar] [CrossRef]
- Wang, Y.X.; Bian, D.M.; Hu, J.; Tang, J.Y.; Wang, C. Optimization Method for Full Bandwidth Beam Hopping Pattern Based on Clustering. Comput. Eng. 2020, 46, 169–176. [Google Scholar]
- Lei, L.; Lagunas, E.; Yuan, Y.X.; Kibria, M.G.; Chatzinotas, S.; Ottersten, B. Deep Learning for Beam Hopping in Multibeam Satellite Systems. In Proceedings of the VTC2020-Spring, Antwerp, Belgium, 25–28 May 2020. [Google Scholar]
- Lei, L.; Lagunas, E.; Yuan, Y.X.; Kibria, M.G.; Chatzinotas, S.; Ottersten, B. Beam Illumination Pattern Design in Satellite Networks: Learning and Optimization for Efficient Beam Hopping. IEEE Access 2020, 8, 136655–136667. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, X.D.; Zhang, G.X. Joint Precoding Schemes for Flexible Resource Allocation in High Throughput Satellite Systems Based on Beam Hopping. China Commun. 2021, 18, 48–61. [Google Scholar] [CrossRef]
- Lin, Z.Y.; Ni, Z.Y.; Kuang, L.L.; Jiang, C.X.; Huang, Z. Dynamic Beam Pattern and Bandwidth Allocation Based on Multi-Agent Deep Reinforcement Learning for Beam Hopping Satellite Systems. IEEE Trans. Veh. Technol. 2022, 71, 3917–3930. [Google Scholar] [CrossRef]
- Hu, X.; Wang, L.B.; Wang, Y.; Xu, S.J.; Liu, Z.J.; Wang, W.D. Dynamic Beam Hopping for DVB-S2X GEO Satellite: A DRL-Powered GA Approach. IEEE Commun. Lett. 2022, 26, 808–812. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, Y.C.; Liao, X.L.; Liu, Z.J.; Wang, W.D.; Channouchi, F.M. Dynamic Beam Hopping Method Based on Multi-Objective Deep Reinforcement Learning for Next Generation Satellite Broadband Systems. IEEE Trans. Broadcast. 2020, 66, 630–646. [Google Scholar] [CrossRef]
- Wu, Z.G.; Ren, P.Y.; Xu, D.Y. Flexible Resource Allocation for Differentiated QoS Provisioning in Beam-Hopping Satellite Communications System. In Proceedings of the VTC2022-Spring, Helsinki, Finland, 19–22 June 2022. [Google Scholar]
- Wang, Y.; Chen, Y.; Qiao, Y.F.; Luo, H.J.; Wang, X.L.; Li, R.; Wang, J. Cooperative Beam Hopping for Accurate Positioning in Ultra-Dense LEO Satellite Networks. In Proceedings of the 2021 ICC Workshops, Montreal, QC, Canada, 14–23 June 2021. [Google Scholar]
- Wang, A.Y.; Lei, L.; Lagunas, E.; P´erez-Neira, A.I.; Chatzinotas, S.; Ottersten, B. Joint Optimization of Beam-Hopping Design and NOMA-Assisted Transmission for Flexible Satellite Systems. IEEE Trans. Wirel. Commun. 2022, 21, 8846–8858. [Google Scholar] [CrossRef]
- Chen, L.; Ha, V.N.; Lagunas, E.; Wu, L.L.; Chatzinotas, S.; Ottersten, B. The Next Generation of Beam Hopping Satellite Systems: Dynamic Beam Illumination with Selective Precoding. IEEE Trans. Wireless Commun. 2022. Early Access. [Google Scholar] [CrossRef]
- Nelson, J.G.; Fonseca; Jacques, S. Multi-Beam Reflector Antenna System Combining Beam Hopping and Size Reduction of Effectively Used Spots. IEEE Antennas Propag. Mag. 2012, 54, 88–99. [Google Scholar]
- Tang, W.J. Research and Design on a Phased Array Antenna. Ph.D. Thesis, Xidian University, Xi’an, China, 2017. [Google Scholar]
- Zhang, G.X.; Wang, Y.F.; Ding, X.J.; Hong, T.; Liu, Z.W.; Zhang, C. Research on Several Key Technologies of Satellite Internet. J. Commun. 2021, 42, 1–14. [Google Scholar]
- Sharma, S.K.; Chatzinotas, S.; Ottersten, B. Cognitive Beamhopping for Spectral Coexistence of Multibeam Satellites. Int. J. Satell. Commun. Netw. 2014, 33, 69–91. [Google Scholar] [CrossRef]
- ITU-R P.618-13-2017; Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems. International Telecommunication Union: Geneva, Switzerland, 2017.
- Mengali, A.; Gaudenzi, R.D.; Stefanovic, C. On the Modeling and Performance Assessment of Random Access with SIC. IEEE J. Select. Areas Commun. 2018, 36, 292–303. [Google Scholar] [CrossRef]
- Matricciani, E. Geocentric Spherical Surfaces Emulating the Geostationary Orbit at Any Latitude with Zenith Links. Future Internet 2020, 12, 16. [Google Scholar] [CrossRef]
- Matricciani, E.; Riva, C. Transfer Functions and Linear Distortions in Ultra-Wideband Channels Faded by Rain in GeoSurf Satellite Constellations. Future Internet 2022, 15, 17. [Google Scholar] [CrossRef]







| City | Rain Attenuation (dB) | |
|---|---|---|
| 99.9% Availability | 99.99% Availability | |
| Beijing | ||
| Shanghai | ||
| Sanya | ||
| Chongqing | ||
| Parameter Type | Value |
|---|---|
| frame length (bits) | 128 |
| encode style | Convolutional/Turbo |
| code rate | 1/2 |
| modulation style | QPSK |
| spread spectrum factor | 128 |
| spread spectrum code | m-sequences |
| Eb/N0 (dB) | 4, 8, 12, 16 |
| preamble length (chips) | 100–2000 |
| mean value of Poisson arrival | 0.1, 0.2, 0.3, 0.4, 0.5 |
| symbol rate (ksyms/s) | 4.8 |
| number of beams | 4 |
| number of cells | 25 |
| number of STs | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gou, L.; Bian, D.; Dong, B.; Nie, Y. Improved Spread Spectrum Aloha Protocol and Beam-Hopping Approach for Return Channel in Satellite Internet of Things. Sensors 2023, 23, 2116. https://doi.org/10.3390/s23042116
Gou L, Bian D, Dong B, Nie Y. Improved Spread Spectrum Aloha Protocol and Beam-Hopping Approach for Return Channel in Satellite Internet of Things. Sensors. 2023; 23(4):2116. https://doi.org/10.3390/s23042116
Chicago/Turabian StyleGou, Liang, Dongming Bian, Baogui Dong, and Yulei Nie. 2023. "Improved Spread Spectrum Aloha Protocol and Beam-Hopping Approach for Return Channel in Satellite Internet of Things" Sensors 23, no. 4: 2116. https://doi.org/10.3390/s23042116
APA StyleGou, L., Bian, D., Dong, B., & Nie, Y. (2023). Improved Spread Spectrum Aloha Protocol and Beam-Hopping Approach for Return Channel in Satellite Internet of Things. Sensors, 23(4), 2116. https://doi.org/10.3390/s23042116








