An Improved Parameter Identification Algorithm for the Friction Model of Electro-Hydraulic Servo Systems
Abstract
:1. Introduction
2. System Model
2.1. LuGre Friction Model
2.2. Identification Model
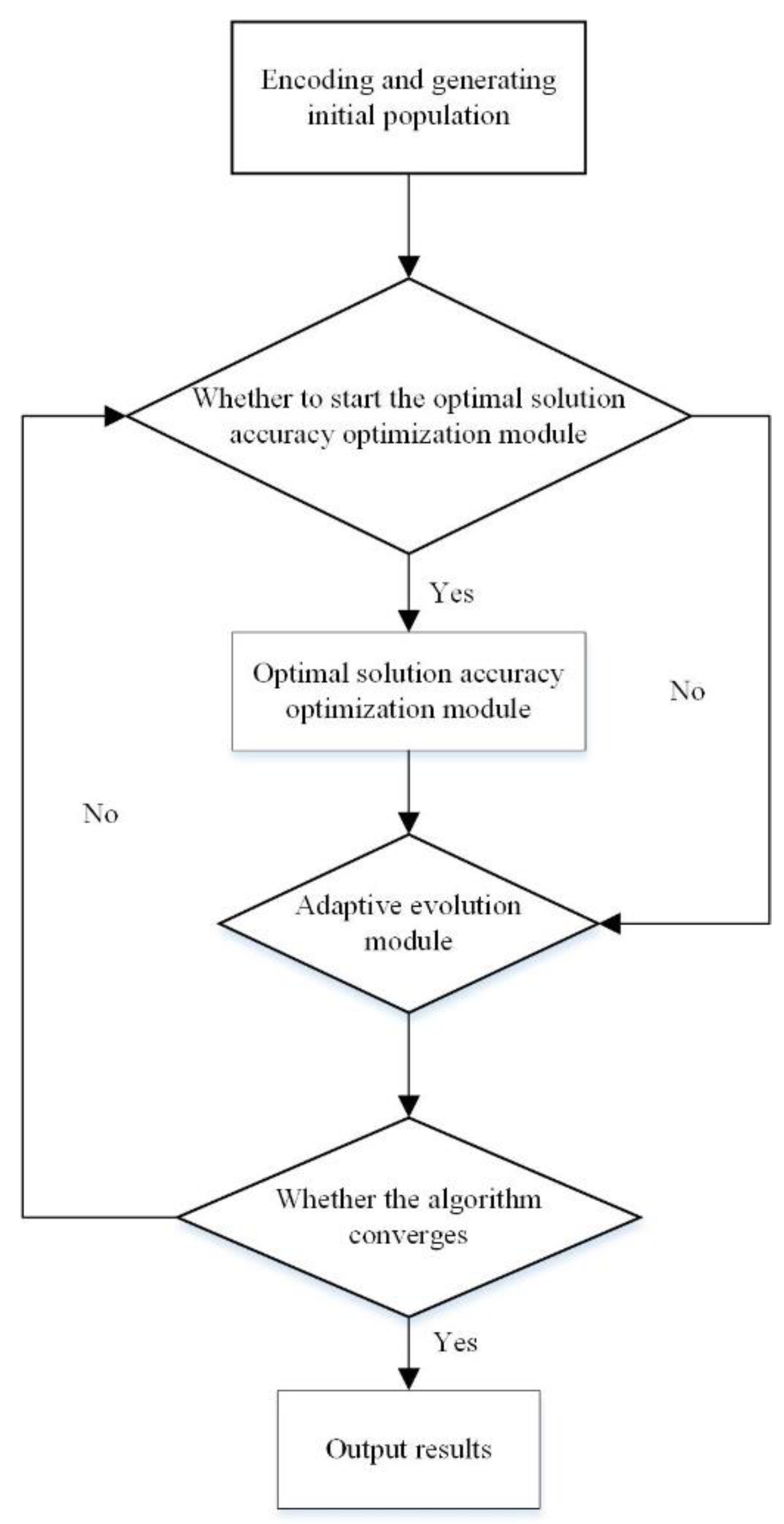
3. Improved Adaptive Genetic Identification Algorithm
3.1. Adaptive Evolution Module Design
3.2. Optimal Solution Accuracy Optimization Module Design
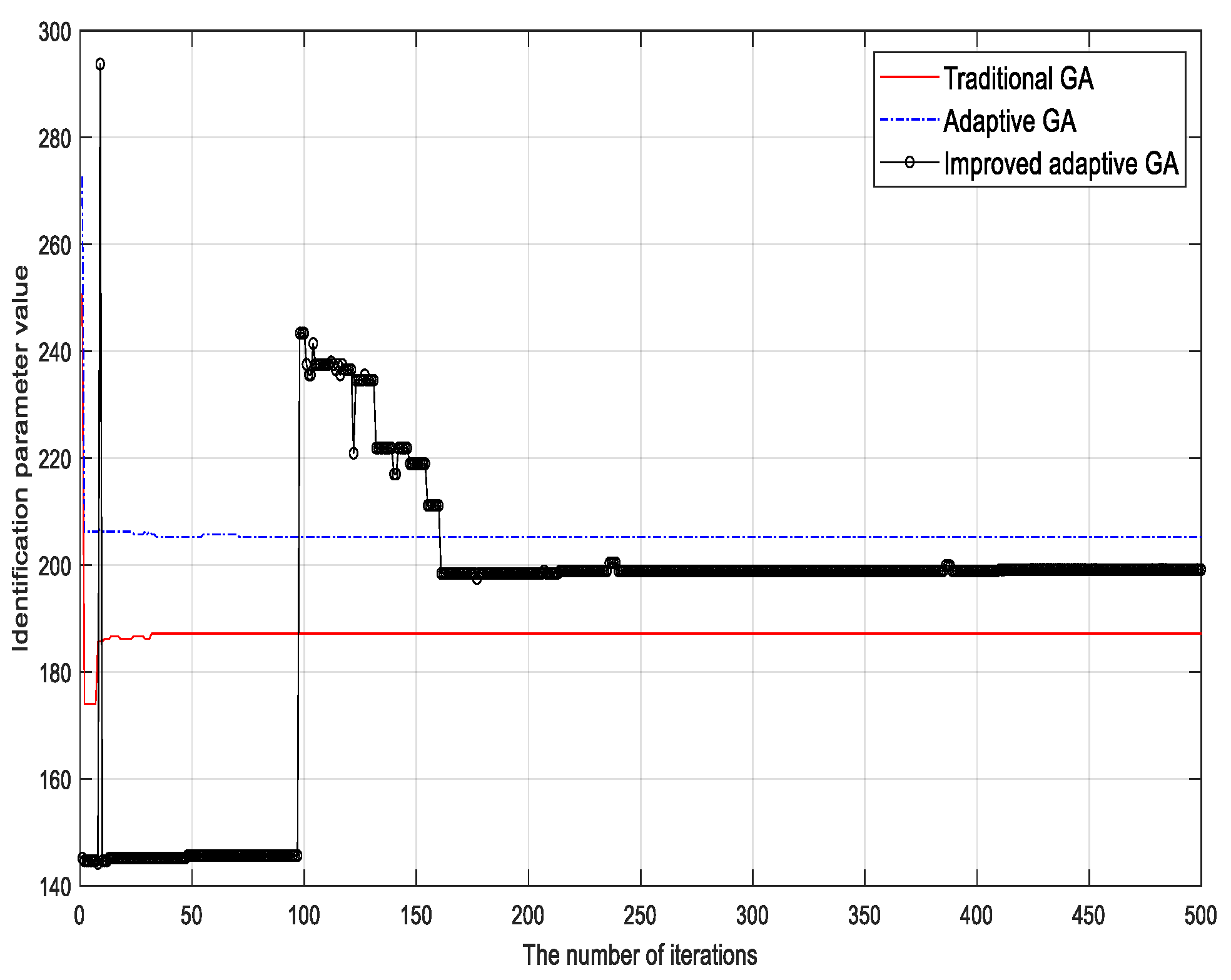
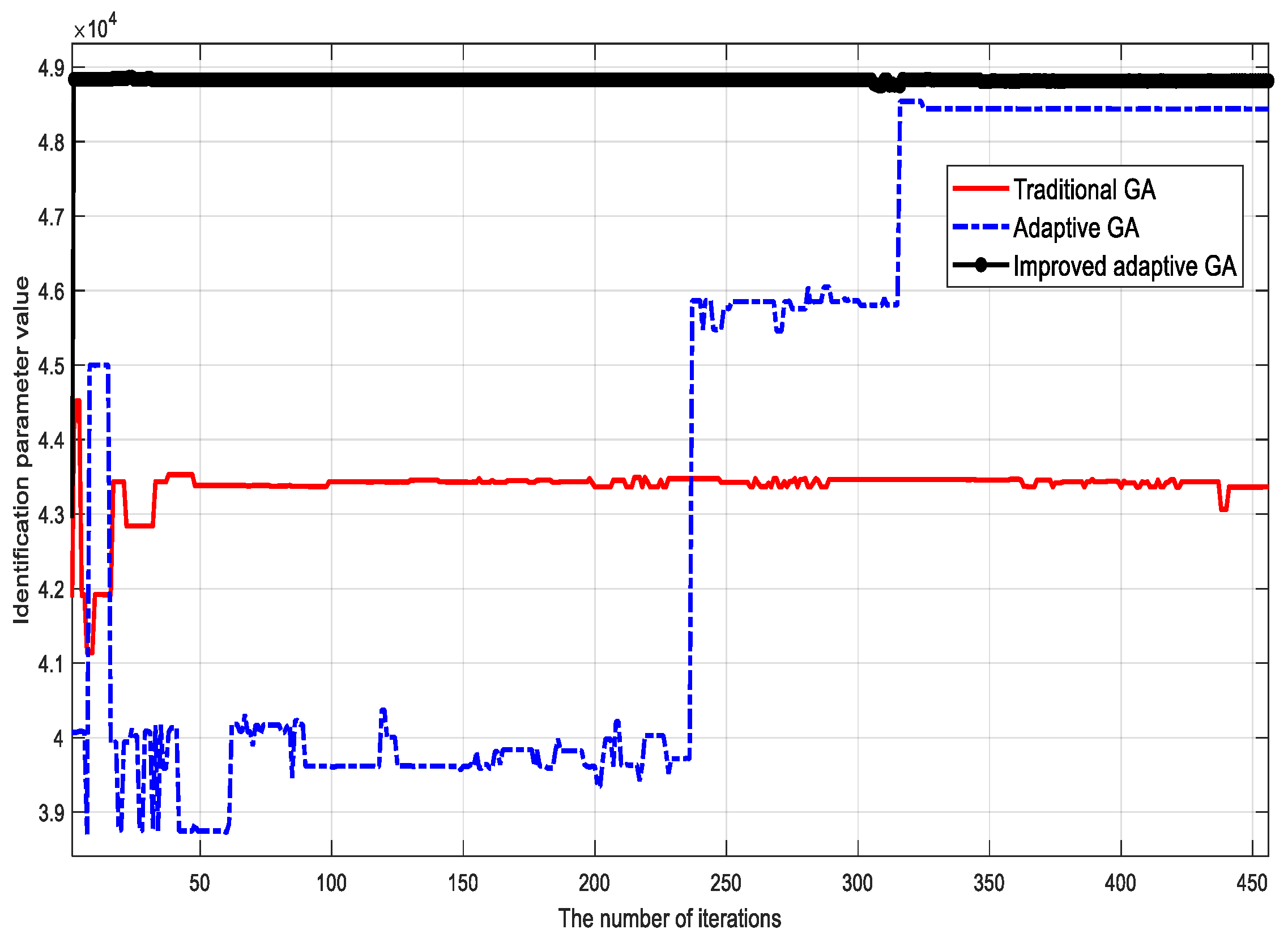
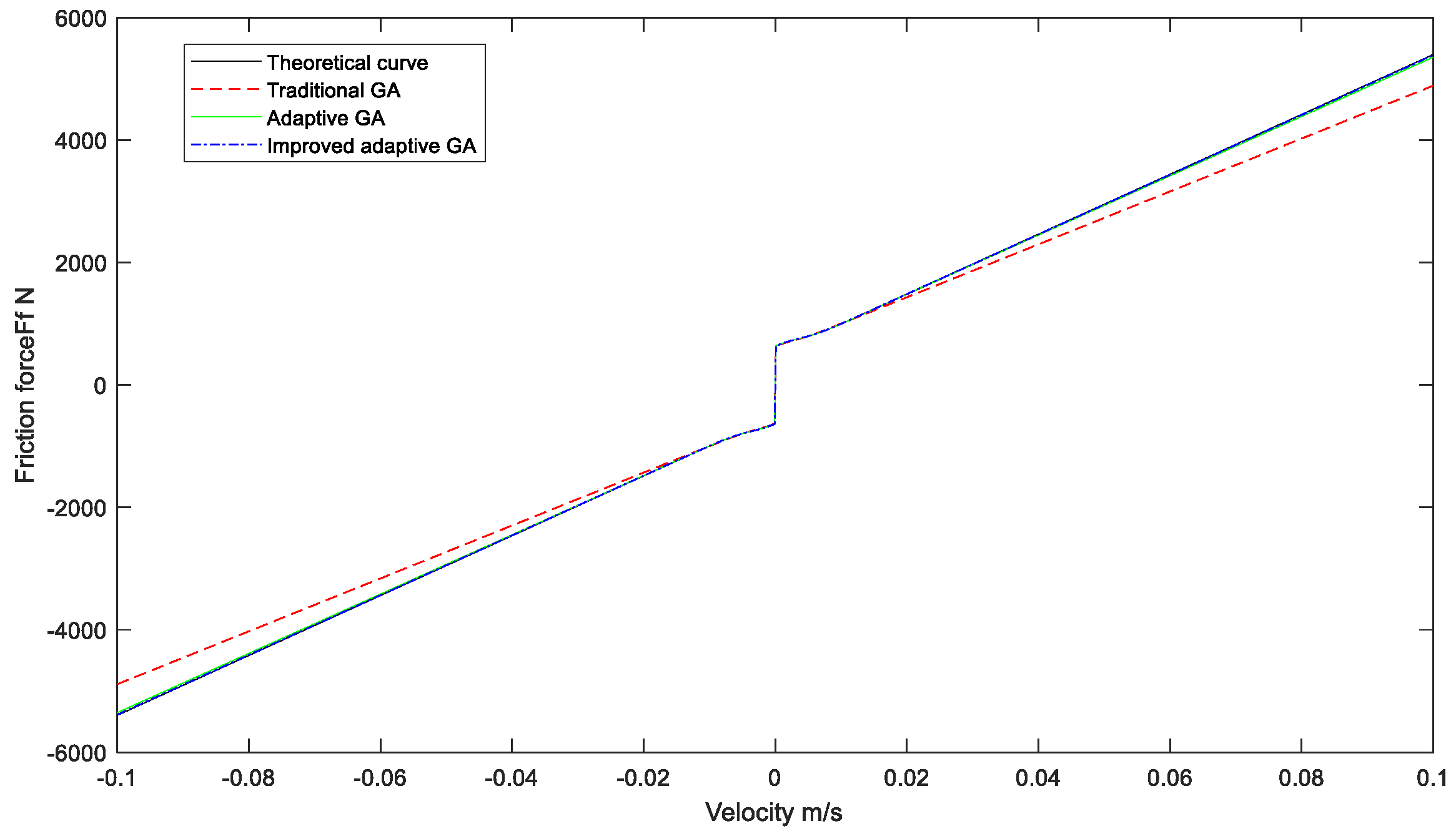
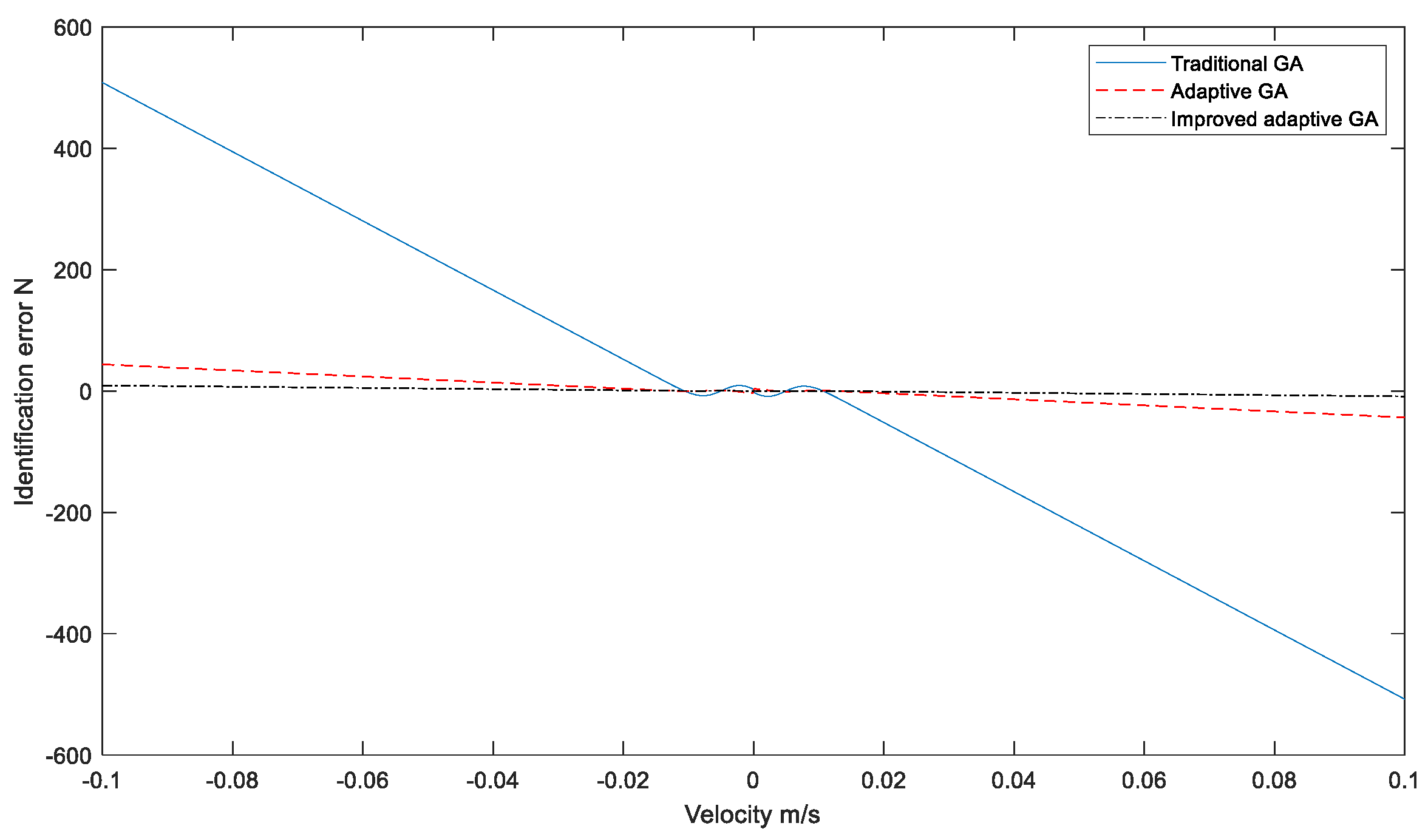
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baghestan, K.; Rezaei, S.M.; Talebi, H.A.; Zareinejad, M. An energy-saving nonlinear position control strategy for electro-hydraulic servo systems. ISA Trans. 2015, 59, 268–279. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Yan, H. Nonlinear adaptive robust control of the electro-hydraulic servo system. Appl. Sci. 2020, 10, 4494. [Google Scholar] [CrossRef]
- Tivay, A.; Zareinejad, M.; Rezaei, S.M.; Baghestan, K. A switched energy saving position controller for variable-pressure electro-hydraulic servo systems. ISA Trans. 2014, 53, 1297–1306. [Google Scholar] [CrossRef] [PubMed]
- Sang, Y.; Gao, H.; Xiang, F. Practical friction models and friction compensation in high-precision electro-hydraulic servo force control systems. Instrum. Sci. Technol. 2014, 42, 184–199. [Google Scholar] [CrossRef]
- Gao, B.; Shen, W.; Zheng, L.; Zhang, W.; Zhao, H. A Review of Key Technologies for Friction Nonlinearity in an Electro-Hydraulic Servo System. Machines 2022, 10, 568. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z. Research on friction disturbance compensation method in low-speed region of permanent magnet synchronous motor. In Proceedings of the 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 4–6 March 2022; pp. 2056–2060. [Google Scholar]
- Xue, L. Parameters Identification and Friction Compensation Based on the LuGre Model in Servo System. Master’s Thesis, University of Jinan, Jinan, China, 2013. [Google Scholar]
- Liu, B.; Yao, H.; Nie, S. Parameter Identification of LuGre Friction Model Based on Interval Analysis. China Mech. Eng. 2013, 24, 2647. [Google Scholar]
- He, Y.; Wang, J.; Hao, R. Adaptive robust dead-zone compensation control of electro-hydraulic servo systems with load disturbance rejection. J. Syst. Sci. Complex. 2015, 28, 341–359. [Google Scholar] [CrossRef]
- Goforth, F.J.; Gao, Z. An active disturbance rejection control solution for hysteresis compensation. In Proceedings of the 2008 American Control Conference, Seattle, DC, USA, 11–13 June 2008; pp. 2202–2208. [Google Scholar]
- Le Tien, L.; Albu-Schaffer, A.; De Luca, A.; Hirzinger, G. Friction observer and compensation for control of robots with joint torque measurement. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3789–3795. [Google Scholar]
- Freidovich, L.; Robertsson, A.; Shiriaev, A.; Johansson, R. LuGre-model-based friction compensation. IEEE Trans. Control Syst. Technol. 2009, 18, 194–200. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S. High performance adaptive control of mechanical servo system with LuGre friction model: Identification and compensation. J. Dyn. Syst. Meas. Control 2012, 134, 011021. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, K.; Wang, H.; Zhong, D.; Su, J.; Liu, Z. Research on adaptive friction compensation of digital hydraulic cylinder based on LuGre friction model. Shock Vib. 2021, 2021, 8854424. [Google Scholar] [CrossRef]
- Zhang, W.; Li, P.; Xu, H. An active disturbance rejection friction compensation in permanent magnet synchronous motor servo system. In Proceedings of the 30th Chinese Control Conference, Shenyang, China, 9–11 June 2018; pp. 3715–3719. [Google Scholar]
- Xu, L. Application of the Newton iteration algorithm to the parameter estimation for dynamical systems. J. Comput. Appl. Math. 2015, 288, 33–43. [Google Scholar] [CrossRef]
- De Wit, C.C.; Lischinsky, P. Adaptive friction compensation with partially known dynamic friction model. Int. J. Adapt. Control Signal Process. 1997, 11, 65–80. [Google Scholar] [CrossRef]
- Rutenbar, R.A. Simulated annealing algorithms: An overview. IEEE Circuits Devices Mag. 1989, 5, 19–26. [Google Scholar] [CrossRef]
- Li, J.; Cheng, J.-H.; Shi, J.-Y.; Huang, F. Brief introduction of back propagation (BP) neural network algorithm and its improvement. In Advances in Computer Science and Information Engineering: Volume 2; Springer: Berlin/Heidelberg, Germany, 2012; pp. 553–558. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks. Studies in Computational Intelligence; Springer: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar]
- Irakoze, R.; Yakoub, K.; Kaddouri, A. Identification of piezoelectric LuGre model based on particle swarm optimization and real-coded genetic algorithm. In Proceedings of the 2015 IEEE 28th Canadian Conference on Electrical and Computer Engineering (CCECE), Halifax, NS, Canada, 3–6 May 2015; pp. 1451–1457. [Google Scholar]
- Chen, Q.; Bao, J.; Wang, M.; Ye, H.; Peng, F. Simulated Annealing Algorithm for Friction Parameters Identification. TELKOMNIKA Indones. J. Electr. Eng. 2013, 11, 245–252. [Google Scholar] [CrossRef]
- Ding, S.; Su, C.; Yu, J. An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm-A literature review. In Proceedings of the 2019 international conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar]
- Johanastrom, K.; Canudas-De-Wit, C. Revisiting the LuGre friction model. IEEE Control Syst. Mag. 2008, 28, 101–114. [Google Scholar] [CrossRef]
- Yue, F.; Li, X. Robust adaptive integral backstepping control for opto-electronic tracking system based on modified LuGre friction model. ISA Trans. 2018, 80, 312–321. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.-C.; Tsai, C.-M.; Chung, C.-L. A study of optical design and optimization of zoom optics with liquid lenses through modified genetic algorithm. Opt. Express 2011, 19, 16291–16302. [Google Scholar] [CrossRef] [PubMed]




| Parameter Type | Value |
|---|---|
| Search range of the bristle stiffness coefficient σ0 | [0, 5 × 109] |
| Search range of the microscopic damping coefficient σ1 | [0, 1000] |
| Search range of the viscous friction coefficient σ2 | [0, 50,000] |
| Search range of the Coulomb friction force Fc | [0, 1000] |
| Search range of the maximum static friction force Fs | [0, 1000] |
| Search range of the Stribeck velocity vs | [0.001, 0.1] |
| Sampling period t0 | 0.001 s |
| Crossover coefficient k1 | 0.8 |
| Mutation coefficient k2 | 0.7 |
| Starting coefficient γ | 0.1 |
| Starting coefficient α | 0.6 |
| Constant β | 0.4 |
| Number of iterations m | 500 |
| Parameter Type | Value |
|---|---|
| Bristle stiffness coefficient σ0 | 3.9 × 109 N/m |
| Microscopic damping coefficient σ1 | 200 N/(m/s) |
| Viscous friction coefficient σ2 | 48,900 N/(m/s) |
| Coulomb friction force Fc | 506 N |
| Maximum static friction force Fs | 632 N |
| Stribeck velocity vs | 0.005 m/s |
| Piston rod mass M | 200 kg |
| Parameter Type | Different Genetic Algorithm | Identification Value | Error (%) |
|---|---|---|---|
| Bristle stiffness coefficient σ0 | Traditional | 3.9003 × 109 | 0.0077 |
| Adaptive | 3.8996 × 109 | 0.010 | |
| Improved adaptive | 3.8999 × 109 | 0.0026 | |
| Microscopic damping coefficient σ1 | Same as above | 187.19 | 6.4 |
| 205.23 | 2.6 | ||
| 201.37 | 0.69 | ||
| Viscous friction coefficient σ2 | 4.32 × 104 | 57 | |
| 4.84 × 104 | 1.0 | ||
| 4.88 × 104 | 0.20 | ||
| Coulomb friction force Fc | 567.94 | 12 | |
| 512.22 | 1.2 | ||
| 507.01 | 0.20 | ||
| Difference between the maximum static friction force Fs and the Coulomb friction force Fc | 61.58 | 51 | |
| 123.20 | 2.2 | ||
| 125.10 | 0.71 | ||
| Stribeck velocity vs | 0.00400 | 20 | |
| 0.00480 | 4.0 | ||
| 0.00498 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, J.; Zhou, F.; Zheng, J. An Improved Parameter Identification Algorithm for the Friction Model of Electro-Hydraulic Servo Systems. Sensors 2023, 23, 2076. https://doi.org/10.3390/s23042076
Liao J, Zhou F, Zheng J. An Improved Parameter Identification Algorithm for the Friction Model of Electro-Hydraulic Servo Systems. Sensors. 2023; 23(4):2076. https://doi.org/10.3390/s23042076
Chicago/Turabian StyleLiao, Jian, Fuming Zhou, and Jianbo Zheng. 2023. "An Improved Parameter Identification Algorithm for the Friction Model of Electro-Hydraulic Servo Systems" Sensors 23, no. 4: 2076. https://doi.org/10.3390/s23042076
APA StyleLiao, J., Zhou, F., & Zheng, J. (2023). An Improved Parameter Identification Algorithm for the Friction Model of Electro-Hydraulic Servo Systems. Sensors, 23(4), 2076. https://doi.org/10.3390/s23042076





