Pixel-Domain Just Noticeable Difference Modeling with Heterogeneous Color Features
(This article belongs to the Section Intelligent Sensors)
Abstract
1. Introduction
- (1)
- We carefully extract the color features that affect perception in the image, and on this basis, analyze the interaction relationship between color regions from the perspective of visual energy competition; then, accordingly propose color contrast intensity.
- (2)
- According to the characteristics of visual perception, color complexity and color distribution dispersion are regarded as visual suppression sources, and color contrast intensity is regarded as a visual stimulus source. Then, they are unified to information communication framework to quantify the degree of influence on perception.
- (3)
- The color uncertainty and the color saliency are applied to improve the conventional JND model, taking the masking and attention effect into consideration, wherein color saliency serves as an adjusting factor to modulate the masking effect based on color uncertainty.
2. Analysis of Color Feature Parameters
2.1. Existing Color Feature Parameters
2.2. Feasibility Analysis of Heterogeneous Color Feature Fusion
2.3. Interaction Analysis between Color Feature Quantities
- (1)
- With the same dispersion, the larger the homogeneous color area is, the more visual energy allocated to this color area compared with other color areas.
- (2)
- On the condition of same area proportion, if the distribution of one homogeneous color region is more concentrated than that of other regions, it will pose a positive stimulation effect on vision and vice versa.
- (3)
- As the distance between different color regions and the fixation point increases, the competitive relationship gradually weakens.
3. The Proposed JND Model
3.1. Color Uncertainty Measurement
3.2. Color Saliency Measurement
3.3. The Proposed JND Model
4. Experimental Results and Analysis
4.1. Noise Injection Method
4.2. Ablation Experiments
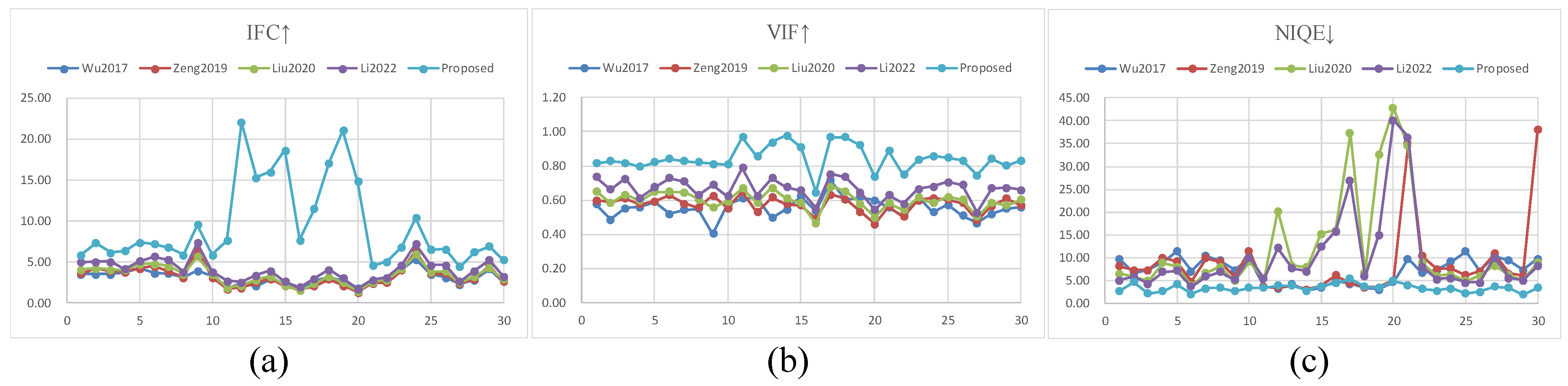
4.3. Comparison Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wen Chang, H.; Yang, H.; Gan, Y.; hui Wang, M. Sparse Feature Fidelity for Perceptual Image Quality Assessment. IEEE Trans. Image Process. 2013, 22, 4007–4018. [Google Scholar] [CrossRef]
- Men, H.; Lin, H.; Saupe, D. Spatiotemporal Feature Combination Model for No-Reference Video Quality Assessment. In Proceedings of the 2018 Tenth International Conference on Quality of Multimedia Experience (QoMEX), Cagliari, Italy, 29 May–1 June 2018; pp. 1–3. [Google Scholar]
- Liu, Y.; Gu, K.; Wang, S.; Zhao, D.; Gao, W. Blind Quality Assessment of Camera Images Based on Low-Level and High-Level Statistical Features. IEEE Trans. Multimed. 2019, 21, 135–146. [Google Scholar] [CrossRef]
- Korhonen, J. Two-Level Approach for No-Reference Consumer Video Quality Assessment. IEEE Trans. Image Process. 2019, 28, 5923–5938. [Google Scholar] [CrossRef]
- Gegenfurtner, K.R. Cortical mechanisms of colour vision. Nat. Rev. Neurosci. 2003, 4, 563–572. [Google Scholar] [CrossRef]
- Bonnardel, N.; Piolat, A.; Bigot, L.L. The impact of colour on Website appeal and users’ cognitive processes. Displays 2011, 32, 69–80. [Google Scholar] [CrossRef]
- Kwon, K.J.; Kim, M.B.; Heo, C.; Kim, S.G.; Baek, J.; Kim, Y.H. Wide color gamut and high dynamic range displays using RGBW LCDs. Displays 2015, 40, 9–16. [Google Scholar] [CrossRef]
- wen Chang, H.; Zhang, Q.; Wu, Q.; Gan, Y. Perceptual image quality assessment by independent feature detector. Neurocomputing 2015, 151, 1142–1152. [Google Scholar] [CrossRef]
- wen Chang, H.; Du, C.Y.; Bi, X.D.; hui Wang, M. Color Image Quality Evaluation based on Visual Saliency and Gradient Information. In Proceedings of the 2021 7th International Symposium on System and Software Reliability (ISSSR), Chongqing, China, 23–24 September 2021; pp. 64–72. [Google Scholar]
- Falomir, Z.; Cabedo, L.M.; Abril, L.G.; Sanz, I. A model for qualitative colour comparison using interval distances. Displays 2013, 34, 250–257. [Google Scholar] [CrossRef]
- Qin, S.; Shu, G.; Yin, H.; Xia, J.; Heynderickx, I. Just noticeable difference in black level, white level and chroma for natural images measured in two different countries. Displays 2010, 31, 25–34. [Google Scholar] [CrossRef]
- Post, D.L.; Goode, W.E. Palette designer: A color-code design tool. Displays 2020, 61, 101929. [Google Scholar] [CrossRef]
- Liu, A.; Lin, W.; Paul, M.; Deng, C.; Zhang, F. Just Noticeable Difference for Images With Decomposition Model for Separating Edge and Textured Regions. IEEE Trans. Circuits Syst. Video Technol. 2010, 20, 1648–1652. [Google Scholar] [CrossRef]
- Wu, J.; Shi, G.; Lin, W.; Liu, A. Just Noticeable Difference Estimation for Images With Free-Energy Principle. IEEE Trans. Multimed. 2013, 15, 1705–1710. [Google Scholar] [CrossRef]
- Wu, J.; Li, L.; Dong, W.; Shi, G.; Lin, W.; Kuo, C.C.J. Enhanced Just Noticeable Difference Model for Images With Pattern Complexity. IEEE Trans. Image Process. 2017, 26, 2682–2693. [Google Scholar] [CrossRef]
- Shen, X.; Ni, Z.; Yang, W.; Zhang, X.; Kwong, S. Just Noticeable Distortion Profile Inference: A Patch-Level Structural Visibility Learning Approach. IEEE Trans. Image Process. 2021, 30, 26–38. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, W. Asymmetric Foveated Just-Noticeable-Difference Model for Images With Visual Field Inhomogeneities. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 4064–4074. [Google Scholar] [CrossRef]
- Bae, S.H.; Kim, M. A Novel Generalized DCT-Based JND Profile Based on an Elaborate CM-JND Model for Variable Block-Sized Transforms in Monochrome Images. IEEE Trans. Image Process. 2014, 23, 3227–3240. [Google Scholar]
- Itti, L.; Koch, C.; Niebur, E. A Model of Saliency-Based Visual Attention for Rapid Scene Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Meur, O.L.; Callet, P.L.; Barba, D.; Thoreau, D. A coherent computational approach to model bottom-up visual attention. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 802–817. [Google Scholar] [CrossRef]
- Hefei, L.; Zheng-ding, L.; Fu-hao, Z.; Rui-xuan, L. An Energy Modulated Watermarking Algorithm Based on Watson Perceptual Model. J. Softw. 2006, 17, 1124. [Google Scholar]
- Liu, A.; Verma, M.; Lin, W. Modeling the masking effect of the human visual system with visual attention model. In Proceedings of the 2009 7th International Conference on Information, Communications and Signal Processing (ICICS), Macau, China, 8–10 December 2009; pp. 1–5. [Google Scholar]
- Zhang, D.; Gao, L.; Zang, D.; Sun, Y. A DCT-domain JND model based on visual attention for image. In Proceedings of the 2013 IEEE International Conference on Signal and Image Processing Applications, Melaka, Malaysia, 8–10 October 2013; pp. 1–4. [Google Scholar]
- Berthier, M.; Garcin, V.; Prencipe, N.; Provenzi, E. The relativity of color perception. J. Math. Psychol. 2021, 103, 102562. [Google Scholar] [CrossRef]
- Chen, H.; Hu, R.; Hu, J.; Wang, Z. Temporal color Just Noticeable Distortion model and its application for video coding. In Proceedings of the 2010 IEEE International Conference on Multimedia and Expo, Singapore, 19–23 July 2010; pp. 713–718. [Google Scholar]
- Yang, X.; Lin, W.; Lu, Z.; Ong, E.P.; Yao, S. Just-noticeable-distortion profile with nonlinear additivity model for perceptual masking in color images. In Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ’03), Hong Kong, China, 6–10 April 2003; Volume 3. [Google Scholar]
- Xue, F.; Jung, C. Chrominance just-noticeable-distortion model based on human colour perception. Electron. Lett. 2014, 50, 1587–1589. [Google Scholar] [CrossRef]
- Boev, A.; Poikela, M.; Gotchev, A.P.; Aksay, A. Modelling of the Stereoscopic HVS. 2009. Available online: https://www.semanticscholar.org/paper/Modelling-of-the-stereoscopic-HVS-Boev-Poikela/7938431f4ba009666153ed410a653651cc440aab (accessed on 6 January 2023).
- Jaramillo, B.O.; Kumcu, A.; Platisa, L.; Philips, W. Evaluation of color differences in natural scene color images. Signal Process. Image Commun. 2019, 71, 128–137. [Google Scholar] [CrossRef]
- Wan, W.; Zhou, K.; Zhang, K.; Zhan, Y.; Li, J. JND-Guided Perceptually Color Image Watermarking in Spatial Domain. IEEE Access 2020, 8, 164504–164520. [Google Scholar] [CrossRef]
- Jin, J.; Yu, D.; Lin, W.; Meng, L.; Wang, H.; Zhang, H. Full RGB Just Noticeable Difference (JND) Modelling. arXiv 2022, arXiv:abs/2203.00629. [Google Scholar]
- Lucassen, T. A new universal colour image fidelity metric. Displays 2003, 24, 197–207. [Google Scholar]
- Gu, K.; Zhai, G.; Yang, X.; Zhang, W. An efficient color image quality metric with local-tuned-global model. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 506–510. [Google Scholar]
- Yang, K.; Gao, S.; Li, C.; Li, Y. Efficient Color Boundary Detection with Color-Opponent Mechanisms. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2810–2817. [Google Scholar]
- Fareed, M.M.S.; Chun, Q.; Ahmed, G.; Asif, M.R.; Zeeshan, M. Saliency detection by exploiting multi-features of color contrast and color distribution. Comput. Electr. Eng. 2017, 70, 551–566. [Google Scholar] [CrossRef]
- Shi, C.; Lin, Y. No Reference Image Sharpness Assessment Based on Global Color Difference Variation. 2019. Available online: https://github.com/AlAlien/CDV (accessed on 5 May 2022).
- Cheng, M.M.; Warrell, J.H.; Lin, W.Y.; Zheng, S.; Vineet, V.; Crook, N. Efficient Salient Region Detection with Soft Image Abstraction. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 2–8 December 2013; pp. 1529–1536. [Google Scholar]
- Cheng, M.M.; Zhang, G.X.; Mitra, N.J.; Huang, X.; Hu, S. Global contrast based salient region detection. In Proceedings of the 24th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 409–416. [Google Scholar]
- jin Yoon, K.; Kweon, I.S. Color image segmentation considering human sensitivity for color pattern variations. In Proceedings of the SPIE Optics East, Boston, MA, USA, 28–31 October 2001. [Google Scholar]
- Sheikh, H.R.; Bovik, A.C. A visual information fidelity approach to video quality assessment. In The First International Workshop on Video Processing and Quality Metrics for Consumer Electronics; 2005; Volume 7, pp. 2117–2128. Available online: https://utw10503.utweb.utexas.edu/publications/2005/hrs_vidqual_vpqm2005.pdf (accessed on 6 January 2023).
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; Volume 3. [Google Scholar]
- Wang, Z.; Li, Q. Video quality assessment using a statistical model of human visual speed perception. J. Opt. Soc. Am. Opt. Image Sci. Vis. 2007, 24, B61–B69. [Google Scholar] [CrossRef]
- Wang, Z.; Shang, X. Spatial Pooling Strategies for Perceptual Image Quality Assessment. In Proceedings of the 2006 International Conference on Image Processing, Atlanta, Georgia, 8–11 October 2006; pp. 2945–2948. [Google Scholar]
- Simoncelli, E.P.; Stocker, A.A. Noise characteristics and prior expectations in human visual speed perception. Nat. Neurosci. 2006, 9, 578–585. [Google Scholar]
- Xing, Y.; Yin, H.; Zhou, Y.; Chen, Y.; Yan, C. Spatiotemporal just noticeable difference modeling with heterogeneous temporal visual features. Displays 2021, 70, 102096. [Google Scholar] [CrossRef]
- Wang, H.; Yu, L.; Liang, J.; Yin, H.; Li, T.; Wang, S. Hierarchical Predictive Coding-Based JND Estimation for Image Compression. IEEE Trans. Image Process. 2020, 30, 487–500. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, Z. Energy coding in biological neural networks. Cogn. Neurodynamics 2007, 1, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Feldman, H.; Friston, K.J. Attention, Uncertainty, and Free-Energy. Front. Hum. Neurosci. 2010, 4, 215. [Google Scholar] [CrossRef] [PubMed]
- Jiménez, J.; Barco, L.; D??Az, J.A.; Hita, E.; Romero, J. Assessment of the visual effectiveness of chromatic signals for CRT colour monitor stimuli. Displays 2000, 21, 151–154. [Google Scholar] [CrossRef]
- Pardo-Vazquez, J.L.; Castiñeiras, J.J.L.; Valente, M.; Costa, T.R.D.; Renart, A. Weber’s law is the result of exact temporal accumulation of evidence. bioRxiv 2018, 333559. [Google Scholar] [CrossRef]
- Yang, X.; Ling, W.S.; Lu, Z.; Ong, E.P.; Yao, S. Just noticeable distortion model and its applications in video coding. Signal Process. Image Commun. 2005, 20, 662–680. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, J.; Yuan, Z.; Liu, T.; Zheng, N. Automatic salient object segmentation based on context and shape prior. In Proceedings of the British Machine Vision Conference, Dundee, UK, 29 August–2 September 2011. [Google Scholar]
- Meng, Y.; Guo, L. Color image coding by utilizing the crossed masking. In Proceedings of the IEEE (ICASSP ’05) International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 18–23 March 2005; Volume 2, pp. ii/389–ii/392. [Google Scholar]
- Watson, A.B.; Solomon, J.A. Model of visual contrast gain control and pattern masking. J. Opt. Soc. Am. Opt. Image Sci. Vis. 1997, 14, 2379–2391. [Google Scholar] [CrossRef]
- Shang, X.; Liang, J.; Wang, G.; Zhao, H.; Wu, C.; Lin, C. Color-Sensitivity-Based Combined PSNR for Objective Video Quality Assessment. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 1239–1250. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Jin, L.; Ieremeiev, O.; Lukin, V.; Egiazarian, K.; Astola, J.; Vozel, B.; Chehdi, K.; Carli, M.; Battisti, F.; et al. Image database TID2013: Peculiarities, results and perspectives. Signal Process. Image Commun. 2015, 30, 57–77. [Google Scholar] [CrossRef]
- Le Callet, P.; Autrusseau, F. Subjective QualityAssessment IRCCyN/IVC Database. 2005. [Google Scholar]
- Judd, T. Learning to predict where humans look. In Proceedings of the IEEE 12th International Conference on Computer Vision (ICCV), Kyoto, Japan, 27 September–4 October 2009. [Google Scholar]
- Zeng, Z.; Zeng, H.; Chen, J.; Zhu, J.; Zhang, Y.; Ma, K.K. Visual attention guided pixel-wise just noticeable difference model. IEEE Access 2019, 7, 132111–132119. [Google Scholar] [CrossRef]
- Liu, X.; Zhan, X.; Wang, M. A novel edge-pattern-based just noticeable difference model for screen content images. In Proceedings of the 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 3–5 July 2020; pp. 386–390. [Google Scholar]
- Li, J.; Yu, L.; Wang, H. Perceptual redundancy model for compression of screen content videos. IET Image Process. 2022, 16, 1724–1741. [Google Scholar] [CrossRef]
- Sheikh, H.; Bovik, A.; de Veciana, G. An information fidelity criterion for image quality assessment using natural scene statistics. IEEE Trans. Image Process. 2005, 14, 2117–2128. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, H.; Bovik, A. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef] [PubMed]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Larson, E.C.; Chandler, D.M. Most apparent distortion: Full-reference image quality assessment and the role of strategy. J. Electron. Imaging 2009, 19, 011006. [Google Scholar]
- Zhang, L.; Shen, Y.; Li, H. VSI: A Visual Saliency-Induced Index for Perceptual Image Quality Assessment. IEEE Trans. Image Process. 2014, 23, 4270–4281. [Google Scholar] [CrossRef]
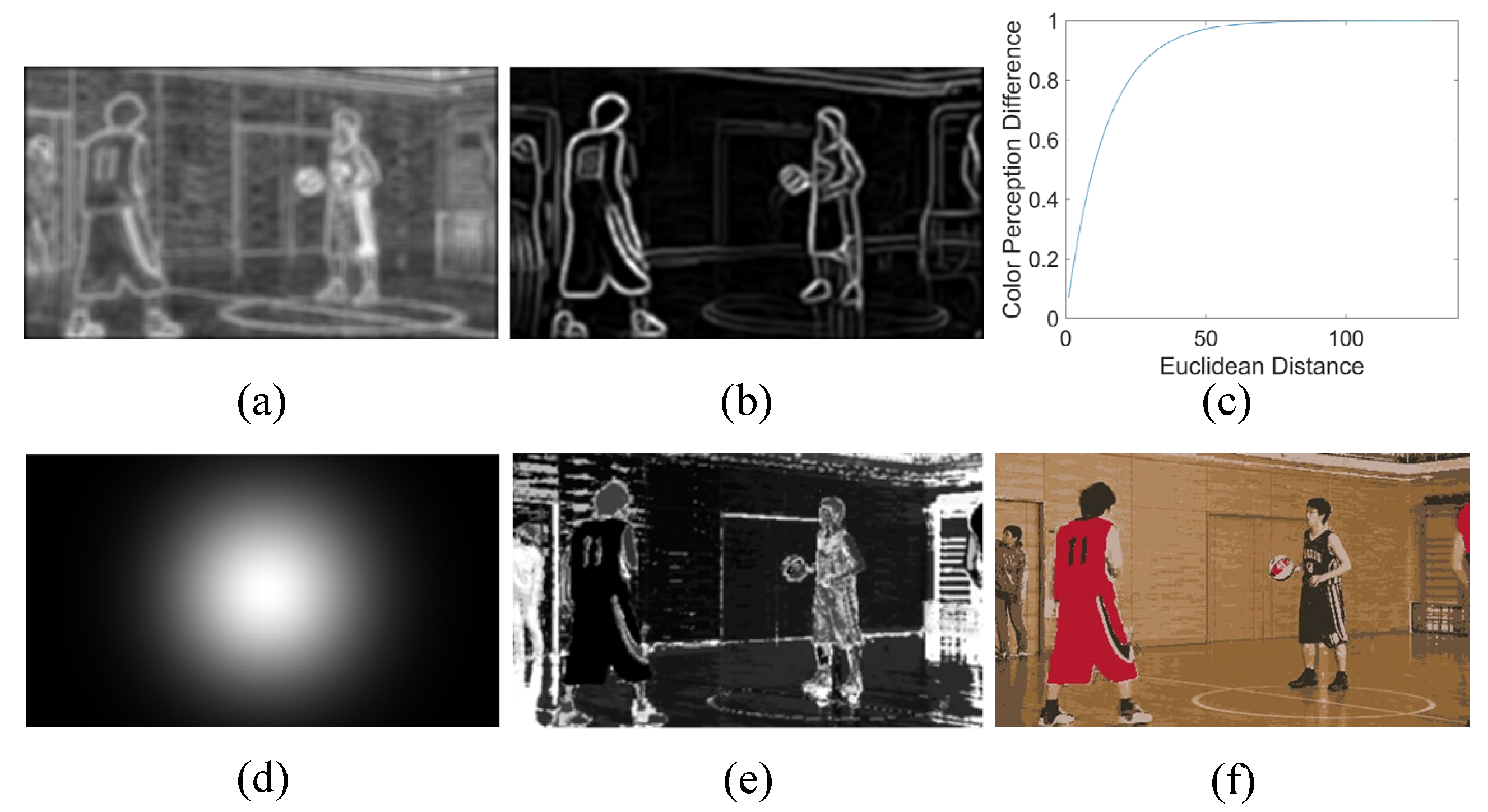


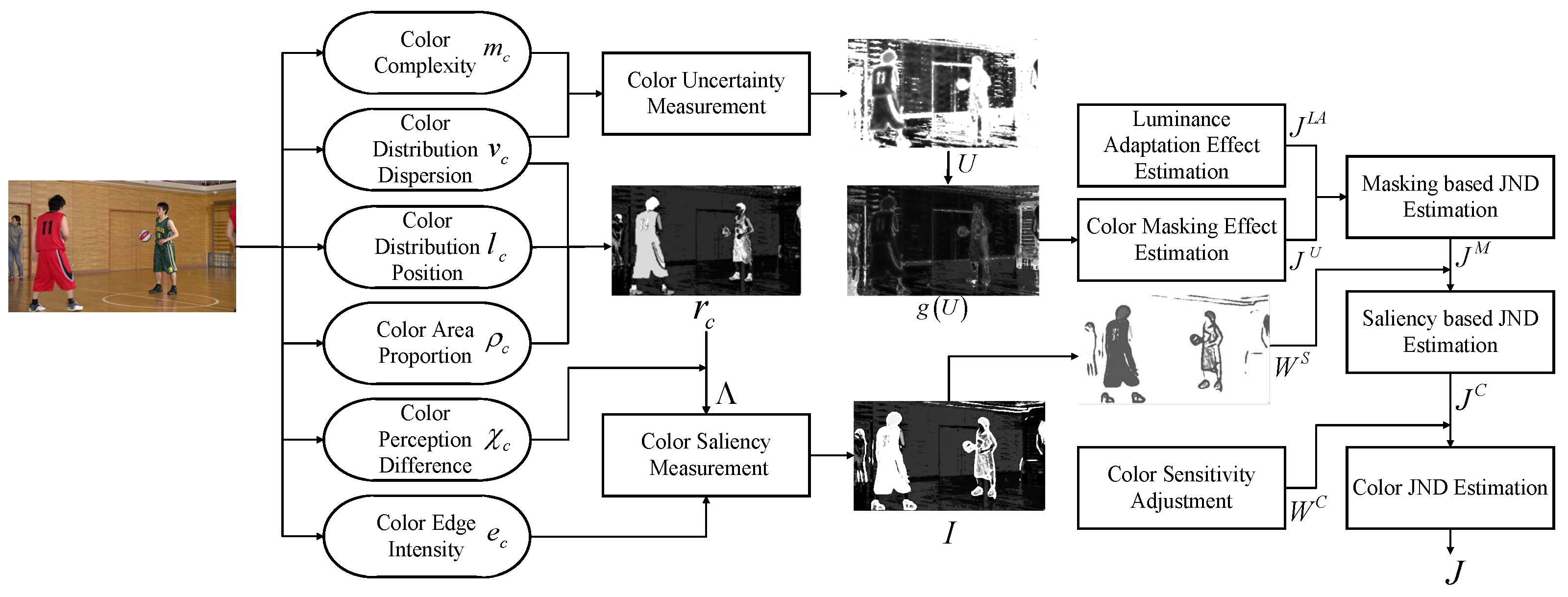



| Color Feature Parameter | Symbol | Effect |
|---|---|---|
| Color Complexity | Masking | |
| Color Edge Intensity | Saliency | |
| Color Distribution Position | Saliency | |
| Color Perception Difference | Saliency | |
| Color Distribution Dispersion | Masking | |
| Color Area Proportion | Saliency |
| Subjective Score | Scoring Criteria |
|---|---|
| 0 | The right figure has the same subjective quality as the left figure. |
| −1 | The right image is slightly worse than the left image. |
| −2 | The right image is of poorer subjective quality than the left image. |
| −3 | The right image is much worse than the left image. |
| Image Name | Wu2017 [15] | Zeng2019 [59] | Liu2020 [60] | Li2022 [61] | Proposed | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | MOS | PSNR | MOS | PSNR | MOS | PSNR | MOS | PSNR | MOS | |
| T1 | 36.51 | −0.32 | 35.85 | −0.30 | 36.29 | −0.30 | 31.00 | −0.20 | 32.03 | −0.06 |
| T2 | 35.47 | −0.30 | 35.27 | −0.30 | 36.34 | −0.26 | 31.72 | −0.16 | 32.23 | −0.06 |
| T3 | 36.39 | −0.24 | 35.78 | −0.22 | 36.32 | −0.24 | 32.04 | −0.18 | 28.94 | −0.10 |
| T4 | 31.51 | −0.22 | 34.74 | −0.12 | 33.55 | −0.08 | 32.25 | −0.08 | 31.58 | −0.06 |
| T5 | 35.21 | −0.24 | 36.25 | −0.26 | 36.75 | −0.18 | 34.67 | −0.10 | 31.92 | −0.10 |
| T6 | 33.99 | −0.32 | 36.43 | −0.28 | 35.35 | −0.22 | 34.92 | −0.10 | 34.34 | −0.08 |
| T7 | 33.80 | −0.34 | 33.41 | −0.40 | 33.80 | −0.36 | 29.35 | −0.34 | 28.25 | −0.14 |
| T8 | 34.69 | −0.28 | 36.84 | −0.24 | 37.32 | −0.18 | 34.80 | −0.12 | 34.06 | −0.06 |
| T9 | 34.06 | −0.16 | 36.38 | −0.22 | 35.14 | −0.18 | 33.36 | −0.10 | 29.81 | −0.08 |
| T10 | 36.95 | −0.24 | 36.52 | −0.30 | 37.21 | −0.26 | 32.52 | −0.16 | 35.01 | −0.06 |
| Avg | 34.86 | −0.27 | 35.75 | −0.26 | 35.81 | −0.23 | 32.66 | −0.15 | 31.82 | −0.08 |
| I1 | 35.90 | −0.28 | 36.16 | −0.22 | 37.97 | −0.16 | 37.09 | −0.14 | 30.81 | −0.12 |
| I2 | 31.40 | −0.40 | 35.62 | −0.30 | 35.44 | −0.30 | 32.46 | −0.20 | 31.71 | −0.08 |
| I3 | 34.57 | −0.22 | 36.52 | −0.22 | 37.07 | −0.18 | 35.66 | −0.12 | 30.48 | −0.10 |
| I4 | 33.92 | −0.34 | 34.21 | −0.24 | 34.70 | −0.20 | 29.58 | −0.12 | 27.55 | −0.08 |
| I5 | 34.76 | −0.22 | 34.52 | −0.20 | 35.52 | −0.16 | 29.81 | −0.12 | 27.76 | −0.06 |
| I6 | 33.17 | −0.26 | 36.39 | −0.22 | 36.44 | −0.12 | 34.77 | −0.10 | 31.13 | −0.10 |
| I7 | 34.87 | −0.40 | 35.67 | −0.30 | 37.21 | −0.22 | 33.57 | −0.10 | 30.94 | −0.06 |
| I8 | 35.90 | −0.34 | 36.01 | −0.30 | 37.53 | −0.18 | 33.72 | −0.08 | 33.24 | −0.12 |
| I9 | 28.62 | −0.14 | 36.49 | −0.06 | 33.26 | −0.06 | 33.21 | −0.06 | 29.60 | −0.06 |
| I10 | 36.16 | −0.24 | 35.21 | −0.14 | 35.69 | −0.10 | 30.69 | −0.08 | 30.66 | −0.08 |
| Avg | 33.93 | −0.28 | 35.68 | −0.22 | 36.08 | −0.17 | 33.06 | −0.11 | 30.39 | −0.09 |
| L1 | 38.34 | −0.20 | 38.30 | −0.14 | 38.04 | −0.12 | 37.58 | −0.04 | 32.00 | −0.06 |
| L2 | 36.72 | −0.18 | 33.33 | −0.18 | 33.58 | −0.14 | 29.13 | −0.08 | 27.87 | −0.08 |
| L3 | 34.09 | −0.18 | 36.93 | −0.16 | 37.89 | −0.14 | 35.14 | −0.08 | 30.96 | −0.06 |
| L4 | 34.83 | −0.24 | 35.62 | −0.18 | 35.84 | −0.12 | 33.07 | −0.10 | 34.01 | −0.14 |
| L5 | 37.52 | −0.24 | 35.35 | −0.24 | 35.41 | −0.22 | 30.80 | −0.12 | 30.17 | −0.10 |
| L6 | 34.71 | −0.16 | 31.87 | −0.14 | 31.56 | −0.10 | 25.96 | −0.08 | 24.49 | −0.06 |
| L7 | 40.20 | −0.16 | 37.66 | −0.14 | 38.30 | −0.08 | 35.43 | −0.08 | 35.82 | −0.08 |
| L8 | 36.47 | −0.28 | 36.70 | −0.30 | 37.08 | −0.24 | 34.30 | −0.10 | 33.83 | −0.08 |
| L9 | 37.62 | −0.26 | 35.02 | −0.26 | 35.51 | −0.22 | 31.69 | −0.16 | 31.31 | −0.10 |
| L10 | 37.45 | −0.18 | 33.02 | −0.32 | 33.22 | −0.28 | 28.10 | −0.20 | 28.21 | −0.12 |
| Avg | 36.80 | −0.21 | 35.38 | −0.21 | 35.64 | −0.17 | 32.12 | −0.10 | 30.87 | −0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, T.; Yin, H.; Wang, H.; Sheng, N.; Xing, Y. Pixel-Domain Just Noticeable Difference Modeling with Heterogeneous Color Features. Sensors 2023, 23, 1788. https://doi.org/10.3390/s23041788
Hu T, Yin H, Wang H, Sheng N, Xing Y. Pixel-Domain Just Noticeable Difference Modeling with Heterogeneous Color Features. Sensors. 2023; 23(4):1788. https://doi.org/10.3390/s23041788
Chicago/Turabian StyleHu, Tingyu, Haibing Yin, Hongkui Wang, Ning Sheng, and Yafen Xing. 2023. "Pixel-Domain Just Noticeable Difference Modeling with Heterogeneous Color Features" Sensors 23, no. 4: 1788. https://doi.org/10.3390/s23041788
APA StyleHu, T., Yin, H., Wang, H., Sheng, N., & Xing, Y. (2023). Pixel-Domain Just Noticeable Difference Modeling with Heterogeneous Color Features. Sensors, 23(4), 1788. https://doi.org/10.3390/s23041788





