Risk Assessment and Experimental Light-Balloon Deployment of a Stratospheric Vertical VLF Transmitter
Abstract
1. Introduction: VLF Emitted from Airborne Sources
2. VLF Theory of Propagation from High Altitudes
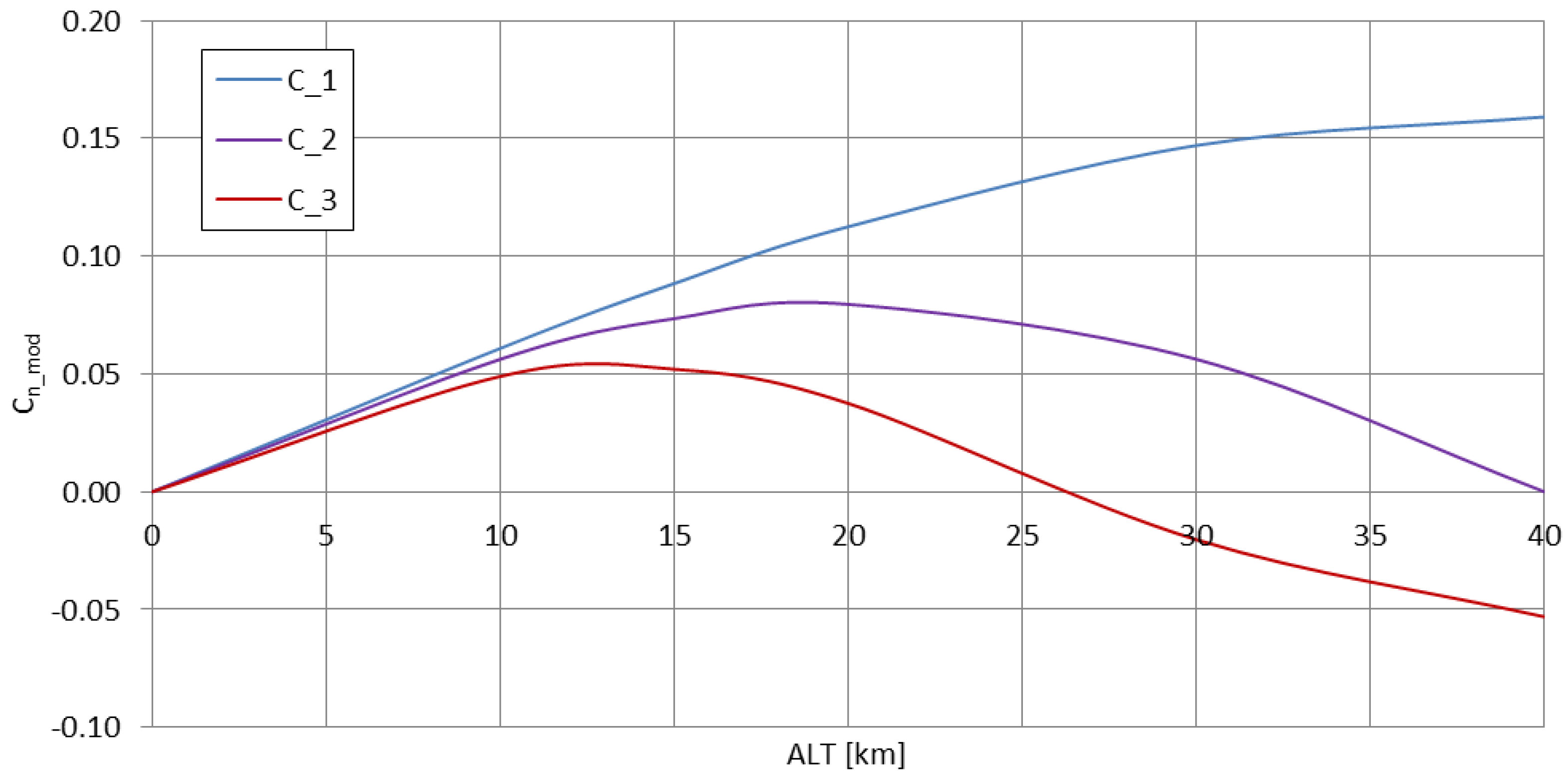
2.1. Mode Magnitudes
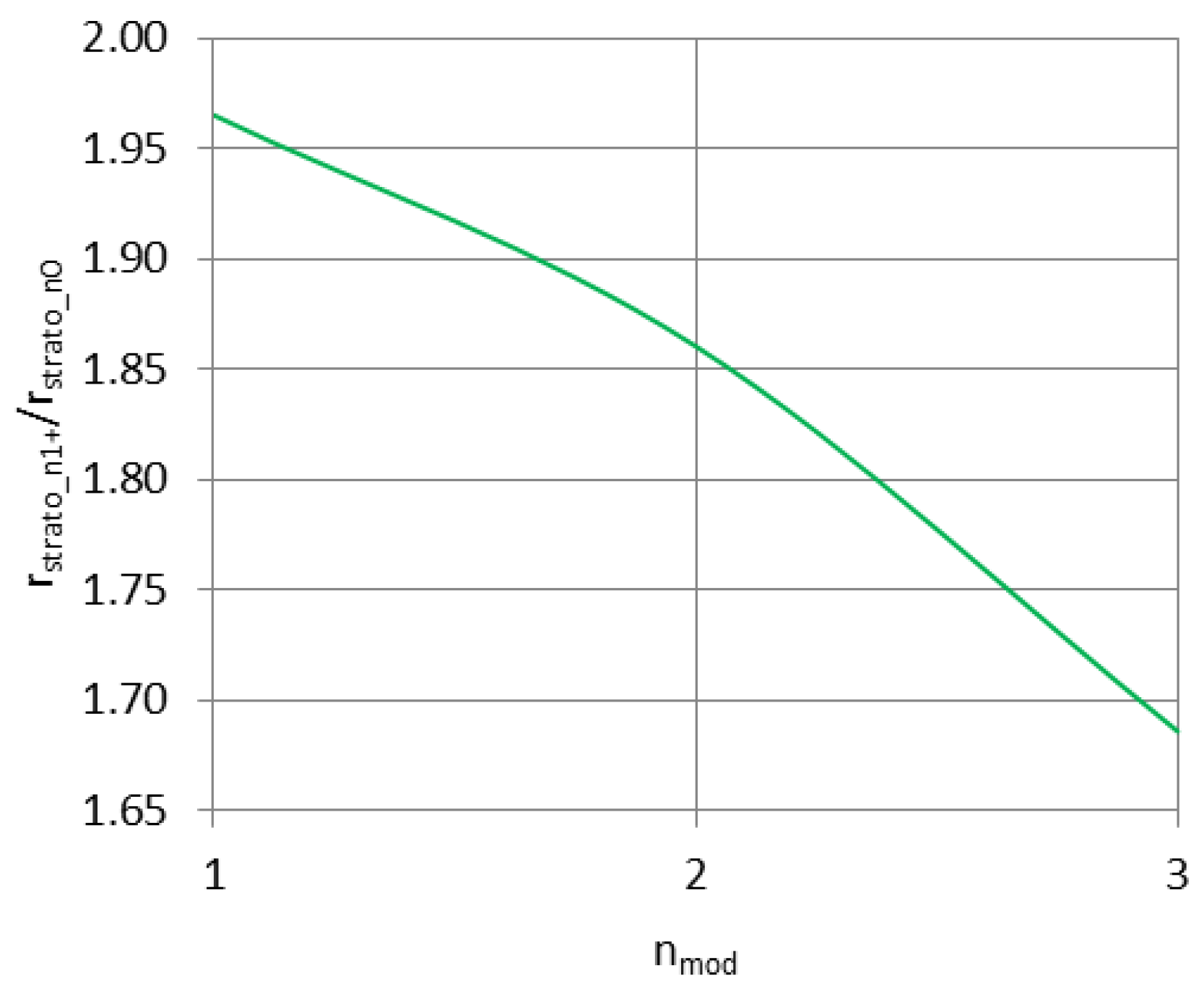
2.2. Mode Excitation Efficiencies
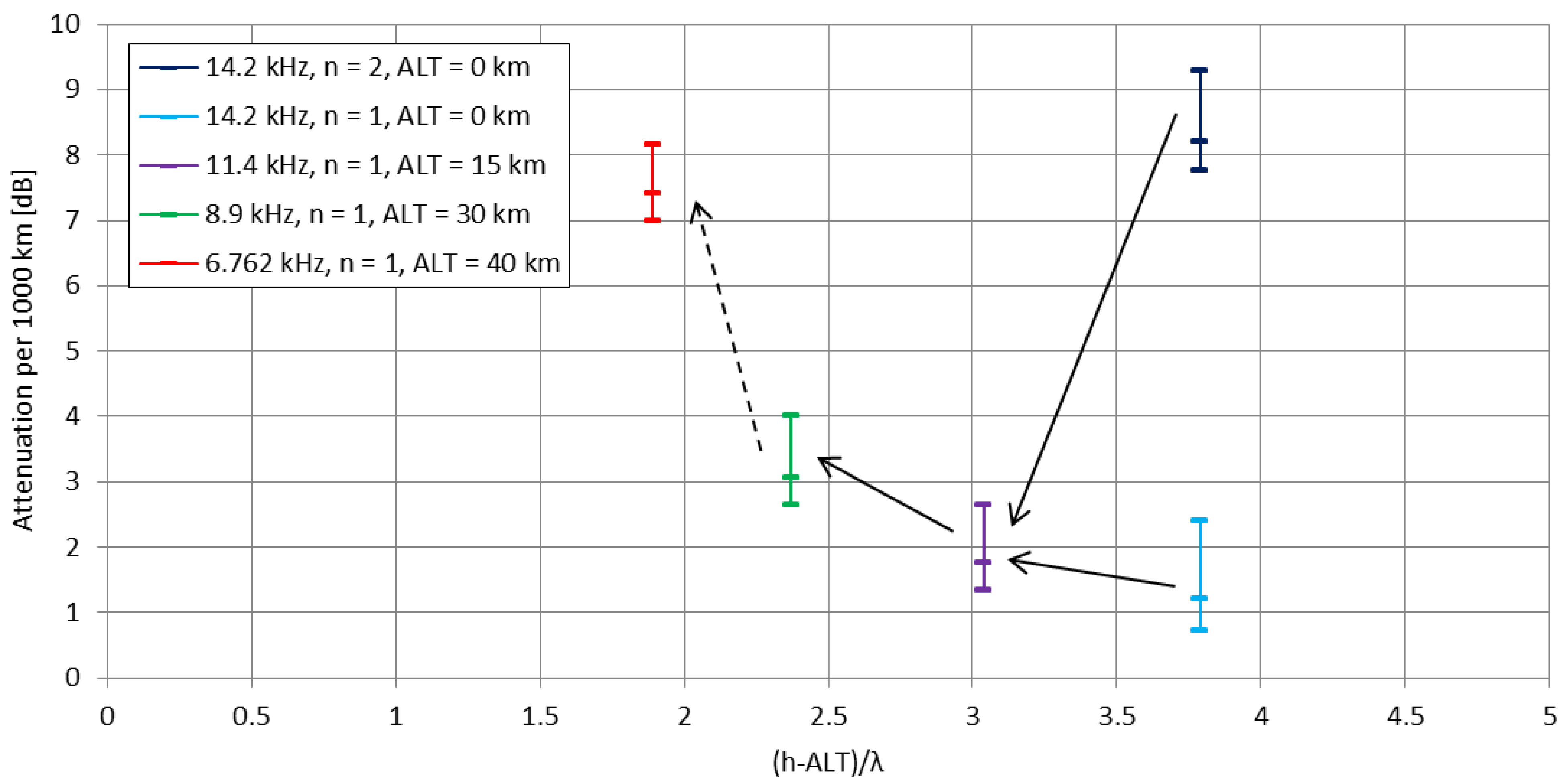
2.3. Modes’ Attenuation: Hypothesis of Apparent Frequency Decrease
3. Mission Specifications
4. Risk Assessments
4.1. Mechanical
| No. | Description | Probability | Severity | Probability × Severity | Mitigation |
|---|---|---|---|---|---|
| M1 | Antenna wire break | 4 | 2 | 8 | Division of antenna wire into radiating wire (metal) and supporting tether (poliethylene, multi-thread), with mandatory strength against breaking <230 N |
| M2 | Cable disconnections | 4 | 3 | 12 | Screw connections, cables threaded through circuit boards to remove loads from the solderings |
| M3 | Excessive loads on the mission components | 5 | 2 | 10 | Entire mission designed as a linear structure, with all tethers connected to each other’s ends |
| M4 | Equipment detachment in flight | 4 | 2 | 8 | Additional tethers to external equipment (if needed) |
| M5 | Explosion due to lack of degassing | 4 | 2 | 8 | Avoidance of creation of sealed spaces—addition of small air drains |
| M6 | Early balloon burst | 3 | 2 | 6 | Choice of high-quality balloon |
| M7 | Damages due to balloon burst deceleration | 2 | 3 | 6 | Affixation of components resistant to high accelerations |
| M8 | Damages due to landing deceleration | 2 | 4 | 8 | Affixation of components resistant to high accelerations |
| M9 | Damages due to landing on uneven terrain | 2 | 4 | 8 | Sufficiently thick and shock-absorbing walls of the gondola |
| M10 | Loss of gondola integrity | 5 | 1 | 5 | Temperature- and shock-resistant gondola hatch |
4.2. Thermal
| No. | Description | Probability | Severity | Probability × Severity | Mitigation |
|---|---|---|---|---|---|
| T1 | Loss of glue joints performance in freezing temperatures | 5 | 1 | 5 | Use of low-temperature-resistant substances/qualified for space use |
| T2 | Shattering of cable insulation due to freezing temperatures | 4 | 1 | 4 | Exclusion of low-resistant insulations for all insulated cables |
| T3 | Freezing temperature on the frequency generator | 4 | 3 | 12 | Sufficient passive thermal control—surrounding insulation |
| T4 | Freezing temperature on the upper navigation unit | 3 | 3 | 9 | Sufficient passive thermal control—surrounding insulation |
| T5 | Freezing temperature on the lower navigation unit | 3 | 3 | 9 | Use of stratosphere-qualified commercial-off-the-shelf navigation transmitter |
| T6 | Freezing temperature on the battery pack | 4 | 3 | 12 | Sufficient passive thermal control—surrounding insulation |
| T7 | Excessive temperature on the power amplifier | 4 | 4 | 16 | Heat sink attached to the power amplifier’s transistors |
| T8 | Excessive temperature on the power amplifier components | 4 | 4 | 16 | Affixation of heat bridges connected to the main heat sink |
| T9 | Uneven temperature distribution on the transistors | 3 | 3 | 9 | Power amplifier with multiple transistors and load resistors; use of a common heat sink |
| T10 | Fire breakout onboard the gondola | 5 | 1 | 5 | Sufficient electrical insulation on high-voltage and prone-to-overload circuits, efficient heat transfer from hot components |
| T11 | The Joule-Thompson effect during the re-entry phase | 4 | 4 | 16 | Sufficient passive thermal control—surrounding insulation |
4.3. Electrical
| No. | Description | Probability | Severity | Probability × Severity | Mitigation |
|---|---|---|---|---|---|
| E1 | Short-circuit due to condensed water | 4 | 1 | 4 | Affixation of silica-based desiccants inside the gondola |
| E2 | Excessive electric potential on electronic components due to pyroelectric behaviour of water | 4 | 1 | 4 | Affixation of silica-based desiccants inside the gondola |
| E3 | Corona appearance on the transmitter circuitry | 4 | 2 | 8 | Lacquering of the circuitry, use of lower voltages |
| E4 | Corona apearance on the antenna wire | 3 | 5 | 15 | Corona dischargers concentrating the discharges away from the wire |
| E5 | Transmitter overload due to corona appearance | 4 | 4 | 16 | Automatic detection of overloading with transmitter decoupling/low antenna-transmitter coupling |
| E6 | Transmitter overload due to lightning strike | 5 | 2 | 10 | Automatic detection of overloading with transmitter decoupling/low antenna-transmitter coupling |
| E7 | Flashover on the main antenna insulator towards the main gondola | 4 | 3 | 12 | Proper design of the ‘mushroom’ upper insulator |
| E8 | Interference with other instruments onboard the gondola (near field of the VLF antenna) | 3 | 2 | 6 | Design of the instrumentation within the constraint of operation in the VLF near-field (shieldings, additional filters, digital protocols) |
| E9 | Low stability of the frequency generator | 3 | 3 | 9 | Additional frequency stabilization circuit, passive thermal control around the generator |
| E10 | Loss of power on transmitter subsystems | 4 | 2 | 8 | Division of power source into multiple, separate, independent power sources |
| E11 | Transmitter malfunction (other) | 4 | 2 | 8 | Transmitter ground testing on a dummy load |
| E12 | Transistor gate breakdown | 4 | 1 | 4 | Choice of transistor type with high durability heritage; multiplication of transistors in the power amplifier |
| E13 | Electrical discharge from the system during landing | 2 | 1 | 2 | Corona dischargers concentrating the discharges away from the wire |
4.4. Operational
| No. | Description | Probability | Severity | Probability × Severity | Mitigation |
|---|---|---|---|---|---|
| O1 | Incorrect antenna deployment | 4 | 2 | 8 | Elaborated antenna launch procedure |
| O2 | Antenna damage during deployment | 4 | 3 | 12 | Proper choice of launch/deployment site, with sufficient clearance |
| O3 | Air traffic hazard due to antenna length | 5 | 2 | 10 | Affixation of radar reflectors, optical warning systems and a double system of navigation/transponder units (on both ends of the antenna) |
| O4 | Low optical- and radar visibility of the mission | 5 | 2 | 10 | Affixation of large radar reflectors and optical warning signs colored in red or bright orange |
| O5 | Parachute coiling | 5 | 1 | 5 | Sufficiently long parachute tethers |
| O6 | Antenna wire coiling during descent phase | 3 | 3 | 9 | Use of antenna end-weight for movement and re-entry stabilization |
| O7 | Loss of mission tracking | 4 | 2 | 8 | Redundant navigation system |
| O8 | Loss of landing site location | 4 | 2 | 8 | Redundant navigation system, live mission tracking, repeated flight/landing predictions |
| O9 | Landing on water | 4 | 1 | 4 | Positive buoyancy of the gondola |
| O10 | Landing on high-voltage power lines | 5 | 1 | 5 | Antenna wire breaking when subjected to high-voltage short-circuit |
| O11 | Landing on a frequented road | 4 | 1 | 4 | High visibility of the entire flight train |
| O12 | Inflicting damage on external environment when landing | 4 | 1 | 4 | Hard flight train components and main gondola built from/shielded with softened/elastic materials |
| O13 | Reduced amount of delivered RF data due to E5 and E6 risk mitigation | 4 | 3 | 12 | Employment of a large amount of reception points/locations with sensitive receivers and large/ferrite antennas |
4.5. Analysis of Highest-Grade Risks
| No. | Description | Probability | Severity | Probability × Severity | Mitigation |
|---|---|---|---|---|---|
| E5 | Transmitter overload due to corona appearance | 4 | 4 | 16 | Automatic detection of overloading with transmitter decoupling/low antenna-transmitter coupling |
| T7 | Excessive temperature of the power amplifier | 4 | 4 | 16 | Heat sink attached to the power amplifier’s transistors |
| T8 | Excessive temperature of the power amplifier components | 4 | 4 | 16 | Affixation of heat bridges connected to the main heat sink |
| T11 | The Joule-Thompson effect during the re-entry phase | 4 | 4 | 16 | Sufficient passive thermal control—surrounding insulation |
| E4 | Corona appearance on the antenna wire | 3 | 5 | 15 | Corona dischargers concentrating the discharges away from the wire |
| M2 | Cable disconnections | 4 | 3 | 12 | Screw connections, cables threaded through circuit boards to remove loads from the solderings |
| T3 | Freezing temperature on the frequency generator | 4 | 3 | 12 | Sufficient passive thermal control—surrounding insulation |
| T6 | Freezing temperature on the battery pack | 4 | 3 | 12 | Sufficient passive thermal control—surrounding insulation |
| O2 | Antenna damage during deployment | 4 | 3 | 12 | Proper choice of launch/deployment site, with sufficient clearance |
| E7 | Flashover on the main antenna insulator towards the main gondola | 4 | 3 | 12 | Proper design of the ‘mushroom’ upper insulator |
| O13 | Reduced amount of delivered RF data due to E5 and E6 risk mitigation | 4 | 3 | 12 | Employment of a large amount of reception points/locations with sensitive receivers and large/ferrite antennas |
| O3 | Air traffic hazard due to antenna length | 5 | 2 | 10 | Affixation of radar reflectors, optical warning systems and a double system of navigation/transponder units (on both ends of the antenna) |
| O4 | Low optical- and radar visibility of the mission | 5 | 2 | 10 | Affixation of large radar reflectors and optical warning signs colored in red or bright orange |
| M3 | Excessive loads on the mission components | 5 | 2 | 10 | Entire mission designed as a linear structure, with all tethers connected to each other’s ends |
| E6 | Transmitter overload due to lightning strike | 5 | 2 | 10 | Automatic detection of overloading with transmitter decoupling/low antenna-transmitter coupling |
5. Experimental Deployment
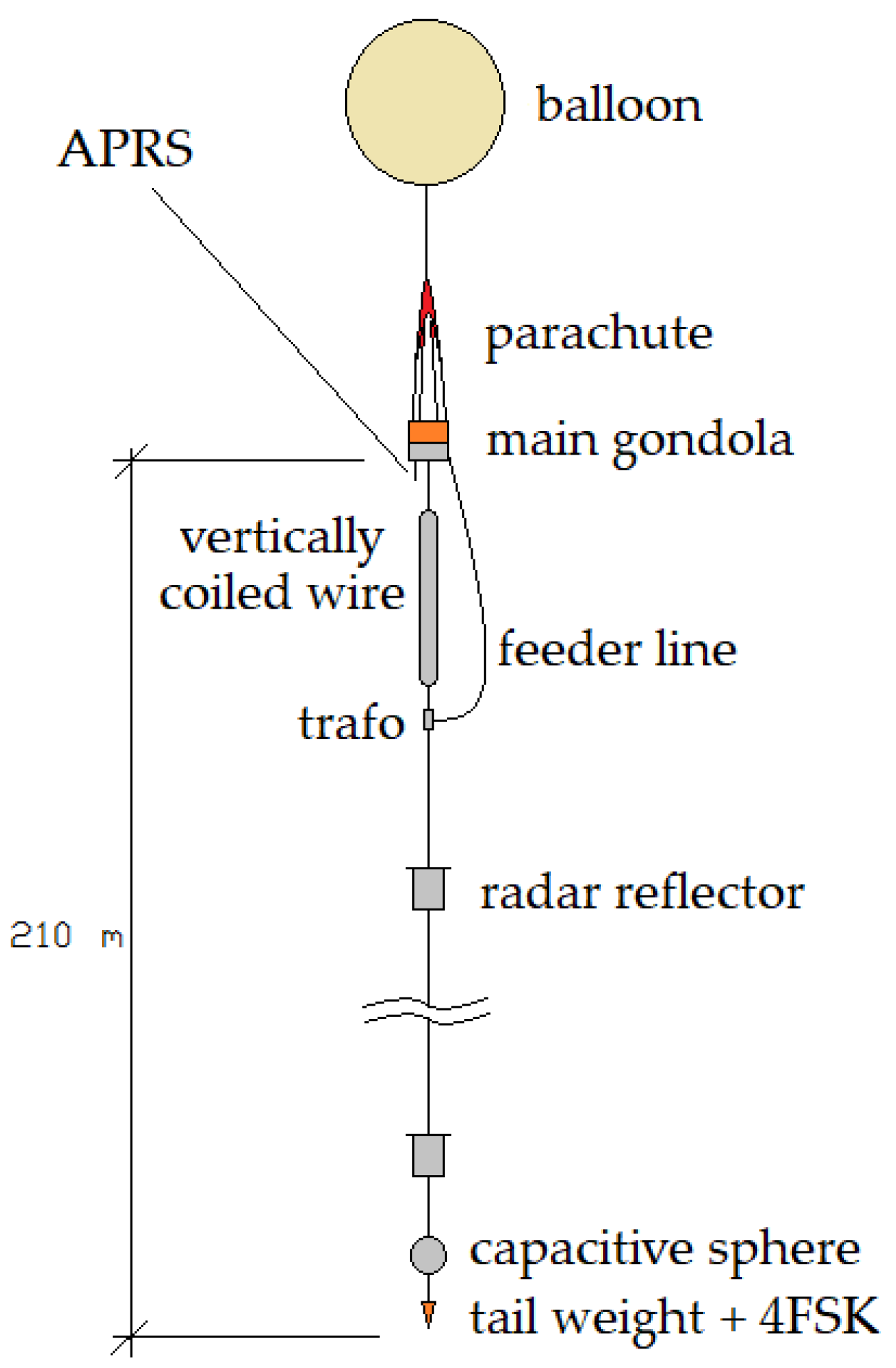
5.1. Mission Design
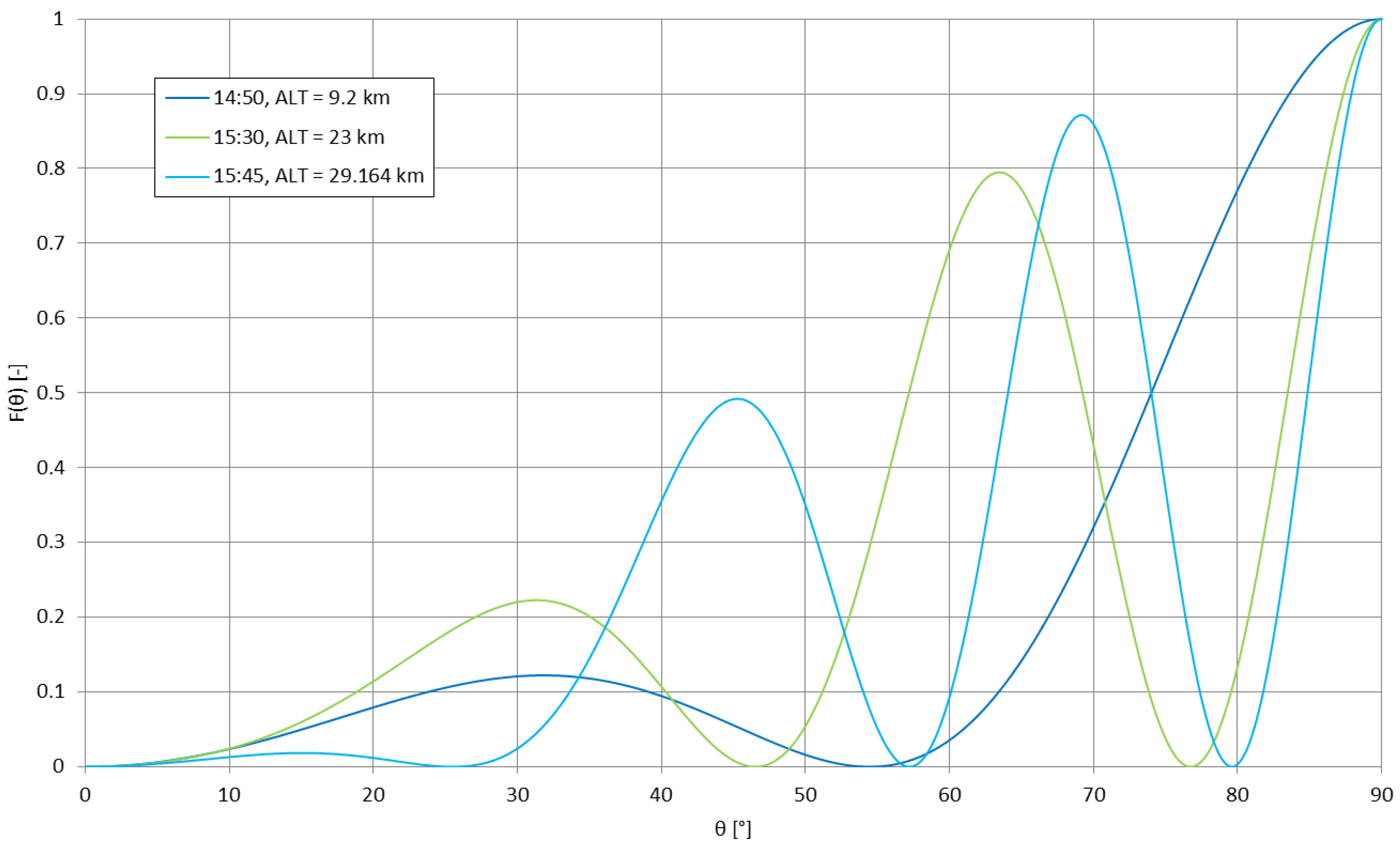
5.2. Flight Performance
6. The Analysis of Flight Results
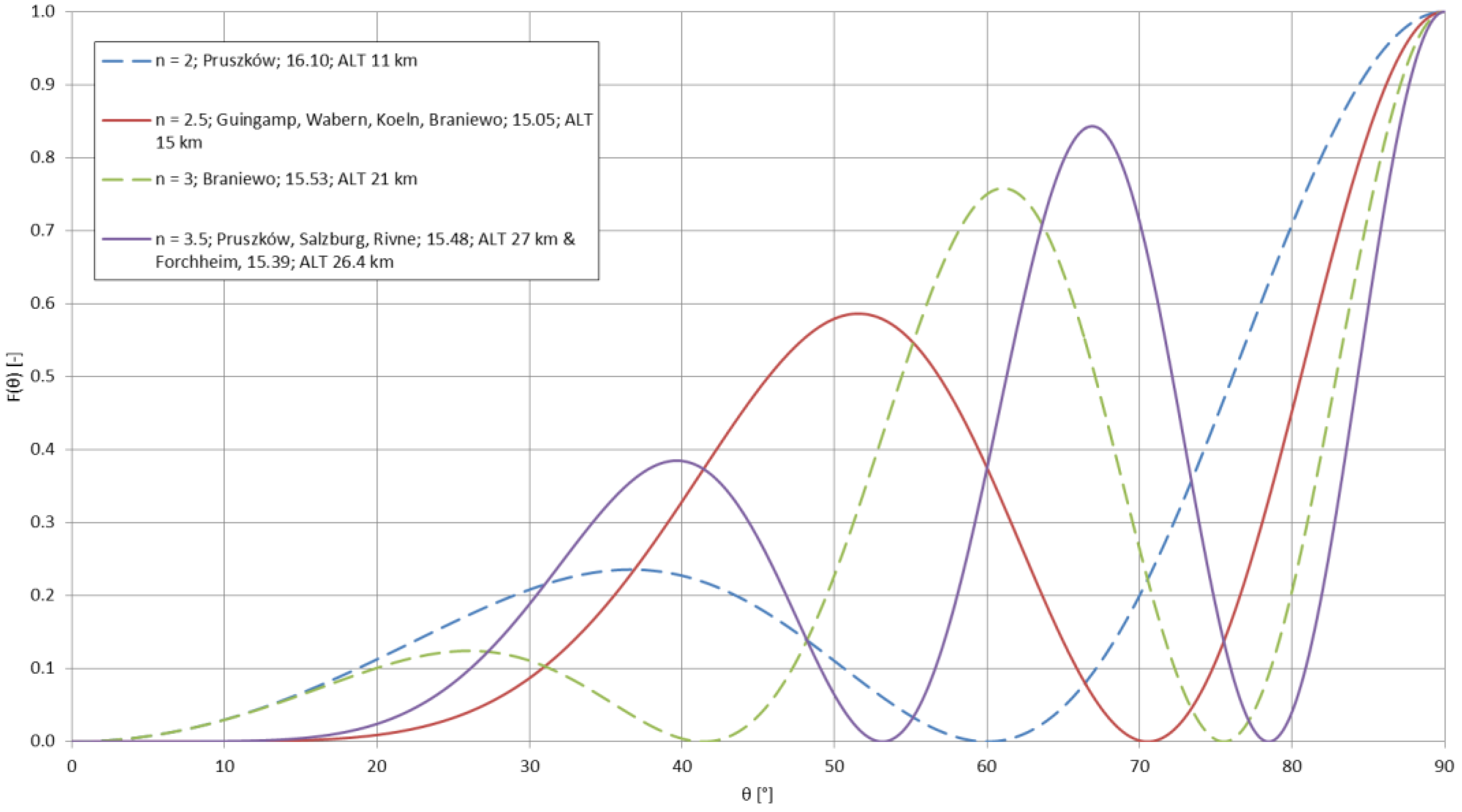
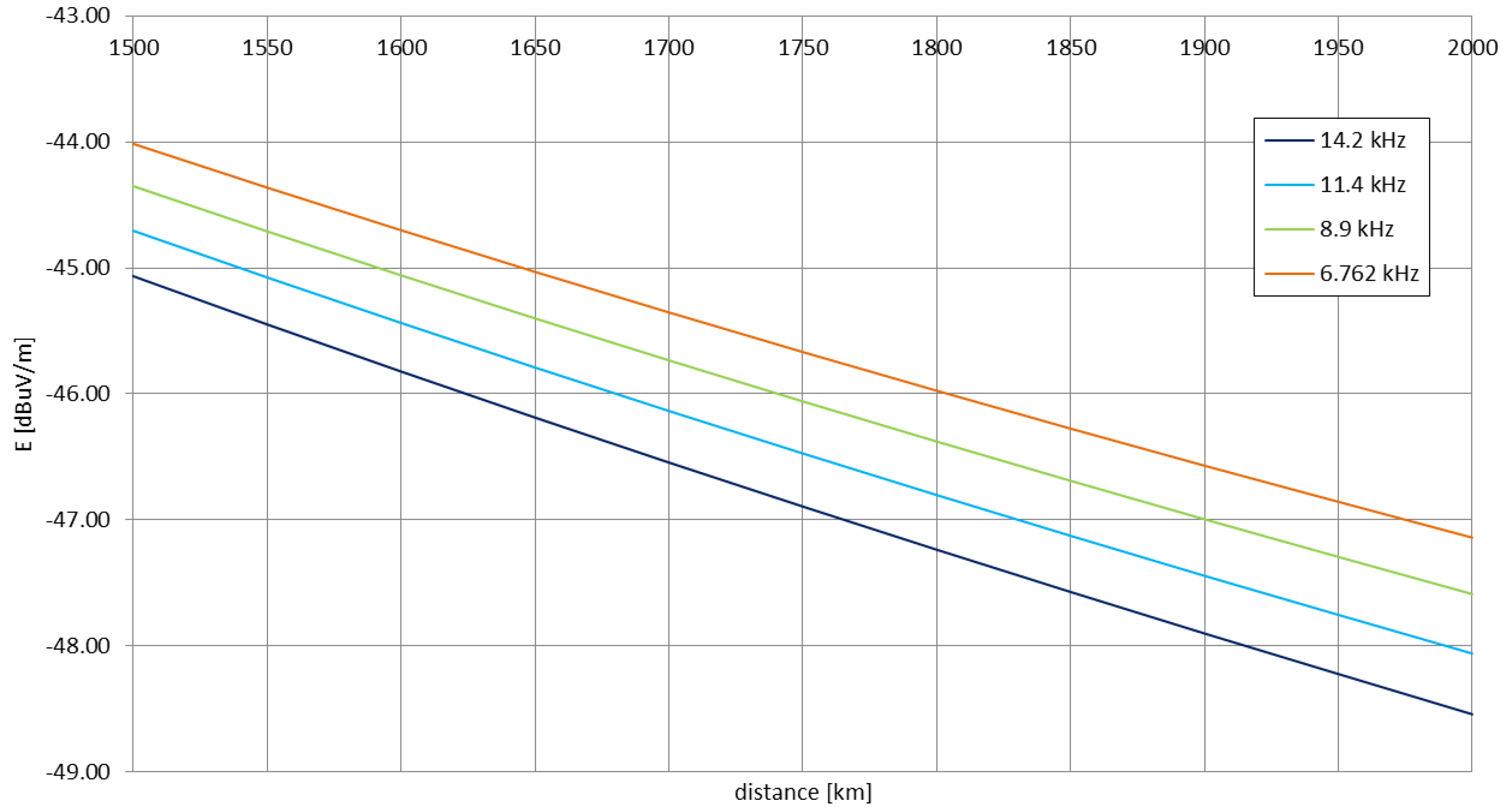
6.1. Experimental Signal Coverage
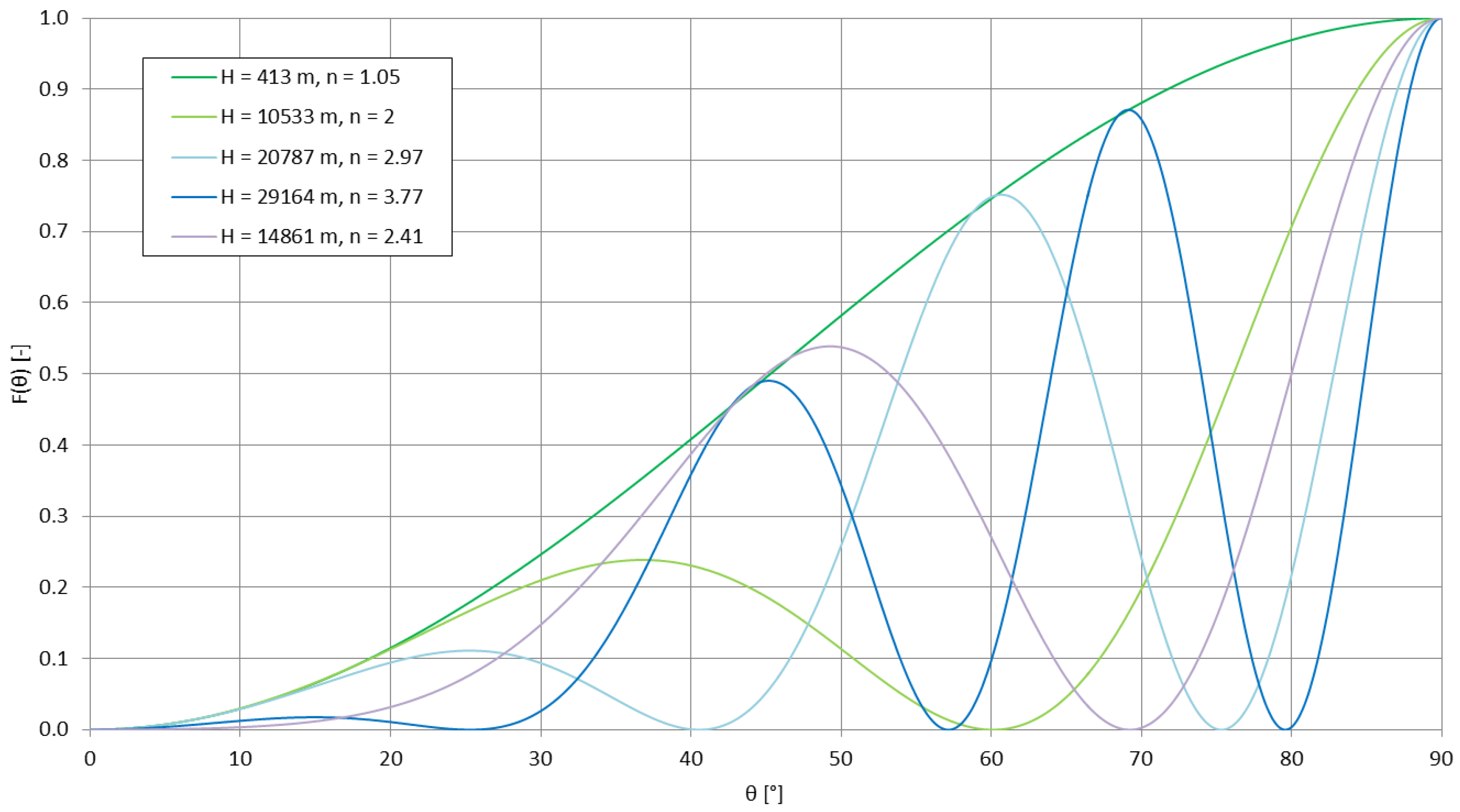
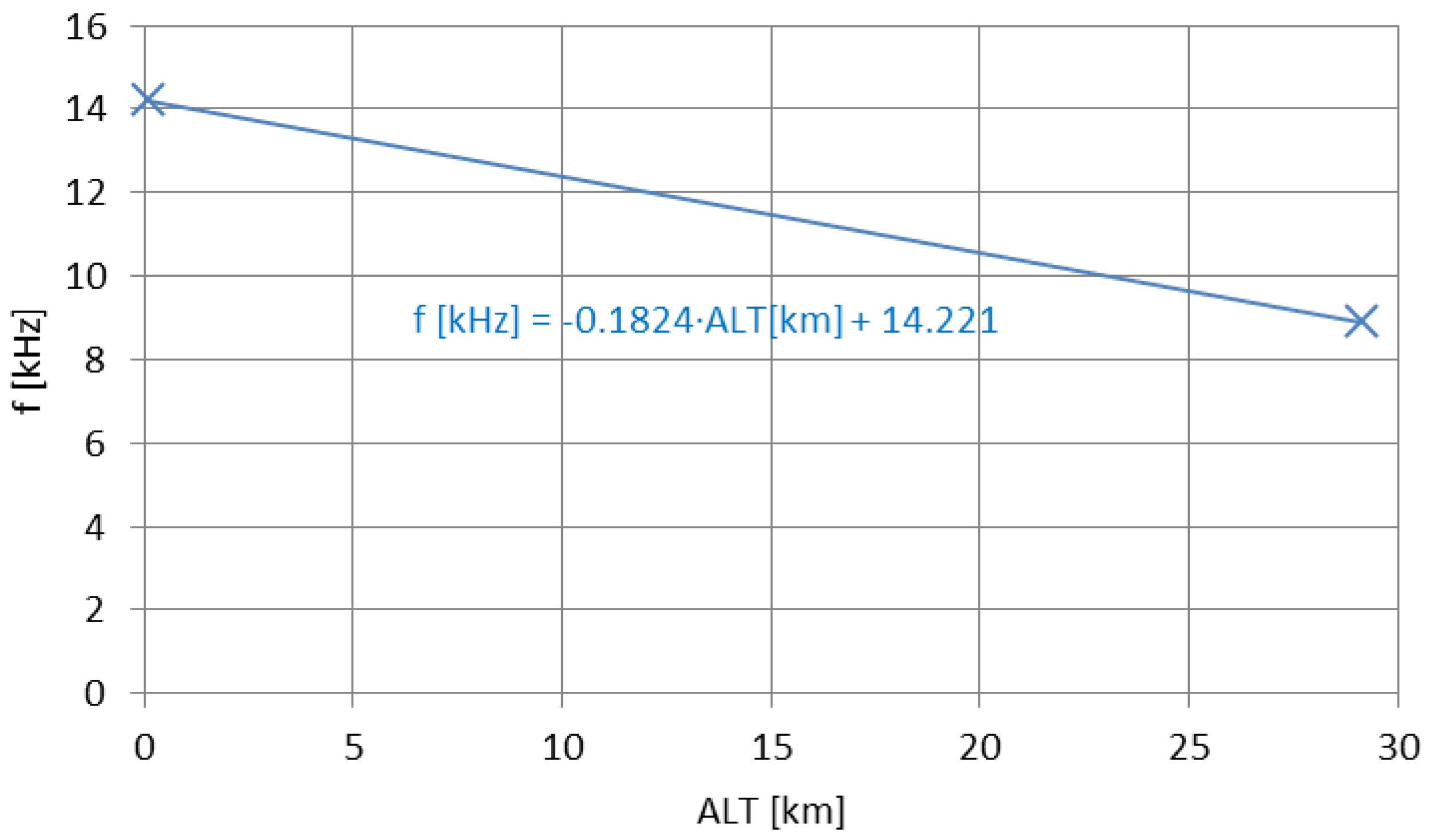
6.2. The Evolution of the Antenna Radiation Pattern
6.3. Simulated Signal Coverages
7. Discussion
7.1. Simulations vs. Experimental Signal Coverage
7.2. Comparison with Low Frequency Experiments
7.3. Possible Ameliorations and System Employment
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bulletin, B. Reference Signals, Frequency and Time; VNIIFTRI: Moscow, Russia, 2018. [Google Scholar]
- Kirsch, R. Groundwater Geophysics: A Tool for Hydrogeology, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Thierry, A. Simple Earth-Ionosphere Waveguide Calculation. 2003. Available online: www.vlf.it/thierry/waveguide_propagation.html (accessed on 20 May 2021).
- Bazilevskaya, G.A.; Kalinin, M.S.; Krainev, M.B.; Makhmutov, V.S.; Svirzhevskaya, A.K.; Svirzhevsky, N.S.; Stozhkov, Y.I.; Gvozdevsky, B.B. Long-Term Evolution of the Occurrence Rate of Magnetospheric Electron Precipitation into the Earth’s Atmosphere. Bullettin Russ. Acad. Sci. Phys. 2019, 83, 584–587. [Google Scholar] [CrossRef]
- Watt, A.D. VLF Radio Engineering; Pergamon Press Inc.: Oxford, UK, 1967. [Google Scholar]
- Belrose, J.S. VLF/LF Transmitting Antennas. In Proceedings of the AGARD Conference: ELF/VLF/LF Radio Propagation and System Aspects, Brussels, Belgium, 28 September–2 October 1992. [Google Scholar]
- Alexanderson, E.F.W. Transatlantic Radio Communication. Proc. Am. Inst. Electr. Eng. 1919, 38, 1077–1093. [Google Scholar] [CrossRef]
- Alexanderson, E.F.W.; Reoch, A.E.; Taylor, C.H. The Electrical Plant of Transocean Radio Telegraphy. Trans. Am. Inst. Electr. Eng. 1923, 42, 707–717. [Google Scholar] [CrossRef]
- Brown, W.W.; Lowe, J.E. Designs and efficiencies of large air core inductances. Proc. Inst. Radio Eng. 1925, 13, 755–766. [Google Scholar] [CrossRef]
- Lindenblad, N.; Brown, W.W. Main considerations in antenna design. Proc. Inst. Radio Eng. 1926, 14, 291–323. [Google Scholar] [CrossRef]
- Slaby, A. The Radiotelegraphy; Verlag von Leonhard Simion: Berlin/Heidelberg, Germany, 1901. [Google Scholar]
- Field, E.C., Jr.; Kies, L.R.; Bannister, P.R.; Ingram, R.F.; Hopkins, W.D.; Roberts, M.A. An aerostat-supported ELF/VLF transmitter. Radio Sci. 1989, 24, 235–246. [Google Scholar] [CrossRef]
- Crawford, R.L.; Jordan, K.L. Tethered Aerostat VLF/LF Transmitter System Design Considerations. In Proceedings of the AGARD Conference: ELF/VLF/LF Radio Propagation and System Aspects, Brussels, Belgium, 28 September–2 October 1992. [Google Scholar]
- Durrant, R.F. Radio experiences in the R-34. Radio Amateur News, December 1919; 295. [Google Scholar]
- Burrows, M.L. ELF Communications Antennas; Peter Peregrinus Ltd.: Herts, UK, 1978. [Google Scholar]
- Hall, W.C. Electrostatic dischargers for aircraft. J. Appl. Phys. 1947, 18, 759–765. [Google Scholar] [CrossRef]
- Galejs, J. VLF fields of elevated sources. Radio Sci. 1970, 5, 1163–1168. [Google Scholar] [CrossRef]
- Pappert, R.A. Effects of elevation and ground conductivity on horizontal dipole excitation of the earth-ionosphere waveguide. Radio Sci. 1970, 5, 579–590. [Google Scholar] [CrossRef]
- Pappert, R.A.; Bickel, J.E. Vertical and horizontal VLF fields excited by dipoles of arbitrary orientation and elevation. Radio Sci. 1970, 5, 1445–1452. [Google Scholar] [CrossRef]
- Miś, T.A. The concept of an airborne VLF transmitter with vertical electric dipole antenna. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018. [Google Scholar] [CrossRef]
- Miś, T.A.; Modelski, J. Stratospheric VLF Vertical Electric Mono- And Dipole Antenna Tests in 2014–2015. In Proceedings of the 2018 Baltic URSI Symposium (URSI), Poznań, Poland, 14–17 May 2018; pp. 566–570. [Google Scholar]
- Sikö, A. Babice Station to the stratosphere. Alternatorn 2015, 2, 6–7. [Google Scholar]
- Wait, J.R. The Mode Theory of VLF Ionospheric Propagation for Finite Ground Conductivity. Proc. Inst. Radio Eng. 1957, 6, 760–767. [Google Scholar] [CrossRef]
- Šulić, D.M.; Srećković, V.A.; Mihajlov, A.A. A study of VLF signals variations associated with the changes of ionization level in the D-region in consequence of solar conditions. Adv. Space Res. 2016, 57, 1029–1043. [Google Scholar] [CrossRef]
- Nunn, D. On the numerical modelling of the VLF Trimpi effect. J. Atmos. Sol.-Terr. Phys. 1997, 59, 537–560. [Google Scholar] [CrossRef]
- EMC Handbook. Section 6.1. Propagation Considerations; Don White Consultants, Inc.: Warrenton, VA, USA, 1976. [Google Scholar]
- Dobrott, D.; Ishimaru, A. East-West Effect on VLF Mode Transmission Across the Earth’s Magnetic Field. J. Res. Natl. Bur. Stand. Sect. D Radio Propag. 1961, 65D, 47–52. [Google Scholar] [CrossRef]
- Poisel, R.A. Antenna Systems and Electronic Warfare Applications; Artech House: Norwood, MA, USA, 2012. [Google Scholar]
- Jankiewicz, Z. Balloons and Dirigibles; WMON: Warsaw, Poland, 1982. [Google Scholar]
- Swedish Space Corporation. BEXUS User Manual v7.5; Swedish Space Corporation: Solna, Sweden, 2020. [Google Scholar]
- Miś, T.A. The Design of the Stratospheric Research Dirigible. Bachelor’s Thesis, Warsaw University of Technology, Faculty of Power and Aerospace Engineering, Division of Mechanics, Warsaw, Poland, 2015. [Google Scholar]
- SERA—Standardised European Rules of the Air. Commission Implementing Regulation No. 923/2012. Off. J. Eur. Union 2012, 281, 1–66. [Google Scholar]
- Miś, T.A. Experiment-based risk evaluation for a stratospheric VLF antenna system. In Proceedings of the IEEE International Symposium on Antennas and Propagation & USNC-URSI Radio Science Meeting, Denver, CO, USA, 10–15 July 2022. [Google Scholar]
- Miś, T.A.; Jasiński, K.; Gajewska, P.; Węgrzyn, E.; Nowakowski, A.; Płonka, M.; Koryciński, I.; Mierzejewski, P.; Maciszewski, K. Balloon micro Lifeform-and-Meteorite Assembler (BuLMA) project for the BEXUS 22 launch campaign. In Proceedings of the 23rd ESA Symposium on European Rocket & Balloon Programmes and Related Research, European Space Agency, Visby, Sweden, 11–15 June 2017. [Google Scholar]
- Masłowski, A.; Miś, T.A.; Grabowski, D.; Owczarzak, M. BEXUS27 LUSTRO—Design and Test of the Light and Ultraviolet Strato- and Tropospheric Radiation Observer. In Proceedings of the 24th ESA Symposium on Rocket and Balloon Programmes and Related Research, European Space Agency, Bremen, Germany, 16–20 June 2019. [Google Scholar]
- Babikov, M.A.; Komarov, N.S.; Sergeyev, A.S. High Voltage Technology; WN-T: Warsaw, Poland, 1967. [Google Scholar]
- Imianitov, I.M.; Chubarina, E.V.; Shwarts, J.M. The Electricity of Clouds; National Scientific Publisher: Warsaw, Poland, 1974. [Google Scholar]
- Kowalska, B.; Łabudzki, S. Electrical discharges on the airplane. LOT Flight Pers. Bull. 1981, 2, 13–25. [Google Scholar]
- Sweers, G.; Birch, B.; Gokcen, J. Lightning strikes: Protection, inspection and repair. Aero Q. 2012, 4, 19–28. [Google Scholar]
- Miś, T.A.; Modelski, J. In-Flight Electromagnetic Compatibility of Airborne Vertical VLF Antennas. Sensors 2022, 22, 5302. [Google Scholar] [CrossRef]
- Miś, T.A.; Modelski, J.; Ciuba, M. Model investigations on electric discharges over balloon-borne stratospheric VLF antennas. Energies 2022, 15, 6805. [Google Scholar] [CrossRef]
- Nautel. Lightning Protection for Radio Transmitter Stations. In Information Booklet; Nautel: Hacketts Cove, NS, Canada, 1996. [Google Scholar]
- Miś, T.A. Design and thermal analysis of POWER MOSFET power amplifiers for LF and VLF special transmitting systems. Telecommun. Rev. Telecommun. News 2020, 1, 7–8. [Google Scholar] [CrossRef]
- BX22 BuLMA Student Experiment Documentation, version 5.0; REXUS/BEXUS Programme: Warsaw, Poland, 2017.
- Miś, T.A. Flashover Analysis of Near-Space Antenna Mounting Insulators. In Proceedings of the 13th European Conference on Antennas and Propagation (EuCAP), Kraków, Poland, 31 March–4 April 2019. [Google Scholar]
- Piccard, A. To the Stratosphere and into the Ocean’s Deep; Publisher: Iskry, Warsaw, 1964. [Google Scholar]
- List of equipment falling within the scope of ‘Class 1’. In Article 1(3) of Commission Decision 2000/299/EC; European Commission: Brussels, Belgium, 2018.
- Kopcewicz, T. Atmospheric Physics. Part I. Aerology; PWN: Warsaw, Poland, 1956. [Google Scholar]
- Kopcewicz, T. The Atmosphere of the Earth; PZWS: Warsaw, Poland, 1948. [Google Scholar]
- Lush, W.G.; Johnston, F.E.; Finch, J.L. Trans-oceanic radio station—Warsaw, Poland. Proc. Inst. Radio Eng. 1925, 13, 571–588. [Google Scholar] [CrossRef]
- Raczek, J.B.; Łada, M.; Śladowski, D.; Chrapek, J.J.; Orda-Sztark, S.; Miś, T.A. The History of the Radiotelegraphic Department Babice-Boernerowo; Profbud Group: Warsaw, Poland, 2017. [Google Scholar]
- Kulikovski, A.A.; Bogdanov, A.F.; Vasin, V.V.; Dulin, W.N.; Ilin, V.A.; Krivitskiy, V.H.; Kuznietsov, V.A.; Labutin, V.K.; Molochkov, Y.B.; Piertsov, S.V.; et al. Radioelectronics—Handbook; WKiŁ: Warsaw, Poland, 1971; Volume 1. [Google Scholar]
- Miś, T.A. The results of IGLUNA 2019 trans-ice longwave communication system tests. In Proceedings of the MIKON Conference, Warsaw, Poland, 5–8 October 2020. [Google Scholar]
- Miś, T.A.; Modelski, J. The Analysis of Experimental Deployment of IGLUNA 2019 Trans-Ice Longwave System. Remote Sens. 2020, 12, 4045. [Google Scholar] [CrossRef]
- Lombardi, M.A. The use of GPS disciplined oscillators as primary frequency standards for calibration and metrology laboratories. MEASURE 2008, 3, 56–65. [Google Scholar] [CrossRef]
- Bem, D.J. Auxiliary Materials for Propagation Calculations; Wrocław University of Science and Technology: Wrocław, Poland, 1974. [Google Scholar]
- Fraser-Smith, A.C.; Bannister, P.R. Reception of ELF signals at antipodal distances. Radio Sci. 1998, 33, 83–88. [Google Scholar] [CrossRef]
- ITU. Recommendation ITU-R P.527-4. In Electrical Characteristics of the Surface of the Earth; ITU: Geneva, Switzerland, 2017. [Google Scholar]
- Gasdia, F.; Marshall, R.A. A New Longwave Mode Propagator for the Earth–Ionosphere Waveguide. IEEE Trans. Antennas Propag. 2021, 69, 8675–8688. [Google Scholar] [CrossRef]
- Bem, D.J. Antenna Array in the Radio Broadcasting Centre Solec Kujawski (Polish Radio, JSC). Telecommun. Rev. Telecommun. News 2000, 8–9, 577–585. [Google Scholar]
- Terman, F.E. Radio Engineering; PWT: Warsaw, Poland, 1952; Volume 2. [Google Scholar]
- Rogers, T. Longwave, Now and Then. A Frequency Order Guide to Longwave Radio Stations and a Look Back at the Past. 2022. Available online: http://www.dxguides.info/2021/01/blog-post_9.html (accessed on 16 January 2023).
- Miś, T.A.; Modelski, J. Environmental Sensitivity of Large Stealth Longwave Antenna Systems. Remote Sens. 2021, 13, 3946. [Google Scholar] [CrossRef]
- Czerwiński, D. Test Circuit for the D Class Power Amplifier Module. Bachelor’s Thesis, Technological-Agricultural Academy, Bydgoszcz, Poland, 2006. [Google Scholar]







| Severity | Probability | ||
|---|---|---|---|
| 1 | No/minor damage | 1 | Extremely low |
| 2 | Damage not affecting performance | 2 | Low |
| 3 | Loss of performance | 3 | Medium |
| 4 | Subsystem shutdown | 4 | High |
| 5 | Mission destruction | 5 | Very high |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miś, T.A.; Modelski, J. Risk Assessment and Experimental Light-Balloon Deployment of a Stratospheric Vertical VLF Transmitter. Sensors 2023, 23, 1073. https://doi.org/10.3390/s23031073
Miś TA, Modelski J. Risk Assessment and Experimental Light-Balloon Deployment of a Stratospheric Vertical VLF Transmitter. Sensors. 2023; 23(3):1073. https://doi.org/10.3390/s23031073
Chicago/Turabian StyleMiś, Tomasz Aleksander, and Józef Modelski. 2023. "Risk Assessment and Experimental Light-Balloon Deployment of a Stratospheric Vertical VLF Transmitter" Sensors 23, no. 3: 1073. https://doi.org/10.3390/s23031073
APA StyleMiś, T. A., & Modelski, J. (2023). Risk Assessment and Experimental Light-Balloon Deployment of a Stratospheric Vertical VLF Transmitter. Sensors, 23(3), 1073. https://doi.org/10.3390/s23031073









