Signal Processing and Waveform Re-Tracking for SAR Altimeters on High Mobility Platforms with Vertical Movement and Antenna Mis-Pointing
Abstract
1. Introduction
2. Numerical Mean Echo Power Model for SAR Altimetry
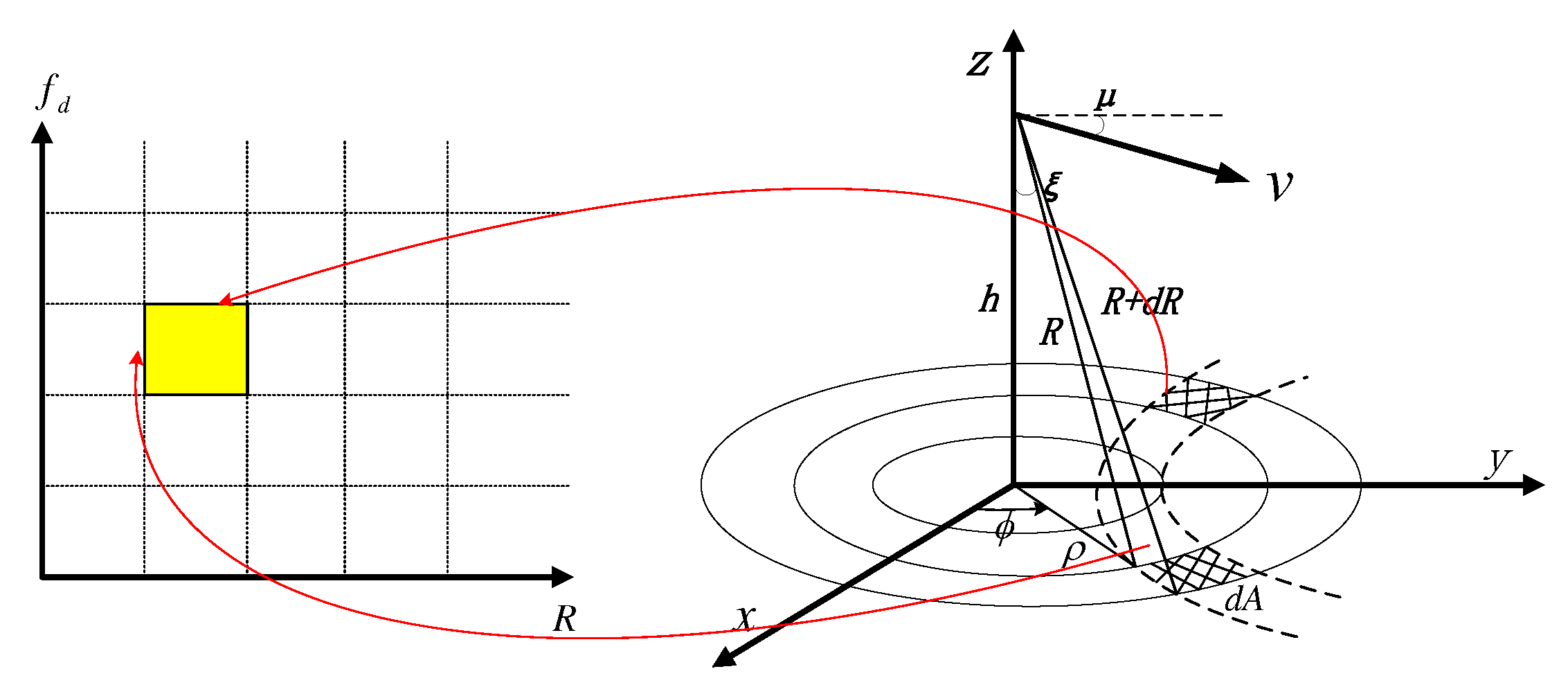
2.1. Altimetric Scenario
2.2. Radar Signal Model
2.3. Pulse Compression
2.4. Along-Track FFT
2.5. Backscattered Waveform Power Model
3. Semi-Analytical Echo Model of Airborne SAR Altimeters
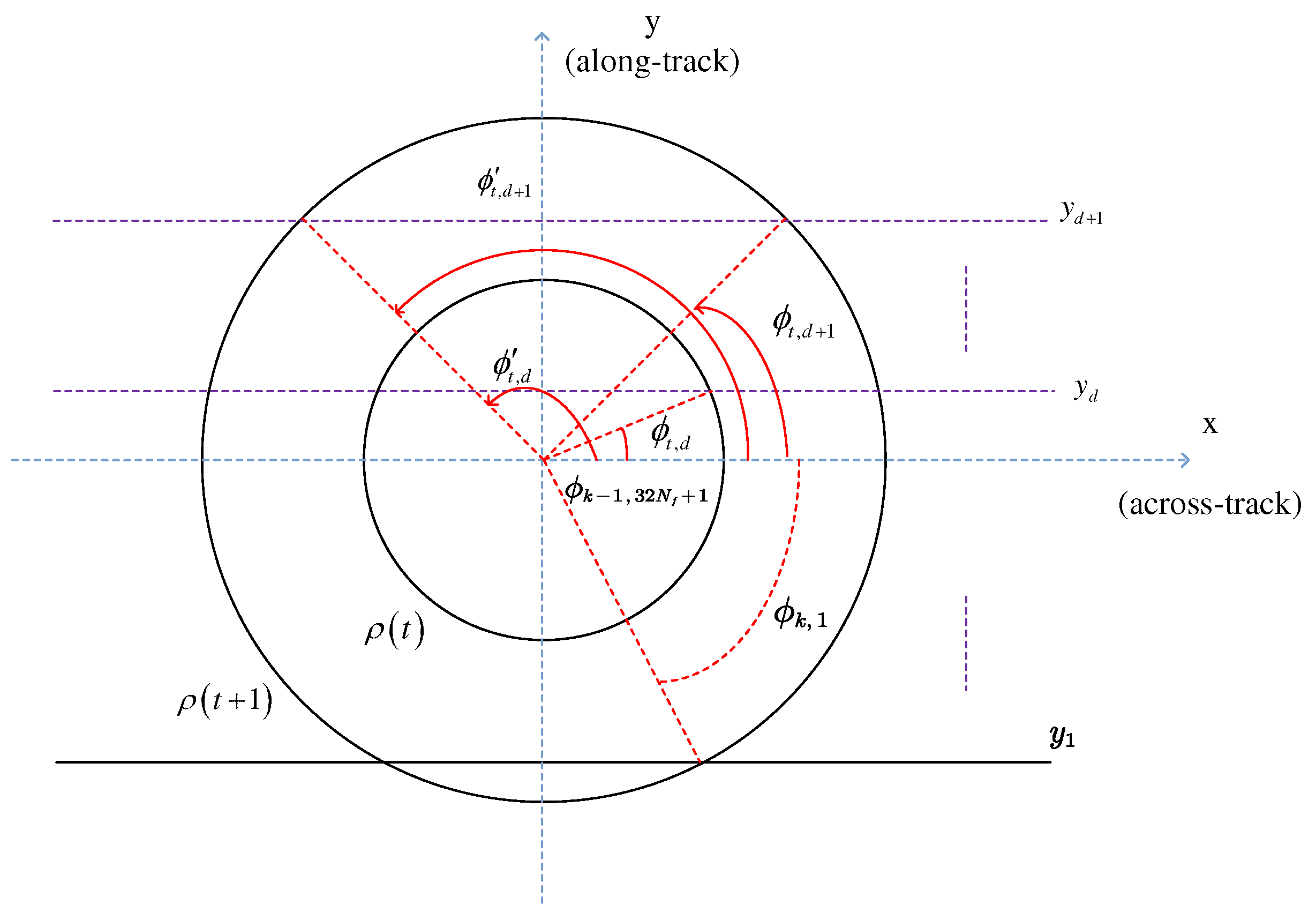
3.1. Convolution Model
3.2. Semi-Analytical Expression of
3.3. Multilooking
| Algorithm 1 Delay Compensation for Airborne SAR Altimetry |
Input: range r, Doppler frequency , The reflected power , minimum height
|
3.4. Analysis of the Semianalytical Echo Model
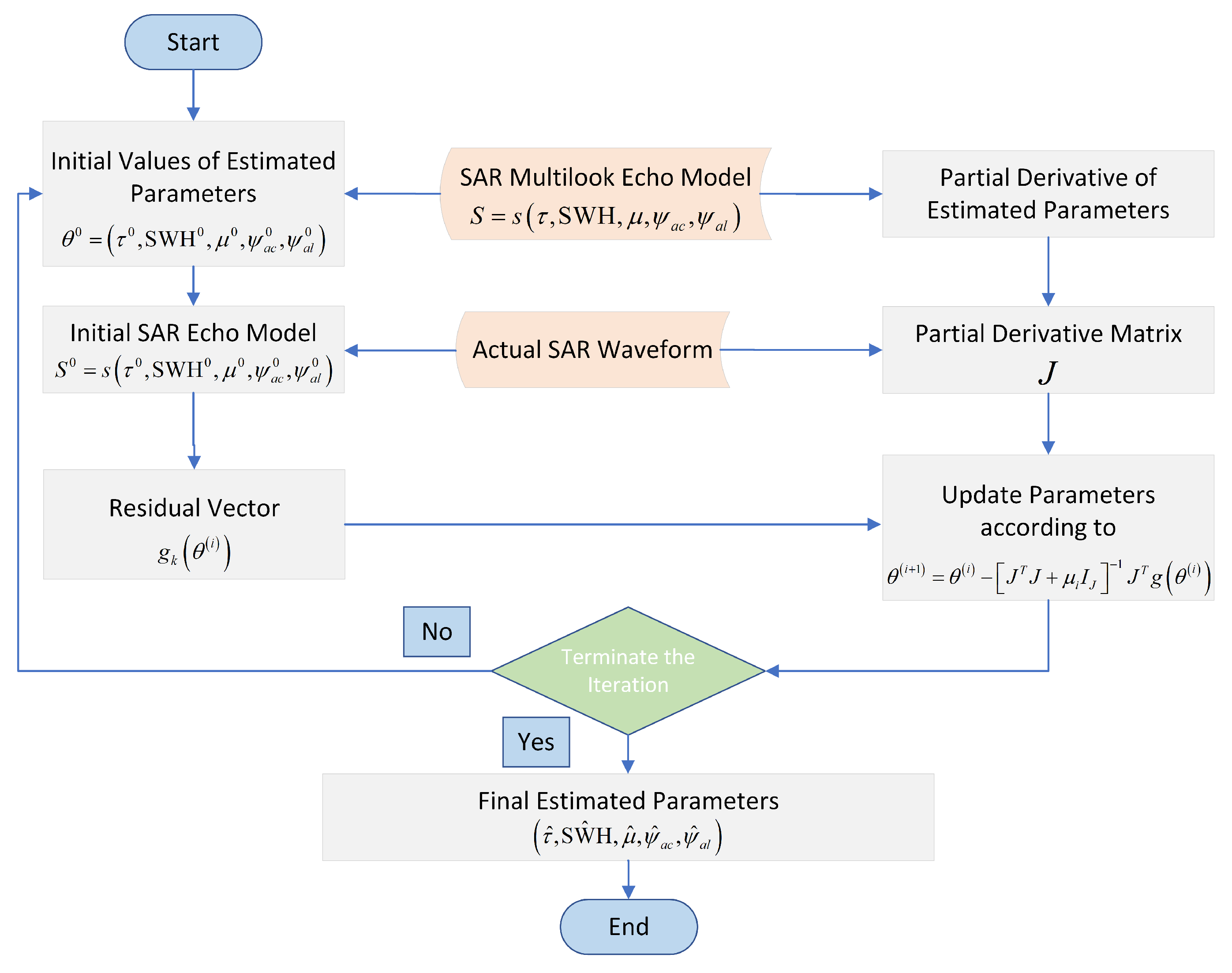
4. Re-Tracking Algorithm Based on Echo Model Fitting
5. Results
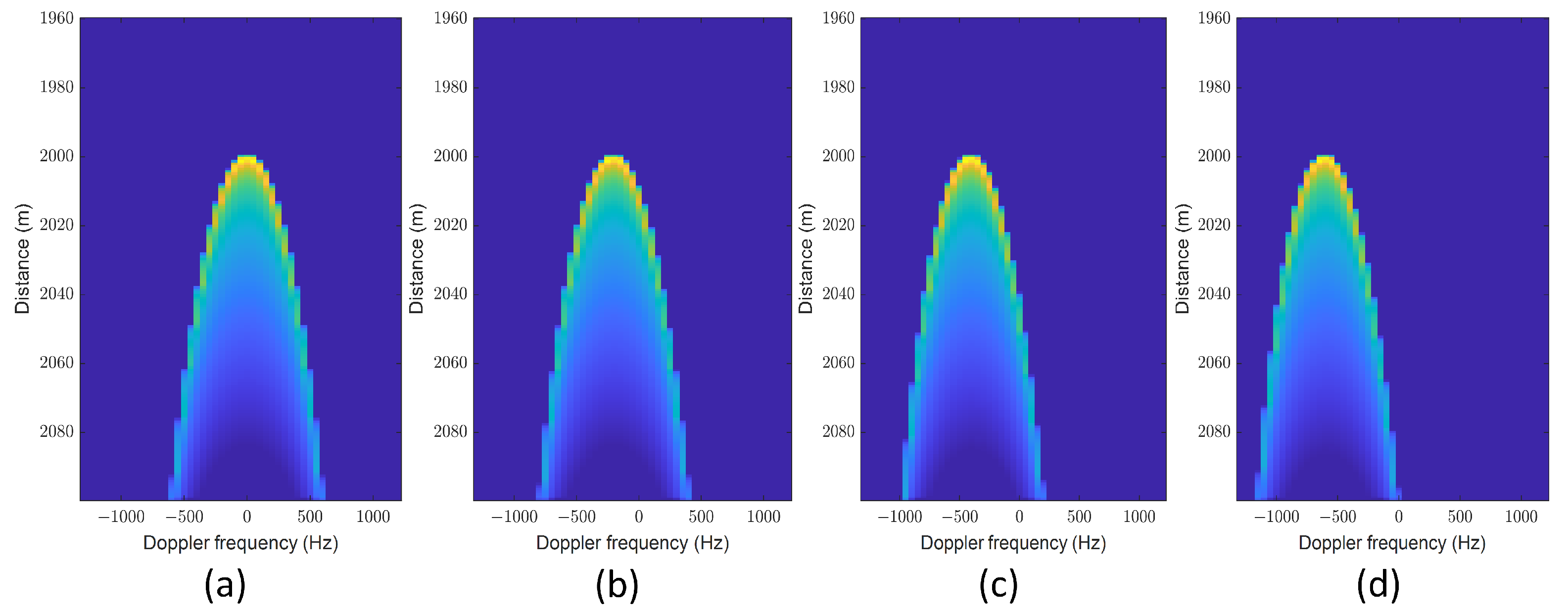
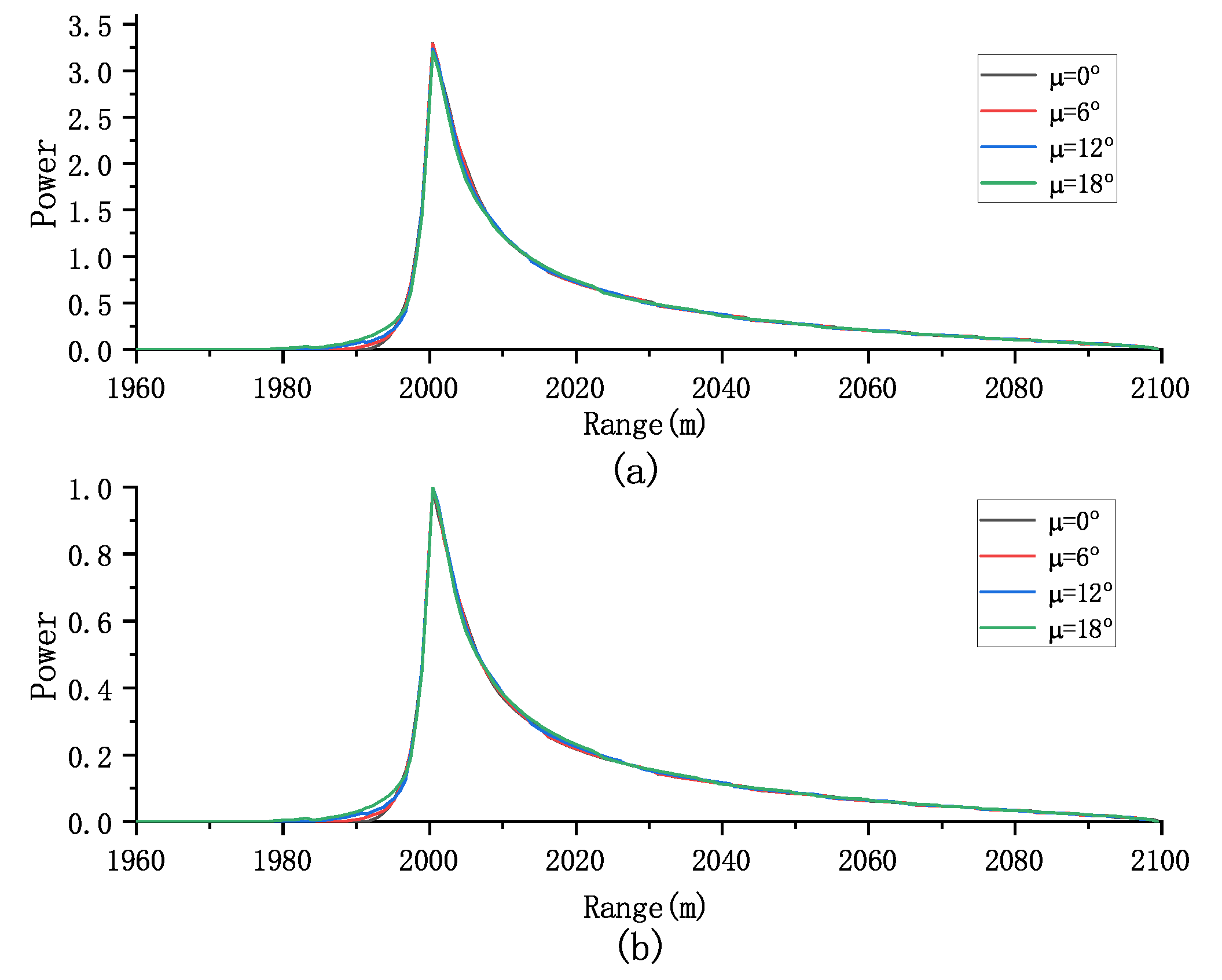
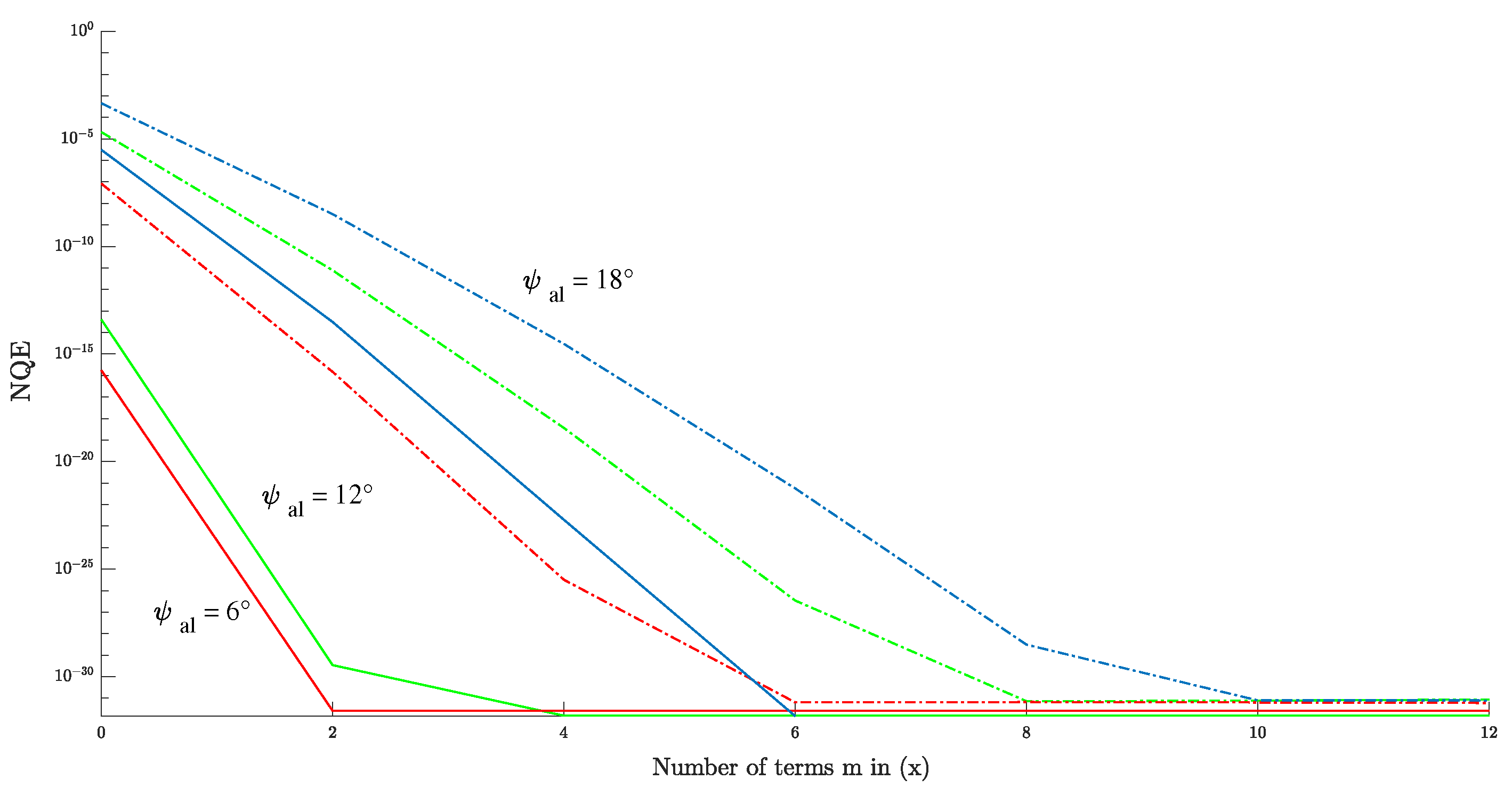
5.1. Analysis of the FSIR Approximations
5.2. Comparison with Numerical Waveforms
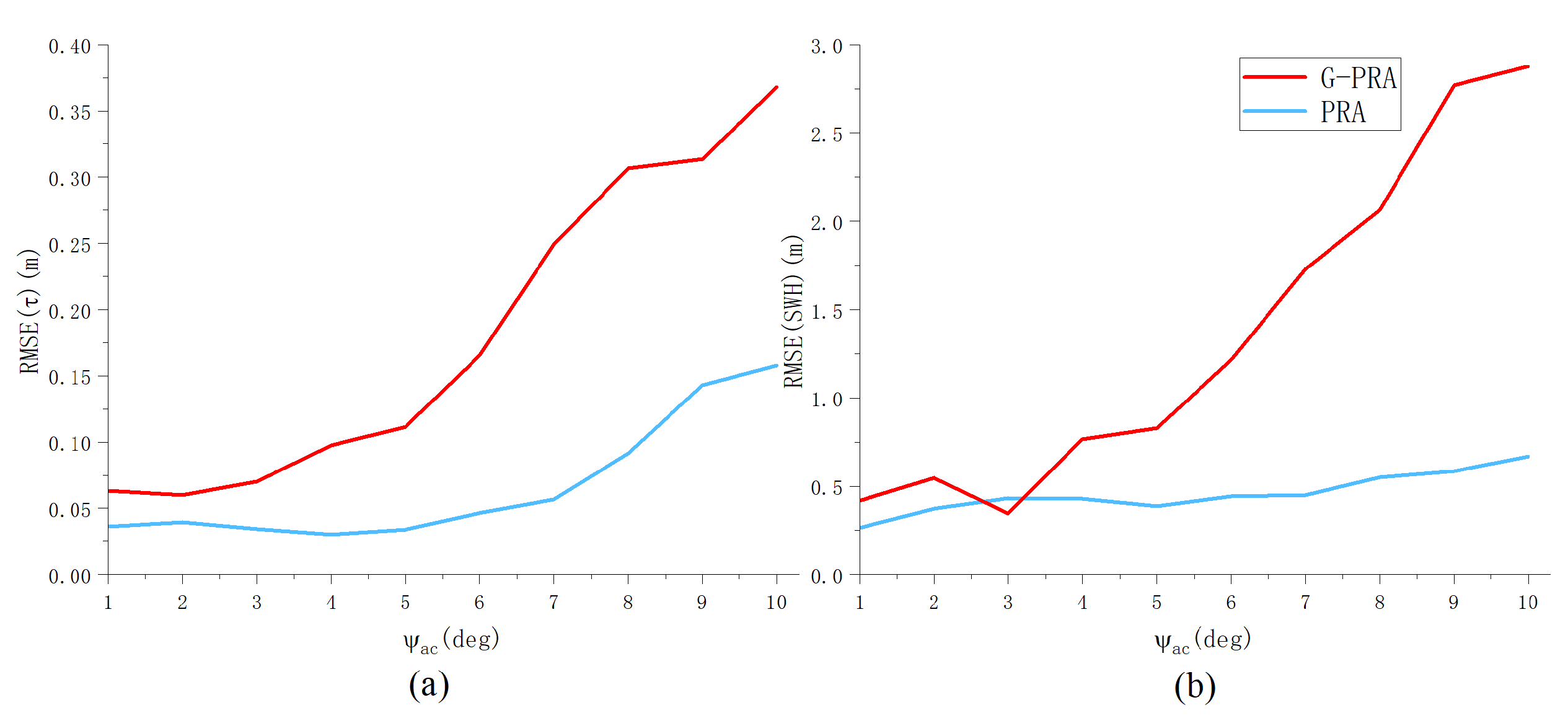
5.3. Analysis of Re-Tracking Precision
6. Conclusions
- (1)
- An analytical expression that considers mis-pointing angles, circular antenna patterns, and vertical velocity is introduced for the echo model. The proposed model shows that the across-track mis-pointing angle affects the shape and the amplitude of the altimetric echo, whereas the along-track mis-pointing angle mainly affects the amplitude of the echo. When we consider (), the expansion order is adequate to achieve the required level of error, which means that the global NQE is less than .
- (2)
- A novel delay compensation method based on sinc interpolation is proposed to obtain the multilook echo in order to optimally handle non-integer delays and maintain the signal frequency characteristics. Compared with the generalized model, the proposed semi-analytic model is closer to the fully numerical waveform at different values of mis-pointing angle and , especially when the roll angle is large.
- (3)
- A five-parameter estimation strategy using the least squares procedure is proposed for SAR altimeters with vertical movement. The performance of the proposed model is evaluated using simulated data for typical airborne scenarios, analyzing the influence of different mis-pointing angles and flight path angle on parameter estimation. When the mis-pointing angles are within 10 degrees, the RMSE of obtained by the re-tracking method fitted by the proposed model is less than 0.2 m, and increases more slowly compared to the one fitted by the generalized model.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hügler, P.; Geiger, M.; Waldschmidt, C. 77 GHz radar-based altimeter for unmanned aerial vehicles. In Proceedings of the 2018 IEEE Radio and Wireless Symposium (RWS), Anaheim, CA, USA, 15–18 January 2018; pp. 129–132. [Google Scholar]
- Hügler, P.; Roos, F.; Schartel, M.; Geiger, M.; Waldschmidt, C. Radar Taking Off: New Capabilities for UAVs. IEEE Microw. Mag. 2018, 19, 43–53. [Google Scholar] [CrossRef]
- Schartel, M.; Burr, R.; Schoeder, P.; Rossi, G.; Hügler, P.; Mayer, W.; Waldschmidt, C. Radar-based altitude over ground estimation of UAVs. In Proceedings of the 2018 11th German Microwave Conference (GeMiC), Freiburg, Germany, 12–14 March 2018; pp. 103–106. [Google Scholar]
- Meng, Y.; Wang, W.; Han, H.; Ban, J. A visual/inertial integrated landing guidance method for UAV landing on the ship. Aerosp. Sci. Technol. 2019, 85, 474–480. [Google Scholar] [CrossRef]
- Labun, J.; Krchňák, M.; Kurdel, P.; Češkovič, M.; Nekrasov, A.; Gamcová, M. Possibilities of Increasing the Low Altitude Measurement Precision of Airborne Radio Altimeters. Electronics 2018, 7, 191. [Google Scholar] [CrossRef]
- Labun, J.; Kurdel, P.; Češkovič, M.; Nekrasov, A.; Gamec, J. Low Altitude Measurement Accuracy Improvement of the Airborne FMCW Radio Altimeters. Electronics 2019, 8, 888. [Google Scholar] [CrossRef]
- Başpınar, Ö.O.; Omuz, B.; Öncü, A. Detection of the Altitude and On-the-Ground Objects Using 77-GHz FMCW Radar Onboard Small Drones. Drones 2023, 7, 86. [Google Scholar] [CrossRef]
- Legresy, B.; Papa, F.; Remy, F.; Vinay, G.; Van den Bosch, M.; Zanife, O.Z. ENVISAT radar altimeter measurements over continental surfaces and ice caps using the ICE-2 retracking algorithm. Remote Sens. Environ. 2005, 95, 150–163. [Google Scholar] [CrossRef]
- Maus, S.; Green, C.M.; Fairhead, J.D. Improved ocean-geoid resolution from retracked ERS-1 satellite altimeter waveforms. Geophys. J. Int. 1998, 134, 243–253. [Google Scholar] [CrossRef][Green Version]
- Sandwell, D.T.; Smith, W.H. Retracking ERS-1 altimeter waveforms for optimal gravity field recovery. Geophys. J. Int. 2005, 163, 79–89. [Google Scholar] [CrossRef]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y.; Boy, F.; Moreau, T. A Generalized Semi-Analytical model for delay/Doppler altimetry. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 5126–5129. [Google Scholar]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y.; Boy, F.; Moreau, T. Including antenna mispointing in a semi-analytical model for delay/Doppler altimetry. IEEE Trans. Geosci. Remote Sens. 2014, 53, 598–608. [Google Scholar] [CrossRef]
- Rodríguez, E. Altimetry for non-Gaussian oceans: Height biases and estimation of parameters. J. Geophys. Res. Ocean. 1988, 93, 14107–14120. [Google Scholar] [CrossRef]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y.; Snoussi, H. Bayesian Estimation of Smooth Altimetric Parameters: Application to Conventional and Delay/Doppler Altimetry. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2207–2219. [Google Scholar] [CrossRef]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y. Nonlinear regression using smooth Bayesian estimation. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 2634–2638. [Google Scholar]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Hayne, G. Radar altimeter mean return waveforms from near-normal-incidence ocean surface scattering. IEEE Trans. Antennas Propag. 1980, 28, 687–692. [Google Scholar] [CrossRef]
- Amarouche, L.; Thibaut, P.; Zanife, O.; Dumont, J.; Vincent, P.; Steunou, N. Improving the Jason-1 ground retracking to better account for attitude effects. Marine Geodesy 2004, 27, 171–197. [Google Scholar] [CrossRef]
- Raney, R.K. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Phalippou, L.; Enjolras, V. Re-tracking of SAR altimeter ocean power-waveforms and related accuracies of the retrieved sea surface height, significant wave height and wind speed. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 3533–3536. [Google Scholar]
- Yang, S.; Liu, H.; Xu, K.; Xu, X. The mean echo model and data process of SAR altimeter. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 2077–2080. [Google Scholar]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y.; Thibaut, P.; Boy, F. A semi-analytical model for delay/Doppler altimetry and its estimation algorithm. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4248–4258. [Google Scholar] [CrossRef]
- Wingham, D.; Phalippou, L.; Mavrocordatos, C.; Wallis, D. The mean echo and echo cross product from a beamforming interferometric altimeter and their application to elevation measurement. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2305–2323. [Google Scholar] [CrossRef]
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR altimeter backscattered waveform model. IEEE Trans. Geosci. Remote Sens. 2014, 53, 911–919. [Google Scholar] [CrossRef]
- Egido, A.; Smith, W.H. Fully focused SAR altimetry: Theory and applications. IEEE Trans. Geosci. Remote Sens. 2016, 55, 392–406. [Google Scholar] [CrossRef]
- Buchhaupt, C.; Fenoglio, L.; Becker, M.; Kusche, J. Impact of vertical water particle motions on focused SAR altimetry. Adv. Space Res. 2021, 68, 853–874. [Google Scholar] [CrossRef]
- Ehlers, F.; Schlembach, F.; Kleinherenbrink, M.; Slobbe, C. Validity assessment of SAMOSA retracking for fully-focused SAR altimeter waveforms. Adv. Space Res. 2023, 71, 1377–1396. [Google Scholar] [CrossRef]
- Schlembach, F.; Passaro, M.; Dettmering, D.; Bidlot, J.; Seitz, F. Interference-sensitive coastal SAR altimetry retracking strategy for measuring significant wave height. Remote Sens. Environ. 2022, 274, 112968. [Google Scholar] [CrossRef]
- Dinardo, S.; Fenoglio-Marc, L.; Buchhaupt, C.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Benveniste, J. Coastal SAR and plrm altimetry in german bight and west baltic sea. Adv. Space Res. 2018, 62, 1371–1404. [Google Scholar] [CrossRef]
- McKean, J.; Roering, J. Objective landslide detection and surface morphology mapping using high-resolution airborne laser altimetry. Geomorphology 2004, 57, 331–351. [Google Scholar] [CrossRef]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y.; Thibaut, P. A new model for peaky altimetric waveforms. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 2825–2828. [Google Scholar]
- Chalup, S.; Maire, F. A study on hill climbing algorithms for neural network training. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 2014–2021. [Google Scholar]
- Galaktionov, I.; Kudryashov, A.; Sheldakova, J.; Nikitin, A. The use of modified hill-climbing algorithm for laser beam focusing through the turbid medium. In Laser Resonators, Microresonators, and Beam Control XIX; SPIE: Washington, DC, USA, 2017; Volume 10090, pp. 164–177. [Google Scholar]
- Li, J.f.; Li, W.; Huang, R. An efficient method for solving a matrix least squares problem over a matrix inequality constraint. Comput. Optim. Appl. 2016, 63, 393–423. [Google Scholar] [CrossRef]
- Hernando, L.; Mendiburu, A.; Lozano, J.A. Hill-Climbing algorithm: Let’s go for a walk before finding the optimum. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–7. [Google Scholar]
- Ranganathan, A. The levenberg-marquardt algorithm. Tutoral LM Algorithm 2004, 11, 101–110. [Google Scholar]
- Liu, X.; Kong, W.; Sun, H.; Lu, Y. Performance analysis of Ku/Ka dual-band SAR altimeter from an airborne experiment over South China Sea. Remote Sens. 2022, 14, 2362. [Google Scholar] [CrossRef]
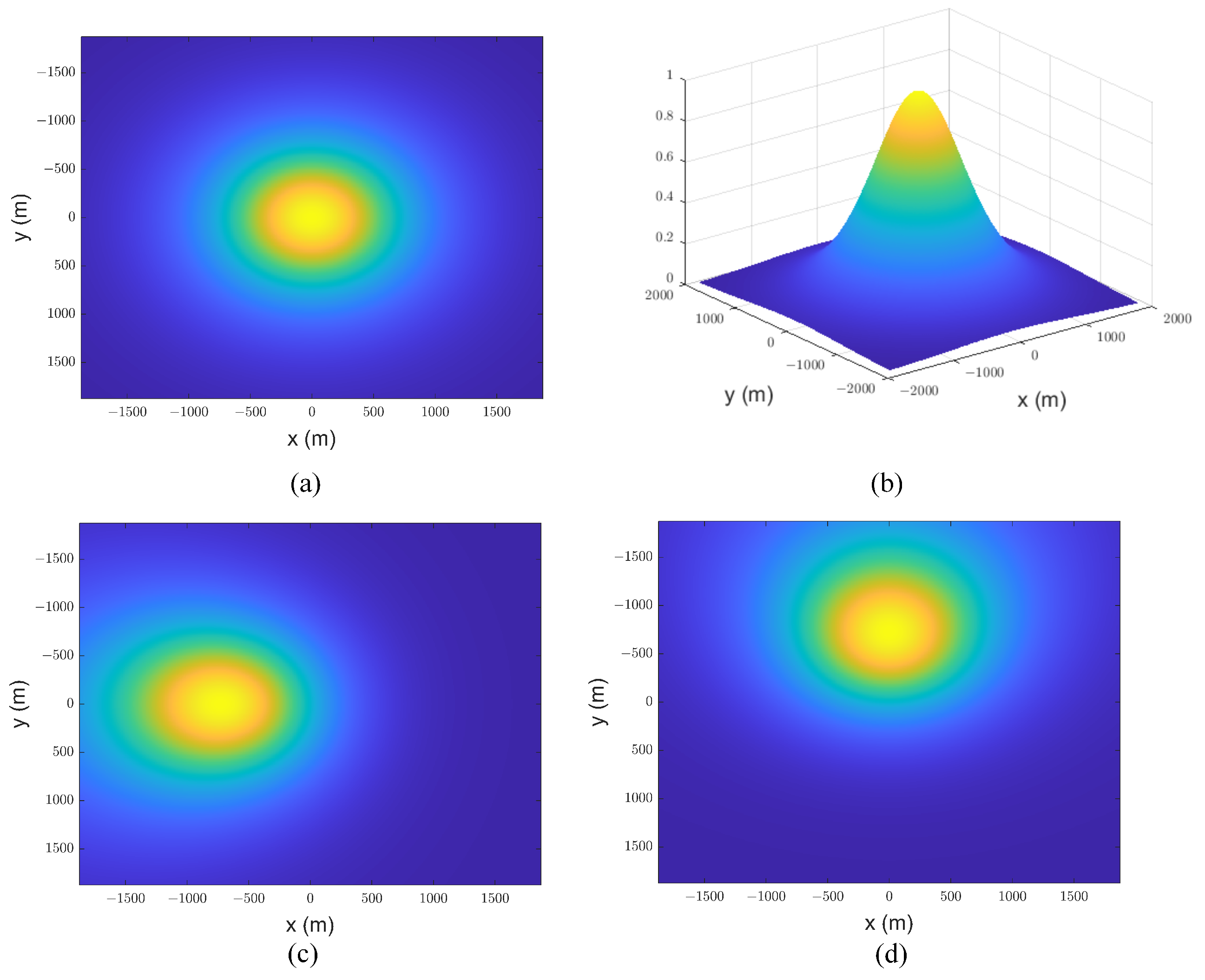







| Parameter | Value |
|---|---|
| Frequency | 2.95 GHz |
| Wavelength () | 0.1 cm |
| Bandwidth (B) | 100 MHz |
| Mean flight altitude (h) | 2000 m |
| Pulse repetition frequency (PRF) | 5000 Hz |
| 3dB Antenna beam width () | |
| Velocity () | 100 m/s |
| Pulse per burst | 100 pulses |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Jing, W.; Liu, X.; Huang, B.; Jiang, G. Signal Processing and Waveform Re-Tracking for SAR Altimeters on High Mobility Platforms with Vertical Movement and Antenna Mis-Pointing. Sensors 2023, 23, 9266. https://doi.org/10.3390/s23229266
Wang Q, Jing W, Liu X, Huang B, Jiang G. Signal Processing and Waveform Re-Tracking for SAR Altimeters on High Mobility Platforms with Vertical Movement and Antenna Mis-Pointing. Sensors. 2023; 23(22):9266. https://doi.org/10.3390/s23229266
Chicago/Turabian StyleWang, Qiankai, Wen Jing, Xiang Liu, Bo Huang, and Ge Jiang. 2023. "Signal Processing and Waveform Re-Tracking for SAR Altimeters on High Mobility Platforms with Vertical Movement and Antenna Mis-Pointing" Sensors 23, no. 22: 9266. https://doi.org/10.3390/s23229266
APA StyleWang, Q., Jing, W., Liu, X., Huang, B., & Jiang, G. (2023). Signal Processing and Waveform Re-Tracking for SAR Altimeters on High Mobility Platforms with Vertical Movement and Antenna Mis-Pointing. Sensors, 23(22), 9266. https://doi.org/10.3390/s23229266





