Bridge Model Updating Based on Wavelet Neural Network and Wind-Driven Optimization
Abstract
:1. Introduction
2. Wavelet Neural Network
2.1. WNN Structure
2.2. WNN Training
2.3. Improved WNN
3. Wind-Driven Optimization Algorithm
3.1. Fundamentals of the Algorithm
3.2. Derivation of Update Equations
3.3. Realisation of WDO
4. Verification of the Proposed Method
4.1. Finite Element Model
4.2. Establishment of WNN
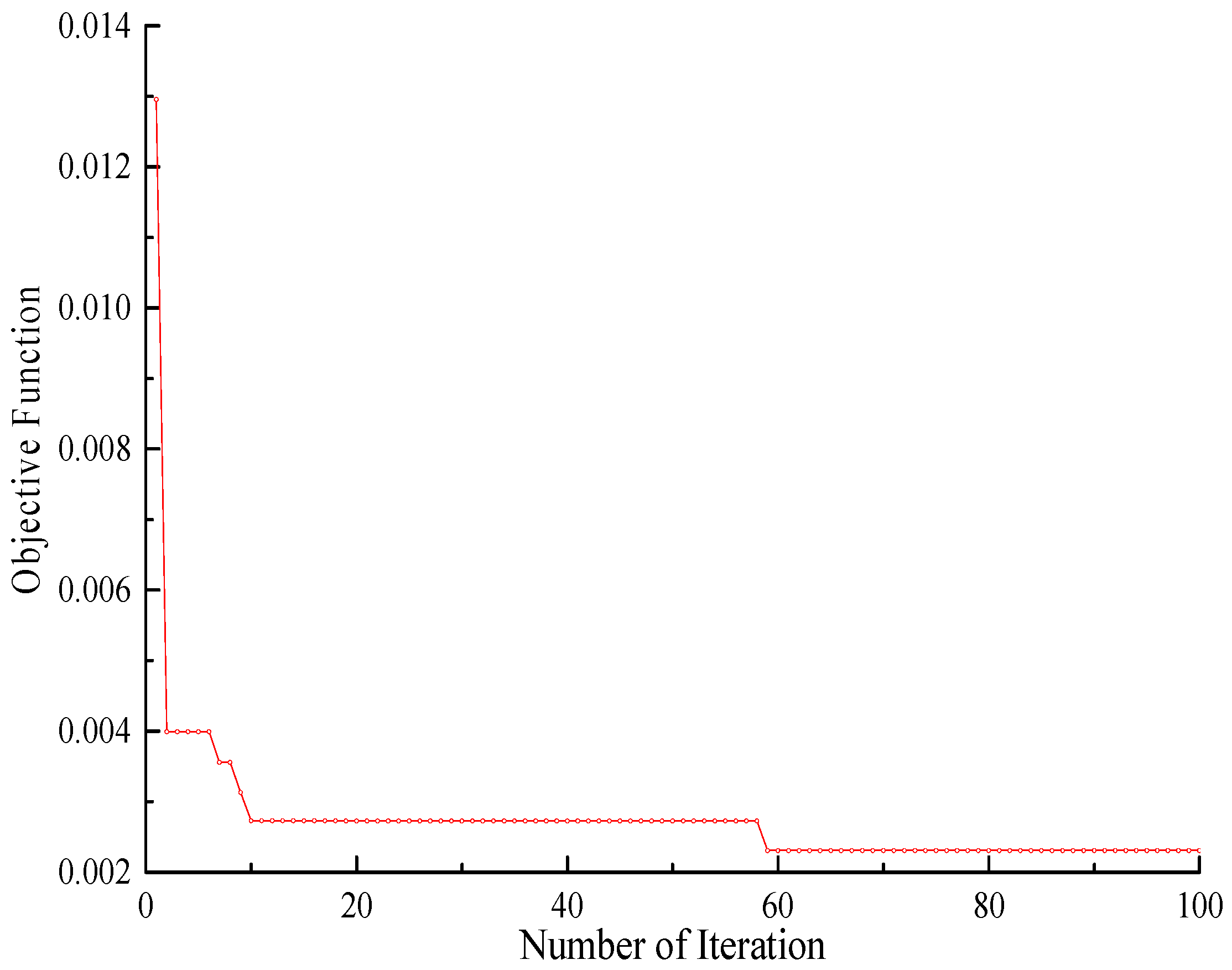
4.3. Results of Algorithm Optimization
5. Finite Element Model Updating of Ningbo Bund Bridge
5.1. Introduction of Ningbo Bund Bridge
5.2. Finite Element Model of Ningbo Bund Bridge
5.3. Selection of Updating Parameters
5.4. Establishment of WNN
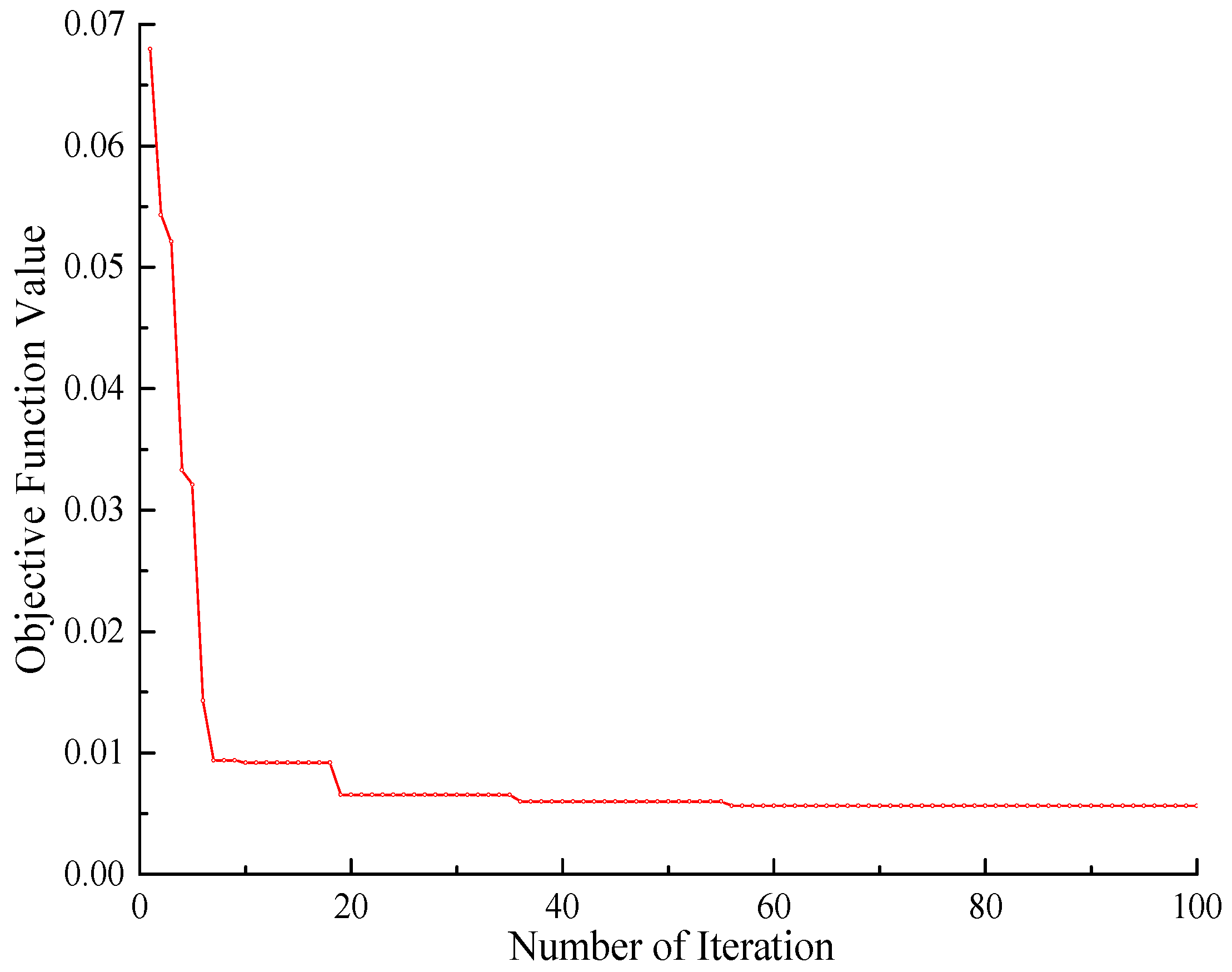
5.5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chrysanidis, T. Experimental and numerical research on cracking characteristics of medium-reinforced prisms under variable uniaxial degrees of elongation. Eng. Fail. Anal. 2023, 145, 107014. [Google Scholar] [CrossRef]
- Chrysanidis, T.A.; Panoskaltsis, V.P. Experimental investigation on cracking behavior of reinforced concrete tension ties. Case Stud. Constr. Mater. 2022, 16, e00810. [Google Scholar] [CrossRef]
- Chrysanidis, T.; Mousama, D.; Tzatzo, E.; Alamanis, N.; Zachos, D. Study of the Effect of a Seismic Zone to the Construction Cost of a Five-Story Reinforced Concrete Building. Sustainability 2022, 14, 10076. [Google Scholar] [CrossRef]
- Gong, C.; Wang, Y.; Peng, Y.; Ding, W.; Lei, M.; Da, Z.; Shi, C. Three-dimensional coupled hydromechanical analysis of localized joint leakage in segmental tunnel linings. Tunn. Undergr. Space Technol. 2022, 130, 104726. [Google Scholar] [CrossRef]
- Razavi, M.; Hadidi, A. Structural damage identification through sensitivity-based finite element model updating and wavelet packet transform component energy. Structures 2021, 33, 4857–4870. [Google Scholar] [CrossRef]
- Aloisio, A.; Pasca, D.P.; Battista, L.D.; Rosso, M.M.; Cucuzza, R.; Marano, G.C.; Alaggio, R. Indirect assessment of concrete resistance from FE model updating and Young’s modulus estimation of a multi-span PSC viaduct: Experimental tests and validation. Structures 2022, 37, 686–697. [Google Scholar] [CrossRef]
- Liu, C.; Huang, X.; Zhao, Y.; Miao, J. Vibration analysis of concrete T-beam at elevated temperatures based on modified finite element model. J. Build. Eng. 2022, 52, 104381. [Google Scholar] [CrossRef]
- Cheng, X.X.; Song, Z.Y. Modal experiment and model updating for Yingzhou Bridge. Structures 2021, 32, 746–759. [Google Scholar] [CrossRef]
- Li, J. Study of Surrogate Model Approximation and Surrogate-Enhanced Structural Reliability Analysis. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2013. (In Chinese). [Google Scholar]
- Jin, R.; Chen, W.; Simpson, T.W. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Zhou, Q.R.; Ou, J.P. Finite element model updating of long-span cable-stayed bridge based on the response surface method of radial basis function. China Railw. Sci. 2012, 33, 8–15. (In Chinese) [Google Scholar]
- Wan, H.P.; Ren, W.X.; Wei, J.H. Structural finite element model updating based on Gaussian process response surface methodology. J. Vib. Shock 2013, 31, 82–87. (In Chinese) [Google Scholar]
- Yang, C.; Xie, Y.M.; Long, Q. Sheet metal forming springback prediction based on agent model of radius basis function. Mach. Tool Hydraul. 2013, 41, 8–11. (In Chinese) [Google Scholar]
- Peng, L.; Liu, L.; Long, T. Satellite bus truss structure optimization using radial basis function. J. Nanjing Univ. Aeronaut. Astronaut. 2014, 46, 475–480. (In Chinese) [Google Scholar]
- Deng, L.; Cai, C.S. Bridge model updating using response surface method and genetic algorithm. J. Bridge Eng. 2010, 15, 553–564. [Google Scholar] [CrossRef]
- Zhong, J.; Gou, H.; Zhao, H.; Zhao, T.; Wang, X. Comparison of several model updating methods based on full-scale model test of track beam. Structures 2022, 35, 46–54. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Li, D.; Zhou, D.; Xin, D. Finite Element Model Updating of Bridge Structures Based on Improved Response Surface Methods. Struct. Control Health Monit. 2023, 2023, 2488951. [Google Scholar] [CrossRef]
- Yang, H.; Yao, W.X. 2D surrogate model of wing lift distribution based on radial basis function. Chin. J. Comput. Mech. 2008, 25, 797–802. (In Chinese) [Google Scholar]
- Chen, S.Z.; Zhong, Q.M.; Hou, S.T.; Wu, G. Two-stage stochastic model updating method for highway bridges based on long-gauge strain sensing. Structures 2022, 37, 1165–1182. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. South. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Levin, R.I.; Lieven, N.A.J. Dynamic finite element model updating using neural networks. J. Sound Vib. 1998, 210, 593–607. [Google Scholar] [CrossRef]
- Park, Y.S.; Kim, S.; Kim, N.; Lee, J.J. Finite element model updating considering boundary conditions using neural networks. Eng. Struct. 2017, 150, 511–519. [Google Scholar] [CrossRef]
- Nejad, R.M.; Sina, N.; Moghadam, D.G.; Branco, R.; Macek, W.; Berto, F. Artificial neural network based fatigue life assessment of friction stir welding AA2024-T351 aluminum alloy and multi-objective optimization of welding parameters. Int. J. Fatigue 2022, 160, 106840. [Google Scholar] [CrossRef]
- Masoudi, N.R.; Sina, N.; Ma, W.; Liu, Z.; Berto, F.; Gholami, A. Optimization of fatigue life of pearlitic Grade 900A steel based on the combination of genetic algorithm and artificial neural network. Int. J. Fatigue 2022, 162, 106975. [Google Scholar] [CrossRef]
- Han, F.; Yang, J. A New Multi-Resolution Wavelet Neural Network for Bridge Health Monitoring. Intell. Autom. Soft Comput. 2010, 16, 771–776. [Google Scholar] [CrossRef]
- Xu, Z.; Xin, J.Z.; Tang, Q.Z.; Xiao, W.N.; Li, S.J. Finite element model updating based on response surface method and sparrow search algorithm. Sci. Technol. Eng. 2021, 21, 9094–9101. (In Chinese) [Google Scholar]
- Qin, S.Q.; Liao, S.P.; Huang, C.L.; Tang, J. Adaptive Kriging model based finite element model updating of a cable-stayed pedestrian bridge. Acta Sci. Nat. Univ. Sunyatseni 2021, 60, 43–53. (In Chinese) [Google Scholar]
- Qin, S.Q.; Gan, Y.W.; Kang, J.T. Model updating of Nanzhonghuan Bridge based on improved gravitational search algorithm. J. Vib. Shock 2021, 40, 116–124+136. (In Chinese) [Google Scholar]
- Yang, Y.X.; Yang, F.L.; Yu, H.B.; Chai, W.H. Single beam finite element model modification based on a weighted response surface method and chaos particle swarm optimization algorithm. J. Lanzhou Univ. 2021, 57, 823–829. (In Chinese) [Google Scholar]
- Zhou, Z.; Zhang, J.; Gong, C. Hybrid semantic segmentation for tunnel lining cracks based on Swin Transformer and convolutional neural network. Comput.-Aided Civ. Infrastruct. Eng. 2023, 38, 2491–2510. [Google Scholar] [CrossRef]
- Gou, H.; Zhao, T.; Qin, S.; Zheng, X.; Pipinato, A.; Bao, Y. In-situ testing and model updating of a long-span cable-stayed railway bridge with hybrid girders subjected to a running train. Eng. Struct. 2022, 253, 113823. [Google Scholar] [CrossRef]
- Ponsi, F.; Bassoli, E.; Vincenzi, L. A multi-objective optimization approach for FE model updating based on a selection criterion of the preferred Pareto-optimal solution. Structures 2021, 33, 916–934. [Google Scholar] [CrossRef]
- Xiao, S.Z. Wavelet Neural Network Theory and Application; Northeastern University Press: Shenyang, China, 2006. (In Chinese) [Google Scholar]
- Zhang, Q.H.; Benveniste, A. Wavelet networks. IEEE Trans. Neural Netw. 1992, 3, 889–898. [Google Scholar] [CrossRef] [PubMed]
- Durbin, R.; Rumelhart, D.E. Product units: A computationally powerful and biologically plausible extension to backpropagation networks. Neural Comput. 1989, 1, 133–142. [Google Scholar] [CrossRef]
- Billings, S.A.; Zheng, G.L. Radial basis function network configuration using genetic algorithms. Neural Netw. 1995, 8, 877–890. [Google Scholar] [CrossRef]
- Xiao, S.M.; Yan, Y.J.; Jiang, B.L. Damage identification for bridge structures based on the wavelet neural network method. Appl. Math. Mech. 2016, 37, 149–159. (In Chinese) [Google Scholar]
- Ulagammai, M.; Venkatesh, P.; Kannan, P.S.; Padhy, N.P. Application of bacterial foraging technique trained artificial and wavelet neural networks in load forecasting. Neurocomputing 2007, 70, 2659–2667. [Google Scholar] [CrossRef]
- Alexandridis, A.K.; Zapranis, A.D. Wavelet neural networks: A practical guide. Neural Netw. 2013, 42, 1–27. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhao, Y.G.; Li, P.P. Efficient approach for dynamic reliability analysis based on uniform design method and Box-Cox transformation. Mech. Syst. Signal Process. 2022, 172, 108967. [Google Scholar] [CrossRef]
- Tong, F. A Maritime Accident Forecast Based on BP Neural Network and Carried out by MATLAB. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2005. (In Chinese). [Google Scholar]
- Bayraktar, Z.; Komurcu, M.; Werner, D.H. Wind Driven Optimization (WDO): A novel nature-inspired optimization algorithm and its application to electromagnetics. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar]
- Ibrahim, I.A.; Hossain, M.J.; Duck, B.C.; Nadarajah, M. An improved wind driven optimization algorithm for parameters identification of a triple-diode photovoltaic cell model. Energy Convers. Manag. 2020, 213, 112872. [Google Scholar] [CrossRef]
- Zhong, L.; Zhou, Y.; Luo, Q.; Zhong, K. Wind driven dragonfly algorithm for global optimization. Concurr. Comput. Pract. Exp. 2021, 33, e6054. [Google Scholar] [CrossRef]
- Ren, Z.L.; Zhang, R.J.; Tian, Y.B. Wind driven optimization algorithm. J. Jiangsu Univ. Sci. Technol. (Nat. Sci. Ed.) 2015, 29, 153–158. (In Chinese) [Google Scholar]
- Fang, K.T. Uniform Design and Uniform Design Table; Science Press: Beijing, China, 1994. (In Chinese) [Google Scholar]
- Komarizadehasl, S.; Huguenet, P.; Lozano, F.; Lozano-Galant, J.A.; Turmo, J. Operational and analytical modal analysis of a bridge using low-cost wireless Arduino-based accelerometers. Sensors 2022, 22, 9808. [Google Scholar] [CrossRef]
- Hu, Z.R.; Wang, Y.W. Analysis on construction control technology of single-tower and four-cable plane space special-shaped cable-stayed bridge. J. China Foreign Highw. 2015, 35, 155–160. (In Chinese) [Google Scholar]
- Zapico, J.L.; Gonzalez, M.P.; Friswell, M.I.; Taylor, C.; Crewe, A. Finite element model updating of a small scale bridge. J. Sound Vib. 2003, 268, 993–1012. [Google Scholar] [CrossRef]
- Yuan, A.M. Studies on Several Key Problems of Finite Element Model Updating Based on the Sensitivity Analysis. Ph.D. Thesis, Southeastern University, Nanjing, China, 2006. (In Chinese). [Google Scholar]


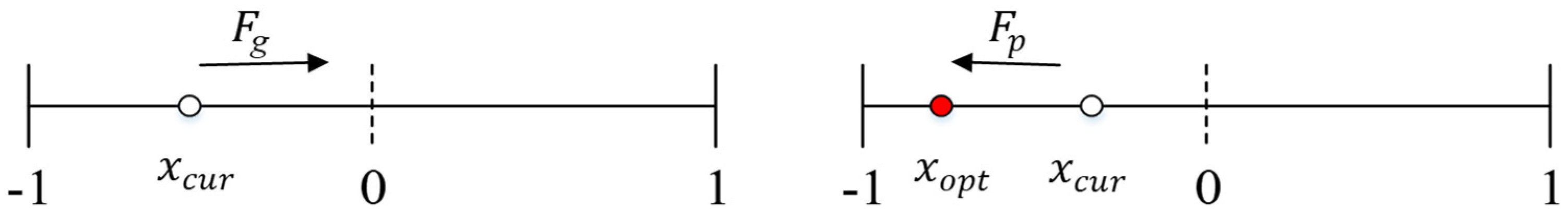








| Correlation Coefficient | g | c | RT | |
|---|---|---|---|---|
| Range | [0.8, 0.9] | [0.6, 0.7] | [0.05, 3.6] | [1.0, 2.0] |
| Parameter | E1 (×104 MPa) | E2 (×104 MPa) | E3 (×104 MPa) | ρ (×101 kg/m3) |
|---|---|---|---|---|
| Initial value | 3.250 | 3.250 | 3.250 | 2.500 |
| Actual value | 2.925 | 2.762 | 2.600 | 2.750 |
| Difference/% | 11.11 | 17.67 | 25.00 | −9.09 |
| Responses | Initial Value | Actual Value | Difference (%) | |
|---|---|---|---|---|
| Natural frequency/Hz | 1st order | 15.151 | 13.295 | 13.96 |
| 2nd order | 19.383 | 17.040 | 13.75 | |
| 3rd order | 28.203 | 24.788 | 13.78 | |
| 4th order | 59.869 | 52.429 | 14.19 | |
| 5th order | 67.678 | 59.568 | 13.61 | |
| 6th order | 81.533 | 71.722 | 13.68 | |
| Displacement/mm | C1 | −17.033 | −19.243 | −11.48 |
| C2 | 9.843 | 11.589 | −15.07 | |
| C3 | −17.033 | −20.926 | −18.60 | |
| Parameter | Optimal Position of Air Particles | Corrected Value |
|---|---|---|
| E1/×104 MPa | −0.444 | 2.889 |
| E2/×104 MPa | −0.576 | 2.782 |
| E3/×104 MPa | −0.674 | 2.702 |
| ρ/×103 kg/m3 | 0.470 | 2.849 |
| Parameter | E1 (×104 MPa) | E2 (×104 MPa) | E3 (×104 MPa) | ρ (×103 kg/m3) |
|---|---|---|---|---|
| Updated value | 2.890 | 2.782 | 2.702 | 2.849 |
| Actual value | 2.925 | 2.762 | 2.600 | 2.805 |
| Difference/% | −1.22 | 0.74 | 3.92 | 1.57 |
| Responses | Network Value | Updated Value | Actual Value | Difference I (%) | Difference II (%) | |
|---|---|---|---|---|---|---|
| Natural frequency/Hz | 1st order | 13.415 | 13.274 | 13.295 | 0.90 | −0.16 |
| 2nd order | 17.174 | 16.996 | 17.040 | 0.78 | −0.26 | |
| 3rd order | 24.973 | 24.714 | 24.788 | 0.75 | −0.30 | |
| 4th order | 52.996 | 52.416 | 52.429 | 1.08 | −0.02 | |
| 5th order | 59.955 | 59.377 | 59.568 | 0.65 | −0.32 | |
| 6th order | 72.214 | 71.453 | 71.722 | 0.69 | −0.37 | |
| Displacement /mm | C1 | −19.263 | −19.361 | −19.243 | 0.10 | 0.61 |
| C2 | 11.367 | 11.468 | 11.589 | −1.91 | −1.04 | |
| C3 | −20.082 | −20.305 | −20.926 | −4.03 | −2.97 | |
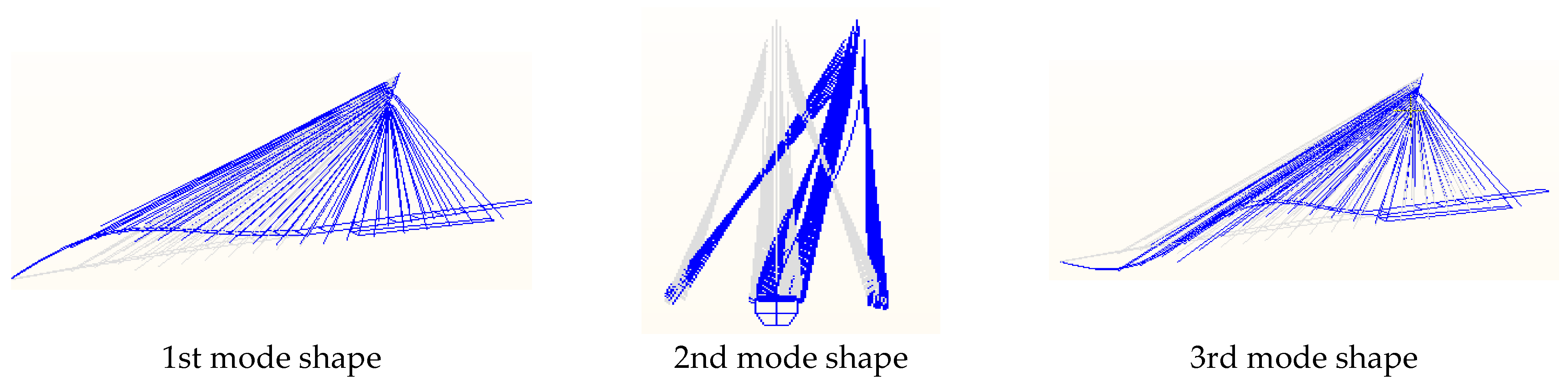
| Order of Natural Frequency | Measured Value (Hz) | Calculated Value (Hz) | Difference (%) | Description of Mode Shape |
|---|---|---|---|---|
| 1 | 0.55 | 0.49 | −10.9% | 225 m span main girder vertical bending vibration |
| 2 | 0.73 | 0.78 | 6.8% | Lateral vibration of the bridge tower |
| 3 | 0.86 | 0.88 | 2.3% | 225 m span main girder vertical bending vibration |
| 4 | 1.26 | 1.21 | −3.9% | Lateral bending vibration of the main beam |
| 5 | 1.34 | 1.41 | 5.2% | Torsional vibration of the main beam |
| 6 | 1.40 | 1.46 | 4.3% | Vertical bending vibration of the main beam |
| 7 | 1.64 | 1.76 | 7.3% | Lateral vibration of the bridge tower |
| 8 | 1.98 | 2.09 | 5.6% | Torsional vibration of the main beam |
| E1 | E2 | E3 | E5 | ρ1 | ρ2 | ρ3 |
|---|---|---|---|---|---|---|
| (×104 MPa) | (×104 MPa) | (×104 MPa) | (×104 MPa) | (×103 kg/m3) | (×103 kg/m3) | (×103 kg/m3) |
| 2.06 | 2.06 | 2.06 | 2.06 | 12.59 | 8.05 | 8.05 |
| Parameter | Updated Value | Initial Value | Difference (%) |
|---|---|---|---|
| E1/×104 MPa | 1.95 | 2.06 | −5.3% |
| E2/×104 MPa | 1.92 | 2.06 | −6.8% |
| E3/×104 MPa | 2.09 | 2.06 | 1.5% |
| E5/×104 MPa | 2.15 | 2.06 | 4.4% |
| ρ1/×103 kg/m3 | 12.68 | 12.59 | 0.7% |
| ρ2/×103 kg/m3 | 7.88 | 8.05 | −1.9% |
| ρ3/×103 kg/m3 | 8.43 | 8.05 | 4.7% |
| Structural Response | Updated Value | Measured Value | Difference (%) | |
|---|---|---|---|---|
| Natural frequency/Hz | 1st order | 0.53 | 0.55 | −3.6% |
| 2nd order | 0.75 | 0.73 | 2.7% | |
| 3rd order | 0.87 | 0.86 | 1.1% | |
| 4th order | 1.22 | 1.26 | 3.2% | |
| 5th order | 1.35 | 1.34 | 0.7% | |
| 6th order | 1.44 | 1.40 | 2.9% | |
| 7th order | 1.69 | 1.64 | 3.0% | |
| 8th order | 2.01 | 1.98 | 1.5% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Zeng, B.; Zhou, Y.; Song, Y.; Zhang, T.; Su, H.; Wang, J. Bridge Model Updating Based on Wavelet Neural Network and Wind-Driven Optimization. Sensors 2023, 23, 9185. https://doi.org/10.3390/s23229185
He H, Zeng B, Zhou Y, Song Y, Zhang T, Su H, Wang J. Bridge Model Updating Based on Wavelet Neural Network and Wind-Driven Optimization. Sensors. 2023; 23(22):9185. https://doi.org/10.3390/s23229185
Chicago/Turabian StyleHe, Haifang, Baojun Zeng, Yulong Zhou, Yuanyuan Song, Tianneng Zhang, Han Su, and Jian Wang. 2023. "Bridge Model Updating Based on Wavelet Neural Network and Wind-Driven Optimization" Sensors 23, no. 22: 9185. https://doi.org/10.3390/s23229185
APA StyleHe, H., Zeng, B., Zhou, Y., Song, Y., Zhang, T., Su, H., & Wang, J. (2023). Bridge Model Updating Based on Wavelet Neural Network and Wind-Driven Optimization. Sensors, 23(22), 9185. https://doi.org/10.3390/s23229185







