Resource Allocation Optimization in IoT-Enabled Water Quality Monitoring Systems
Abstract
:1. Introduction
- We propose the design of a NOMA-enabled protocol for IoT-enabled water quality monitoring systems;
- We propose the integration of edge computing with water quality monitoring systems;
- We propose resource allocation optimization methods, including a Dinkelbach algorithm-based optimization method for optimizing wireless energy transfer and wireless information transfer, as well as a dynamic resource allocation method for hybrid access point (HAP) resource allocation for data collection;
- We provide a comparison of the proposed method with a comparable baseline method.
2. Related Work
3. Proposed Method
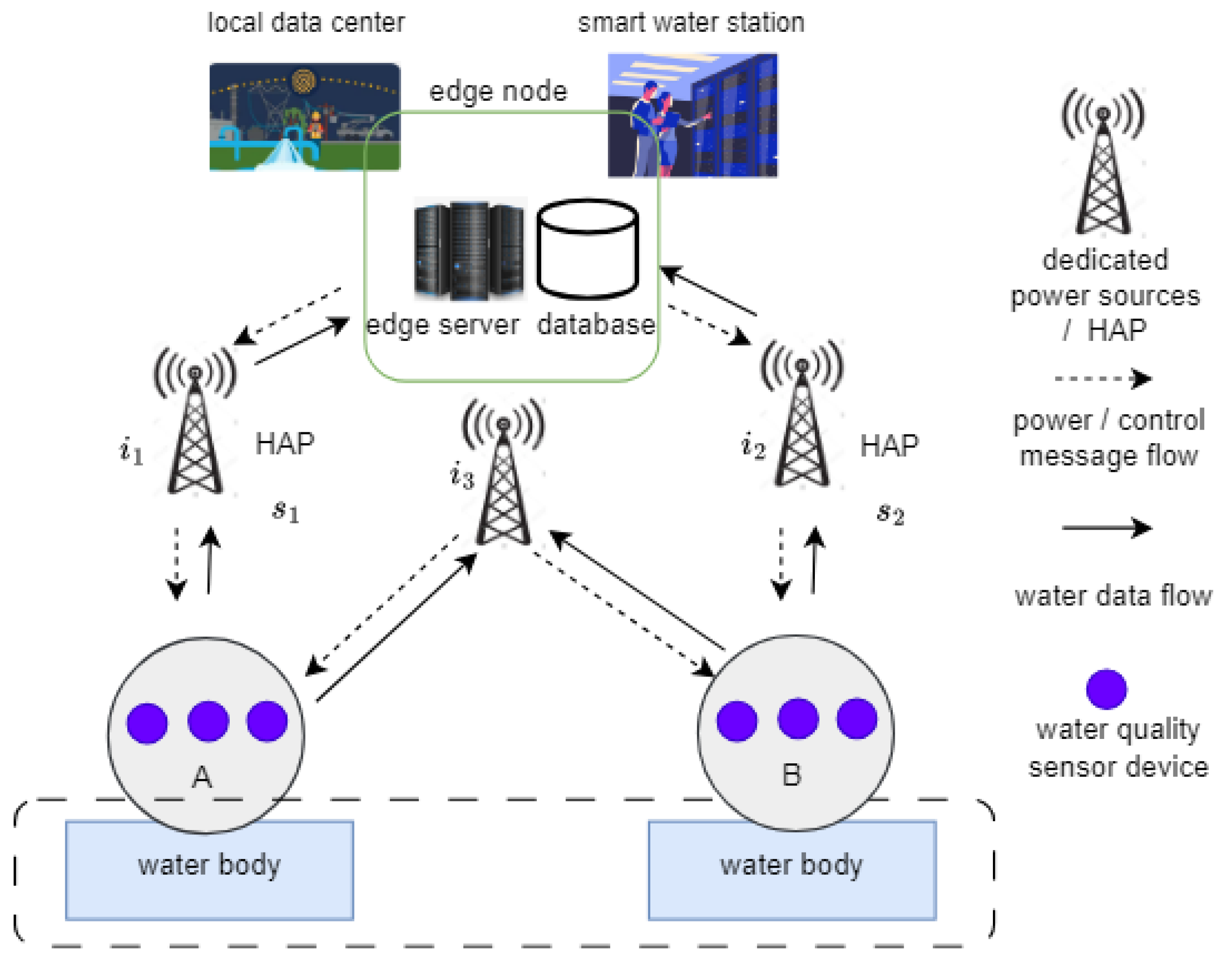
3.1. System Architecture
3.2. System Model
4. Mathematical Model
4.1. Transformation of the Objective Function
4.2. Optimal Solution
| Algorithm 1 Resource Allocation Algorithm |
|
| Algorithm 2 Proposed Dinkelbach-based Iteration Algorithm |
|
4.3. Dynamic HAP Resource Allocation Algorithm
| Algorithm 3 HAP allocation in the WIT Phase |
|
5. Results and Discussions
5.1. Performance Comparison of Different Methods
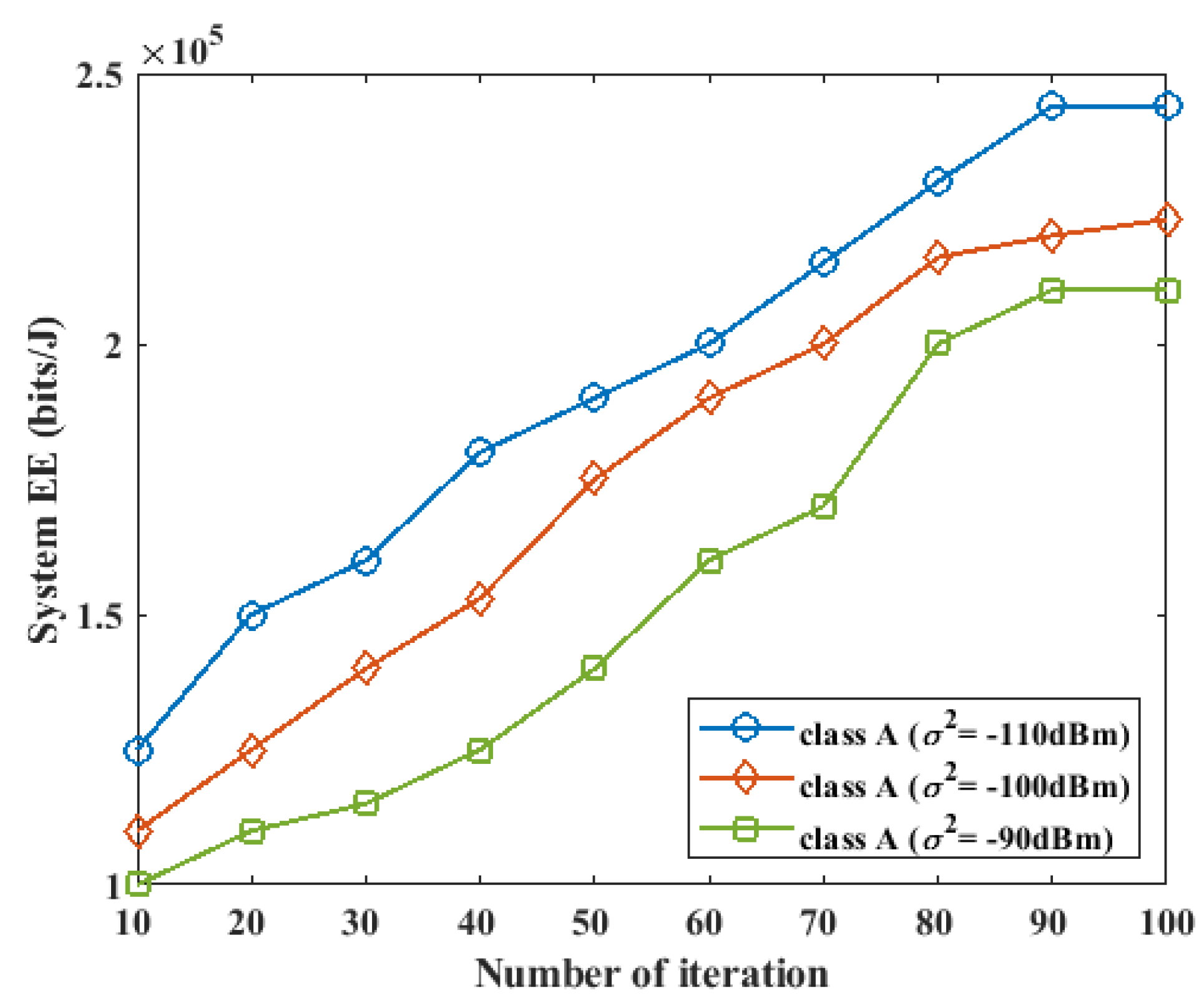
5.2. Impact of Noise Power on Energy Efficiency
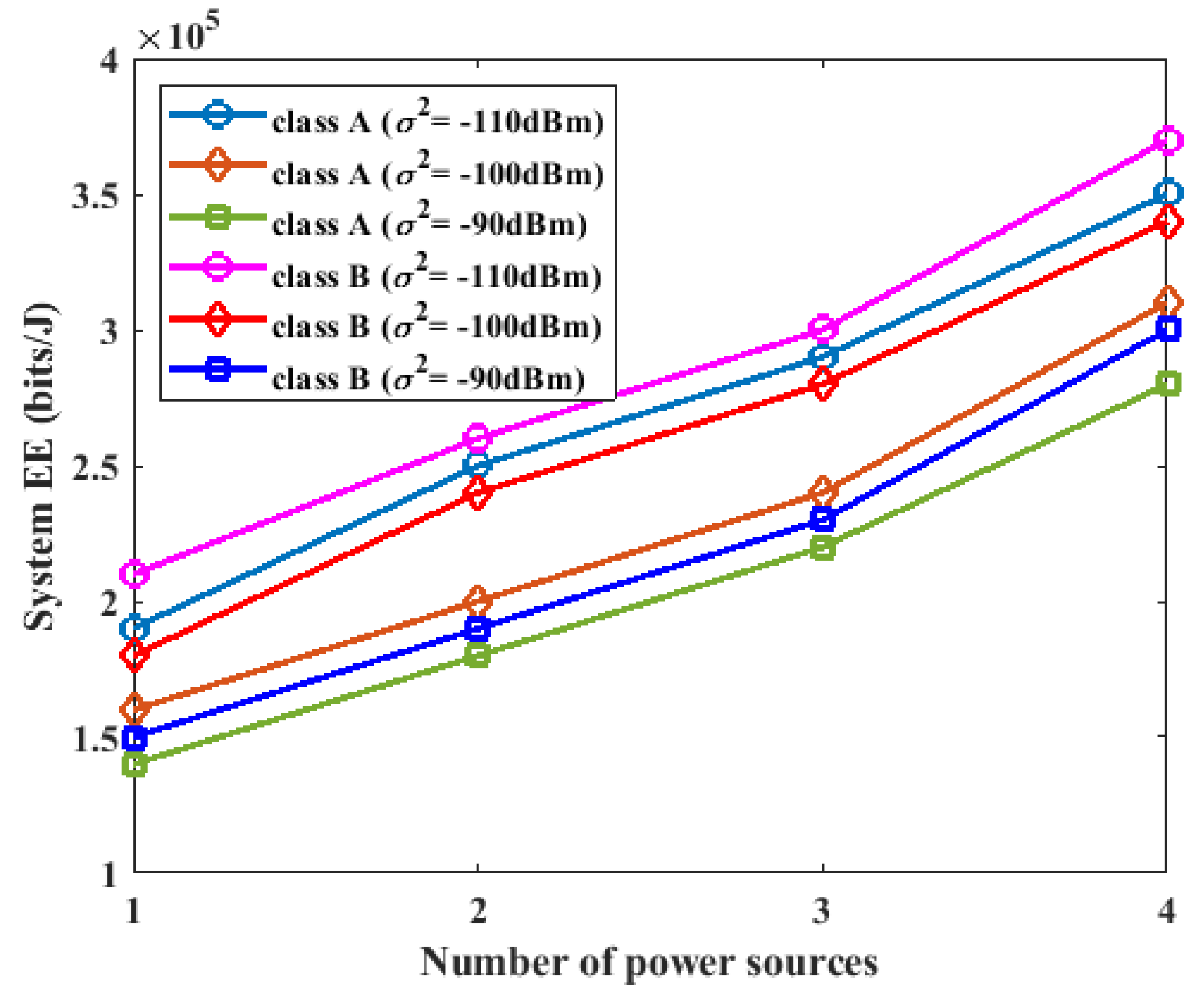
5.3. Effect of the Number of Power Sources on Energy Efficiency
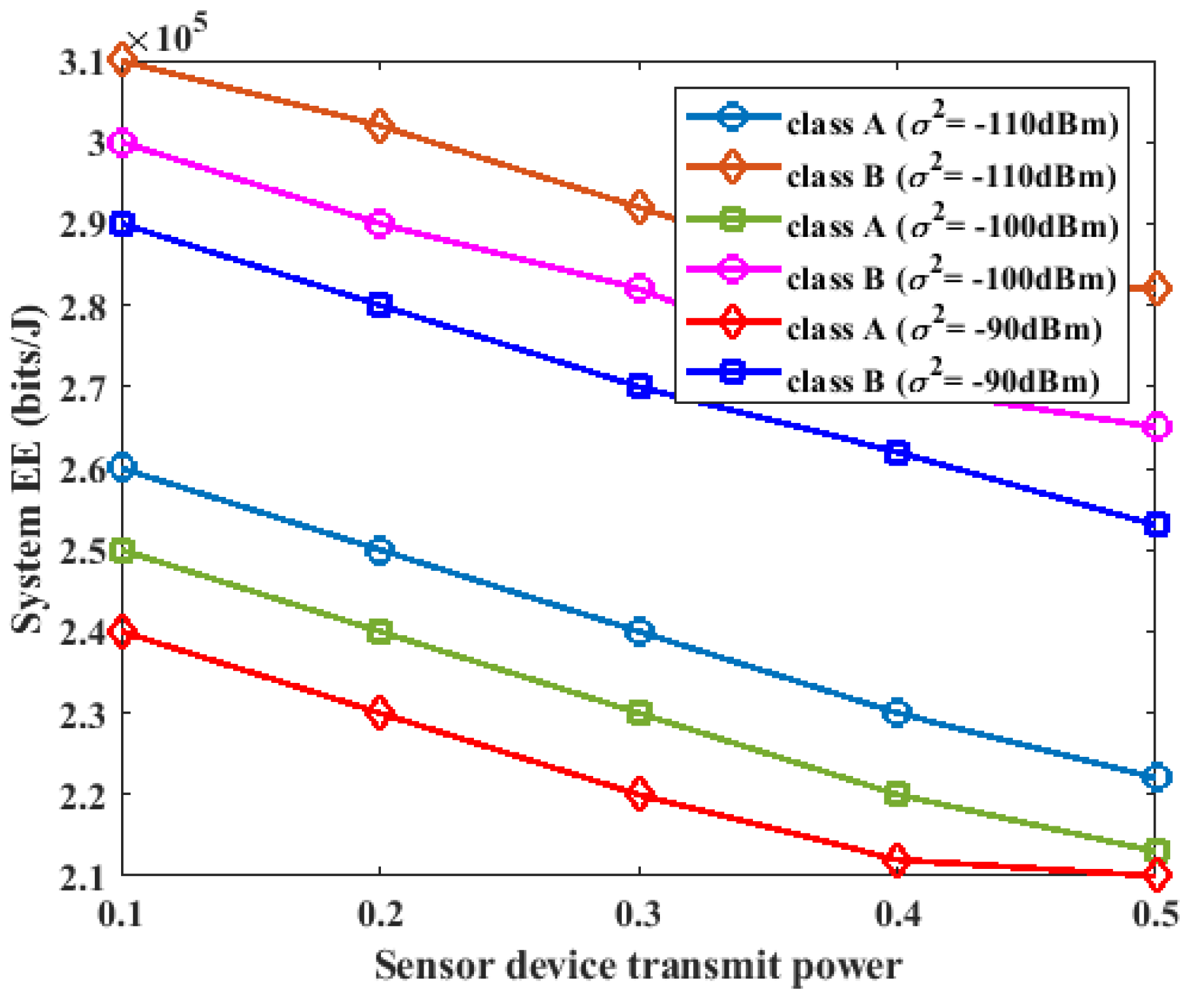
5.4. Impact of Sensor Device Transmit Power on Energy Efficiency
5.5. Impact of QoS Data Requirements on the System EE
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Olatinwo, S.O.; Joubert, T.H. A bibliometric analysis and review of resource management in internet of water things: The use of game theory. Water 2022, 14, 1636. [Google Scholar] [CrossRef]
- Li, J.; Ma, R.; Cao, Z.; Xue, K.; Xiong, J.; Hu, M.; Feng, X. Satellite detection of surface water extent: A review of methodology. Water 2022, 14, 1148. [Google Scholar] [CrossRef]
- Jan, F.; Min-Allah, N.; Düştegör, D. Iot based smart water quality monitoring: Recent techniques, trends and challenges for domestic applications. Water 2021, 13, 1729. [Google Scholar] [CrossRef]
- Radhakrishnan, N.; Pillai, A.S. Comparison of water quality classification models using machine learning. In Proceedings of the 2020 5th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 10–12 June 2020; IEEE: New York, NY, USA, 2020; pp. 1183–1188. [Google Scholar]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef] [PubMed]
- Brown, D. The discovery of water channels (aquaporins). Ann. Nutr. Metab. 2017, 70, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Madni, H.A.; Umer, M.; Ishaq, A.; Abuzinadah, N.; Saidani, O.; Alsubai, S.; Hamdi, M.; Ashraf, I. Water-Quality Prediction Based on H2O AutoML and Explainable AI Techniques. Water 2023, 15, 475. [Google Scholar] [CrossRef]
- du Plessis, A.; du Plessis, A. Global water scarcity and possible conflicts. In Freshwater Challenges of South Africa and Its Upper Vaal River: Current State and Outlook; Springer: Cham, Switzerland, 2017; pp. 45–62. [Google Scholar]
- Van Vliet, M.T.; Jones, E.R.; Flörke, M.; Franssen, W.H.; Hanasaki, N.; Wada, Y.; Yearsley, J.R. Global water scarcity including surface water quality and expansions of clean water technologies. Environ. Res. Lett. 2021, 16, 024020. [Google Scholar] [CrossRef]
- Doaemo, W.; Betasolo, M.; Montenegro, J.F.; Pizzigoni, S.; Kvashuk, A.; Femeena, P.V.; Mohan, M. Evaluating the Impacts of Environmental and Anthropogenic Factors on Water Quality in the Bumbu River Watershed, Papua New Guinea. Water 2023, 15, 489. [Google Scholar] [CrossRef]
- Devane, M.L.; Moriarty, E.; Weaver, L.; Cookson, A.; Gilpin, B. Fecal indicator bacteria from environmental sources; strategies for identification to improve water quality monitoring. Water Res. 2020, 185, 116204. [Google Scholar] [CrossRef]
- Li, P.; Wu, J. Drinking water quality and public health. Expo. Health 2019, 11, 73–79. [Google Scholar] [CrossRef]
- Li, P. Groundwater quality in western China: Challenges and paths forward for groundwater quality research in western China. Expo. Health 2016, 8, 305–310. [Google Scholar] [CrossRef]
- Villar Miguelez, C.; Monzon Baeza, V.; Parada, R.; Monzo, C. Guidelines for Renewal and Securitization of a Critical Infrastructure Based on IoT Networks. Smart Cities 2023, 6, 728–743. [Google Scholar] [CrossRef]
- Khatri, P.; Gupta, K.K.; Gupta, R.K. Assessment of water quality parameters in real-time environment. SN Comput. Sci. 2020, 1, 340. [Google Scholar] [CrossRef]
- Aranda, J.; Mendez, D.; Carrillo, H. Multimodal wireless sensor networks for monitoring applications: A review. J. Circuits Syst. Comput. 2020, 29, 2030003. [Google Scholar] [CrossRef]
- Martínez, R.; Vela, N.; El Aatik, A.; Murray, E.; Roche, P.; Navarro, J.M. On the use of an IoT integrated system for water quality monitoring and management in wastewater treatment plants. Water 2020, 12, 1096. [Google Scholar] [CrossRef]
- Olatinwo, D.D.; Abu-Mahfouz, A.M.; Hancke, G.P. Towards achieving efficient MAC protocols for WBAN-enabled IoT technology: A review. EURASIP J. Wirel. Commun. Netw. 2021, 2021, 60. [Google Scholar] [CrossRef]
- Olatinwo, S.O.; Joubert, T.H. Deep Learning for Resource Management in Internet of Things Networks: A Bibliometric Analysis and Comprehensive Review; Institute of Electrical and Electronics Engineers: Los Alamitos, CA, USA, 2022. [Google Scholar]
- Ji, L.; Guo, S. Energy-efficient cooperative resource allocation in wireless-powered mobile edge computing. IEEE Internet Things J. 2018, 6, 4744–4754. [Google Scholar] [CrossRef]
- Ahmed, M.; Alshahrani, H.M.; Alruwais, N.; Asiri, M.M.; Al Duhayyim, M.; Khan, W.U.; Nauman, A.; Khurshaid, T. Joint optimization of UAV-IRS placement and resource allocation for wireless powered mobile edge computing networks. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101646. [Google Scholar] [CrossRef]
- Sun, M.; Xu, X.; Huang, Y.; Wu, Q.; Tao, X.; Zhang, P. Resource management for computation offloading in D2D-aided wireless powered mobile-edge computing networks. IEEE Internet Things J. 2020, 8, 8005–8020. [Google Scholar] [CrossRef]
- Cao, L.; Yue, Y.; Zhang, Y. A data collection strategy for heterogeneous wireless sensor networks based on energy efficiency and collaborative optimization. Comput. Intell. Neurosci. 2021, 2021, 9808449. [Google Scholar] [CrossRef]
- Sun, X.; Su, Y.; Huang, Y.; Tan, J.; Yi, J.; Hu, T.; Zhu, L. Edge computing-based ERBS time synchronization algorithm in WSNs. Wirel. Commun. Mob. Comput. 2020, 2020, 8840367. [Google Scholar] [CrossRef]
- Zeng, X. Game theory-based energy efficiency optimization model for the Internet of Things. Comput. Commun. 2022, 183, 171–180. [Google Scholar] [CrossRef]
- Olatinwo, S.O.; Joubert, T.H. Energy efficiency maximization in a wireless powered IoT sensor network for water quality monitoring. Comput. Netw. 2020, 176, 107237. [Google Scholar] [CrossRef]
- Ansere, J.A.; Kamal, M.; Gyamfi, E.; Sam, F.; Tariq, M.; Mohammed, A. Energy efficient resource optimization in cooperative Internet of Things networks. Internet Things 2020, 12, 100302. [Google Scholar] [CrossRef]
- Ji, B.; Song, K.; Li, C.; Zhu, W.P.; Yang, L. Energy harvest and information transmission design in internet-of-things wireless communication systems. AEU-Int. J. Electron. Commun. 2018, 87, 124–127. [Google Scholar] [CrossRef]
- DWAF. South African Water Quality Guidelines: Volume 1: Domestic Water Use; Department of Water Affairs and Forestry: Pretoria, South Africa, 1996.
- World Health Organization Guidelines for Drinking-Water Quality; World Health Organization: Geneva, Switzerland, 2004; Volume 1.
- World Health Organization Manganese in Drinking-Water: Background Document for Development of WHO Guidelines for Drinking-Water Quality; Technical Documents; World Health Organization: Geneva, Switzerland, 2004.
- Tyagi, S.; Sharma, B.; Singh, P.; Dobhal, R. Water quality assessment in terms of water quality index. Am. J. Water Resour. 2013, 1, 34–38. [Google Scholar] [CrossRef]
- Vamvakas, P.; Tsiropoulou, E.E.; Papavassiliou, S.; Baras, J.S. Optimization and resource management in NOMA wireless networks supporting real and non-real time service bundling. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; IEEE: New York, NY, USA, 2017; pp. 697–703. [Google Scholar]
- Salh, A.; Shah, N.S.M.; Audah, L.; Abdullah, Q.; Jabbar, W.A.; Mohamad, M. Energy-efficient power allocation and joint user association in multiuser-downlink massive MIMO system. IEEE Access 2019, 8, 1314–1326. [Google Scholar] [CrossRef]
- Dinkelbach, W. On nonlinear fractional programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Energy-efficient resource allocation for secure OFDMA systems. IEEE Trans. Veh. Technol. 2012, 61, 2572–2585. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]






| Reference | Contribution of Related Works | Contribution of the Proposed Work |
|---|---|---|
| [20] | The authors designed a resource allocation algorithm to manage edge computation resource allocation in a network where all IoT devices participate in data transmission in the same cycle. | Unlike [20], we introduced a dynamic resource allocation method and an optimization-based method to jointly optimize energy harvesting and data transmission in a sequential multi-class WPCN, where each class of sensors operates sequentially to improve the overall system energy efficiency. |
| [21] | The authors designed a wireless- powered network where IoT devices perform complex tasks. Additionally, IoT devices can only send their data to a single base station. | Contrary to [21], we shifted complex tasks from IoT devices to reduce energy consumption. Additionally, we contributed a dynamic resource allocation method to optimally allocate multiple hybrid access points to improve system energy efficiency. |
| [22] | The authors designed a resource management scheme to offload computations in the network IoT devices concurrently. | Unlike [22], we introduced a sequential multi-class WPCN strategy for offloading computations in a sequential manner. Additionally, we contributed a dynamic resource allocation method to improve the overall system energy efficiency. |
| [25] | The authors designed a game theory-based resource allocation method to improve energy efficiency in cooperative network settings. | Unlike [25], we proposed a dynamic resource allocation method and an optimization-based method to jointly optimize the allocation of system resources to improve the overall system energy efficiency in sequential multi-class WPCN settings. |
| [26] | The authors designed a wireless- powered communication network with only one hybrid access point. | Different from [26], we contributed a sequential multi-class WPCN with dynamically allocated hybrid access points to improve energy efficiency. |
| [27] | The authors designed a wireless- powered cooperative IoT network where devices transmit data in the same cycle. | Different from [27], we contributed a sequential multi-class WPCN where devices transmit data in different cycles to improve energy efficiency. |
| [28] | The authors designed a wireless- powered communication network where IoT devices uses a multi-hop communication strategy to communi- cate with a single base station. | Contrary to [28], we contributed a sequential multi-class WPCN where IoT devices uses single-hop communication to communicate with dynamically allocated hybrid access points to improve energy efficiency. |
| Requirement | Range |
|---|---|
| pH sensor | 0–14 |
| Conductivity sensor | 100 μS/cm–200 mS/cm |
| E. coli sensor | 1–1000 CFU/100 mL |
| Residual chlorine sensor | 0–10 mg/L |
| Dissolved oxygen sensor | 0–20 mg/L |
| Transmitter/HAP | 1 W–3 W |
| Edge node | ≤5 m from HAPs |
| ZigBee radio | Above 100 m |
| Acronymn | Definition |
|---|---|
| IoT | Internet of Things |
| NOMA | Non-orthogonal multiple access |
| HAP | Hybrid access point |
| WEH | Wireless energy transfer |
| WIT | Wireless information transfer |
| Time slot for wireless information transfer | |
| Time slot for wireless energy transfer | |
| and | Downlink communication channel gains |
| and | Uplink communication channel gains |
| HAP transmission power | |
| SIC | Successive interference cancellation |
| B | System’s bandwidth |
| DL | Downlink |
| UL | Uplink |
| Power sources | |
| Energy harvested by K sensor devices | |
| Energy harvested by L sensor devices | |
| Energy used by each sensor device k for UL data transfer | |
| Energy used by each sensor device l for UL data transfer |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olatinwo, S.O.; Joubert, T.H. Resource Allocation Optimization in IoT-Enabled Water Quality Monitoring Systems. Sensors 2023, 23, 8963. https://doi.org/10.3390/s23218963
Olatinwo SO, Joubert TH. Resource Allocation Optimization in IoT-Enabled Water Quality Monitoring Systems. Sensors. 2023; 23(21):8963. https://doi.org/10.3390/s23218963
Chicago/Turabian StyleOlatinwo, Segun O., and Trudi H. Joubert. 2023. "Resource Allocation Optimization in IoT-Enabled Water Quality Monitoring Systems" Sensors 23, no. 21: 8963. https://doi.org/10.3390/s23218963
APA StyleOlatinwo, S. O., & Joubert, T. H. (2023). Resource Allocation Optimization in IoT-Enabled Water Quality Monitoring Systems. Sensors, 23(21), 8963. https://doi.org/10.3390/s23218963






