Research on Three-Dimensional Shape Curve Reconstruction Technology for a Scraper Conveyor on an Intelligent Working Face
Abstract
:1. Introduction
2. Principle of the Analysis and Perception of a Scraper Conveyor’s Shape Curve
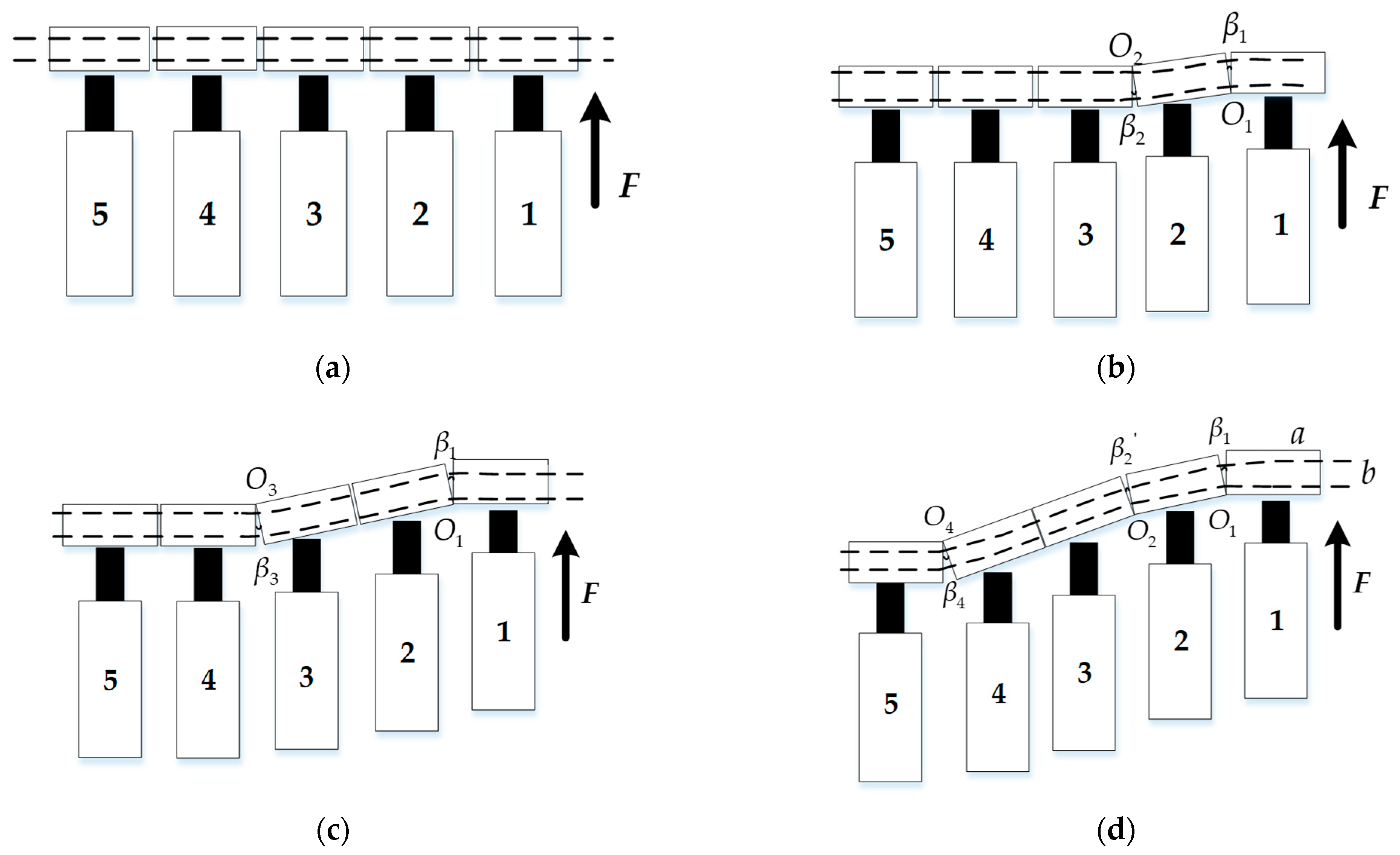
2.1. The Analysis of a Scraper Conveyor’s Shape Curve
2.2. The Principle of the Perception of the Scraper Conveyor’s Shape Curve
2.2.1. The Principle of FBG Strain Sensing
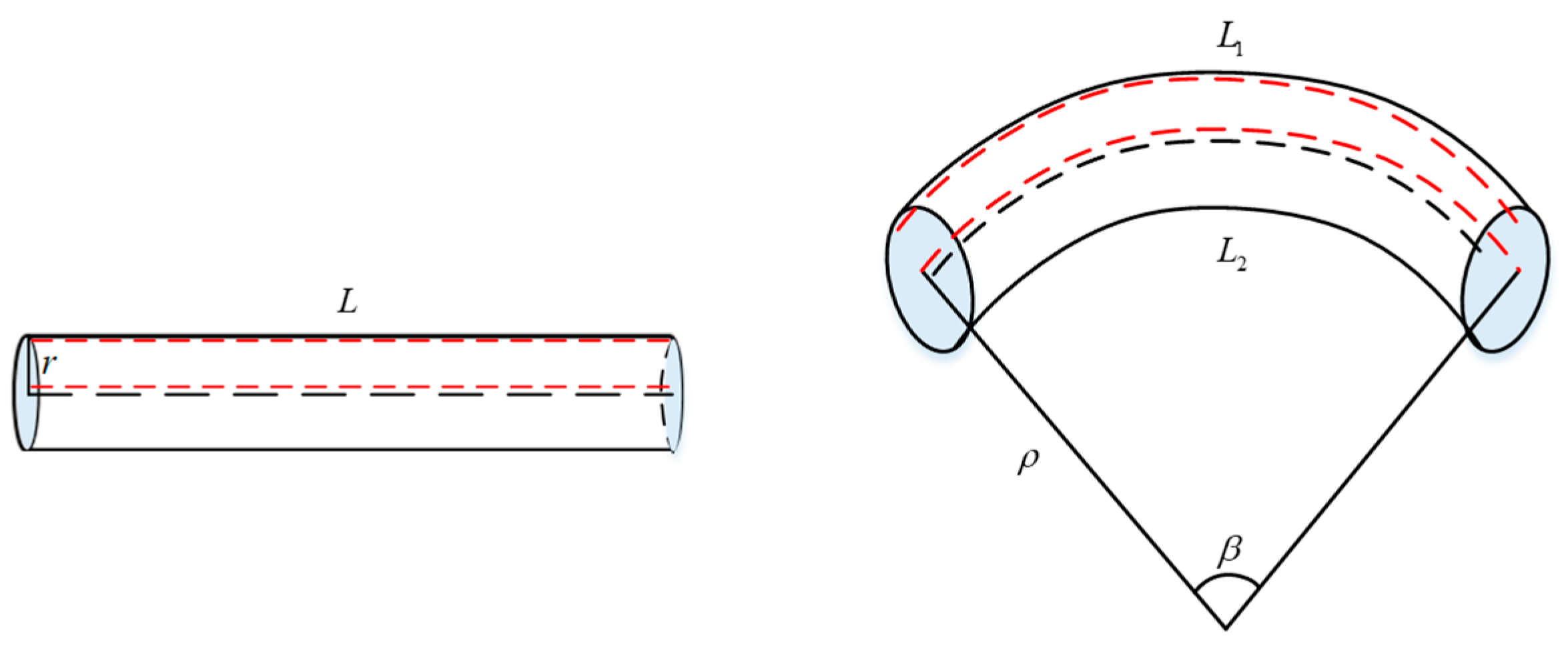
2.2.2. The Fundamental Principle of Spatial Curvature Perception
3. The Key Technology of the Shape Curve Reconstruction of a Scraper Conveyor
3.1. A Shape Curve Reconstruction Method Based on the Discrete Curvature
3.2. Research on the Discrete Curvature Continuation Method
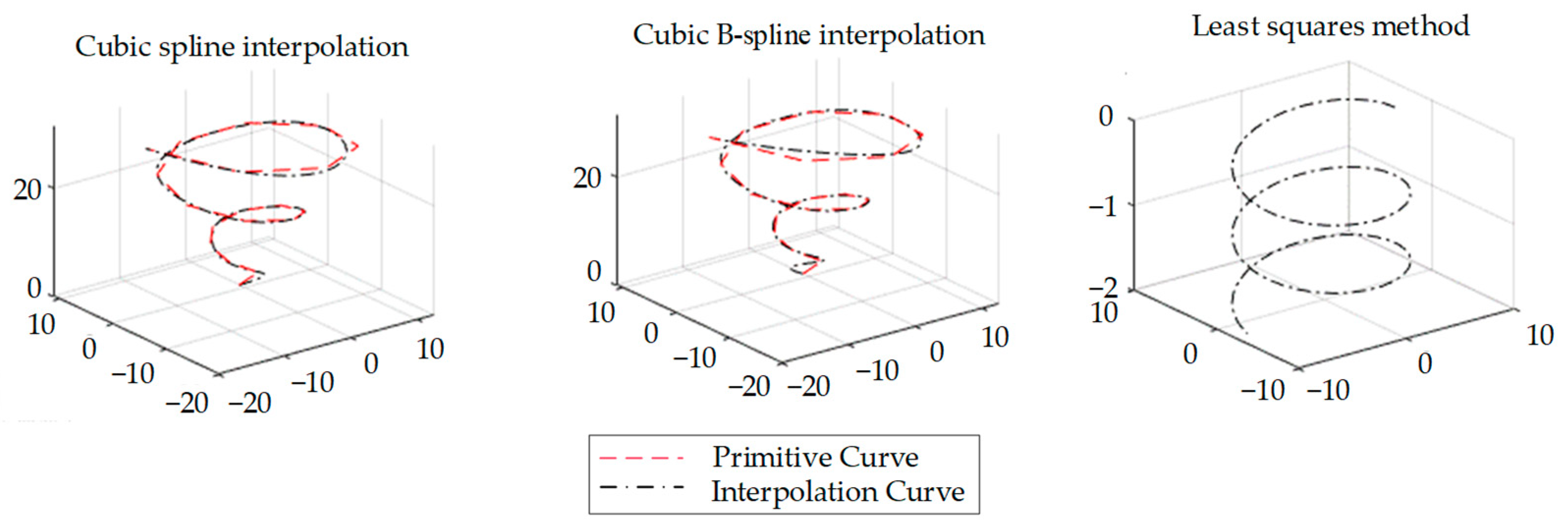
3.2.1. Analysis of the Interpolation and Fitting Methods
3.2.2. Effect Evaluation for the Interpolation and Fitting Methods
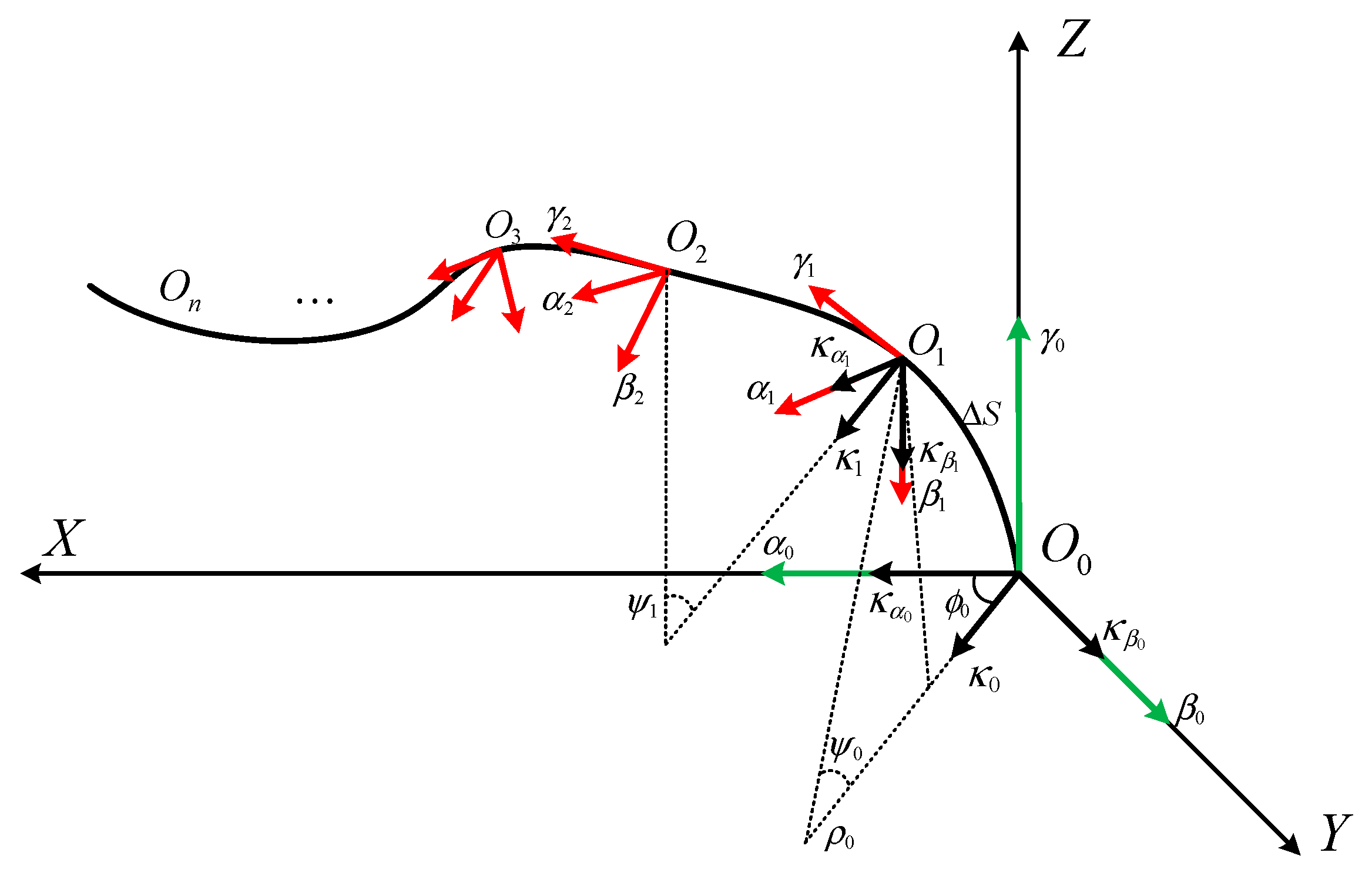
3.3. An Algorithm for Spatial Curve Reconstruction Based on the Frenet Moving Frame
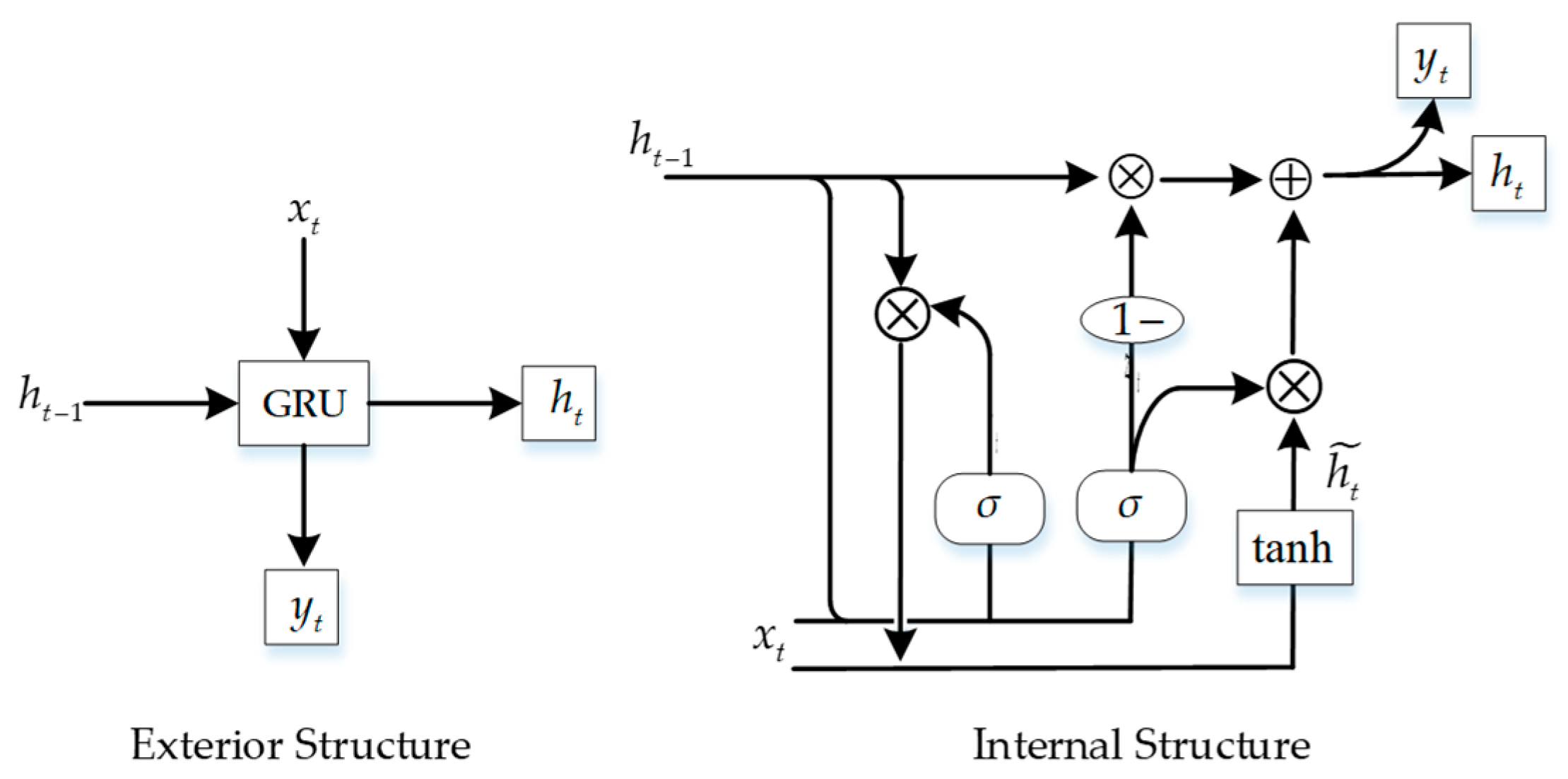
3.4. The Shape Curve Prediction Model for a Scraper Conveyor Based on the GRU
3.4.1. Establishment of the GRU Model
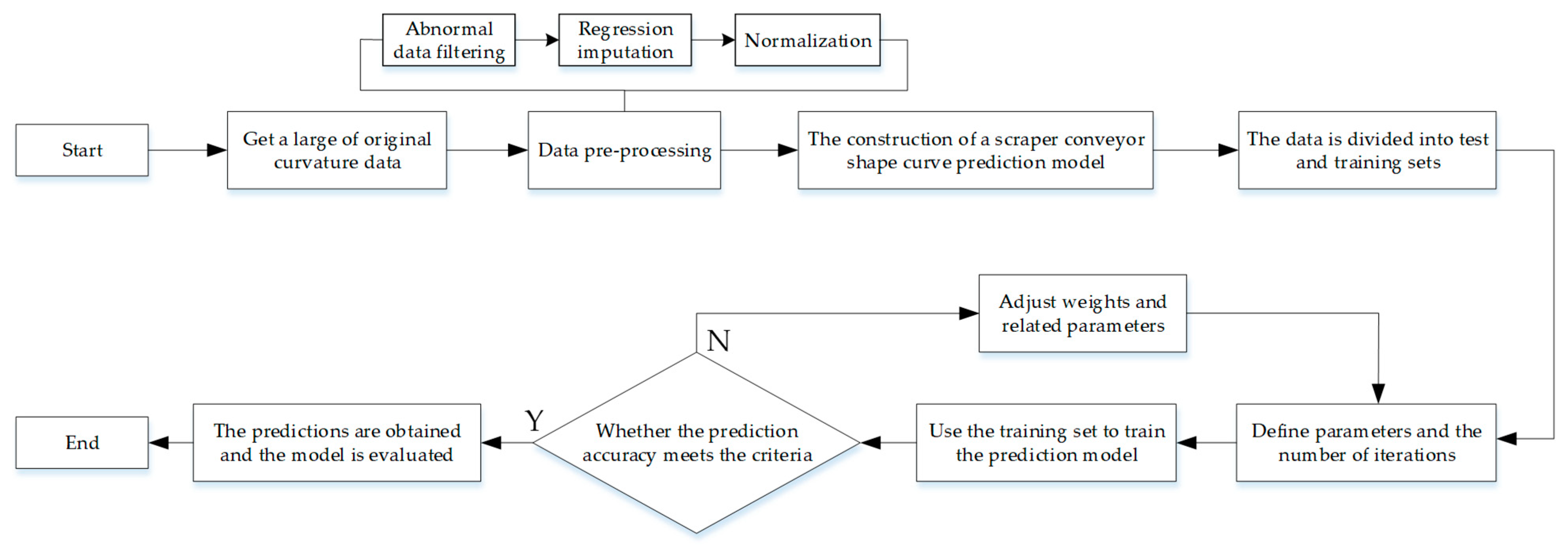
3.4.2. The Prediction and Interpolation Process for the Scraper Conveyor’s Shape Curve
4. The Experimental Testing and Analysis of the Shape Curve Reconstruction Algorithm
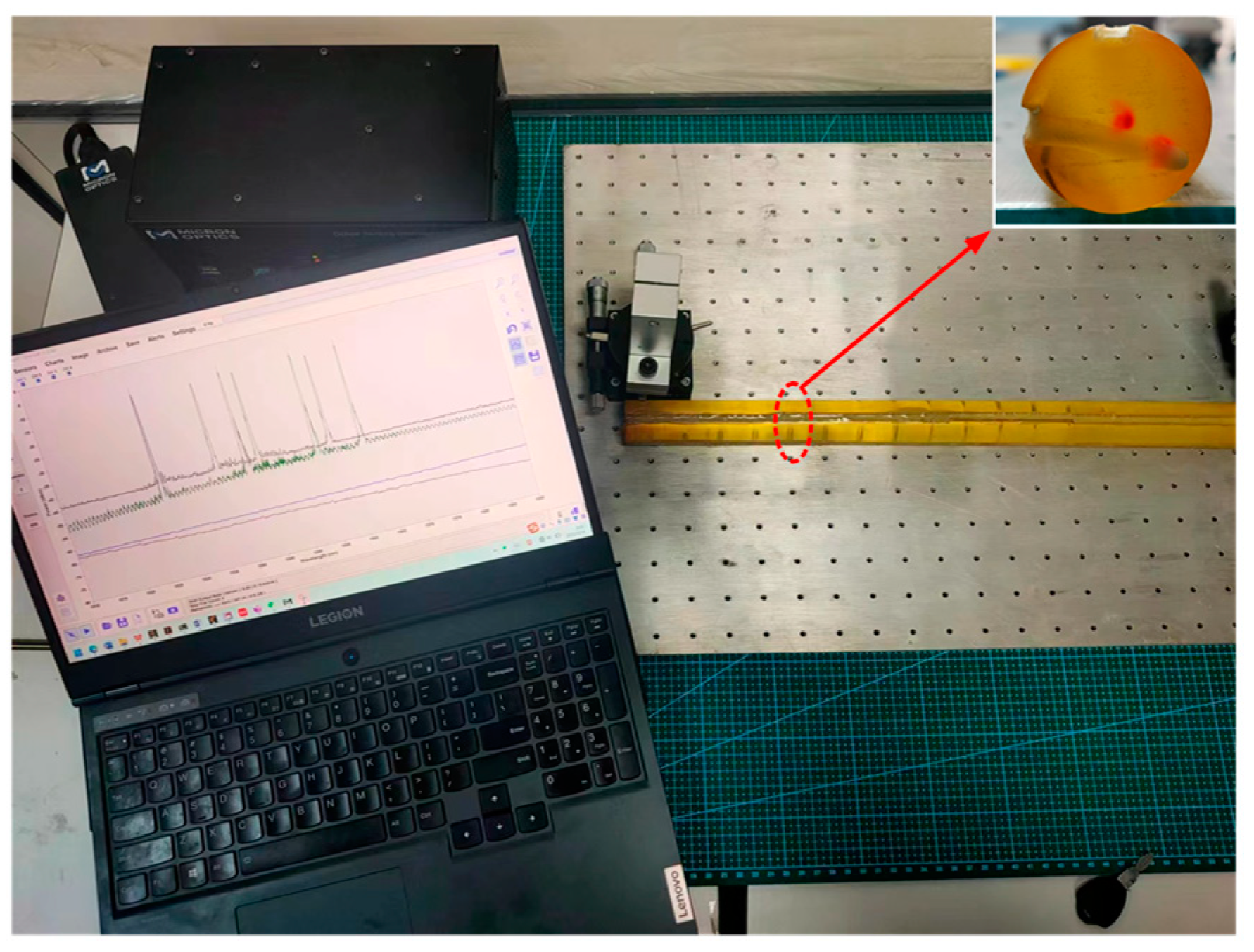
4.1. Construction of an Experimental Platform for the Reconstruction Algorithm
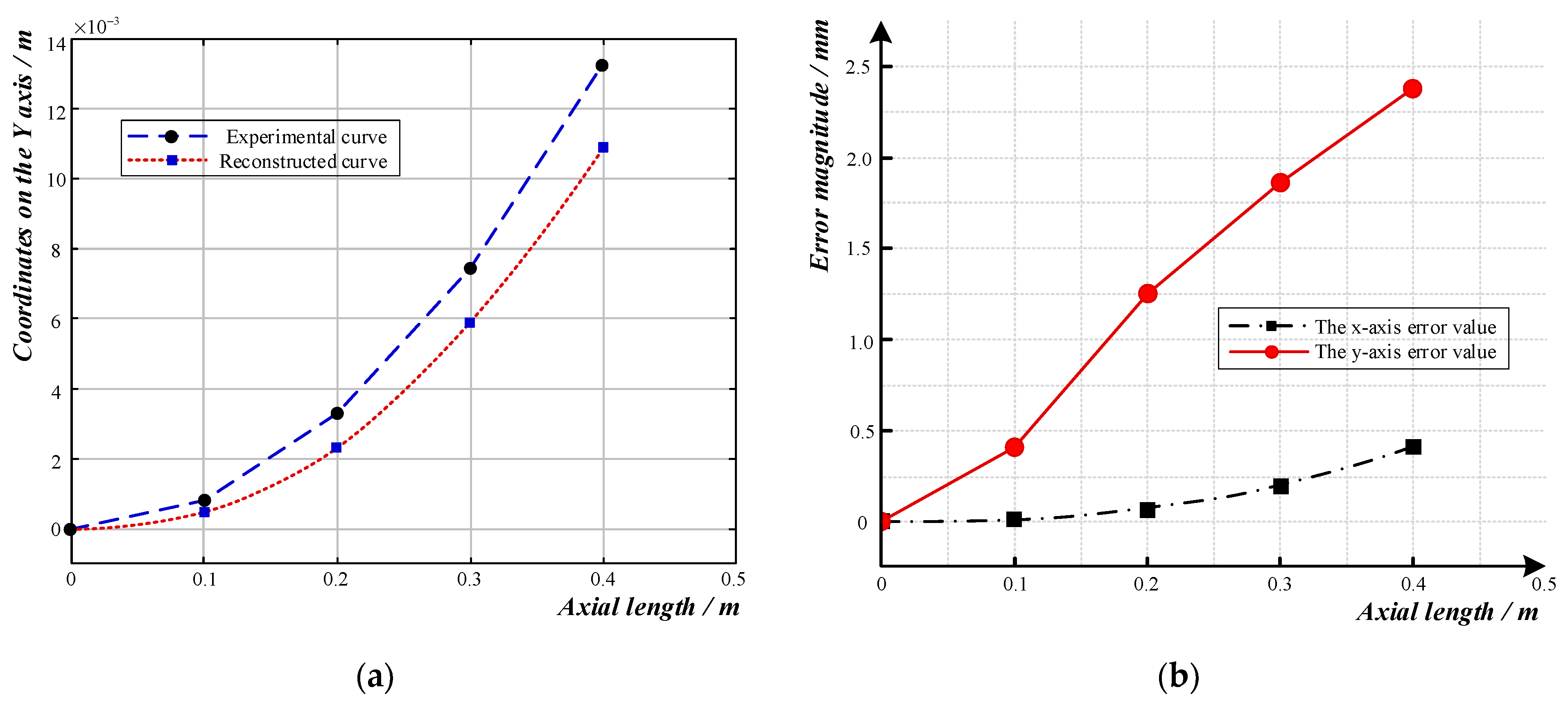
4.2. The Experiment on Shape Curve Reconstruction
5. Conclusions
- A spatial curvature perception theory for a three-dimensional curvature sensor involving FBG is proposed, and a mathematical model that included the central wavelength variation of the FBG, strain, and spatial curvature was established, which established a foundation for the reconstruction of the shape curve of a scraper conveyor.
- The cubic B-spline interpolation method produced a better result when used to continuously interpolate a standard conic curve. The spatial curve reconstruction algorithm based on the Frenet moving frame was able to reconstruct the curve in a fixed coordinate system.
- The shape curve of a scraper conveyor was accurately reconstructed using the prediction model, which was based on the fundamental principle of the GRU model, even if some grating measuring points were damaged over time.
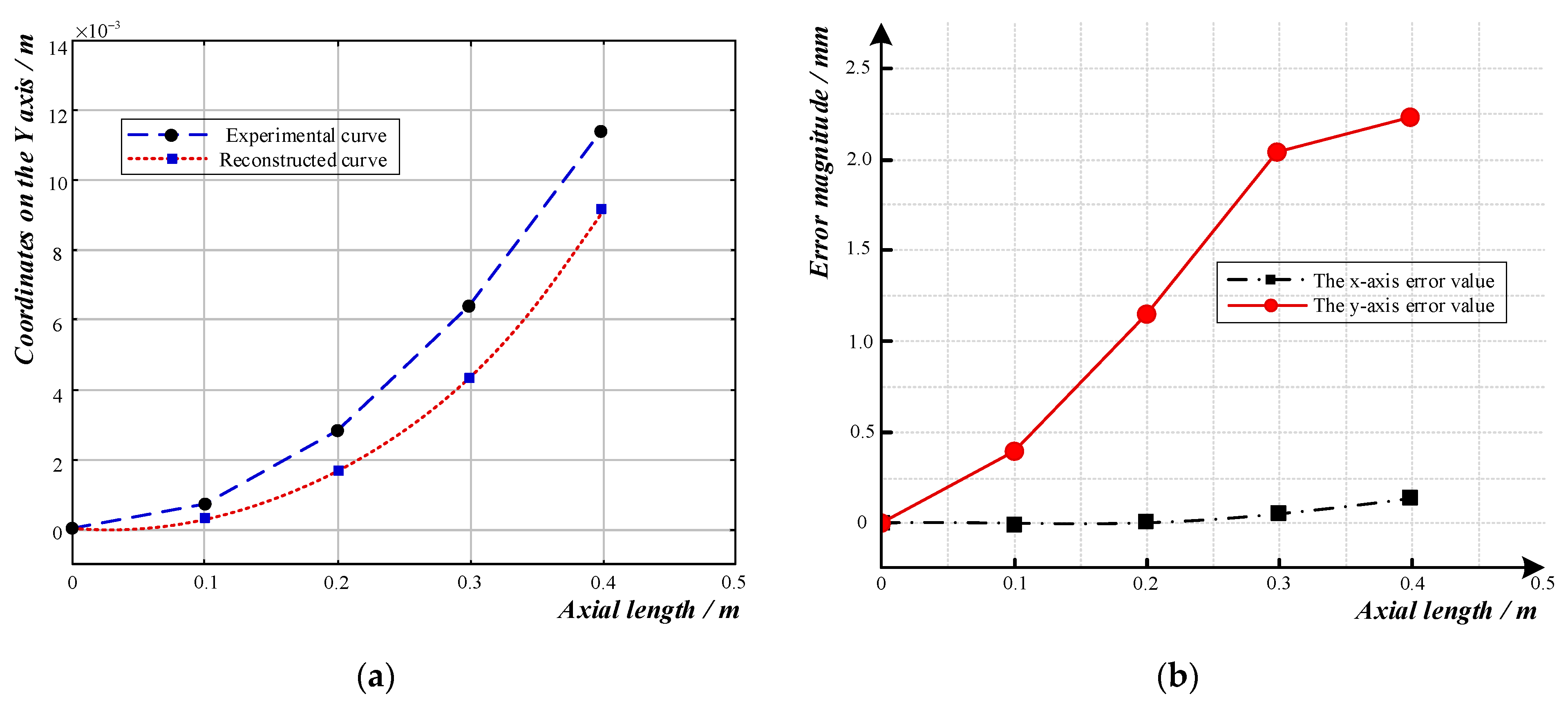
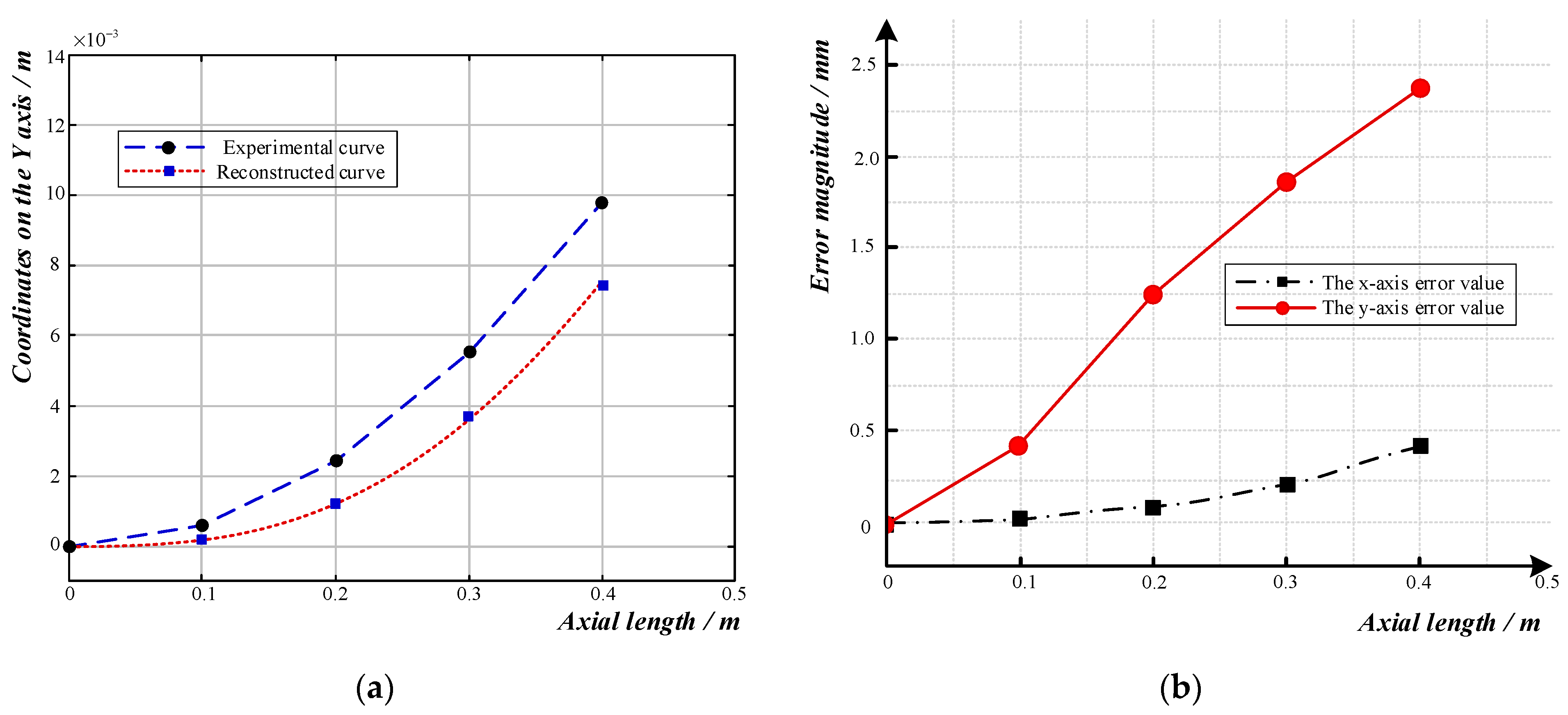
- Indoor experiments showed that the reconstruction curves obtained with the reconstruction algorithm were essentially consistent with the actual shape when the curvature radius of the three-dimensional sensor involving fiber grating was 6 m, 7 m, or 8 m, which proved that the reconstruction algorithm is feasible in practical application.
- During the ‘S’-shaped bending experiment, due to the excessive bending strain on the substrate, the FBG was pulled off. Therefore, based on the principle of symmetry, half of the ‘S’-shaped data were selected for the bending experiment, thus reducing the reliability. There are limitations, and further research is needed to improve this experiment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, G.; Xu, Y.; Ren, H. Intelligent and ecological coal mining as well as clean utilization technology in China: Review and prospects. Int. J. Min. Sci. Technol. 2019, 29, 161–169. [Google Scholar] [CrossRef]
- Lu, E.; Li, W.; Yang, X.; Xu, S. Composite Sliding Mode Control of a Permanent Magnet Direct-Driven System for a Mining Scraper Conveyor. IEEE Access 2017, 5, 22399–22408. [Google Scholar] [CrossRef]
- Einicke, G.A.; Ralston, J.C.; Hargrave, C.O.; Reid, D.C.; Hainsworth, D.W. Longwall mining automation an application of minimum-variance smoothing [Applications of Control]. IEEE Control. Syst. Mag. 2008, 28, 28–37. [Google Scholar] [CrossRef]
- Barter, B. Failure Detection in Longwall Armored Face Conveyors. Fail. Detect. 2011, 2, 158–166. [Google Scholar]
- Kelly, M.S.; Hainsworth, D.W. The Landmark Longwall Automation Project; Acarp project, Report C10100A; CSIRO Exploration & Mining: Perth, Australia, 2005. [Google Scholar]
- Fan, Q.; Li, W.; Hui, J.; Wu, L.; Yu, Z.; Yan, W.; Zhou, L. Integrated Positioning for Coal Mining Machinery in Enclosed Underground Mine Based on SINS/WSN. Sci. World J. 2014, 2014, 460415. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Yang, H.; Xia, T. Research on the Compensation Strategy of the Initial Alignment of the SINS Based on the Dynamic Model of the Shearer. IEEE Access 2019, 7, 36736–36747. [Google Scholar] [CrossRef]
- Kelly, M.; Hainsworth, D.; Caris, C.; Reid, D.; Gurgenci, H. Progress towards longwall automation. In Proceedings of the 5th International Symposium on Mining Science & Technology, Xuzhou, China, 20–22 October 2004. [Google Scholar]
- Zhang, Z.; Wang, S.; Zhang, B.; Li, A. Shape detection of scraper conveyor based on shearer trajectory. J. China Coal Soc. 2015, 40, 2514–2521. [Google Scholar] [CrossRef]
- Hao, S.; Wang, S.; Malekian, R.; Zhang, B.; Liu, W.; Li, Z. A Geometry Surveying Model and Instrument of a Scraper Conveyor in Unmanned Longwall Mining Faces. IEEE Access 2017, 5, 4095–4103. [Google Scholar] [CrossRef]
- Shibo, W.; Boyuan, Z.; Shijia, W.; Shirong, G. Dynamic Precise Positioning Method of Shearer Based on Closing Path Optimal Estimation Model. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1468–1475. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S. Improving the Shearer Positioning Accuracy Using the Shearer Motion Constraints in Longwall Panels. IEEE Access 2020, 8, 52466–52474. [Google Scholar] [CrossRef]
- Xie, J.; Yang, Z.; Wang, X.; Wang, S.; Zhang, Q. A Joint Positioning and Attitude Solving Method for Shearer and Scraper Conveyor under Complex Conditions. Math. Probl. Eng. 2017, 2017, 3793412. [Google Scholar] [CrossRef]
- Li, S.; Xie, J.; Ren, F.; Zhang, X.; Wang, X.; Wang, B. Virtual straightening of scraper conveyor based on the position and attitude solution of industrial robot model. Int. J. Coal Sci. Technol. 2021, 8, 1149–1170. [Google Scholar] [CrossRef]
- Niu, J. Research of Straightness Control System of Fully-mechanized Coal Mining Face. J. Mine Autom. 2015, 41, 4. [Google Scholar]
- Niu, J. Study on Automatic and Intelligent Following Control System of Hydraulic Powered Support in Fully-mechanized Coal Mining Face. Coal Sci. Technol. 2015, 43, 85–91. [Google Scholar]
- Liu, P.; Wang, C. Straightness Measurement Algorithm Based on Machine Vision for Coal Longwall Face. J. Min. Sci. Technol. 2017, 7, 267–273. [Google Scholar]
- Lv, J.; Shi, P.; Wan, Z.; Cheng, J.; Xing, K.; Wang, M.; Gou, H. Research on a Real-Time Monitoring Method for the Three-Dimensional Straightness of a Scraper Conveyor Based on Binocular Vision. Mathematics 2022, 10, 3545. [Google Scholar] [CrossRef]
- Xie, J.-C.; Yang, Z.-J.; Wang, X.-W.; Wang, S.-P.; Zhang, Q. Cooperative solving method of chute postures in the bending section of a scraper conveyor. Adv. Mech. Eng. 2018, 10, 1687814018767684. [Google Scholar] [CrossRef]
- Zhang, F.; Li, C.; Li, H. Study on straightness monitoring method of scraper conveyor in intelligent fully mechanized mining face. Coal Sci. Technol. 2022, 50, 246–255. [Google Scholar] [CrossRef]
- Liang, M.; Fang, X.; Li, S.; Wu, G.; Ma, M.; Zhang, Y. A fiber Bragg grating tilt sensor for posture monitoring of hydraulic supports in coal mine working face. Measurement 2019, 138, 305–313. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y.; Li, C.; Wan, Z.; Li, Y.; Wang, K.; Xu, J. Monitoring of coal mine roadway roof separation based on fiber Bragg grating displacement sensors. Int. J. Rock Mech. Min. Sci. 2015, 74, 128–132. [Google Scholar] [CrossRef]
- Wu, G.; Qiao, F.; Fang, X.; Liang, M.; Song, Y. Straightness Perception Mechanism of Scraper Conveyor Based on the Three-Dimensional Curvature Sensing of FBG. Appl. Sci. 2023, 13, 3619. [Google Scholar] [CrossRef]
- Fang, X.; Feng, H.; Liang, M.; Chen, N.; Lu, N.; Wu, G.; Li, S.; Song, Y. Research on Key Technologies of Fiber Bragg Grating Intelligent Sensing and Safety Decision in Coal Mining. China Coal 2022, 48, 46–56. [Google Scholar]
- Fang, X.; Ning, Y.; Li, S.; Liang, M.; Wu, G.; Gu, C. Research on Key Technique of Straightness Perception of Scraper Conveyor Based on Fiber Grating Mining. Coal Sci. Technol. 2019, 47, 152–158. [Google Scholar]
- Chen, N.; Fang, X.; Feng, H.; Liang, M.; Wu, G.; Song, Y.; Zhang, F. Scraper conveyor shape sensing technology based on orthogonal optical fiber strain. Meas. Sci. Technol. 2023, 34, 125103. [Google Scholar] [CrossRef]
- Song, Y.; Fang, X.; Wu, G.; Chen, N.; Liang, M.; Xu, Z.; Zhang, F. Research on Straightness Perception Compensation Model of FBG Scraper Conveyor Based on Rotation Error Angle. Sensors 2022, 22, 6399. [Google Scholar] [CrossRef]
- Mei, X.; Huang, J. Differential Geometrythe, 4th ed.; Higher Education Press: Beijing, China, 2008. [Google Scholar]
- Zhu, X.; Ji, L.; Zhang, H.; Jin, X.; Yi, J. Analysis of 3D Curve Reconstruction Method Using Orthogonal Curvatures. J. Basic Sci. Eng. 2011, 19, 9. [Google Scholar]
- Wang, J.; Cao, J.; You, J. Logging Curve Reconstruction Based on GRU Neural Network. Oil Geophys. Prospect. 2020, 55, 510–520+468. [Google Scholar] [CrossRef]



| Methods | Advantages | Disadvantages |
|---|---|---|
| Third-order spline interpolation method | 1. This method can produce smooth interpolation curves with good shape-fitting capabilities; 2. This method can reduce error in high-data-point-density cases. | 1. This method requires a lot of calculation, and the time increases significantly for large-scale datasets; 2. In the event of jumps or mutations between data points, the interpolation may not be accurate. |
| Cubic B-spline interpolation method | 1. This method is better at handling data mutation and discontinuity and making the interpolation results more accurate; 2. In the case of high data point density, this method’s error is small. | 1. The calculation time for this method is significant and increases significantly for large-scale datasets; 2. The theory behind it is complex, and the algorithm requires optimization and improvement in real-world applications. |
| The least square fitting method | 1. Models constructed using this method are simple and easy to understand and implement; 2. This method can handle linear relationships well and has high fitting accuracy for data with less noise. | 1. This method is not effective in dealing with nonlinear relationships and may result in a loss of fit accuracy for data with high noise; 2. This method can only handle a limited number of independent variables and has limitations when dealing with high-dimensional data. |
| Technology Index | Parameter |
|---|---|
| Demodulation wavelength range | 1510 nm–1590 nm |
| Strain resolution | 1 pm |
| Channel number | 4 channels (the number of channels can increase to 16) |
| Radius of Curvature /m | Absolute Error of x-Axis End/mm | Absolute Error of y-Axis End/mm | Relative Error of y-Axis End | Mean Absolute Error | RMSE |
|---|---|---|---|---|---|
| 6 | 0.45 | 2.3 | 17.79% | ||
| 7 | 0.1 | 2.1 | 19.61% | ||
| 8 | 0.45 | 2.2 | 22.99% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, F.; Fang, X.; Chen, N.; Liang, M.; Wu, G.; Zhang, F. Research on Three-Dimensional Shape Curve Reconstruction Technology for a Scraper Conveyor on an Intelligent Working Face. Sensors 2023, 23, 8755. https://doi.org/10.3390/s23218755
Qiao F, Fang X, Chen N, Liang M, Wu G, Zhang F. Research on Three-Dimensional Shape Curve Reconstruction Technology for a Scraper Conveyor on an Intelligent Working Face. Sensors. 2023; 23(21):8755. https://doi.org/10.3390/s23218755
Chicago/Turabian StyleQiao, Fukang, Xinqiu Fang, Ningning Chen, Minfu Liang, Gang Wu, and Fan Zhang. 2023. "Research on Three-Dimensional Shape Curve Reconstruction Technology for a Scraper Conveyor on an Intelligent Working Face" Sensors 23, no. 21: 8755. https://doi.org/10.3390/s23218755
APA StyleQiao, F., Fang, X., Chen, N., Liang, M., Wu, G., & Zhang, F. (2023). Research on Three-Dimensional Shape Curve Reconstruction Technology for a Scraper Conveyor on an Intelligent Working Face. Sensors, 23(21), 8755. https://doi.org/10.3390/s23218755







