6G-Powered Efficient Resource Control through IRS-UE Association
Abstract
:1. Introduction
Contributions and Outcomes
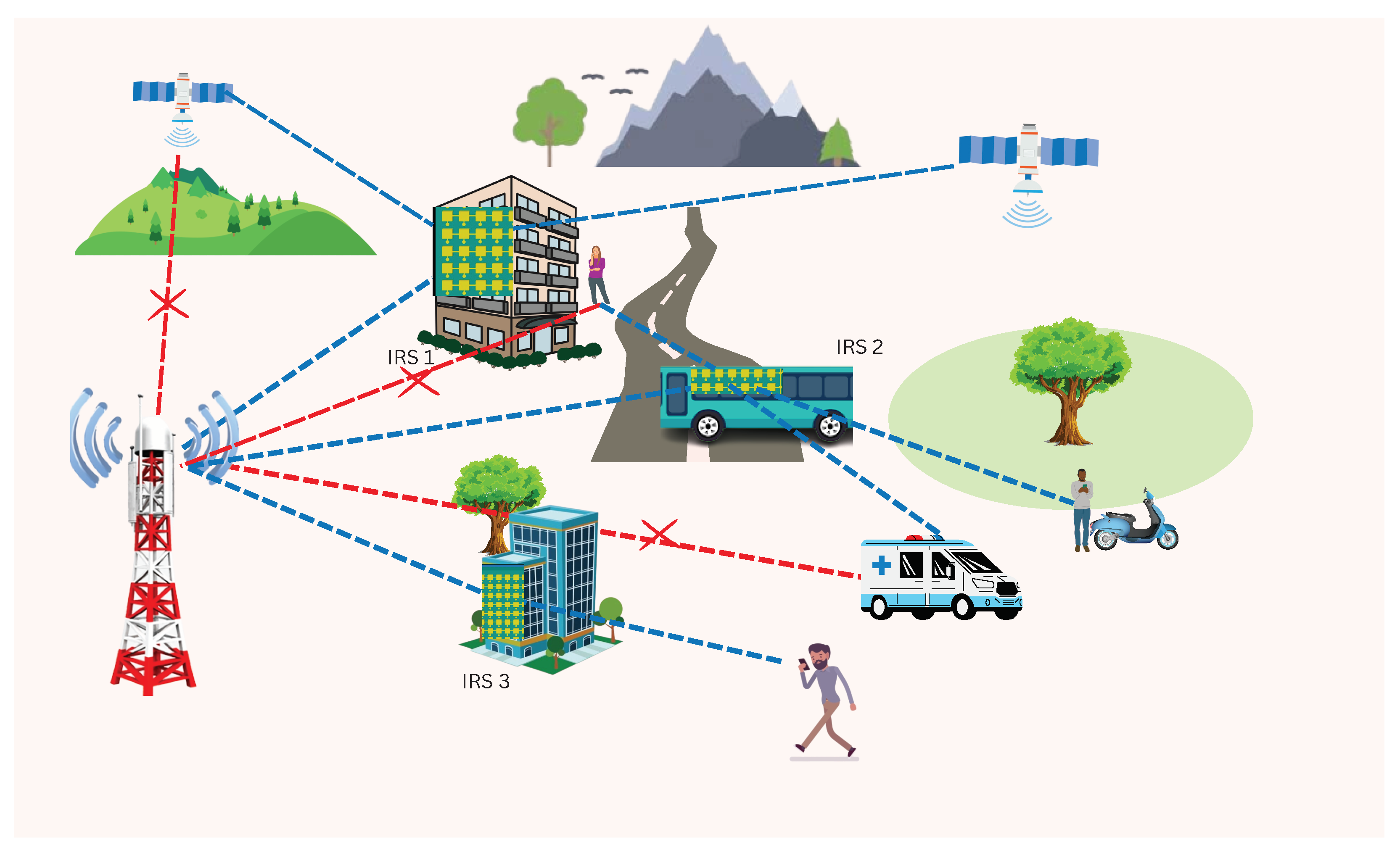
- A distributed IRS system model is considered to serve the user nodes in dead zones, under harsh environments, with the aid of multiple IRSs. The distributed IRS system is compared with the centralized IRS system with one centralized IRS in the system.
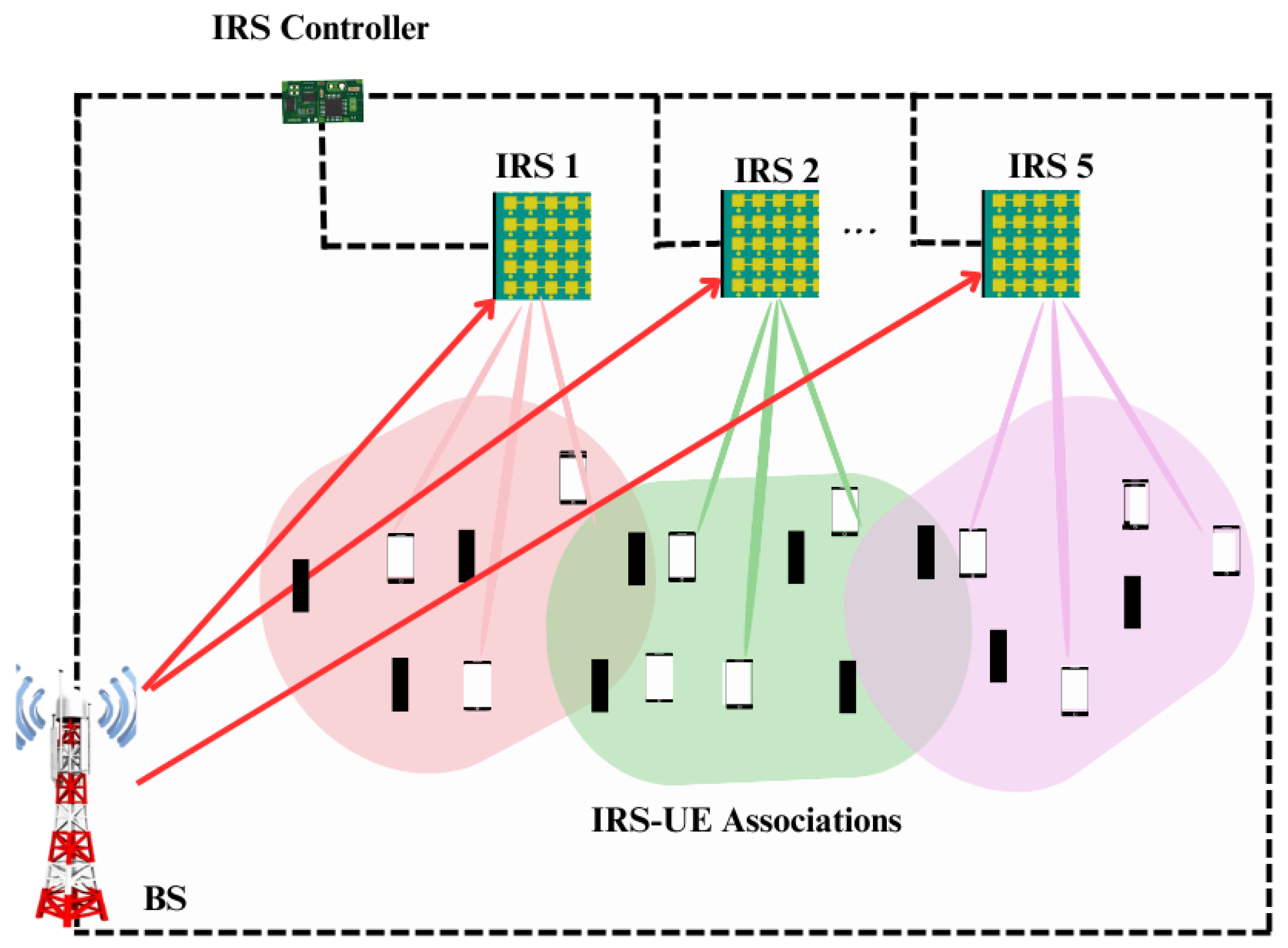
- The increased overhead challenge in a multi-IRS system is overcome by proposing a resource control algorithm, namely IUABP (IRS-UE association based on pilots). The IUABP algorithm assigns subsets of IRSs to user equipment (UE), based on efficient pilot allocation.
- After the selective association, the effective channel between the BS and user nodes via selected IRSs is estimated against all IRS channels.
- The mathematical formulations of the signal processing involved in estimating the channel and the evaluation of the system sum rate is provided.
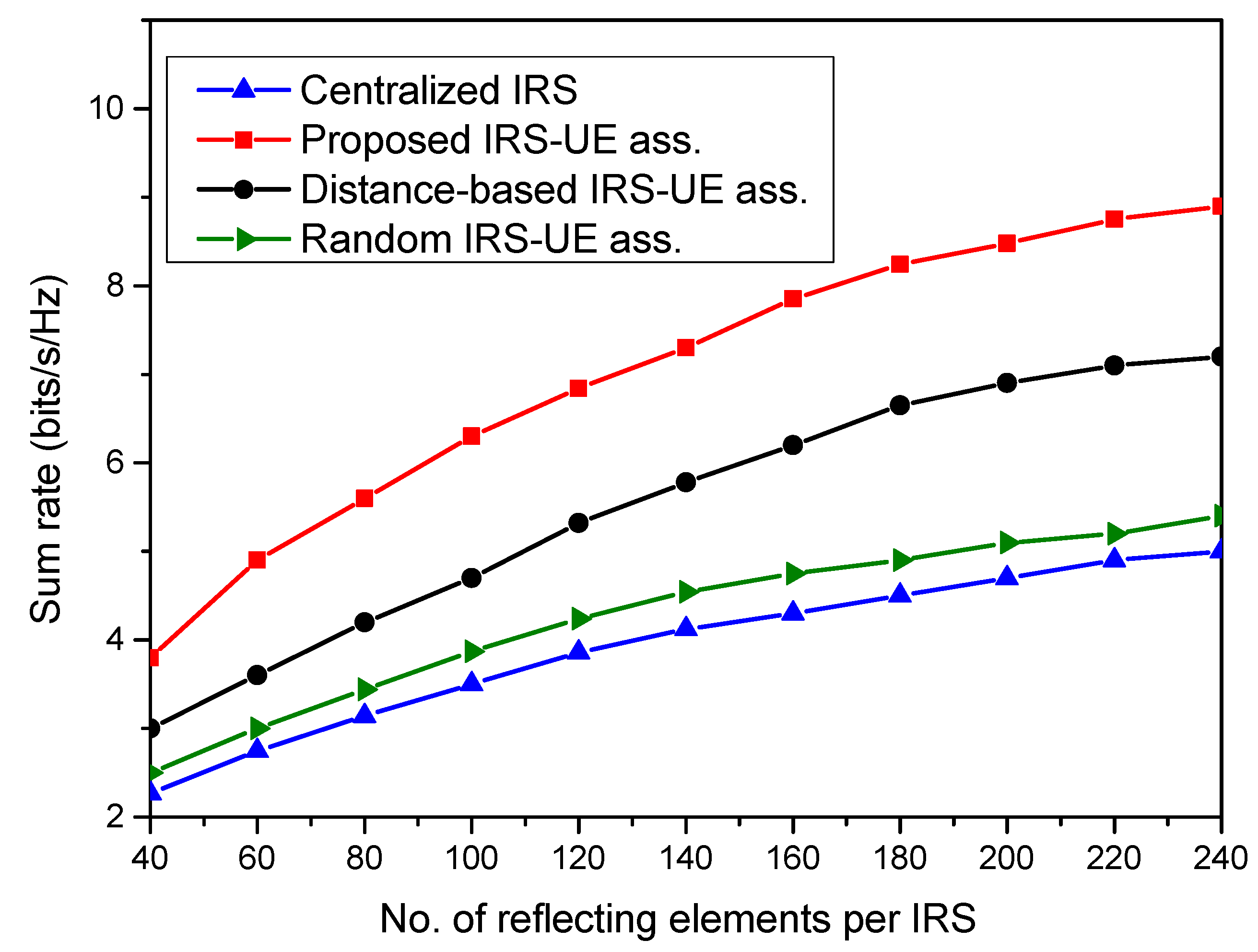
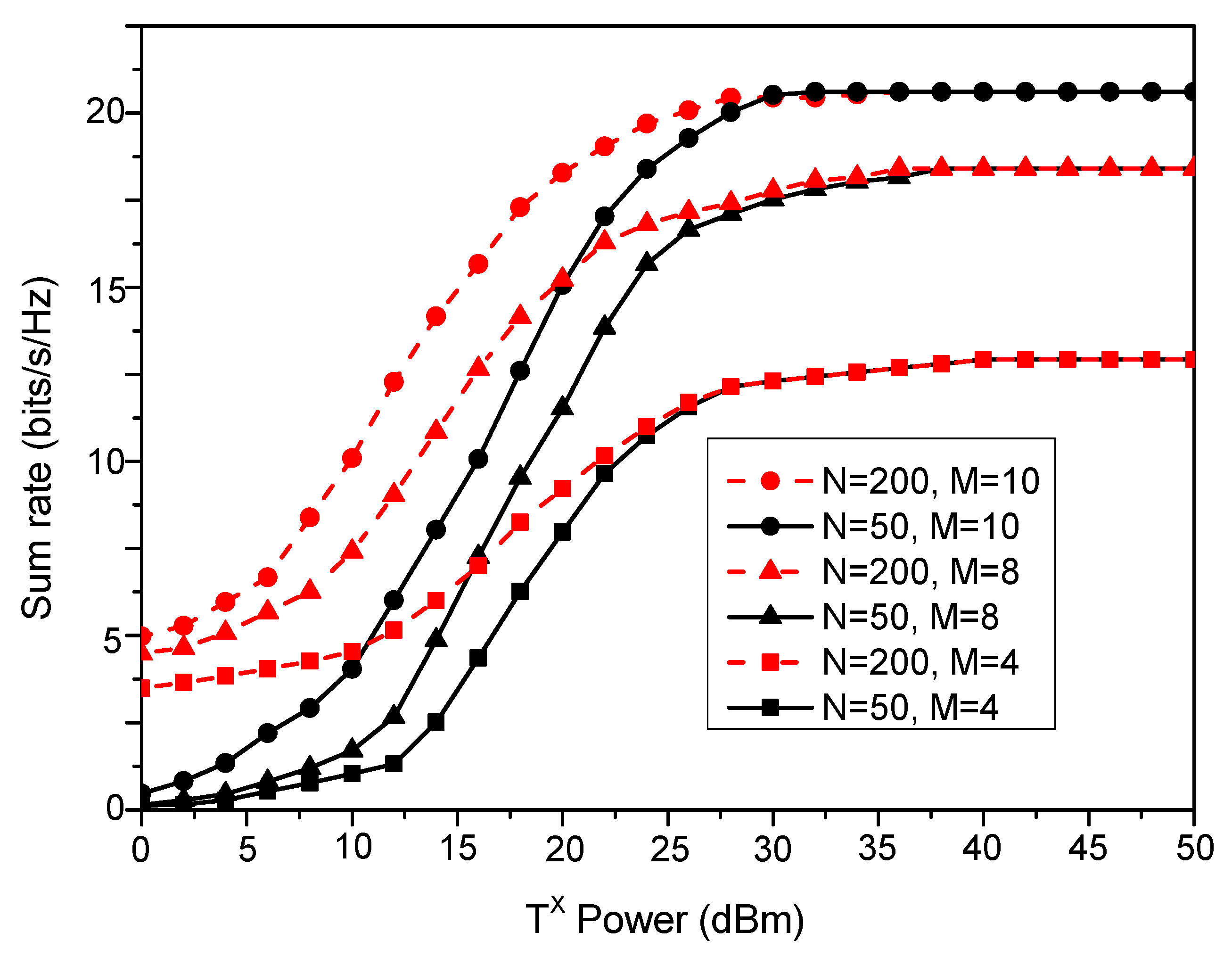
- The performance of the system with the proposed IUABP algorithm is evaluated for the sum rate achieved under different transmit powers, different reflecting elements per IRS, and different IRS numbers.
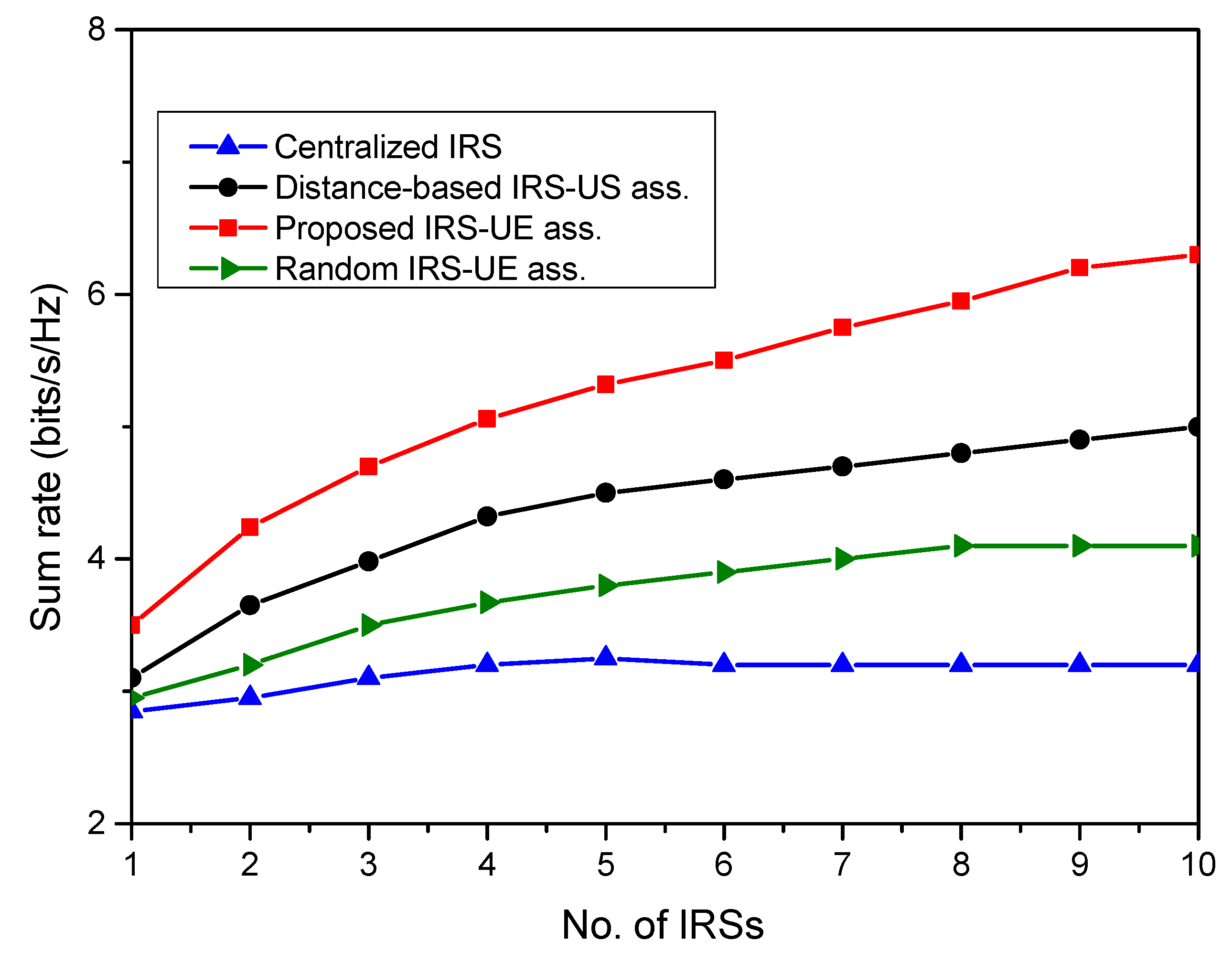
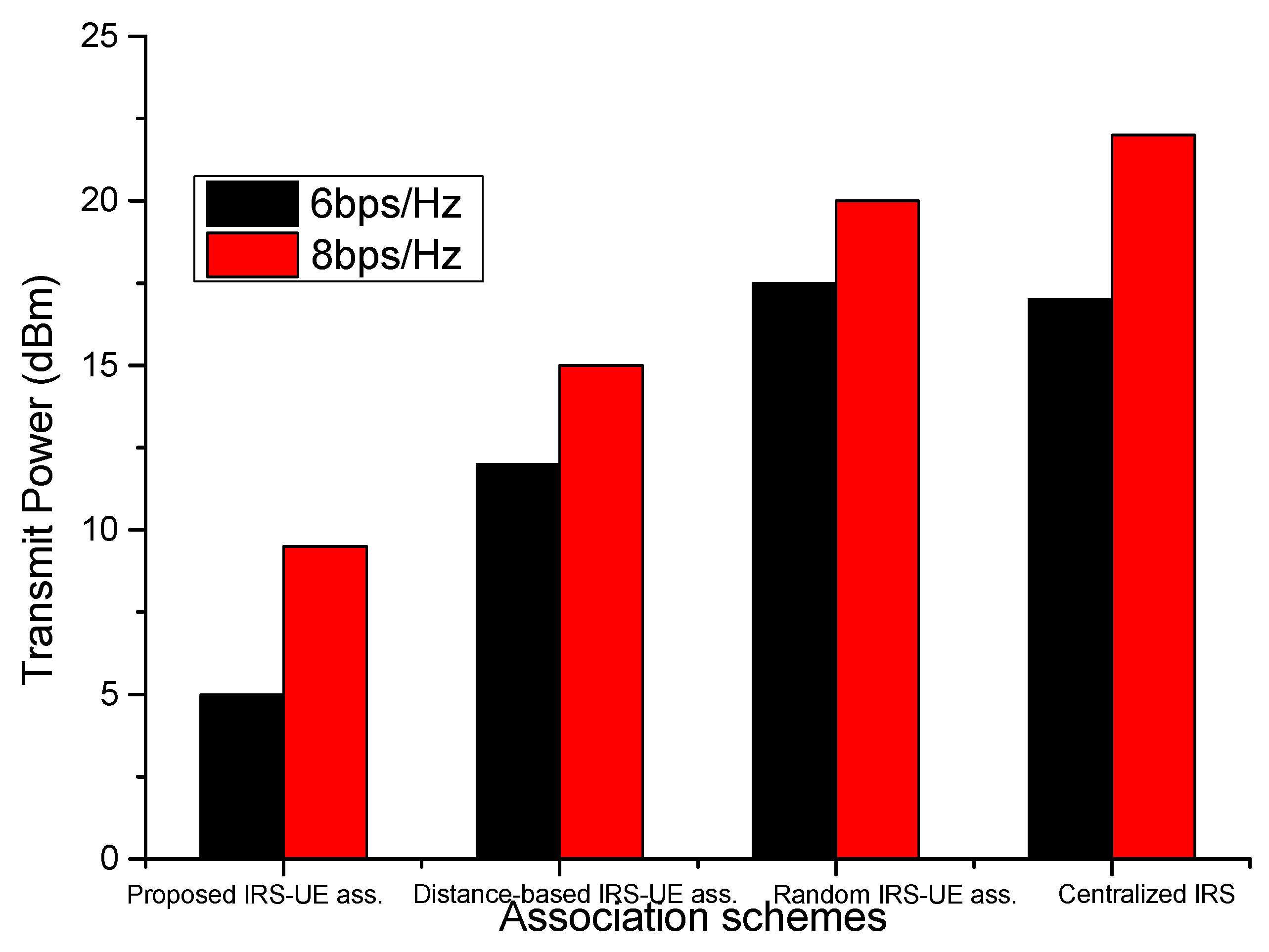
- The proposed algorithm is also compared for performance with a distance-based association scheme and a random association scheme.
2. System Model
2.1. Channel Modeling
2.2. Pilot Transmission and Channel Estimation
2.3. Data Transmission
3. IRS-UE Association
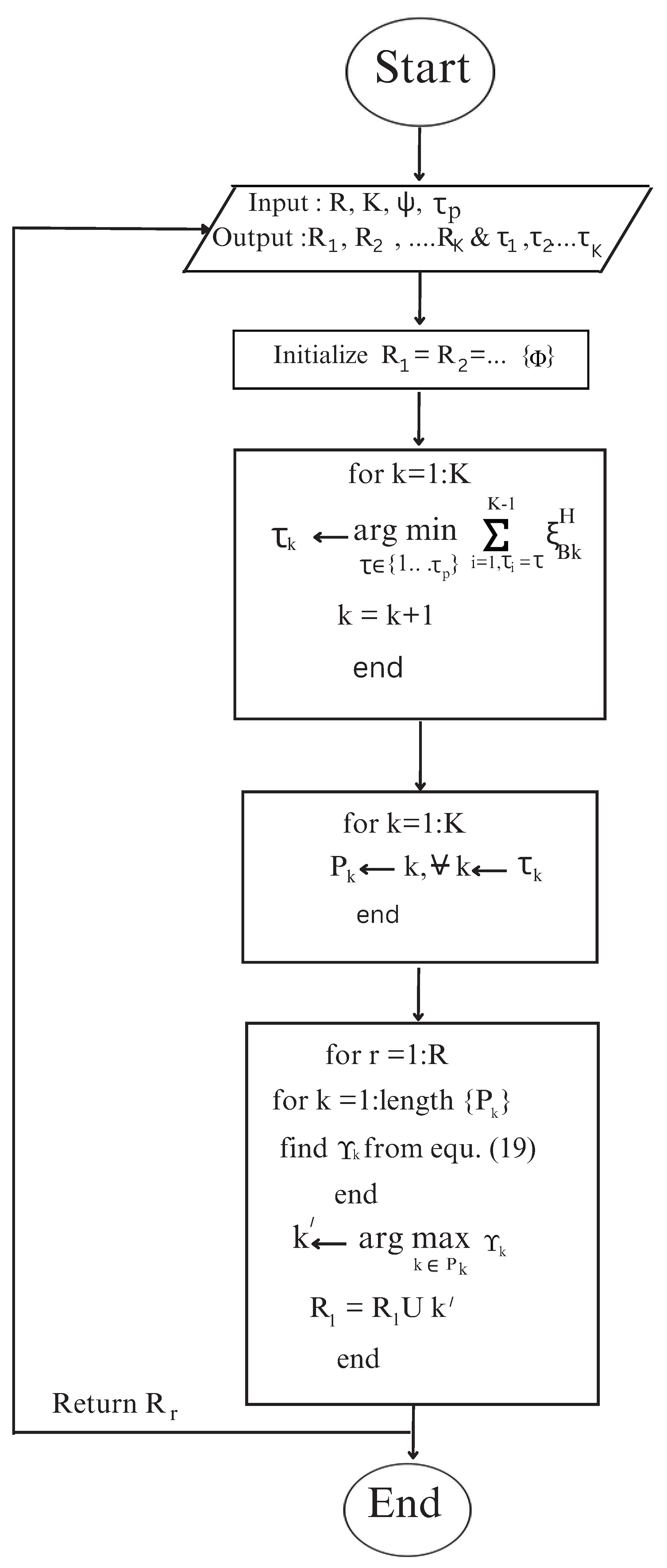
3.1. IUABP Algorithm
| Algorithm 1 IUABP algorithm. |
| Input R, K, , |
| Output , , …, and , , …, |
| 1. Initialization |
| 2. Pilot Assignment |
| for |
| end |
| 3. Formation of user sets with the same pilots |
| for |
| , |
| end |
| 4. IRS-UE Association |
| for |
| for |
| find from Equation (19) |
| end |
| end |
| return |
3.2. Implementation Complexity or Number of Estimated Links
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 6G | sixth-generation |
| IRSs | intelligent reflecting surfaces |
| UE | user equipment |
| 5G | fifth-generation |
| mmWaves | millimeter waves |
| THz | terahertz |
| IoT | Internet of Things |
| BS | base station |
| SISO | single-input single-output |
| MISO | multiple-input single-output |
| MIMO | multiple-input multiple-output |
| D-IRS | distributed IRS |
| QoS | quality-of-service |
| DFT | discrete Fourier transform |
| SINR | signal-to-noise plus interference ratio |
| M2M | machine-to-machine communication |
| LoS | line-of-sight |
| AODs | angles of departure |
| TDD | time division duplex |
| IUABP | IRS-UE association based on pilots |
References
- Jiang, W.; Han, B.; Habibi, M.A.; Schotten, H.D. The Road Towards 6G: A Comprehensive Survey. IEEE Open J. Commun. Soc. 2021, 2, 334–366. [Google Scholar] [CrossRef]
- Wang, C.X.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the Road to 6G: Visions, Requirements, Key Technologies, and Testbeds. IEEE Commun. Surv. Tutor. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- Gui, G.; Liu, M.; Tang, F.; Kato, N.; Adachi, F. 6G: Opening New Horizons for Integration of Comfort, Security, and Intelligence. IEEE Wirel. Commun. 2020, 27, 126–132. [Google Scholar] [CrossRef]
- Chopra, G. A Review on Rate Splitting Multiple Access: Challenges and Future Directions. In Proceedings of the 2023 International Conference on Emerging Smart Computing and Informatics (ESCI), Pune, India, 1–3 March 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Gupta, D.; Rani, S.; Ahmed, S.H.; Garg, S.; Jalil Piran, M.; Alrashoud, M. ICN-Based Enhanced Cooperative Caching for Multimedia Streaming in Resource Constrained Vehicular Environment. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4588–4600. [Google Scholar] [CrossRef]
- Taneja, A.; Alhudhaif, A.; Alsubai, S.; Alqahtani, A. A Novel Multiple Access Scheme for 6G Assisted Massive Machine Type Communication. IEEE Access 2022, 10, 117638–117645. [Google Scholar] [CrossRef]
- Boulogeorgos, A.A.A.; Jornet, J.M.; Alexiou, A. Directional Terahertz Communication Systems for 6G: Fact Check. IEEE Veh. Technol. Mag. 2021, 16, 68–77. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Han, C.; Nie, S. Combating the Distance Problem in the Millimeter Wave and Terahertz Frequency Bands. IEEE Commun. Mag. 2018, 56, 102–108. [Google Scholar] [CrossRef]
- Zheng, H.; Pan, C.; Zhang, C.; Li, X.; He, C.; Yang, Y.; Dai, M. Robust Transmission Design for RIS-Aided Wireless Communication With Both Imperfect CSI and Transceiver Hardware Impairments. IEEE Internet Things J. 2023, 10, 4621–4635. [Google Scholar] [CrossRef]
- Zhu, Y.; Mao, B.; Kawamoto, Y.; Kato, N. Intelligent Reflecting Surface-Aided Vehicular Networks Toward 6G: Vision, Proposal, and Future Directions. IEEE Veh. Technol. Mag. 2021, 16, 48–56. [Google Scholar] [CrossRef]
- Lyu, B.; Ramezani, P.; Hoang, D.T.; Jamalipour, A. IRS-Assisted Downlink and Uplink NOMA in Wireless Powered Communication Networks. IEEE Trans. Veh. Technol. 2022, 71, 1083–1088. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, Y.J.A.; Shi, Y.; Yan, W.; Liu, H. Reconfigurable-Intelligent-Surface Empowered Wireless Communications: Challenges and Opportunities. IEEE Wirel. Commun. 2021, 28, 136–143. [Google Scholar] [CrossRef]
- Özdogan, Ö.; Björnson, E.; Larsson, E.G. Intelligent Reflecting Surfaces: Physics, Propagation, and Pathloss Modeling. IEEE Wirel. Commun. Lett. 2020, 9, 581–585. [Google Scholar] [CrossRef]
- ElMossallamy, M.A.; Zhang, H.; Song, L.; Seddik, K.G.; Han, Z.; Li, G.Y. Reconfigurable Intelligent Surfaces for Wireless Communications: Principles, Challenges, and Opportunities. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 990–1002. [Google Scholar] [CrossRef]
- Di Renzo, M.; Zappone, A.; Debbah, M.; Alouini, M.S.; Yuen, C.; de Rosny, J.; Tretyakov, S. Smart Radio Environments Empowered by Reconfigurable Intelligent Surfaces: How It Works, State of Research, and The Road Ahead. IEEE J. Sel. Areas Commun. 2020, 38, 2450–2525. [Google Scholar] [CrossRef]
- Deng, R.; Di, B.; Zhang, H.; Tan, Y.; Song, L. Reconfigurable Holographic Surface: Holographic Beamforming for Metasurface-Aided Wireless Communications. IEEE Trans. Veh. Technol. 2021, 70, 6255–6259. [Google Scholar] [CrossRef]
- Wen, M.; Zheng, B.; Kim, K.J.; Di Renzo, M.; Tsiftsis, T.A.; Chen, K.C.; Al-Dhahir, N. A Survey on Spatial Modulation in Emerging Wireless Systems: Research Progresses and Applications. IEEE J. Sel. Areas Commun. 2019, 37, 1949–1972. [Google Scholar] [CrossRef]
- Li, J.; Dang, S.; Wen, M.; Li, Q.; Chen, Y.; Huang, Y.; Shang, W. Index Modulation Multiple Access for 6G Communications: Principles, Applications, and Challenges. IEEE Netw. 2023, 37, 52–60. [Google Scholar] [CrossRef]
- Feng, H.; Wang, J.; Fang, Z.; Qian, J.; Chen, K.C. Age of Information in UAV Aided Wireless Sensor Networks Relying on Blockchain. IEEE Trans. Veh. Technol. 2023, 72, 12430–12435. [Google Scholar] [CrossRef]
- Sun, M.; Xu, X.; Qin, X.; Zhang, P. AoI-Energy-Aware UAV-Assisted Data Collection for IoT Networks: A Deep Reinforcement Learning Method. IEEE Internet Things J. 2021, 8, 17275–17289. [Google Scholar] [CrossRef]
- Javed, M.A.; Nguyen, T.N.; Mirza, J.; Ahmed, J.; Ali, B. Reliable Communications for Cybertwin-Driven 6G IoVs Using Intelligent Reflecting Surfaces. IEEE Trans. Ind. Inf. 2022, 18, 7454–7462. [Google Scholar] [CrossRef]
- Chu, Z.; Zhu, Z.; Zhou, F.; Zhang, M.; Al-Dhahir, N. Intelligent Reflecting Surface Assisted Wireless Powered Sensor Networks for Internet of Things. IEEE Trans. Commun. 2021, 69, 4877–4889. [Google Scholar] [CrossRef]
- Taneja, A.; Rani, S.; Raza, S.; Jain, A.; Sefat, S.M. Energy efficient IRS assisted 6G network for Industry 5.0. Sci. Rep. 2023, 13, 12814. [Google Scholar] [CrossRef] [PubMed]
- Pan, Q.; Wu, J.; Zheng, X.; Yang, W.; Li, J. Differential Privacy and IRS Empowered Intelligent Energy Harvesting for 6G Internet of Things. IEEE Internet Things J. 2022, 9, 22109–22122. [Google Scholar] [CrossRef]
- Taneja, A.; Rani, S.; Breñosa, J.; Tolba, A.; Kadry, S. An improved WiFi sensing based indoor navigation with reconfigurable intelligent surfaces for 6G enabled IoT network and AI explainable use case. Future Gener. Comput. Syst. 2023, 149, 294–303. [Google Scholar] [CrossRef]
- Ramezani, P.; Jamalipour, A. Backscatter-Assisted Wireless Powered Communication Networks Empowered by Intelligent Reflecting Surface. IEEE Trans. Veh. Technol. 2021, 70, 11908–11922. [Google Scholar] [CrossRef]
- Zhou, G.; Pan, C.; Ren, H.; Wang, K.; Nallanathan, A. Intelligent Reflecting Surface Aided Multigroup Multicast MISO Communication Systems. IEEE Trans. Signal Process. 2020, 68, 3236–3251. [Google Scholar] [CrossRef]
- Ning, B.; Chen, Z.; Chen, W.; Fang, J. Beamforming Optimization for Intelligent Reflecting Surface Assisted MIMO: A Sum-Path-Gain Maximization Approach. IEEE Wirel. Commun. Lett. 2020, 9, 1105–1109. [Google Scholar] [CrossRef]
- Hashida, H.; Kawamoto, Y.; Kato, N.; Iwabuchi, M.; Murakami, T. Mobility-Aware User Association Strategy for IRS-Aided mm-Wave Multibeam Transmission Towards 6G. IEEE J. Sel. Areas Commun. 2022, 40, 1667–1678. [Google Scholar] [CrossRef]
- Zhi, K.; Pan, C.; Ren, H.; Wang, K. Power Scaling Law Analysis and Phase Shift Optimization of RIS-Aided Massive MIMO Systems With Statistical CSI. IEEE Trans. Commun. 2022, 70, 3558–3574. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Nguyen, D.N.; Renzo, M.D.; Zhang, R. Leveraging Secondary Reflections and Mitigating Interference in Multi-IRS/RIS Aided Wireless Networks. IEEE Trans. Wirel. Commun. 2023, 22, 502–517. [Google Scholar] [CrossRef]
- Li, Z.; Hua, M.; Wang, Q.; Song, Q. Weighted Sum-Rate Maximization for Multi-IRS Aided Cooperative Transmission. IEEE Wirel. Commun. Lett. 2020, 9, 1620–1624. [Google Scholar] [CrossRef]
- Niu, H.; Chu, Z.; Zhou, F.; Pan, C.; Ng, D.W.K.; Nguyen, H.X. Double Intelligent Reflecting Surface-Assisted Multi-User MIMO Mmwave Systems With Hybrid Precoding. IEEE Trans. Veh. Technol. 2022, 71, 1575–1587. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, M.; Saad, W.; Xu, W.; Shikh-Bahaei, M.; Poor, H.V.; Cui, S. Energy-Efficient Wireless Communications With Distributed Reconfigurable Intelligent Surfaces. IEEE Trans. Wirel. Commun. 2022, 21, 665–679. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Ferdinand, N. Distributed Reconfigurable Intelligent Surfaces for Energy-Efficient Indoor Terahertz Wireless Communications. IEEE Internet Things J. 2023, 10, 2728–2742. [Google Scholar] [CrossRef]
- Shabir, M.W.; Nguyen, T.N.; Mirza, J.; Ali, B.; Javed, M.A. Transmit and Reflect Beamforming for Max-Min SINR in IRS-Aided MIMO Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1099–1105. [Google Scholar] [CrossRef]
- Hashida, H.; Kawamoto, Y.; Kato, N. Selective Reflection Control: Distributed IRS-Aided Communication With Partial Channel State Information. IEEE Trans. Veh. Technol. 2022, 71, 11949–11958. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Cui, S. Channel Estimation for Intelligent Reflecting Surface Assisted Multiuser Communications: Framework, Algorithms, and Analysis. IEEE Trans. Wirel. Commun. 2020, 19, 6607–6620. [Google Scholar] [CrossRef]
- Jensen, T.L.; De Carvalho, E. An Optimal Channel Estimation Scheme for Intelligent Reflecting Surfaces Based on a Minimum Variance Unbiased Estimator. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 5000–5004. [Google Scholar] [CrossRef]
- Psomas, C.; Suraweera, H.A.; Krikidis, I. On the Association with Intelligent Reflecting Surfaces in Spatially Random Networks. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Peng, X.; Hu, X.; Zhong, C. Distributed Intelligent Reflecting Surfaces-Aided Communication System: Analysis and Design. IEEE Trans. Green Commun. Netw. 2022, 6, 1932–1944. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L. Rayleigh Fading Modeling and Channel Hardening for Reconfigurable Intelligent Surfaces. IEEE Wirel. Commun. Lett. 2021, 10, 830–834. [Google Scholar] [CrossRef]
- Li, Y.; You, C.; Chun, Y.J. Active-IRS Aided Wireless Network: System Modeling and Performance Analysis. IEEE Commun. Lett. 2023, 27, 487–491. [Google Scholar] [CrossRef]
- Shi, E.; Zhang, J.; He, R.; Jiao, H.; Wang, Z.; Ai, B.; Ng, D.W.K. Spatially Correlated Reconfigurable Intelligent Surfaces-Aided Cell-Free Massive MIMO Systems. IEEE Trans. Veh. Technol. 2022, 71, 9073–9077. [Google Scholar] [CrossRef]
- Van Chien, T.; Ngo, H.Q.; Chatzinotas, S.; Di Renzo, M.; Ottersten, B. Reconfigurable Intelligent Surface-Assisted Cell-Free Massive MIMO Systems Over Spatially-Correlated Channels. IEEE Trans. Wirel. Commun. 2022, 21, 5106–5128. [Google Scholar] [CrossRef]
- Tao, Q.; Zhang, S.; Zhong, C.; Xu, W.; Lin, H.; Zhang, Z. Weighted Sum-Rate of Intelligent Reflecting Surface Aided Multiuser Downlink Transmission With Statistical CSI. IEEE Trans. Wirel. Commun. 2022, 21, 4925–4937. [Google Scholar] [CrossRef]

| Notation | Description |
|---|---|
| R | Number of IRSs |
| N | Number of reflecting elements per IRS |
| M | Number of antennas at the BS |
| K | Number of user equipment |
| Reflection matrix of rth IRS | |
| Direct channel between BS and the kth user node | |
| Channel between BS and the rth IRS | |
| Channel between the rth IRS and the kth user node | |
| Cascaded channel between the kth user node and the BS | |
| pilot transmit power of user k | |
| , | large-scale fading coefficients |
| , | Rician factors |
| elevation angles | |
| azimuth angles | |
| , | Effective angle of departures |
| Pilot length | |
| A set of pilot sequences | |
| Length of coherence block | |
| Set of nodes assigned with the same pilot | |
| Z | Receiver noise |
| Total BS transmit power | |
| Effective channel from the kth node and the BS | |
| Estimates of the effective channel between BS and the kth node | |
| SINR at the kth node | |
| Achievable rate | |
| Received data signal at the kth node | |
| Received pilot signal at the BS | |
| Height f BS from the ground plane | |
| Height of IRS from the ground plane | |
| Height of the user equipment from the ground plane |
| Ref. | Channel Fading Model Used | Advantage | Limitation |
|---|---|---|---|
| [42] | Uncorrelated Rayleigh fading | Commonly used and less complex | The spatial correlations among the reflecting elements of the IRSs are not considered. |
| [43] | Spatially correlated Rayleigh fading | More practical and realistic model. Considers the correlations among the IRS reflecting elements due to their geometric layouts, sizes, and inter-distances. | Computational complexity is more due to the requirement of covariance matrices. |
| [44] | Nakagami-m fading channel | Useful in real-world fading environments with varying multipath propagation degrees. | Channel characteristics are spatially homogeneous |
| [45] | Rician fading model | It provides a more realistic description of channel behavior when there is a strong LOS signal. Better SNR estimation | Not applicable in scenarios without LoS paths, estimation of the k-factor is challenging. |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| N | 100 | 5 | |
| R | 5 | 15 dBm | |
| M | 8 | 10 m | |
| 5 m | m | ||
| K | 40 | 10 mW | |
| 20 GHz | dBm | ||
| 5 | 5 | ||
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqahtani, A.; Taneja, A.; Alqahtani, J.; Alqahtani, N. 6G-Powered Efficient Resource Control through IRS-UE Association. Sensors 2023, 23, 8713. https://doi.org/10.3390/s23218713
Alqahtani A, Taneja A, Alqahtani J, Alqahtani N. 6G-Powered Efficient Resource Control through IRS-UE Association. Sensors. 2023; 23(21):8713. https://doi.org/10.3390/s23218713
Chicago/Turabian StyleAlqahtani, Ali, Ashu Taneja, Jarallah Alqahtani, and Nayef Alqahtani. 2023. "6G-Powered Efficient Resource Control through IRS-UE Association" Sensors 23, no. 21: 8713. https://doi.org/10.3390/s23218713
APA StyleAlqahtani, A., Taneja, A., Alqahtani, J., & Alqahtani, N. (2023). 6G-Powered Efficient Resource Control through IRS-UE Association. Sensors, 23(21), 8713. https://doi.org/10.3390/s23218713





