Structural Uncertainty Analysis of High-Temperature Strain Gauge Based on Monte Carlo Stochastic Finite Element Method
Abstract
1. Introduction
2. Analysis of Temperature Field of High-Temperature Strain Gauge
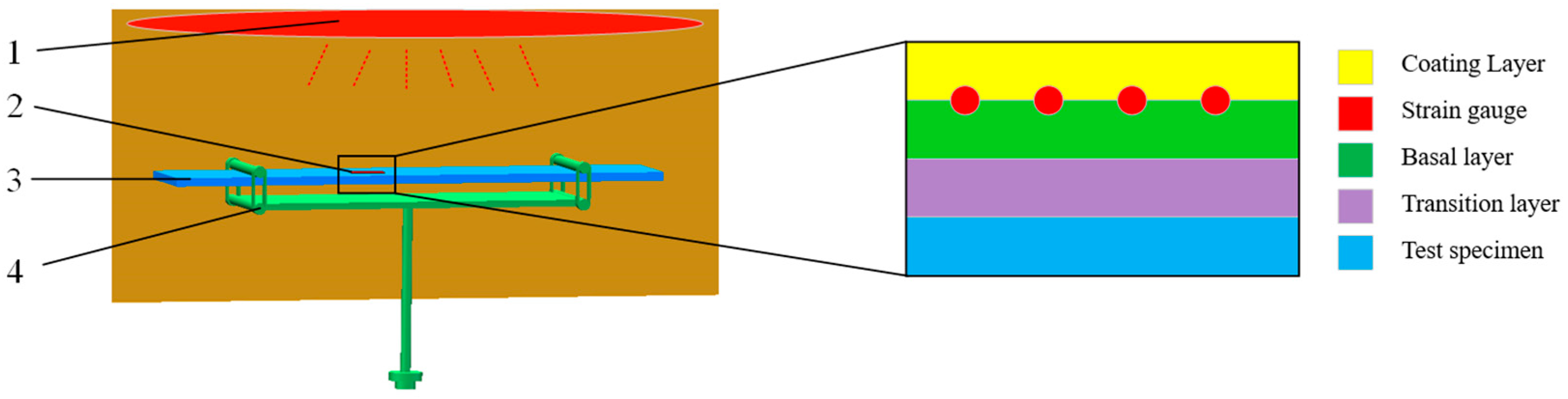
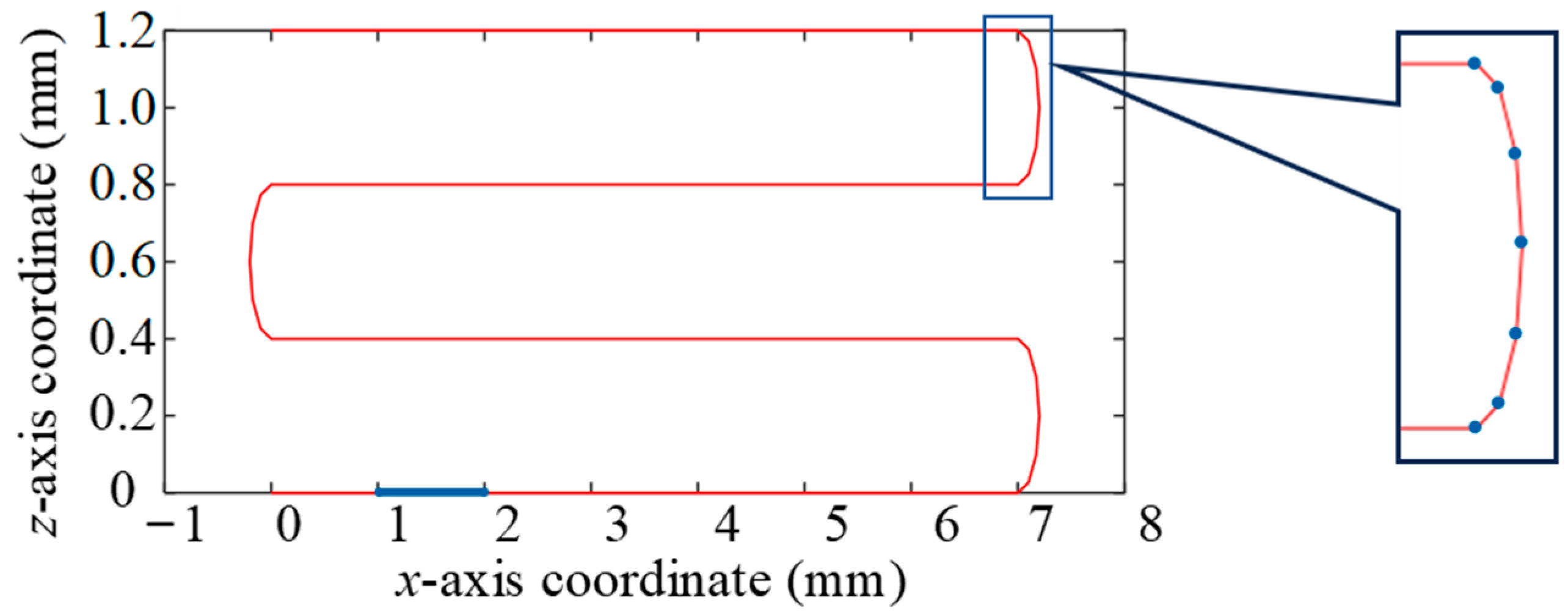
2.1. Problem Description
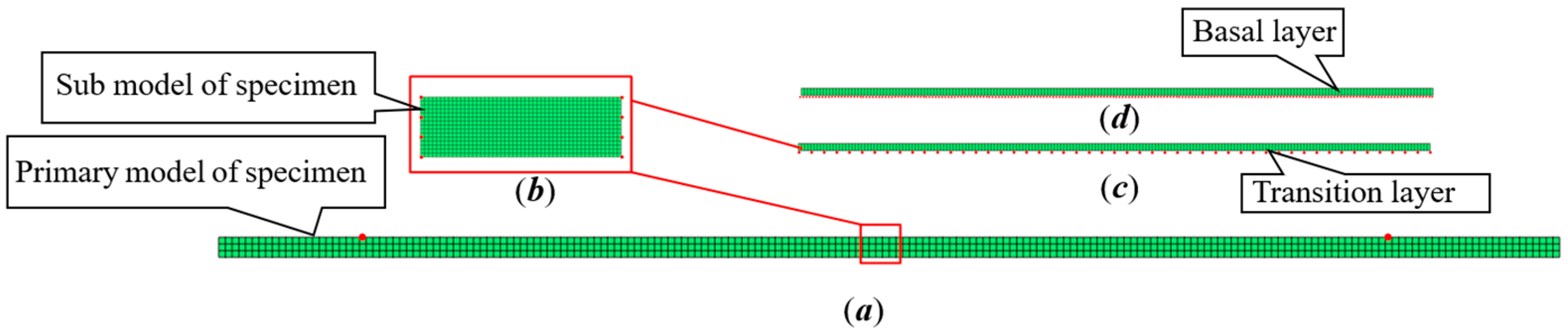
2.2. Establishment of the Primary Sub-Model
2.3. Finite Element Calculation of Temperature Field
3. Thermal Response Analysis of High-Temperature Strain Gauge Based on Coupled Thermo-Mechanical Model
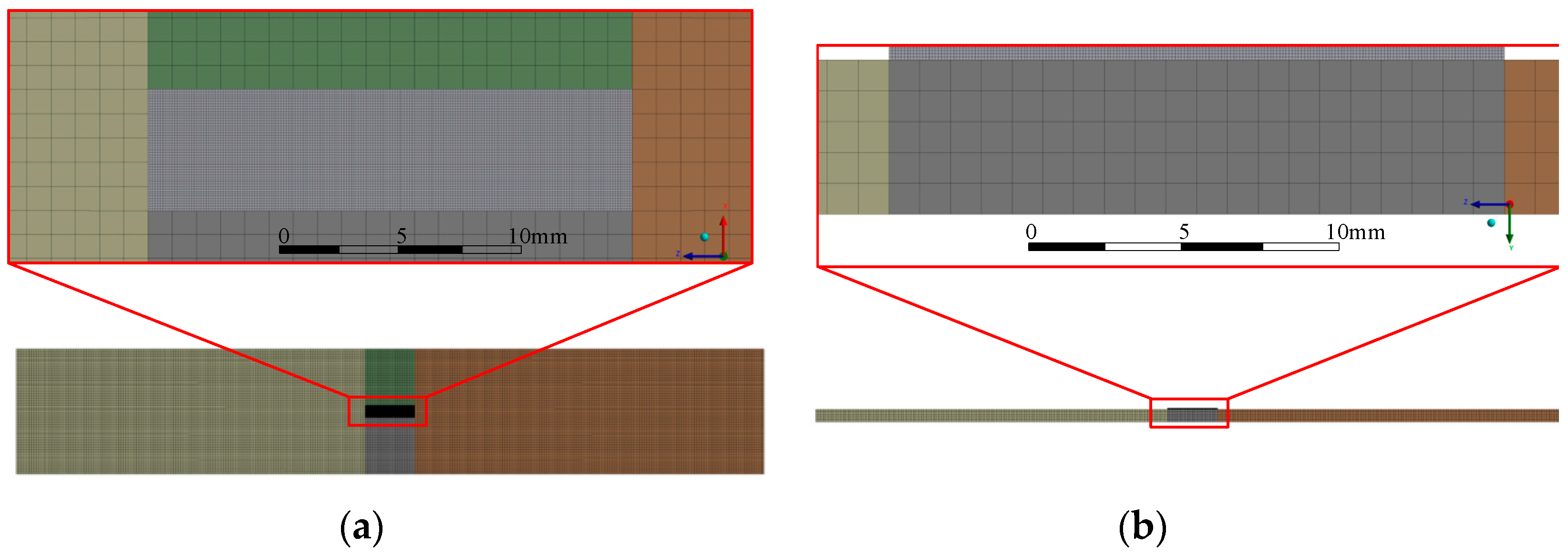
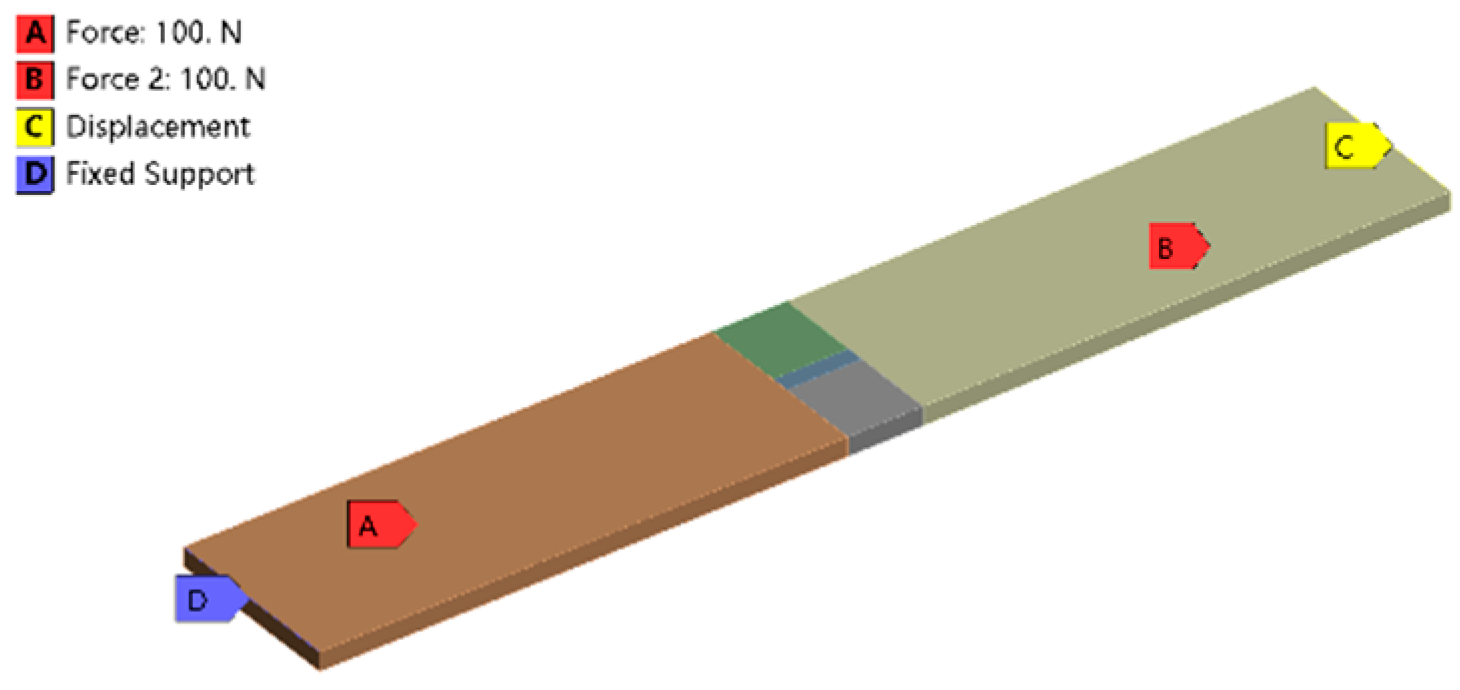
3.1. Establishment of a Primary Sub Model for Thermal Response Analysis
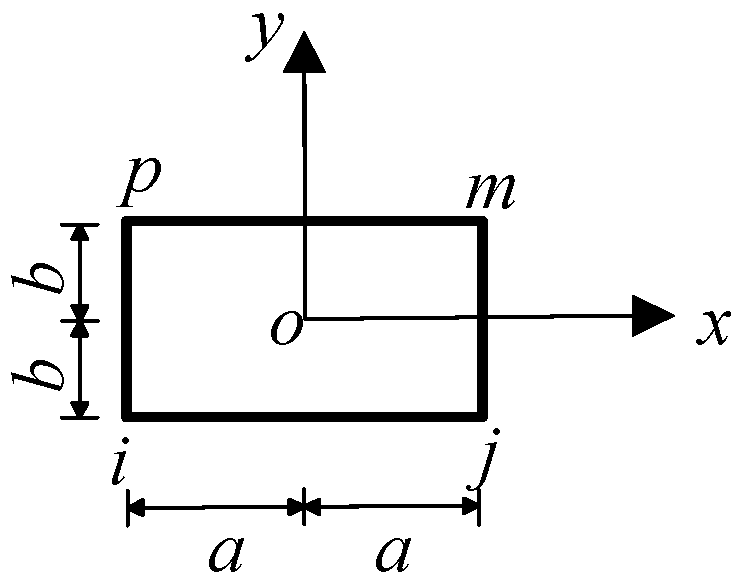
3.2. Transfer of Force in the System
3.3. Element Division and Thermal Response Analysis of Grid Wire
4. Results and Discussion
4.1. ANSYS Verification of the MATLAB Program
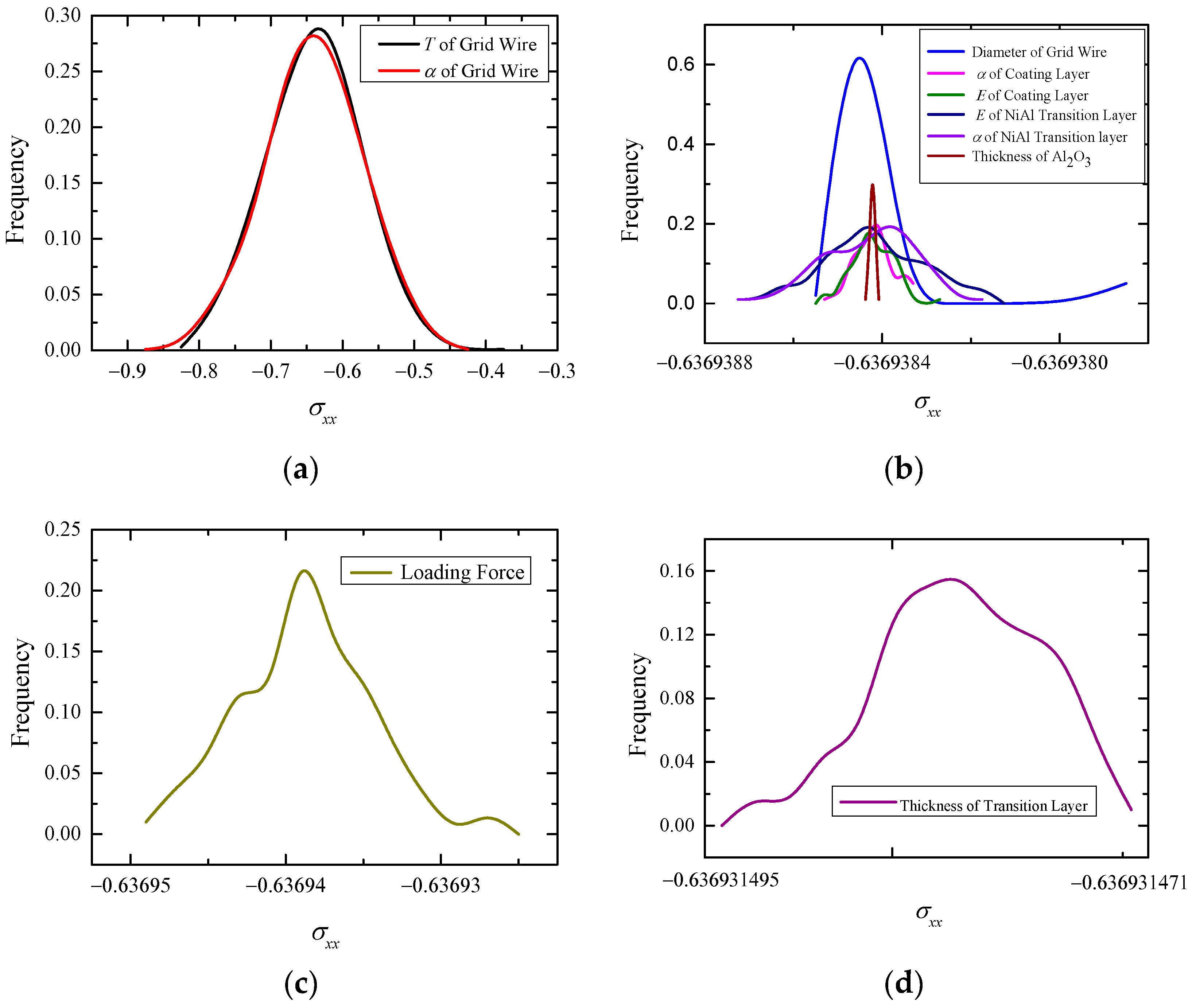
4.2. Uncertainty Analysis of Thermal Response of High-Temperature Grid Wire Based on SFEM
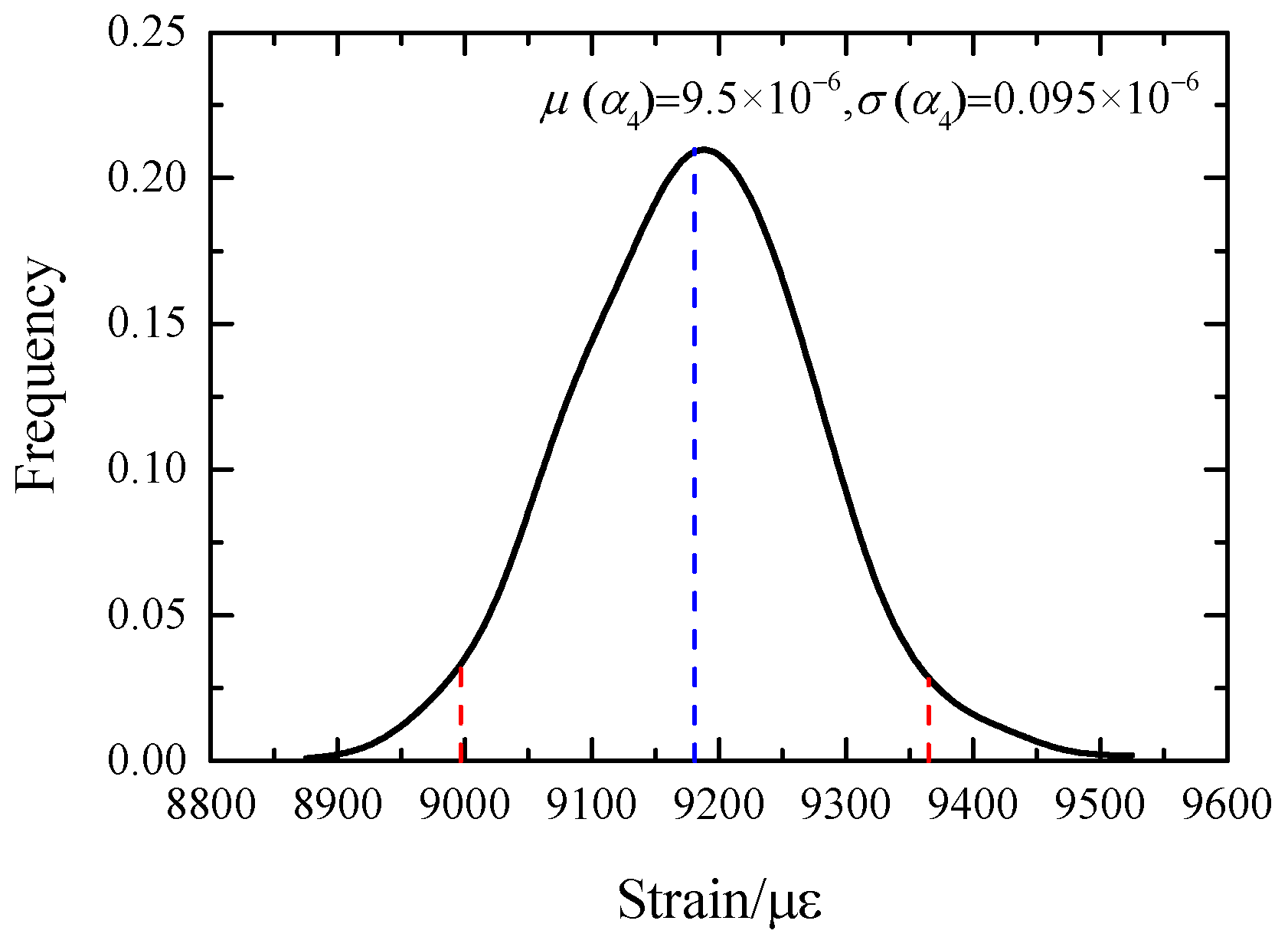
4.3. Uncertainty Analysis of Thermal Expansion Coefficient of Grid Wire Based on SFEM
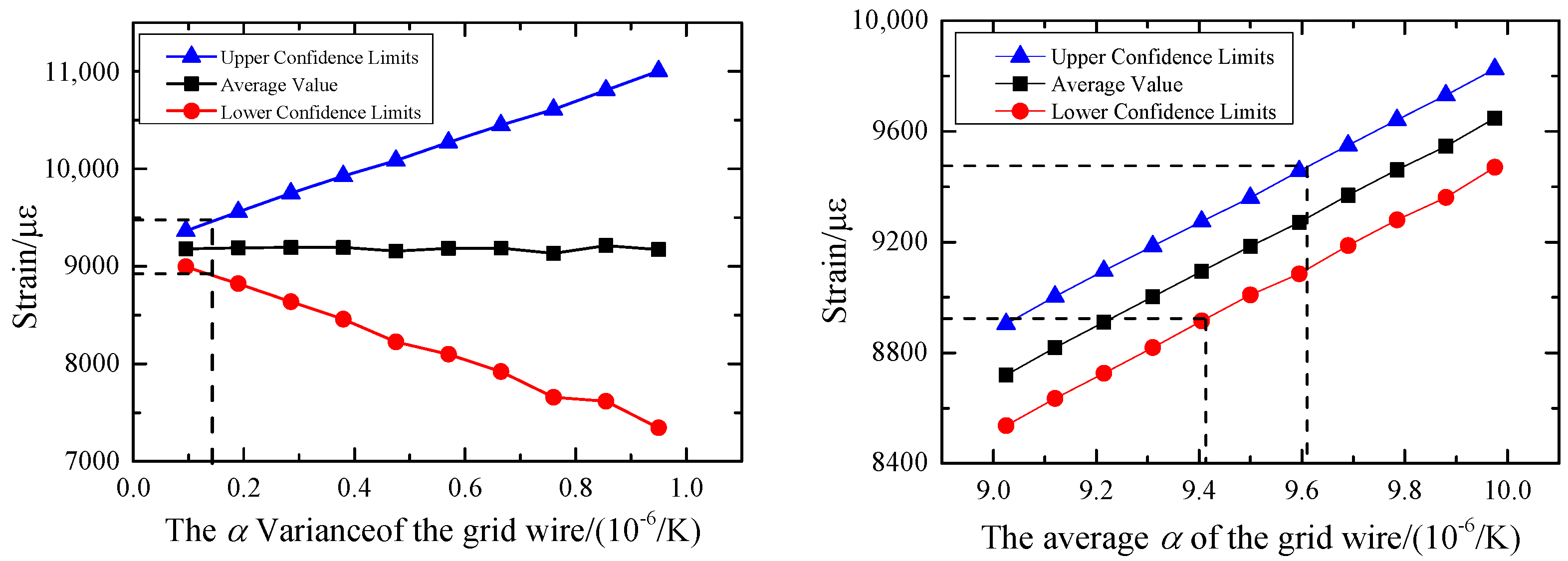
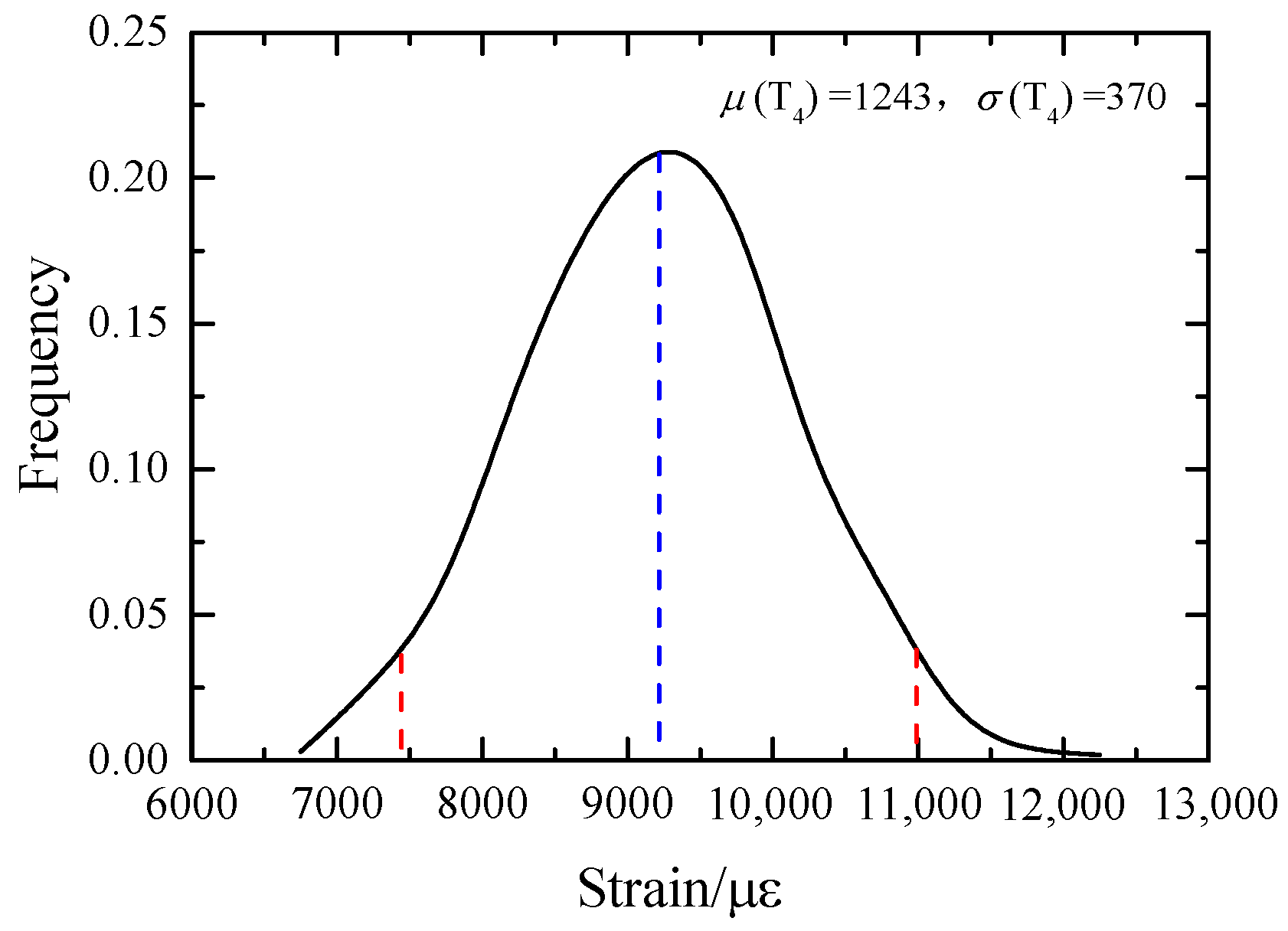
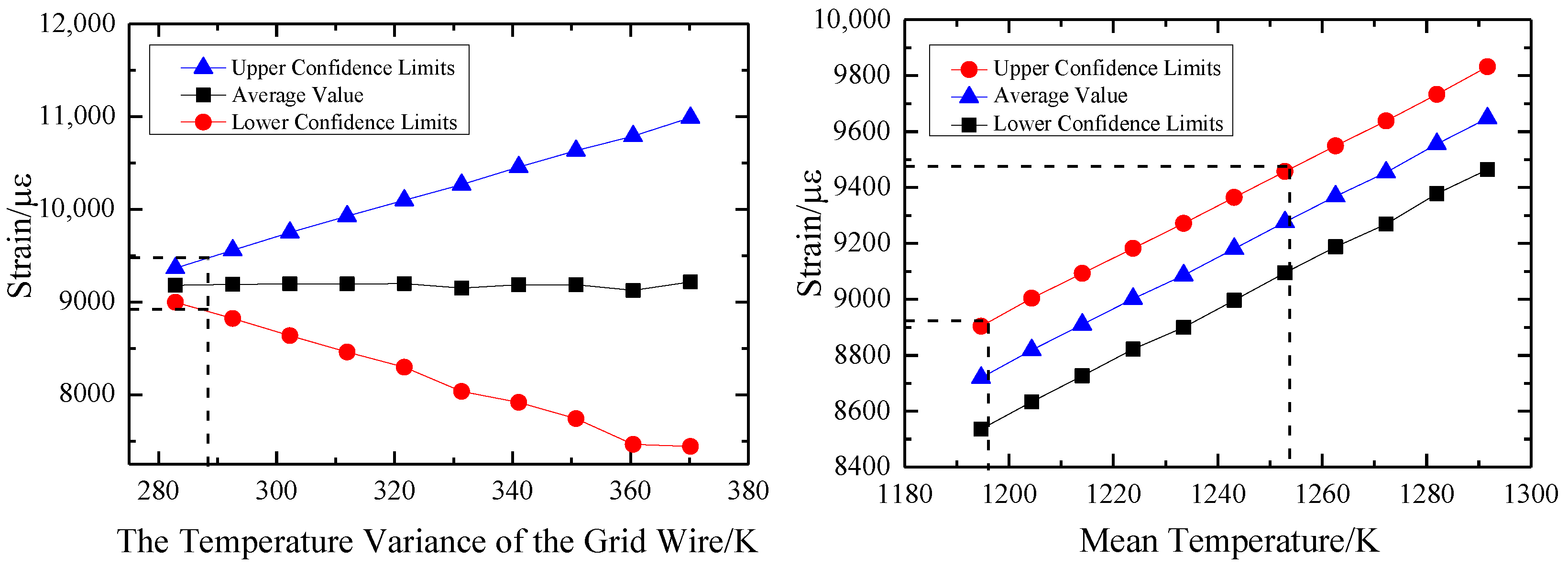
4.4. Uncertainty Analysis of Temperature of Grid Wire Based on SFEM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ai, Y.T.; Liu, M.; Zhang, F.L. Research on Structural optimization Method to improve the life and accuracy of high-temperature strain gauge. Chin. J. Sci. Instr. 2022, 43, 151–161. [Google Scholar]
- Reis, M.; Castro, R.; Mello, O. Calibration uncertainty estimation of a strain-gage external balance. Measurement 2013, 46, 24–33. [Google Scholar] [CrossRef]
- Zhu, B.; Pei, H.F.; Yang, Q. Probabilistic analysis of wave-induced seabed response based on stochastic finite element method. Rock Soil Mechan. 2023, 44, 1545–1556. [Google Scholar]
- Khairi, N.; Rizam, M.S.; Naimah, M.; Nooritawati, M.; Husna, Z. Diameter Stem Changes Detection Sensor Evaluation Using Different Size of Strain Gauge on Dendrobium Stem. Procedia Eng. 2012, 41, 1421–1425. [Google Scholar] [CrossRef]
- Schmid, P.; Zarfl, C.; Balogh, G.; Schmid, U. Gauge Factor of Titanium/Platinum Thin Films up to 350 °C. Procedia Eng. 2014, 87, 172–175. [Google Scholar] [CrossRef][Green Version]
- Kolhapure, R.; Shinde, V.; Kamble, V. Geometrical optimization of strain gauge force transducer using GRA method. Measurement 2017, 101, 111–117. [Google Scholar] [CrossRef]
- Liu, H.; Mao, X.; Yang, Z.; Cui, J.; Jiang, S.; Zhang, W. High temperature static and dynamic strain response of PdCr thin film strain gauge prepared on Ni-based superalloy. Sens. Actuators A Phys. 2019, 298, 111571. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, J.; Chen, Y.; Guo, Z.; Yu, P.; Liu, Y.; Zhao, J. High-sensitive and stretchable resistive strain gauges: Parametric design and DIW fabrication. Compos. Struct. 2019, 223, 110955. [Google Scholar] [CrossRef]
- Enser, H.; Kulha, P.; Sell, J.K.; Jakoby, B.; Hilber, W.; Strauß, B.; Schatzl-Linder, M. Printed Strain Gauges Embedded in Organic Coatings. Procedia Eng. 2016, 168, 822–825. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Xiao, C.; Zhao, Y.; Zhu, Y.; Zhou, Z. Strain Transfer Characteristics of Resistance Strain-Type Transducer Using Elas-tic-Mechanical Shear Lag Theory. Sensors 2018, 18, 2420. [Google Scholar] [CrossRef]
- Gräbner, D.; Dumstorff, G.; Lang, W. Simultaneous Measurement of Strain and Temperature with two Resistive Strain Gauges made from Different Materials. Procedia Manuf. 2018, 24, 258–263. [Google Scholar] [CrossRef]
- Larsen, M.L.; Adhikari, S.; Arora, V. Analysis of stochastically parameterized prestressed beams and frames. Eng. Struct. 2021, 249, 113312. [Google Scholar] [CrossRef]
- Bartłomiej, P.; Marcin, K. Numerical convergence and error analysis for the truncated iterative generalized stochastic pertur-bation-based finite element method. Comput. Methods Appl. Mechan. Eng. 2023, 410, 115993. [Google Scholar]
- Chen, C.; Dawson, C.; Valseth, E. Cross-mode stabilized stochastic shallow water systems using stochastic finite element methods. Comput. Methods Appl. Mech. Eng. 2023, 405, 115873. [Google Scholar] [CrossRef]
- Li, J.; Liu, Q.; Yue, J. Numerical analysis of fully discrete finite element methods for the stochastic Navier-Stokes equations with multiplicative noise. Appl. Numer. Math. 2021, 170, 398–417. [Google Scholar] [CrossRef]
- Ghanem, R.G. Stochastic Finite Elements; Springer: Berlin/Heidelberg, Germany, 2003; pp. 70–92. [Google Scholar]
- Popescu, R.; Deodatis, G.; Nobahar, A. Effects of random heterogeneity of soil properties on bearing capacity. Probabilistic Eng. Mech. 2005, 20, 324–341. [Google Scholar] [CrossRef]
- Lagaros, N.D.; Papadopoulos, V. Optimum design of shell structures with random geometric, material and thickness imperfections. Int. J. Solids Struct. 2006, 43, 6948–6964. [Google Scholar] [CrossRef]
- Palluotto, L.; Dumont, N.; Rodrigues, P.; Gicquel, O.; Vicquelin, R. Assessment of randomized Quasi-Monte Carlo method efficiency in radiative heat transfer simulations. J. Quant. Spectrosc. Radiat. Transf. 2019, 236, 106570. [Google Scholar] [CrossRef]
- Vadlamani, S.; Arun, C.O. A stochastic B-spline wavelet on the interval finite element method for beams. Comput. Struct. 2020, 233, 106246. [Google Scholar] [CrossRef]
- Wang, B.; Cai, Y.; Li, Z.; Ding, C.; Yang, T.; Cui, X. Stochastic stable node-based smoothed finite element method for uncertainty and reliability analysis of thermo-mechanical problems. Eng. Anal. Bound. Elem. 2020, 114, 23–44. [Google Scholar] [CrossRef]
- Do, N.-T.; Tran, T.T. Random vibration analysis of FGM plates subjected to moving load using a refined stochastic finite element method. Def. Technol. 2023, in press. [Google Scholar] [CrossRef]
- Talischi, C.; Paulino, G.H.; Pereira, A.; Menezes, I.F.M. PolyMesher: A general-purpose mesh generator for polygonal elements written in Matlab. Struct. Multidiscip. Optim. 2012, 45, 309–328. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, W.; Wei, J. Analysis of random temperature field for freeway with wide subgrade in cold regions. Cold Reg. Sci. Technol. 2014, 106–107, 22–27. [Google Scholar] [CrossRef]
- Bärnkopf, E.; Jáger, B.; Kövesdi, B. Lateral–torsional buckling resistance of corrugated web girders based on deterministic and stochastic nonlinear analysis. Thin-Walled Struct. 2022, 180, 109880. [Google Scholar] [CrossRef]
- Hong, C.; Yang, Q.; Sun, X.; Chen, W.; Han, K. A theoretical strain transfer model between optical fiber sensors and monitored substrates. Geotext. Geomembranes 2021, 49, 1539–1549. [Google Scholar] [CrossRef]
- He, C.; He, H.; Wang, T.; Pei, J.H. Modification and prediction of finite element model in thermal environment considering uncertain factors. J. Vibrat. Eng. 2018, 31, 1013–1020. [Google Scholar]
- Chen, J.J.; Wang, L.G.; Li, J.P. Thermal analysis of rod structures with random parameters in steady state random temperature field. Eng. Mechan. 2009, 26, 12–15. [Google Scholar]
- Nastos, C.; Zarouchas, D. Probabilistic failure analysis of quasi-isotropic CFRP structures utilizing the stochastic finite element and the Karhunen–Loève expansion methods. Compos. Part B Eng. 2022, 235, 109742. [Google Scholar] [CrossRef]
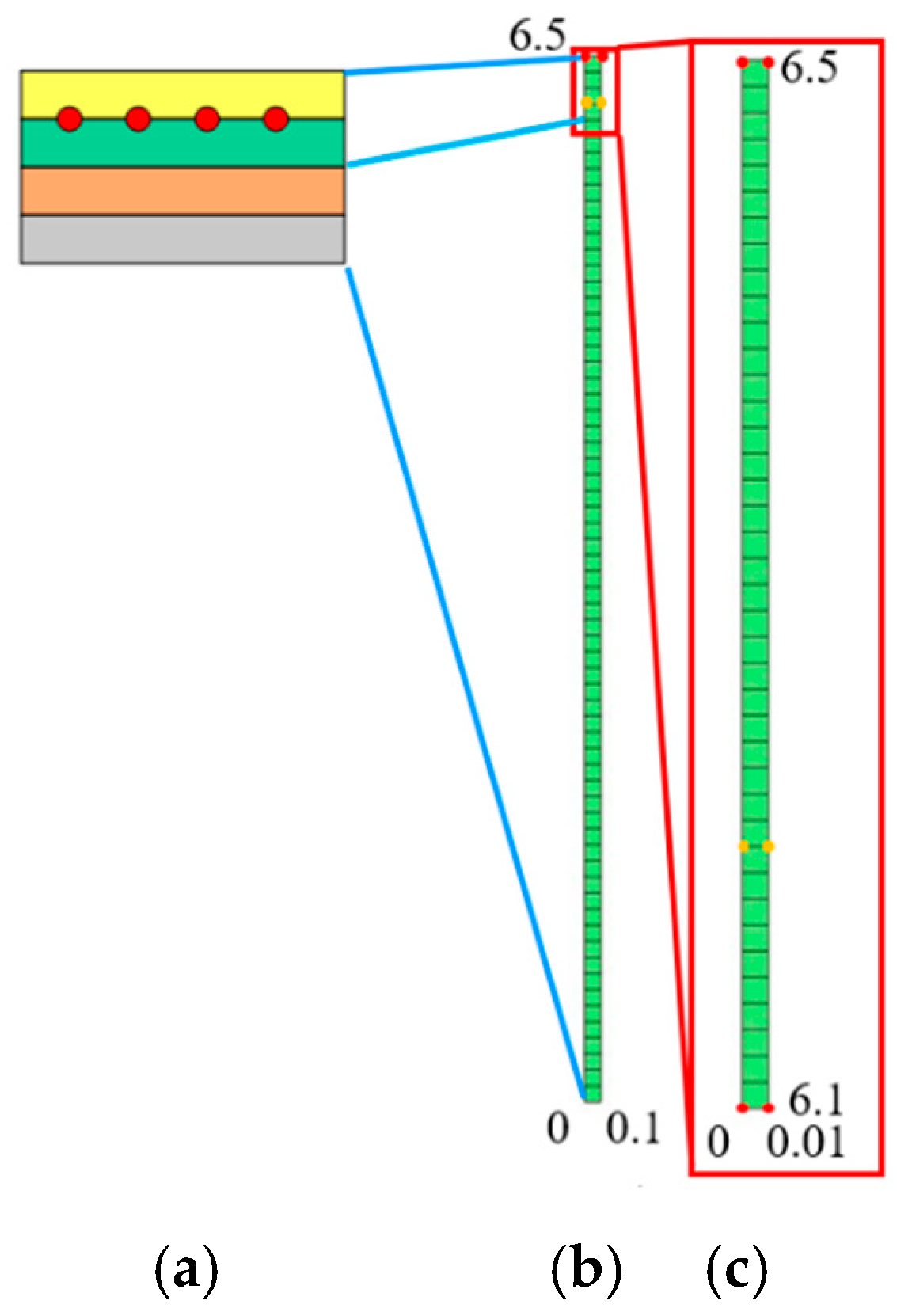
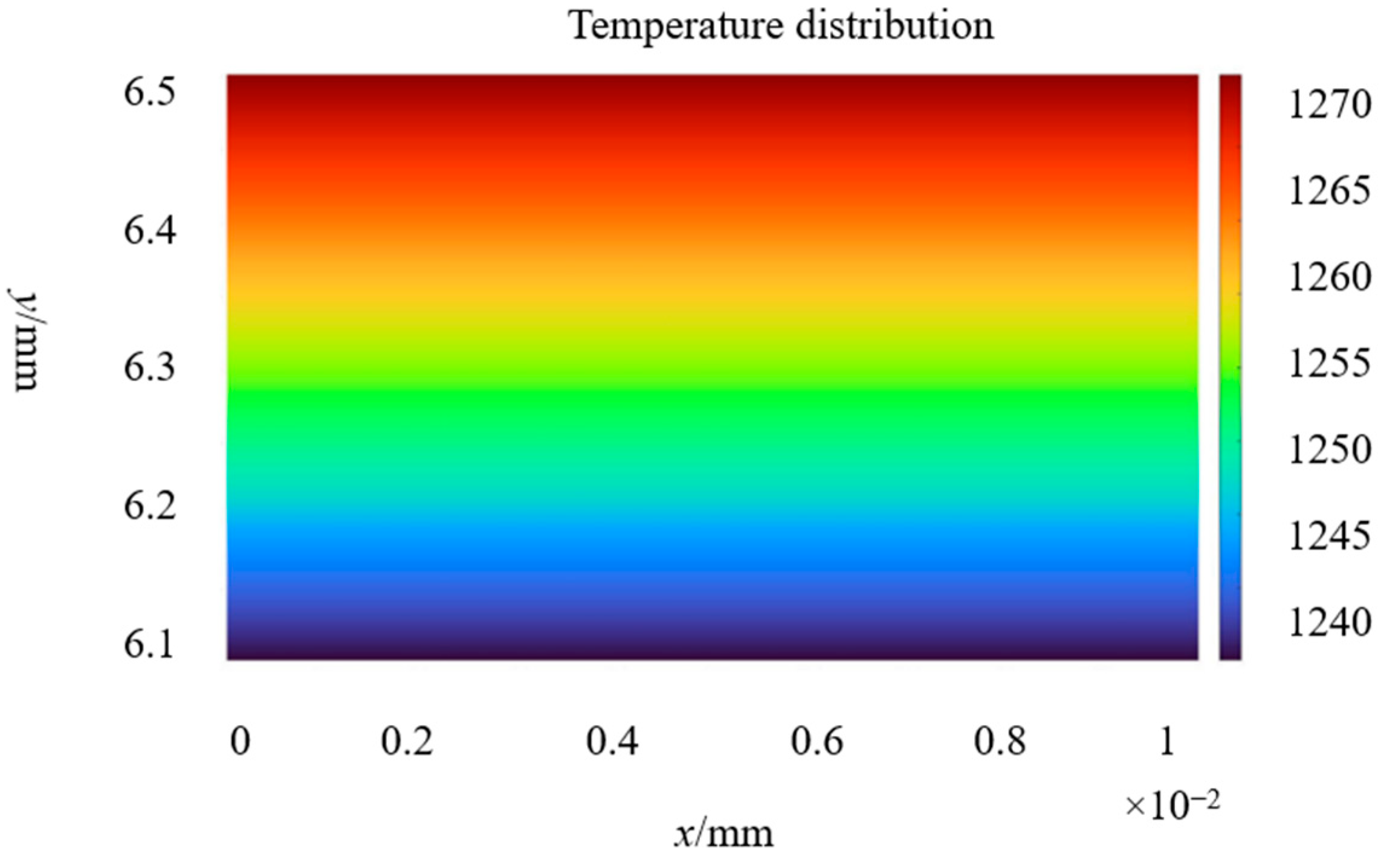




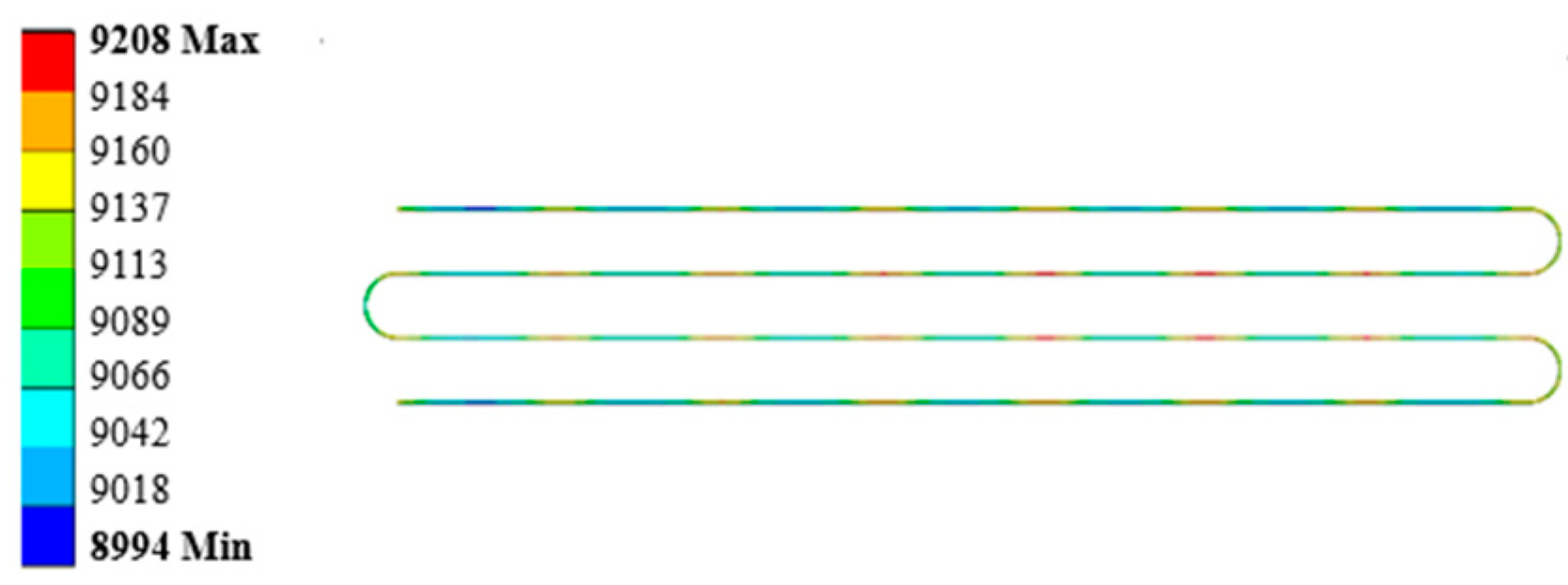
| Nodes | Temperature/K | x Coordinates | y Coordinates |
|---|---|---|---|
| 61 | 1221.87 | 0 | 6 |
| 62 | 1234.52 | 0 | 6.1 |
| 63 | 1244.10 | 0 | 6.2 |
| 64 | 1253.68 | 0 | 6.3 |
| 65 | 1263.26 | 0 | 6.4 |
| 66 | 1272.83 | 0 | 6.5 |
| Nodes | Temperature/K | y Co-ordinate | x Co-ordinate | Nodes | Temperature/K | y Co-ordinate | x Co-ordinate |
|---|---|---|---|---|---|---|---|
| 7 | 1240.97 | 6.16 | 0 | 48 | 1240.97 | 6.16 | 0.01 |
| 8 | 1241.88 | 6.17 | 0 | 49 | 1241.88 | 6.17 | 0.01 |
| 9 | 1242.79 | 6.18 | 0 | 50 | 1242.79 | 6.18 | 0.01 |
| 10 | 1243.70 | 6.19 | 0 | 51 | 1243.70 | 6.19 | 0.01 |
| 11 | 1245.20 | 6.20 | 0 | 52 | 1245.20 | 6.20 | 0.01 |
| 12 | 1246.70 | 6.21 | 0 | 53 | 1246.70 | 6.21 | 0.01 |
| 13 | 1247.61 | 6.22 | 0 | 54 | 1247.61 | 6.22 | 0.01 |
| 14 | 1248.53 | 6.23 | 0 | 55 | 1248.53 | 6.23 | 0.01 |
| Uncertainty Factor | Contents Include |
|---|---|
| Physical parameters | Coefficient of thermal expansion of grid wire α4, thermal expansion coefficient of the covering layer α3, elastic modulus of the substrate E3, thermal expansion coefficient of the transition layer α2, and elastic modulus of the transition layer E2 |
| Geometric dimensions | Grid wire diameter d4, basal thickness h3, and transition layer thickness h2 |
| Load | Force load F and temperature load T4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhang, F.; Ai, Y.; Tian, J.; Wang, Z. Structural Uncertainty Analysis of High-Temperature Strain Gauge Based on Monte Carlo Stochastic Finite Element Method. Sensors 2023, 23, 8647. https://doi.org/10.3390/s23208647
Zhao Y, Zhang F, Ai Y, Tian J, Wang Z. Structural Uncertainty Analysis of High-Temperature Strain Gauge Based on Monte Carlo Stochastic Finite Element Method. Sensors. 2023; 23(20):8647. https://doi.org/10.3390/s23208647
Chicago/Turabian StyleZhao, Yazhi, Fengling Zhang, Yanting Ai, Jing Tian, and Zhi Wang. 2023. "Structural Uncertainty Analysis of High-Temperature Strain Gauge Based on Monte Carlo Stochastic Finite Element Method" Sensors 23, no. 20: 8647. https://doi.org/10.3390/s23208647
APA StyleZhao, Y., Zhang, F., Ai, Y., Tian, J., & Wang, Z. (2023). Structural Uncertainty Analysis of High-Temperature Strain Gauge Based on Monte Carlo Stochastic Finite Element Method. Sensors, 23(20), 8647. https://doi.org/10.3390/s23208647






