VKECE-3D: Energy-Efficient Coverage Enhancement in Three-Dimensional Heterogeneous Wireless Sensor Networks Based on 3D-Voronoi and K-Means Algorithm
Abstract
1. Introduction
- To improve the network homogeneity, a secondary deployment of nodes using a highly destructive polynomial mutation strategy is proposed based on the idea of mutation characteristics;
- After the elbow method determines the quantity of clusters k, the nodes after secondary deployment are divided into several clusters using K-means, and the optimal sensing radius of the computational unit is calculated using 3D-Voronoi partition to lower the quantity of active nodes and improve the network’s QoS;
- Network data communication is divided into single-hop communication and multi-hop communication. The polling working mechanism is established according to the distance of the centroid from near to far. All nodes outside the unit centroid are dormant to lower the nodes’ energy consumption and lengthen the network life cycle.
2. Related Works
3. System Model and Term Definition
3.1. Network Model
3.2. Perceptual Model
3.3. Energy Consumption Model
3.4. Description of Connectivity
3.5. Related Concepts
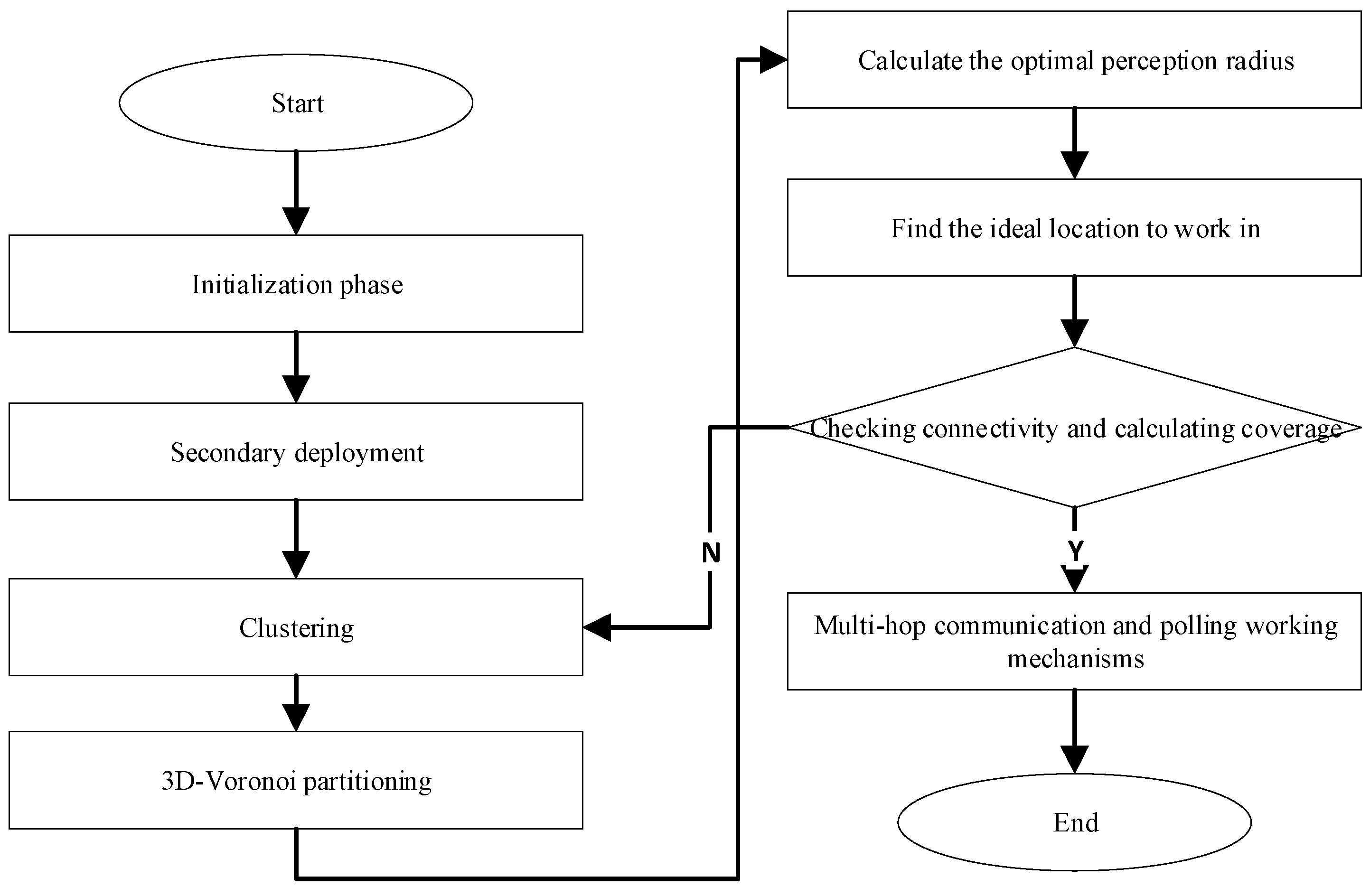
4. Energy-Efficient Coverage Enhancement Algorithm VKECE-3D
4.1. Highly Destructive Polynomial Mutation Strategy
4.2. K-Means Clustering
- Select sample data points at random from the sample data set as the primary cluster center ;
- The Euclidean distance is used to compute the distance between the sample data and the center of each cluster, and the clusters with the smallest distance between them are partitioned;
- After one round of division, recalculate the cluster center of each cluster using Formula (14);
- Repeat the above two operations until the partition result is unchanged.
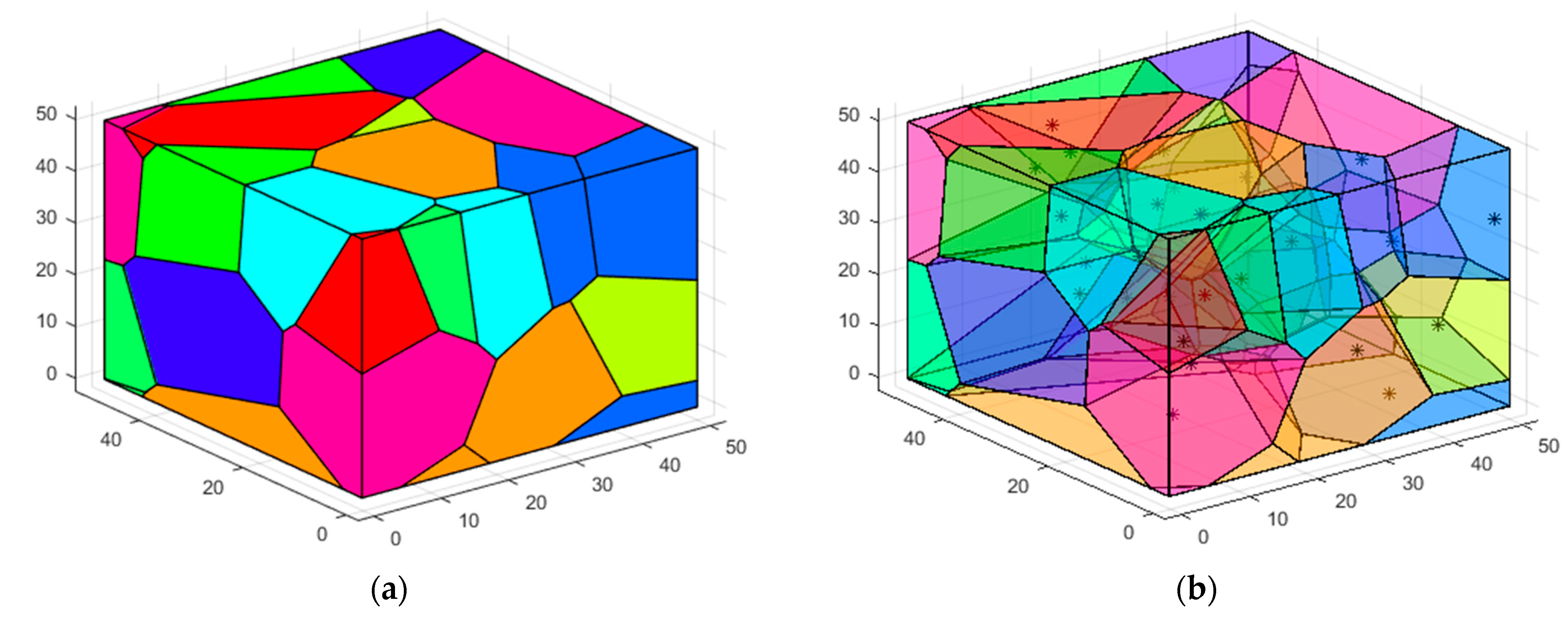
4.3. 3D-Voronoi Partition
- The distance from each center of mass to its 3D-Voronoi vertex is calculated, and the cell’s optimal perceptual radius is confirmed by the greatest distance between them.
- Quantity of 3D-Voronoi cells is equal to the minimum quantity of active nodes needed by the network to achieve the QoS standards. The best deployment position of the active node is defined as the cell’s centroid in 3D-Voronoi space.
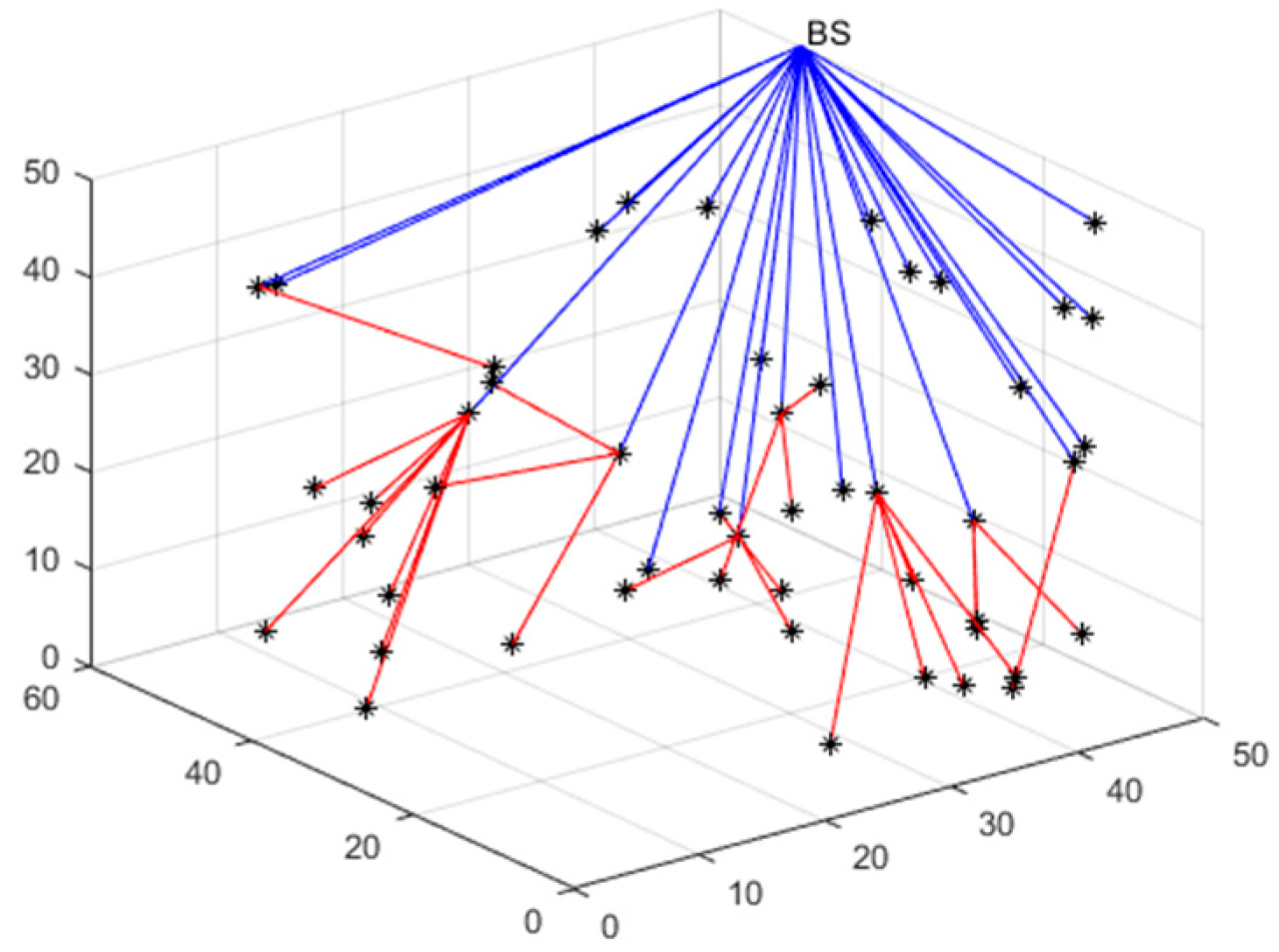
4.4. Multi-Hop Communication and Polling Working Mechanism
4.5. VKECE-3D Algorithm
| Algorithm 1: VKECE-3D |
| Input: Location of N sensor nodes; Maximum number of iterations Output: Deployment Solutions 1: In the target area R, a random deployment method is taken to initialize N sensor nodes. 2: Secondary deployment using highly destructive polynomial mutation strategy nodes 3: for (t = 1, 2…,) 4: Determine the clustering algorithm hyperparameter using the elbow method 5: Cluster the nodes using K-means and find the clustering centers 6: Perform 3D-Voronoi partitioning based on clustering centers 7: The optimal perceptual radius of a cell is defined as the farthest distance from the centroid to the vertex of the 3D-Voronoi cell 8: Within each 3D-Voronoi cell, the node closest to the center of mass moves to the center of mass and starts working, while the rest of the nodes are dormant 9: Verify network connection, Kruskal’s algorithm constructs a minimal spanning tree 10: If the coverage of the network is higher than 90% and the connection of the network satisfies the criteria, stop the loop; otherwise, continue 11: Return best deployment solutions 12: The multi-hop communication and polling working mechanisms start to take effect. |
4.6. Complexity Analysis
5. Simulation Result Analysis
5.1. Experimental Environment
5.2. Method of Comparison
- GHND [20]: GHND (Grid-based Hybrid Network Deployment) is a representative algorithm to ensure energy-efficient deployment schemes based on grid hybrid deployment to upgrade the energy efficiency and load balancing of WSNs. In the network, a technique of splitting and merging is proposed to enhance the uniformity of sensors. The network can enhance the best load balance state by merging the low-density adjacent areas and splitting the high-density adjacent areas. Benefits in load balancing, network life cycle, and efficiency are all high when using this strategy.
- CSPM [39]: CSPM (Cuckoo Search with highly disruptive Polynomial Mutation) is initially designed to improve the problem of scheduling algorithms in cloud computing environments tending to fall into local optima. Its application to WSN node deployments improves node uniformity and thus the coverage of the network.
- CS [43]: CS (Cuckoo Search Algorithm) is a representative of a traditional swarm-intelligence algorithm to deal with 3D problems in ascending dimensions and is a bionic optimization algorithm that simulates the reproductive characteristics of the aggressive nest-seeking and egg-hatching of cuckoos. It has the advantages of setting fewer parameters, a simple process, and fast convergence and has good robustness for many optimization problems. It has been widely used in industrial design and in other practical problems.
- MACHPS [13]: An example of a swarm intelligence algorithm combined with a sleep-wake mechanism is MACHPS (Mobile Assisted Coverage Hole Patching Scheme). It has the potential to vastly improve network coverage and extend the useful life of a network. Before anything else, a scattershot network of sensor nodes is placed across the region of interest and left there to remain motionless or in a sleep state. Second, we partition the whole network into squares called “grids,” and we calculate the coverage percentage for each grid. As a candidate grid, we choose the one with the lowest coverage. Particle swarm optimization (PSO) is then utilized to estimate the mobile locations of sensor nodes, waking up dormant mobile sensors to fill in the coverage hole.
- IPSO-IRCD [44]: IPSO-IRCD is a two-stage coverage optimization strategy that addresses an enhanced particle swarm algorithm with a node coverage schedule. In order to discover potential node placements, IPSO computes the particle fitness value and compares it to the prior ideal value, so avoiding the issue of losing the optimal solution of the original method. To find the best fit between nodes and candidate sites without compromising network coverage, IRCD, an optimization method, takes into account both the coverage increments and the move distance to make its selections. It is a great solution for wireless sensor networks’ coverage redundancy and hole problems.
5.3. Operation Process Simulation
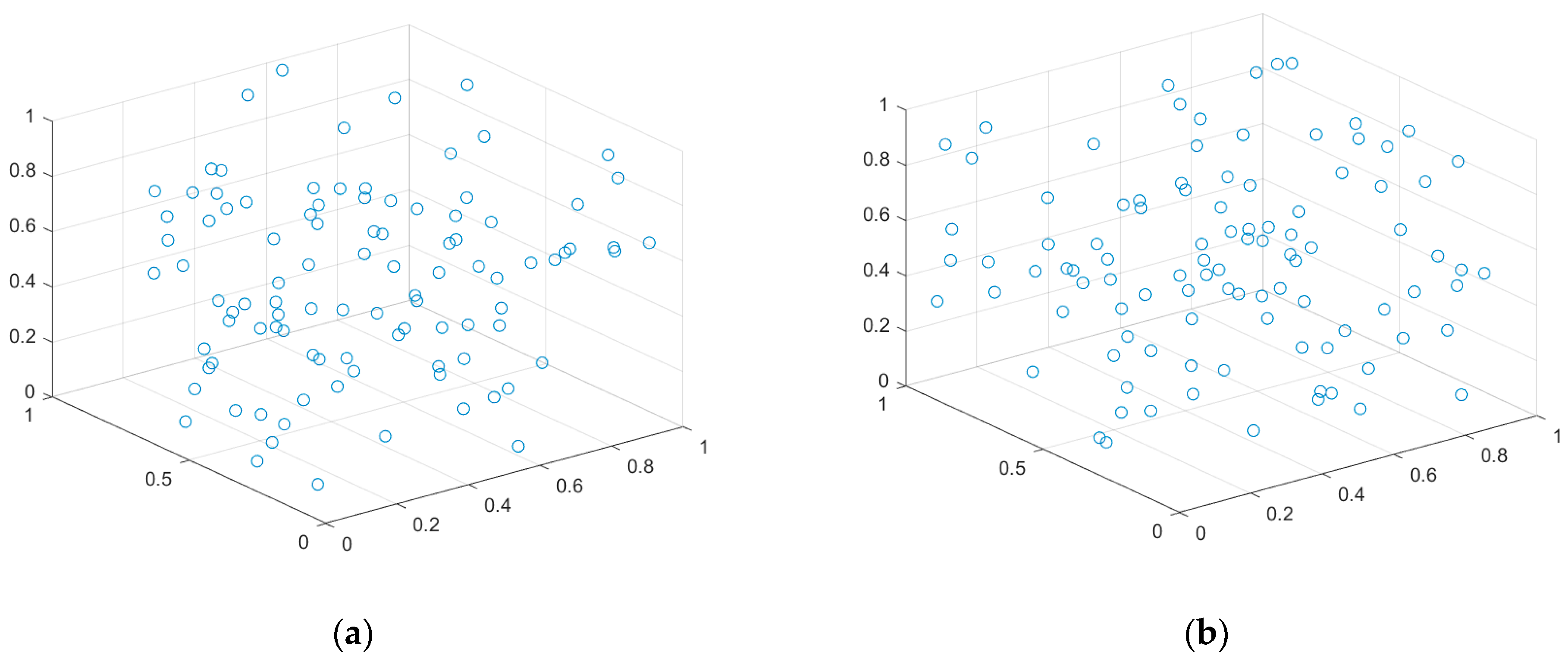
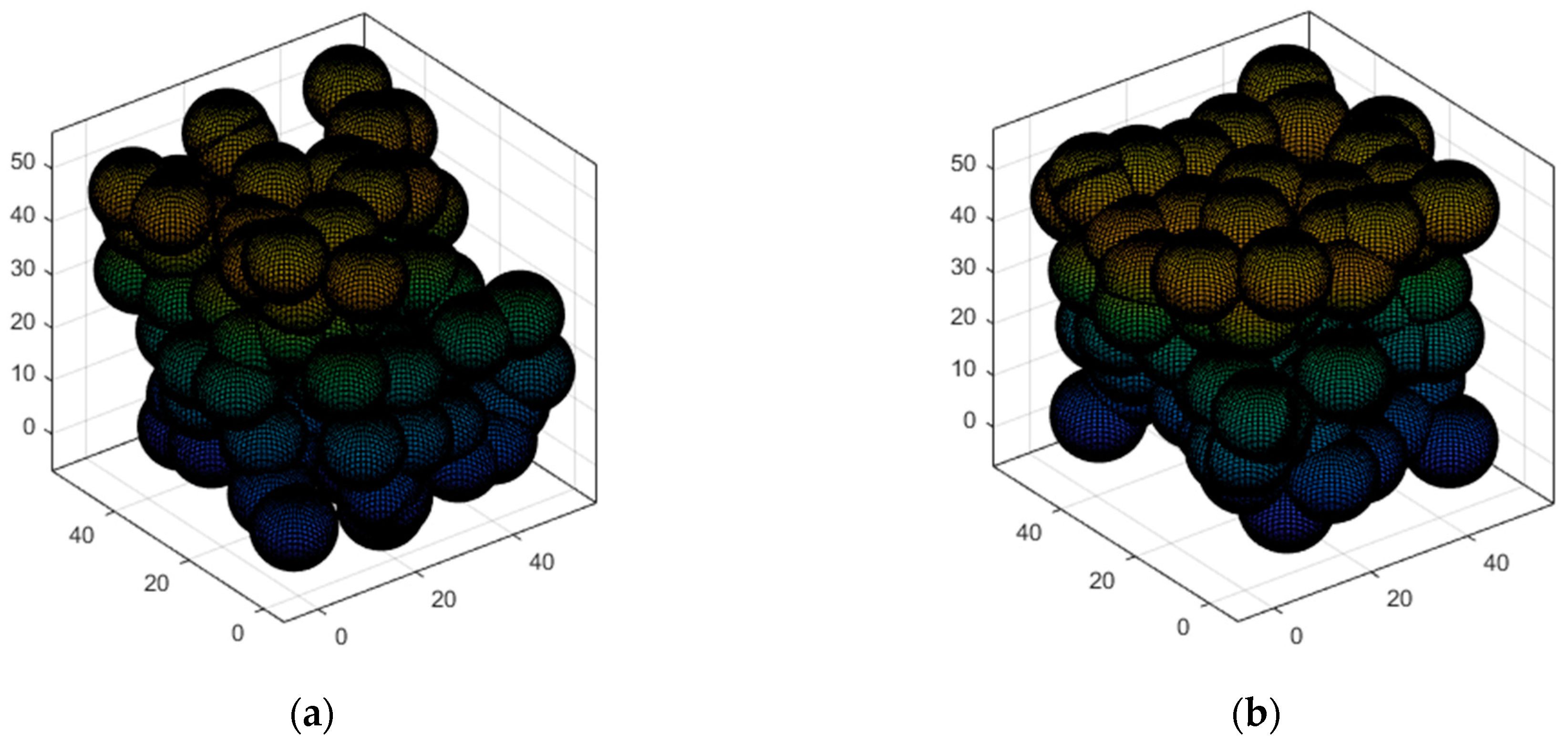
5.3.1. Case 1: Highly Destructive Polynomial Mutation Strategy for the Secondary Deployment of Nodes
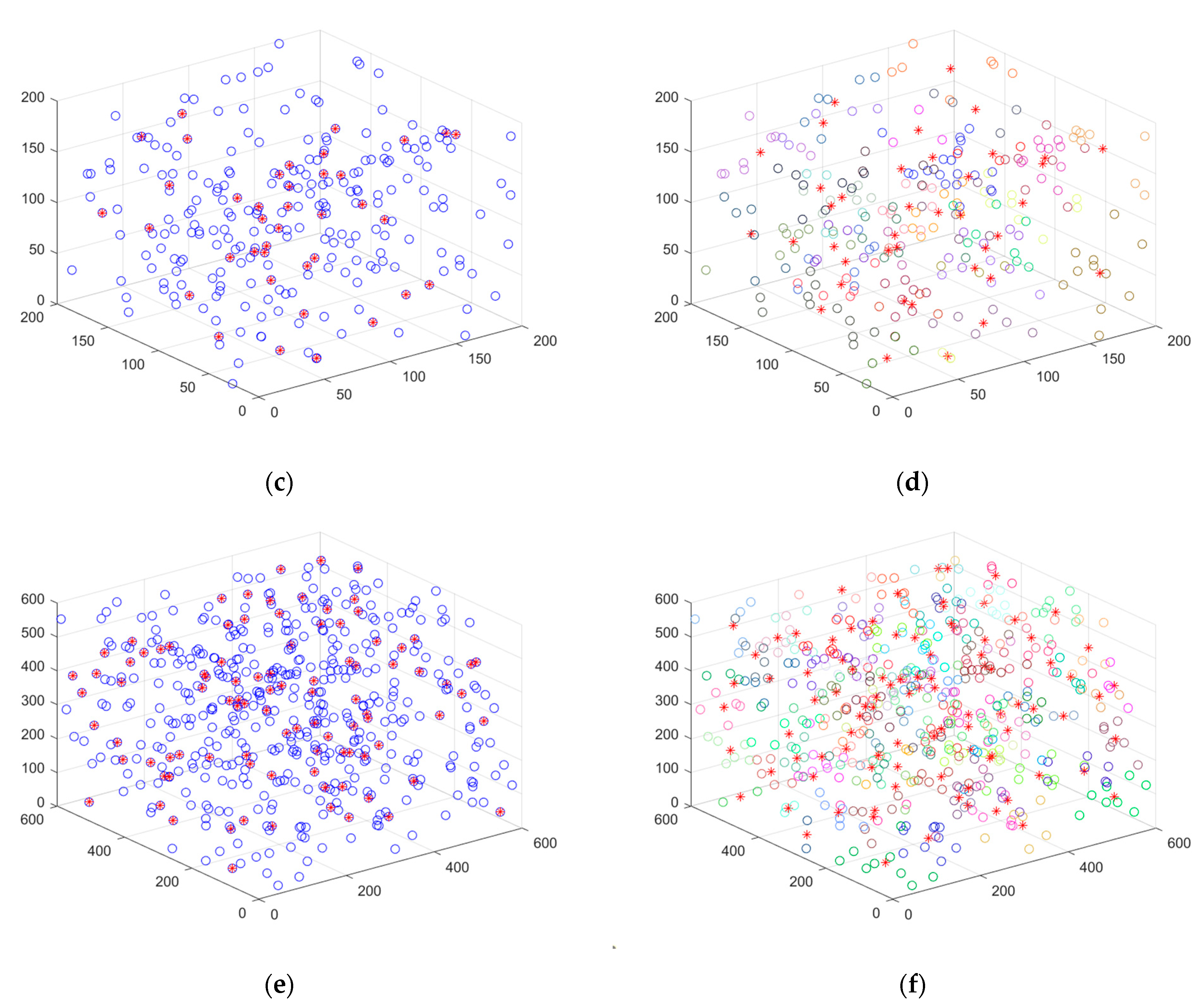
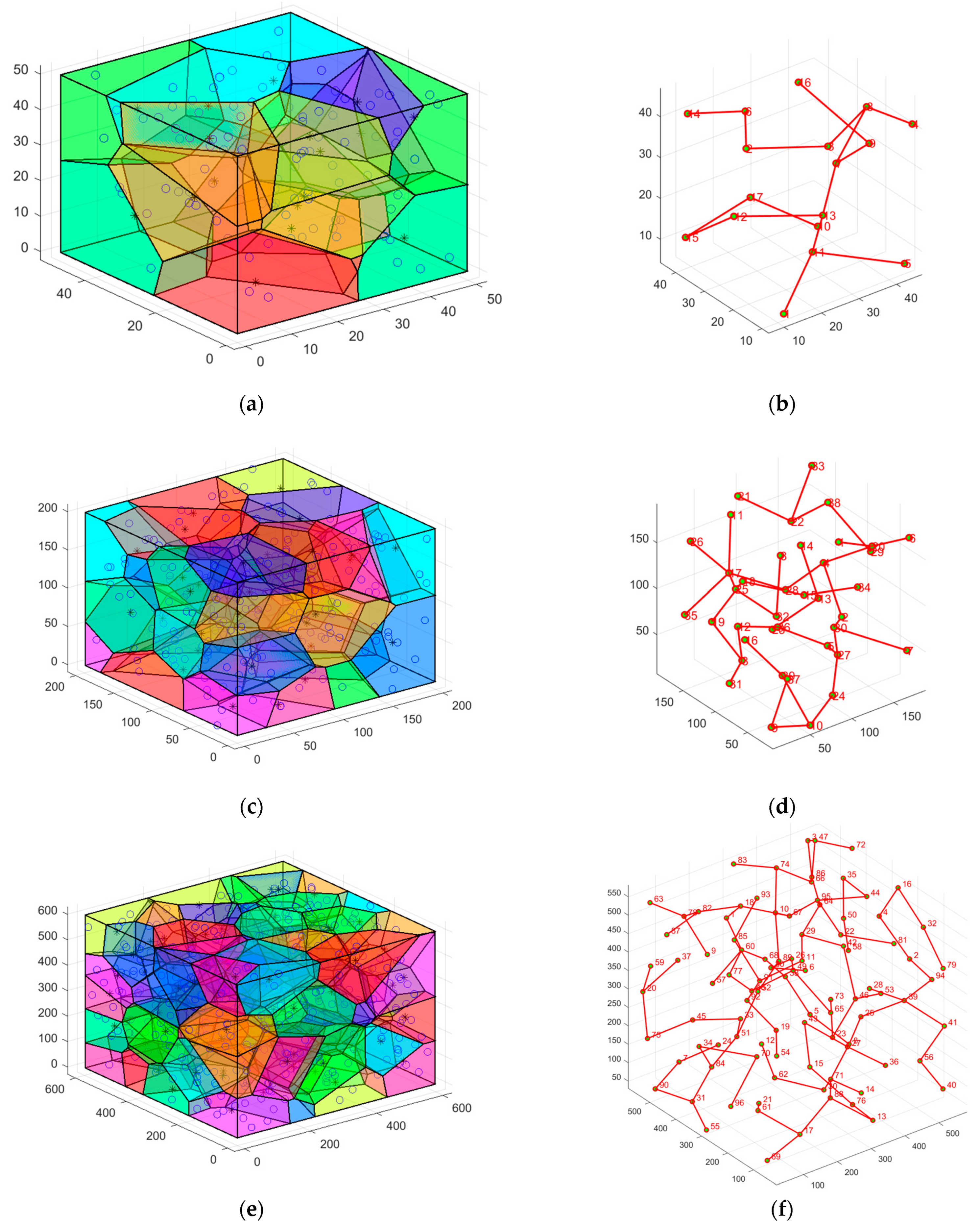
5.3.2. Case 2: K-Means Clustering to Determine the Minimum Quantity of Nodes to Be Deployed in the Network
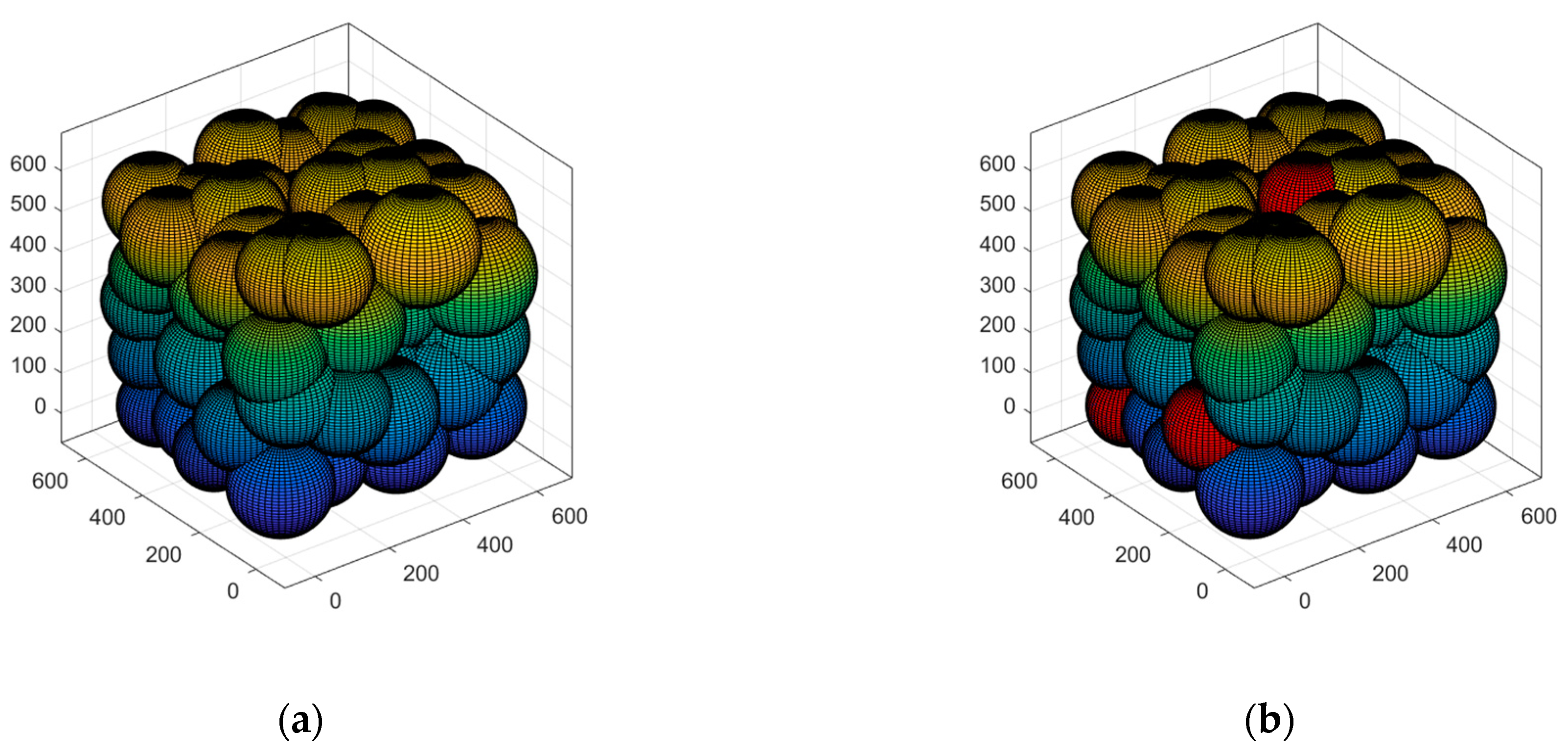
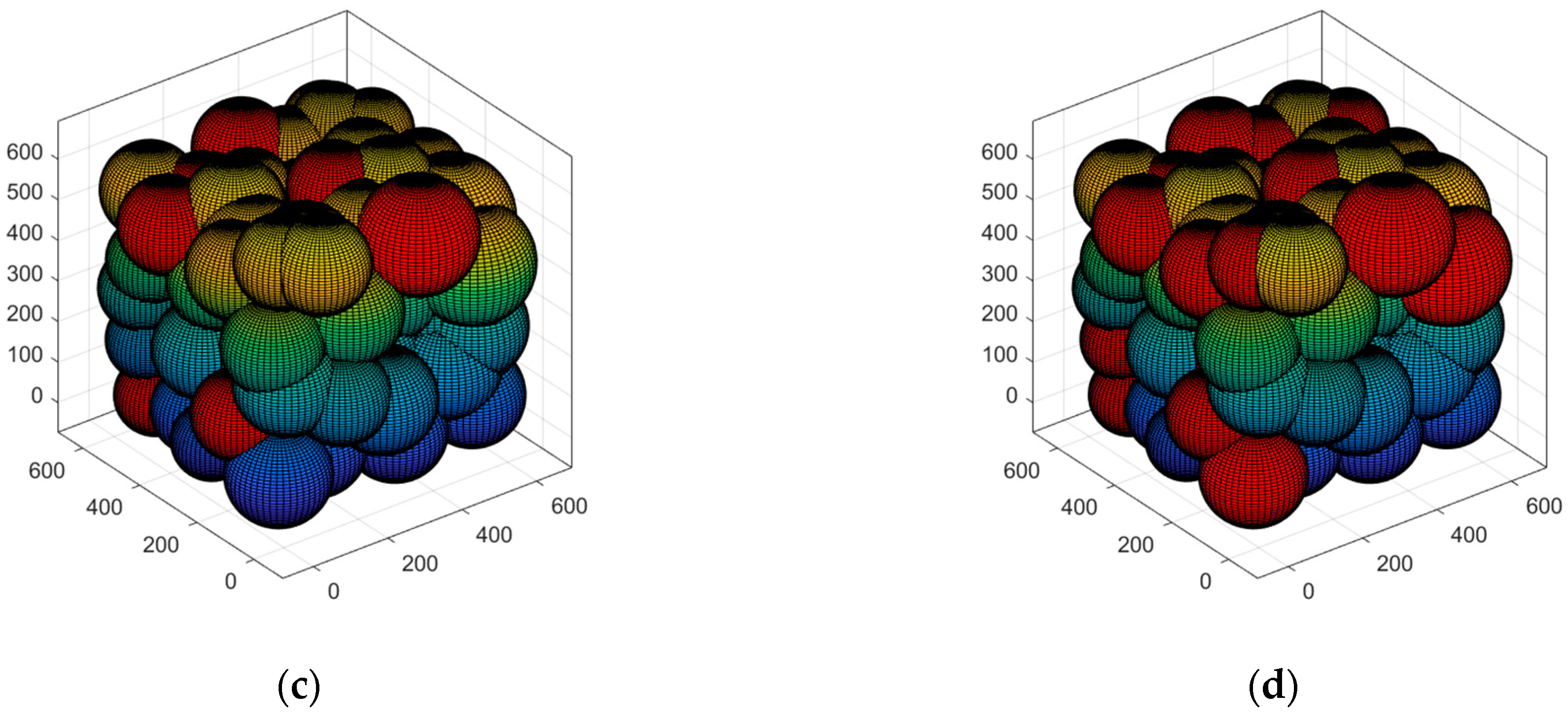
5.3.3. Case 3: Moving the Sensor Nodes to the Optimal Position and Verifying Network Connectivity
5.3.4. Case 4: Multi-Hop Communication and Polling Working Mechanism to Lengthen the Network’s Life Cycle
5.4. Performance Testing
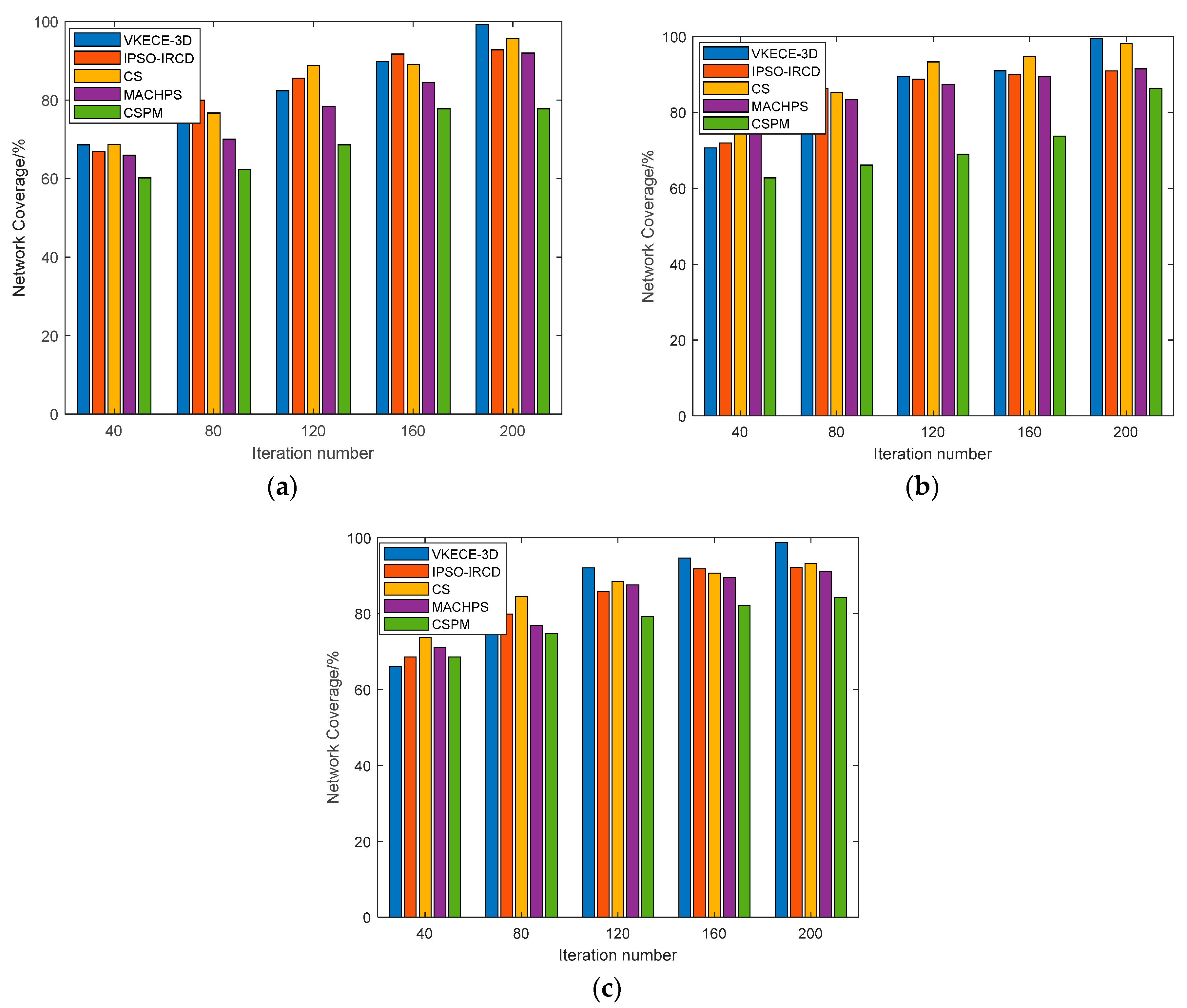
5.4.1. Coverage Performance Testing
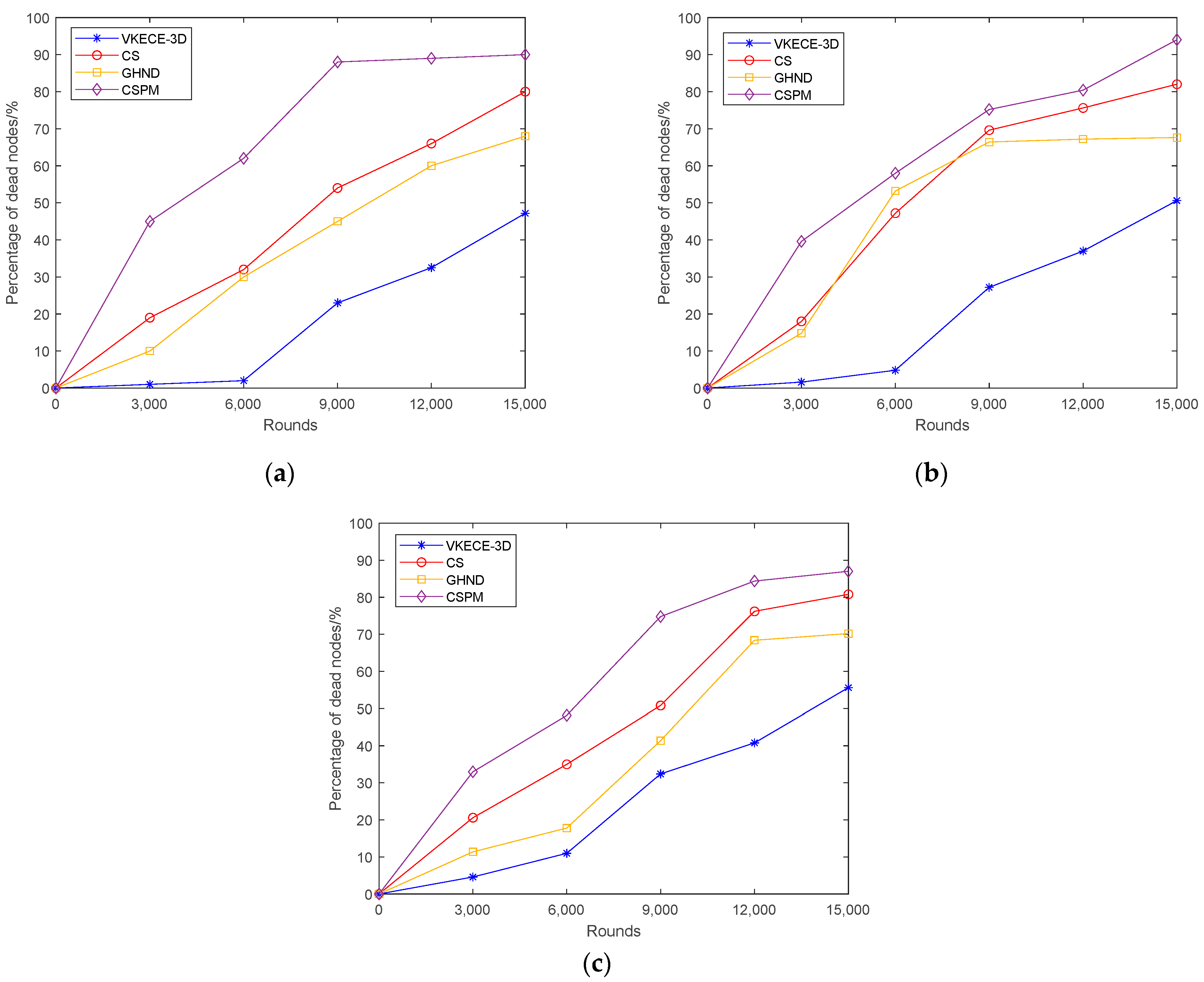
5.4.2. Proportion of Dead Nodes in Different Rounds
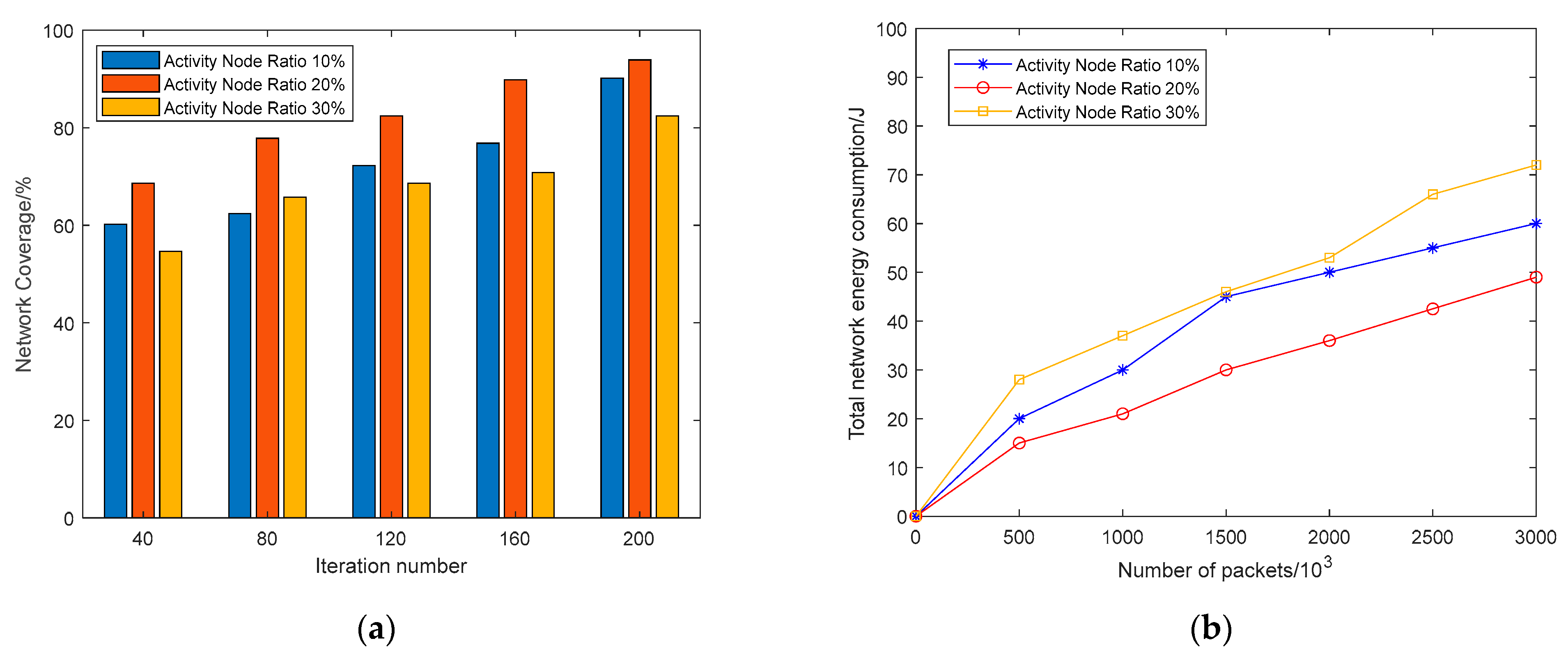
5.4.3. Activity Node Ratio
6. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Temene, N.; Sergiou, C.; Georgiou, C.; Vassiliou, V. A Survey on Mobility in Wireless Sensor Networks. Ad Hoc Networks 2022, 125, 102726. [Google Scholar] [CrossRef]
- Aziz, Z.A.A.; Ameen, S.Y.A. Air pollution monitoring using wireless sensor networks. J. Inf. Technol. Inform. 2021, 1, 20–25. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, F.; Wang, Y. Integration of Wireless Sensor Network and IoT for Smart Environment Monitoring System. J. Interconnect. Netw. 2021, 22, 2143010. [Google Scholar] [CrossRef]
- Ahmad, I.; Shah, K.; Ullah, S. Military applications using wireless sensor networks: A survey. Int. J. Eng. Sci. 2016, 6, 7039–7043. [Google Scholar] [CrossRef]
- Erdelj, M.; Król, M.; Natalizio, E. Wireless Sensor Networks and Multi-UAV systems for natural disaster management. Comput. Netw. 2017, 124, 72–86. [Google Scholar] [CrossRef]
- Torkestani, J.A. An adaptive energy-efficient area coverage algorithm for wireless sensor networks. Ad Hoc Netw. 2013, 11, 1655–1666. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M. Coverage Control Optimization Algorithm for Wireless Sensor Networks Based on Combinatorial Mathematics. Math. Probl. Eng. 2021, 2021, 6066379.1–6066379.8. [Google Scholar] [CrossRef]
- Pananjady, A.; Bagaria, V.K.; Vaze, R. Optimally Approximating the Coverage Lifetime of Wireless Sensor Networks. IEEE/ACM Trans. Netw. 2016, 25, 98–111. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Y.; Xie, D.; Hu, S.; Wang, C.; Li, Y. Coverage Enhancement Strategy for WSNs Based on Virtual Force-Directed Ant Lion Optimization Algorithm. IEEE Sens. J. 2021, 21, 19611–19622. [Google Scholar] [CrossRef]
- Chawra, V.K.; Gupta, G.P. Memetic Algorithm based Energy Efficient Wake-up Scheduling Scheme for Maximizing the Network Lifetime, Coverage and Connectivity in Three-Dimensional Wireless Sensor Networks. Wirel. Pers. Commun. 2022, 123, 1507–1522. [Google Scholar] [CrossRef]
- Zhao, X.-Q.; Cui, Y.-P.; Gao, C.-Y.; Guo, Z.; Gao, Q. Energy-Efficient Coverage Enhancement Strategy for 3-D Wireless Sensor Networks Based on a Vampire Bat Optimizer. IEEE Internet Things J. 2019, 7, 325–338. [Google Scholar] [CrossRef]
- Feng, Y.; Zhao, S.; Liu, H. Analysis of Network Coverage Optimization Based on Feedback K-Means Clustering and Artificial Fish Swarm Algorithm. IEEE Access 2020, 8, 42864–42876. [Google Scholar] [CrossRef]
- Wang, J.; Ju, C.; Kim, H.J.; Sherratt, R.S.; Lee, S. A mobile assisted coverage hole patching scheme based on particle swarm optimization for WSNs. Clust. Comput. 2019, 22, 1787–1795. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, L.; Wu, W.; Lin, L.; Li, Z.; Tong, Y. A Metaheuristic Algorithm for Coverage Enhancement of Wireless Sensor Networks. Wirel. Commun. Mob. Comput. 2022, 2022, 7732989. [Google Scholar] [CrossRef]
- Wang, S.; Yang, X.; Wang, X.; Qian, Z. A Virtual Force Algorithm-Lévy-Embedded Grey Wolf Optimization Algorithm for Wireless Sensor Network Coverage Optimization. Sensors 2019, 19, 2735. [Google Scholar] [CrossRef] [PubMed]
- Deepa, R.; Venkataraman, R. Enhancing Whale Optimization Algorithm with Levy Flight for coverage optimization in wireless sensor networks. Comput. Electr. Eng. 2021, 94, 107359. [Google Scholar] [CrossRef]
- Chowdhury, A.; De, D. FIS-RGSO: Dynamic Fuzzy Inference System Based Reverse Glowworm Swarm Optimization of energy and coverage in green mobile wireless sensor networks. Comput. Commun. 2020, 163, 12–34. [Google Scholar] [CrossRef]
- Yin, J.; Deng, N.; Zhang, J. Wireless Sensor Network coverage optimization based on Yin-Yang pigeon-inspired optimization algorithm for Internet of Things. Internet Things 2022, 19, 100546. [Google Scholar] [CrossRef]
- Xiao, F.; Yang, Y.; Wang, R.; Sun, L. A Novel Deployment Scheme Based on Three-Dimensional Coverage Model for Wireless Sensor Networks. Sci. World J. 2014, 2014, 846784. [Google Scholar] [CrossRef]
- Farman, H.; Javed, H.; Ahmad, J.; Jan, B.; Zeeshan, M. Grid-Based Hybrid Network Deployment Approach for Energy Efficient Wireless Sensor Networks. J. Sens. 2016, 2016, 2326917. [Google Scholar] [CrossRef]
- Charr, J.-C.; Deschinkel, K.; Mansour, R.H.; Hakem, M. Partial coverage optimization under network connectivity constraints in heterogeneous sensor networks. Comput. Netw. 2022, 210, 108928. [Google Scholar] [CrossRef]
- Hao, Z.; Xu, H.; Dang, X.; Qu, N. Method for Patching Three-Dimensional Surface Coverage Loopholes of Hybrid Nodes in Wireless Sensor Networks. J. Sens. 2020, 2020, 6492457. [Google Scholar] [CrossRef]
- Gou, P.; Mao, G.; Zhang, F.; Jia, X. Reconstruction of coverage hole model and cooperative repair optimization algorithm in heterogeneous wireless sensor networks. Comput. Commun. 2020, 153, 614–625. [Google Scholar] [CrossRef]
- Zhang, J.; Chu, H.; Feng, X. Efficient Coverage Hole Detection Algorithm Based on the Simplified Rips Complex in Wireless Sensor Networks. J. Sens. 2020, 2020, 3236970. [Google Scholar] [CrossRef]
- Le Nguyen, P.; Nguyen, K.; Vu, H.; Ji, Y. TELPAC: A time and energy efficient protocol for locating and patching coverage holes in WSNs. J. Netw. Comput. Appl. 2019, 147, 102439. [Google Scholar] [CrossRef]
- Yanfei, J.; Guangda, C.; Liquan, Z. Energy-Efficient Routing Protocol Based on Zone for Heterogeneous Wireless Sensor Networks. J. Electr. Comput. Eng. 2021, 2021, 5557756. [Google Scholar] [CrossRef]
- Katti, A.; Lobiyal, D.K. Node deployment strategies and coverage prediction in 3D wireless sensor network with scheduling. Adv. Comput. Sci. Technol. 2017, 10, 2243–2255. [Google Scholar] [CrossRef]
- Bairagi, K.; Mitra, S.; Bhattacharya, U. Multi-objective optimization for coverage aware energy consumption in wireless 3D video sensor network. Comput. Commun. 2022, 195, 262–280. [Google Scholar] [CrossRef]
- Ali, H.; Tariq, U.U.; Hussain, M.; Lu, L.; Panneerselvam, J.; Zhai, X. ARSH-FATI: A Novel Metaheuristic for Cluster Head Selection in Wireless Sensor Networks. IEEE Syst. J. 2020, 15, 2386–2397. [Google Scholar] [CrossRef]
- Chowdhury, A.; De, D. Energy-efficient coverage optimization in wireless sensor networks based on Voronoi-Glowworm Swarm Optimization-K-means algorithm. Ad Hoc Netw. 2021, 122, 102660. [Google Scholar] [CrossRef]
- Dang, X.; Shao, C.; Hao, Z. Target Detection Coverage Algorithm Based on 3D-Voronoi Partition for Three-Dimensional Wireless Sensor Networks. Mob. Inf. Syst. 2019, 2019, 7542324. [Google Scholar] [CrossRef]
- Gou, P.; Mao, G.; Li, F.; Jia, X. Optimized Algorithm for Recovering Coverage Holes in Heterogeneous Wireless Sensor Networks with Node Stable Matching. J. Sens. Actuators 2019, 32, 908–914+930. [Google Scholar] [CrossRef]
- Wang, L.M.; Li, F.; Qin, Y. Resilient method for recovering coverage holes of wireless sensor networks by using mobile nodes. J. Commun. 2011, 32, 1–8. [Google Scholar] [CrossRef]
- Mahboubi, H.; Moezzi, K.; Aghdam, A.G.; Sayrafian-Pour, K.; Marbukh, V. Self-deployment algorithms for coverage problem in a network of mobile sensors with unidentical sensing ranges. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Zou, Y.; Chakrabarty, K. A Distributed Coverage- and Connectivity-Centric Technique for Selecting Active Nodes in Wireless Sensor Networks. IEEE Trans. Comput. 2005, 54, 978–991. [Google Scholar] [CrossRef]
- Heinzelman, W.; Chandrakasan, A.; Balakrishnan, H. Energy Efficient Communicati-on Protocol for Wireless Microsensor Networks. In Proceedings of the Thirty Third Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; Volume 2, pp. 3005–3014. [Google Scholar] [CrossRef]
- Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks, Graph Theoretic Methods in Multiagent Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Mamun, A.A.; Rajasekaran, S. An efficient minimum spanning tree algorithm. In Proceedings of the 2016 IEEE Symposium on Computers and Communication (ISCC), Messina, Italy, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1047–1052. [Google Scholar] [CrossRef]
- Alawad, N.A.; Abed-Alguni, B.H. Discrete Island-Based Cuckoo Search with Highly Disruptive Polynomial Mutation and Opposition-Based Learning Strategy for Scheduling of Workflow Applications in Cloud Environments. Arab. J. Sci. Eng. 2021, 46, 3213–3233. [Google Scholar] [CrossRef]
- Rai, P.; Singh, S. A survey of clustering techniques. Int. J. Comput. Appl. 2010, 7, 1–5. [Google Scholar] [CrossRef]
- Thinsungnoen, T.; Kaoungku, N.; Durongdumronchai, P.; Kerdprasop, K.; Kerdprasop, N. The clustering validity with silhouette and sum of squared errors. Learning 2015, 3, 44–51. [Google Scholar] [CrossRef]
- Boukerche, A.; Fei, X. A voronoi approach for coverage protocols in wireless sensor networks. In Proceedings of the IEEE GLOBECOM 2007-IEEE Global Telecommunications Conference, Washington, DC, USA, 26–30 November 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 5190–5194. [Google Scholar] [CrossRef]
- Arivudainambi, D.; Balaji, S.; Poorani, T.S. Sensor deployment for target coverage in underwater wireless sensor network. In Proceedings of the 2017 International Conference on Performance Evaluation and Modeling in Wired and Wireless Networks (PEMWN), Paris, France, 28–30 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, J.; Li, H.; Luo, L.; Ou, J.; Zhang, Y. Multiobjective Optimization Strategy of WSN Coverage Based on IPSO-IRCD. J. Sens. 2022, 2022, 7483148. [Google Scholar] [CrossRef]







| Notations | Descriptions |
|---|---|
| R | target area |
| sensing range | |
| communication range | |
| coverage | |
| quantity of K-means algorithm cluster | |
| SSE | sum of the squared errors |
| Q | 3D-Voronoi cell |
| BS | distributed base station |
| Parameter List | Value of Parameter |
|---|---|
| Size of the target area | 50 × 50 × 50 , 200 × 200 × 200 , 600 × 600 × 600 |
| Iteration number | 250 |
| Number of nodes deployed randomly | 100, 250, 500 |
| Initial energy of every sensor | 5 J |
| Threshold battery power | 0.02 J |
| Circuit unit energy consumption | 50 nJ/bit |
| Free space channel parameter () | 10 pJ/bit/m3 |
| Multi-path channel parameter () | 0.0013 pJ/(bit/m4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gou, P.; Guo, B.; Guo, M.; Mao, S. VKECE-3D: Energy-Efficient Coverage Enhancement in Three-Dimensional Heterogeneous Wireless Sensor Networks Based on 3D-Voronoi and K-Means Algorithm. Sensors 2023, 23, 573. https://doi.org/10.3390/s23020573
Gou P, Guo B, Guo M, Mao S. VKECE-3D: Energy-Efficient Coverage Enhancement in Three-Dimensional Heterogeneous Wireless Sensor Networks Based on 3D-Voronoi and K-Means Algorithm. Sensors. 2023; 23(2):573. https://doi.org/10.3390/s23020573
Chicago/Turabian StyleGou, Pingzhang, Baoyong Guo, Miao Guo, and Shun Mao. 2023. "VKECE-3D: Energy-Efficient Coverage Enhancement in Three-Dimensional Heterogeneous Wireless Sensor Networks Based on 3D-Voronoi and K-Means Algorithm" Sensors 23, no. 2: 573. https://doi.org/10.3390/s23020573
APA StyleGou, P., Guo, B., Guo, M., & Mao, S. (2023). VKECE-3D: Energy-Efficient Coverage Enhancement in Three-Dimensional Heterogeneous Wireless Sensor Networks Based on 3D-Voronoi and K-Means Algorithm. Sensors, 23(2), 573. https://doi.org/10.3390/s23020573






