A Front-End Circuit for Two-Wire Connected Resistive Sensors with a Wire-Resistance Compensation
Abstract
:1. Introduction
2. New Front-End Circuit
2.1. Overall Description
2.2. Operating Principle
2.3. Operating Frequency
2.4. Non-Idealities
3. Materials and Methods
4. Experimental Results and Discussion
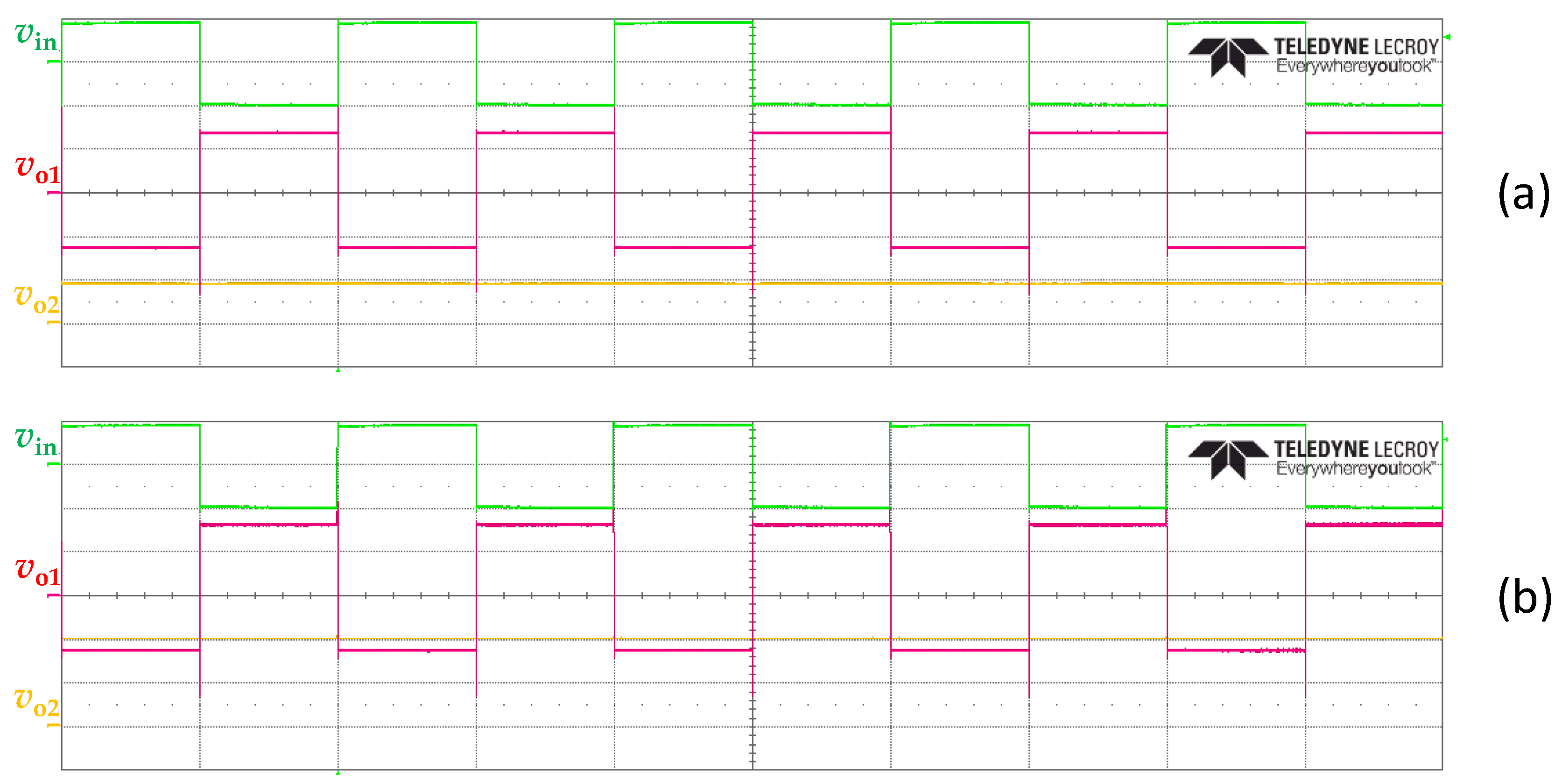
4.1. Experimental Waveforms
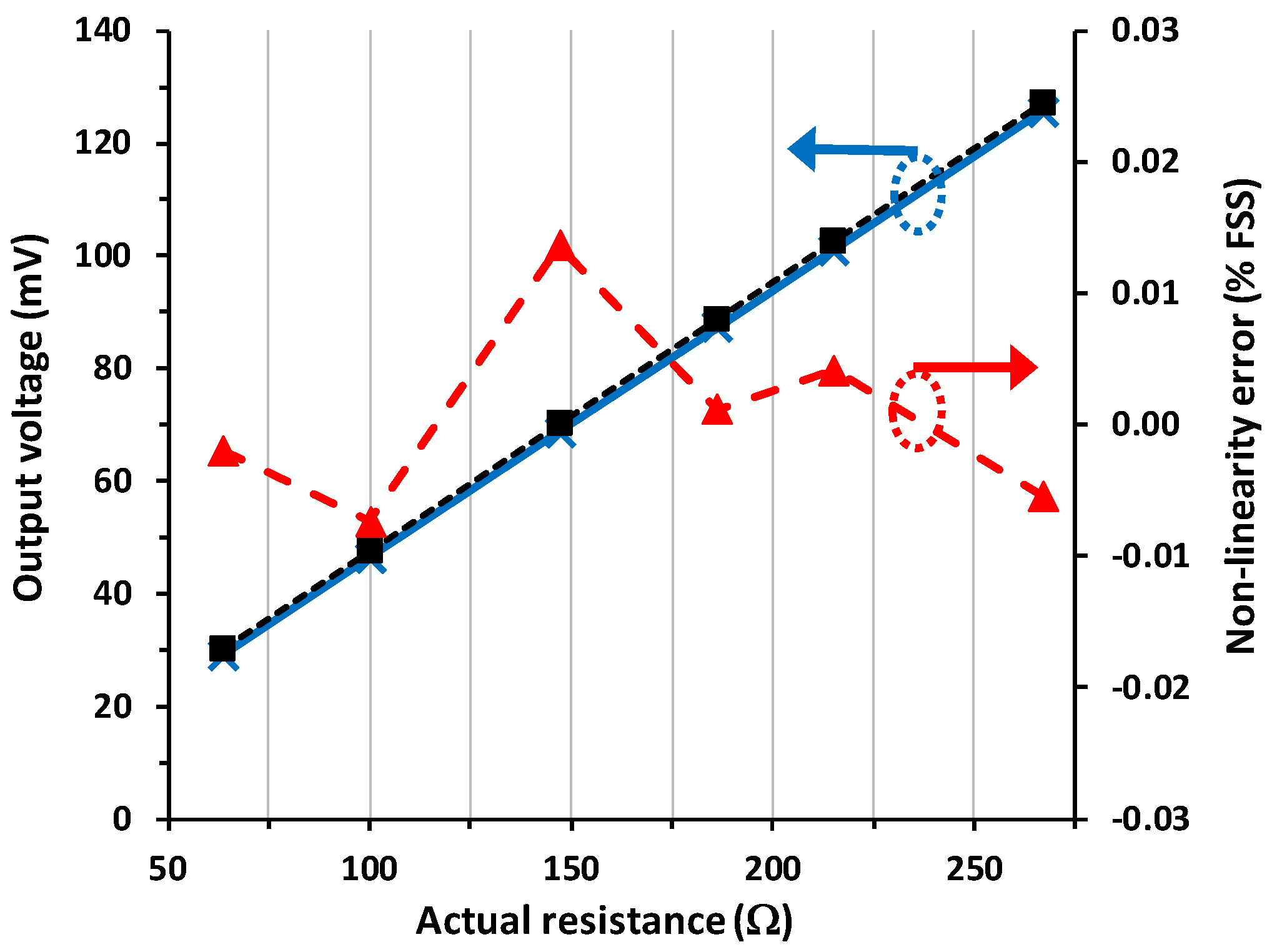
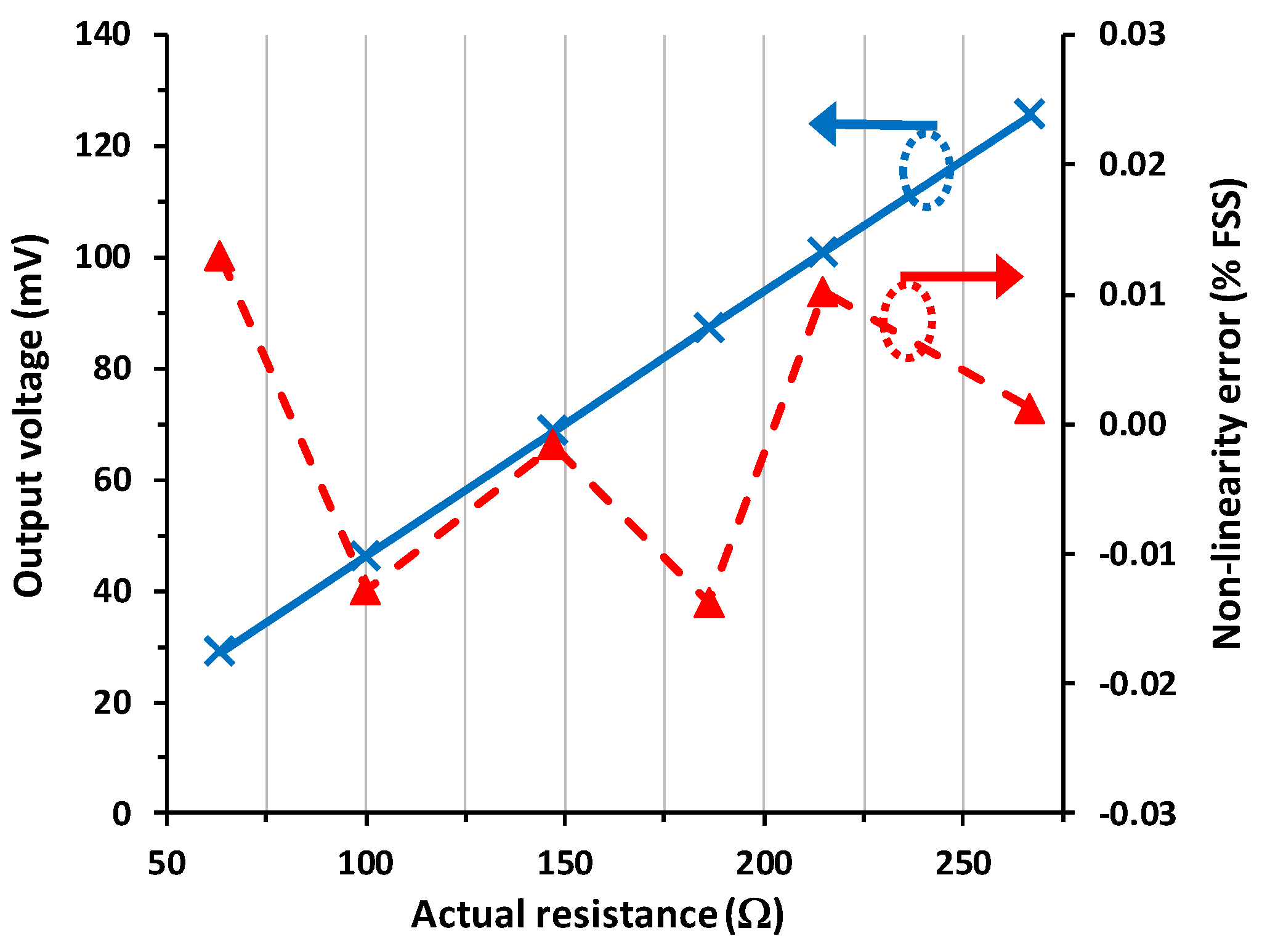
4.2. Input–Output Characteristic
4.3. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hidalgo-López, J.A.; Oballe-Peinado, Ó.; Castellanos-Ramos, J.; Sánchez-Durán, J.A. Two-Capacitor Direct Interface Circuit for Resistive Sensor Measurements. Sensors 2021, 21, 1524. [Google Scholar] [CrossRef] [PubMed]
- Pallàs-Areny, R.; Webster, J.G. Sensors and Signal Conditioning; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Mathew, T.; Elangovan, K.; Sreekantan, A.C. Accurate Interface Schemes for Resistance Thermometers with Lead Resistance Compensation. IEEE Trans. Instrum. Meas. 2023, 72, 2005904. [Google Scholar] [CrossRef]
- Nagarajan, P.R.; George, B.; Kumar, V.J. Improved Single-Element Resistive Sensor-to-Microcontroller Interface. IEEE Trans. Instrum. Meas. 2017, 66, 2736–2744. [Google Scholar] [CrossRef]
- Reverter, F. A Microcontroller-Based Interface Circuit for Three-Wire Connected Resistive Sensors. IEEE Trans. Instrum. Meas. 2022, 71, 2006704. [Google Scholar] [CrossRef]
- Elangovan, K.; Antony, A.; Sreekantan, A.C. Simplified Digitizing Interface-Architectures for Three-Wire Connected Resistive Sensors: Design and Comprehensive Evaluation. IEEE Trans. Instrum. Meas. 2022, 71, 2000309. [Google Scholar] [CrossRef]
- Reverter, F. A direct approach for interfacing four-wire resistive sensors to microcontrollers. Meas. Sci. Technol. 2023, 34, 03700. [Google Scholar] [CrossRef]
- Maiti, T.K.; Kar, A. A new and low cost lead resistance compensation technique for resistive sensors. Measurement 2010, 43, 735–738. [Google Scholar] [CrossRef]
- Anandanatarajan, R.; Mangalanathan, U.; Gandhi, U. Enhanced microcontroller interface of resistive sensors through resistance-to-time converter. IEEE Trans. Instrum. Meas. 2020, 69, 2698–2706. [Google Scholar] [CrossRef]
- Maiti, T.K. A novel lead-wire-resistance compensation technique using two-wire resistance temperature detector. IEEE Sens. J. 2006, 6, 1454–1458. [Google Scholar] [CrossRef]
- Maiti, T.K.; Kar, A. Novel remote measurement technique using resistive sensor as grounded load in an Opamp based V-to-I converter. IEEE Sens. J. 2009, 9, 244–245. [Google Scholar] [CrossRef]
- Rerkratn, A.; Prombut, S.; Kamsri, T.; Riewruja, V.; Petchmaneelumka, W. A Procedure for Precise Determination and Compensation of Lead-Wire Resistance of a Two-Wire Resistance Temperature Detector. Sensors 2022, 22, 4176. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Xiong, S.; Zhou, X. Lead-Wire-Resistance Compensation Technique Using a Single Zener Diode for Two-Wire Resistance Temperature Detectors (RTDs). Sensors 2020, 20, 2742. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Sohail, S.; Mangalanathan, U.; Gandhi, U.; Islam, T. A Novel Dual-Slope Resistance to Digital Converter With Lead Resistance Compensation. IEEE Trans. Instrum. Meas. 2023, 72, 2001410. [Google Scholar] [CrossRef]
- Hidalgo-López, J.A. Direct interface circuits for resistive sensors affected by lead wire resistances. Measurement 2023, 218, 113250. [Google Scholar] [CrossRef]
- Simić, M.; Radovanović, M.; Stavrakis, A.K.; Jeoti, V. Wireless Readout of Resistive Sensors. IEEE Sens. J. 2022, 22, 4235–4245. [Google Scholar] [CrossRef]
- Reverter, F. A Tutorial on Thermal Sensors in the 200th Anniversary of the Seebeck Effect. IEEE Sens. J. 2021, 21, 22122–22132. [Google Scholar] [CrossRef]




| Ref. | Circuit Topology | CCE | Range (Ω) | Max. NLE (% FSS) |
|---|---|---|---|---|
| [4] | MCU and 3 switches | No | [100, 146] | 1.04 1 |
| [8] | 555-timer in astable mode | No | [148, 826] | 1.07 2 |
| [9] | MCU, 555-timer, and 2 switches | No | [100, 150] | 0.33 |
| [10] | 4 switches, 4 S&H, and an amplifier | Yes | [49, 315] | 0.026 2 |
| [11] | Howland current source with a square excitation | Yes | [100, 1300] | 0.41 2 |
| [12] | Bipolar three-step current source | Yes | [100, 214] | Not available |
| This work | Inverting amplifier with a square excitation | Yes | [63, 267] | 0.013 |
| Scenario | Rw1 (Ω) | Rw2 (Ω) | Others |
|---|---|---|---|
| 1 | 0 | 0 | Reference scenario |
| 2 | 3.9 | 3.9 | Emulating a 10 m cable |
| 3 | 3.9 | 2 | Emulating a strong mismatch between the two wires |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reverter, F. A Front-End Circuit for Two-Wire Connected Resistive Sensors with a Wire-Resistance Compensation. Sensors 2023, 23, 8228. https://doi.org/10.3390/s23198228
Reverter F. A Front-End Circuit for Two-Wire Connected Resistive Sensors with a Wire-Resistance Compensation. Sensors. 2023; 23(19):8228. https://doi.org/10.3390/s23198228
Chicago/Turabian StyleReverter, Ferran. 2023. "A Front-End Circuit for Two-Wire Connected Resistive Sensors with a Wire-Resistance Compensation" Sensors 23, no. 19: 8228. https://doi.org/10.3390/s23198228
APA StyleReverter, F. (2023). A Front-End Circuit for Two-Wire Connected Resistive Sensors with a Wire-Resistance Compensation. Sensors, 23(19), 8228. https://doi.org/10.3390/s23198228






