Physical Layer Authenticated Image Encryption for IoT Network Based on Biometric Chaotic Signature for MPFrFT OFDM System
Abstract
:1. Introduction
- 1.
- New robust MCC-MF sine map is designed and analyzed.
- 2.
- New dynamic chaotic biometric (Digital Fingerprint) signature (DCBS) generator based on the combining the biometric signature and the proposed MCC-MF sine map random chaotic sequence output is also designed.
- 3.
- New physical layer authenticated encryption (PLAE) scheme based on the multi-parameter fractional Fourier transform—Orthogonal frequency division multiplexing (MP-FrFT-OFDM) is suggested.
2. Related Preliminary Basics
2.1. Multiple Parameters FrFT
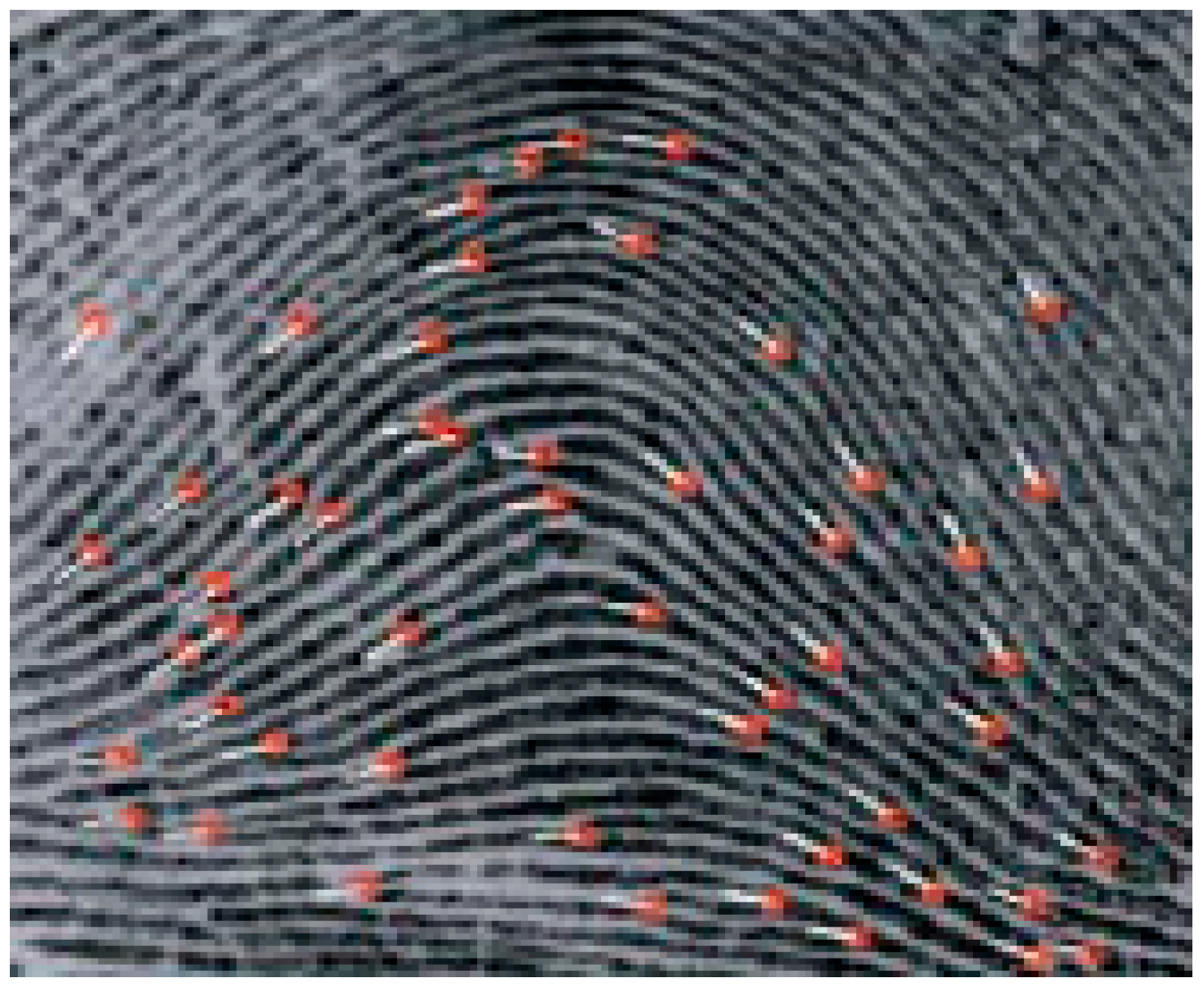
2.2. Biometric Authenticated Secret Key
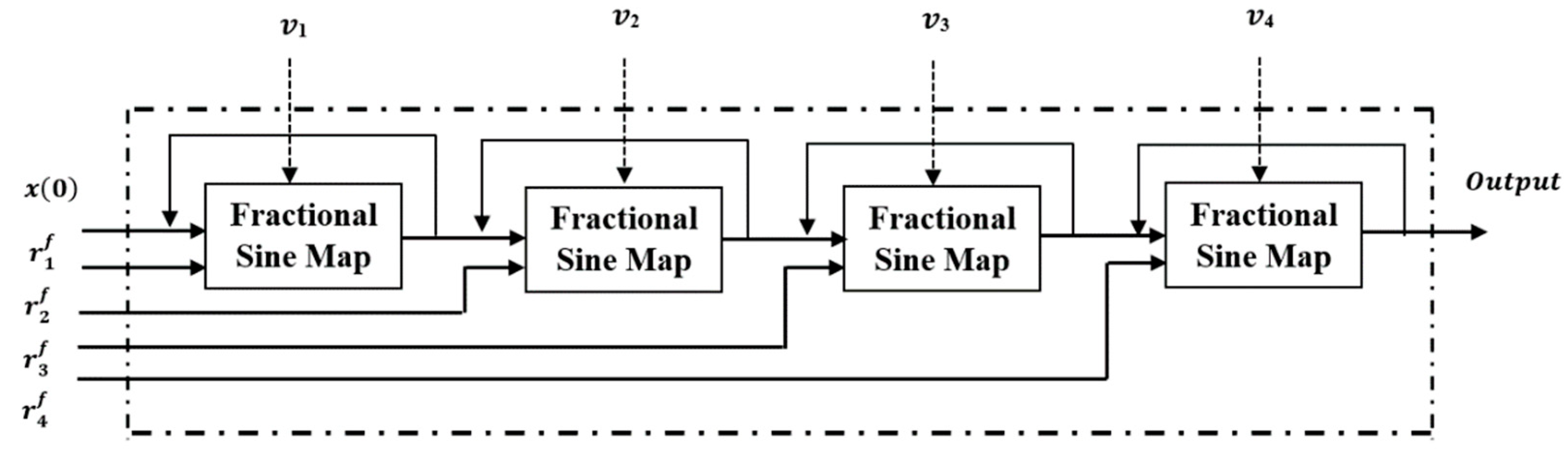
3. Proposed Multi-Cascaded Chaotic Modular Fractional Sine Map (MCC-MF Sine Map)
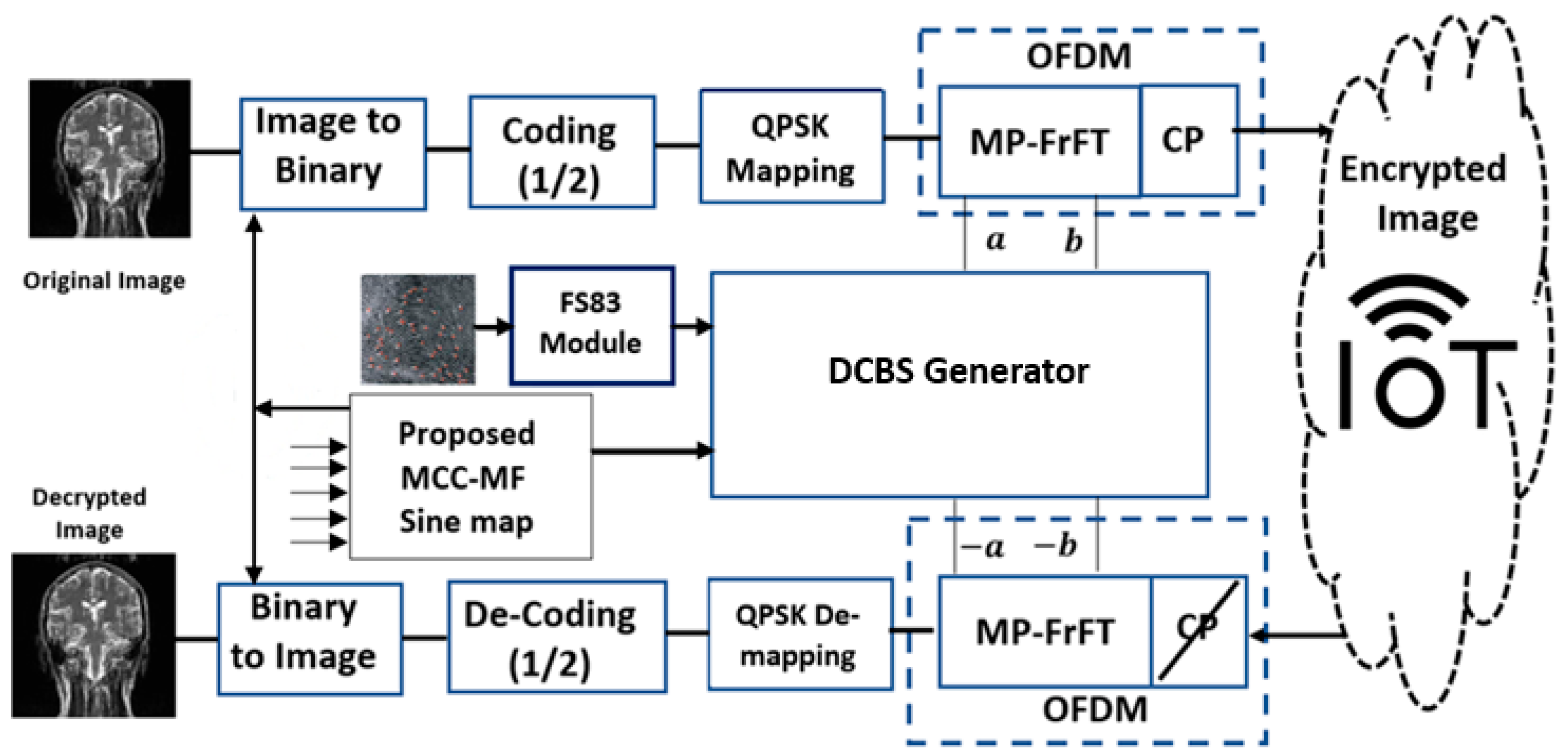
4. Proposed Secure MP-FrFT-OFDM Cryptosystem
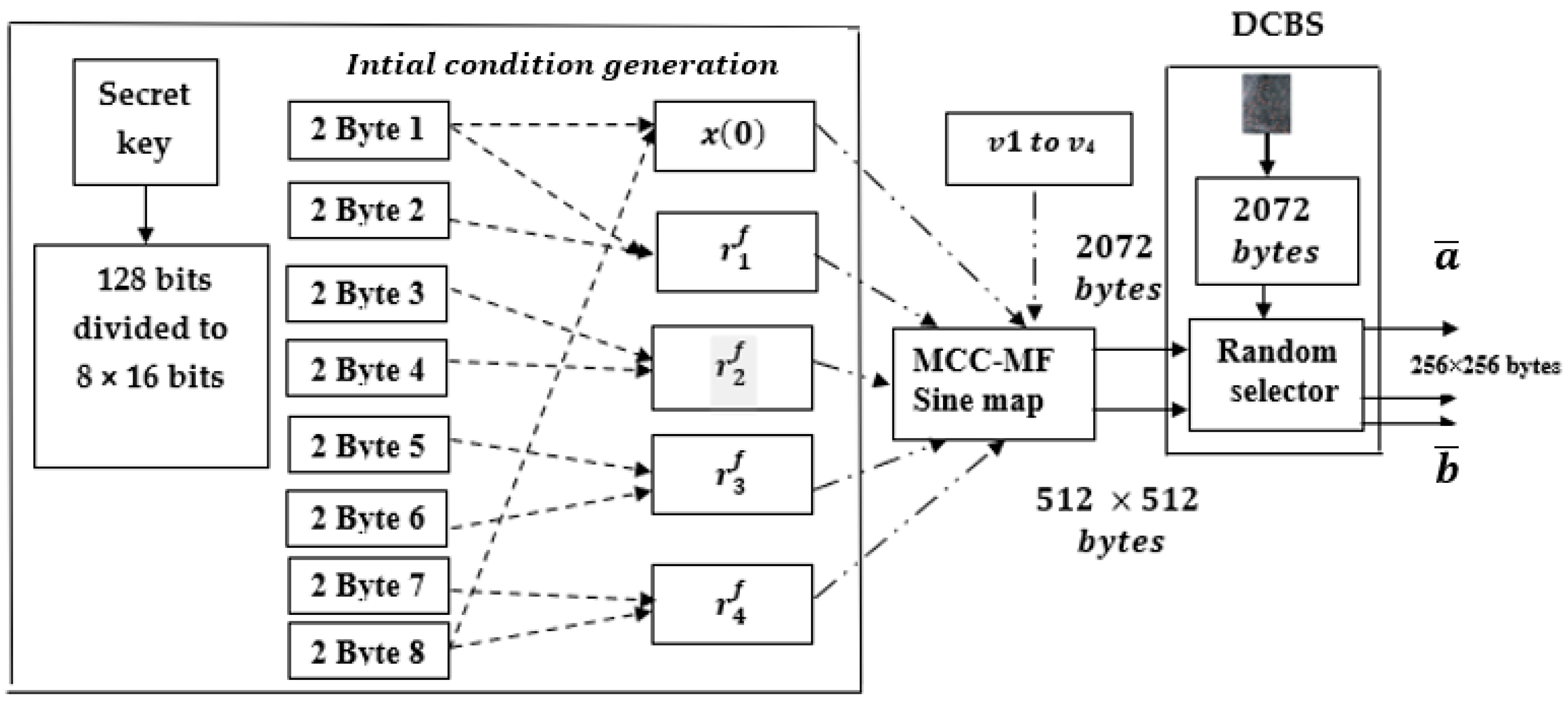
4.1. Proposed DCBS Generator
- 1.
- The secret key (SK) of 128 bits represented by 32 hexadecimal digits “C2250EA6637F5AFAAF0654 9CCD16220A” is used to combined the biometric signature with the fractional number sequence generated from the proposed MCC-MF sine map.
- 2.
- The secret key is divided into eight sections to generate the initial conditions and the different control parameters of the proposed MCC-MF sine map. All secret parameters and the initial condition are decimal precision.
- 3.
- The first eight hexadecimal digits ( ) and the last eight hexadecimal digits number eight are used to generate the fractional initial condition of the proposed MCC-MF sine map as:
- 4.
- The first ( ) and the second () eight hexadecimal digits are used to generate the first fractional secret control parameter () as:
- 5.
- The next three fractional secret control parameters are given as:
- 6.
- The proposed MCC-MF sine map given in Equation (15) is iterated t = 512 × 512 × 8 times by using the generated secret parameters and the fractional secure parameters ( ).
- 7.
- Ignore the first 1000 bits to prove the chaos property of the generated chaotic sequence. In addition, select the last 2072 bytes of the generated chaotic sequence.
- 8.
- Concatenate the chaotic sequence output (2072 bytes) with the 2072 bytes of the biometric signature to generate the dynamic chaotic biometric signature (DCBS).
- 9.
- Finally, randomly select 256 × 256 bytes from the iterated chaotic sequence 512 × 512 bytes for the diffusion process by Xoring with the original image and select the two different 256 vectors ( ), which are used as the secret multi-parameters for the confusion process in the MPFrFT OFDM transform.
4.2. Secure MP-FrFT-OFDM Based on MCC-MF Sine Map and DCBS Generator
4.3. Authenticated Encryption Scheme
- Read the image that was entered.
- Convert the input image into binary format.
- The first encryption step started with the diffusion process by Xoring, which converts the binary image data of 256 × 256 × 8 bits with the select random iterated chaotic sequence of 256 × 256 × 8 bits.
- Apply convolutional coding for the diffusion 256 × 256 × 8 bits.
- Apply QPSK mapping.
- The second encryption step is the confusion process, applying the inverse MPFrFT based OFDM modulation based on the two secret fractional parameter vectors a
- 7.
- Add the cyclic prefix (CP) to the output of the secure MP-FrFT.
- 8.
- Send the encrypted image across an IoT channel to the recipient side.
4.4. Authenticated Decryption
- Receive the authenticated encrypted image data.
- Remove the cyclic prefix (CP) from the received secure MP-FrFT.
- The first step in the decryption is the de-confusion by applying the inverse MP-FrFT-based OFDM on the encrypted image based on the inverse two secret fractional parameter vectors and as follows:
- 4.
- Apply QPSK de-mapping.
- 5.
- Apply convolutional de-coding for the diffusion 256 × 256 × 8 bits.
- 6.
- Convert the authenticated encrypted image into binary format.
- 7.
- The second step in the decryption step is the de-diffusion by Xoring of the authenticated encrypted binary image data of 256 × 256 × 8 bits with the select random iterated chaotic sequence of 256 × 256 × 8 bits.
- 8.
- Apply the required analysis.
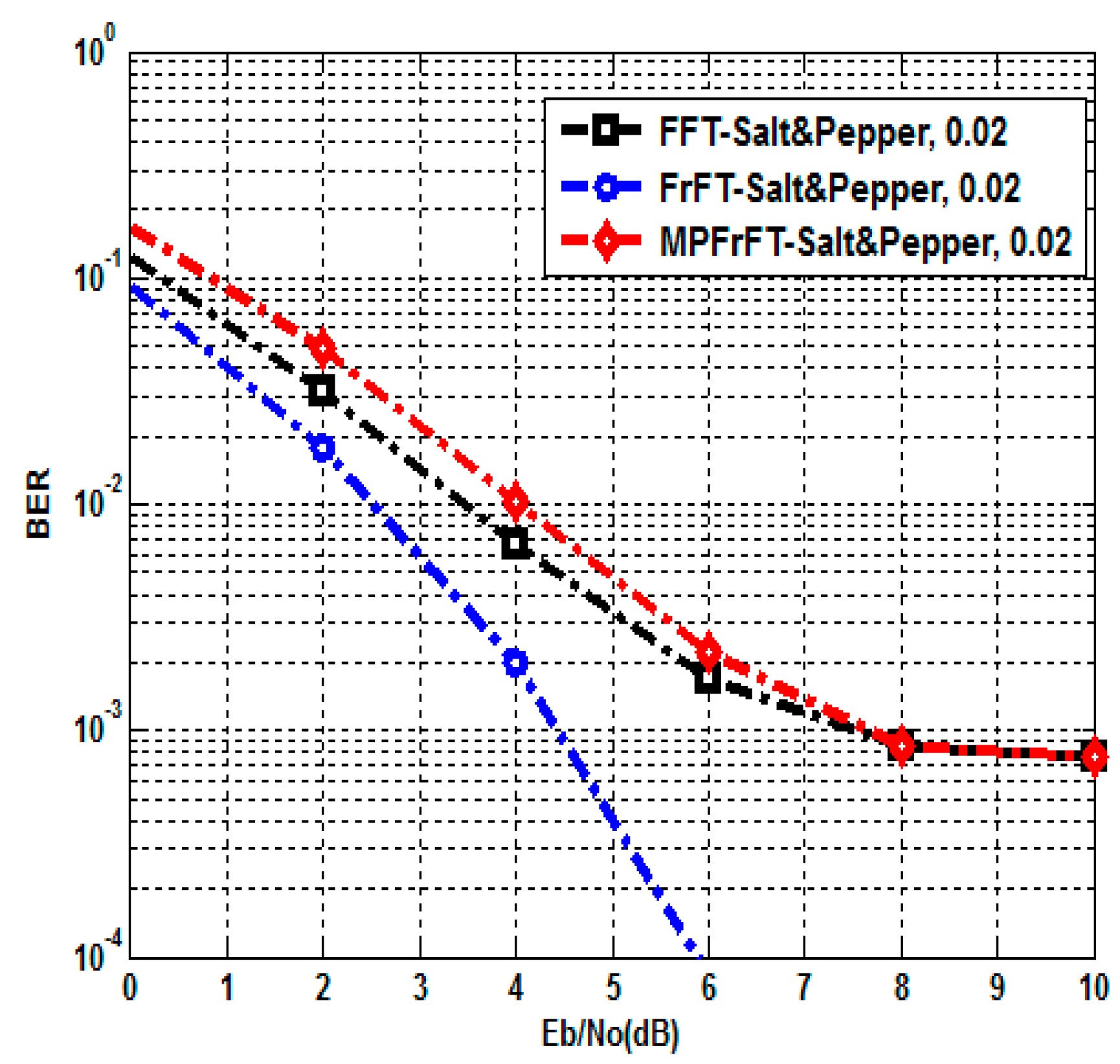
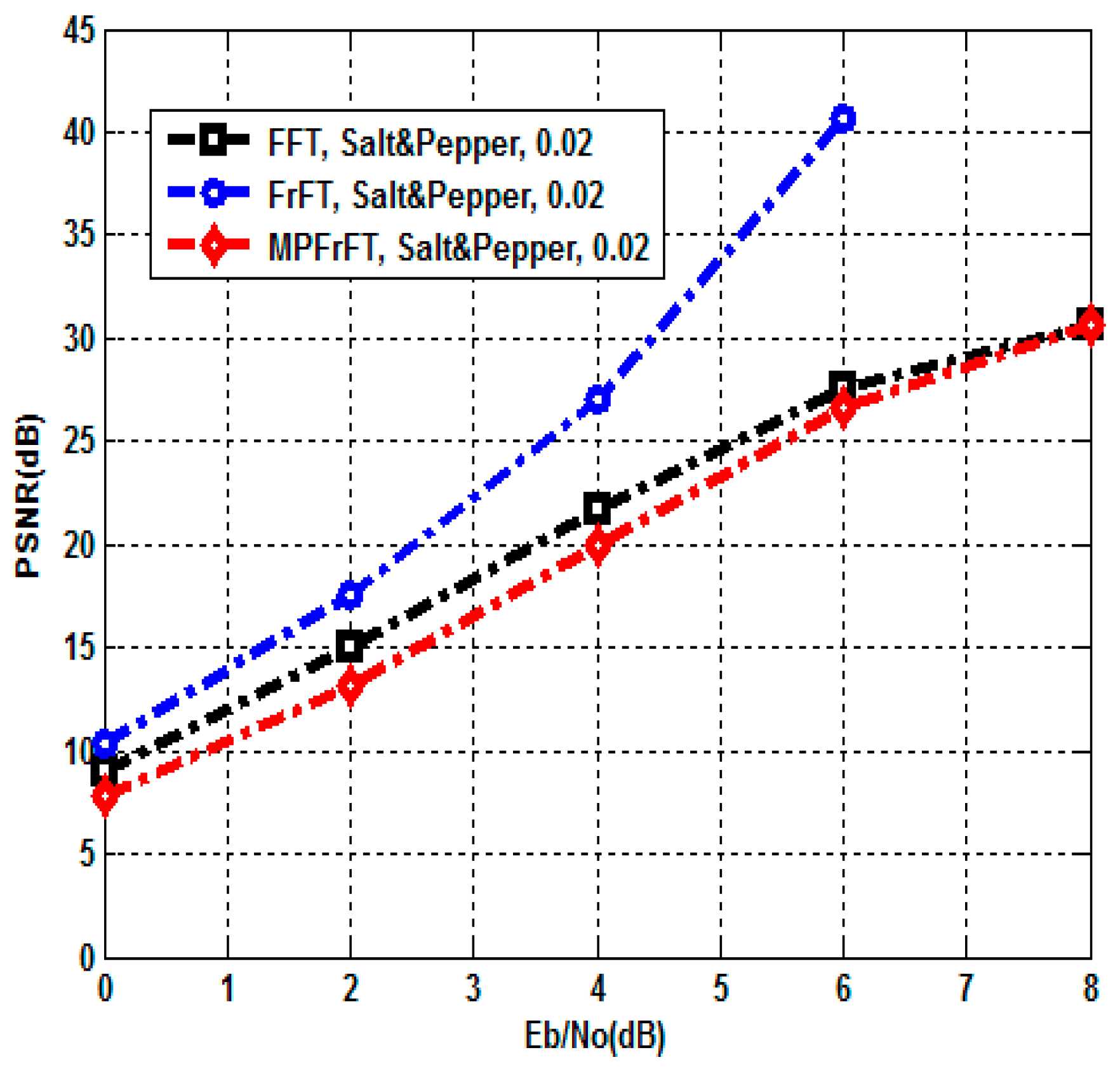
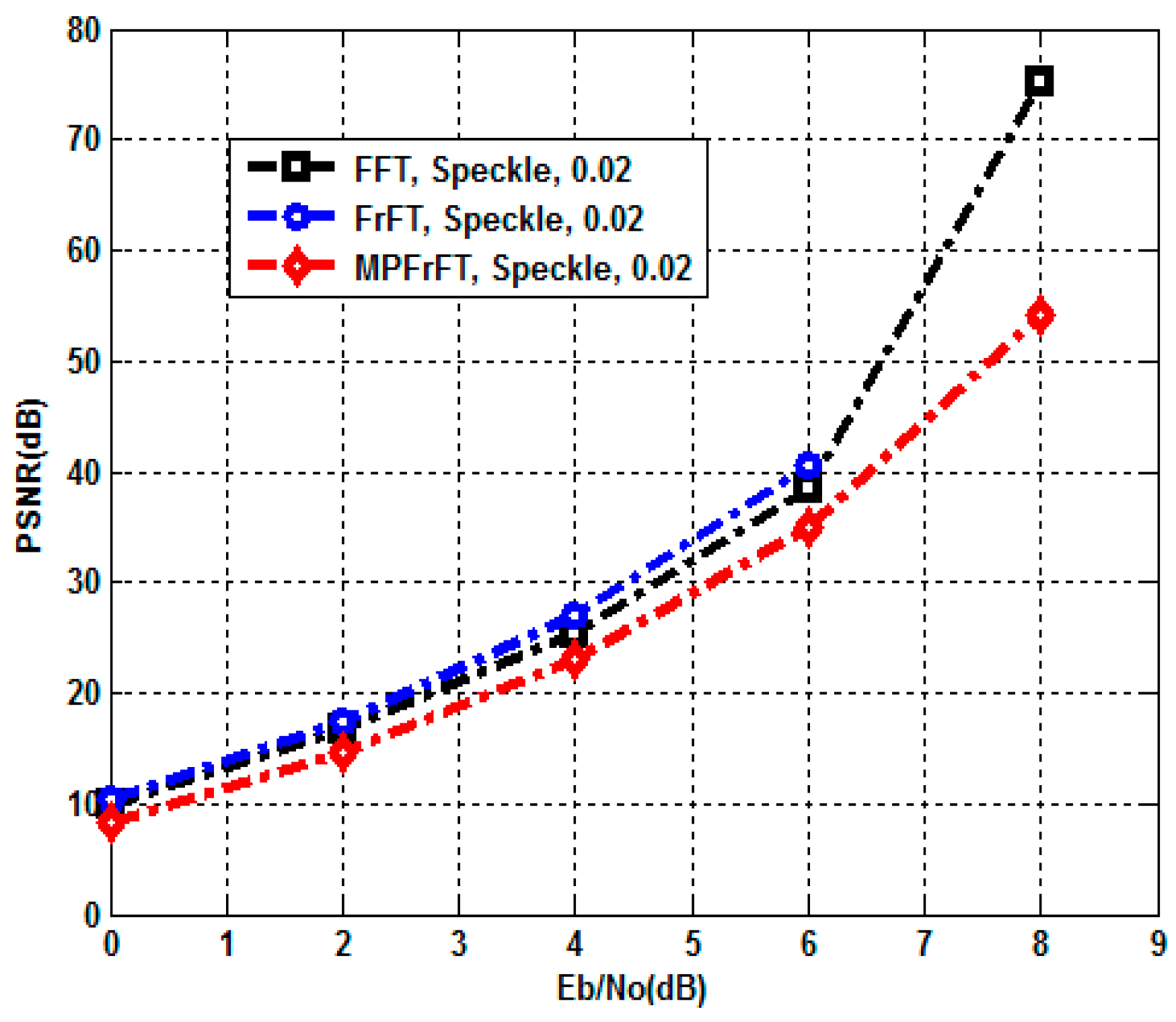
5. Performance Analysis and Results
5.1. Visual Quality Metrics
5.2. Encryption Quality Metrics
5.2.1. Deferential Attack Analysis
5.2.2. Correlation Analysis
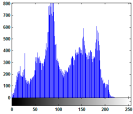
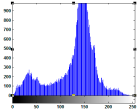
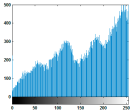
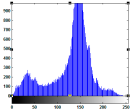
5.2.3. Histogram Analysis
5.2.4. Key Space Analysis
5.2.5. Entropy Analysis
5.2.6. Key Sensitivity Analysis
6. Comparative Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gloukhovtsev, M. IOT Security: Challenges, Solutions & Future Prospects; Knowledge Sharing Article; Dell Inc.: Round Rock, TX, USA, 2018. [Google Scholar]
- Srhir, A.; Mazri, T.; Mohammed, B. Security in the IoT: State-of-the-Art, Issues, Solutions, and Challenges. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 65–75. [Google Scholar] [CrossRef]
- Hou, Y.; Li, G.; Dang, S.; Hu, L.; Hu, A. Physical Layer Encryption Scheme Based on Dynamic Constellation Rotation. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022. [Google Scholar] [CrossRef]
- Salman, H.; Arslan, H. PLS-IoT Enhancement against Eavesdropping via Spatially Distributed Constellation Obfuscation. IEEE Wireless Commun. Lett. 2023, 25, 1–8. [Google Scholar] [CrossRef]
- Ashraf, A.M.; Elmedany, W.M.; Sharif, M.S. Secure IoT Data Transmission at Physical Layer using RC6 Encryption Technique. In Proceedings of the 2022 9th International Conference on Future Internet of Things and Cloud (FiCloud), Online, 22–24 August 2022. [Google Scholar] [CrossRef]
- Liu, J.; Ren, A.; Sun, R.; Du, X.; Guiza, M. A Novel Chaos-Based Physical Layer Security Transmission Scheme for Internet of Things. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019. [Google Scholar]
- Liu, J.; Hu, Q.; Sun, R.; Du, X.; Guizani, M. A Physical Layer Security Scheme with Compressed Sensing in OFDM-based IoT Systems. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020. [Google Scholar] [CrossRef]
- Quan, M.; Jin, Q.; Ba, B.; Zhang, J.; Jian, C. Constellation Encryption Design Based on Chaotic Sequence and the RSA Algorithm. Electronics 2022, 11, 3346. [Google Scholar] [CrossRef]
- Sun, L.; Du, Q. A Review of Physical Layer Security Techniques for Internet of Things: Challenges and Solutions. Entropy 2018, 20, 730. [Google Scholar] [CrossRef] [PubMed]
- Hussain, M.; Du, Q.; Sun, L.; Ren, P. Security enhancement for video transmission via noise aggregation in immersive systems. Multimed. Tools Appl. 2016, 75, 5345–5357. [Google Scholar] [CrossRef]
- Sun, L.; Xu, H. Unequal secrecy protection for untrusted two-way relaying systems: Constellation overlapping and noise aggregation. IEEE Trans. Veh. Technol. 2018, 67, 9681–9695. [Google Scholar] [CrossRef]
- Luby, M. LT codes. In Proceedings of the 43rd IEEE Annual Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 16–19 November 2002; Volume 1, pp. 271–280. [Google Scholar]
- Byers, J.; Luby, M.; Mitzenmacher, M. A digital fountain approach to asynchronous reliable multicast. IEEE J. Sel. Areas Commun. 2002, 20, 1528–1540. [Google Scholar] [CrossRef]
- Zhang, X.; Du, Q. Adaptive low-complexity erasure-correcting code-based protocols for QoS-driven mobile multicast services over wireless networks. IEEE Trans. Veh. Technol. 2006, 55, 1633–1647. [Google Scholar] [CrossRef]
- Shokrollahi, A. Rapter codes. IEEE Trans. Inf. Theory 2006, 52, 2551–2567. [Google Scholar] [CrossRef]
- Nonenmacher, J.; Biersack, E.; Towsley, D. Partity-based loss recovery for reliable multicast transmission. IEEE/ACM Trans. Netw. 1998, 6, 349–361. [Google Scholar] [CrossRef]
- MacKay, D. Fountain codes. IEE Proc. Commun. 2005, 152, 1062–1068. [Google Scholar] [CrossRef]
- Niu, H.; Iwai, M.; Sezaki, K.; Sun, L.; Du, Q. Exploiting fountain codes for secure wireless delivery. IEEE Commun. Lett. 2014, 18, 777–780. [Google Scholar] [CrossRef]
- Boutros, J.; Viterbo, E. Signal space diversity: A power- and bandwidth-efficient diversity technique for the Rayleigh fading channel. IEEE Trans. Inf. Theory 1998, 44, 1453–1467. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, T.; Niu, H. Inter-relay interference in two-path digital relaying systems: Detrimental or beneficial? IEEE Trans. Wirel. Commun. 2011, 10, 2468–2473. [Google Scholar] [CrossRef]
- Lu, H.; Hong, P.L.; Xue, K.P. Analysis on decode-and-forward two-path relay networks: When and how to cooperate. IEEE Trans. Veh. Technol. 2016, 65, 5758–5763. [Google Scholar] [CrossRef]
- Sun, L.; Du, Q.; Ren, P.; Wang, Y. Two birds with one stone: Towards secure and interference-free D2D transmissions via constellation rotation. IEEE Trans. Veh. Technol. 2016, 65, 8767–8774. [Google Scholar] [CrossRef]
- Ren, C.; Chen, J.; Tellambura, C. Spectrum sharing with device-to-device successive relaying and hybrid complex field network coding. IEEE Trans. Veh. Technol. 2017, 66, 7947–7963. [Google Scholar] [CrossRef]
- Xu, H.; Sun, L.; Ren, P.; Du, Q. Securing two-way cooperative systems with an untrusted relay: A constellation-rotation aided approach. IEEE Commun. Lett. 2015, 19, 2270–2273. [Google Scholar] [CrossRef]
- Khan, M.A.; Asim, M.; Jeoti, V.; Manzoor, R.S. On secure OFDM system: Chaos based constellation scrambling. In Proceedings of the 2007 International Conference on Intelligent and Advanced Systems (ICIAS), Kuala Lumpur, Malaysia, 25–28 November 2007; pp. 484–488. [Google Scholar]
- Tseng, D.; Chiu, J. An OFDM speech scrambler without residual intelligibility. In Proceedings of the IEEE Region 10 Conference (TENCON), Taipei, Taiwan, 30 October–2 November 2007; pp. 1–4. [Google Scholar]
- Zhang, L.; Xin, X.; Liu, B.; Wang, Y. Secure OFDM-PON based on chaos scrambling. IEEE Photon. Technol. Lett. 2011, 23, 998–1000. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Hou, W. Secure transmission in OFDM systems by using time domain scrambling. In Proceedings of the 77th IEEE Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar]
- Dzung, D. Data Encryption on the Physical Layer of a Data Transmission System. U.S. Patent 7752430B2, 6 July 2010. [Google Scholar]
- Ma, R.; Dai, L.; Wang, Z.; Wang, J. Secure communication in TDS-OFDM system using constellation rotation and noise insertion. IEEE Trans. Consum. Electron. 2010, 56, 1328–1332. [Google Scholar] [CrossRef]
- Reilly, D.; Kanter, G. Noise-enhanced encryption for physical layer security in an OFDM radio. In Proceedings of the IEEE Radio and Wireless Symposium (RWS), San Diego, CA, USA, 18–22 January 2009; pp. 344–347. [Google Scholar]
- Vukadinovic, V.; Bakowski, K.; Marsch, P.; Garcia, I.D.; Xu, H.; Sybis, M.; Sroka, P.; Wesolowski, K.; Lister, D.; Thibault, I. 3GPP C-V2X and IEEE 802.11 p for vehicle-to-vehicle communications in highway platooning scenarios. Ad Hoc Netw. 2018, 74, 17–29. [Google Scholar] [CrossRef]
- Ometov, A.; Daneshfar, N.; Hazmi, A.; Andreev, S.; Del Carpio, L.F.; Amin, P.; Torsner, J.; Koucheryavy, Y.; Valkama, M. System-level analysis of IEEE 802.11 ah technology for unsaturated MTC traffic. Int. J. Sens. Netw. 2018, 26, 269–282. [Google Scholar] [CrossRef]
- Park, M.; Kenney, T.; Perahia, E.; Stacey, R.; Azizi, S. Method of Packet Classification for 802.11 ax. U.S. Patent 9,882,687, 30 January 2018. [Google Scholar]
- Wang, W.; He, S.; Yang, L.; Zhang, Q.; Jiang, T. Wi-Fi teetertotter: Overclocking OFDM for internet of things. arXiv 2018, arXiv:1801.02811. [Google Scholar]
- Mavromoustakis, C.; Mastorakis, G.; Batalla, J. Internet of Things (IoT) in 5G Mobile Technologies; Springer: Berlin/Heidelberg, Germany, 2016; Volume 8. [Google Scholar]
- Al-Sarawi, S.; Anbar, M.; Alieyan, K.; Alzubaidi, M. Internet of things (IoT) communication protocols. In Proceedings of the IEEE International Conference on Information Technology (ICIT), Amman, Jordan, 17–18 May 2017; pp. 685–690. [Google Scholar]
- Hamamreh, J.M.; Arslan, H. Secure orthogonal transform division multiplexing (OTDM) waveform for 5G and beyond. IEEE Commun. Lett. 2017, 21, 1191–1194. [Google Scholar] [CrossRef]
- Huo, F.; Gong, G. A new efficient physical layer OFDM encryption scheme. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM), Toronto, ON, Canada, 27 April–2 May 2014; pp. 1024–1032. [Google Scholar]
- Dharavathu, K.; Mosa, A. Secure image transmission through crypto-OFDM system using Rubik’s cube algorithm over an AWGN channel. Int. J. Commun. Syst. 2020, 33, e4369. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, B.; Xin, X.; Zhang, Q.; Yu, J.; Wang, Y. Theory and performance analyses in secure CO-OFDM transmission system based on two-dimensional permutation. J. Lightw. Technol. 2013, 31, 74–80. [Google Scholar] [CrossRef]
- Cheng, D.; Gao, Z.; Liu, F.; Liao, X. A general time-domain artificial noise design for OFDM AF relay systems. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC), Shenzhen, China, 2–4 November 2015; pp. 1–6. [Google Scholar]
- Akitaya, T.; Saba, T. Energy efficient artificial fast fading for MISOOFDM systems. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Rahbari, H.; Krunz, M. Exploiting frame preamble waveforms to support new physical-layer functions in OFDM-based 802.11 systems. IEEE Trans. Wirel. Commun. 2017, 16, 3775–3786. [Google Scholar] [CrossRef]
- Karachontzitis, S.; Timotheou, S.; Krikidis, I.; Berberidis, K. Security-aware max-min resource allocation in multiuser OFDMA downlink. IEEE Trans. Inf. Forensics Secur. 2015, 10, 529–542. [Google Scholar] [CrossRef]
- Zhang, B.; Zhan, Q.; Chen, S.; Li, M.; Ren, K.; Wang, C.; Ma, D. Priwhisper: Enabling keyless secure acoustic communication for smartphones. IEEE Internet Things J. 2014, 1, 33–45. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, M.; Li, F.; Tang, J.; Liu, Y.; Chen, L. PAPR reduction based on chaos combined with SLM technique in optical OFDM IM/DD system. Opt. Fiber Technol. 2015, 21, 81–86. [Google Scholar] [CrossRef]
- Allah, O.S.F.; Afifi, A.; El-Shafai, W.; Naeem, E.A.; Alzain, M.A.; Al-Amri, J.F.; Soh, B.; El-Samie, F.E.A. Investigation of Chaotic Image Encryption in Spatial and FrFT Domains for Cybersecurity Applications. IEEE Access 2020, 8, 42491–42503. [Google Scholar]
- Dasgupta, T.; Paral, P.; Bhattacharya, S. Color image encryption based on multiple fractional order chaotic systems. In Proceedings of the International Conference on Control, Instrumentation, Energy and Communication (CIEC), Calcutta, India, 31 January–2 February 2014; pp. 583–587. [Google Scholar]
- Ozaktas, H.M.; Zalevsky, Z.; Kutay, M.A. The Fractional Fourier Transform with Applications in Optics and Signal Processing; Prentice Hall: New York, NY, USA, 2000. [Google Scholar]
- Pei, S.C.; Hsue, W.L. The multiple-parameter discrete fractional Fourier transform. IEEE Signal Proc. Lett. 2006, 13, 329–332. [Google Scholar]
- Zhao, T.; Ran, Q.; Yuan, L.; Chi, Y.; Ma, J. Security of image encryption scheme based on multi-parameter fractional Fourier transform. Opt. Commun. 2016, 376, 47–51. [Google Scholar] [CrossRef]
- Zhou, N.R.; Dong, T.J.; Wu, J.H. Novel image encryption algorithm based on multiple-parameter discrete fractional random transform. Opt. Commun. 2010, 283, 3037–3042. [Google Scholar] [CrossRef]
- Tao, R.; Meng, X.Y.; Wang, Y. Image encryption with multiorders of fractional Fourier transforms. IEEE Trans. Inf. Forensic. Secur. 2010, 5, 734–738. [Google Scholar] [CrossRef]
- Lang, J.; Tao, R.; Wang, Y. Image encryption based on the multiple-parameter discrete fractional Fourier transform and chaos function. Opt. Commun. 2010, 283, 2092–2096. [Google Scholar] [CrossRef]
- Liu, F.; Wang, L.; Xie, J.; Wang, Y.; Zhang, Z. MP-WFRFT and Chaotic Scrambling Aided Directional Modulation Technique for Physical Layer Security Enhancement. IEEE Access 2019, 7, 74459–74470. [Google Scholar] [CrossRef]
- Heidari, A.; Navimipour, N.J.; Jamali, M.A.J.; Akbarpour, S. A hybrid approach for latency and battery lifetime optimization in IoT devices through offloading and CNN learning. Sustain. Comput. Inform. Syst. 2023, 39, 100899. [Google Scholar] [CrossRef]
- Aminizadeh, S.; Heidari, A.; Toumaj, S.; Darbandi, M.; Navimipour, N.J.; Rezaei, M.; Talebi, S.; Azad, P.; Unal, M. The Applications of Machine Learning Techniques in Medical Data Processing based on Distributed Computing and the Internet of Things. Comput. Methods Programs Biomed. 2023, 241, 107745. [Google Scholar] [CrossRef]
- Alhoraibi, L.; Alghazzawi, D.; Alhebshi, R.; Rabie, O.B.J. Physical Layer Authentication in Wireless Networks-Based Machine Learning Approaches. Sensors 2023, 23, 1814. [Google Scholar] [CrossRef]
- Hsue, W.L.; Pei, S.C. The Multiple-Parameter Discrete Fractional Fourier Transform and Its Application. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 July 2006. [Google Scholar]
- Farah, M.B.; Guesmi, R.; Kachouri, A.; Samet, M. A novel chaos based optical image encryption using fractional Fourier transform and DNA sequence operation. Opt. Laser Technol. 2020, 121, 105777. [Google Scholar] [CrossRef]
- Panchal, G.; Samanta, D. A Novel Approach to Fingerprint Biometric-Based Cryptographic Key Generation and its Applications to Storage Security. Comput. Electr. Eng. 2018, 69, 461–478. [Google Scholar] [CrossRef]
- El-Mahallawy, M.S.; Hagras, E.A.; Eldin, A.Z.; Fakhr, M.W. Robust Blind and Secure Biometric Watermarking Based on Partial Multi-Map Chaotic Encryption. In Proceedings of the 4th IFIP International Conference on New Technologies, Mobility and Security, Paris, France, 7–10 February 2011. [Google Scholar]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M. A robust embedded biometric authentication system based on fingerprint and chaotic encryption. Expert Syst. Appl. 2015, 42, 8198–8211. [Google Scholar] [CrossRef]
- Zebbiche, K.; Ghouti, L.; Khelifi, F.; Bouridane, A. Protecting Fingerprint Data Using Watermarking. In Proceedings of the First NASA/ESA Conference on Adaptive Hardware and Systems (AHS’06), Istanbul, Turkey, 15–18 June 2006. [Google Scholar]
- Zhou, Y.; Hua, Z.; Pun, C.M.; Chen, C.L. Cascade Chaotic System with Applications. IEEE Trans. Cybern. 2015, 45, 2001–2012. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. A New Simple One-Dimensional Chaotic Map and Its Application for Image Encryption. Multimed. Tools Appl. 2018, 77, 21445–21462. [Google Scholar] [CrossRef]
- Chen, F.; Luo, X.; Zhou, Y. Existence Results for Nonlinear Fractional Difference Equation. Adv. Differ. Equ. 2011, 2011, 713201. [Google Scholar] [CrossRef]
- Moore, R.E.; Kearfott, R.B.; Cloud, M.J. Introduction to Interval Analysis, Society for Industrial and Applied Mathematics 3600; University City Science Center: Philadelphia, PA, USA, 2009. [Google Scholar]
- Nepomuceno, E.G.; Martins, S.A.M. A lower bound error for free run simulation of the polynomial NARMAX. Syst. Sci. Control. Eng. Open Access J. 2016, 4, 50–58. [Google Scholar] [CrossRef]
- Nepomuceno, E.G.; Martins, S.A.M.; Amaral, G.; Riveret, R. On the lower bound error for discrete maps using associative property. Syst. Sci. Control. Eng. Open Access J. 2017, 5, 462–473. [Google Scholar] [CrossRef]
- Wu, G.-C.; Baleanu, D.; Zeng, S.-D. Discrete chaos in fractional sine and standard maps. Phys. Lett. A 2014, 378, 484–487. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; NIST Special Publication 800-22; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001. [Google Scholar]
- Hagras, E.A.A.; Aldosary, S.; Khaled, H.; Hassan, T.M. Authenticated Public Key Elliptic Curve Based on Deep Convolutional Neural Network for Cybersecurity Image Encryption Application. Sensors 2023, 23, 6589. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Cao, Y.; Xiong, L.; Chen, X. An effective multiple-image encryption algorithm based on 3D cube and hyperchaotic map. J. King Saud. Univ. Comput. Inf. Sci. 2022, 34, 1535–1551. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Xiong, L.; Sha, Y.; Yan, H.; Cao, Y. A fast and efficient multiple images encryption based on single-channel encryption and chaotic system. Nonlinear Dyn. 2022, 108, 613–636. [Google Scholar] [CrossRef]
- Gupta, M.; Singh, V.P.; Gupta, K.K.; Shukla, P.K. An efficient image encryption technique based on two-level security for internet of things. Multimed. Tools Appl. 2022, 82, 5091–5111. [Google Scholar] [CrossRef]




| Test | p-Value | Result |
|---|---|---|
| Monobit frequency | 0.5961 | Success |
| Block frequency | 0.3673 | Success |
| Runs test | 0.7286 | Success |
| Longest run of ones | 0.8837 | Success |
| Binary matrix rank test | 0.2735 | Success |
| Discrete Fourier transform | 0.1942 | Success |
| Non-overlapping template | 0.3061 | Success |
| Overlapping templates | 0.7398 | Success |
| Universal statistical | 0.8394 | Success |
| Linear complexity | 0.7193 | Success |
| Serial test | 0.5037 | Success |
| Approximate entropy | 0.6695 | Success |
| Cumulative sums (forward) | 0.8359 | Success |
| Cumulative sums (revere) | 0.3891 | Success |
| Random excursions | 0.7291 | Success |
| Parameter | Value |
|---|---|
| SK ( | 4071A20C3CB340E95E65AF06549CCD16220A C0D998DEE50C22550EA6637F5AFA |
| 0.918347421094373 | |
| 10.485174284360704 | |
| 18.936817384042791 | |
| 9.195731663827418 | |
| 3.038618376892133 | |
| 0.843728376417384 | |
| 0.172865272648265 | |
| 0.447162948327648 | |
| 0.728395273521837 | |
| Gray-Scale Image | Size | |
|---|---|---|
| Channel coding | Type | Convolutional Encoder |
| Code Rate | ||
| OFDM parameters | Sub-carrier () | 256 |
| FFT length | 256 | |
| Cyclic prefix (CP) | 32 | |
| Attacks | AWGN | |
| Salt and Pepper noise | ||
| Speckle noise | ||
| Key Performance Indicators (KPI) | Visual Quality Metrics (Clarity investigation) | |
| Encryption Quality Metrics (Statistical Analysis) | ||
| , Histogram, Key space |
| Decrypted Image |  | 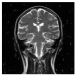 | 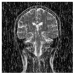 |  |  | |
| Decrypted Image | 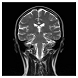 |  | 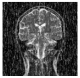 | 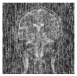 |  | |
| Decrypted Image | 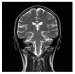 | 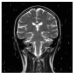 | 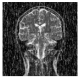 |  |  | |
| FFT | Decrypted Image | 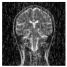 |  |  |
| FrFT | Decrypted Image |  |  | 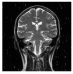 |
| MP-FrFT | Decrypted Image | 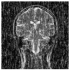 |  | 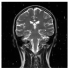 |
| FFT | Decrypted Image |  | 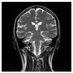 | 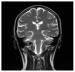 |
| FrFT | Decrypted Image | 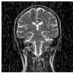 |  |  |
| MP-FrFT | Decrypted Image | 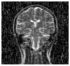 | 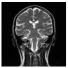 | 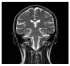 |
| Image | Encryption Scheme | |
|---|---|---|
| Cameraman | ||
| Peppers | ||
| Boat | ||
| Image | Encryption Scheme | |
|---|---|---|
| Cameraman | ||
| Peppers | ||
| Boat | ||
| Image | Encryption Scheme | |
|---|---|---|
| Lena | ||
| Cameraman | ||
| Peppers | ||
| Boat | ||
| Test Image | Original Image Histogram | ||
|---|---|---|---|
| Encryption | Decryption | ||
 |  |  |  |
 | 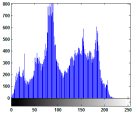 | 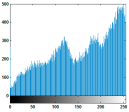 |  |
 |  |  |  |
| Criteria | Proposed | Ref. [48] | Ref. [74] | Ref. [75] | Ref. [76] | Ref. [77] |
|---|---|---|---|---|---|---|
| Key space | - | - | - | |||
| Entropy | 7.9999 | 7.7771 | 7.9997 | 7.9974 | 7.9022 | 7.9973 |
| CC-H | -0.0219 | −0.0002 | 0.0021 | 0.0022 | 0.0044 | |
| CC-V | - | 0.0004 | - | - | ||
| CC-V | - | 0.0001 | - | - | ||
| NPCR (%) | 99.8945 | 99.7400 | 99.611 | 99.6123 | 99.62 | 99.63 |
| UACI (%) | 33.5283 | 27.5200 | 33.471 | 33.46 | 33.46 | – |
| Authentication | ✓ | × | ✓ | × | × | × |
| Encryption | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagras, E.A.A.; Aldosary, S.; Khaled, H.; Hassan, T.M. Physical Layer Authenticated Image Encryption for IoT Network Based on Biometric Chaotic Signature for MPFrFT OFDM System. Sensors 2023, 23, 7843. https://doi.org/10.3390/s23187843
Hagras EAA, Aldosary S, Khaled H, Hassan TM. Physical Layer Authenticated Image Encryption for IoT Network Based on Biometric Chaotic Signature for MPFrFT OFDM System. Sensors. 2023; 23(18):7843. https://doi.org/10.3390/s23187843
Chicago/Turabian StyleHagras, Esam A. A., Saad Aldosary, Haitham Khaled, and Tarek M. Hassan. 2023. "Physical Layer Authenticated Image Encryption for IoT Network Based on Biometric Chaotic Signature for MPFrFT OFDM System" Sensors 23, no. 18: 7843. https://doi.org/10.3390/s23187843
APA StyleHagras, E. A. A., Aldosary, S., Khaled, H., & Hassan, T. M. (2023). Physical Layer Authenticated Image Encryption for IoT Network Based on Biometric Chaotic Signature for MPFrFT OFDM System. Sensors, 23(18), 7843. https://doi.org/10.3390/s23187843





