Low-Latency Collaborative Predictive Maintenance: Over-the-Air Federated Learning in Noisy Industrial Environments
Abstract
:1. Introduction
1.1. Related Work
1.2. Our Contributions
- We propose a hierarchical approach to PM, building upon our prior work [1]. The key distinction lies in the utilization of OACC for the FL algorithm at the factory level. This choice is motivated by the benefits of low latency, making it suitable for PM applications while also improving spectral efficiency. At higher levels, such as fog and cloud servers, occasional requests are made to the factory level for the aggregate model, enabling averaging over multiple factory parameters, FedAvg. Our primary emphasis is on the factory level, specifically investigating FLOACC as the focal point of our research.
- We propose FSVRG-OACC as a distributed approach to solve the optimization problem for PM at the factory level based on OACC. FSVRG-OACC leverages analog over-the-air aggregation, which enables it to effectively handle highly noisy communication channels and allows for improved convergence in minimizing the cost function associated with the ML algorithm.
- FSVRG-OACC facilitates the transmission of local gradient updates by individual agents, capitalizing on the advantages of computation over the air. This algorithm effectively mitigates the impact of channel perturbations on convergence by incorporating the effects of the communication channel into the algorithm update process. The utilization of FSVRG-OACC ensures that convergence is not compromised, enabling efficient and robust optimization in the presence of varying channel conditions.
- The simulation results demonstrate the substantial reduction in convergence sensitivity to noise achieved by our proposed algorithm. This finding holds significant implications for the implementation of ML algorithms on analog over-the-air aggregation in highly noisy industrial environments.
2. System Model
2.1. Federated Edge Learning System
- Model averaging: In this approach, each agent minimizes its local loss function and transmits the model parameters to the PS for aggregation. In the second round of iteration, the agent receives the updated model from the PS.
- Gradient averaging: In this approach, each agent calculates the gradient of its loss function and transmits the gradient to the PS for aggregation. In the second round of iteration, the agent can update its model based on the gradient averaging received from the PS.
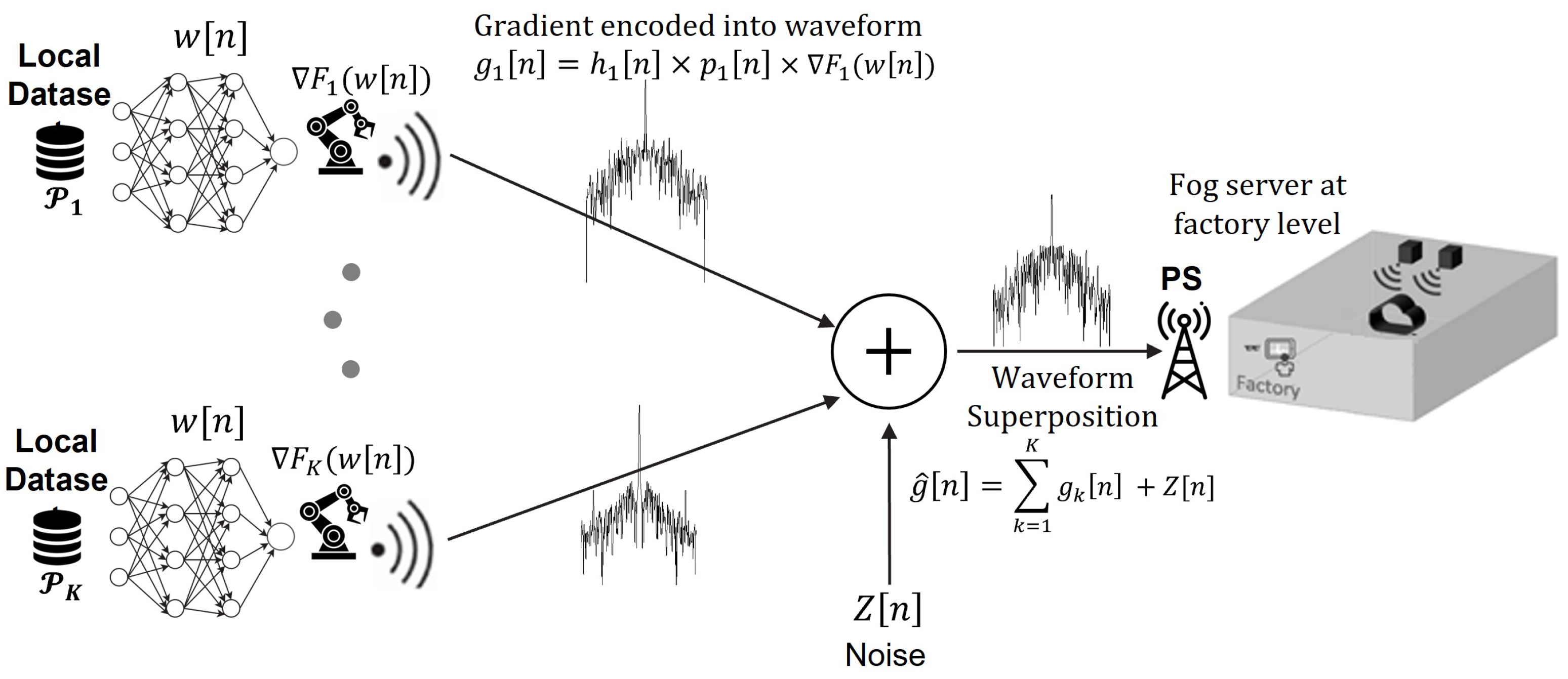
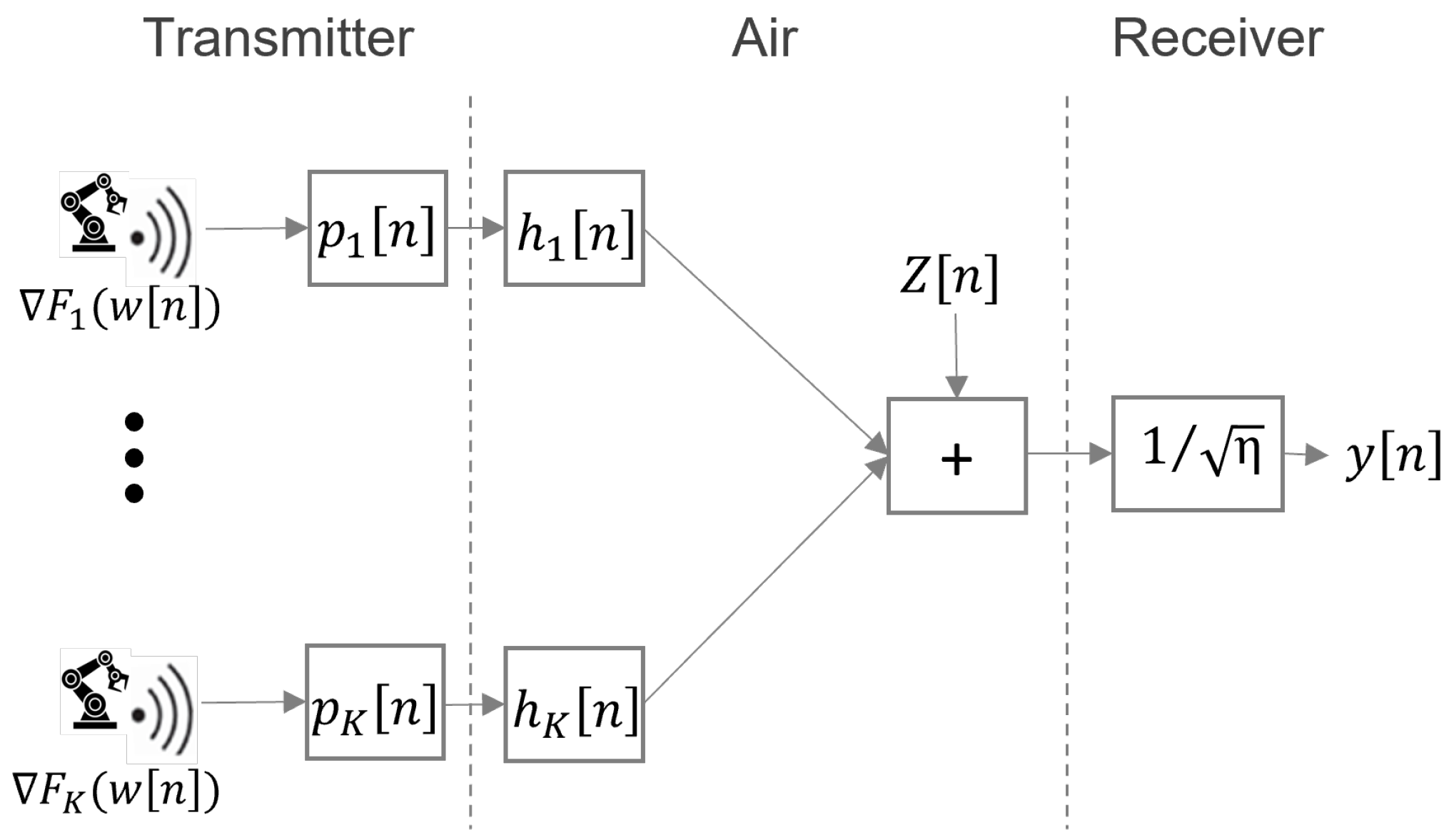
2.2. Fl Over-the-Air Communication and Computation
2.3. Effective Noise and Definition of SNR in FLOACC
3. Proposed Adaptive FSVRG-OACC Algorithm
3.1. Baseline Algorithms
3.2. Fsvrg-Oacc Algorithm
| Algorithm 1: Federated SVRG |
 |
| Algorithm 2: FSVRG With Over-the-Air Communication and Computation (FSVRG-OACC) |
 |
4. Performance Evaluation of FSVRG-OACC
4.1. Algorithm Implementation
4.2. Performance of FSVRG-OACC
4.2.1. General Performance
- In the case of FD003, it is evident that both the GD-MT and FSVRG algorithms fail to converge under the given noise environment and transmission power settings. Consequently, these algorithms are excluded from the accuracy analysis. On the other hand, the GD-GT and SGD-GT algorithms demonstrate convergence, but they exhibit significant fluctuations during the convergence phase. In contrast, our proposed FSVRG-OACC method shows excellent convergence performance under the same environmental conditions and noise levels.As depicted in the accuracy plot for FD003, both SGD-DT and GD-GT algorithms experience a considerable drop in accuracy. However, our proposed algorithm achieves an average accuracy of and demonstrates higher stability compared to the other algorithms.
- In the case of FD004, we observed similar results, although this dataset presents greater challenges due to its inclusion of six fault modes, making the prediction algorithm significantly more complex compared to other CMAPSS datasets. Despite these difficulties, our proposed FSVRG-OACC algorithm demonstrates robust convergence, with only minimal fluctuations occurring after the convergence stage. These fluctuations can be attributed to the estimation anomalies present in the most challenging instances of the dataset.In the accuracy plot, our proposed method achieved a commendable accuracy of on the model. In contrast, the average accuracy of the other two converged methods is lower than that of the proposed method, and their accuracy values exhibited less fluctuation during the communication rounds.
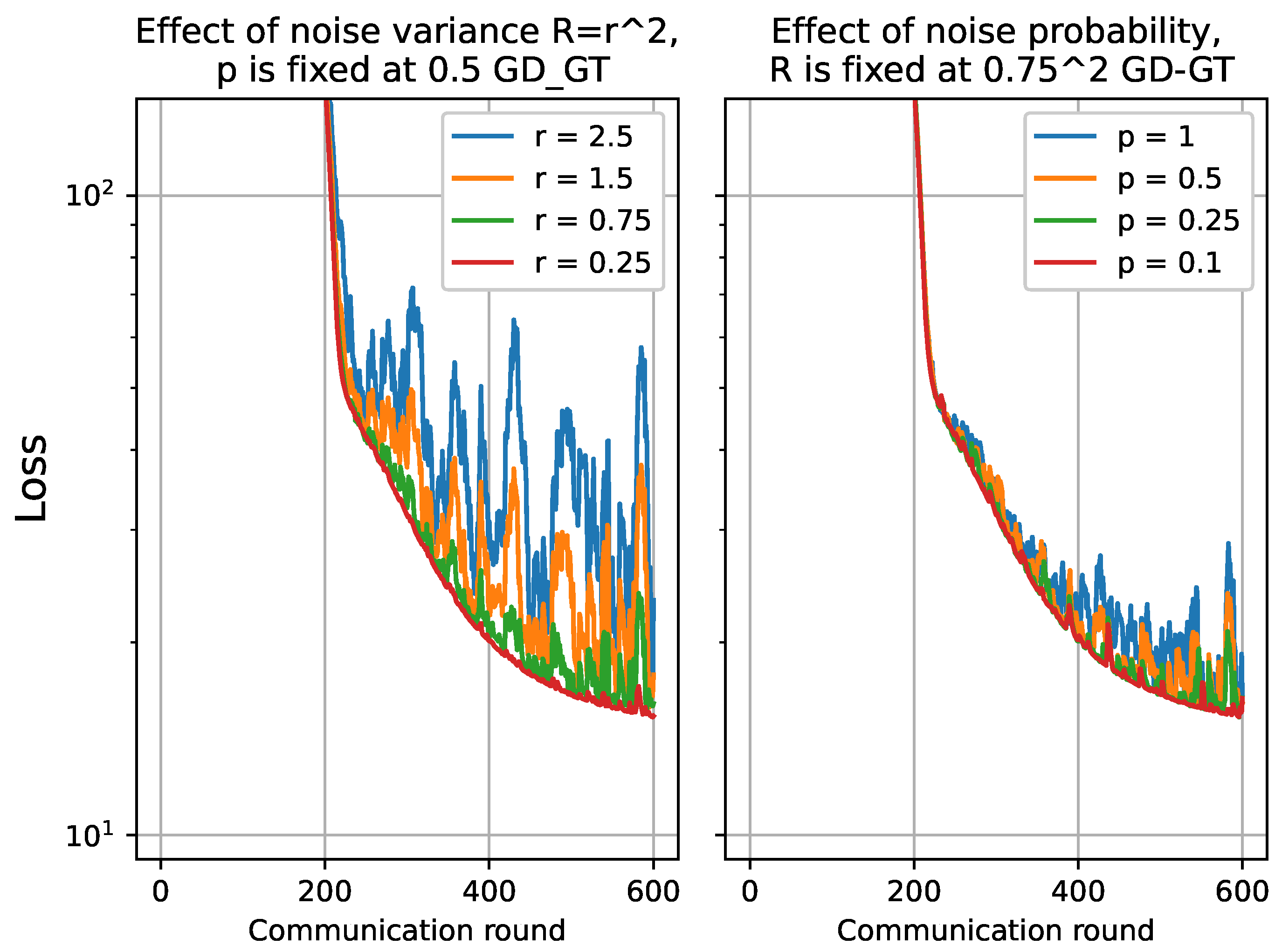
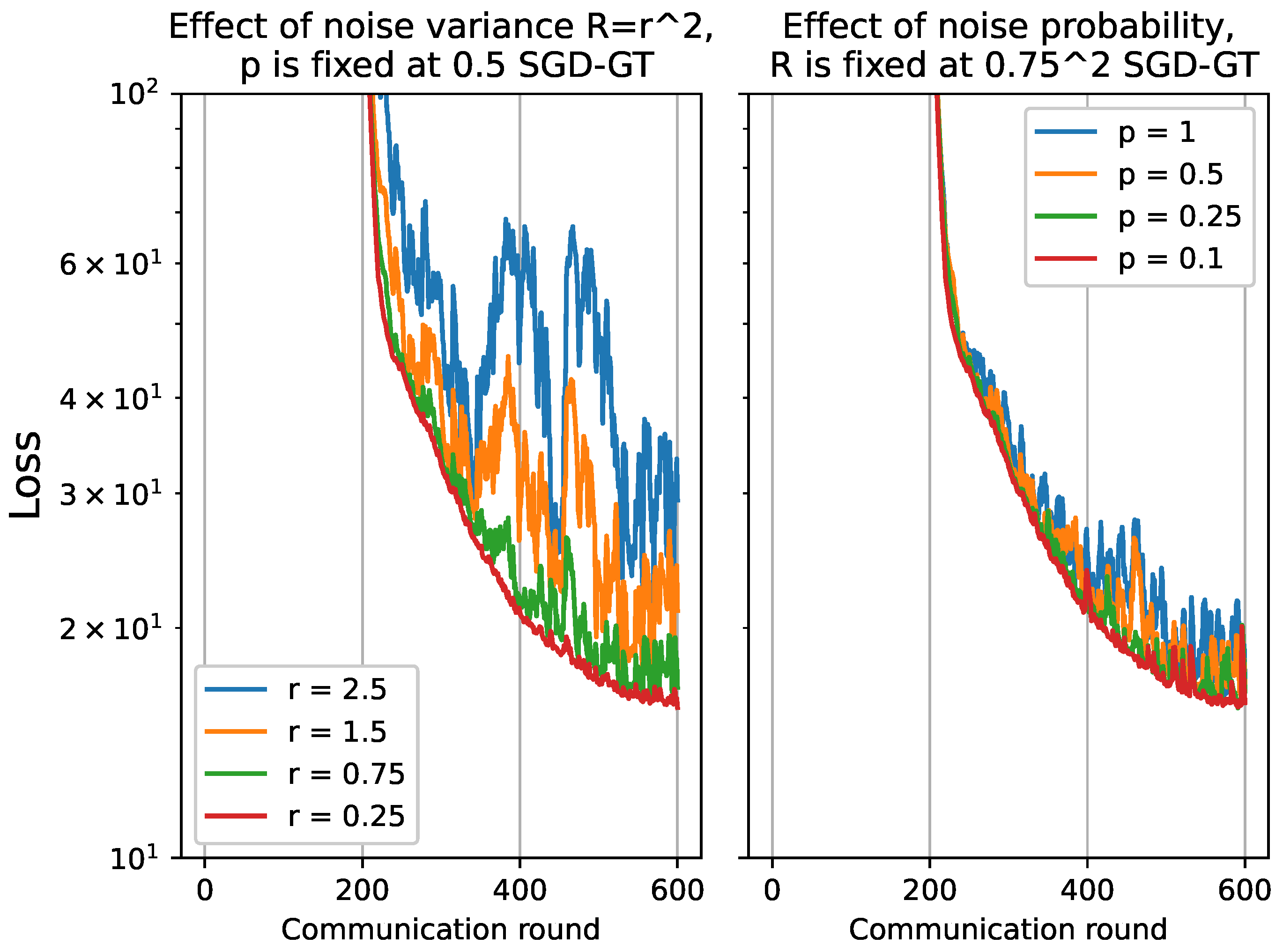
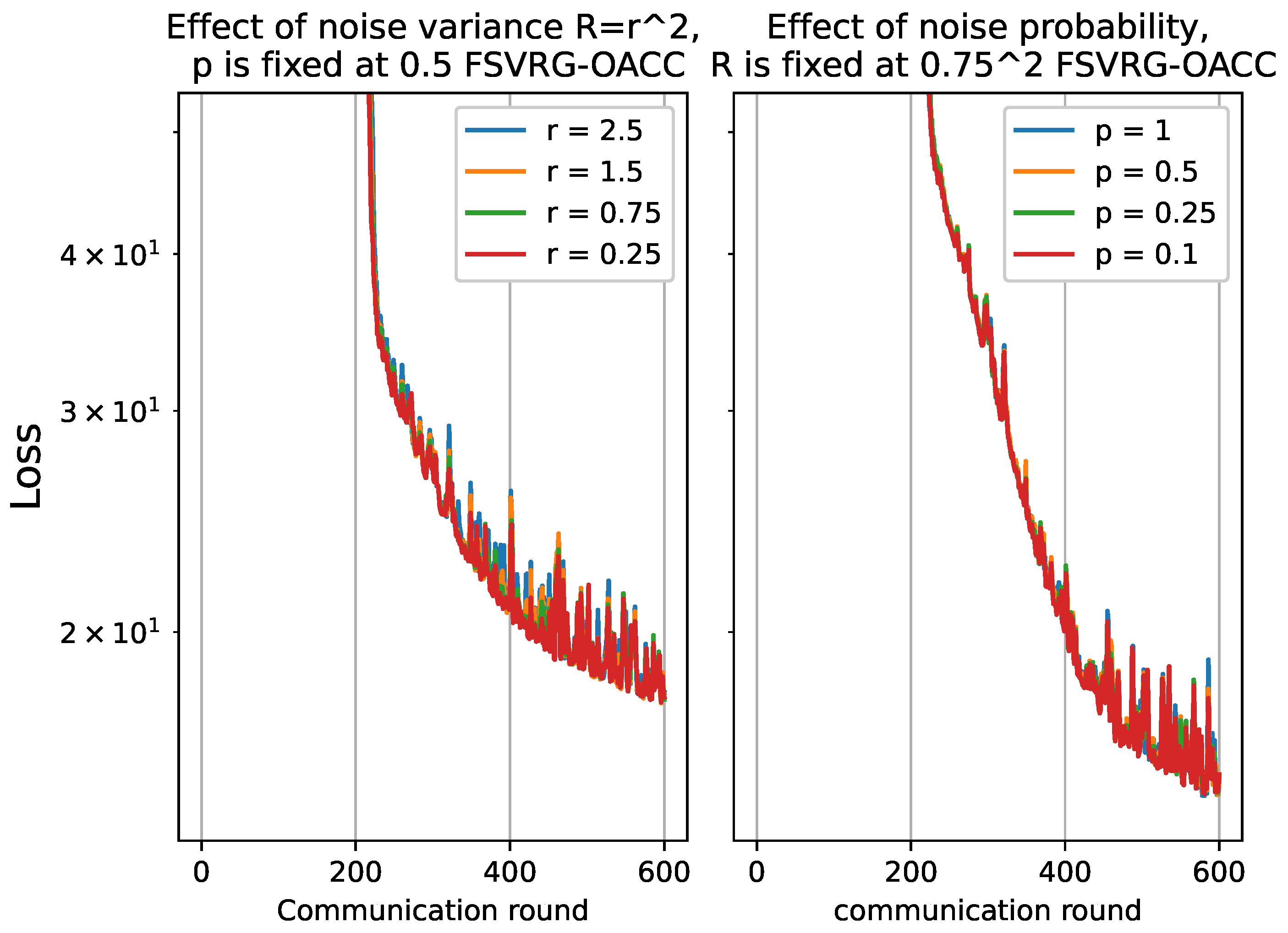
4.2.2. Performance of FSVRG-OACC with Varying Noise Level
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IoT | Internet of Things |
| ML | Machine Learning |
| PM | Predictive Maintenance |
| PS | Parameter Server |
| FL | Federated Learning |
| OACC | Over-the-Air Communication and Computation |
| SNR | Signal-to-Noise Ratio |
| FedAvg | Federated Averaging |
| OFDM | Orthogonal Frequency-Division Multiplexing |
| GD | Gradient Descent |
| SGD | Stochastic Gradient Descent |
| non-IID | non-independent and not identically distributed |
| FSVRG | Federated Stochastic Variance Reduced Gradient |
| FLOACC | Federated Learning Over-the-Air Communication and Computation |
| FSVRG-OACC | Federated Stochastic Variance Reduced Gradient-Over-the-Air Communication and Computation |
References
- Bemani, A.; Björsell, N. Aggregation Strategy on Federated Machine Learning Algorithm for Collaborative Predictive Maintenance. Sensors 2022, 22, 6252. [Google Scholar] [CrossRef] [PubMed]
- Amiri, M.M.; Gündüz, D. Machine Learning at the Wireless Edge: Distributed Stochastic Gradient Descent Over-the-Air. IEEE Trans. Signal Process. 2020, 68, 2155–2169. [Google Scholar] [CrossRef]
- Konečný, J.; McMahan, H.B.; Yu, F.X.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated learning: Strategies for improving communication efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Peng, C.; Hu, Q.; Wang, Z.; Liu, R.W.; Xiong, Z. Online-Learning-Based Fast-Convergent and Energy-Efficient Device Selection in Federated Edge Learning. IEEE Internet Things J. 2023, 10, 5571–5582. [Google Scholar] [CrossRef]
- Liu, S.; Yu, J.; Deng, X.; Wan, S. FedCPF: An Efficient-Communication Federated Learning Approach for Vehicular Edge Computing in 6G Communication Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1616–1629. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Xue, H.; Zhang, H.; Liu, Q.; Niyato, D.; Han, Z. Digital twin-assisted edge computation offloading in industrial Internet of Things with NOMA. IEEE Trans. Veh. Technol. 2022. [Google Scholar] [CrossRef]
- Zheng, S.; Shen, C.; Chen, X. Design and Analysis of Uplink and Downlink Communications for Federated Learning. IEEE J. Sel. Areas Commun. 2021, 39, 2150–2167. [Google Scholar] [CrossRef]
- Amiri, M.M.; Gündüz, D. Federated Learning Over Wireless Fading Channels. IEEE Trans. Wirel. Commun. 2020, 19, 3546–3557. [Google Scholar] [CrossRef]
- Krouka, M.; Elgabli, A.; Ben Issaid, C.; Bennis, M. Communication-Efficient Federated Learning: A Second Order Newton-Type Method With Analog Over-the-Air Aggregation. IEEE Trans. Green Commun. Netw. 2022, 6, 1862–1874. [Google Scholar] [CrossRef]
- Jing, S.; Xiao, C. Federated Learning via Over-the-Air Computation With Statistical Channel State Information. IEEE Trans. Wirel. Commun. 2022, 21, 9351–9365. [Google Scholar] [CrossRef]
- Yang, P.; Jiang, Y.; Wang, T.; Zhou, Y.; Shi, Y.; Jones, C.N. Over-the-Air Federated Learning via Second-Order Optimization. IEEE Trans. Wirel. Commun. 2022, 21, 10560–10575. [Google Scholar] [CrossRef]
- Du, J.; Jiang, B.; Jiang, C.; Shi, Y.; Han, Z. Gradient and Channel Aware Dynamic Scheduling for Over-the-Air Computation in Federated Edge Learning Systems. IEEE J. Sel. Areas Commun. 2023, 41, 1035–1050. [Google Scholar] [CrossRef]
- Konečný, J.; McMahan, B.; Ramage, D. Federated optimization: Distributed optimization beyond the datacenter. arXiv 2015, arXiv:1511.03575. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.Y. Communication-efficient learning of deep networks from decentralized data. Proc. Artif. Intell. Statist. 2017, 54, 1273–1282. [Google Scholar]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, Y.; Huang, K. Broadband Analog Aggregation for Low-Latency Federated Edge Learning. IEEE Trans. Wirel. Commun. 2020, 19, 491–506. [Google Scholar] [CrossRef]
- Chen, M.; Yang, Z.; Saad, W.; Yin, C.; Poor, H.V.; Cui, S. A Joint Learning and Communications Framework for Federated Learning Over Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 269–283. [Google Scholar] [CrossRef]
- Yang, H.H.; Liu, Z.; Quek, T.Q.; Poor, H.V. Scheduling Policies for Federated Learning in Wireless Networks. IEEE Trans. Commun. 2020, 68, 317–333. [Google Scholar] [CrossRef]
- Krouka, M.; Elgabli, A.; Issaid, C.B.; Bennis, M. Communication-Efficient and Federated Multi-Agent Reinforcement Learning. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 311–320. [Google Scholar] [CrossRef]
- Ang, F.; Chen, L.; Zhao, N.; Chen, Y.; Wang, W.; Yu, F.R. Robust Federated Learning With Noisy Communication. IEEE Trans. Commun. 2020, 68, 3452–3464. [Google Scholar] [CrossRef]
- Amiri, M.M.; Gündüz, D.; Kulkarni, S.R.; Poor, H.V. Convergence of Federated Learning Over a Noisy Downlink. IEEE Trans. Wirel. Commun. 2022, 21, 1422–1437. [Google Scholar] [CrossRef]
- Wei, X.; Shen, C. Federated Learning Over Noisy Channels: Convergence Analysis and Design Examples. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1253–1268. [Google Scholar] [CrossRef]
- Guo, H.; Zhu, Y.; Ma, H.; Lau, V.K.; Huang, K.; Li, X.; Nong, H.; Zhou, M. Over-the-Air Aggregation for Federated Learning: Waveform Superposition and Prototype Validation. J. Commun. Inf. Netw. 2021, 4, 429–442. [Google Scholar] [CrossRef]
- Cao, X.; Zhu, G.; Xu, J.; Huang, K. Optimized Power Control for Over-the-Air Computation in Fading Channels. IEEE Trans. Wirel. Commun. 2020, 19, 7498–7513. [Google Scholar] [CrossRef]
- Liu, W.; Zang, X.; Li, Y.; Vucetic, B. Over-the-Air Computation Systems: Optimization, Analysis and Scaling Laws. IEEE Trans. Wirel. Commun. 2020, 19, 5488–5502. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, T. A proximal stochastic gradient method with progressive variance reduction. SIAM J. Optim. 2014, 24, 2057–2075. [Google Scholar] [CrossRef]
- Konečný, J.; McMahan, H.B.; Ramage, D.; Richtárik, P. Federated optimization: Distributed machine learning for on-device intelligence. arXiv 2016, arXiv:1610.02527. [Google Scholar]
- Li, X.; Ding, Q.; Sun, J.Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef]




| Model | Loss Function |
|---|---|
| Linear regression | |
| Logistic regression | |
| K-means | |
| Cross-Entropy | |
| Squared-SVM |
| Dataset | Evaluation Metrics | Optimizer | ||
|---|---|---|---|---|
| GD-GT | SGD-GT | FSVRG-OACC | ||
| FD003 | Runtime | 45.8 s | 21.3 s | 66.7 s |
| Final accuracy | 76% | 61% | 91% | |
| FD004 | Runtime | 70 s | 20 s | 105 s |
| Final accuracy | 42% | 41% | 61% | |
| Dataset | Evaluation Metrics | Optimizer | ||
|---|---|---|---|---|
| GD-GT | SGD-GT | FSVRG | ||
| FD003 | Runtime | 69 s | 20.5 s | 161 s |
| Final accuracy | 94.2% | 92.2% | 91.7% | |
| FD004 | Runtime | 143.5 s | 45.5 s | 337 s |
| Final accuracy | 78.4% | 71.7% | 86.6% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bemani, A.; Björsell, N. Low-Latency Collaborative Predictive Maintenance: Over-the-Air Federated Learning in Noisy Industrial Environments. Sensors 2023, 23, 7840. https://doi.org/10.3390/s23187840
Bemani A, Björsell N. Low-Latency Collaborative Predictive Maintenance: Over-the-Air Federated Learning in Noisy Industrial Environments. Sensors. 2023; 23(18):7840. https://doi.org/10.3390/s23187840
Chicago/Turabian StyleBemani, Ali, and Niclas Björsell. 2023. "Low-Latency Collaborative Predictive Maintenance: Over-the-Air Federated Learning in Noisy Industrial Environments" Sensors 23, no. 18: 7840. https://doi.org/10.3390/s23187840
APA StyleBemani, A., & Björsell, N. (2023). Low-Latency Collaborative Predictive Maintenance: Over-the-Air Federated Learning in Noisy Industrial Environments. Sensors, 23(18), 7840. https://doi.org/10.3390/s23187840








