Characterization of the iPhone LiDAR-Based Sensing System for Vibration Measurement and Modal Analysis
Abstract
1. Introduction
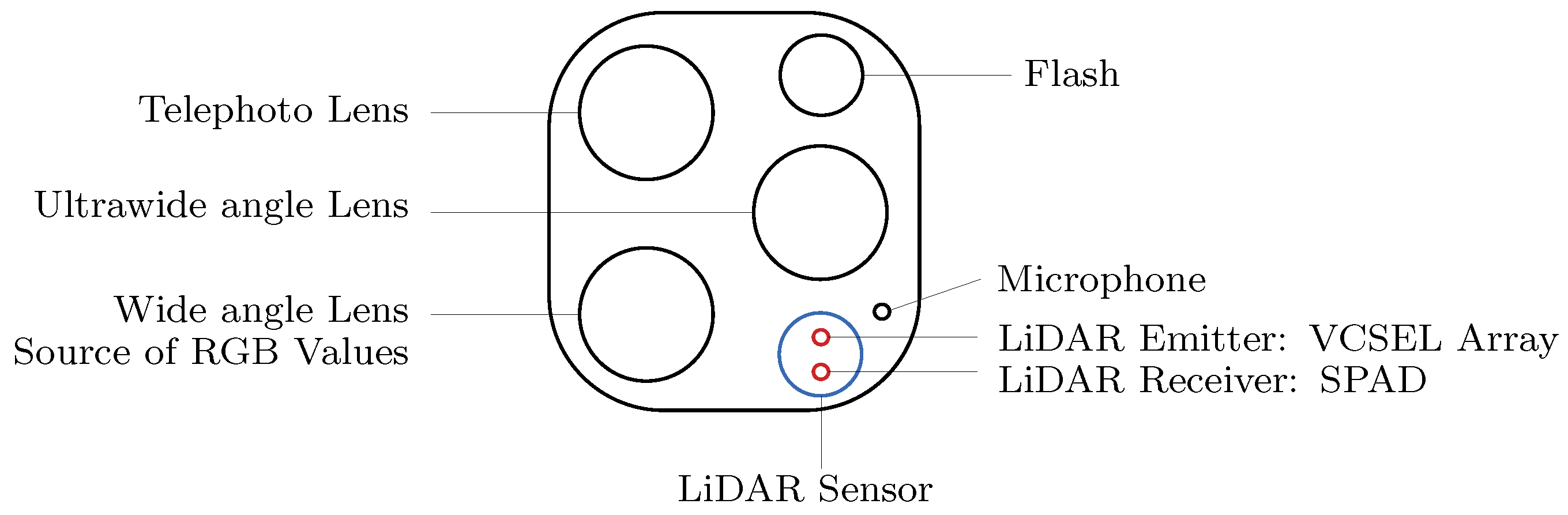
2. iPhone 13 Pro LiDAR Properties
3. Sensor Characterization
3.1. Problem Statement
- (i)
- We characterise the LiDAR sensing system available on the iPhone 13 Pro and similar Apple devices regarding its static measurement properties, exploring its accuracy with different phone-to-target distances, noise floors, and lighting conditions.
- (ii)
- We define the dynamic characteristics and capabilities of the sensor regarding dynamic accuracy, range, and sampling rate effects, and further relate these to applications and limitations of LiDAR in modal analysis.
3.2. Static Measurement Characteristics
3.3. Dynamic Properties
3.3.1. Setup
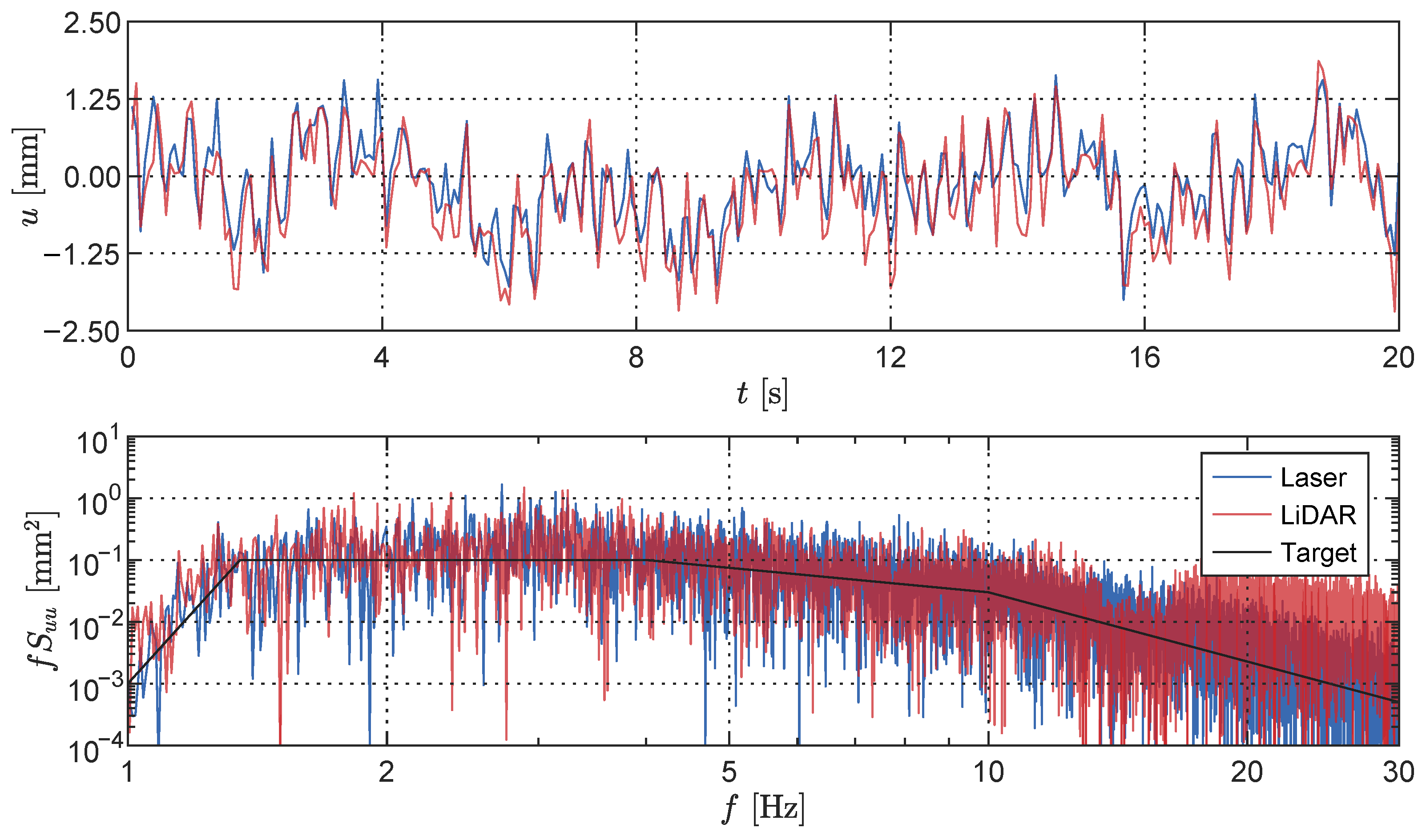
3.3.2. Accuracy and Noise Characterisation
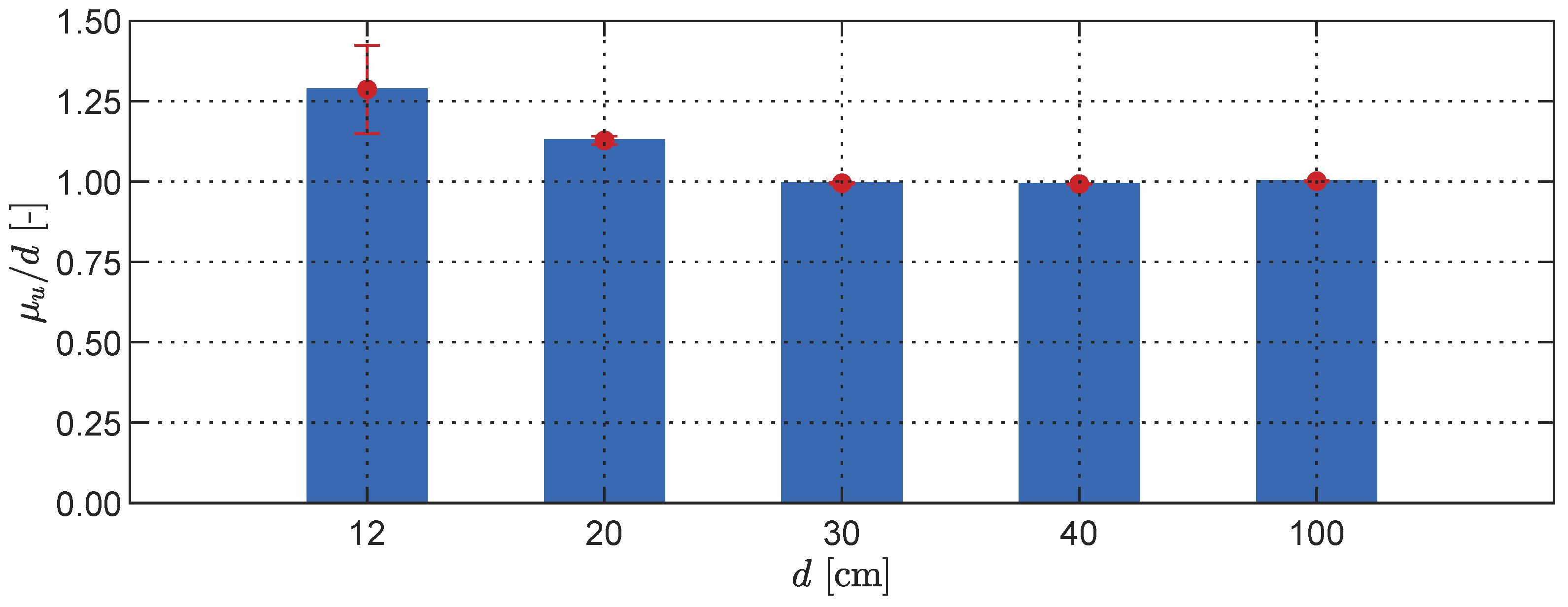
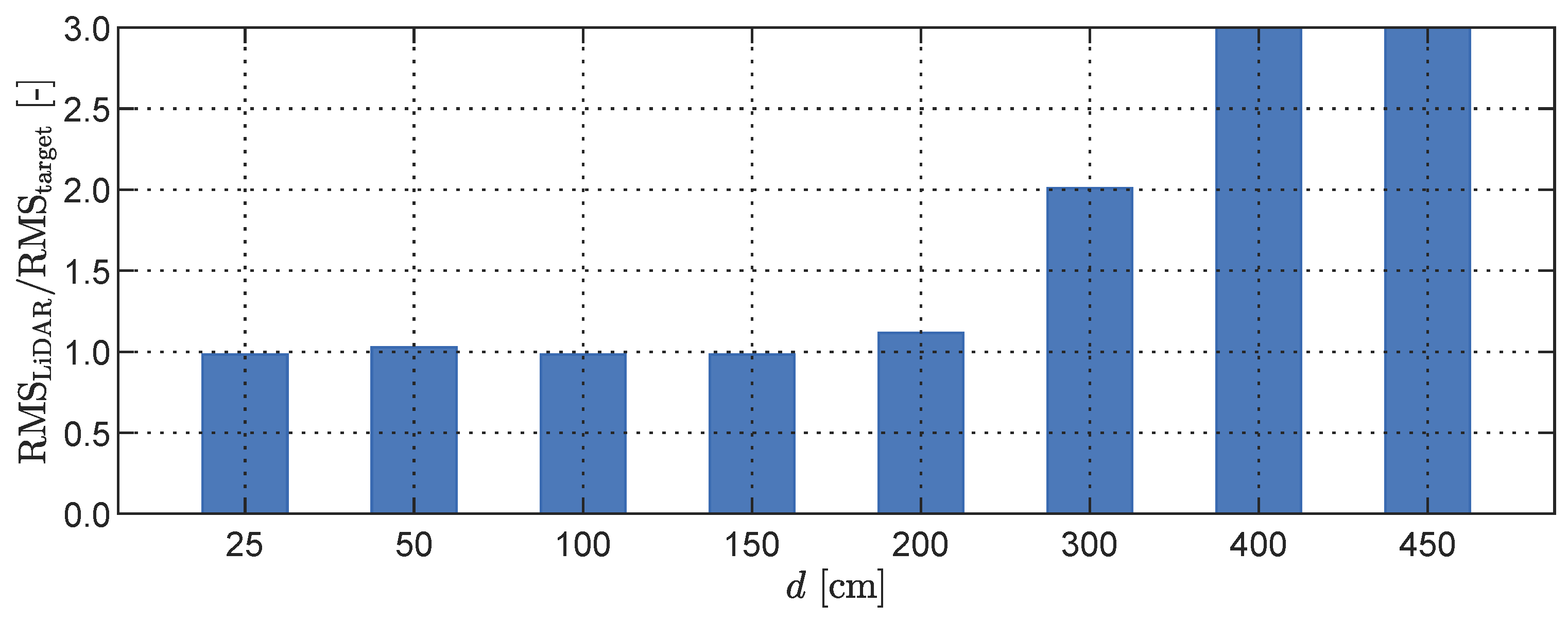
3.3.3. Phone-to-Target Distance
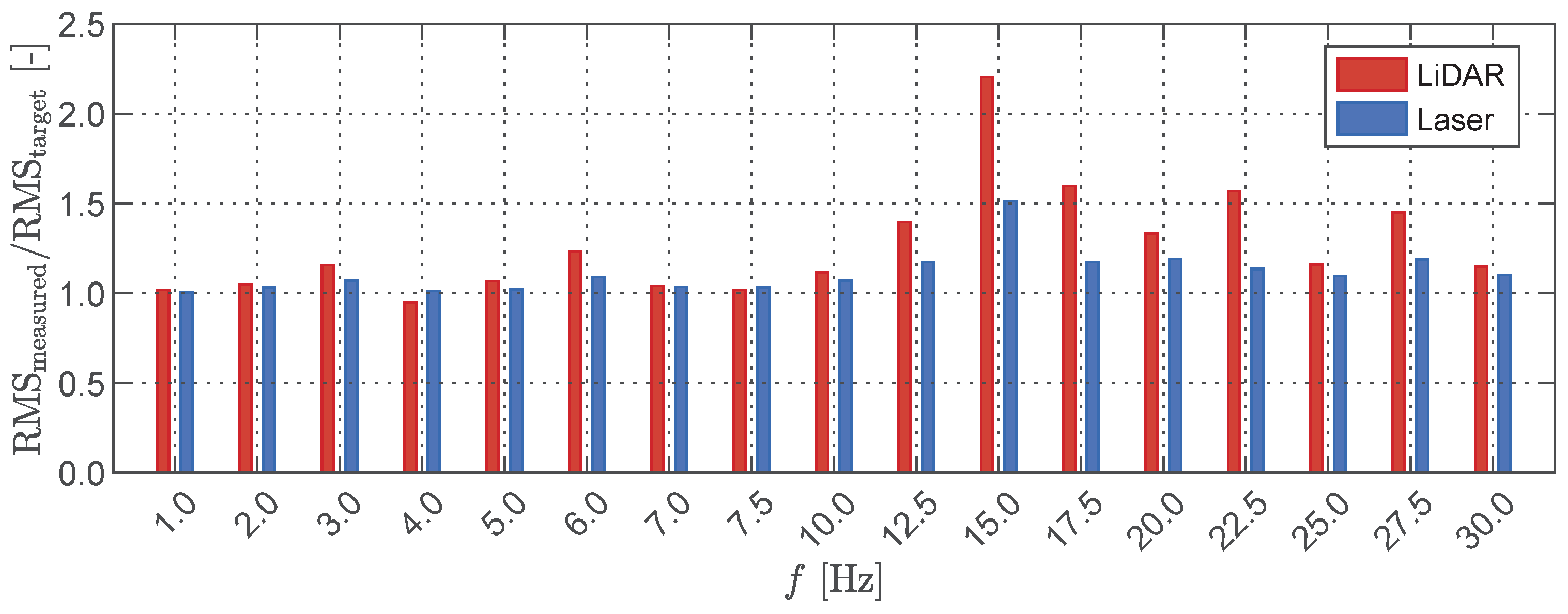
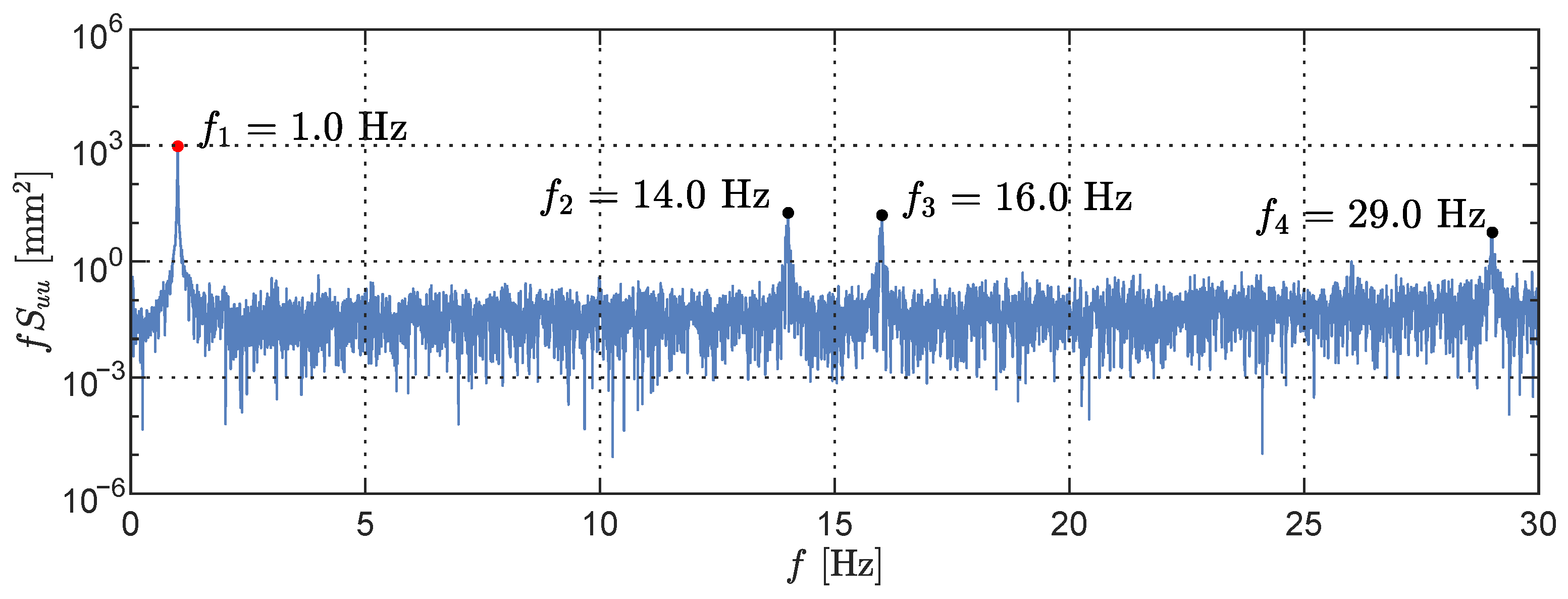
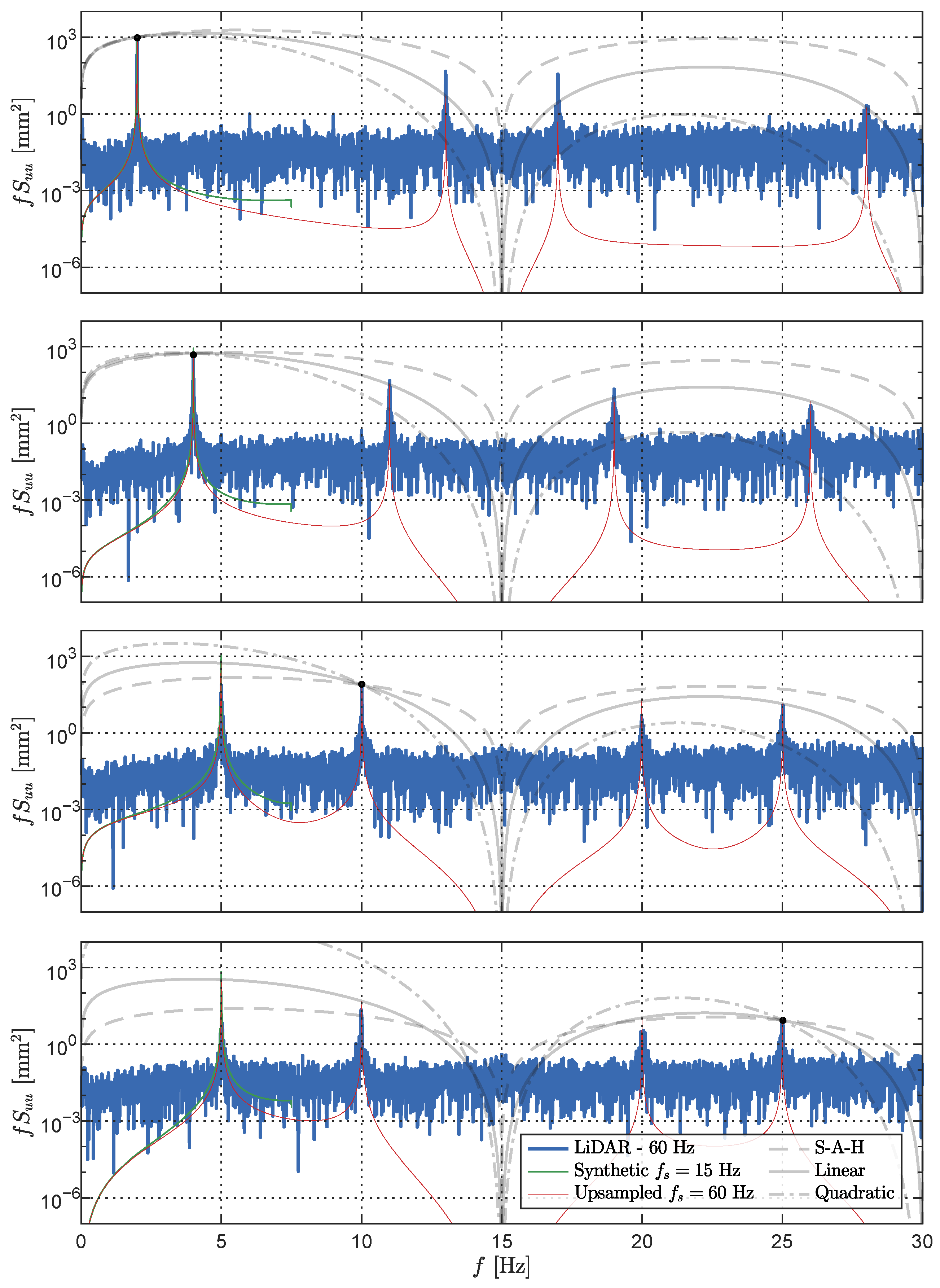
3.3.4. Effective Sampling Rate
4. Experiment
4.1. Setup
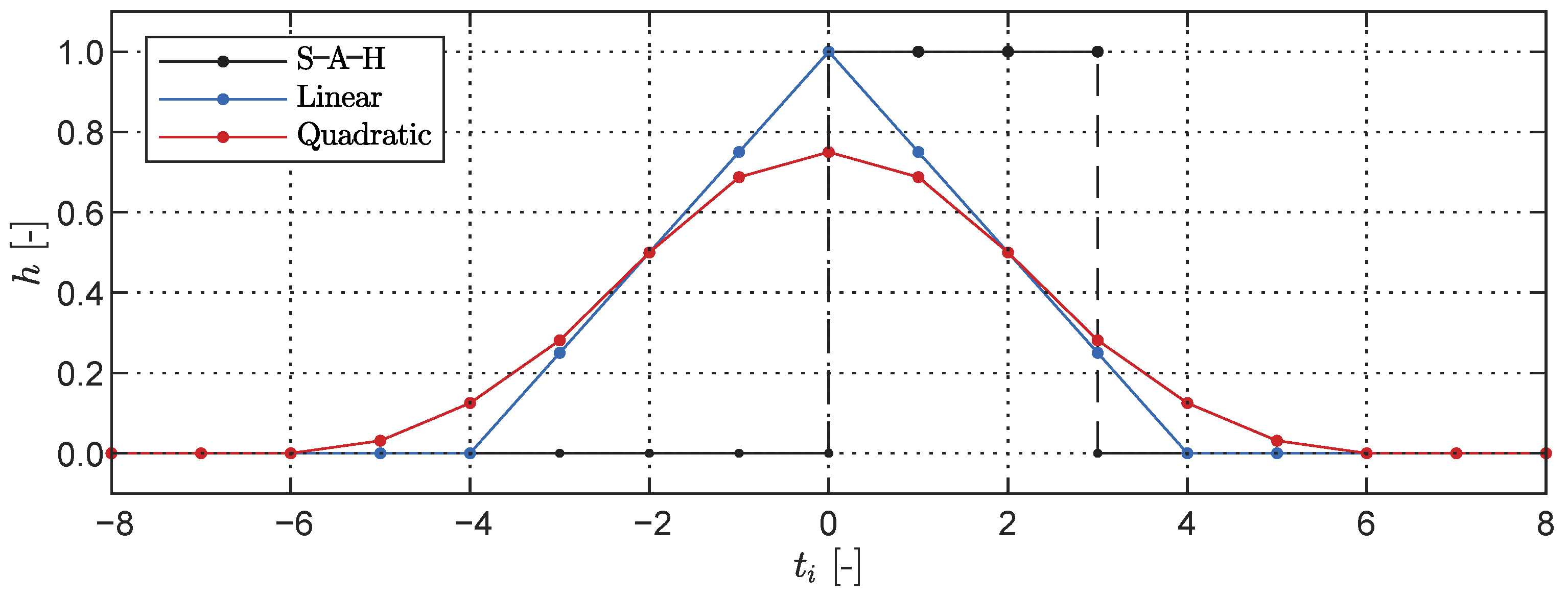
4.2. Data Preprocessing
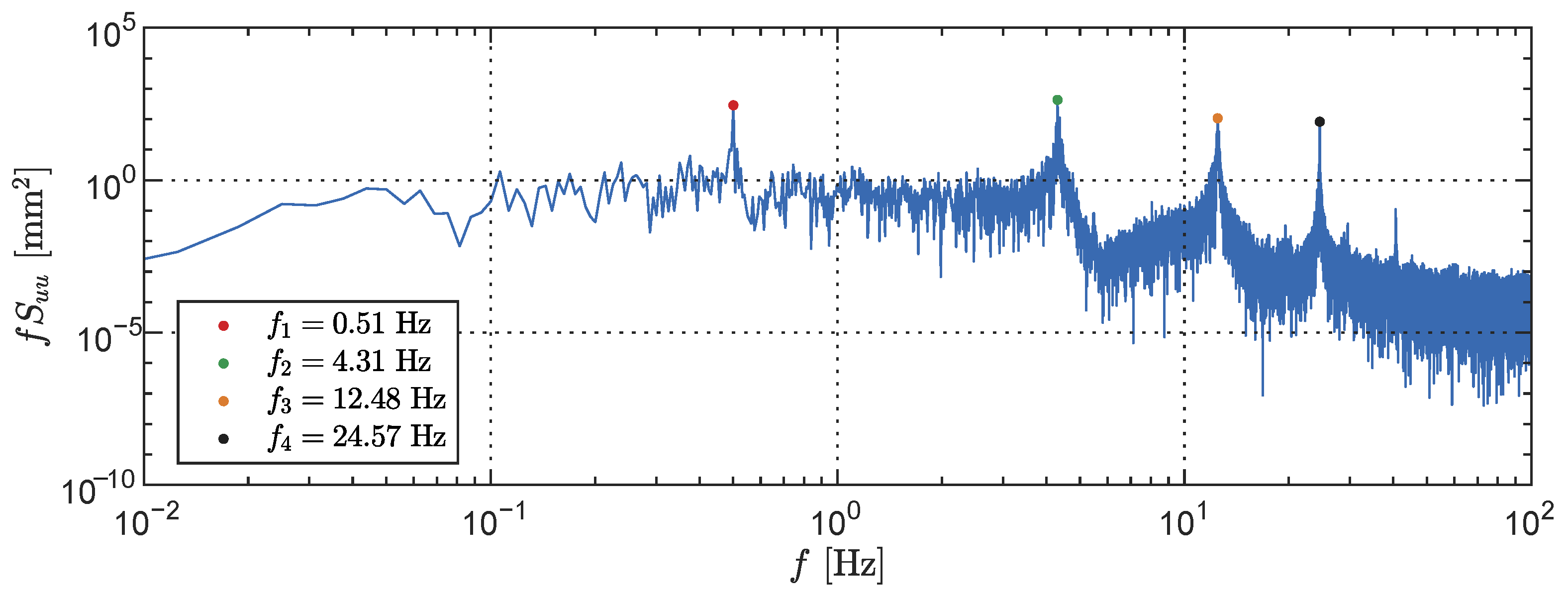
4.3. Modal Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- iPhone 13 Pro is a trademark of Apple Inc., registered in the U.S. and other countries and regions.
- Debeunne, C.; Vivet, D. A review of visual-LiDAR fusion based simultaneous localization and mapping. Sensors 2020, 20, 2068. [Google Scholar] [CrossRef]
- Kim, T.; Park, T.H. Extended Kalman filter (EKF) design for vehicle position tracking using reliability function of radar and lidar. Sensors 2020, 20, 4126. [Google Scholar] [CrossRef]
- De Silva, V.; Roche, J.; Kondoz, A. Robust fusion of LiDAR and wide-angle camera data for autonomous mobile robots. Sensors 2018, 18, 2730. [Google Scholar] [CrossRef] [PubMed]
- Roriz, R.; Cabral, J.; Gomes, T. Automotive LiDAR Technology: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6282–6297. [Google Scholar] [CrossRef]
- Luetzenburg, G.; Kroon, A.; Bjørk, A.A. Evaluation of the Apple iPhone 12 Pro LiDAR for an Application in Geosciences. Sci. Rep. 2021, 11, 22221. [Google Scholar] [CrossRef]
- Tamimi, R. Relative Accuracy found within iPhone Data Collection. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 43, 303–308. [Google Scholar] [CrossRef]
- Tatsumi, S.; Yamaguchi, K.; Furuya, N. ForestScanner: A mobile application for measuring and mapping trees with LiDAR-equipped iPhone and iPad. Methods Ecol. Evol. 2023, 14, 1603–1609. [Google Scholar] [CrossRef]
- Tavani, S.; Billi, A.; Corradetti, A.; Mercuri, M.; Bosman, A.; Cuffaro, M.; Seers, T.; Carminati, E. Smartphone assisted fieldwork: Towards the digital transition of geoscience fieldwork using LiDAR-equipped iPhones. Earth-Sci. Rev. 2022, 227, 103969. [Google Scholar] [CrossRef]
- Mikalai, Z.; Andrey, D.; Hawas, H.; Tetiana, H.; Oleksandr, S. Human body measurement with the iPhone 12 Pro LiDAR scanner. In Proceedings of the AIP Conference Proceedings, Vitebsk, Belarus, 8–10 June 2021; AIP Publishing: Melville, NY, USA, 2022; Volume 2430. [Google Scholar] [CrossRef]
- Sony, S.; Laventure, S.; Sadhu, A. A literature review of next-generation smart sensing technology in structural health monitoring. Struct. Control Health Monit. 2019, 26, e2321. [Google Scholar] [CrossRef]
- Pires, I.M.; Garcia, N.M.; Pombo, N.; Flórez-Revuelta, F. From data acquisition to data fusion: A comprehensive review and a roadmap for the identification of activities of daily living using mobile devices. Sensors 2016, 16, 184. [Google Scholar] [CrossRef]
- Pittaluga, F.; Tasneem, Z.; Folden, J.; Tilmon, B.; Chakrabarti, A.; Koppal, S.J. Towards a MEMS-based Adaptive LIDAR. In Proceedings of the 2020 International Conference on 3D Vision (3DV), Fukuoka, Japan, 25–28 November 2020; pp. 1216–1226. [Google Scholar] [CrossRef]
- Morgenthal, G.; Höpfner, H. The application of smartphones to measuring transient structural displacements. J. Civ. Struct. Health Monit. 2012, 2, 149–161. [Google Scholar] [CrossRef]
- Riley, C.; Millar, J.D.; Lozano, S.; Clair, S.S. Using Mobile Devices to Teach Structural Dynamics and Structural Health Monitoring. In Proceedings of the 2016 ASEE Annual Conference & Exposition, New Orleans, LA, USA, 26 June–28 August 2016. [Google Scholar] [CrossRef]
- Morgenthal, G.; Rau, S.; Taraben, J.; Abbas, T. Determination of stay-cable forces using highly mobile vibration measurement devices. J. Bridge Eng. 2018, 23, 04017136. [Google Scholar] [CrossRef]
- Tondo, G.R.; Rau, S.; Kavrakov, I.; Morgenthal, G. Physics-Informed Gaussian Process Model for Euler-Bernoulli Beam Elements. In Proceedings of the IABSE Symposium, Prague, Czech Republic, 25–27 May 2022; pp. 445–452. [Google Scholar] [CrossRef]
- Goyal, D.; Pabla, B. The vibration monitoring methods and signal processing techniques for structural health monitoring: A review. Arch. Comput. Methods Eng. 2016, 23, 585–594. [Google Scholar] [CrossRef]
- Chawdhury, S.; Morgenthal, G. Numerical simulations of aeroelastic instabilities to optimize the performance of flutter-based electromagnetic energy harvesters. J. Intell. Mater. Syst. Struct. 2018, 29, 479–495. [Google Scholar] [CrossRef]
- Hallermann, N.; Morgenthal, G.; Rodehorst, V. Vision-based deformation monitoring of large scale structures using Unmanned Aerial Systems. In Proceedings of the IABSE Symposium Madrid. International Association for Bridge and Structural Engineering, Madrid, Spain, 3–5 September 2014; Volume 102, pp. 2852–2859. [Google Scholar] [CrossRef]
- Gueguen, P.; Jolivet, V.; Michel, C.; Schveitzer, A.S. Comparison of velocimeter and coherent lidar measurements for building frequency assessment. Bull. Earthq. Eng. 2010, 8, 327–338. [Google Scholar] [CrossRef]
- Morgenthal, G.; Hallermann, N.; Kersten, J.; Taraben, J.; Debus, P.; Helmrich, M.; Rodehorst, V. Framework for automated UAS-based structural condition assessment of bridges. Autom. Constr. 2019, 97, 77–95. [Google Scholar] [CrossRef]
- Kaartinen, E.; Dunphy, K.; Sadhu, A. LiDAR-based structural health monitoring: Applications in civil infrastructure systems. Sensors 2022, 22, 4610. [Google Scholar] [CrossRef]
- Silva, M.F.; Green, A.; Morales, J.; Meyerhofer, P.; Yang, Y.; Figueiredo, E.; Costa, J.C.; Mascareñas, D. 3D structural vibration identification from dynamic point clouds. Mech. Syst. Signal Process. 2022, 166, 108352. [Google Scholar] [CrossRef]
- Benedetti, E.; Branzanti, M.; Colosimo, G.; Mazzoni, A.; Moroni, M.; Crespi, M. A new approach for real-time structural monitoring. Coordinates 2015, 11, 37–45. [Google Scholar]
- Smisek, J.; Jancosek, M.; Pajdla, T. 3D with Kinect. In Consumer Depth Cameras for Computer Vision: Research Topics and Applications; Springer: London, UK, 2013; pp. 3–25. [Google Scholar] [CrossRef]
- Järvenpää, A. Metrological Characterization of a Consumer Grade Flash LiDAR Device. Master’s Thesis, Aalto University, Espoo, Finland, 2021. [Google Scholar]
- Chen, G.; Wiede, C.; Kokozinski, R. Data processing approaches on SPAD-based d-TOF LiDAR systems: A review. IEEE Sens. J. 2020, 21, 5656–5667. [Google Scholar] [CrossRef]
- Kim, W.; Tanaka, M.; Okutomi, M.; Sasaki, Y. Pixelwise Dynamic Convolution Neural Network for LiDAR Depth Data Interpolation. IEEE Sens. J. 2021, 21, 27736–27747. [Google Scholar] [CrossRef]
- Xu, X.; Al-Dahle, A.; Garg, K. Shared Sensor Data across Sensor Processing Pipelines. U.S. Patent 10671068, 19 September 2020. [Google Scholar]
- Norman, M.; Tao, M.; Bujold, E.; Soussan, S.; Roelke, V.; Anneheim, G.; Zaragoza, J.; Ciurea, F. Efficient Scene Depth Map Enhancement for Low Power Devices. U.S. Patent 20190362511A1, 28 November 2019. [Google Scholar]
- Vogt, M.; Rips, A.; Emmelmann, C. Comparison of iPad Pro®’s LiDAR and TrueDepth capabilities with an industrial 3D scanning solution. Technologies 2021, 9, 25. [Google Scholar] [CrossRef]
- Teppati Losè, L.; Spreafico, A.; Chiabrando, F.; Giulio Tonolo, F. Apple LiDAR Sensor for 3D Surveying: Tests and Results in the Cultural Heritage Domain. Remote Sens. 2022, 14, 4157. [Google Scholar] [CrossRef]
- Allain, R. What is the Angular Field of View for an iPhone 13? Available online: https://rjallain.medium.com/what-is-the-angular-field-of-view-for-an-iphone-13-199969482531 (accessed on 26 June 2022).
- Mathie, M.; Basilakis, J.; Celler, B. A system for monitoring posture and physical activity using accelerometers. In Proceedings of the 2001 Conference Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Istanbul, Turkey, 25–28 October 2001; Volume 4, pp. 3654–3657. [Google Scholar] [CrossRef]
- Coskun, D.; Incel, O.D.; Ozgovde, A. Phone position/placement detection using accelerometer: Impact on activity recognition. In Proceedings of the 2015 IEEE Tenth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Singapore, 7–9 April 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, Y.; Wang, S.; Chen, Z. FallAlarm: Smart Phone Based Fall Detecting and Positioning System. Procedia Comput. Sci. 2012, 10, 617–624. [Google Scholar] [CrossRef]
- Apple Inc. ARKit Documentation. Available online: https://developer.apple.com/documentation/arkit/ (accessed on 3 July 2023).
- Panglosse, A.; Martin-Gonthier, P.; Marcelot, O.; Virmontois, C.; Saint-Pé, O.; Magnan, P. Modeling, Simulation Methods and Characterization of Photon Detection Probability in CMOS-SPAD. Sensors 2021, 21, 5860. [Google Scholar] [CrossRef]
- Kohneh Poushi, S.S.; Mahmoudi, H.; Steindl, B.; Hofbauer, M.; Zimmermann, H. Comprehensive Modeling of Photon Detection Probability in CMOS-based SPADs. In Proceedings of the 2020 IEEE SENSORS, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Xiaoyong, Y. Apple LIDAR Demystified: SPAD, VCSEL, and Fusion. 4D Sensing & AIoT. Available online: https://4sense.medium.com/apple-lidar-demystified-spad-vcsel-and-fusion-aa9c3519d4cb (accessed on 26 June 2023).
- Kashani, A.G.; Olsen, M.J.; Parrish, C.E.; Wilson, N. A Review of LIDAR Radiometric Processing: From Ad Hoc Intensity Correction to Rigorous Radiometric Calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. Reference-based stochastic subspace identification for output-only modal analysis. Mech. Syst. Signal Process. 1999, 13, 855–878. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. Reference based stochastic subspace identification in civil engineering. Inverse Probl. Eng. 2000, 8, 47–74. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Orlowitz, E.; Brandt, A. Influence of Noise in Correlation Function Estimates for Operational Modal Analysis. In Proceedings of the Topics in Modal Analysis & Testing; Mains, M., Dilworth, B.J., Eds.; Springer: Cham, Switzerland, 2019; Volume 9, pp. 55–64. [Google Scholar] [CrossRef]
- Kudu, F.N.; Uçak, Ş.; Osmancikli, G.; Türker, T.; Bayraktar, A. Estimation of damping ratios of steel structures by Operational Modal Analysis method. J. Constr. Steel Res. 2015, 112, 61–68. [Google Scholar] [CrossRef]
- Zahid, F.B.; Ong, Z.C.; Khoo, S.Y. A review of operational modal analysis techniques for in-service modal identification. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–18. [Google Scholar] [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]








| Target Distance | Measurement | ||
|---|---|---|---|
| [cm] | [cm] | [cm] | SNR [dB] |
| 12 | 15.4 | 0.65 | 27.6 |
| 20 | 22.6 | 0.10 | 46.7 |
| 30 | 29.9 | 0.05 | 55.5 |
| 40 | 39.7 | 0.03 | 63.0 |
| 100 | 100.1 | 0.09 | 61.4 |
| [Hz] | [Hz] | [Hz] | [Hz] | [Hz] |
|---|---|---|---|---|
| 2.0 | 2.0 | 13.0 | 17.0 | 28.0 |
| 4.0 | 4.0 | 11.0 | 19.0 | 26.0 |
| 10.0 | 5.0 | 10.0 | 20.0 | 25.0 |
| 25.0 | 5.0 | 10.0 | 20.0 | 25.0 |
| Mode | Frequencies | Damping Ratios | |||||
|---|---|---|---|---|---|---|---|
| [-] | [Hz] | [Hz] | [Hz] | [Hz] | [-] | [-] | [-] |
| 1 | 0.51 | - | 0.50 | 0.04 | 0.0006 | 0.0048 | 0.0026 |
| 2 | 4.31 | - | 4.45 | 0.08 | 0.0049 | 0.0139 | 0.0091 |
| 3 | 12.48 | 2.52 | 2.55 | 0.14 | 0.0027 | 0.0182 | 0.0099 |
| 4 | 24.57 | 5.43 | 5.48 | 0.27 | 0.0007 | 0.0012 | 0.0008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tondo, G.R.; Riley, C.; Morgenthal, G. Characterization of the iPhone LiDAR-Based Sensing System for Vibration Measurement and Modal Analysis. Sensors 2023, 23, 7832. https://doi.org/10.3390/s23187832
Tondo GR, Riley C, Morgenthal G. Characterization of the iPhone LiDAR-Based Sensing System for Vibration Measurement and Modal Analysis. Sensors. 2023; 23(18):7832. https://doi.org/10.3390/s23187832
Chicago/Turabian StyleTondo, Gledson Rodrigo, Charles Riley, and Guido Morgenthal. 2023. "Characterization of the iPhone LiDAR-Based Sensing System for Vibration Measurement and Modal Analysis" Sensors 23, no. 18: 7832. https://doi.org/10.3390/s23187832
APA StyleTondo, G. R., Riley, C., & Morgenthal, G. (2023). Characterization of the iPhone LiDAR-Based Sensing System for Vibration Measurement and Modal Analysis. Sensors, 23(18), 7832. https://doi.org/10.3390/s23187832





