Destriping of Remote Sensing Images by an Optimized Variational Model
Abstract
:1. Introduction
- (1)
- We utilize the gradient information obtained from remote sensing image decomposition to design regularization constraints in different directions, effectively avoiding the ripple effect during the destriping process.
- (2)
- The quasinorm is introduced into the proposed model to better capture the relevant sparsity properties, thereby preserving a greater amount of fine details in the underlying image.
- (3)
- The fast ADMM algorithm is employed to solve the destriping model. It reduces the computational time, enabling efficient processing of large-scale data.
2. Related Work
2.1. Characteristics of Stripe Noise and UTV Model
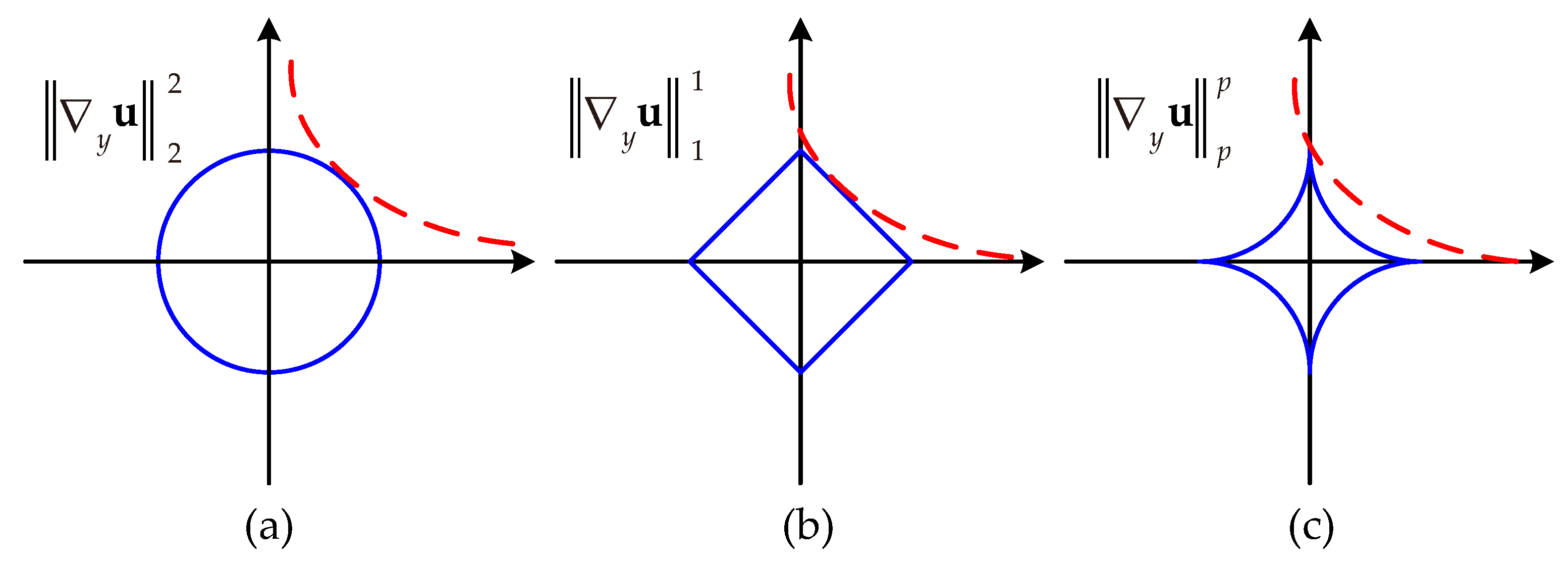
2.2. The Sparsity Analysis of the Quasinorm
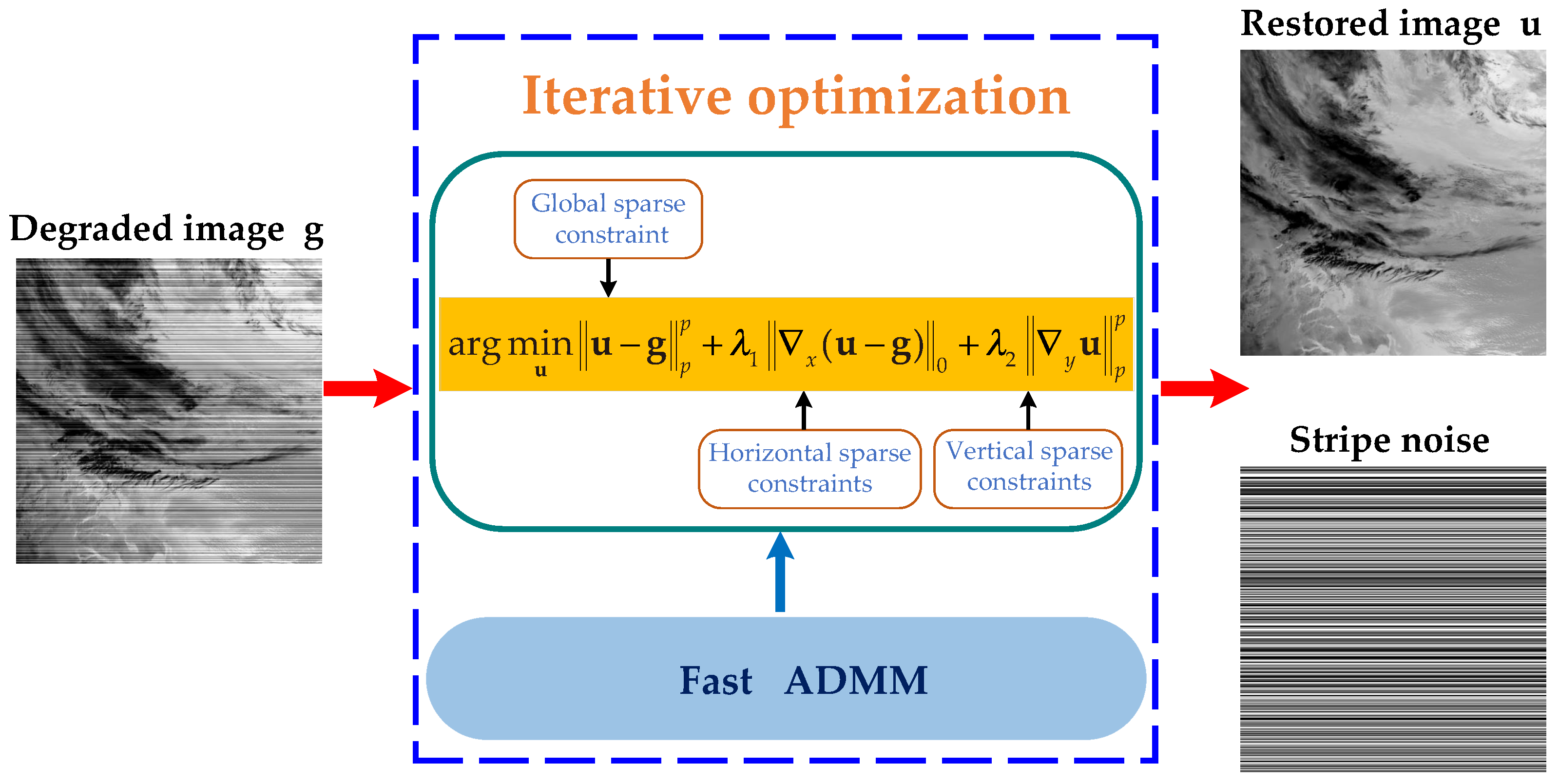
3. Proposed Method
3.1. The Proposed Model
3.1.1. Global Sparsity Constraint
3.1.2. Local Sparsity Constraint
3.2. The Solution Based on Fast ADMM
- (1)
- The subproblem related to is
- (2)
- The subproblem related to is
- (3)
- The subproblem related to is
- (4)
- The subproblem related to is
| Algorithm 1: The proposed destriping model with Fast ADMM |
| Input: Degraded image and related parameter , , , , and |
| 1: Initialize: Set , , , . |
| 2: While: and |
| 3: update by using Equation (13) |
| 4: update , , and by using Equations (17), (21) and (24) |
| 5: update , , and by using Equations (25)–(27) |
| 6: update by using Equation (28) |
| 7: if , then |
| 8: update , and by using Equations (29)–(31) |
| 9: else |
| 10: , , , , |
| 11: end if |
| 12: |
| 13: End While |
| Output: Destriped image |
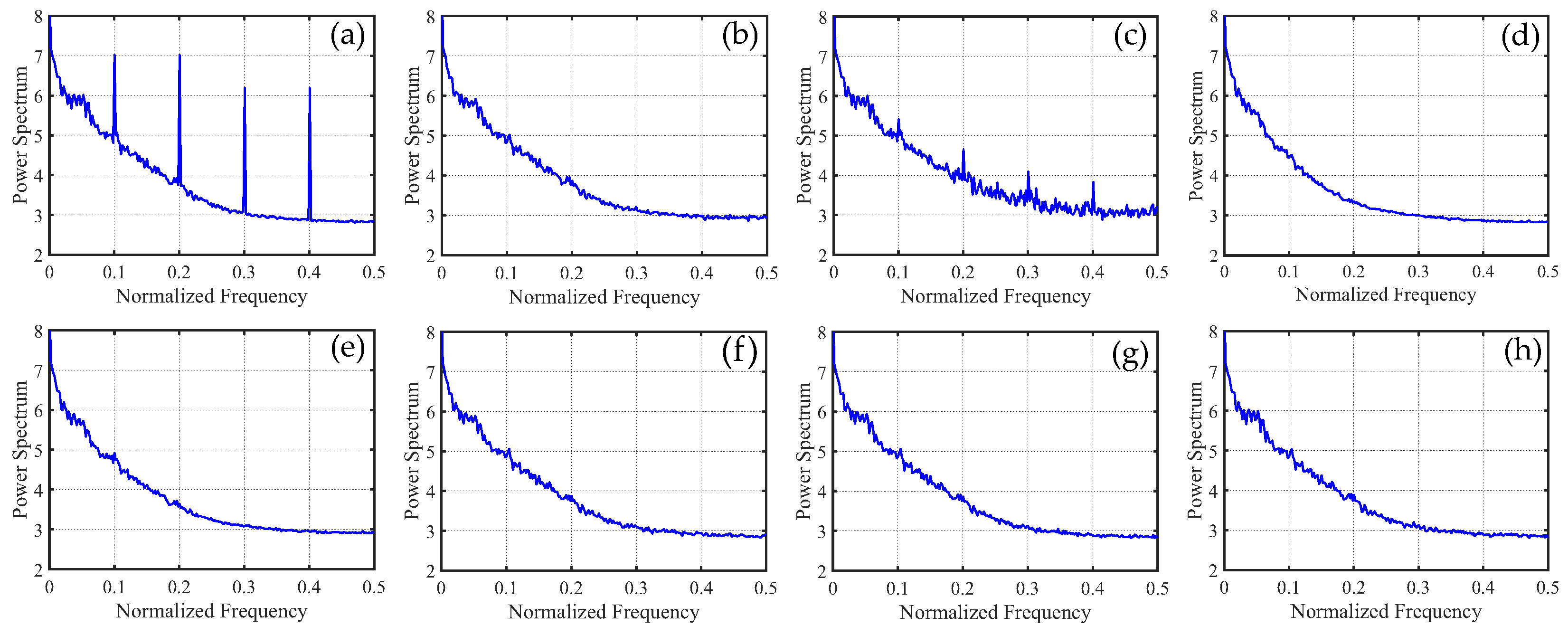
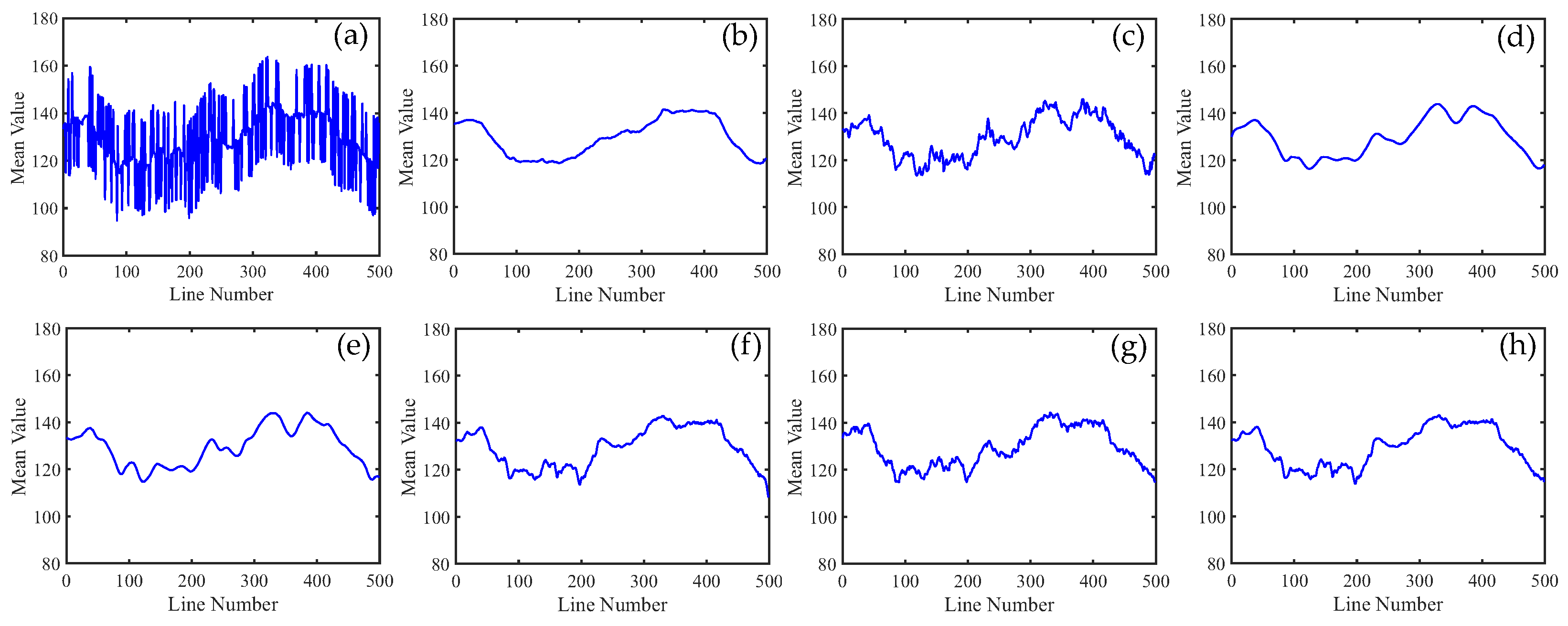
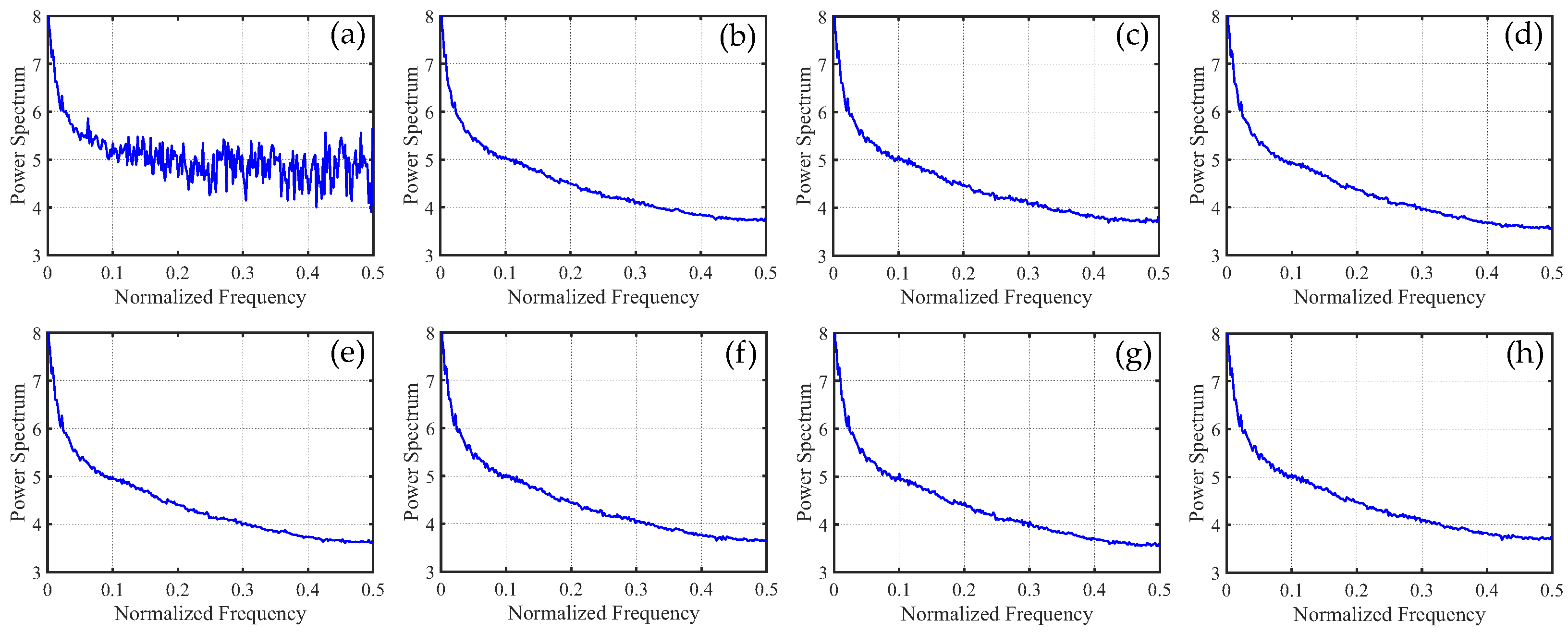
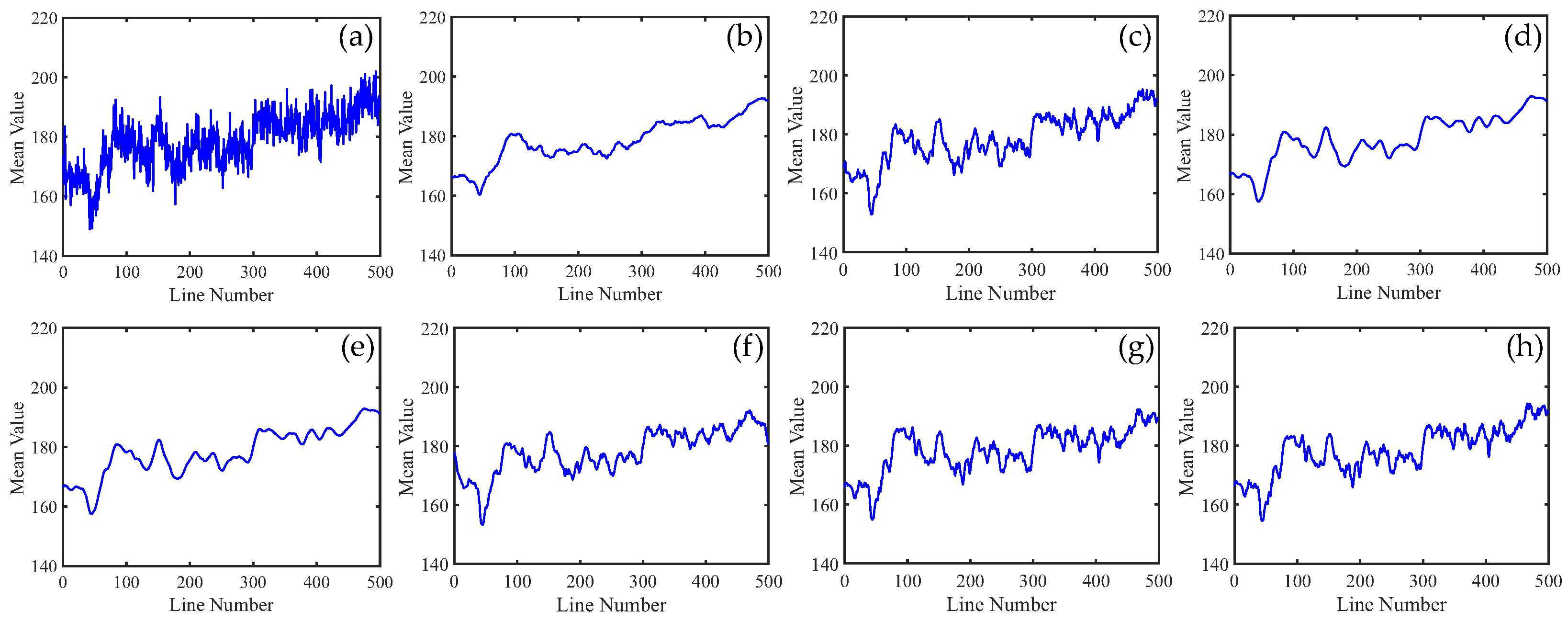
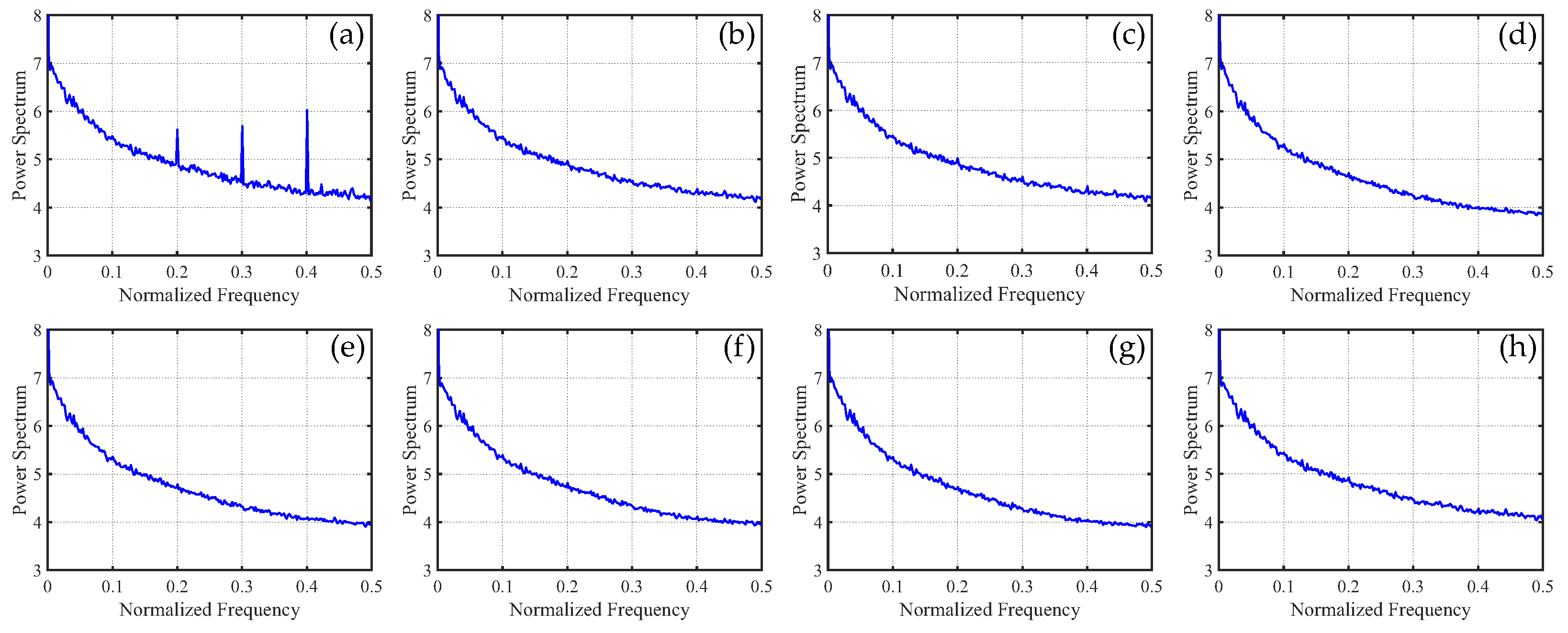
4. Experiment Results
4.1. Simulated Data Experiments
4.1.1. Periodic Stripe Noise
4.1.2. Nonperiodic Stripe Noise
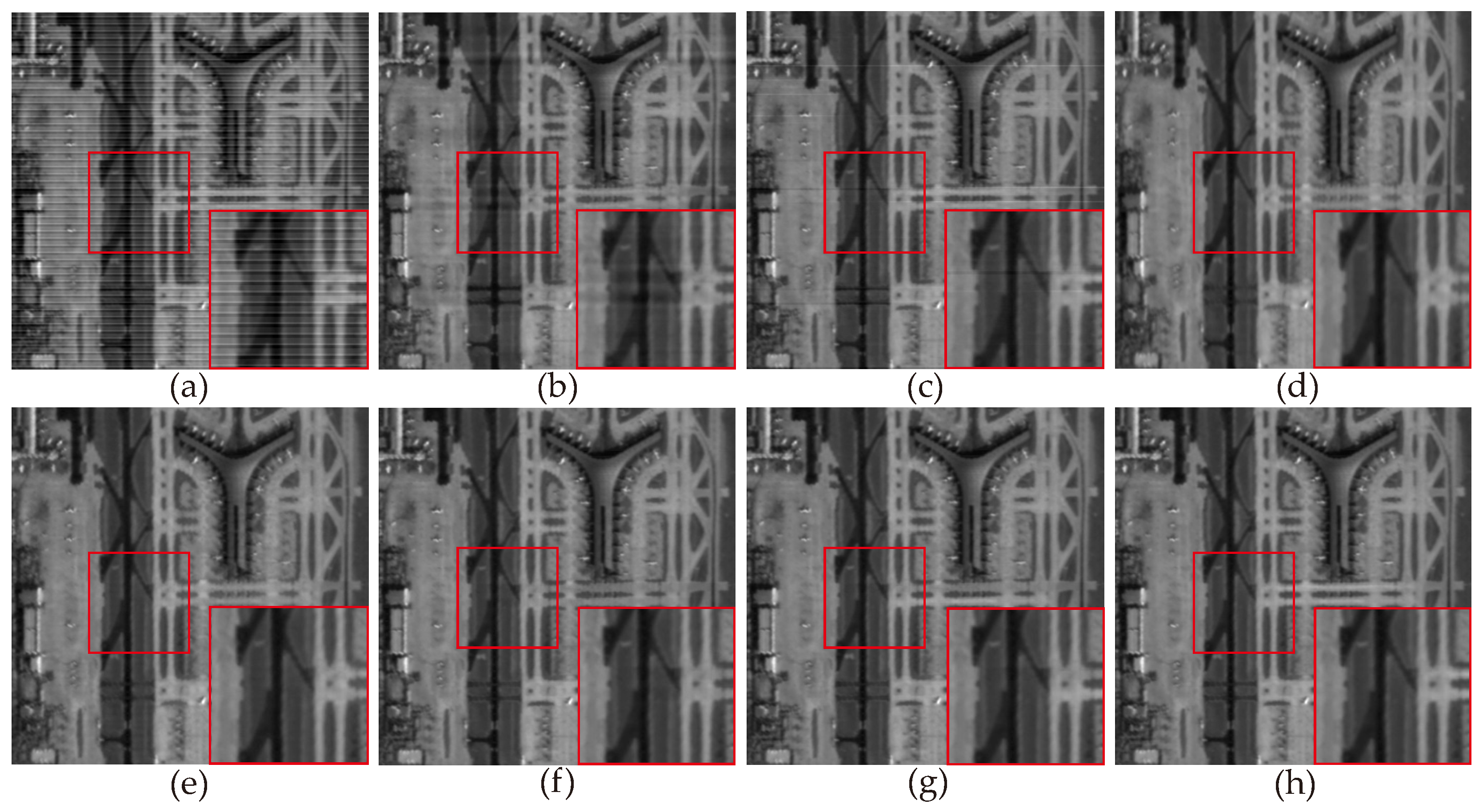
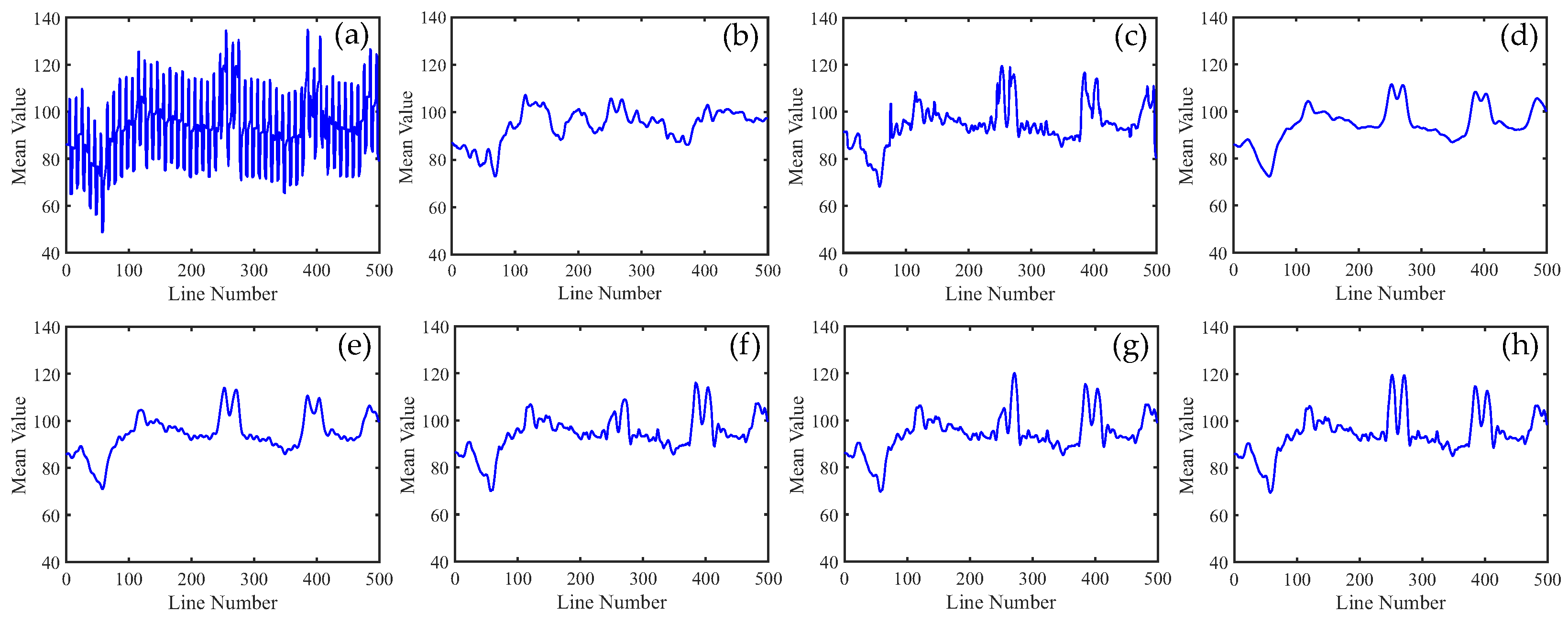
4.2. Real Data Experiments
5. Discussion
5.1. Discussion of Experiment Results
5.2. Analysis of the Parameters
- (1)
- When the stripe noise is weak, it is generally recommended to select a larger value for , which increases the weight of the horizontal stripe component, better preserving the details of the underlying image.
- (2)
- When the stripe noise is strong, it is generally recommended to select a larger value for , which increases the weight of the vertical image component, enhancing the destriping capability.
5.3. Limitation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| MODIS | Multidisciplinary Digital Publishing Institute |
| VIIRS | Visible Infrared Imaging Radiometer Suite |
| FFT | Fast Fourier Transform |
| PSNR | Peak Signal to Noise Ratio |
| SSIM | Structural Similarity |
| MRD | Mean Relative Deviation |
| ICV | Inverse Coefficient of Variation |
References
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Bouali, M.; Ladjal, S. Toward optimal destriping of MODIS data using a unidirectional variational model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet—Fourier filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar] [CrossRef]
- Chen, J.; Shao, Y.; Guo, H.; Wang, W.; Zhu, B. Destriping CMODIS data by power filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2119–2124. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, M.Y.; Tisse, C.L. Effective strip noise removal for low-textured infrared images based on 1-D guided filtering. IEEE Trans. Circuits Syst. Video Technol. 2015, 26, 2176–2188. [Google Scholar] [CrossRef]
- Torres, J.; Infante, S.O. Wavelet analysis for the elimination of striping noise in satellite images. Opt. Eng. 2001, 40, 1309–1314. [Google Scholar]
- Gadallah, F.; Csillag, F.; Smith, E. Destriping multisensor imagery with moment matching. Int. J. Remote Sens. 2000, 21, 2505–2511. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A MAP-based algorithm for destriping and inpainting of remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2008, 47, 1492–1502. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Restoration of Aqua MODIS band 6 using histogram matching and local least squares fitting. IEEE Trans. Geosci. Remote Sens. 2008, 47, 613–627. [Google Scholar] [CrossRef]
- Carfantan, H.; Idier, J. Statistical linear destriping of satellite-based pushbroom-type images. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1860–1871. [Google Scholar] [CrossRef]
- Shen, H.; Jiang, W.; Zhang, H.; Zhang, L. A piece-wise approach to removing the nonlinear and irregular stripes in MODIS data. Int. J. Remote Sens. 2014, 35, 44–53. [Google Scholar] [CrossRef]
- Xiao, P.; Guo, Y.; Zhuang, P. Removing stripe noise from infrared cloud images via deep convolutional networks. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Zhong, S.; Liao, W. HSI-DeNet: Hyperspectral image restoration via convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 667–682. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Li, Q.; Li, Z.; Zhang, T.; Sang, N.; Xiong, S. Unidirectional variation and deep CNN denoiser priors for simultaneously destriping and denoising optical remote sensing images. Int. J. Remote Sens. 2019, 40, 5737–5748. [Google Scholar] [CrossRef]
- Guan, J.; Lai, R.; Xiong, A. Learning spatiotemporal features for single image stripe noise removal. IEEE Access 2019, 7, 144489–144499. [Google Scholar] [CrossRef]
- Huang, Z.; Zhu, Z.; Wang, Z.; Li, X.; Xu, B.; Zhang, Y.; Fang, H. D3CNNs: Dual Denoiser Driven Convolutional Neural Networks for Mixed Noise Removal in Remotely Sensed Images. Remote Sens. 2023, 15, 443. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.Z.; Deng, L.J.; Zhao, X.L.; Wang, M. Group sparsity based regularization model for remote sensing image stripe noise removal. Neurocomputing 2017, 267, 95–106. [Google Scholar] [CrossRef]
- Yang, J.H.; Zhao, X.L.; Ma, T.H.; Chen, Y.; Huang, T.Z.; Ding, M. Remote sensing images destriping using unidirectional hybrid total variation and nonconvex low-rank regularization. J. Comput. Appl. Math. 2020, 363, 124–144. [Google Scholar] [CrossRef]
- Zhou, G.; Fang, H.; Yan, L.; Zhang, T.; Hu, J. Removal of stripe noise with spatially adaptive unidirectional total variation. Optik 2014, 125, 2756–2762. [Google Scholar] [CrossRef]
- Dou, H.X.; Huang, T.Z.; Deng, L.J.; Zhao, X.L.; Huang, J. Directional ℓ0 Sparse Modeling for Image Stripe Noise Removal. Remote Sens. 2018, 10, 361. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Wu, T.; Zhong, S. Remote sensing image stripe noise removal: From image decomposition perspective. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7018–7031. [Google Scholar] [CrossRef]
- Goldstein, T.; O’Donoghue, B.; Setzer, S.; Baraniuk, R. Fast alternating direction optimization methods. SIAM J. Imaging Sci. 2014, 7, 1588–1623. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Y.; Lin, F.; Chen, Y.; Yu, F.; Cai, Z. Impulse noise denoising using total variation with overlapping group sparsity and Lp-pseudo-norm shrinkage. Appl. Sci. 2018, 8, 2317. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Peng, Z.; Wu, J.; Wang, Z. Infrared image super-resolution reconstruction based on quaternion fractional order total variation with Lp quasinorm. Appl. Sci. 2018, 8, 1864. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, L.; Gao, S. Non-convex fractional-order derivative for single image blind restoration. Appl. Math. Model. 2022, 102, 207–227. [Google Scholar] [CrossRef]
- Liu, L.; Xu, L.; Fang, H. Simultaneous intensity bias estimation and stripe noise removal in infrared images using the global and local sparsity constraints. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1777–1789. [Google Scholar] [CrossRef]
- Chen, Y.; He, W.; Yokoya, N.; Huang, T.Z. Hyperspectral image restoration using weighted group sparsity-regularized low-rank tensor decomposition. IEEE Trans. Cybern. 2019, 50, 3556–3570. [Google Scholar] [CrossRef]
- Yuan, G.; Ghanem, B. l0tv: A new method for image restoration in the presence of impulse noise. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5369–5377. [Google Scholar]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing information reconstruction of remote sensing data: A technical review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Shen, H.; Yuan, Q.; Jiao, Y.; Zhang, L. Stripe noise separation and removal in remote sensing images by consideration of the global sparsity and local variational properties. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3049–3060. [Google Scholar] [CrossRef]
- Wu, X.; Qu, H.; Zheng, L.; Gao, T.; Zhang, Z. A remote sensing image destriping model based on low-rank and directional sparse constraint. Remote Sens. 2021, 13, 5126. [Google Scholar] [CrossRef]
- Woodworth, J.; Chartrand, R. Compressed sensing recovery via nonconvex shrinkage penalties. Inverse Probl. 2016, 32, 075004. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, Z.; Gholami, A.; Yan, J.; Li, S. Seismic signal sparse time–frequency representation by Lp-quasinorm constraint. Digit. Signal Process. 2019, 87, 43–59. [Google Scholar] [CrossRef]
- Jiao, Y.; Jin, B.; Lu, X. A primal dual active set with continuation algorithm for the ℓ0-regularized optimization problem. Appl. Comput. Harmon. Anal. 2015, 39, 400–426. [Google Scholar] [CrossRef]
- Wang, J.; Xia, Q.; Xia, B. Fast image restoration method based on the L0, L1, and L1 gradient minimization. Mathematics 2022, 10, 3107. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Y.; Xiang, W. Single-frame-based column fixed-pattern noise correction in an uncooled infrared imaging system based on weighted least squares. Appl. Opt. 2019, 58, 9141–9153. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.L.; Huang, T.Z.; Zhao, X.L.; Huang, J.; Ma, T.H.; Zheng, Y.B. Reweighted block sparsity regularization for remote sensing images destriping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4951–4963. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Wang, J.L.; Huang, T.Z.; Ma, T.H.; Zhao, X.L.; Chen, Y. A sheared low-rank model for oblique stripe removal. Appl. Math. Comput. 2019, 360, 167–180. [Google Scholar] [CrossRef]
- Zeng, Q.; Qin, H.; Yan, X.; Yang, T. Fourier domain anomaly detection and spectral fusion for stripe noise removal of TIR imagery. Remote Sens. 2020, 12, 3714. [Google Scholar] [CrossRef]
- Nichol, J.E.; Vohora, V. Noise over water surfaces in Landsat TM images. Int. J. Remote Sens. 2004, 25, 2087–2093. [Google Scholar] [CrossRef]
- LAADS DAAC. Available online: https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 12 May 2023).
- MAXAR Resources. Available online: http://www.digitalglobe.com/product-samples (accessed on 12 May 2023).
- Earth at Night. Available online: https://earthobservatory.nasa.gov/images/event/79869/earth-at-night (accessed on 12 May 2023).
- Song, Q.; Wang, Y.; Yan, X.; Gu, H. Remote sensing images stripe noise removal by double sparse regulation and region separation. Remote Sens. 2018, 10, 998. [Google Scholar] [CrossRef]














| Image | Method | r = 0.2 | r = 0.5 | r = 0.8 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Intensity | Intensity | Intensity | ||||||||
| 20 | 50 | 80 | 20 | 50 | 80 | 20 | 50 | 80 | ||
| PSNR | WAFT | 43.4022 | 41.0526 | 36.4039 | 38.7461 | 34.4116 | 31.1280 | 36.7882 | 33.7920 | 26.0641 |
| WLS | 46.0724 | 39.4454 | 35.3322 | 41.6714 | 36.1614 | 30.6251 | 35.0809 | 31.1331 | 27.3167 | |
| UTV | 39.2602 | 38.1358 | 34.5581 | 38.3960 | 34.8853 | 32.3572 | 37.7028 | 33.2023 | 30.5506 | |
| SAUTV | 41.0473 | 38.9131 | 37.4996 | 39.3513 | 35.3723 | 34.7114 | 36.0768 | 35.1770 | 29.5822 | |
| GSLV | 43.1521 | 40.6223 | 38.0372 | 41.2094 | 38.5517 | 33.7158 | 39.8349 | 37.9538 | 30.5086 | |
| RBSUTV | 48.6146 | 43.7358 | 37.4996 | 41.4725 | 35.2497 | 32.3088 | 33.3342 | 29.8573 | 27.9977 | |
| Proposed | 46.5692 | 43.3382 | 39.6116 | 44.8139 | 41.0586 | 35.5250 | 41.2979 | 38.6075 | 32.6568 | |
| SSIM | WAFT | 0.9920 | 0.9909 | 0.9809 | 0.9853 | 0.9676 | 0.9351 | 0.9792 | 0.9654 | 0.9361 |
| WLS | 0.9968 | 0.9956 | 0.9922 | 0.9976 | 0.9958 | 0.9881 | 0.9956 | 0.9914 | 0.9309 | |
| UTV | 0.9901 | 0.9878 | 0.9755 | 0.9883 | 0.9774 | 0.9661 | 0.9864 | 0.9697 | 0.9497 | |
| SAUTV | 0.9982 | 0.9925 | 0.9918 | 0.9949 | 0.9905 | 0.9885 | 0.9902 | 0.9879 | 0.9585 | |
| GSLV | 0.9984 | 0.9945 | 0.9932 | 0.9968 | 0.9943 | 0.9852 | 0.9974 | 0.9936 | 0.9644 | |
| RBSUTV | 0.9995 | 0.9986 | 0.9882 | 0.9966 | 0.9787 | 0.9742 | 0.9696 | 0.9381 | 0.9155 | |
| Proposed | 0.9993 | 0.9983 | 0.9949 | 0.9987 | 0.9982 | 0.9936 | 0.9975 | 0.9946 | 0.9741 | |
| Image | Method | r = 0.2 | r = 0.5 | r = 0.8 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Intensity | Intensity | Intensity | ||||||||
| 20 | 50 | 80 | 20 | 50 | 80 | 20 | 50 | 80 | ||
| PSNR | WAFT | 34.2481 | 31.4194 | 30.6256 | 33.2016 | 30.7178 | 29.0722 | 32.7578 | 27.5066 | 24.6842 |
| WLS | 39.3885 | 33.8543 | 29.9705 | 38.9246 | 32.4222 | 28.1826 | 36.4057 | 26.0033 | 24.2943 | |
| UTV | 36.3369 | 32.9826 | 31.8258 | 33.7618 | 30.4517 | 29.9246 | 32.2136 | 28.7507 | 25.9453 | |
| SAUTV | 38.2431 | 33.1458 | 32.0741 | 35.7210 | 32.6039 | 30.5993 | 33.7555 | 30.0501 | 27.2049 | |
| GSLV | 41.0957 | 40.5213 | 36.9920 | 39.2048 | 36.6313 | 32.6001 | 38.8471 | 34.5522 | 28.9274 | |
| RBSUTV | 43.0943 | 38.4611 | 35.2614 | 38.8061 | 36.9439 | 32.7291 | 33.4630 | 27.5817 | 24.9959 | |
| Proposed | 42.4628 | 40.6482 | 37.5273 | 42.0398 | 37.6390 | 33.5871 | 41.0827 | 35.0869 | 30.6429 | |
| SSIM | WAFT | 0.9882 | 0.9813 | 0.9660 | 0.9863 | 0.9679 | 0.9049 | 0.9858 | 0.9243 | 0.8919 |
| WLS | 0.9974 | 0.9794 | 0.9448 | 0.9950 | 0.9635 | 0.9290 | 0.9921 | 0.9245 | 0.8717 | |
| UTV | 0.9758 | 0.9617 | 0.9551 | 0.9628 | 0.9471 | 0.9339 | 0.9567 | 0.9388 | 0.9004 | |
| SAUTV | 0.9885 | 0.9753 | 0.9629 | 0.9803 | 0.9723 | 0.9606 | 0.9774 | 0.9616 | 0.9246 | |
| GSLV | 0.9987 | 0.9963 | 0.9798 | 0.9982 | 0.9855 | 0.9699 | 0.9968 | 0.9686 | 0.9102 | |
| RBSUTV | 0.9997 | 0.9952 | 0.9756 | 0.9984 | 0.9911 | 0.9722 | 0.9801 | 0.9028 | 0.8692 | |
| Proposed | 0.9995 | 0.9967 | 0.9862 | 0.9991 | 0.9903 | 0.9784 | 0.9976 | 0.9785 | 0.9539 | |
| Image | Index | WAFT | WLS | UTV | SAUTV | GSLV | RBSUTV | Proposed |
|---|---|---|---|---|---|---|---|---|
| MODIS | MRD (%) | 3.9013 | 5.7286 | 4.3230 | 3.9782 | 2.9361 | 6.9148 | 3.3134 |
| data D7 | ICV | 48.49 | 49.94 | 63.37 | 54.09 | 73.11 | 41.17 | 56.10 |
| MODIS | MRD (%) | 3.6293 | 1.6754 | 2.8951 | 1.2567 | 3.7674 | 2.0363 | 1.1608 |
| data D8 | ICV | 83.97 | 73.80 | 80.15 | 88.23 | 74.29 | 84.12 | 89.74 |
| MODIS | MRD (%) | 2.3294 | 1.4604 | 2.0018 | 1.1688 | 1.8633 | 2.2361 | 1.0299 |
| data D9 | ICV | 79.15 | 72.47 | 107.47 | 112.93 | 90.29 | 76.21 | 101.63 |
| MODIS | MRD (%) | 6.2981 | 5.1454 | 7.1068 | 6.2015 | 4.8334 | 5.5062 | 2.3385 |
| data D10 | ICV | 101.13 | 109.64 | 163.37 | 127.50 | 137.58 | 114.04 | 172.35 |
| Image Size | 200 × 200 | 300 × 300 | 400 × 400 | 500 × 500 | 600 × 600 | 700 × 700 |
|---|---|---|---|---|---|---|
| ADMM | 1.1871 | 2.9263 | 6.0689 | 9.2549 | 13.3545 | 18.2670 |
| Fast ADMM | 0.3352 | 0.9538 | 1.8967 | 3.0324 | 4.1232 | 5.8862 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, F.; Wu, S.; Zhang, Q.; Liu, Y.; Sun, H. Destriping of Remote Sensing Images by an Optimized Variational Model. Sensors 2023, 23, 7529. https://doi.org/10.3390/s23177529
Yan F, Wu S, Zhang Q, Liu Y, Sun H. Destriping of Remote Sensing Images by an Optimized Variational Model. Sensors. 2023; 23(17):7529. https://doi.org/10.3390/s23177529
Chicago/Turabian StyleYan, Fei, Siyuan Wu, Qiong Zhang, Yunqing Liu, and Haonan Sun. 2023. "Destriping of Remote Sensing Images by an Optimized Variational Model" Sensors 23, no. 17: 7529. https://doi.org/10.3390/s23177529
APA StyleYan, F., Wu, S., Zhang, Q., Liu, Y., & Sun, H. (2023). Destriping of Remote Sensing Images by an Optimized Variational Model. Sensors, 23(17), 7529. https://doi.org/10.3390/s23177529






