Optimizing Machine Learning Algorithms for Landslide Susceptibility Mapping along the Karakoram Highway, Gilgit Baltistan, Pakistan: A Comparative Study of Baseline, Bayesian, and Metaheuristic Hyperparameter Optimization Techniques
Abstract
1. Introduction
- As numerous ML programmers devote significant time to adjusting the hyperparameters, notably for huge datasets or intricate ML algorithms having numerous hyperparameters, it decreases the degree of human labor required.
- It boosts the efficacy of ML models. Numerous ML hyperparameters have diverse optimal values to attain the best results on different datasets or problems.
- It boosts the replicability of the frameworks and techniques. Several ML algorithms may solely be justly assessed when the identical degree of hyperparameter adjustment is applied; consequently, utilizing the equivalent HPO approach to several ML algorithms also assists in recognizing the ideal ML model for a specific problem.
- It encompasses three well-known machine learning algorithms (SVM, RF, and KNN) and their fundamental hyperparameters.
- It assesses conventional HPO methodologies, their pros and cons, to facilitate their application to different ML models by selecting the fitting algorithm in pragmatic circumstances.
- It investigates the impact of HPO techniques on the comprehensive precision of landslide susceptibility mapping.
- It contrasts the increase in precision from the starting point and predetermined parameters to fine-tuned parameters and their impact on three renowned machine learning methods.
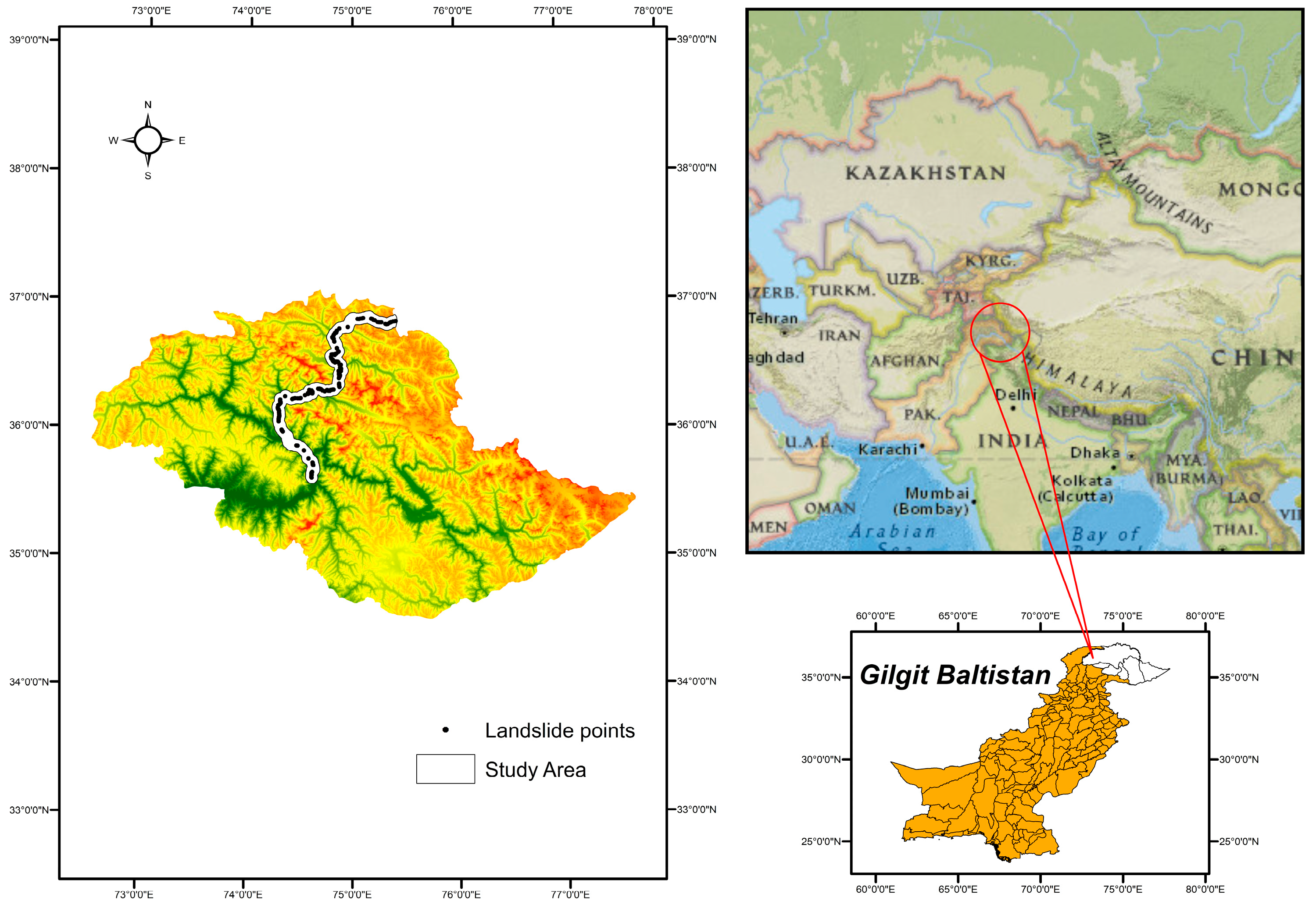
Study Area
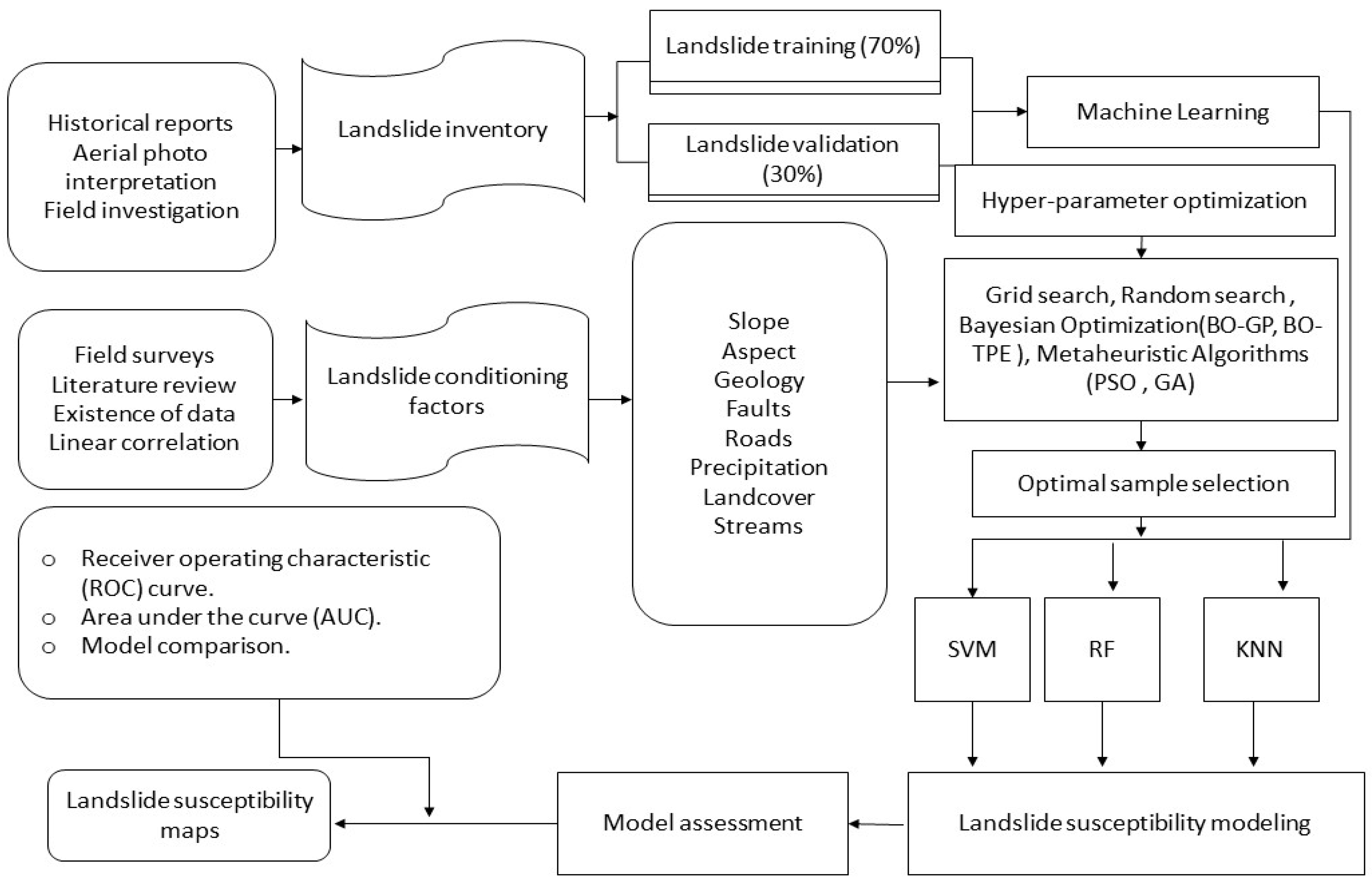
2. Methodology
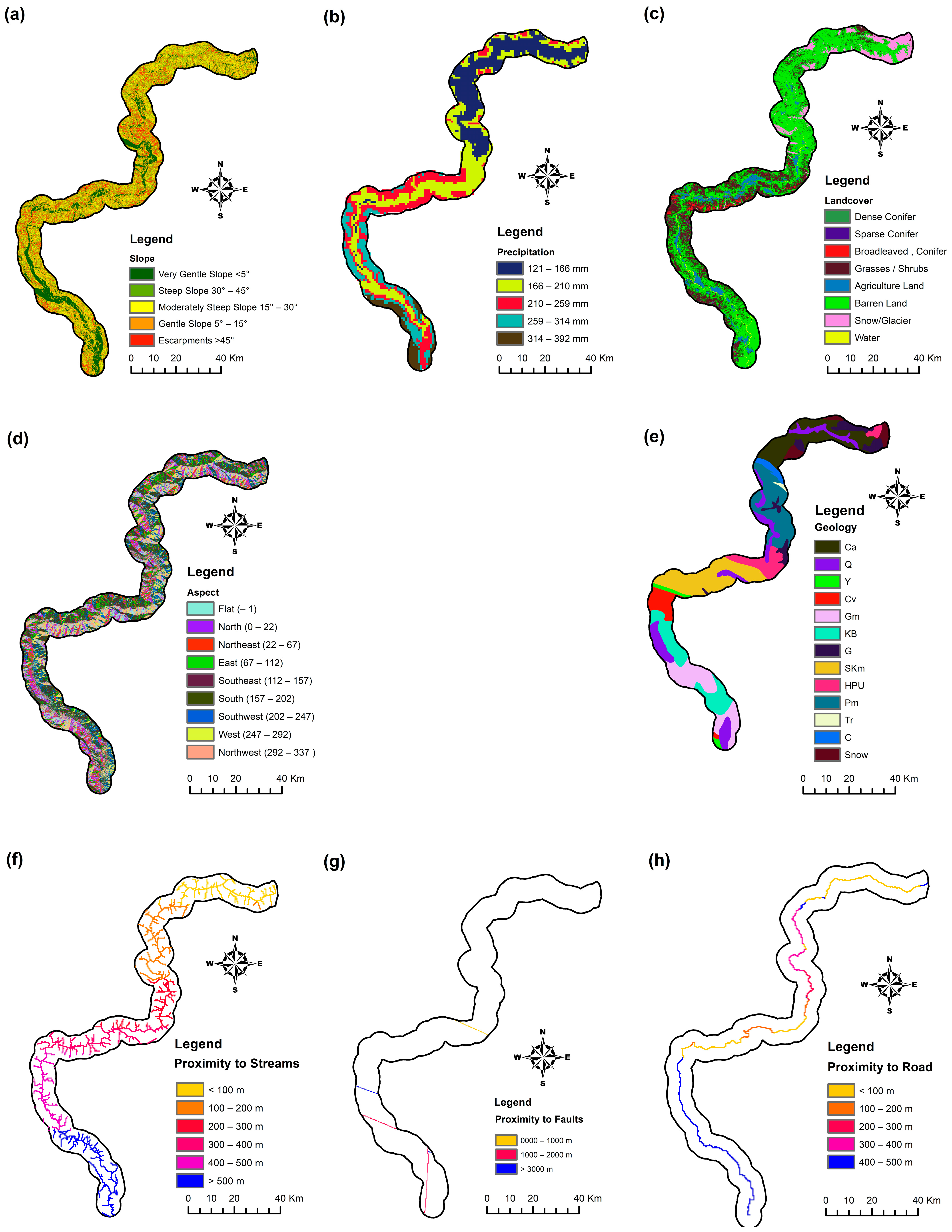
Landslide Conditioning Factors
3. Hyperparameters
3.1. Discrete Hyperparameter
3.2. Continuous Hyperparameter
3.3. Conditional Hyperparameters
3.4. Categorical Hyperparameters
3.5. Big Hyperparameter Configuration Space with Different Types of Hyperparameters
4. Hyperparameter Optimization Techniques
4.1. Babysitting
4.2. Grid Search
- Commence with a wide exploration region and sizable stride length.
- Utilizing prior effective hyperparameter settings, diminish the exploration area and stride length.
- Persist in repeating step 2 until the optimum outcome is achieved.
4.3. Random Search
Bayesian Optimization
- Create a surrogate probabilistic model of the target function.
- Find the best hyperparameter values on the surrogate model.
- Employ these hyperparameter values to the existing target function for evaluation.
- Add the most recent observations to the surrogate model.
- Repeat steps 2 through 4 until the allotted number of iterative cycles is reached.
4.4. BO-GP
4.5. BO-TPE
4.6. Metaheuristic Algorithms
4.7. Genetic Algorithm (GA)
- Commence by randomly initializing the genes, chromosomes, and population that depict the whole exploration space, as well as the hyperparameters and their corresponding values.
- Identify the fitness function, which embodies the main objective of an ML model, and employ the findings to evaluate each member of the current generation.
- Use chromosome methodologies such as crossover, mutation, and selection to generate a new generation consisting of the subsequent hyperparameter values that will be evaluated.
- Continue executing steps 2 and 3 until the termination criteria are met.
- Conclude the process and output the optimal hyperparameter configuration.
4.8. Particle Swarm Optimization (PSO)
5. Mathematical and Hyperparameter Optimization
5.1. Mathematical Optimization
5.2. Hyperparameter Optimization
- Choose the performance measurements and the objective function.
- Identify the hyperparameters that need tuning, list their categories, and select the optimal optimization method.
- Train the ML model using the default hyperparameter setup or common values for the baseline model.
- Commence the optimization process with a broad search space, selected through manual testing and/or domain expertise, as the feasible hyperparameter domain.
- If required, explore additional search spaces or narrow down the search space based on the regions where best-functioning hyperparameter values have been recently evaluated.
- Finally, provide the hyperparameter configuration that exhibits the best performance.
6. Hyperparameters in Machine Learning Models
6.1. KNN
6.2. SVM
6.3. Random Forest (Tree-Based Models)
7. Results
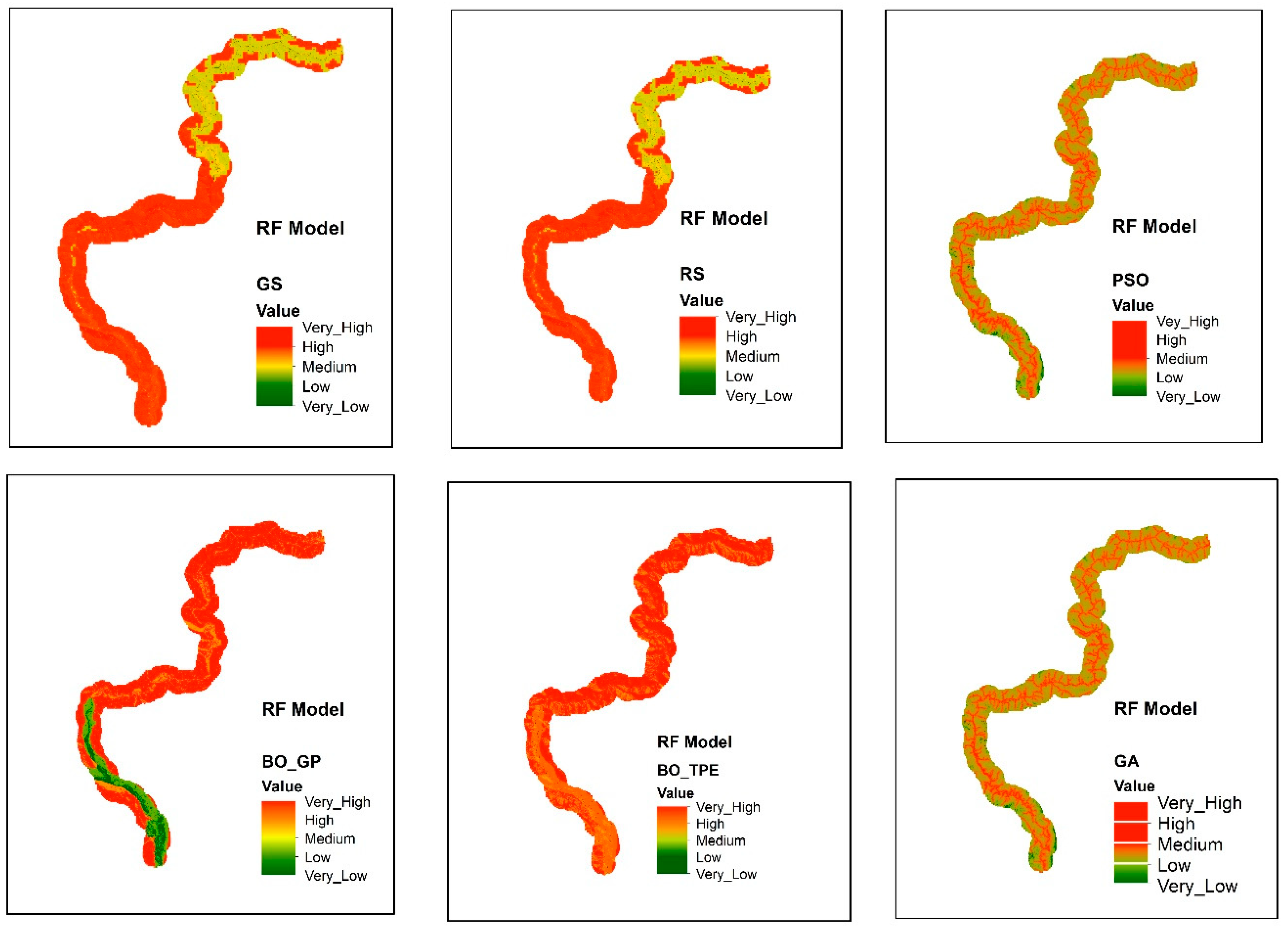
7.1. Landslide Susceptibility Maps
7.1.1. Random Forest
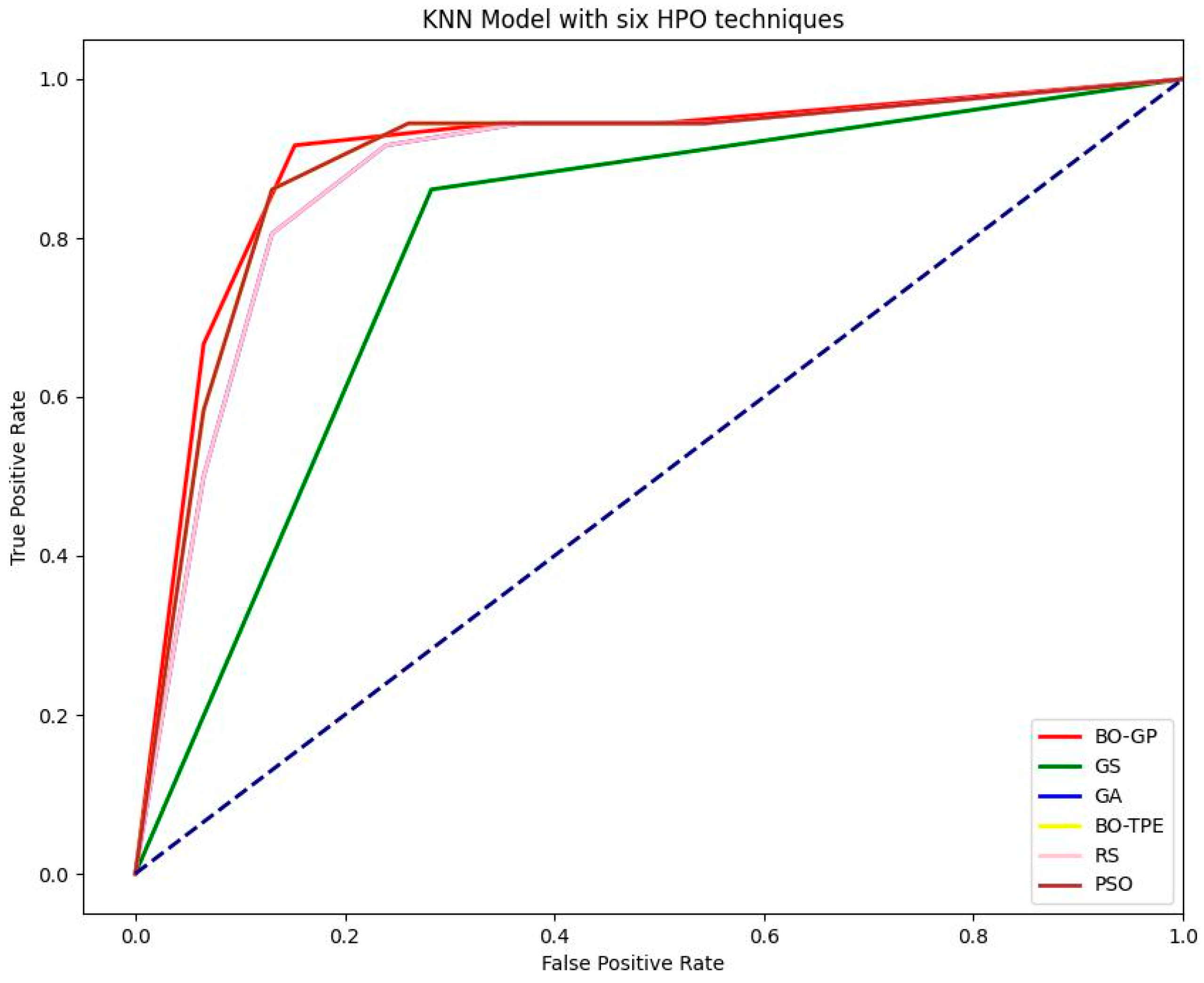
7.1.2. KNN
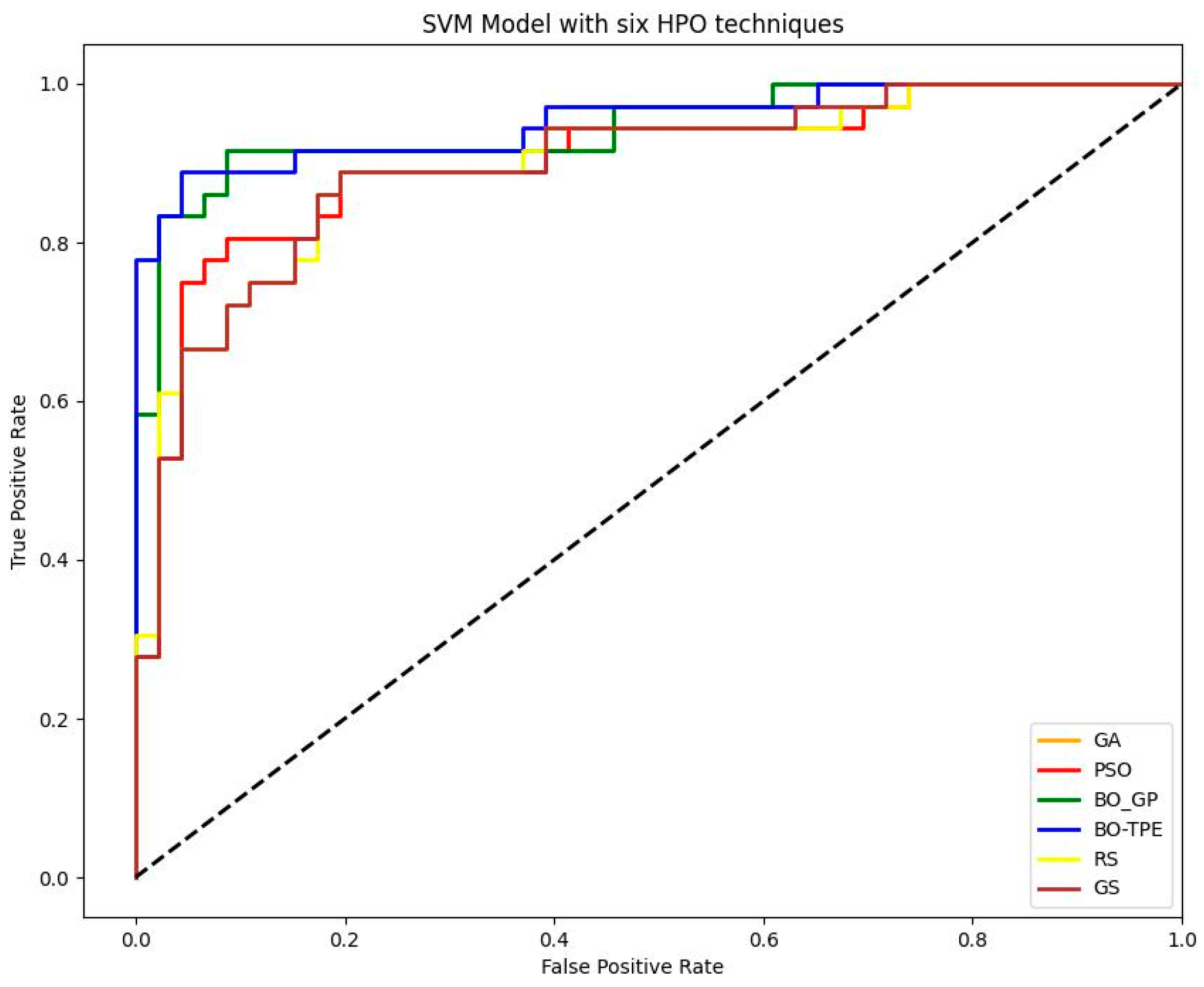
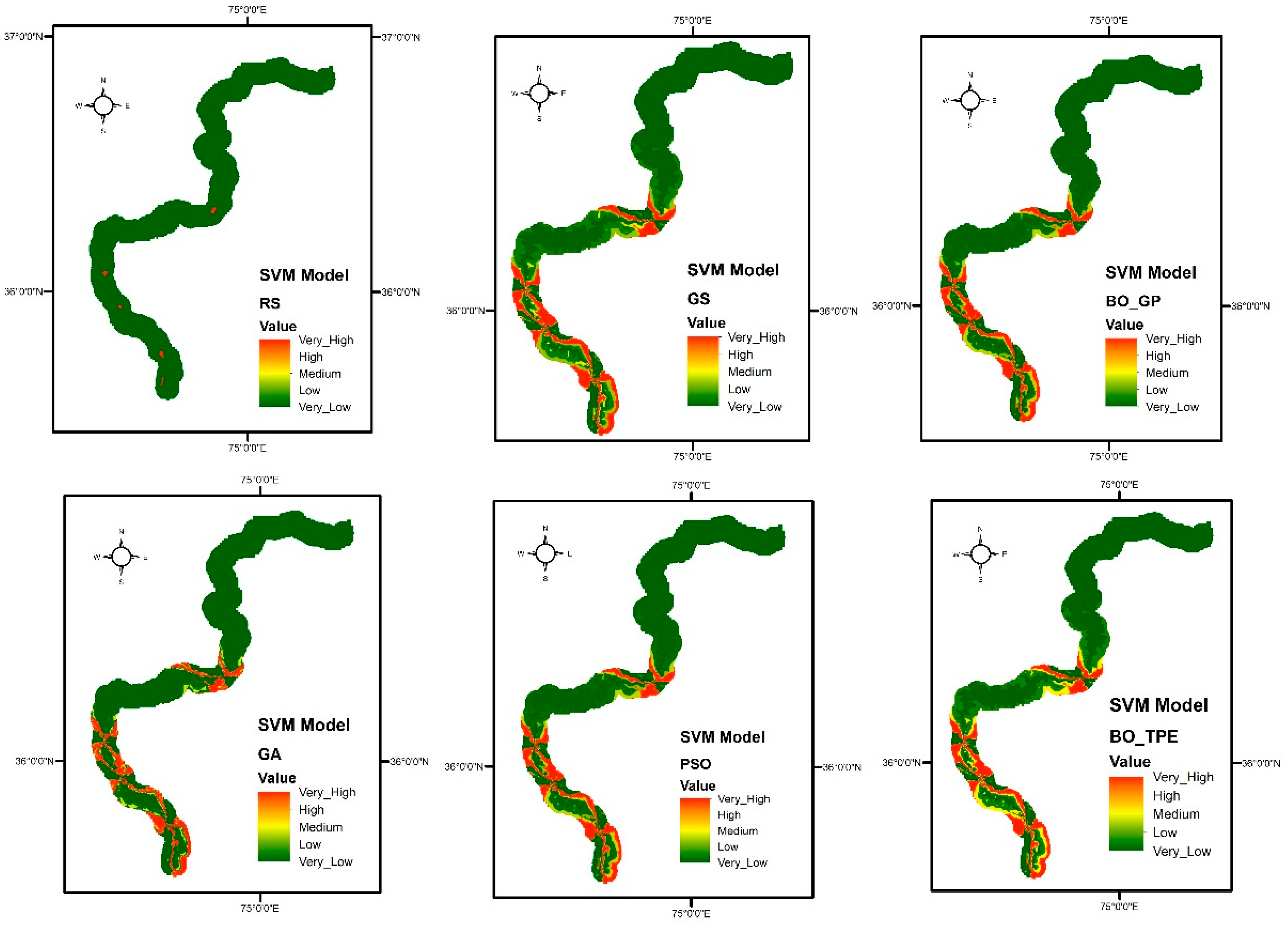
7.1.3. SVM
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Polanco, C. Add a new comment. Science 2014, 346, 684–685. [Google Scholar]
- Zöller, M.-A.; Huber, M.F. Benchmark and survey of automated machine learning frameworks. J. Artif. Intell. Res. 2021, 70, 409–472. [Google Scholar] [CrossRef]
- Elshawi, R.; Maher, M.; Sakr, S. Automated machine learning: State-of-the-art and open challenges. arXiv 2019, arXiv:1906.02287. [Google Scholar]
- DeCastro-García, N.; Munoz Castaneda, A.L.; Escudero Garcia, D.; Carriegos, M.V. Effect of the sampling of a dataset in the hyperparameter optimization phase over the efficiency of a machine learning algorithm. Complexity 2019, 2019, 6278908. [Google Scholar] [CrossRef]
- Abreu, S. Automated architecture design for deep neural networks. arXiv 2019, arXiv:1908.10714. [Google Scholar]
- Olof, S.S. A Comparative Study of Black-Box Optimization Algorithms for Tuning of Hyper-Parameters in Deep Neural Networks; Luleå University of Technology: Luleå, Sweden, 2018. [Google Scholar]
- Luo, G. A review of automatic selection methods for machine learning algorithms and hyper-parameter values. Netw. Model. Anal. Health Inform. Bioinform. 2016, 5, 18. [Google Scholar] [CrossRef]
- Maclaurin, D.; Duvenaud, D.; Adams, R. Gradient-based hyperparameter optimization through reversible learning. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2113–2122. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2011; Volume 24. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Eggensperger, K.; Feurer, M.; Hutter, F.; Bergstra, J.; Snoek, J.; Hoos, H.; Leyton-Brown, K. Towards an empirical foundation for assessing bayesian optimization of hyperparameters. In Proceedings of the NIPS Workshop on Bayesian Optimization in Theory and Practice, Lake Tahoe, NV, USA, 10 December 2013. [Google Scholar]
- Eggensperger, K.; Hutter, F.; Hoos, H.; Leyton-Brown, K. Efficient benchmarking of hyperparameter optimizers via surrogates. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- Yao, Q.; Wang, M.; Chen, Y.; Dai, W.; Li, Y.-F.; Tu, W.-W.; Yang, Q.; Yu, Y. Taking human out of learning applications: A survey on automated machine learning. arXiv 2018, arXiv:1810.13306. [Google Scholar]
- Lessmann, S.; Stahlbock, R.; Crone, S.F. Optimizing hyperparameters of support vector machines by genetic algorithms. In Proceedings of the IC-AI, Las Vegas, NV, USA, 27–30 June 2005; p. 82. [Google Scholar]
- Lorenzo, P.R.; Nalepa, J.; Kawulok, M.; Ramos, L.S.; Pastor, J.R. Particle swarm optimization for hyper-parameter selection in deep neural networks. In Proceedings of the Genetic and Evolutionary Computation Conference, Berlin, Germany, 15–19 July 2017; pp. 481–488. [Google Scholar]
- Li, H.; Chaudhari, P.; Yang, H.; Lam, M.; Ravichandran, A.; Bhotika, R.; Soatto, S. Rethinking the hyperparameters for fine-tuning. arXiv 2020, arXiv:2002.11770. [Google Scholar]
- Poojary, R.; Raina, R.; Mondal, A.K. Effect of data-augmentation on fine-tuned CNN model performance. IAES Int. J. Artif. Intell. 2021, 10, 84. [Google Scholar] [CrossRef]
- Cattan, Y.; Choquette-Choo, C.A.; Papernot, N.; Thakurta, A. Fine-tuning with differential privacy necessitates an additional hyperparameter search. arXiv 2022, arXiv:2210.02156. [Google Scholar]
- Ahmad, Z.; Li, J.; Mahmood, T. Adaptive Hyperparameter Fine-Tuning for Boosting the Robustness and Quality of the Particle Swarm Optimization Algorithm for Non-Linear RBF Neural Network Modelling and Its Applications. Mathematics 2023, 11, 242. [Google Scholar] [CrossRef]
- Shen, X.; Plested, J.; Caldwell, S.; Zhong, Y.; Gedeon, T. AMF: Adaptable Weighting Fusion with Multiple Fine-tuning for Image Classification. arXiv 2022, arXiv:2207.12944. [Google Scholar]
- Iqbal, J.; Ali, M.; Ali, A.; Raza, D.; Bashir, F.; Ali, F.; Hussain, S.; Afzal, Z. Investigation of cryosphere dynamics variations in the upper indus basin using remote sensing and gis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 44, 59–63. [Google Scholar] [CrossRef]
- Jamil, A.; Khan, A.A.; Bayram, B.; Iqbal, J.; Amin, G.; Yesiltepe, M.; Hussain, D. Spatio-temporal glacier change detection using deep learning: A case study of Shishper Glacier in Hunza. In Proceedings of the International Symposium on Applied Geoinformatics, Istanbul, Turkey, 7–9 November 2019. [Google Scholar]
- Watanabe, S.; Hutter, F. c-TPE: Generalizing tree-structured Parzen estimator with inequality constraints for continuous and categorical hyperparameter optimization. arXiv 2022, arXiv:2211.14411. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Zhao, M.; Li, J. Tuning the hyper-parameters of CMA-ES with tree-structured Parzen estimators. In Proceedings of the 2018 Tenth International Conference on Advanced Computational Intelligence (ICACI), Xiamen, China, 29–31 March 2018; pp. 613–618. [Google Scholar]
- Kelkar, K.M.; Bakal, J. Hyper parameter tuning of random forest algorithm for affective learning system. In Proceedings of the 2020 Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 August 2020; pp. 1192–1195. [Google Scholar]
- Liu, R.; Liu, E.; Yang, J.; Li, M.; Wang, F. Optimizing the hyper-parameters for SVM by combining evolution strategies with a grid search. In Proceedings of the Intelligent Control and Automation: International Conference on Intelligent Computing, ICIC 2006, Kunming, China, 16–19 August 2006; pp. 712–721. [Google Scholar]
- Kalita, D.J.; Singh, V.P.; Kumar, V. A survey on SVM hyper-parameters optimization techniques. In Social Networking and Computational Intelligence: Proceedings of SCI-2018, Bhopal, India, 5–6 October 2018; Springer: Singapore, 2020; pp. 243–256. [Google Scholar]
- Polepaka, S.; Kumar, R.R.; Katukam, S.; Potluri, S.V.; Abburi, S.D.; Peddineni, M.; Islavath, N.; Anumandla, M.R. Heart Disease Prediction-based on Conventional KNN and Tuned-Hyper Parameters of KNN: An Insight. In Proceedings of the 2023 International Conference on Computer Communication and Informatics (ICCCI), Fujisawa, Japan, 23–25 June 2023; pp. 1–3. [Google Scholar]
- Koutsoukas, A.; Monaghan, K.J.; Li, X.; Huan, J. Deep-learning: Investigating deep neural networks hyper-parameters and comparison of performance to shallow methods for modeling bioactivity data. J. Cheminform. 2017, 9, 42. [Google Scholar] [CrossRef]
- Ogilvie, H.A.; Heled, J.; Xie, D.; Drummond, A.J. Computational performance and statistical accuracy of *BEAST and comparisons with other methods. Syst. Biol. 2016, 65, 381–396. [Google Scholar] [CrossRef]
- Pritsker, M. Evaluating value at risk methodologies: Accuracy versus computational time. J. Financ. Serv. Res. 1997, 12, 201–242. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Head, T.; MechCoder; Louppe, G.; Shcherbatyi, I.; fcharras; Zé Vinícius; cmmalone; Schröder, C.; nel215; Campos, N.; et al. scikit-optimize/scikit-optimize: v0.5.2. 2018. Available online: https://zenodo.org/record/1207017 (accessed on 4 July 2023).
- Komer, B.; Bergstra, J.; Eliasmith, C. Hyperopt-sklearn: Automatic hyperparameter configuration for scikit-learn. In ICML Workshop on AutoML; Citeseer: Austin, TX, USA, 2014. [Google Scholar]
- Claesen, M.; Simm, J.; Popovic, D.; Moreau, Y.; De Moor, B. Easy hyperparameter search using optunity. arXiv 2014, arXiv:1412.1114. [Google Scholar]
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and efficient hyperparameter optimization at scale. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1437–1446. [Google Scholar]
- Olson, R.S.; Moore, J.H. TPOT: A tree-based pipeline optimization tool for automating machine learning. In Proceedings of the Workshop on Automatic Machine Learning, New York, NY, USA, 24 June 2016; pp. 66–74. [Google Scholar]
- Dhuime, B.; Bosch, D.; Garrido, C.J.; Bodinier, J.-L.; Bruguier, O.; Hussain, S.S.; Dawood, H. Geochemical architecture of the lower-to middle-crustal section of a paleo-island arc (Kohistan Complex, Jijal–Kamila area, northern Pakistan): Implications for the evolution of an oceanic subduction zone. J. Petrol. 2009, 50, 531–569. [Google Scholar] [CrossRef]
- Rahman, N.U.; Song, H.; Benzhong, X.; Rehman, S.U.; Rehman, G.; Majid, A.; Iqbal, J.; Hussain, G. Middle-Late Permian and Early Triassic foraminiferal assemblages in the Western Salt Range, Pakistan. Rud. -Geološko-Naft. Zb. 2022, 37, 161–196. [Google Scholar] [CrossRef]
- Baloch, M.Y.J.; Zhang, W.; Al Shoumik, B.A.; Nigar, A.; Elhassan, A.A.; Elshekh, A.E.; Bashir, M.O.; Ebrahim, A.F.M.S.; Iqbal, J. Hydrogeochemical mechanism associated with land use land cover indices using geospatial, remote sensing techniques, and health risks model. Sustainability 2022, 14, 16768. [Google Scholar] [CrossRef]
- Iqbal, J.; Amin, G.; Su, C.; Haroon, E.; Baloch, M.Y.J. Assessment of Landcover Impacts on the Groundwater Quality Using Hydrogeochemical and Geospatial Techniques. 2023. Available online: https://www.researchsquare.com/article/rs-2771650/v1 (accessed on 4 July 2023).
- Tong, Y.; Yu, B. Research on hyper-parameter optimization of activity recognition algorithm based on improved cuckoo search. Entropy 2022, 24, 845. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Lin, J.; Bischl, B. ReinBo: Machine learning pipeline conditional hierarchy search and configuration with Bayesian optimization embedded reinforcement learning. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: International Workshops of ECML PKDD 2019, Würzburg, Germany, 16–20 September 2019; Proceedings, Part I, 2020. pp. 68–84. [Google Scholar]
- Nguyen, D.; Gupta, S.; Rana, S.; Shilton, A.; Venkatesh, S. Bayesian optimization for categorical and category-specific continuous inputs. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Ilievski, I.; Akhtar, T.; Feng, J.; Shoemaker, C. Efficient hyperparameter optimization for deep learning algorithms using deterministic RBF surrogates. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Witt, C. Worst-case and average-case approximations by simple randomized search heuristics. In Proceedings of the STACS 2005: 22nd Annual Symposium on Theoretical Aspects of Computer Science, Stuttgart, Germany, 24–26 February 2005; Proceedings 22, 2005. pp. 44–56. [Google Scholar]
- Hutter, F.; Kotthoff, L.; Vanschoren, J. Automated Machine Learning: Methods, Systems, Challenges; Springer Nature: Berlin, Germany, 2019. [Google Scholar]
- Nguyen, V. Bayesian optimization for accelerating hyper-parameter tuning. In Proceedings of the 2019 IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), Sardinia, Italy, 3–5 June 2019; pp. 302–305. [Google Scholar]
- Sanders, S.; Giraud-Carrier, C. Informing the use of hyperparameter optimization through metalearning. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 1051–1056. [Google Scholar]
- Hazan, E.; Klivans, A.; Yuan, Y. Hyperparameter optimization: A spectral approach. arXiv 2017, arXiv:1706.00764. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Proceedings of the Learning and Intelligent Optimization: 5th International Conference, LION 5, Rome, Italy, 17–21 January 2011; Selected Papers 5, 2011. pp. 507–523. [Google Scholar]
- Dewancker, I.; McCourt, M.; Clark, S. Bayesian Optimization Primer. 2015. Available online: https://static.sigopt.com/b/20a144d208ef255d3b981ce419667ec25d8412e2/static/pdf/SigOpt_Bayesian_Optimization_Primer.pdf (accessed on 4 July 2023).
- Gogna, A.; Tayal, A. Metaheuristics: Review and application. J. Exp. Theor. Artif. Intell. 2013, 25, 503–526. [Google Scholar] [CrossRef]
- Itano, F.; de Sousa, M.A.d.A.; Del-Moral-Hernandez, E. Extending MLP ANN hyper-parameters Optimization by using Genetic Algorithm. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Kazimipour, B.; Li, X.; Qin, A.K. A review of population initialization techniques for evolutionary algorithms. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 2585–2592. [Google Scholar]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M. A novel population initialization method for accelerating evolutionary algorithms. Comput. Math. Appl. 2007, 53, 1605–1614. [Google Scholar] [CrossRef]
- Lobo, F.G.; Goldberg, D.E.; Pelikan, M. Time complexity of genetic algorithms on exponentially scaled problems. In Proceedings of the 2nd Annual Conference on Genetic and Evolutionary Computation, Las Vegas, NV, USA, 10–12 July 2000; pp. 151–158. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Parameter selection in particle swarm optimization. In Proceedings of the Evolutionary Programming VII: 7th International Conference, EP98, San Diego, CA, USA, 25–27 March 1998; Proceedings 7, 1998. pp. 591–600. [Google Scholar]
- Yan, X.-H.; He, F.-Z.; Chen, Y.-L. 基于野草扰动粒子群算法的新型软硬件划分方法. 计算机科学技术学报 2017, 32, 340–355. [Google Scholar]
- Min-Yuan, C.; Kuo-Yu, H.; Merciawati, H. Multiobjective Dynamic-Guiding PSO for Optimizing Work Shift Schedules. J. Constr. Eng. Manag. 2018, 144, 04018089. [Google Scholar]
- Wang, H.; Wu, Z.; Wang, J.; Dong, X.; Yu, S.; Chen, C. A new population initialization method based on space transformation search. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjian, China, 14–16 August 2009; pp. 332–336. [Google Scholar]
- Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A survey of optimization methods from a machine learning perspective. IEEE Trans. Cybern. 2019, 50, 3668–3681. [Google Scholar] [CrossRef]
- McCarl, B.A.; Spreen, T.H. Applied Mathematical Programming Using Algebraic Systems; Texas A&M University: Cambridge, MA, USA, 1997. [Google Scholar]
- Bubeck, S. Konvex optimering: Algoritmer och komplexitet. Found. Trends® Mach. Learn. 2015, 8, 231–357. [Google Scholar] [CrossRef]
- Abbas, F.; Zhang, F.; Iqbal, J.; Abbas, F.; Alrefaei, A.F.; Albeshr, M. Assessing the Dimensionality Reduction of the Geospatial Dataset Using Principal Component Analysis (PCA) and Its Impact on the Accuracy and Performance of Ensembled and Non-ensembled Algorithms. Preprints 2023, 2023070529. [Google Scholar] [CrossRef]
- Abbas, F.; Zhang, F.; Abbas, F.; Ismail, M.; Iqbal, J.; Hussain, D.; Khan, G.; Alrefaei, A.F.; Albeshr, M.F. Landslide Susceptibility Mapping: Analysis of Different Feature Selection Techniques with Artificial Neural Network Tuned by Bayesian and Metaheuristic Algorithms. Preprints 2023, 2023071467. [Google Scholar] [CrossRef]
- Shahriari, B.; Bouchard-Côté, A.; Freitas, N. Unbounded Bayesian optimization via regularization. In Proceedings of the Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; pp. 1168–1176. [Google Scholar]
- Diaz, G.I.; Fokoue-Nkoutche, A.; Nannicini, G.; Samulowitz, H. An effective algorithm for hyperparameter optimization of neural networks. IBM J. Res. Dev. 2017, 61, 9:1–9:11. [Google Scholar] [CrossRef]
- Gambella, C.; Ghaddar, B.; Naoum-Sawaya, J. Optimization problems for machine learning: A survey. Eur. J. Oper. Res. 2021, 290, 807–828. [Google Scholar] [CrossRef]
- Sparks, E.R.; Talwalkar, A.; Haas, D.; Franklin, M.J.; Jordan, M.I.; Kraska, T. Automating model search for large scale machine learning. In Proceedings of the Sixth ACM Symposium on Cloud Computing, Kohala Coast, HI, USA, 27–29 August 2015; pp. 368–380. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Chen, C.; Yan, C.; Li, Y. A robust weighted least squares support vector regression based on least trimmed squares. Neurocomputing 2015, 168, 941–946. [Google Scholar] [CrossRef]
- Yang, L.; Muresan, R.; Al-Dweik, A.; Hadjileontiadis, L.J. Image-based visibility estimation algorithm for intelligent transportation systems. IEEE Access 2018, 6, 76728–76740. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, R.; Yang, Y.; Hauptmann, A. Modified logistic regression: An approximation to SVM and its applications in large-scale text categorization. In Proceedings of the Twentieth International Conference on Machine Learning (ICML-2003), Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Soliman, O.S.; Mahmoud, A.S. A classification system for remote sensing satellite images using support vector machine with non-linear kernel functions. In Proceedings of the 2012 8th International Conference on Informatics and Systems (INFOS), Giza, Egypt, 14–16 May 2012; pp. BIO-181–BIO-187. [Google Scholar]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Manias, D.M.; Jammal, M.; Hawilo, H.; Shami, A.; Heidari, P.; Larabi, A.; Brunner, R. Machine learning for performance-aware virtual network function placement. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Yang, L.; Moubayed, A.; Hamieh, I.; Shami, A. Tree-based intelligent intrusion detection system in internet of vehicles. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Injadat, M.; Salo, F.; Nassif, A.B.; Essex, A.; Shami, A. Bayesian optimization with machine learning algorithms towards anomaly detection. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Arjunan, K.; Modi, C.N. An enhanced intrusion detection framework for securing network layer of cloud computing. In Proceedings of the 2017 ISEA Asia Security and Privacy (ISEASP), Surat, India, 29 January–1 February 2017; pp. 1–10. [Google Scholar]
- Dietterich, T.G. Ensemble methods in machine learning. In Proceedings of the Multiple Classifier Systems: First International Workshop, MCS 2000, Cagliari, Italy, 21–23 June 2000; Proceedings 1, 2000. pp. 1–15. [Google Scholar]
- Ning, C.; You, F. Optimization under uncertainty in the era of big data and deep learning: When machine learning meets mathematical programming. Comput. Chem. Eng. 2019, 125, 434–448. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hogg, T.; Portnov, D. Quantum optimization. Inf. Sci. 2000, 128, 181–197. [Google Scholar] [CrossRef]


| ML Model | Hyperparameter | Type | Search Space |
|---|---|---|---|
| RF Classifier | n_estimators | Discrete | [10, 100] |
| max_depth | Discrete | [5, 50] | |
| min_samples_split | Discrete | [2, 11] | |
| min_samples_leaf | Discrete | [1, 11] | |
| criterion | Categorical | [’gini’, ’entropy’] | |
| max_features | Discrete | [1, 64] | |
| SVM Classifier | C | Continuous | [0.1, 50] |
| Kernel | Categorical | [’linear’, ’poly’, ’rbf’, ’sigmoid’] | |
| KNN Classifier | n_neighbors | Discrete | [1, 20] |
| Factors | Classes | Class Percentage % | Landslide Percentage % | Reclassification |
|---|---|---|---|---|
| Slope (°) | Very Gentle Slope < 5° | 17.36 | 21.11 | Geometrical interval reclassification |
| Gentle Slope 5–15° | 20.87 | 28.37 | ||
| Moderately Steep Slope 15–30° | 26.64 | 37.89 | ||
| Steep Slope 30–45° | 24.40 | 10.90 | ||
| Escarpments > 45° | 10.71 | 1.73 | ||
| Aspect | Flat (−1) | 22.86 | 7.04 | Remained unmodified (as in source data) |
| North (0–22) | 21.47 | 7.03 | ||
| Northeast (22–67) | 14.85 | 5.00 | ||
| East (67–112) | 8.00 | 11.86 | ||
| Southeast (112–157) | 5.22 | 14.3 | ||
| South (157–202) | 2.84 | 14.40 | ||
| Southwest (202–247) | 6.46 | 12.41 | ||
| West (247–292) | 7.19 | 16.03 | ||
| Northwest (292–337) | 11.07 | 11.96 | ||
| Land Cover | Dense Conifer | 0.38 | 12.73 | |
| Sparse Conifer | 0.25 | 12.80 | ||
| Broadleaved, Conifer | 1.52 | 10.86 | ||
| Grasses/Shrubs | 25.54 | 10.3 | ||
| Agriculture Land | 5.78 | 10.40 | ||
| Soil/Rocks | 56.55 | 14.51 | ||
| Snow/Glacier | 8.89 | 12.03 | ||
| Water | 1.06 | 16.96 | ||
| Geology | Cretaceous sandstone | 13.70 | 6.38 | |
| Devonian–Carboniferous | 12.34 | 5.80 | ||
| Chalt Group | 1.43 | 8.43 | ||
| Hunza plutonic unit | 4.74 | 10.74 | ||
| Paragneisses | 11.38 | 11.34 | ||
| Yasin group | 10.80 | 10.70 | ||
| Gilgit complex | 5.80 | 9.58 | ||
| Trondhjemite | 15.65 | 9.32 | ||
| Permian massive limestone | 6.51 | 6.61 | ||
| Permanent ice | 12.61 | 3.51 | ||
| Quaternary alluvium | 0.32 | 8.65 | ||
| Triassic massive limestone and dolomite | 1.58 | 7.80 | ||
| snow | 3.08 | 2.00 | ||
| Proximity to Stream (meter) | 0–100 m | 19.37 | 18.52 | Geometrical interval reclassification |
| 100–200 | 10.26 | 21.63 | ||
| 200–300 | 10.78 | 25.16 | ||
| 300–400 | 13.95 | 26.12 | ||
| 400–500 | 18.69 | 6.23 | ||
| >500 | 26.92 | 2.34 | ||
| Proximity to Road (meter) | 0–100 m | 81.08 | 25.70 | |
| 100–200 | 10.34 | 25.19 | ||
| 200–300 | 6.72 | 27.09 | ||
| 300–400 | 1.25 | 12.02 | ||
| 400–500 | 0.60 | 10.00 | ||
| Proximity to Fault (meter) | 000–1000 m | 29.76 | 27.30 | |
| 2000–3000 | 36.25 | 37.40 | ||
| >3000 | 34.15 | 35.03 |
| HPO Method | Strengths | Limitations | Time Complexity |
|---|---|---|---|
| GS | Straightforward | Inefficient without categorical HPs and time-consuming. | O() |
| RS | It is more effective than GS and supports parallelism. | Does not take into account prior outcomes. Ineffective when used with conditional HPs. | O(n) |
| BO-GP | For continuous HPs, fast convergence speed. | Poor parallelization ability; ineffective with conditional HPs. | |
| BO-TPE | Effective with all HP types. Maintains conditional dependencies. | Poor parallelization ability. | |
| GA | All HPs are effective with it, and it does not need excellent initialization. | Poor parallelization ability. | |
| PSO | Enables parallelization; is effective with all sorts of HPs. | Needs to be initialized properly. |
| Optimization Algorithm | Accuracy (%) | CT(s) |
|---|---|---|
| GS | 0.90730 | 4.70 |
| RS | 0.92663 | 3.91 |
| BO-GP | 0.93266 | 16.94 |
| BO-TPE | 0.94112 | 1.43 |
| GA | 0.94957 | 4.90 |
| PSO | 0.95923 | 3.12 |
| Optimization Algorithm | Accuracy (%) | CT(s) |
|---|---|---|
| BO-TPE | 0.95289 | 0.55 |
| BO-GP | 0.94565 | 5.78 |
| PSO | 0.90277 | 0.43 |
| GA | 0.90277 | 1.18 |
| RS | 0.89855 | 0.73 |
| GS | 0.89794 | 1.23 |
| Optimization Algorithm | Accuracy (%) | CT(s) |
|---|---|---|
| BO-GP | 0.90247 | 1.21 |
| BO-TPE | 0.89462 | 2.23 |
| PSO | 0.89462 | 1.65 |
| GA | 0.88194 | 2.43 |
| RS | 0.88194 | 6.41 |
| GS | 0.78925 | 7.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, F.; Zhang, F.; Ismail, M.; Khan, G.; Iqbal, J.; Alrefaei, A.F.; Albeshr, M.F. Optimizing Machine Learning Algorithms for Landslide Susceptibility Mapping along the Karakoram Highway, Gilgit Baltistan, Pakistan: A Comparative Study of Baseline, Bayesian, and Metaheuristic Hyperparameter Optimization Techniques. Sensors 2023, 23, 6843. https://doi.org/10.3390/s23156843
Abbas F, Zhang F, Ismail M, Khan G, Iqbal J, Alrefaei AF, Albeshr MF. Optimizing Machine Learning Algorithms for Landslide Susceptibility Mapping along the Karakoram Highway, Gilgit Baltistan, Pakistan: A Comparative Study of Baseline, Bayesian, and Metaheuristic Hyperparameter Optimization Techniques. Sensors. 2023; 23(15):6843. https://doi.org/10.3390/s23156843
Chicago/Turabian StyleAbbas, Farkhanda, Feng Zhang, Muhammad Ismail, Garee Khan, Javed Iqbal, Abdulwahed Fahad Alrefaei, and Mohammed Fahad Albeshr. 2023. "Optimizing Machine Learning Algorithms for Landslide Susceptibility Mapping along the Karakoram Highway, Gilgit Baltistan, Pakistan: A Comparative Study of Baseline, Bayesian, and Metaheuristic Hyperparameter Optimization Techniques" Sensors 23, no. 15: 6843. https://doi.org/10.3390/s23156843
APA StyleAbbas, F., Zhang, F., Ismail, M., Khan, G., Iqbal, J., Alrefaei, A. F., & Albeshr, M. F. (2023). Optimizing Machine Learning Algorithms for Landslide Susceptibility Mapping along the Karakoram Highway, Gilgit Baltistan, Pakistan: A Comparative Study of Baseline, Bayesian, and Metaheuristic Hyperparameter Optimization Techniques. Sensors, 23(15), 6843. https://doi.org/10.3390/s23156843









