Figure 1.
Linear antenna array (a) without EPP and (b) with EPP.
Figure 1.
Linear antenna array (a) without EPP and (b) with EPP.
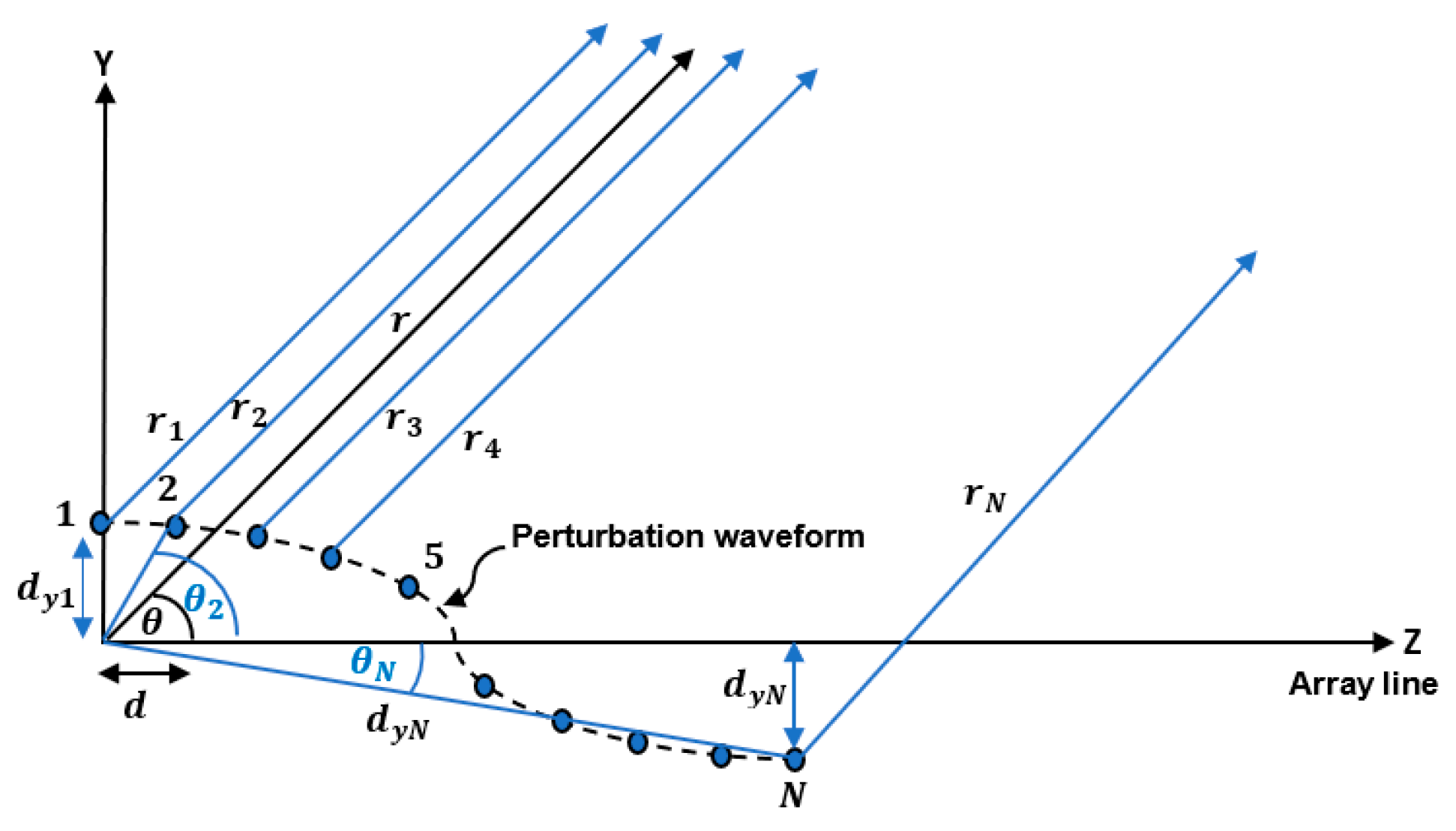
Figure 2.
Geometry of a linear array of elements aligned along the Z-axis and has position perturbation along the Y-axis.
Figure 2.
Geometry of a linear array of elements aligned along the Z-axis and has position perturbation along the Y-axis.
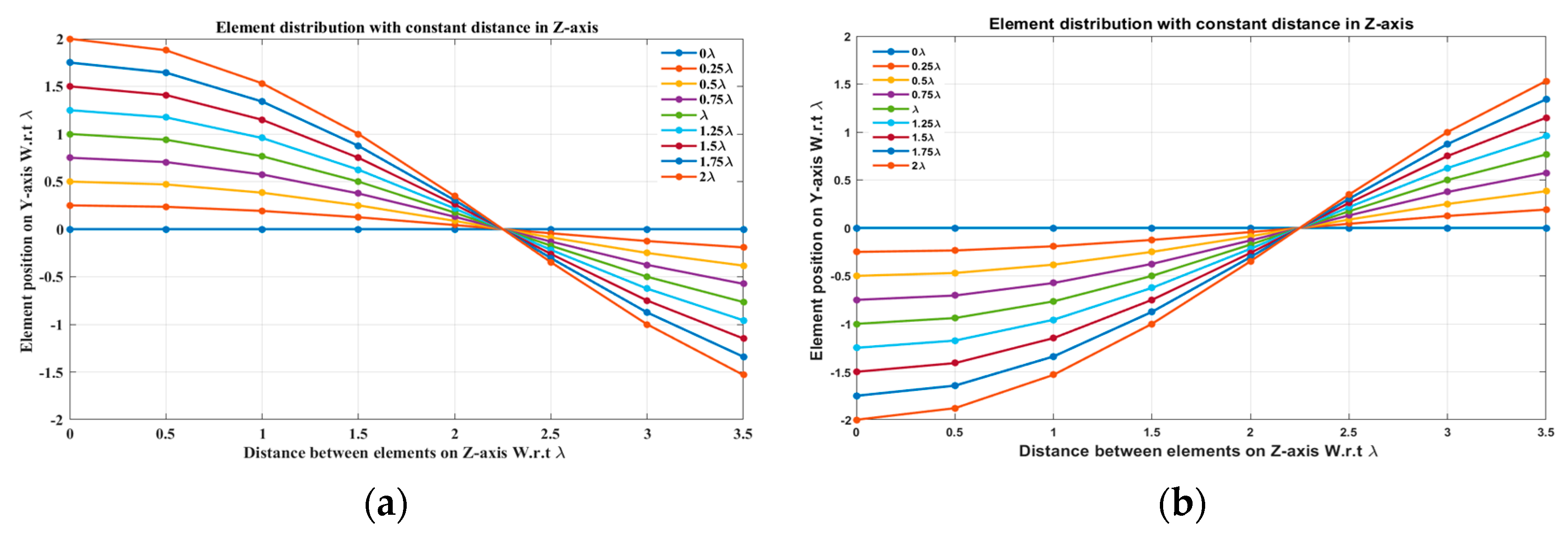
Figure 3.
The triangular relation between the element position in the Y-direction and the distance from the reference antenna element.
Figure 3.
The triangular relation between the element position in the Y-direction and the distance from the reference antenna element.
Figure 4.
Geometry of a linear array of elements aligned along the Z-axis and has position perturbation along the Y-axis indicating the far field radiation from the first antenna element.
Figure 4.
Geometry of a linear array of elements aligned along the Z-axis and has position perturbation along the Y-axis indicating the far field radiation from the first antenna element.
Figure 5.
Geometry of a linear array of elements aligned along the Z-axis and has position perturbation along the Y-axis indicating the far field radiation from the second antenna element.
Figure 5.
Geometry of a linear array of elements aligned along the Z-axis and has position perturbation along the Y-axis indicating the far field radiation from the second antenna element.
Figure 6.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 6.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
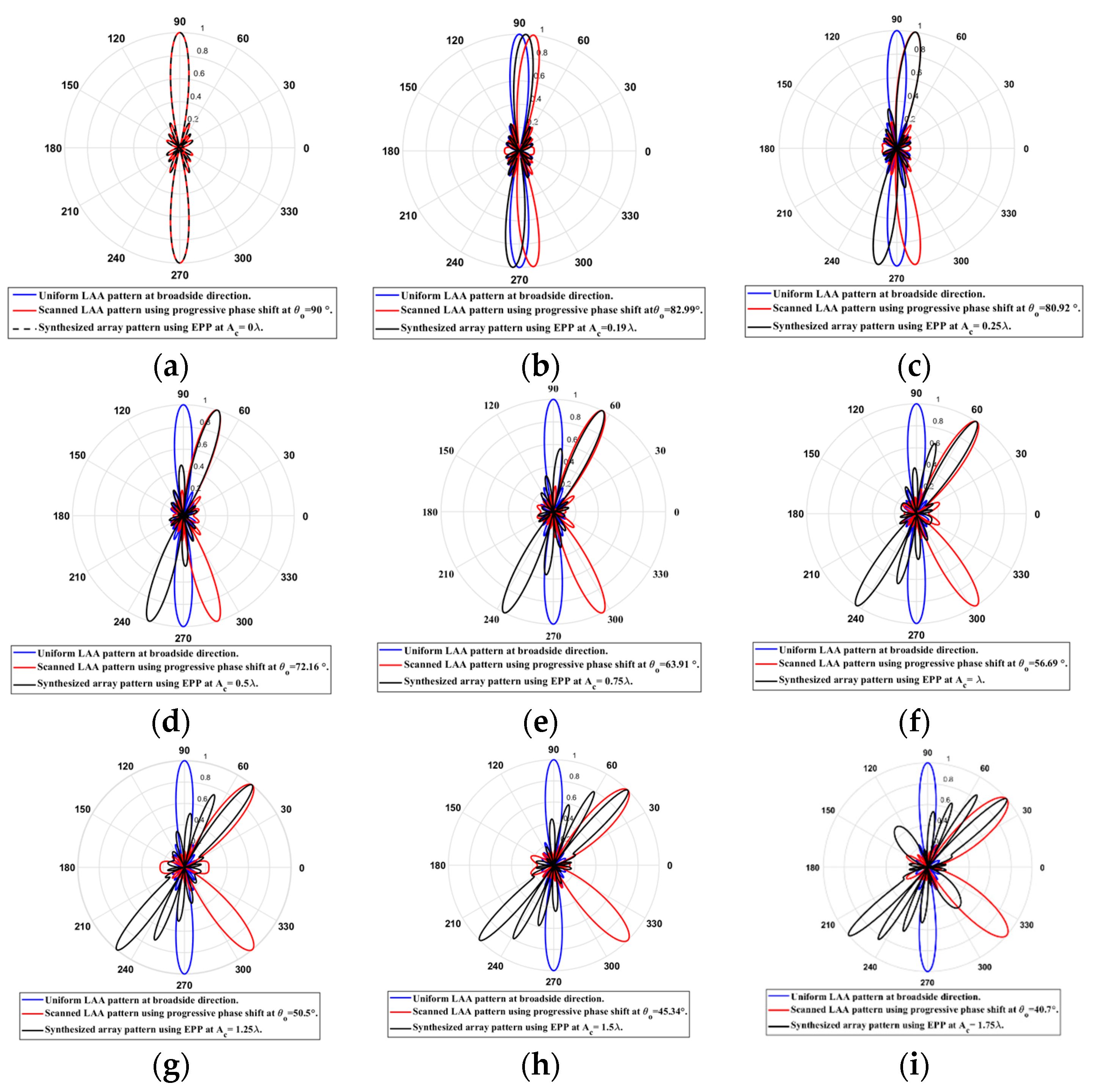
Figure 7.
Polar plots of the synthesized radiation patterns using the EPP-BSA approach for 8-element LAA at compression ratio and (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h), (i), and (j) and changing from positive to negative.
Figure 7.
Polar plots of the synthesized radiation patterns using the EPP-BSA approach for 8-element LAA at compression ratio and (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h), (i), and (j) and changing from positive to negative.
Figure 8.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element ULAA at compression ratio for and changing from negative to positive.
Figure 8.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element ULAA at compression ratio for and changing from negative to positive.
Figure 9.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 9.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 10.
Polar plots of the synthesized radiation patterns using the EPP-BSA approach for an 8-element ULAA at compression ratio and (a) , (b) , (c) , (d) , (e) , (f) , (g), (h), and (i) and changing from positive to negative.
Figure 10.
Polar plots of the synthesized radiation patterns using the EPP-BSA approach for an 8-element ULAA at compression ratio and (a) , (b) , (c) , (d) , (e) , (f) , (g), (h), and (i) and changing from positive to negative.
Figure 11.
Relation between changes in the main beam scanning angle around the broadside direction and side lobe level changes.
Figure 11.
Relation between changes in the main beam scanning angle around the broadside direction and side lobe level changes.
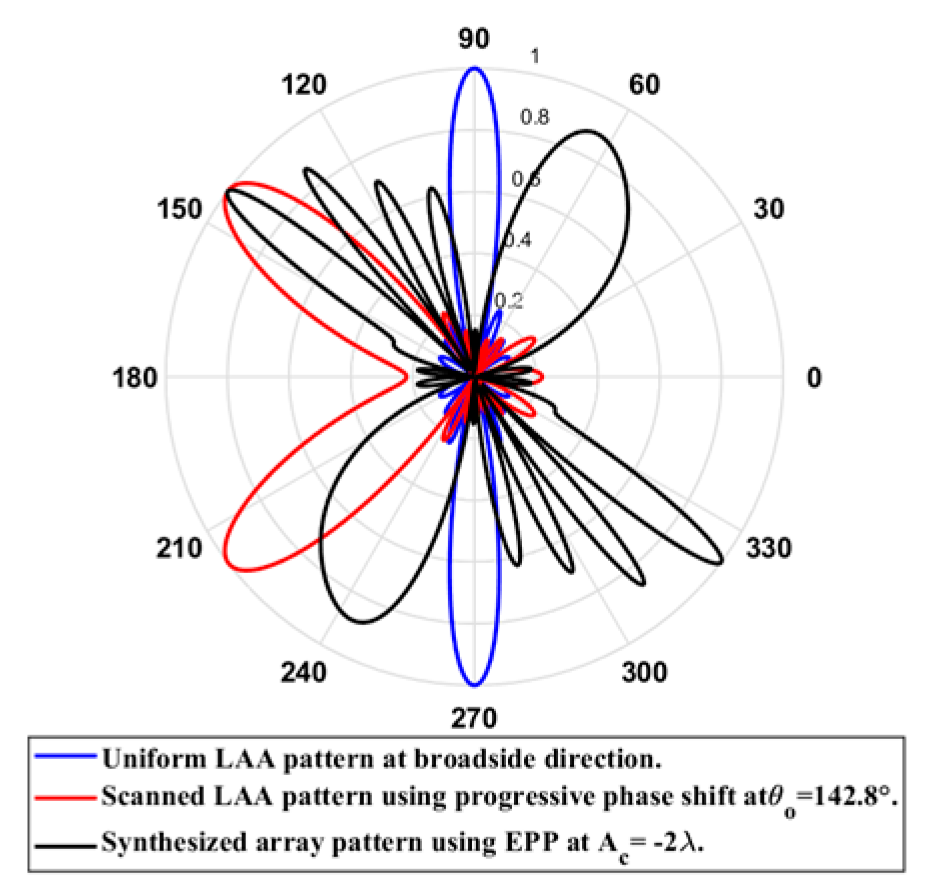
Figure 12.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element ULAA at compression ratio for and changing from negative to positive.
Figure 12.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element ULAA at compression ratio for and changing from negative to positive.
Figure 13.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 13.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 14.
Polar plots of the synthesized radiation patterns using the EPP-BSA approach for an 8-element ULAA at compression ratio at (a), (b) , (c) , (d) (e) , (f) , (g) , (h) , (i), (j), and (k) and changing from positive to negative.
Figure 14.
Polar plots of the synthesized radiation patterns using the EPP-BSA approach for an 8-element ULAA at compression ratio at (a), (b) , (c) , (d) (e) , (f) , (g) , (h) , (i), (j), and (k) and changing from positive to negative.
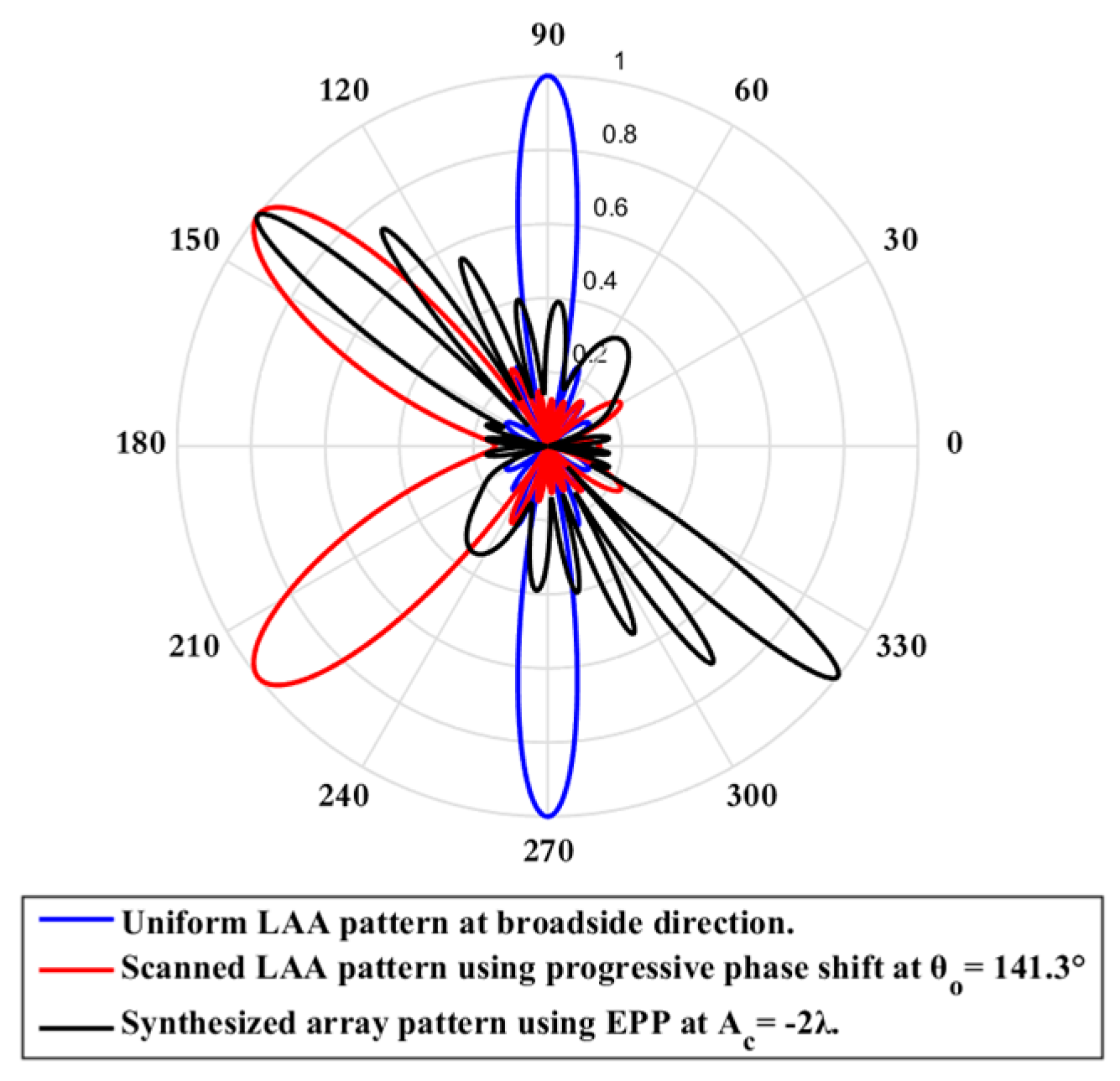
Figure 15.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element ULAA at compression ratio for and changing from negative to positive.
Figure 15.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element ULAA at compression ratio for and changing from negative to positive.
Figure 16.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 16.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 17.
Polar plots of the synthesized radiation patterns using the EPP techniques for 8-element ULAA at compression ratio at: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i), (j), and (k) and changing from positive to negative.
Figure 17.
Polar plots of the synthesized radiation patterns using the EPP techniques for 8-element ULAA at compression ratio at: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i), (j), and (k) and changing from positive to negative.
Figure 18.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element ULAA at compression ratio for and changing from negative to positive.
Figure 18.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element ULAA at compression ratio for and changing from negative to positive.
Figure 19.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 19.
The EPPs of the array elements at compression ratio for (a) is changing from positive to negative and (b) is changing from negative to positive.
Figure 20.
Polar plots of the synthesized radiation patterns using the EPP-BSA approach for 8-element uniform LAA at compression ratio equal to 0.5 at: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i), (j), and (k) and changing from positive to negative.
Figure 20.
Polar plots of the synthesized radiation patterns using the EPP-BSA approach for 8-element uniform LAA at compression ratio equal to 0.5 at: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i), (j), and (k) and changing from positive to negative.
Figure 21.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element uniform LAA due to compression ratio equal to for and changing from negative to positive.
Figure 21.
Polar plot of the synthesized radiation pattern using the EPP-BSA approach for 8-element uniform LAA due to compression ratio equal to for and changing from negative to positive.
Figure 22.
(a) Dimensions of dipole antenna, (b) H-plane pattern, and (c) E-plane pattern.
Figure 22.
(a) Dimensions of dipole antenna, (b) H-plane pattern, and (c) E-plane pattern.
Figure 23.
The scattering parameter (reflection coefficient) against the frequency for the designed dipole antenna.
Figure 23.
The scattering parameter (reflection coefficient) against the frequency for the designed dipole antenna.
Figure 24.
The 3D radiation pattern plots of the synthesized antenna arrays using CST software package applying the proposed EPP-BSA approach for an 8-element ULAA for at: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i) , and changing from positive to negative.
Figure 24.
The 3D radiation pattern plots of the synthesized antenna arrays using CST software package applying the proposed EPP-BSA approach for an 8-element ULAA for at: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i) , and changing from positive to negative.
Figure 25.
Polar plots of the synthesized antenna arrays radiation patterns using CST software package applying the proposed EPP-BSA approach for an 8-element ULAA for at: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i) , and changing from positive to negative.
Figure 25.
Polar plots of the synthesized antenna arrays radiation patterns using CST software package applying the proposed EPP-BSA approach for an 8-element ULAA for at: (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i) , and changing from positive to negative.
Figure 26.
The triangular relation between the element position in the Y-direction and the distance from the reference antenna element.
Figure 26.
The triangular relation between the element position in the Y-direction and the distance from the reference antenna element.
Figure 27.
The synthesized array factor using odd excitations compared to the original array factor of the 8-element ULAA.
Figure 27.
The synthesized array factor using odd excitations compared to the original array factor of the 8-element ULAA.
Figure 28.
The synthesized array factor using even excitations compared to the original array factor of the 8-element ULAA.
Figure 28.
The synthesized array factor using even excitations compared to the original array factor of the 8-element ULAA.
Figure 29.
The EPPs of the synthesized array elements at compression ratio for is changing from positive to negative.
Figure 29.
The EPPs of the synthesized array elements at compression ratio for is changing from positive to negative.
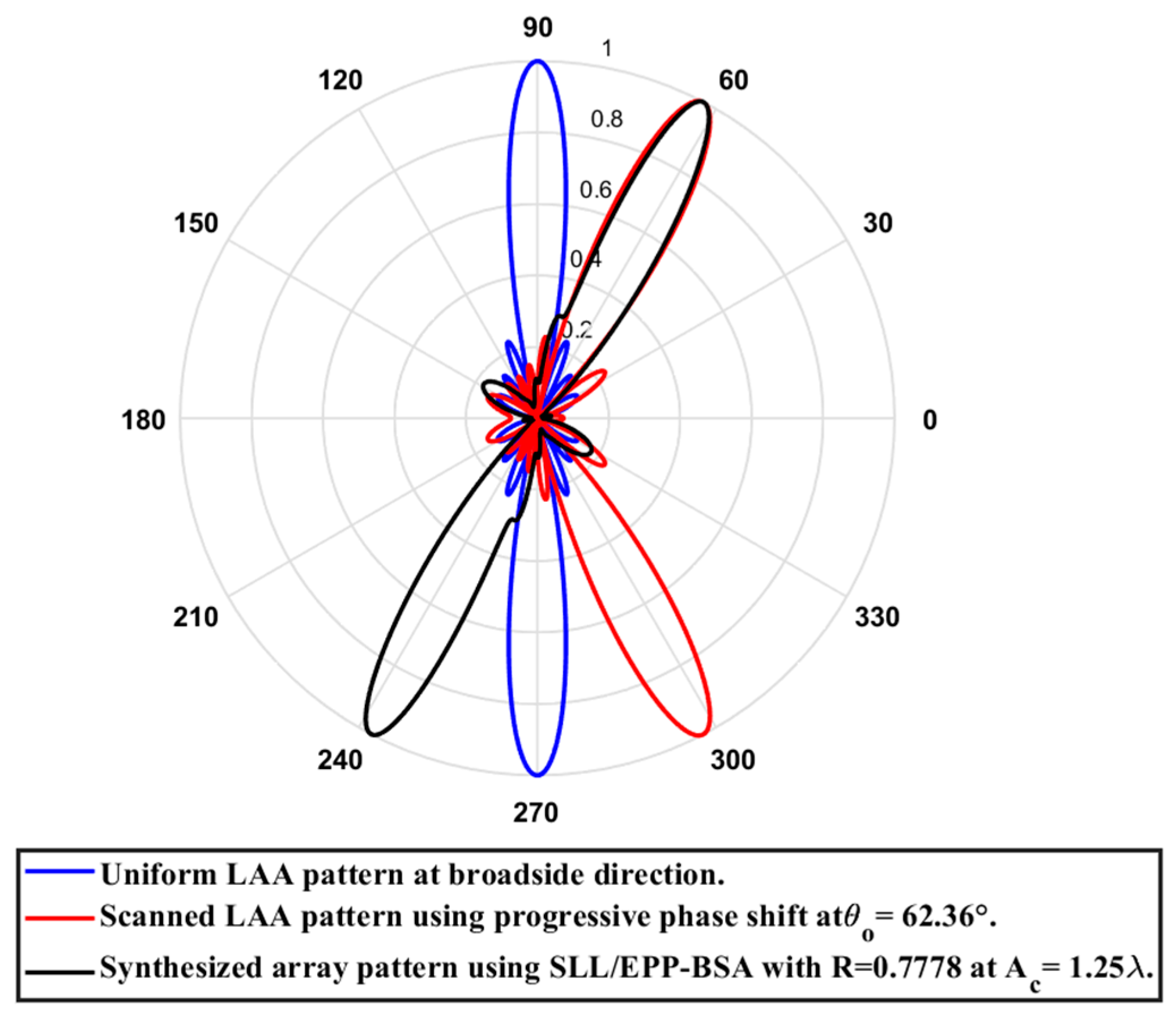
Figure 30.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 30.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 31.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 31.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 32.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 32.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 33.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 33.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 34.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 34.
Polar plot of the synthesized radiation pattern using the SLL/EPP-BSA approach at compression ratio and .
Figure 35.
Element distribution of the proposed ) PAA configuration and the element distributions of the elements of the actual array using the proposed EPP-BSA approach at uniform element spacing on the Z-axis and changing from positive to negative.
Figure 35.
Element distribution of the proposed ) PAA configuration and the element distributions of the elements of the actual array using the proposed EPP-BSA approach at uniform element spacing on the Z-axis and changing from positive to negative.
Figure 36.
The implementation of the proposed ) PAA configuration using CST microwave studio utilizing a dipole antenna with resonance frequency .
Figure 36.
The implementation of the proposed ) PAA configuration using CST microwave studio utilizing a dipole antenna with resonance frequency .
Figure 37.
CST-simulated 3D radiation patterns using the PAA thinning for implementation of the proposed EPP-BSA approach for 8-element ULAA at : (a) , (b) , (c) , (d) , and changing from positive to negative.
Figure 37.
CST-simulated 3D radiation patterns using the PAA thinning for implementation of the proposed EPP-BSA approach for 8-element ULAA at : (a) , (b) , (c) , (d) , and changing from positive to negative.
Figure 38.
CST simulated polar plots of the radiation patterns using the PAA thinning for implementation of the proposed EPP-BSA approach for 8-element ULAA at : (a) , (b) , (c) , (d) , and changing from positive to negative.
Figure 38.
CST simulated polar plots of the radiation patterns using the PAA thinning for implementation of the proposed EPP-BSA approach for 8-element ULAA at : (a) , (b) , (c) , (d) , and changing from positive to negative.
Table 1.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element uniform LAA at compression ratio .
Table 1.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element uniform LAA at compression ratio .
| Figure | | , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| Figure 7a | | | | | |
| Figure 7b | | | | |
| Figure 7c | | | | |
| Figure 7d | | | | |
| Figure 7e | | | | |
| Figure 7f | | | | |
| Figure 7g | | | | |
| Figure 7h | | | | |
| Figure 7i | | | | |
| Figure 7j | | | | |
Table 2.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 2.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| Figure | | , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| Figure 10a | | 90° | | | |
| Figure 10b | | 81.44° | | |
| Figure 10c | | 73.19° | | |
| Figure 10d | | | | |
| Figure 10e | | | | |
| Figure 10f | | | | |
| Figure 10g | | | | |
| Figure 10h | | | | |
| Figure 10i | | | | |
Table 3.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 3.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| Figure | | , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| Figure 14a | | | | | |
| Figure 14b | | | | |
| Figure 14c | | | | |
| Figure 14d | | | | |
| Figure 14e | | | | |
| Figure 14f | | | | |
| Figure 14g | | | | |
| Figure 14h | | | | |
| Figure 14i | | | | |
| Figure 14j | | | | |
| Figure 14k | | | | |
Table 4.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 4.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| Figure | | , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| Figure 17a | | | | | |
| Figure 17b | | | | |
| Figure 17c | | | | |
| Figure 17d | | | | |
| Figure 17e | | | | |
| Figure 17f | | | | |
| Figure 17g | | | | |
| Figure 17h | | | | |
| Figure 17i | | | | |
| Figure 17j | | | | |
| Figure 17k | | | | |
Table 5.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 5.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| Figure | | , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| Figure 19a | | | | | |
| Figure 19b | | | | |
| Figure 19c | | | | |
| Figure 19d | | | | |
| Figure 19e | | | | |
| Figure 19f | | | | |
| Figure 19g | | | | |
| Figure 19h | | | | |
| Figure 19i | | | | |
| Figure 19j | | | | |
| Figure 19k | | | | |
Table 6.
Comparison between the five test cases of compression ratio. The optimal value is in bold.
Table 6.
Comparison between the five test cases of compression ratio. The optimal value is in bold.
| No. | Compression Ratio | | Scan Angle Range with Respect to Broadside Direction | SLL | HPBW |
|---|
| 1 | | to | From | | Constant |
| to 1.5 | From | | Decreased by |
| 2 | | to | From | | Constant |
| to | From | | Decreased by |
| 3 | | to | From | | Constant |
| to | From | | Decreased by |
| 4 | | to | From | | Constant |
| to | From | | Increase by |
| 5 | | to | From | | Constant |
| to | From | | Increased by |
Table 7.
The CST simulation results for changing from 0 to compared to the MATLAB simulation results indicating the resultant scan angle, SLL, and HPBW.
Table 7.
The CST simulation results for changing from 0 to compared to the MATLAB simulation results indicating the resultant scan angle, SLL, and HPBW.
| CST Results | MATLAB Results |
|---|
| Scan Angle | HPBW | SLL | Scan Angle | HPBW | SLL |
|---|
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
Table 8.
The synthesized excitation coefficients and , element spacing , SLL, and HPBW.
Table 8.
The synthesized excitation coefficients and , element spacing , SLL, and HPBW.
| Original ULAA | The Synthesized Array Using Odd Excitations | The Synthesized Array Using Even Excitations |
|---|
| N = 8 elements | N = 8 elements | N = 7 elements |
| | |
| 1 | | 1 | | 2 |
| 1 | | 3 | | 4 |
| 1 | | 5 | | 6 |
| 1 | | 7 | | 8 |
| 1 | | 7 | | 6 |
| 1 | | 5 | | 4 |
| 1 | | 3 | | 2 |
| 1 | | 1 | | |
| | |
| | |
Table 9.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 9.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| | | | |
| | | |
| | | |
| | | |
| | | |
| Grating lobe appearance |
|
|
|
Table 10.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 10.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| | | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| Grating lobe appearance |
|
|
Table 11.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 11.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| | | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| Grating lobe appearance |
|
|
Table 12.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 12.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| | | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| Grating lobe appearance |
|
Table 13.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
Table 13.
The relation between the amplitude changes of the cosine waveform and the scanning angle, HPBW, SLL, and maximum scanning range for 8-element ULAA at compression ratio .
| , in °
| SLL (dB) | HPBW in ° | Maximum Scanning Range |
|---|
| | | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Table 14.
A comparison between the actual elements’ positions in Y-direction compared to the corresponding quantized elements’ positions in Y-direction at fixed element spacing in Z-direction for the realization of EPP-BSA approach using the proposed PAA thinning.
Table 14.
A comparison between the actual elements’ positions in Y-direction compared to the corresponding quantized elements’ positions in Y-direction at fixed element spacing in Z-direction for the realization of EPP-BSA approach using the proposed PAA thinning.
| | Number of Antenna Element on Z-Direction |
|---|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|---|
| Exact position | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Quantized position | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Exact position | 0.5 | 0.46 | 0.35 | 0.19 | 0 | −0.19 | −0.35 | −0.46 |
| Quantized position | 0.5 | 0.5 | 0.4 | 0.2 | 0 | −0.2 | −0.4 | −0.5 |
| Exact position | 1 | 0.9 | 0.7 | 0.4 | 0 | −0.4 | −0.7 | −0.9 |
| Quantized position | 1 | 0.9 | 0.7 | 0.4 | 0 | −0.4 | −0.7 | −0.9 |
| Exact position | 2 | 1.848 | 1.414 | 0.7654 | 0 | −0.7654 | −1.414 | −1.848 |
| Quantized position | 2 | 1.8 | 1.4 | 0.7 | 0 | −0.7 | −1.4 | −1.8 |
Table 15.
A comparison between the CST simulation results and MATLAB simulation results of the proposed EPP/BSA approach using the proposed PAA thinning and actual EPP/BSA indicating the resultant scan angle, SLL, and HPBW at .
Table 15.
A comparison between the CST simulation results and MATLAB simulation results of the proposed EPP/BSA approach using the proposed PAA thinning and actual EPP/BSA indicating the resultant scan angle, SLL, and HPBW at .
| CST Simulation Results Using PAA Thinning | CST Simulation Results Using Actual EPP/BSA | MATLAB Simulation Results Using Actual EPP/BSA |
|---|
| Scan Angle | HPBW | SLL | Scan Angle | HPBW | SLL | Scan Angle | HPBW | SLL |
|---|
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
Table 16.
Comparison with state-of-the-art works.
Table 16.
Comparison with state-of-the-art works.
| Ref. | Beam Steering Range (BSR) | Maximum SLL | HPBW |
|---|
| [19] | by switching eight different sampling states of the switching mechanism. | in this 3-bit phase shifter. | Whenever the main beam’s direction changes, the HPBW correspondingly changes. |
| [20] | . | . | Whenever the main beam’s direction changes, the HPBW correspondingly changes. |
| [21] | . | , respectively. | , respectively. |
| [22] | Continuous beam steering from . | | . |
| [23] | Continuous beam steering from . | Not available | Not available |
| [24] | . | Not available | Not available |
| This work | . | at the edges of the steering range. | at the edges of the steering range. |
| . | over the entire steering range. | Constant HPBW over the entire steering range. |