An Enhanced Flower Pollination Algorithm with Gaussian Perturbation for Node Location of a WSN
Abstract
1. Introduction
- (1)
- A localization algorithm based on the enhanced flower pollination algorithm with Gaussian perturbation and the DV-Hop method is proposed. The superiority and robustness of the proposed algorithm are verified by extensive simulation experiments.
- (2)
- An enhancement strategy based on Lévy flight is proposed to improve the search capability of the algorithm.
- (3)
- A Gaussian perturbation strategy for balancing global exploration and local exploitation search capabilities is proposed.
2. Background
2.1. DV-Hop Method
2.1.1. Calculating the Minimum Number of Hops
2.1.2. Estimating the Distance between Anchor Nodes and Unknown Nodes
2.1.3. Estimating Unknown Node Coordinates
2.2. Flower Pollination Algorithm
2.2.1. Global Pollination
2.2.2. Local Pollination
2.2.3. Transition Probability
3. Proposed EFPA-G Approach
3.1. Enhanced Strategy
3.2. Gaussian Perturbation
3.3. Objective Function
3.4. EFPA-G Algorithm
| Algorithm 1 Proposed EFPA-G Algorithm |
Input: The maximum number of iterations , population size N, transition probability P; Output: Optimal solution;
|
3.5. Complexity Analysis
4. Numerical Results and Discussions
4.1. Parameters Settings
- (1)
- Flower pollination algorithm (FPA): transition probability ;
- (2)
- Flower pollination algorithm based on cloud mutation (CMFPA) [31]: transition probability ;
- (3)
- Modified particle swarm optimization (MPSO) [32]: inertia weight ∼, acceleration factors ;
- (4)
- Marine predators algorithm (MPA) [33]: fish aggregating devices , constant number ;
- (5)
- Ranking-based adaptive cuckoo search algorithm (RACS) [34]: the maximum size of the archive , exponent parameter , the pre-determined number of cycles , initial crossover rate ;
- (6)
- Proposed EFPA-G algorithm: transition probability .
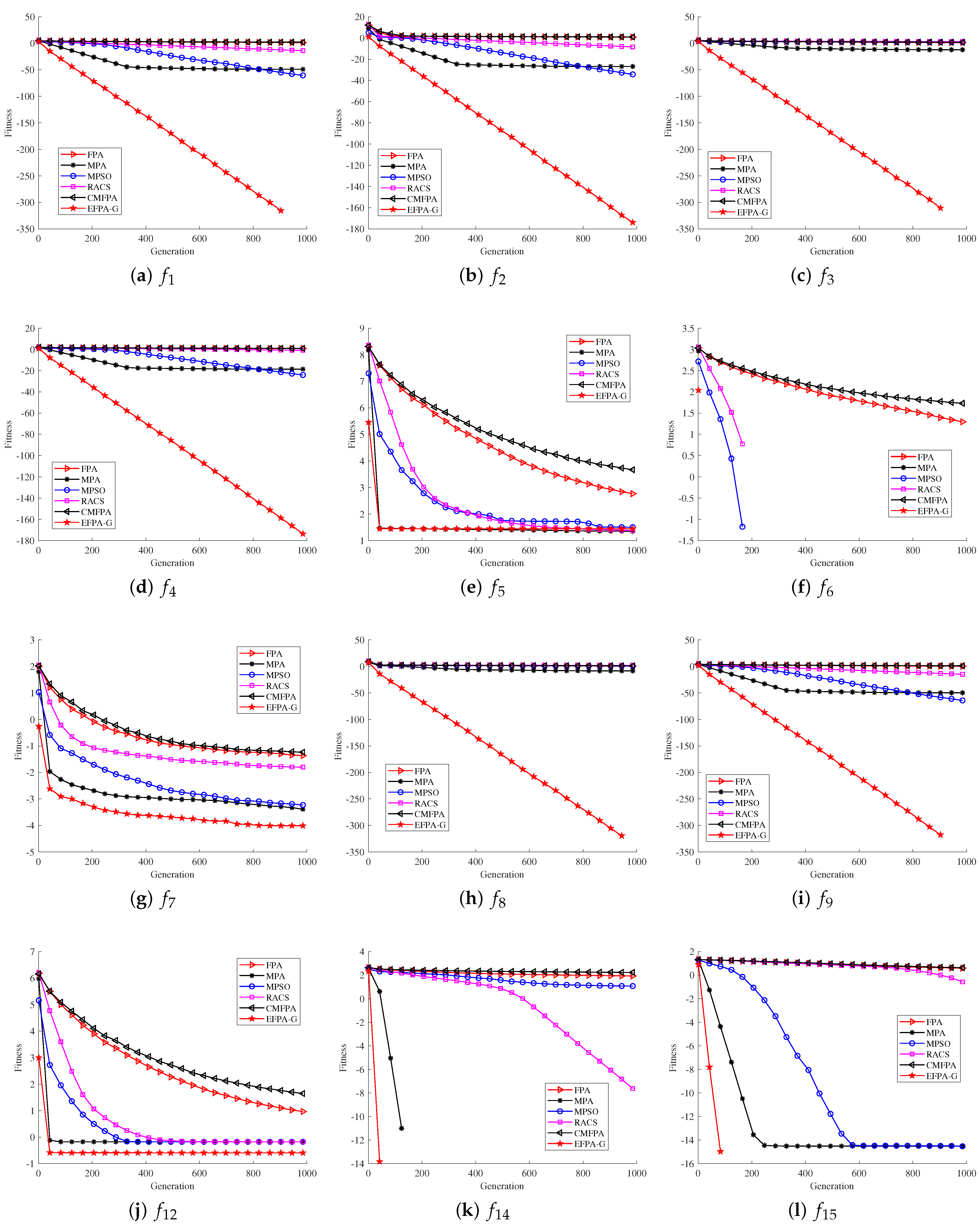
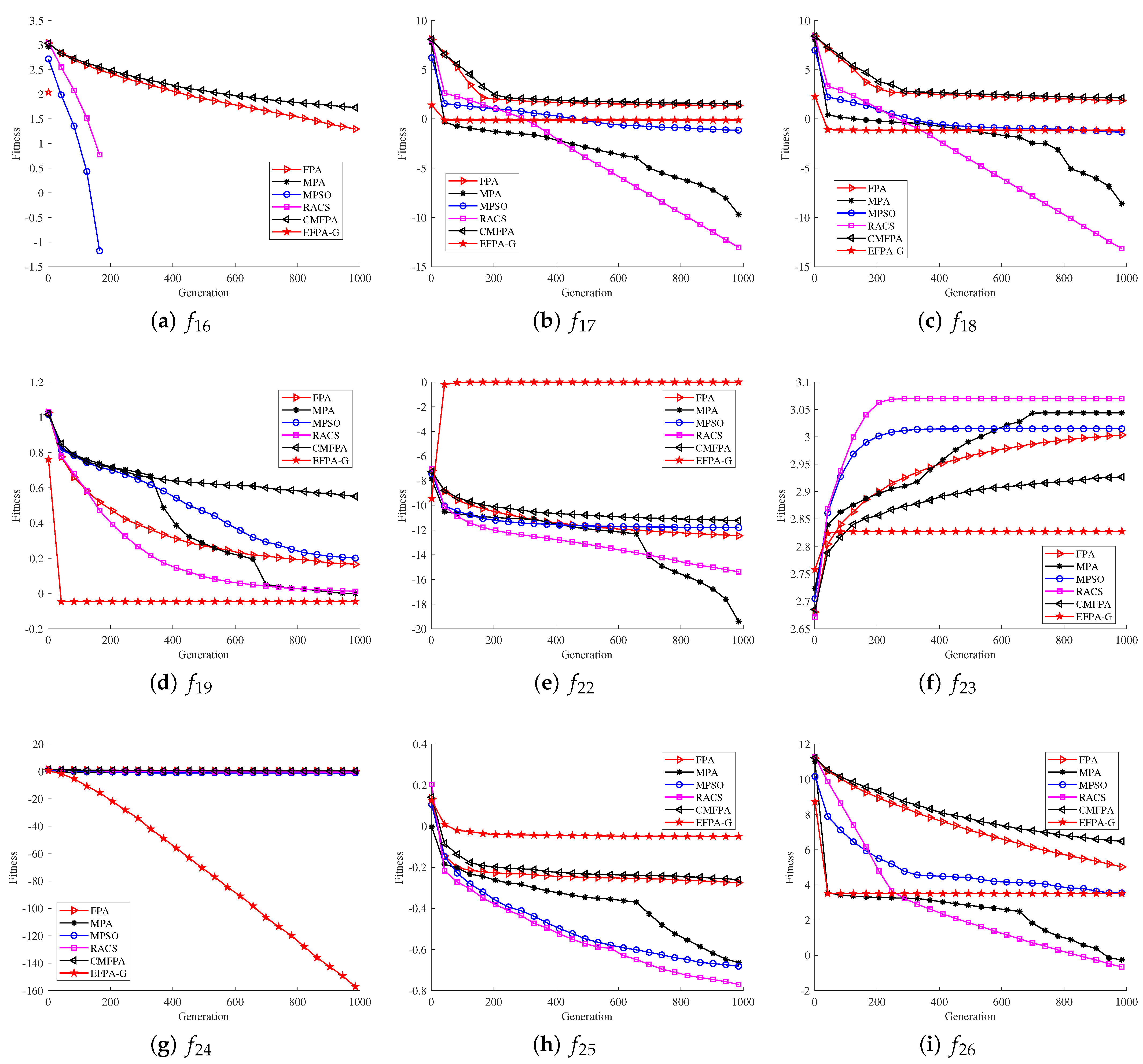
4.2. Benchmark Test
4.2.1.
4.2.2.
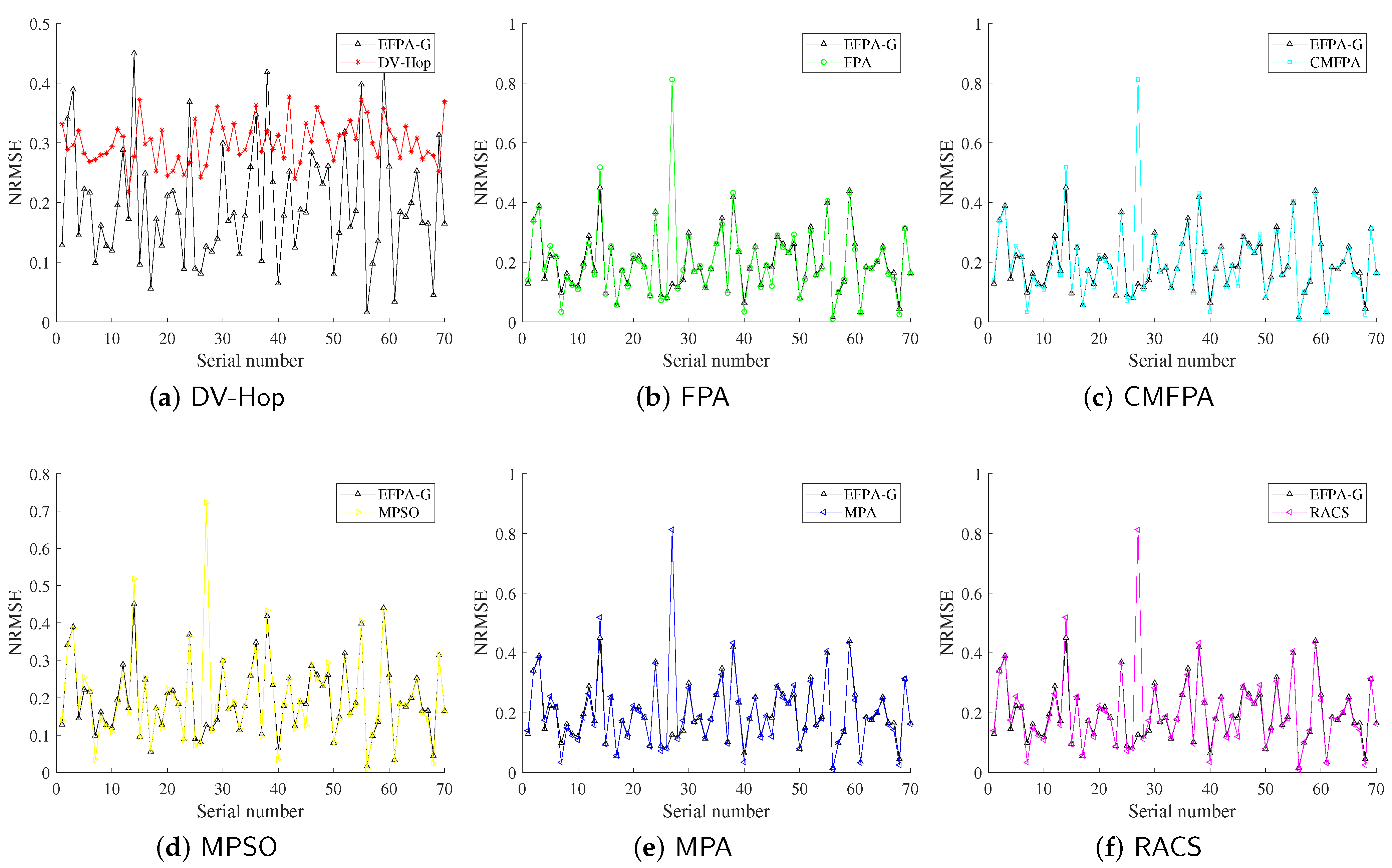
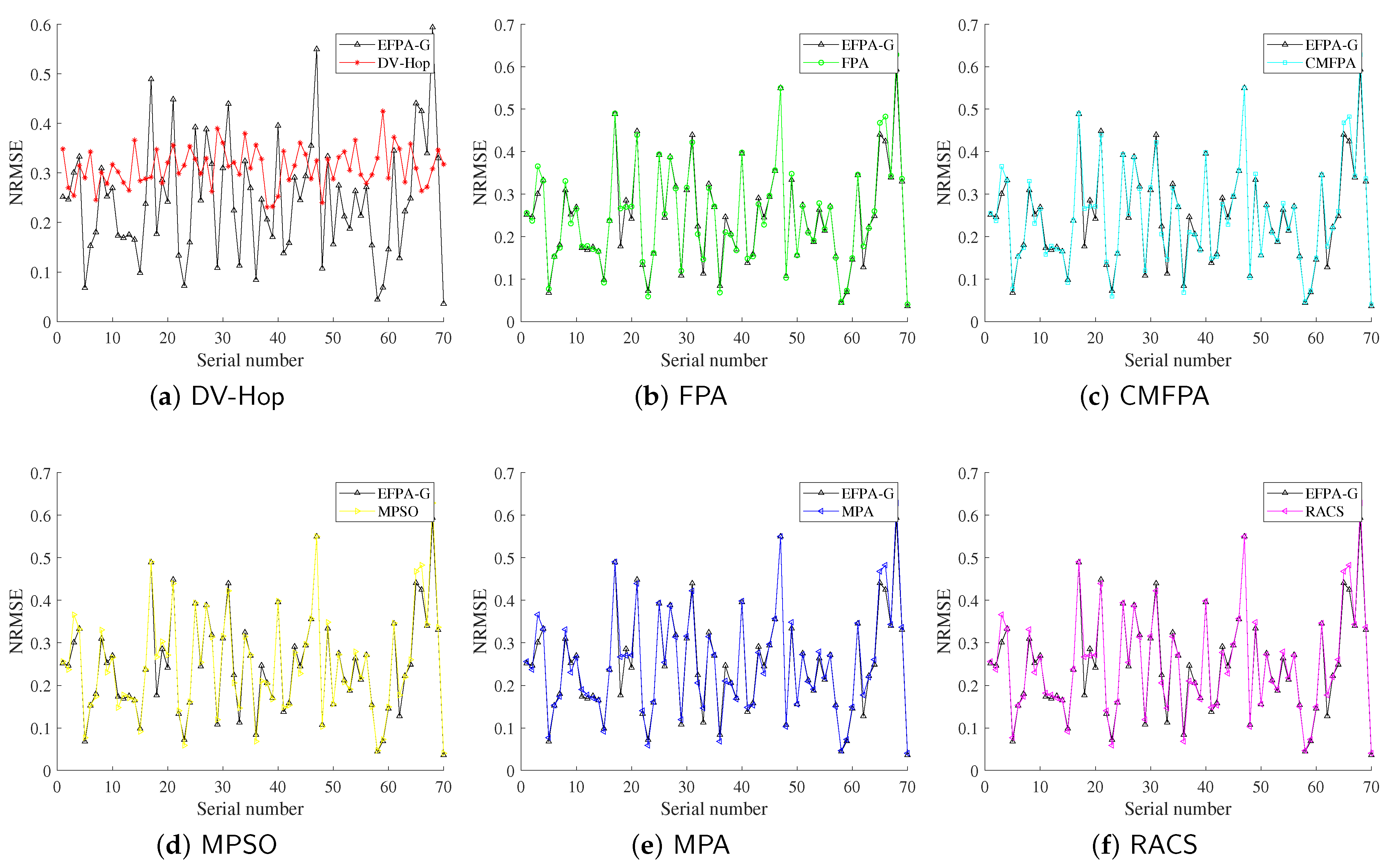
4.3. Simulation for WSN
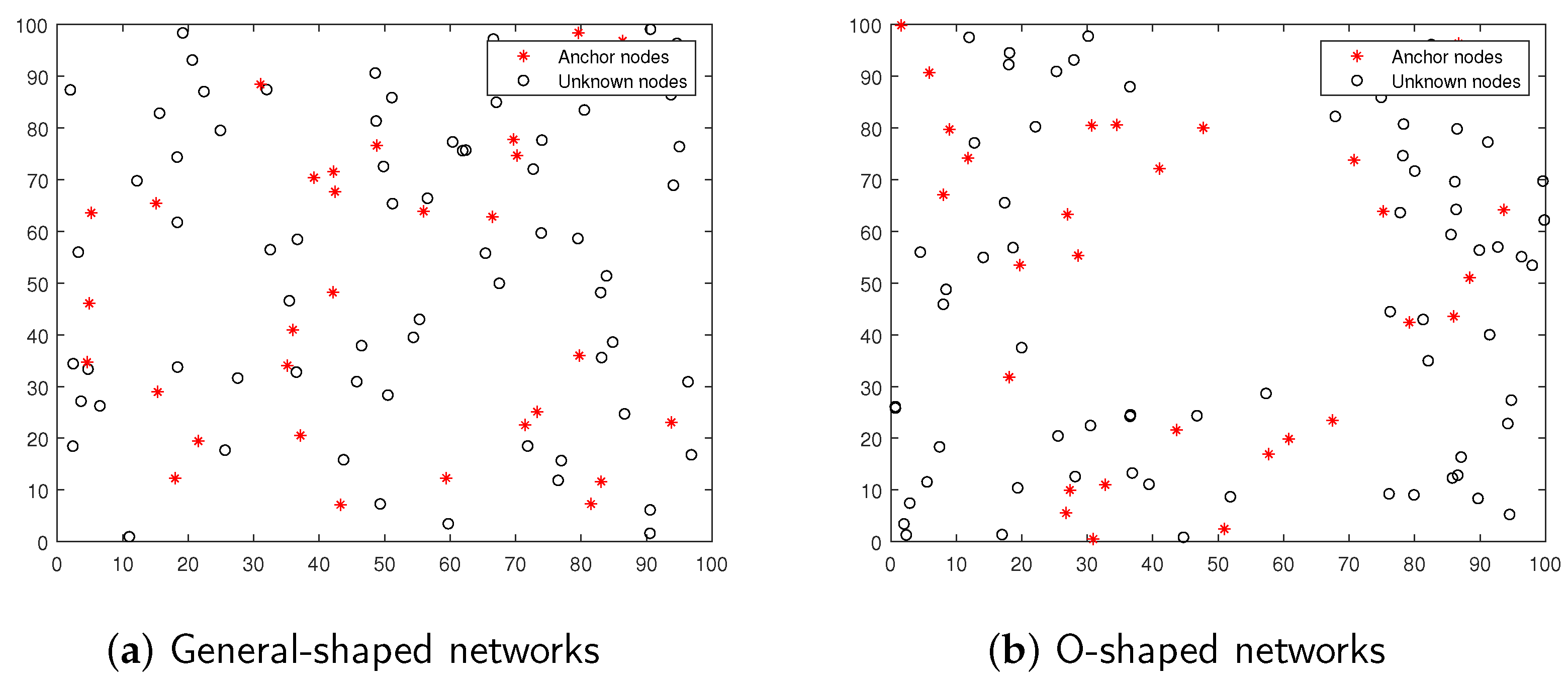
4.3.1. General Simulation
4.3.2. Effect of the Proportion of Anchor Nodes
4.3.3. Effect of Node Communication Radius
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6g internet of things: A comprehensive survey. IEEE Internet Things J. 2022, 9, 359–383. [Google Scholar] [CrossRef]
- Bianchi, V.; Ciampolini, P.; Munari, I.D. Rssi-based indoor localization and identification for zigbee wireless sensor networks in smart homes. IEEE Trans. Instrum. Meas. 2019, 68, 566–575. [Google Scholar] [CrossRef]
- Sundhari, R.M.; Jaikumar, K. Iot assisted hierarchical computation strategic making (HCSM) and dynamic stochastic optimization technique (DSOT) for energy optimization in wireless sensor networks for smart city monitoring. Comput. Commun. 2020, 150, 226–234. [Google Scholar] [CrossRef]
- Du, C.; Gao, S.; Jia, N.; Kong, D.; Jiang, J.; Tian, G.; Su, Y.; Wang, Q.; Li, C. A high-accuracy least-time-domain mixture features machine-fault diagnosis based on wireless sensor network. IEEE Syst. J. 2020, 14, 4101–4109. [Google Scholar] [CrossRef]
- Liu, X.; Yin, J.; Zhang, S.; Ding, B.; Guo, S.; Wang, K. Range-based localization for sparse 3-d sensor networks. IEEE Internet Things J. 2019, 6, 753–764. [Google Scholar] [CrossRef]
- Tu, Q.; Liu, Y.; Han, F.; Liu, X.; Xie, Y. Range-free localization using reliable anchor pair selection and quantum-behaved salp swarm algorithm for anisotropic wireless sensor networks. Ad Hoc Netw. 2021, 113, 102406. [Google Scholar] [CrossRef]
- Wang, L.; Su, D.; Liu, M.; Du, X. Modified zeroing neurodynamics models for range-based wsn localization from aoa and tdoa measurements. IEEE Sens. J. 2022, 22, 13716–13726. [Google Scholar] [CrossRef]
- Shen, H.; Ding, Z.; Dasgupta, S.; Zhao, C. Multiple source localization in wireless sensor networks based on time of arrival measurement. IEEE Trans. Signal Process. 2014, 62, 1938–1949. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, J.; Wei, W.; Qin, T.; Fan, Y.; Long, F.; Yang, J. A hybrid bald eagle search algorithm for time difference of arrival localization. Appl. Sci. 2022, 12, 5221. [Google Scholar] [CrossRef]
- Wang, P.; Zhou, R.; Fan, X.; Zhao, D. A distance estimation model for dv-hop localization in wsns. IEEE Trans. Veh. Technol. 2023, 72, 5290–5299. [Google Scholar] [CrossRef]
- Xue, D. Research of localization algorithm for wireless sensor network based on dv-hop. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 218. [Google Scholar] [CrossRef]
- Messous, S.; Liouane, H.; Liouane, N. Improvement of dv-hop localization algorithm for randomly deployed wireless sensor networks. Telecommun. Syst. 2020, 73, 75–86. [Google Scholar] [CrossRef]
- Cheikhrouhou, O.; Bhatti, G.M.; Alroobaea, R. A hybrid dv-hop algorithm using rssi for localization in large-scale wireless sensor networks. Sensors 2018, 18, 1469. [Google Scholar] [CrossRef] [PubMed]
- Messous, S.; Liouane, H.; Cheikhrouhou, O.; Hamam, H. Improved recursive dv-hop localization algorithm with rssi measurement for wireless sensor networks. Sensors 2021, 21, 4152. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Su, S.; Shao, F. Improved dv-hop algorithm using locally weighted linear regression in anisotropic wireless sensor networks. Wirel. Pers. Commun. 2018, 98, 3335–3353. [Google Scholar] [CrossRef]
- Liouane, H.; Messous, S.; Cheikhrouhou, O. Regularized least square multi-hops localization algorithm based on dv-hop for wireless sensor networks. Telecommun. Syst. 2022, 80, 349–358. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Du, X.; Stanimirovi, P.S.; Jin, L. An improved dv-hop algorithm for wireless sensor networks based on neural dynamics. Neurocomputing 2022, 491, 172–185. [Google Scholar] [CrossRef]
- Ou, X.; Wu, M.; Pu, Y.; Tu, B.; Zhang, G.; Xu, Z. Cuckoo search algorithm with fuzzy logic and gauss–cauchy for minimizing localization error of wsn. Appl. Soft Comput. 2022, 125, 109211. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar]
- Chen, Y.; Pi, D.; Xu, Y. Neighborhood global learning based flower pollination algorithm and its application to unmanned aerial vehicle path planning. Expert Syst. Appl. 2021, 170, 114505. [Google Scholar]
- Mohanty, S.; Dash, R. A flower pollination algorithm based chebyshev polynomial neural network for net asset value prediction. Evol. Intell. 2023, 16, 115–131. [Google Scholar] [CrossRef]
- Kaya, E. Quick flower pollination algorithm (QFPA) and its performance on neural network training. Soft Comput. 2022, 26, 9729–9750. [Google Scholar] [CrossRef]
- Cao, H.Q.; Nguyen, H.X.; Tran, T.N.-C.; Tran, H.N.; Jeon, J.W. A robot calibration method using a neural network based on a butterfly and flower pollination algorithm. IEEE Trans. Ind. Electron. 2022, 69, 3865–3875. [Google Scholar] [CrossRef]
- Ozsoydan, F.B.; Baykasoglu, A. A species-based flower pollination algorithm with increased selection pressure in abiotic local pollination and enhanced intensification. Knowl.-Based Syst. 2021, 225, 107125. [Google Scholar] [CrossRef]
- Mergos, P.E. Optimum design of 3d reinforced concrete building frames with the flower pollination algorithm. J. Build. Eng. 2021, 44, 102935. [Google Scholar] [CrossRef]
- Dao, T.-K.; Nguyen, T.-T.; Nguyen, V.-T.; Nguyen, T.-D. A hybridized flower pollination algorithm and its application on microgrid operations planning. Appl. Sci. 2022, 12, 6487. [Google Scholar] [CrossRef]
- Sasikumar, A.; Subramaniyaswamy, V.; Jannali, R.; Rao, V.S.; Ravi, L. Design and area optimization of cmos operational amplifier circuit using hybrid flower pollination algorithm for iot end-node devices. Microprocess. Microsyst. 2022, 93, 104610. [Google Scholar]
- Ozsoydan, F.B.; Baykasoglu, A. Chaos and intensification enhanced flower pollination algorithm to solve mechanical design and unconstrained function optimization problems. Expert Syst. Appl. 2021, 184, 115496. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Ding, Y.; Xu, J.; Liu, Z. An improved DV-Hop localization algorithm for wireless sensor networks. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications, Wuhan, China, 31 May–2 June 2018; pp. 1831–1836. [Google Scholar]
- Chen, Y.; Pi, D. An innovative flower pollination algorithm for continuous optimization problem. Appl. Math. Model. 2020, 83, 237–265. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.-W.; Tu, L.-P. A modified particle swarm optimization using adaptive strategy. Expert Syst. Appl. 2020, 152, 113353. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine predators algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar]
- Wei, J.; Niu, H. A ranking-based adaptive cuckoo search algorithm for unconstrained optimization. Expert Syst. Appl. 2022, 204, 117428. [Google Scholar]
| Name | Function | Range | |
|---|---|---|---|
| Sphere | 0 | ||
| Schwefel 2.22 | 0 | ||
| Schwefel 1.2 | 0 | ||
| Schwefel 2.21 | 0 | ||
| Rosenbrock | 0 | ||
| Step | 0 | ||
| Quartic | 0 | ||
| Zakharov | 0 | ||
| Sum Squares | 0 | ||
| Ridge | −5 | ||
| Xin-She Yang 3 | −1 | ||
| Dixon&Price | 0 | ||
| Schwefel 2.26 | 0 | ||
| Rastrigin | 0 | ||
| Ackley 1 | 0 | ||
| Griewank | 0 | ||
| Generalized pen- alized function 1 | 0 | ||
| Generalized pen- alized function 2 | 0 | ||
| Periodic | 0.9 | ||
| Ackley 4 | −4.59 | ||
| Xin-She Yang 2 | 0 | ||
| Xin-She Yang 4 | −1 | ||
| Styblinski-Tank | 0 | ||
| Salomon | |||
| Happy Cat | 0 | ||
| Qing | 0 |
| Function | Algorithm | Function | Algorithm | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FPA | CMFPA | MPSO | MPA | RACS | EFPA-G | FPA | CMFPA | MPSO | MPA | RACS | EFPA-G | ||||
| Ave | 2.11E+01 | 1.19E+02 | 6.69E-62 | 9.61E-50 | 8.34E-15 | 0.00E+00 | Ave | 8.45E+01 | 1.68E+02 | 1.17E+01 | 0.00E+00 | 1.19E-08 | 0.00E+00 | ||
| Std | 1.26E+01 | 7.99E+01 | 3.66E-61 | 1.05E-49 | 6.55E-15 | 0.00E+00 | Std | 1.38E+01 | 1.39E+01 | 1.32E+01 | 0.00E+00 | 8.19E-09 | 0.00E+00 | ||
| Ave | 6.21E+00 | 1.00E+01 | 1.39E-35 | 1.33E-27 | 2.75E-09 | 1.77E-178 | Ave | 3.81E+00 | 4.26E+00 | 2.96E-15 | 3.08E-15 | 1.78E-01 | 0.00E+00 | ||
| Std | 2.03E+00 | 2.06E+00 | 4.54E-35 | 1.72E-27 | 8.79E-10 | 0.00E+00 | Std | 1.03E+00 | 8.13E-01 | 1.35E-15 | 1.23E-15 | 4.26E-01 | 0.00E+00 | ||
| Ave | 1.86E+01 | 8.07E+01 | 2.60E+02 | 7.83E-13 | 1.16E+03 | 0.00E+00 | Ave | 6.30E-01 | 1.02E+00 | 0.00E+00 | 0.00E+00 | 1.53E-13 | 0.00E+00 | ||
| Std | 9.71E+00 | 3.31E+01 | 1.54E+02 | 2.82E-12 | 5.61E+02 | 0.00E+00 | Std | 1.40E-01 | 4.63E-02 | 0.00E+00 | 0.00E+00 | 6.53E-13 | 0.00E+00 | ||
| Ave | 7.71E+00 | 9.89E+00 | 3.13E-25 | 2.70E-19 | 1.30E-01 | 7.58E-177 | Ave | 2.26E+01 | 3.14E+01 | 6.54E-02 | 5.95E-11 | 5.02E-14 | 7.64E-01 | ||
| Std | 1.49E+00 | 1.75E+00 | 7.68E-25 | 2.34E-19 | 3.43E-02 | 0.00E+00 | Std | 7.89E+00 | 1.54E+01 | 1.24E-01 | 2.55E-11 | 3.08E-14 | 4.24E-01 | ||
| Ave | 5.45E+02 | 4.47E+03 | 3.19E+01 | 2.24E+01 | 2.38E+01 | 2.78E+01 | Ave | 6.96E+01 | 1.29E+02 | 4.33E-02 | 7.40E-10 | 3.34E-14 | 7.22E-02 | ||
| Std | 4.30E+02 | 3.15E+03 | 3.17E+01 | 6.19E-01 | 3.96E+00 | 4.98E+00 | Std | 3.36E+01 | 8.84E+01 | 3.80E-02 | 3.21E-10 | 3.06E-14 | 3.70E-02 | ||
| Ave | 1.87E+01 | 5.26E+01 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | Ave | 1.46E+00 | 3.51E+00 | 1.59E+00 | 1.00E+00 | 1.03E+00 | 9.00E-01 | ||
| Std | 5.46E+00 | 1.48E+01 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | Std | 6.81E-02 | 5.06E-01 | 5.13E-01 | 2.01E-03 | 6.42E-03 | 4.52E-16 | ||
| Ave | 4.27E-02 | 5.71E-02 | 5.73E-04 | 4.08E-04 | 1.53E-02 | 9.56E-05 | Ave | 1.15E+01 | 2.14E+01 | −3.93E+01 | −4.71E+01 | −4.81E+01 | −4.69E+01 | ||
| Std | 1.36E-02 | 1.90E-02 | 2.95E-04 | 2.30E-04 | 4.10E-03 | 6.88E-05 | Std | 9.23E+00 | 9.55E+00 | 3.02E+00 | 1.94E+00 | 1.21E+00 | 4.47E+00 | ||
| Ave | 4.70E+00 | 1.03E+01 | 6.02E+00 | 4.05E-09 | 3.81E+01 | 0.00E+00 | Ave | 5.87E-12 | 6.34E-12 | 4.23E-11 | 7.30E-12 | 3.66E-12 | 7.98E-11 | ||
| Std | 2.84E+00 | 5.64E+00 | 8.05E+00 | 4.15E-09 | 1.27E+01 | 0.00E+00 | Std | 2.32E-12 | 2.91E-12 | 4.29E-11 | 2.84E-12 | 2.07E-13 | 2.30E-10 | ||
| Ave | 2.20E+00 | 1.37E+01 | 4.78E-66 | 1.68E-50 | 7.77E-16 | 0.00E+00 | Ave | 3.35E-13 | 5.58E-12 | 1.62E-12 | 7.93E-21 | 3.59E-16 | −1.00E+00 | ||
| Std | 1.08E+00 | 6.90E+00 | 1.09E-65 | 3.13E-50 | 3.31E-16 | 0.00E+00 | Std | 5.79E-14 | 1.57E-12 | 1.43E-12 | 3.42E-21 | 1.72E-16 | 0.00E+00 | ||
| Ave | −4.59E+00 | −3.85E+00 | −5.00E+00 | −5.00E+00 | −5.00E+00 | −1.50E+00 | Ave | −1.01E+03 | −8.47E+02 | −1.03E+03 | −1.11E+03 | −1.17E+03 | −6.73E+02 | ||
| Std | 1.09E-01 | 2.63E-01 | 0.00E+00 | 1.77E-12 | 6.26E-10 | 8.97E-01 | Std | 1.27E+01 | 2.47E+01 | 3.96E+01 | 2.12E+01 | 1.79E-13 | 3.93E+01 | ||
| Ave | −2.56E-01 | −2.98E-01 | 9.95E-01 | 1.99E-01 | 9.95E-01 | −1.00E+00 | Ave | 2.49E+00 | 2.55E+00 | 9.99E-02 | 1.10E-01 | 3.55E-01 | 1.33E-159 | ||
| Std | 8.96E-01 | 8.64E-01 | 3.39E-16 | 9.91E-01 | 3.39E-16 | 0.00E+00 | Std | 3.29E-01 | 4.23E-01 | 6.30E-09 | 3.05E-02 | 4.97E-02 | 7.29E-159 | ||
| Ave | 8.63E+00 | 4.28E+01 | 6.67E-01 | 6.67E-01 | 6.67E-01 | 2.55E-01 | Ave | 5.31E-01 | 5.48E-01 | 2.06E-01 | 2.16E-01 | 1.68E-01 | 8.92E-01 | ||
| Std | 3.97E+00 | 2.59E+01 | 1.96E-07 | 1.06E-09 | 4.35E-05 | 6.84E-03 | Std | 9.33E-02 | 6.84E-02 | 7.30E-02 | 4.65E-02 | 2.33E-02 | 2.02E-01 | ||
| Ave | −2.70E+02 | −1.79E+02 | −3.15E+02 | −3.36E+02 | −4.19E+02 | −1.41E+02 | Ave | 9.19E+04 | 2.88E+06 | 3.52E+03 | 5.40E-01 | 1.98E-01 | 3.24E+03 | ||
| Std | 6.91E+00 | 7.94E+00 | 2.01E+01 | 1.71E+01 | 1.00E+00 | 2.09E+01 | Std | 7.72E+04 | 3.60E+06 | 1.11E+04 | 1.66E+00 | 8.29E-02 | 8.43E+02 | ||
| Function | Algorithm | Function | Algorithm | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FPA | CMFPA | MPSO | MPA | RACS | EFPA-G | FPA | CMFPA | MPSO | MPA | RACS | EFPA-G | ||||
| Ave | 3.50E+02 | 1.26E+03 | 1.43E-45 | 3.84E-46 | 7.23E-08 | 0.00E+00 | Ave | 1.78E+02 | 3.33E+02 | 1.53E+01 | 0.00E+00 | 1.40E+00 | 0.00E+00 | ||
| Std | 1.25E+02 | 4.98E+02 | 7.41E-45 | 7.34E-46 | 2.93E-08 | 0.00E+00 | Std | 1.97E+01 | 2.21E+01 | 3.36E+01 | 0.00E+00 | 9.42E-01 | 0.00E+00 | ||
| Ave | 1.61E+01 | 2.20E+01 | 5.64E-32 | 3.88E-26 | 5.07E-05 | 1.80E-178 | Ave | 4.49E+00 | 4.35E+00 | 4.19E-01 | 3.32E-15 | 1.23E+01 | 0.00E+00 | ||
| Std | 1.70E+00 | 2.81E+00 | 2.11E-31 | 4.70E-26 | 1.03E-05 | 0.00E+00 | Std | 1.22E+00 | 1.06E+00 | 1.91E+03 | 9.01E-16 | 4.33E+00 | 0.00E+00 | ||
| Ave | 3.77E+02 | 7.17E+02 | 2.84E+03 | 2.48E-08 | 1.17E+04 | 0.00E+00 | Ave | 1.08E+00 | 1.35E+00 | 0.00E+00 | 0.00E+00 | 1.26E-08 | 0.00E+00 | ||
| Std | 1.22E+02 | 2.57E+02 | 1.91E+03 | 1.02E-07 | 1.94E+03 | 0.00E+00 | Std | 2.88E-02 | 9.60E-02 | 0.00E+00 | 0.00E+00 | 1.83E-08 | 0.00E+00 | ||
| Ave | 1.25E+01 | 1.35E+01 | 3.54E-22 | 1.36E-17 | 2.33E+00 | 1.74E-175 | Ave | 3.23E+01 | 3.58E+01 | 2.50E+00 | 2.52E-09 | 9.05E-07 | 1.63E+00 | ||
| Std | 1.91E+00 | 1.58E+00 | 1.39E-21 | 9.06E-18 | 4.29E-01 | 0.00E+00 | Std | 8.86E+00 | 1.56E+01 | 3.24E+00 | 6.82E-10 | 5.27E-07 | 6.35E-01 | ||
| Ave | 1.26E+04 | 1.03E+05 | 4.92E+03 | 4.34E+01 | 5.76E+01 | 4.85E+01 | Ave | 1.51E+02 | 1.85E+02 | 1.22E+00 | 4.90E-03 | 3.59E-07 | 1.12E-01 | ||
| Std | 8.62E+03 | 6.20E+04 | 2.00E+04 | 5.44E-01 | 2.00E+01 | 6.88E-03 | Std | 6.45E+01 | 7.93E+01 | 1.41E+00 | 7.86E-03 | 1.22E-07 | 5.15E-02 | ||
| Ave | 9.58E+01 | 1.71E+02 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | Ave | 3.11E+00 | 6.80E+00 | 2.30E+00 | 1.01E+00 | 1.35E+00 | 9.00E-01 | ||
| Std | 1.38E+01 | 2.75E+01 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | Std | 2.02E-01 | 6.73E-01 | 6.13E-01 | 7.12E-03 | 5.44E-02 | 4.52E-16 | ||
| Ave | 1.52E-01 | 1.81E-01 | 8.88E-04 | 6.65E-04 | 3.05E-02 | 8.43E-05 | Ave | 5.09E+01 | 7.40E+01 | 5.64E-32 | −7.44E+01 | −6.85E+01 | −7.95E+01 | ||
| Std | 5.13E-02 | 5.37E-02 | 3.87E-04 | 3.84E-04 | 6.91E-03 | 9.02E-05 | Std | 1.37E+01 | 1.17E+01 | 6.51E+00 | 2.74E+00 | 1.45E+00 | 6.96E+00 | ||
| Ave | 5.52E+01 | 8.81E+01 | 9.81E+01 | 6.66E-05 | 2.88E+02 | 0.00E+00 | Ave | 1.96E-20 | 1.92E-20 | 8.90E-17 | 1.97E-20 | 3.71E-20 | 9.85E-19 | ||
| Std | 1.66E+01 | 2.01E+01 | 5.53E+01 | 6.29E-05 | 5.32E+01 | 0.00E+00 | Std | 8.23E-21 | 7.09E-21 | 4.87E-16 | 6.74E-21 | 2.56E-21 | 2.37E-18 | ||
| Ave | 6.94E+01 | 2.37E+02 | 9.73E-56 | 1.77E-46 | 1.43E-08 | 0.00E+00 | Ave | 5.31E-21 | 3.44E-19 | 3.35E-20 | 3.93E-22 | 9.24E-22 | −1.00E+00 | ||
| Std | 2.26E+01 | 7.41E+01 | 5.32E-55 | 2.91E-46 | 4.21E-09 | 0.00E+00 | Std | 5.86E-22 | 1.32E-19 | 5.13E-20 | 2.15E-21 | 1.15E-22 | 0.00E+00 | ||
| Ave | −3.47E+00 | −1.48E+00 | −5.00E+00 | −5.00E+00 | −5.00E+00 | −1.41E+00 | Ave | −1.57E+03 | −1.25E+03 | −1.71E+03 | −1.77E+03 | −1.96E+03 | −1.07E+03 | ||
| Std | 2.93E-01 | 5.64E-01 | 1.65E-16 | 1.77E-11 | 2.99E-06 | 1.01E+00 | Std | 2.42E+01 | 4.17E+01 | 4.41E+01 | 3.19E+01 | 2.41E-07 | 7.78E+01 | ||
| Ave | −1.83E-01 | 6.93E-02 | 9.92E-01 | −5.22E-02 | 9.92E-01 | −1.00E+00 | Ave | 4.66E+00 | 4.84E+00 | 9.99E-02 | 1.43E-01 | 7.64E-01 | 3.57E-159 | ||
| Std | 8.98E-01 | 8.79E-01 | 3.39E-16 | 9.94E-01 | 3.39E-16 | 0.00E+00 | Std | 5.32E-01 | 5.70E-01 | 1.26E-08 | 5.04E-02 | 7.15E-02 | 1.90E-158 | ||
| Ave | 2.26E+02 | 1.14E+03 | 5.24E+00 | 6.67E-01 | 6.80E-01 | 2.56E-01 | Ave | 6.41E-01 | 6.84E-01 | 4.38E-01 | 4.46E-01 | 3.75E-01 | 9.90E-01 | ||
| Std | 1.56E+02 | 4.97E+02 | 2.51E+01 | 3.00E-09 | 2.79E-02 | 1.49E-02 | Std | 6.72E-02 | 5.15E-02 | 8.45E-02 | 5.99E-02 | 4.25E-02 | 2.73E-01 | ||
| Ave | −2.39E+02 | −1.41E+02 | −2.64E+02 | −3.22E+02 | −4.18E+02 | −1.55E+02 | Ave | 9.06E+06 | 8.09E+07 | 2.31E+06 | 8.69E+01 | 9.28E+01 | 1.87E+04 | ||
| Std | 7.17E+00 | 7.54E+00 | 2.58E+01 | 1.27E+01 | 1.27E+00 | 5.49E+01 | Std | 5.34E+06 | 5.29E+07 | 8.35E+06 | 1.25E+02 | 2.08E+01 | 2.11E+03 | ||
| General-Shaped Network | O-Shaped Network | |||||||
|---|---|---|---|---|---|---|---|---|
| Algorithm | Average | Best | Std | Algorithm | Average | Best | Std | |
| Normalized Root Mean Square Error (NRMSE %) | DV-Hop | 30.1224% | 24.4230% | 2.94E-02 | DV-Hop | 31.2086% | 25.3410% | 3.23E-02 |
| FPA | 20.2731% | 20.2595% | 1.86E-04 | FPA | 24.9798% | 24.9442% | 3.60E-04 | |
| CMFPA | 20.2648% | 20.2629% | 8.87E-06 | CMFPA | 25.0067% | 24.9509% | 3.25E-04 | |
| MPSO | 20.1720% | 19.3034% | 3.39E-03 | MPSO | 25.0103% | 24.8910% | 4.42E-04 | |
| MPA | 20.2650% | 20.2649% | 6.17E-08 | MPA | 25.0280% | 25.0280% | 4.20E-07 | |
| RACS | 20.2650% | 20.2650% | 2.71E-15 | RACS | 25.0159% | 24.9552% | 2.76E-04 | |
| EFPA-G | 19.5182% | 19.0583% | 2.21E-03 | EFPA-G | 24.5535% | 24.0744% | 1.56E-03 | |
| Mean Distance Error (MDE) | DV-Hop | 7.53E+00 | 6.11E+00 | 7.35E-01 | DV-Hop | 7.80E+00 | 6.34E+00 | 8.07E-01 |
| FPA | 5.07E+00 | 5.06E+00 | 4.64E-03 | FPA | 6.24E+00 | 6.24E+00 | 9.01E-03 | |
| CMFPA | 5.07E+00 | 5.07E+00 | 2.22E-04 | CMFPA | 6.25E+00 | 6.24E+00 | 8.13E-03 | |
| MPSO | 5.04E+00 | 4.83E+00 | 8.48E-02 | MPSO | 6.25E+00 | 6.22E+00 | 1.10E-02 | |
| MPA | 5.07E+00 | 5.07E+00 | 1.54E-06 | MPA | 6.26E+00 | 6.26E+00 | 1.05E-05 | |
| RACS | 5.07E+00 | 5.07E+00 | 6.79E-14 | RACS | 6.25E+00 | 6.24E+00 | 6.91E-03 | |
| EFPA-G | 4.88E+00 | 4.76E+00 | 5.52E-02 | EFPA-G | 6.14E+00 | 6.02E+00 | 3.90E-02 | |
| Algorithm | Proportion of Anchor Nodes (%) | ||||
|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | ||
| General-shaped network | DV-Hop | 39.38% | 31.29% | 30.12% | 30.48% |
| FPA | 26.85% | 20.50% | 20.27% | 18.97% | |
| CMFPA | 26.84% | 20.44% | 20.27% | 18.97% | |
| MPSO | 26.85% | 20.49% | 20.17% | 18.47% | |
| MPA | 26.84% | 20.44% | 20.27% | 18.97% | |
| RACS | 26.84% | 20.44% | 20.27% | 18.97% | |
| EFPA-G | 25.94% | 20.45% | 19.52% | 18.02% | |
| O-shaped network | DV-Hop | 37.66% | 31.49% | 31.21% | 29.70% |
| FPA | 34.14% | 25.50% | 24.98% | 25.79% | |
| CMFPA | 33.91% | 25.51% | 25.01% | 25.79% | |
| MPSO | 34.10% | 25.52% | 25.01% | 25.78% | |
| MPA | 33.92% | 25.51% | 25.03% | 25.79% | |
| RACS | 33.97% | 25.51% | 25.02% | 25.79% | |
| EFPA-G | 33.41% | 25.45% | 24.56% | 25.14% | |
| Algorithm | Communication Radius of Nodes (m) | ||||
|---|---|---|---|---|---|
| 15 | 20 | 25 | 30 | ||
| General-shaped network | DV-Hop | 158.78% | 43.64% | 30.12% | 29.42% |
| FPA | 72.53% | 22.31% | 20.27% | 21.74% | |
| CMFPA | 71.83% | 22.31% | 20.27% | 21.74% | |
| MPSO | 71.90% | 22.68% | 20.17% | 21.58% | |
| MPA | 71.83% | 22.31% | 20.27% | 21.74% | |
| RACS | 71.84% | 22.31% | 20.26% | 21.74% | |
| EFPA-G | 71.43% | 22.14% | 19.52% | 20.98% | |
| O-shaped network | DV-Hop | 156.64% | 42.18% | 31.21% | 29.71% |
| FPA | 48.12% | 38.45% | 24.98% | 23.16% | |
| CMFPA | 48.12% | 38.22% | 25.01% | 23.16% | |
| MPSO | 47.97% | 39.05% | 25.01% | 23.17% | |
| MPA | 48.12% | 38.23% | 25.03% | 23.15% | |
| RACS | 48.12% | 38.12% | 25.02% | 23.16% | |
| EFPA-G | 46.53% | 37.17% | 24.55% | 22.33% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Yuan, T.; Xie, W.; Yang, Z.; Yu, D. An Enhanced Flower Pollination Algorithm with Gaussian Perturbation for Node Location of a WSN. Sensors 2023, 23, 6463. https://doi.org/10.3390/s23146463
Zheng J, Yuan T, Xie W, Yang Z, Yu D. An Enhanced Flower Pollination Algorithm with Gaussian Perturbation for Node Location of a WSN. Sensors. 2023; 23(14):6463. https://doi.org/10.3390/s23146463
Chicago/Turabian StyleZheng, Jun, Ting Yuan, Wenwu Xie, Zhihe Yang, and Dan Yu. 2023. "An Enhanced Flower Pollination Algorithm with Gaussian Perturbation for Node Location of a WSN" Sensors 23, no. 14: 6463. https://doi.org/10.3390/s23146463
APA StyleZheng, J., Yuan, T., Xie, W., Yang, Z., & Yu, D. (2023). An Enhanced Flower Pollination Algorithm with Gaussian Perturbation for Node Location of a WSN. Sensors, 23(14), 6463. https://doi.org/10.3390/s23146463





