Numerical Analysis of GNSS Signal Outage Effect on EOPs Solutions Using Tightly Coupled GNSS/IMU Integration: A Simulated Case Study in Sweden
Abstract
1. Introduction
2. Materials and Methods
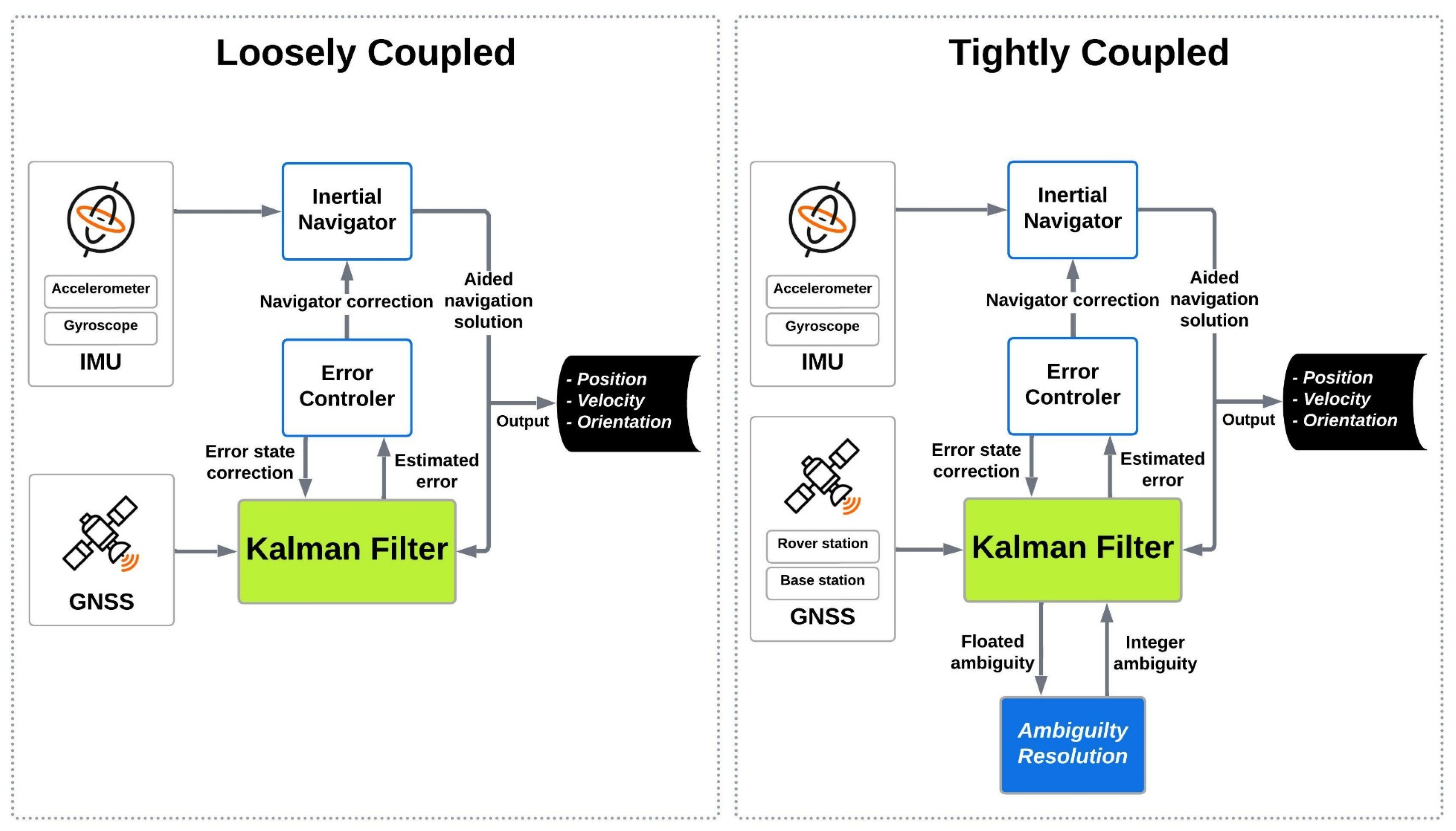
2.1. Loosely and Tightly Coupled Integration
2.2. Single and Network-Based PPK Solution
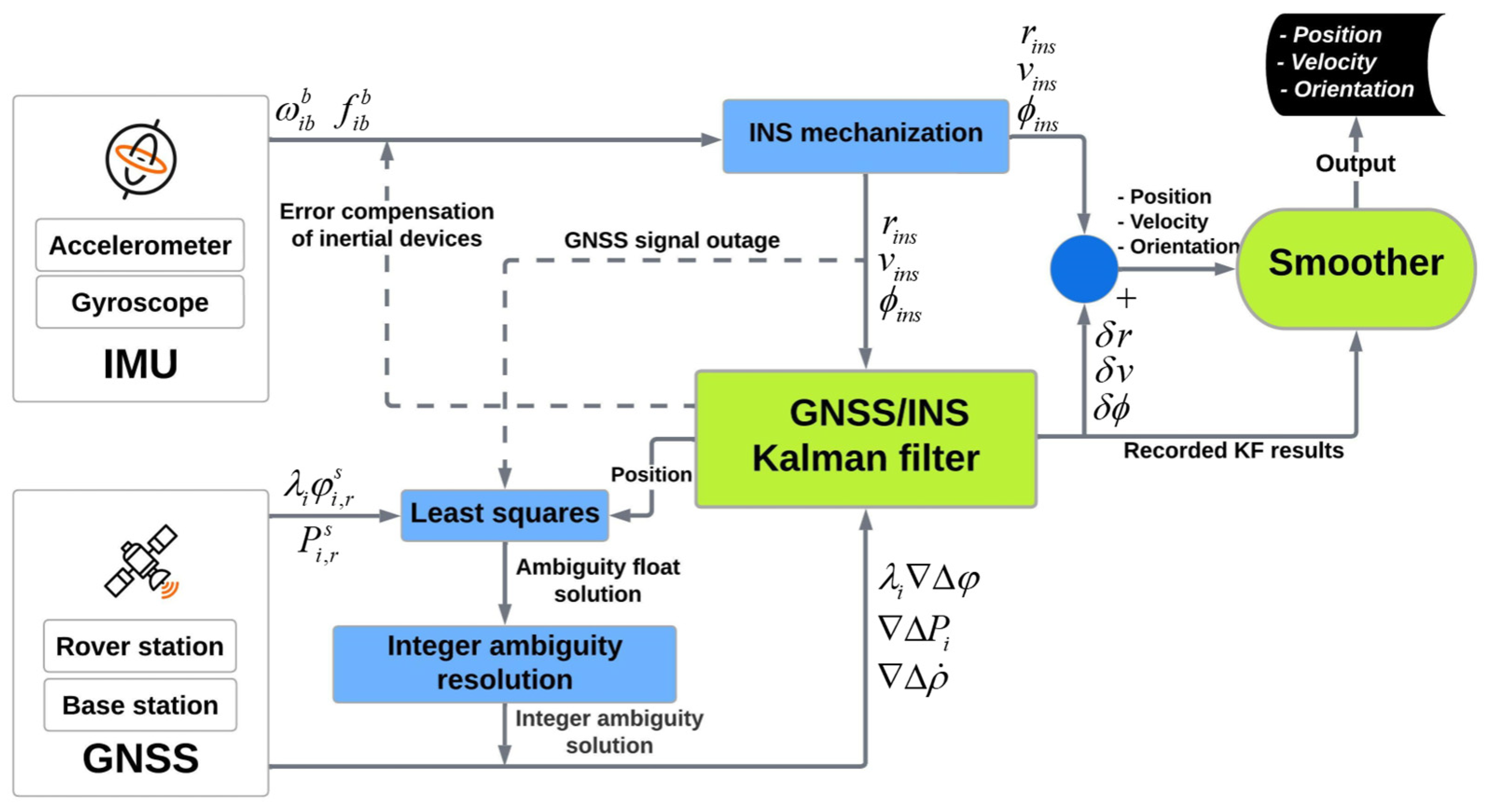
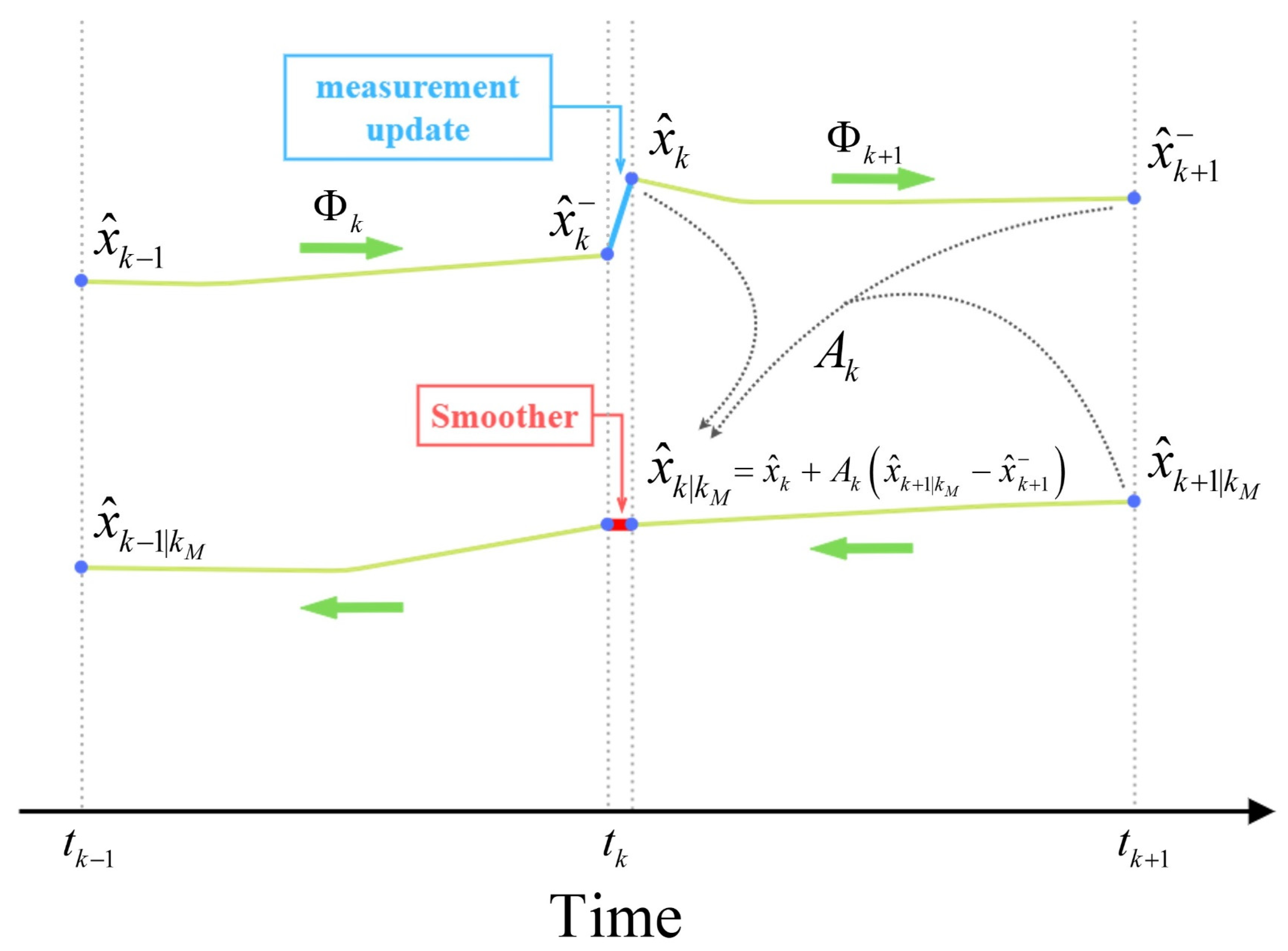
2.3. GNSS/IMU Processing Using KF and Smoothing Method
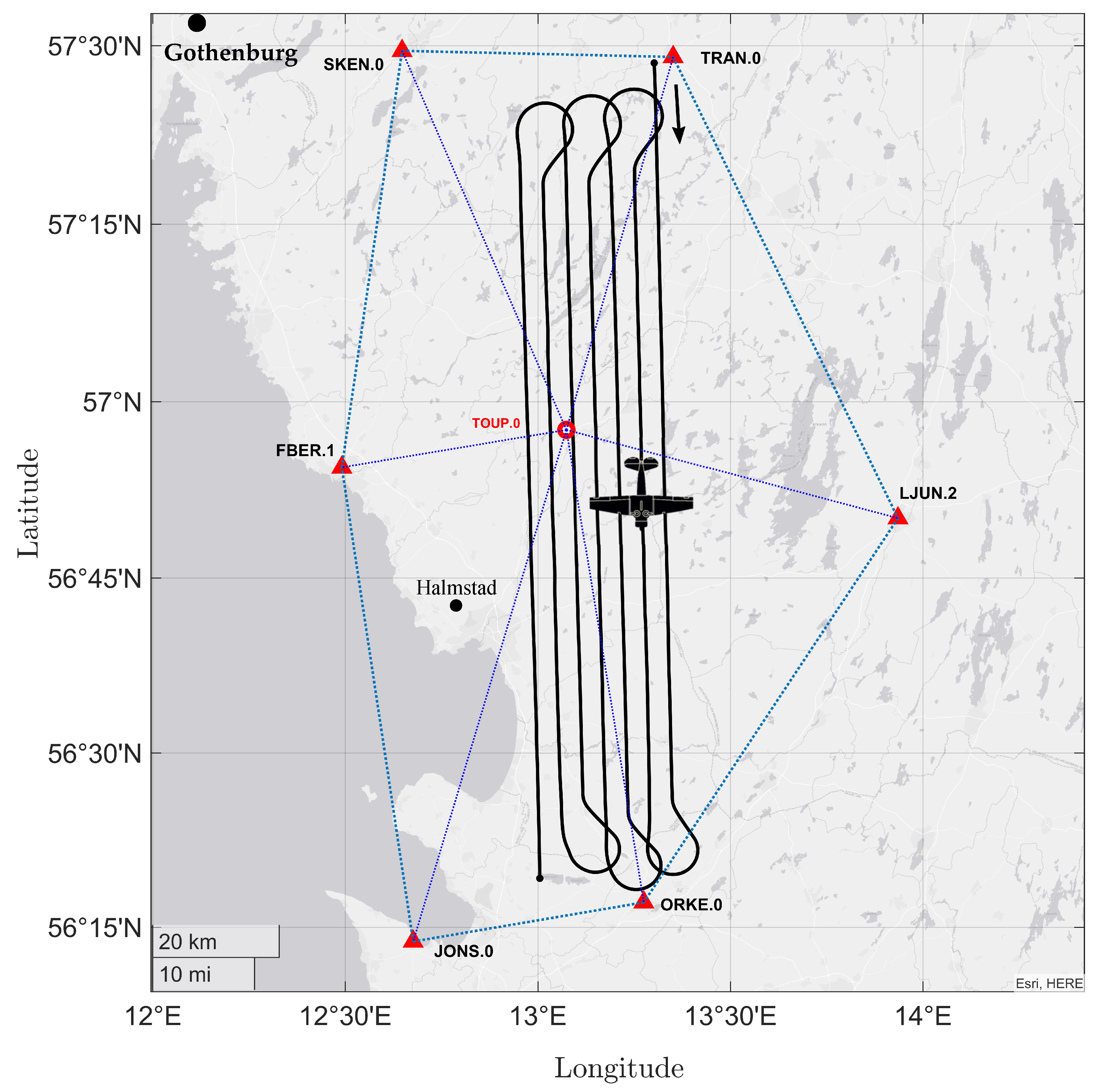
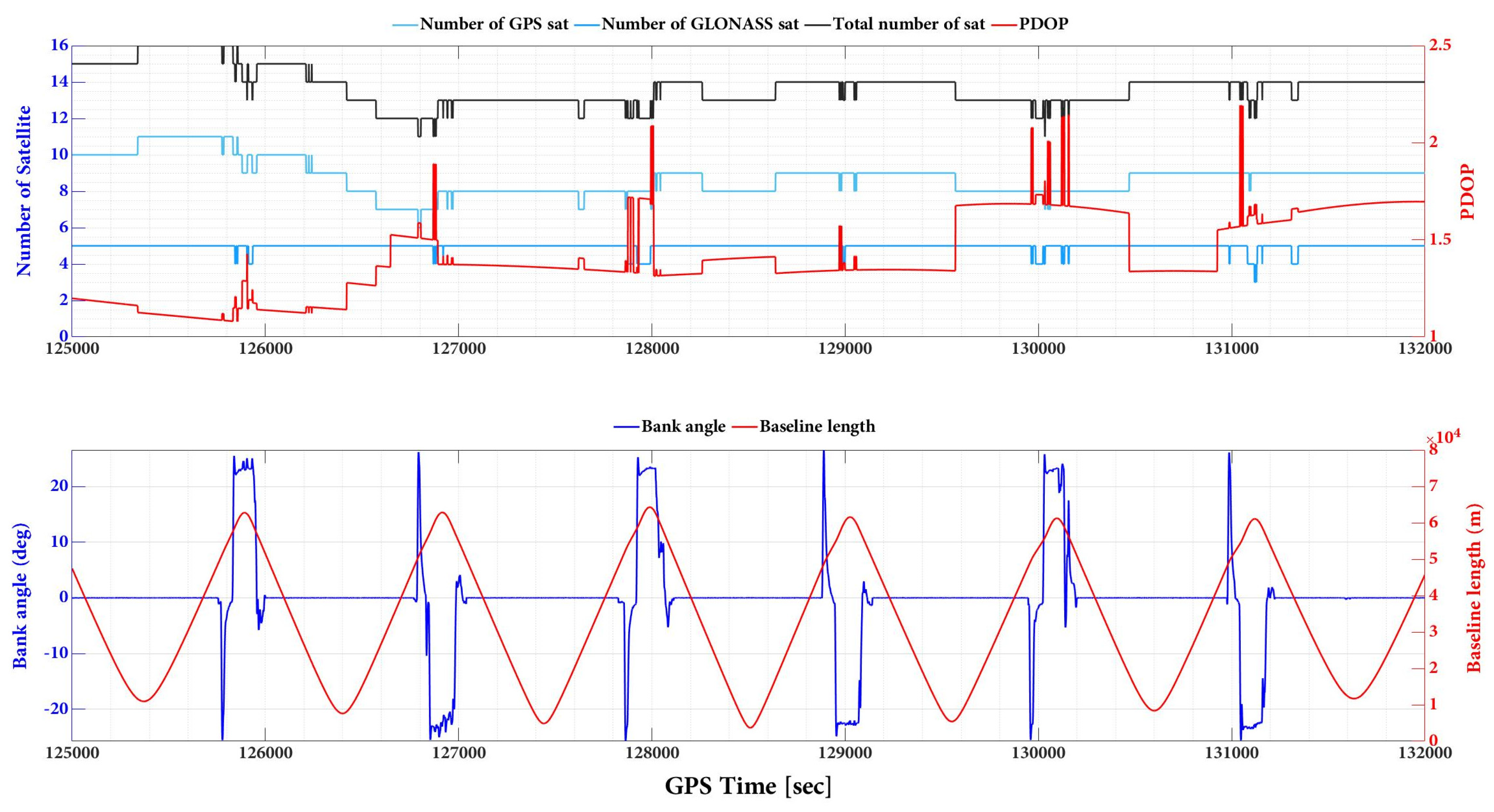
2.4. Data and Analysis
3. Results and Discussion
3.1. Comparison of Single and Network-Based PPK Solutions
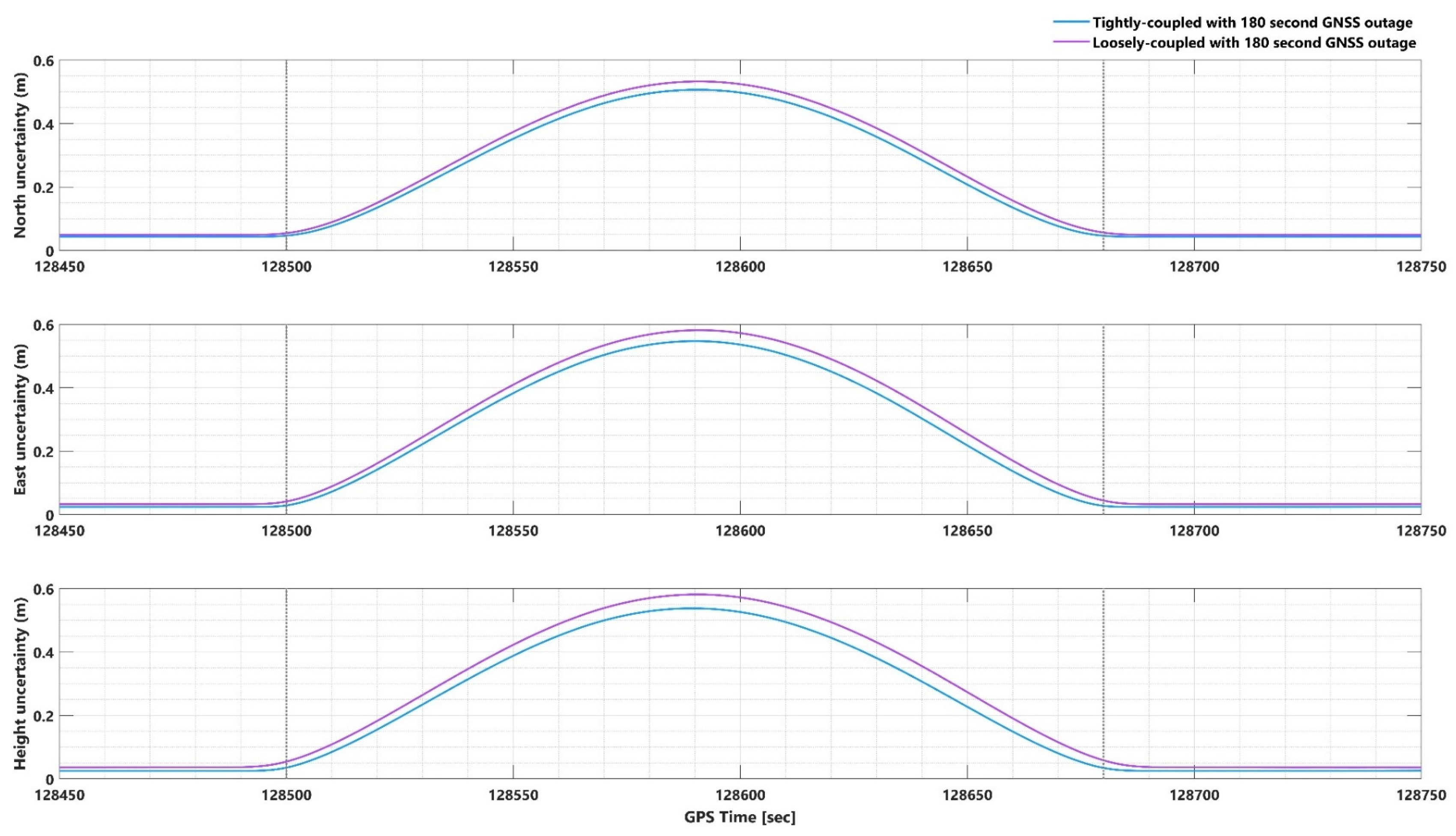
3.2. Impact of GNSS Signal Outage on EOPs
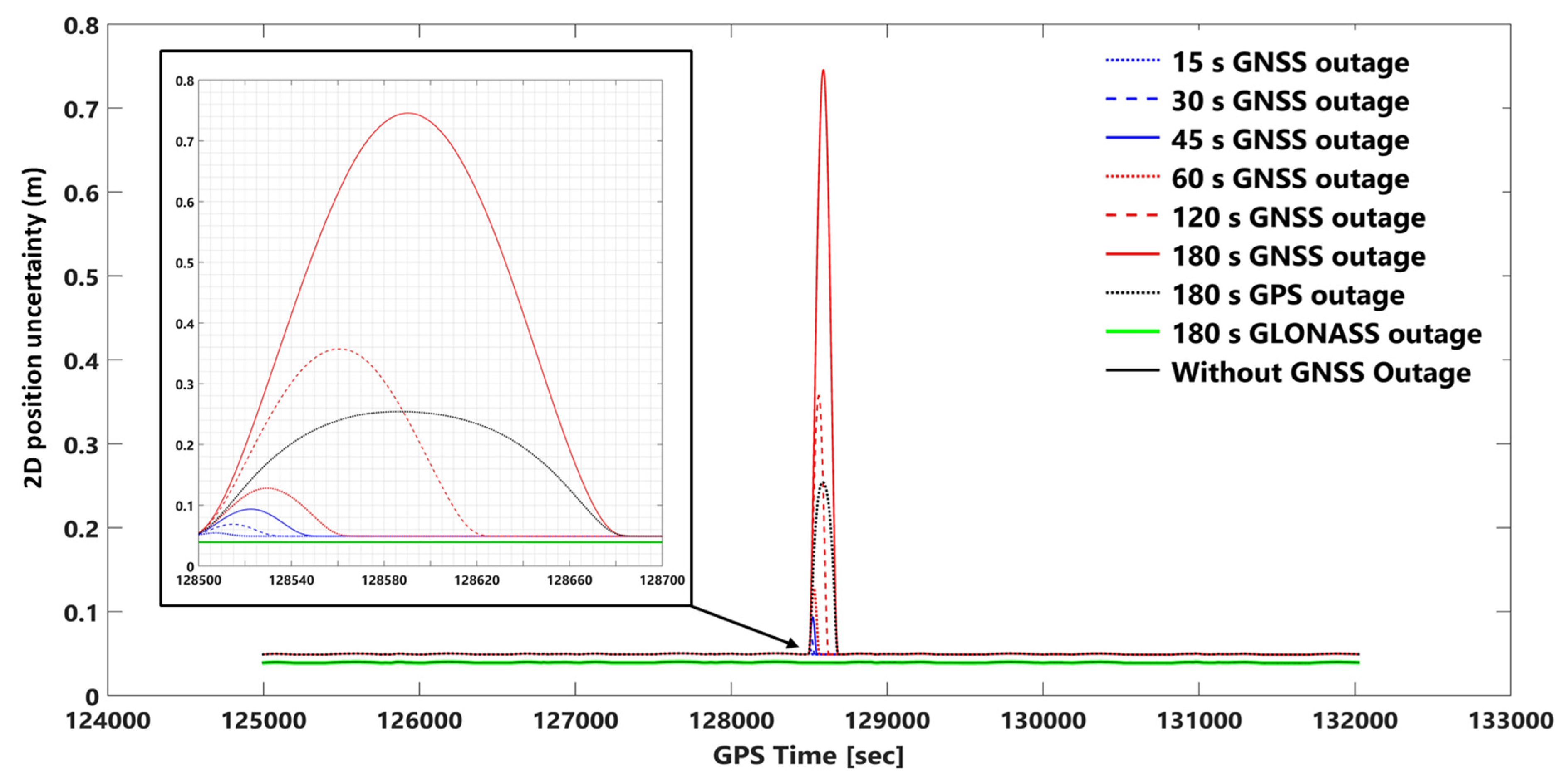
3.2.1. Smooth and Forward KF Processing Comparison Using 2D Position and Height Uncertainties
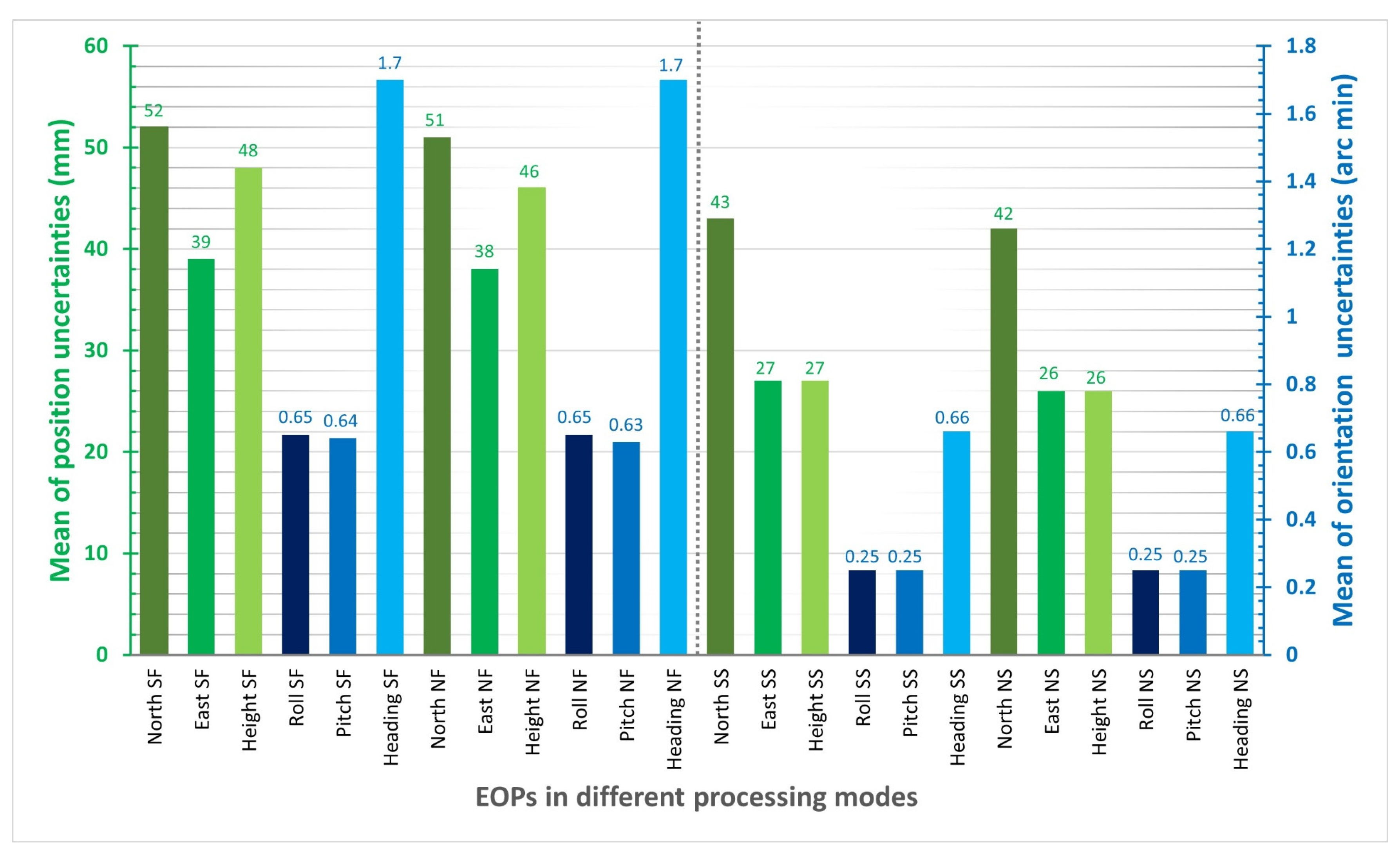
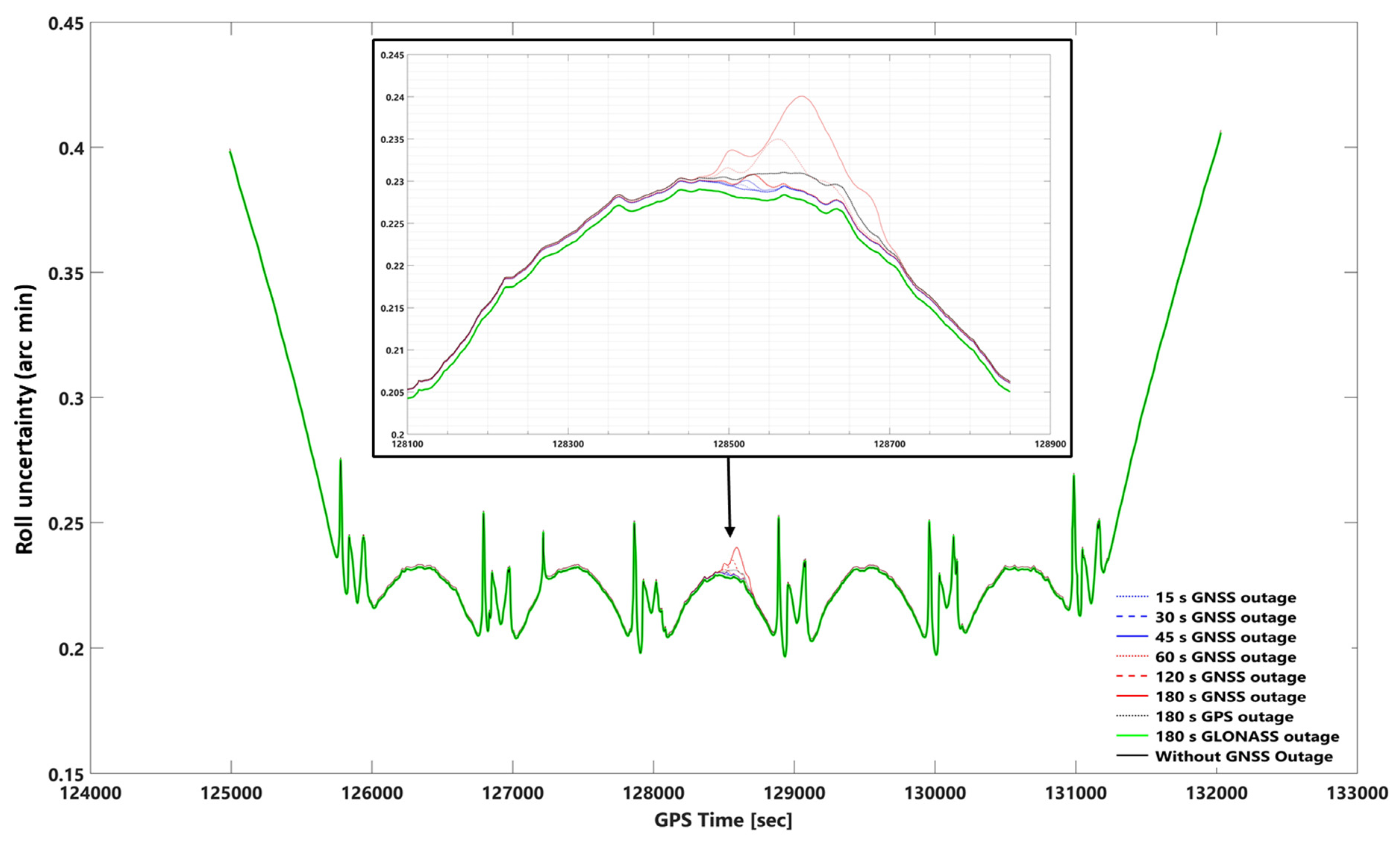
3.2.2. Smooth and Forward KF Processing Comparison Using Orientation Uncertainties
3.3. Kalman Filter
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morton, Y.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Leick, A. GPS Satellite Surveying; John Wiley & Sons: Hoboken, NJ, USA, 1990; Available online: https://trid.trb.org/view/368731 (accessed on 22 October 2021).
- Li, B.; Verhagen, S.; Teunissen, P.J.G. Robustness of GNSS integer ambiguity resolution in the presence of atmospheric biases. GPS Solut. 2014, 18, 283–296. [Google Scholar] [CrossRef]
- Takasu, T.; Yasuda, A. Evaluation of RTK-GPS performance with low-cost single-frequency GPS receivers. In Proceedings of the International Symposium on GPS/GNSS 2008, Tokyo, Japan, 11–14 November 2008; pp. 852–861. Available online: http://www.gnss-pnt.org/symposium2008/abstract/oral/B12a/7-727-a.pdf (accessed on 25 October 2021).
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined GPS + BDS for short to long baseline RTK positioning. Meas. Sci. Technol. 2015, 26, 045801. [Google Scholar] [CrossRef]
- Joosten, P.; Irsigler, M. GNSS ambiguity resolution in the presence of multipath. In Proceedings of the ION GPS/GNSS 2003, Portland, OR, USA, 9–12 September 2003. [Google Scholar]
- Feng, W.; Zhao, Y.; Zhou, L.; Huang, D.; Hassan, A. Fast cycle slip determination for high-rate multi-GNSS RTK using modified geometry-free phase combination. GPS Solut. 2020, 24, 42. [Google Scholar] [CrossRef]
- Skone, S.H. The impact of magnetic storms on GPS receiver performance. J. Geod. 2001, 75, 457–468. [Google Scholar] [CrossRef]
- Jouybari, A.; Amiri, H.; Ardalan, A.A.; Zahraee, N.K. Methods comparison for attitude determination of a lightweight buoy by raw data of IMU. Meas. J. Int. Meas. Confed. 2019, 135, 348–354. [Google Scholar] [CrossRef]
- Jouybari, A.; Ardalan, A.A.; Rezvani, M.H. Experimental comparison between Mahoney and Complementary sensor fusion algorithm for attitude determination by raw sensor data of Xsens IMU on buoy. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2017, 42, 497–502. [Google Scholar] [CrossRef]
- Nassar, S.; Noureldin, A.; El-Sheimy, N. Improving positioning accuracy during kinematic DGPS outage periods using SINS/DGPS integration and SINS data de-noising. Surv. Rev 2004, 37, 426–438. [Google Scholar] [CrossRef]
- Liu, H.; Nassar, S.; El-sheimy, N. Performance Evaluation of Different Optimal Smoothers for Land-Vehicle Navigation Using Integrated GPS/INS Systems. 2009. Available online: https://www.researchgate.net/publication/280721038_Performance_Evaluation_of_Different_Optimal_Smoothers_for_Land-Vehicle_Navigation_Using_Integrated_GPSINS_Systems (accessed on 10 November 2021).
- Liu, H.; Nassar, S.; El-Sheimy, N. Two-filter smoothing for accurate INS/GPS land-vehicle navigation in urban centers. IEEE Trans. Veh. Technol. 2010, 59, 4256–4267. [Google Scholar] [CrossRef]
- Dougherty, E.R. Random Processes for Image and Signal Processing; SPIE Optical Engineering Press: Bellingham, WA, USA, 2009. [Google Scholar] [CrossRef]
- Vaclavovic, P.; Dousa, J. Backward smoothing for precise GNSS applications. Adv. Sp. Res. 2015, 56, 1627–1634. [Google Scholar] [CrossRef]
- Chiang, K.-W.; Duong, T.T.; Liao, J.-K.; Lai, Y.-C.; Chang, C.-C.; Cai, J.-M.; Huang, S.-C. On-Line Smoothing for an Integrated Navigation System with Low-Cost MEMS Inertial Sensors. Sensors 2012, 12, 17372–17389. [Google Scholar] [CrossRef]
- Rauch, H.E.; Tung, F.; Striebel, C.T. Maximum likelihood estimates of linear dynamic systems. AIAA J. 1965, 3, 1445–1450. [Google Scholar] [CrossRef]
- Bryson, A.E.; Frazier, M. Smoothing for linear and nonlinear dynamic systems. In Proceedings of the Optimum System Synthesis Conference, Los Angeles, CA, USA, 17–20 June 1963; pp. 353–364. [Google Scholar]
- Zhang, Y.; Li, X.R. Fixed-interval smoothing algorithm based on singular value decomposition. In Proceedings of the 1996 IEEE International Conference on Control Applications, Dearborn, MI, USA, 15–18 September 1996; pp. 916–921. [Google Scholar] [CrossRef]
- Park, P.G.; Kailath, T. New square-root smoothing algorithms. IEEE Trans. Automat. Control 1996, 41, 727–732. [Google Scholar] [CrossRef]
- Desai, U.B.; Weinert, H.L.; Yusypchuk, G.J. Discrete-time complementary models and smoothing algorithms: The correlated noise case. Proc. IEEE Conf. Decis. Control. 1981, 3, 1048–1053. [Google Scholar] [CrossRef]
- Mayne, D.Q. A solution of the smoothing problem for linear dynamic systems. Automatica 1966, 4, 73–92. [Google Scholar] [CrossRef]
- Cao, Y.; Mao, X. Improved filtering-smoothing algorithm for GPS positioning. In Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems (ITSC 2008), Beijing, China, 12–15 October 2008; pp. 857–861. [Google Scholar] [CrossRef]
- Chiang, K.-W.; Chang, H.-W.; Li, C.-Y.; Huang, Y.-W. An Artificial Neural Network Embedded Position and Orientation Determination Algorithm for Low Cost MEMS INS/GPS Integrated Sensors. Sensors 2009, 9, 2586–2610. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Zhu, F. A method of improving ambiguity fixing rate for post-processing kinematic GNSS data. Satell. Navig 2020, 1, 20. [Google Scholar] [CrossRef]
- Al Bitar, N.; Gavrilov, A. A new method for compensating the errors of integrated navigation systems using artificial neural networks. Meas. J. Int. Meas. Confed. 2020, 168, 108391. [Google Scholar] [CrossRef]
- Nassar, S.; El-Sheimy, N. Wavelet analysis for improving INS and INS/DGPS navigation accuracy. J. Navig. 2005, 58, 119–134. [Google Scholar] [CrossRef]
- Wen, W.; Bai, X.; Kan, Y.C.; Hsu, L.T. Tightly Coupled GNSS/INS Integration via Factor Graph and Aided by Fish-Eye Camera. IEEE Trans. Veh. Technol 2019, 68, 10651–10662. [Google Scholar] [CrossRef]
- Zhang, G.; Wen, W.; Xu, B.; Hsu, L.T. Extending Shadow Matching to Tightly-Coupled GNSS/INS Integration System. IEEE Trans. Veh. Technol. 2020, 69, 4979–4991. [Google Scholar] [CrossRef]
- Titterton, D.; Weston, J. Strapdown Inertial Navigation Technology, 2nd ed.; Book review; IEEE Press: Piscataway, NJ, USA, 2005; Volume 20. [Google Scholar] [CrossRef]
- Elbahnasawy, M.; Shamseldin, T.; Habib, A. Image-assisted GNSS/INS navigation for UAV-based mobile mapping systems during GNSS outages. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 417–425. [Google Scholar] [CrossRef]
- Hutton, J.; Ip, A.; Bourke, T.; Scherzinger, B.; Gopaul, N.; Canter, P. Tight Integration of GNSS Post-processed Virtual Reference Station with Inertial Data for Increased Accuracy and Productivity of Airborne Mapping. XXIst ISPRS Congr. Technol. Comm. V 2008, 37, 829–834. [Google Scholar]
- Shi, B.; Wang, M.; Wang, Y.; Bai, Y.; Lin, K.; Yang, F. Effect analysis of GNSS/INS processing strategy for sufficient utilization of urban environment observations. Sensors 2021, 21, 620. [Google Scholar] [CrossRef]
- Hol, J.D.; Dijkstra, F.; Luinge, H.; Schöny, T.B. Tightly coupled UWB/IMU pose estimation. In Proceedings of the 2009 IEEE International Conference on Ultra-Wideband, Vancouver, BC, Canada, 9–11 September 2009; pp. 688–692. [Google Scholar] [CrossRef]
- Taddia, Y.; Stecchi, F.; Pellegrinelli, A. Coastal mapping using dji phantom 4 RTK in post-processing kinematic mode. Drones 2020, 4, 9. [Google Scholar] [CrossRef]
- Hutton, J.; Bourke, T.; Scherzinger, B.; Hill, R. New developments of inertial navigation systems at Applanix. Photogramm. Week 2007, 7, 201–213. [Google Scholar]
- MacIntosh, D. Surveying Practices in the Drone Age: An Accuracy and Slope Assessment of UAV-Derived Elevation Products; California State University: Sacramento, CA, USA, 2019; pp. 1–126. [Google Scholar]
- Stöcker, C.; Nex, F.; Koeva, M.; Gerke, M. Quality assessment of combined IMU/GNSS data for direct georeferencing in the context of UAV-based mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2017, 42, 355–361. [Google Scholar] [CrossRef]
- Ocalan, T. Accuracy assessment of GPS precise point Positioning (PPP) technique using different web-based online services in a forest environment. Sumar. List 2016, 140, 357–368. [Google Scholar] [CrossRef]
- Zhang, H.; Aldana-Jague, E.; Clapuyt, F.; Wilken, F.; Vanacker, V.; Van Oost, K. Evaluating the potential of post-processing kinematic (PPK) georeferencing for UAV-based structure-from-motion (SfM) photogrammetry and surface change detection. Earth Surf. Dyn 2019, 7, 807–827. [Google Scholar] [CrossRef]
- Eker, R.; Alkan, E.; Aydın, A. A Comparative Analysis of UAV-RTK and UAV-PPK Methods in Mapping Different Surface Types. Eur. J. For. Eng. 2021, 7, 12–25. [Google Scholar] [CrossRef]
- El-Diasty, M. Evaluation of KSACORS-based network GNSS-INS integrated system for Saudi coastal hydrographic surveys. Geomat. Nat. Hazards Risk 2020, 11, 1426–1446. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of ionosphere-constrained precise point positioning and inertial navigation systems. Sensors 2015, 15, 5783–5802. [Google Scholar] [CrossRef]
- Bruton, A.M.; Mostafa, M.M.R.; Scherzinger, B. Airborne DGPS without dedicated base stations for mapping applications. In Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, UT, USA, 11–14 September 2001; Volume 8. [Google Scholar]
- Wanninger, L. Virtual reference stations (VRS). GPS Solut. 2003, 7, 143–144. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.-R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Niu, X.; Zhang, Q.; Gong, L.; Liu, C.; Zhang, H.; Shi, C.; Wang, J.; Coleman, M. Development and evaluation of gnss/ins data processing software for position and orientation systems. Surv. Rev. 2015, 47, 87–98. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, F.; Tao, X.; Duan, R. New optimal smoothing scheme for improving relative and absolute accuracy of tightly coupled GNSS/SINS integration. GPS Solut. 2017, 21, 861–872. [Google Scholar] [CrossRef]
- Zhang, Q.; Niu, X.; Shi, C. Assessment of the effect of GNSS sampling rate on GNSS/INS relative accuracy on different time scales for precision measurements. Meas. J. Int. Meas. Confed. 2019, 145, 583–593. [Google Scholar] [CrossRef]
- Mönikes, R.; Teltschik, A.; Wendel, J.; Trommer, G.F. Post-processing GNSS/INS measurements using a tightly coupled fixed-interval smoother performing carrier phase ambiguity resolution. In Proceedings of the IEEE/ION PLANS 2006, San Diego, CA, USA, 25–27 April 2006; pp. 283–290. [Google Scholar] [CrossRef]
- Brown, R.G.; Hwang, P.Y.C. Introduction to random signals and applied Kalman filtering: With MATLAB exercises and solutions. In Introduction to Random Signals and Applied Kalman Filtering: With MATLAB Exercises and Solutions; Wiley: New York, NY, USA, 1997; Available online: https://ui.adsabs.harvard.edu/abs/1997itrs.book.....B/abstract (accessed on 9 February 2023).
- Shin, E.-H. Estimation Techniques for Low-Cost Inertial Navigation. Ph.D. Thesis, The University of Galgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Applanix, Datasheet Pos Av 510 Immediate Answers from Airborne Direct Georeferencing. Available online: https://www.applanix.com/downloads/products/specs/pos_av_510.pdf (accessed on 1 March 2023).
- Elamin, A.; Abdelaziz, N.; El-Rabbany, A. A GNSS/INS/LiDAR Integration Scheme for UAV-Based Navigation in GNSS-Challenging Environments. Sensors 2022, 22, 9908. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Traugott, J.; Scherzinger, B.; Miranda, C.; Kipka, A. A New Integration method for MEMS based GNSS/INS Multi-sensor systems. In Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015; Volume 1, pp. 209–218. [Google Scholar]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter. 2006, pp. 1–16. Available online: https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf (accessed on 1 March 2023).






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jouybari, A.; Bagherbandi, M.; Nilfouroushan, F. Numerical Analysis of GNSS Signal Outage Effect on EOPs Solutions Using Tightly Coupled GNSS/IMU Integration: A Simulated Case Study in Sweden. Sensors 2023, 23, 6361. https://doi.org/10.3390/s23146361
Jouybari A, Bagherbandi M, Nilfouroushan F. Numerical Analysis of GNSS Signal Outage Effect on EOPs Solutions Using Tightly Coupled GNSS/IMU Integration: A Simulated Case Study in Sweden. Sensors. 2023; 23(14):6361. https://doi.org/10.3390/s23146361
Chicago/Turabian StyleJouybari, Arash, Mohammad Bagherbandi, and Faramarz Nilfouroushan. 2023. "Numerical Analysis of GNSS Signal Outage Effect on EOPs Solutions Using Tightly Coupled GNSS/IMU Integration: A Simulated Case Study in Sweden" Sensors 23, no. 14: 6361. https://doi.org/10.3390/s23146361
APA StyleJouybari, A., Bagherbandi, M., & Nilfouroushan, F. (2023). Numerical Analysis of GNSS Signal Outage Effect on EOPs Solutions Using Tightly Coupled GNSS/IMU Integration: A Simulated Case Study in Sweden. Sensors, 23(14), 6361. https://doi.org/10.3390/s23146361








