Nonlinear Ultrasonic Imaging for Porosity Evaluation
Abstract
1. Introduction
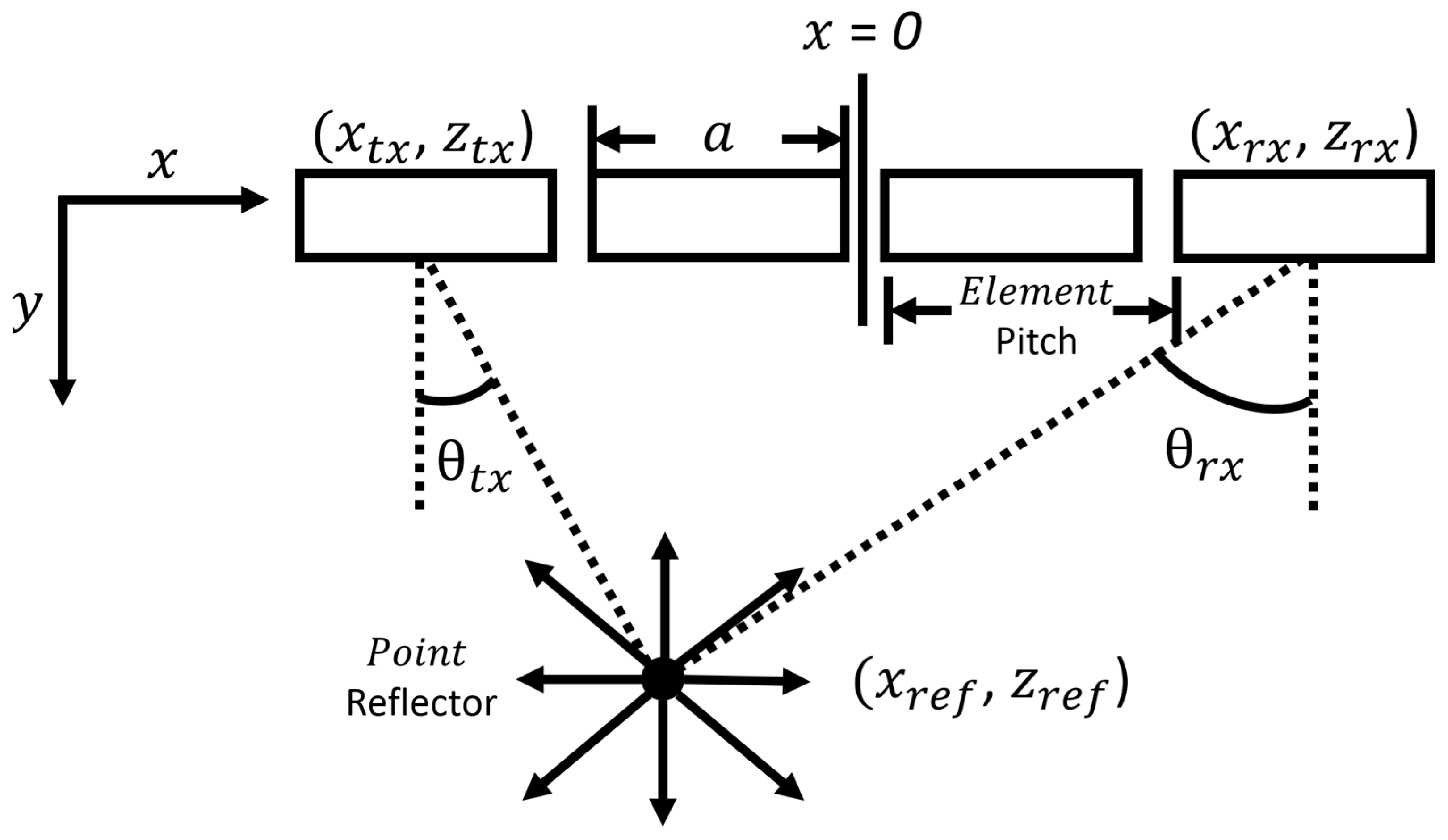
2. Nonlinear Ultrasound Approach
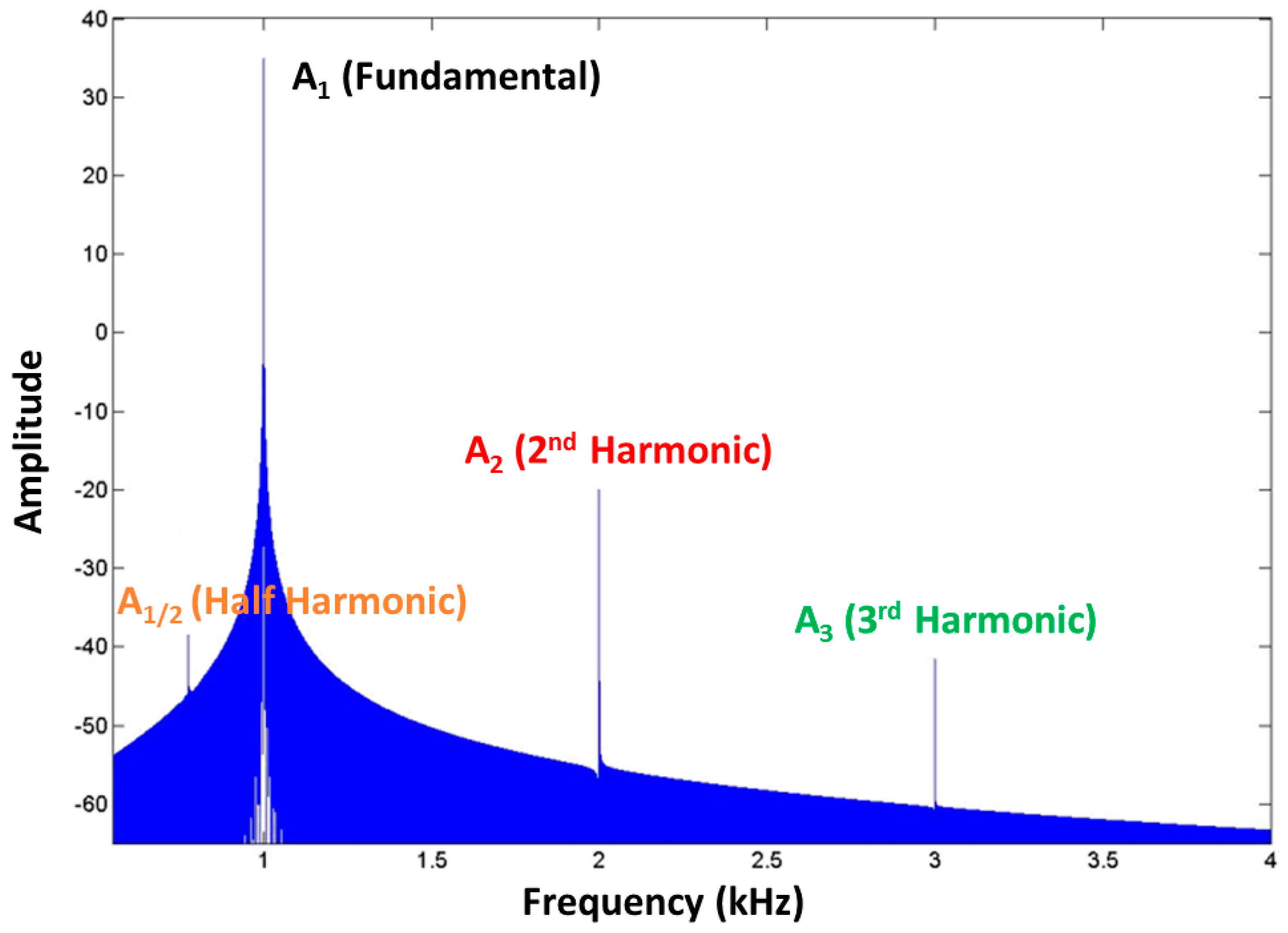
2.1. Subharmonic Method
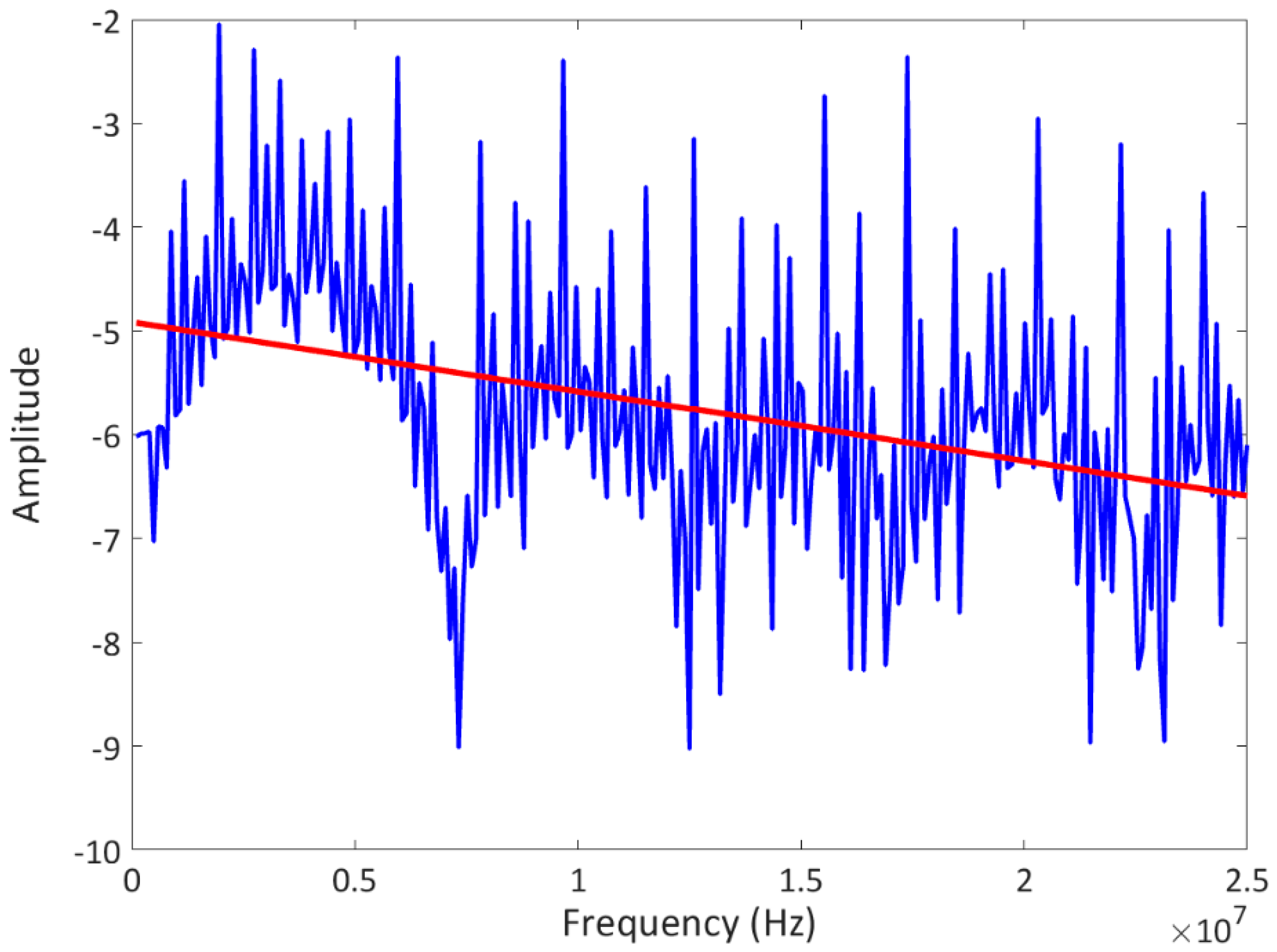
2.2. Attenuation Coefficient Method
3. Experimental Setup
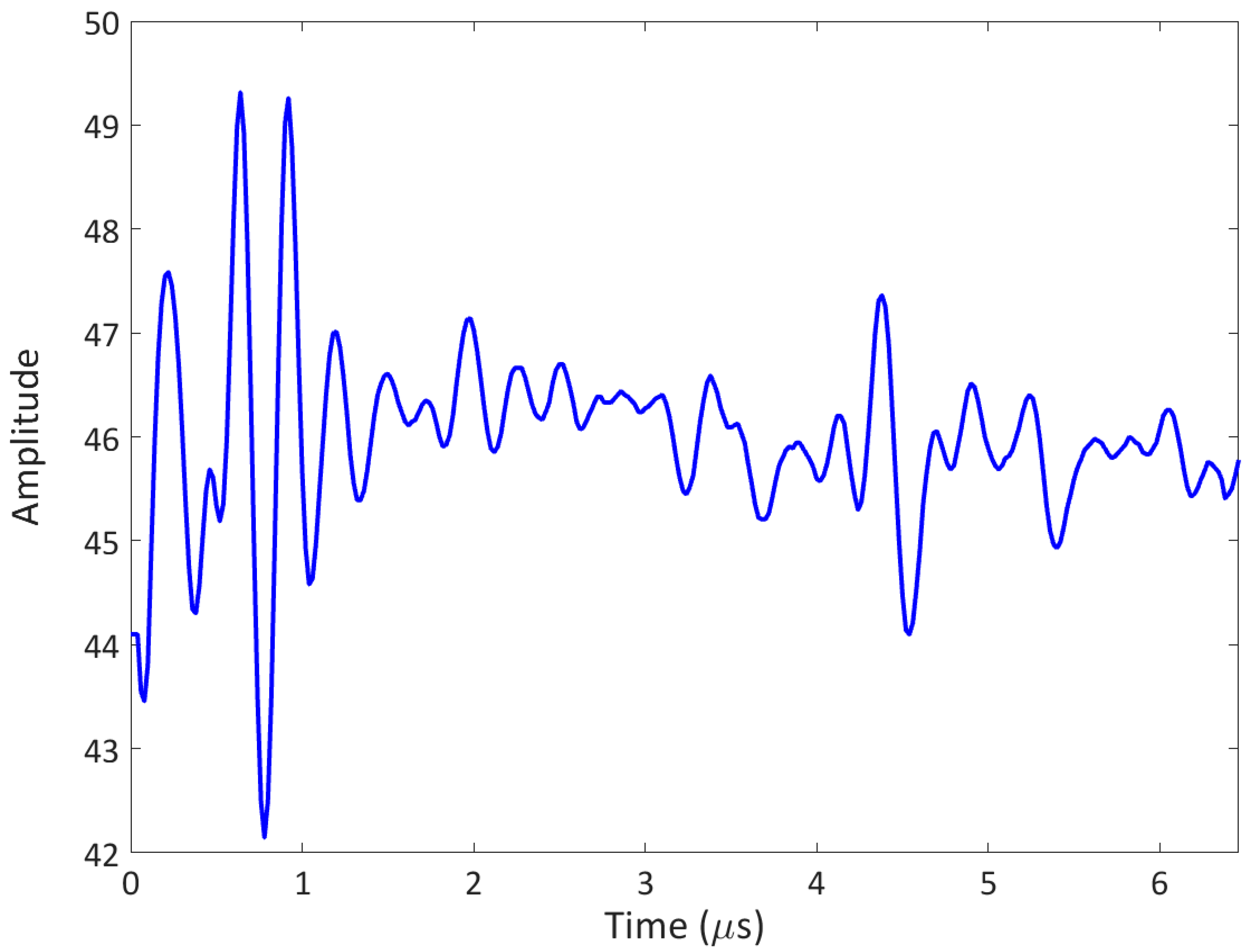
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rubin, A.M.; Jerina, K.L. Evaluation of porosity in composite aircraft structures. Mech. Compos. Mater. 1994, 30, 587–600. [Google Scholar] [CrossRef]
- Stone, D.; Clarke, B. Ultrasonic attenuation as a measure of void content in carbon-fibre reinforced plastics. Non Destr. Test. 1975, 8, 137–145. [Google Scholar] [CrossRef]
- Bowles, K.J.; Frimpong, S. Void Effects on the Interlaminar Shear Strength of Unidirectional Graphite-Fiber-Reinforced Composites. J. Compos. Mater. 1992, 26, 1487–1509. [Google Scholar] [CrossRef]
- Müller de Almeida, S.F.; de Mas Santacreu, A.C. Environmental effects in composite laminates with voids. Polym. Polym. Compos. 1995, 3, 193–204. [Google Scholar]
- Jeong, H. Effects of Voids on the Mechanical Strength and Ultrasonic Attenuation of Laminated Composites. J. Compos. Mater. 1997, 31, 276–292. [Google Scholar] [CrossRef]
- Suarez, J.C.; Molleda, F.; Guemes, A. Void content in carbon fibre/epoxy resin composites and its effects on compressive properties. ICCM/9 Compos. Prop. Appl. 1993, 6, 589–596. [Google Scholar]
- de Almeida, S.F.M.; Neto, Z.D.S.N. Effect of void content on the strength of composite laminates. Compos. Struct. 1994, 28, 139–148. [Google Scholar] [CrossRef]
- Costa, M.L.; Almeida, S.F.M.; Rezende, M.C. The influence of porosity on the interlaminar shear strength of carbon/epoxy and carbon/bismaleimide fabric laminates. Compos. Sci. Technol. 2001, 61, 2101–2108. [Google Scholar] [CrossRef]
- Fernlund, G.; Wells, J.; Fahrang, L.; Kay, J.; Poursartip, A. Causes and remedies for porosity in composite manufacturing. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 139, p. 012002. [Google Scholar]
- Martin, B.G. Ultrasonic wave propagation in fiber-reinforced solids containing voids. J. Appl. Phys. 1977, 48, 3368–3373. [Google Scholar] [CrossRef]
- Reynolds, W.N.; Wilkinson, S.J. The analysis of fibre-reinforced porous composite materials by the measurement of ultrasonic wave velocities. Ultrasonics 1978, 16, 159–163. [Google Scholar] [CrossRef]
- Hsu, D.K. Ultrasonic Measurements of Porosity in Woven Graphite Polyimide Composites. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1988; pp. 1063–1068. [Google Scholar]
- Nair, S.M.; Hsu, D.K.; Rose, J.H. Porosity estimation using the frequency dependence of the ultrasonic attenuation. J. Nondestruct. Eval. 1989, 8, 13–26. [Google Scholar] [CrossRef]
- Bhat, M.R.; Binoy, M.P.; Surya, N.M.; Murthy, C.R.L.; Engelbart, R.W. Non-destructive evaluation of porosity and its effect on mechanical properties of carbon fiber reinforced polymer composite materials. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2012; Volume 1430, pp. 1080–1087. [Google Scholar]
- Karabutov, A.A.; Podymova, N.B. Quantitative analysis of the influence of voids and delaminations on acoustic attenuation in CFRP composites by the laser-ultrasonic spectroscopy method. Compos. Part B Eng. 2014, 56, 238–244. [Google Scholar] [CrossRef]
- Pelivanov, I.; O’donnell, M. Imaging of porosity in fiber-reinforced composites with a fiber-optic pump–probe laser-ultrasound system. Compos. Part A Appl. Sci. Manuf. 2015, 79, 43–51. [Google Scholar] [CrossRef]
- Ishii, Y.; Biwa, S.; Kuraishi, A. Influence of porosity on ultrasonic wave velocity, attenuation and interlaminar interface echoes in composite laminates: Finite element simulations and measurements. Compos. Struct. 2016, 152, 645–653. [Google Scholar] [CrossRef]
- Stamopoulos, A.G.; Tserpes, K.I.; Prucha, P.; Vavrik, D. Evaluation of porosity effects on the mechanical properties of carbon fiber-reinforced plastic unidirectional laminates by X-ray computed tomography and mechanical testing. J. Compos. Mater. 2016, 50, 2087–2098. [Google Scholar] [CrossRef]
- Mayr, G.; Gresslehner, K.H.; Hendorfer, G. Non-destructive testing procedure for porosity determination in carbon fibre reinforced plastics using pulsed thermography. Quant. Infrared Thermogr. J. 2017, 14, 263–274. [Google Scholar] [CrossRef]
- ASTM D. 3171-2006; Standard Test Method for Constituent Content of Composite Materials. ASTM: West Conshohocken, PA, USA, 2006.
- Plessix, B.D.P.D.; Lefébure, P.; Boyard, N.; Le Corre, S.; Lefèvre, N.; Jacquemin, F.; Sobotka, V.; Du Roscoat, S.R. In situ real-time 3D observation of porosity growth during composite part curing by ultra-fast synchrotron X-ray microtomography. J. Compos. Mater. 2019, 53, 4105–4116. [Google Scholar] [CrossRef]
- Oromiehie, E.; Garbe, U.; Prusty, B.G. Porosity analysis of carbon fibre-reinforced polymer laminates manufactured using automated fibre placement. J. Compos. Mater. 2020, 54, 1217–1231. [Google Scholar] [CrossRef]
- Podymova, N.B.; Kalashnikov, I.E.; Bolotova, L.K.; Kobeleva, L.I. Laser-ultrasonic nondestructive evaluation of porosity in particulate reinforced metal-matrix composites. Ultrasonics 2019, 99, 105959. [Google Scholar] [CrossRef]
- Song, P.; Liu, J.; Liu, L.; Wang, F.; Sun, X.; Liu, Z.; Xu, L. Contactless inspection of CFRP artificial disbonds using combined laser thermography and laser ultrasonics with optical microphone. Compos. Struct. 2022, 297, 115971. [Google Scholar] [CrossRef]
- Pelivanov, I.; Ambroziński, Ł.; Khomenko, A.; Koricho, E.G.; Cloud, G.L.; Haq, M.; O’Donnell, M. High resolution imaging of impacted CFRP composites with a fiber-optic laser-ultrasound scanner. Photoacoustics 2016, 4, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Ashwell, D.G.; Chauhan, A.P. A study of ½-subharmonic oscillations by the method of harmonic balance. J. Sound Vib. 1973, 27, 313–324. [Google Scholar] [CrossRef]
- Lauterborn, W. Numerical investigation of nonlinear oscillations of gas bubbles in liquids. J. Acoust. Soc. Am. 1976, 59, 283–293. [Google Scholar] [CrossRef]
- Leighton, T.G.; Lingard, R.J.; Walton, A.J.; Field, J.E. Acoustic bubble sizing by combination of subharmonic emissions with imaging frequency. Ultrasonics 1991, 29, 319–323. [Google Scholar] [CrossRef]
- Sojahrood, A.J.; Earl, R.; Haghi, H.; Li, Q.; Porter, T.M.; Kolios, M.C.; Karshafian, R. Nonlinear dynamics of acoustic bubbles excited by their pressure-dependent subharmonic resonance frequency: Influence of the pressure amplitude, frequency, encapsulation and multiple bubble interactions on oversaturation and enhancement of the subharmonic signal. Nonlinear Dyn. 2021, 103, 429–466. [Google Scholar]
- Dutta, D.; Sohn, H.; Harries, K.A.; Rizzo, P. A nonlinear acoustic technique for crack detection in metallic structures. Struct. Health Monit. 2009, 8, 251–262. [Google Scholar] [CrossRef]
- Fierro, G.M.; Ciampa, F.; Ginzburg, D.; Onder, E.; Meo, M. Nonlinear ultrasound modelling and validation of fatigue damage. J. Sound Vib. 2015, 343, 121–130. [Google Scholar] [CrossRef]
- Fierro, G.P.M.; Meo, M. Residual fatigue life estimation using a nonlinear ultrasound modulation method. Smart Mater. Struct. 2015, 24, 025040. [Google Scholar] [CrossRef]
- Morris, W.L.; Buck, O.; Inman, R.V. Acoustic harmonic generation due to fatigue damage in high-strength aluminum. J. Appl. Phys. 1979, 50, 6737–6741. [Google Scholar] [CrossRef]
- Donskoy, D.M.; Sutin, A.M. Vibro-Acoustic Modulation Nondestructive Evaluation Technique. J. Intell. Mater. Syst. Struct. 1998, 9, 765–771. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue 2001, 23, 487–490. [Google Scholar] [CrossRef]
- Hillis, A.J.; Neild, S.A.; Drinkwater, B.W.; Wilcox, P.D. Global crack detection using bispectral analysis. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; The Royal Society: London, UK, 2006; Volume 462, pp. 1515–1530. [Google Scholar]
- Boccardi, S.; Calla, D.; Fierro, G.-P.; Ciampa, F.; Meo, M. Nonlinear Damage Detection and Localisation Using a Time Domain Approach. Struct. Health Monit. 2015, 9804, 209–215. [Google Scholar]
- Fierro, G.P.M.; Calla’, D.; Ginzburg, D.; Ciampa, F.; Meo, M. Nonlinear ultrasonic stimulated thermography for damage assessment in isotropic fatigued structures. J. Sound Vib. 2017, 404, 102–115. [Google Scholar] [CrossRef]
- Boccardi, S.; Callá, D.; Ciampa, F.; Meo, M. Nonlinear elastic multi-path reciprocal method for damage localisation in composite materials. Ultrasonics 2018, 82, 239–245. [Google Scholar] [CrossRef] [PubMed]
- Meo, M.; Zumpano, G. Nonlinear elastic wave spectroscopy identification of impact damage on a sandwich plate. Compos. Struct. 2005, 71, 469–474. [Google Scholar] [CrossRef]
- Scalerandi, M.; Gliozzi, A.S.; Bruno, C.L.E.; Masera, D.; Bocca, P. A scaling method to enhance detection of a nonlinear elastic response. Appl. Phys. Lett. 2008, 92, 101912. [Google Scholar] [CrossRef]
- Ciampa, F.; Pickering, S.; Scarselli, G.; Meo, M. Nonlinear damage detection in composite structures using bispectral analysis. In Health Monitoring of Structural and Biological Systems; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9064, p. 906402. [Google Scholar]
- Van Den Abeele, K.A.; Johnson, P.A.; Sutin, A. Nonlinear elastic wave spectroscopy (NEWS) techniques to discern material damage, part I: Nonlinear wave modulation spectroscopy (NWMS). J. Res. Nondestruct. Eval. 2000, 12, 17–30. [Google Scholar] [CrossRef]
- Straka, L.; Yagodzinskyy, Y.; Landa, M.; Hänninen, H. Detection of structural damage of aluminum alloy 6082 using elastic wave modulation spectroscopy. NDT E Int. 2008, 41, 554–563. [Google Scholar] [CrossRef]
- Fierro, G.P.M.; Meo, M. Identification of the Location and Level of Loosening in a Multi-bolt Structure using Nonlinear Ultrasound. In Proceedings of the 11th International Workshop on Structural Health Monitoring 2017: Real-Time Material State Awareness and Data-Driven Safety Assurance, IWSHM 2017, Stanford, CA, USA, 12–14 September 2017. [Google Scholar]
- Fierro, G.P.M.; Meo, M. Nonlinear imaging (NIM) of flaws in a complex composite stiffened panel using a constructive nonlinear array (CNA) technique. Ultrasonics 2016, 74, 30–47. [Google Scholar] [CrossRef]
- Fierro, G.-P.M.; Pinto, F.; Iacono, S.D.; Martone, A.; Amendola, E.; Meo, M. Monitoring of self-healing composites: A nonlinear ultrasound approach. Smart Mater. Struct. 2017, 26, 115015. [Google Scholar] [CrossRef]
- Dionysopoulos, D.; Fierro, G.-P.M.; Meo, M.; Ciampa, F. Imaging of barely visible impact damage on a composite panel using nonlinear wave modulation thermography. NDT E Int. 2018, 95, 9–16. [Google Scholar] [CrossRef]
- Dos Santos, S.; Prevorovsky, Z. Imaging of human tooth using ultrasound based chirp-coded nonlinear time reversal acoustics. Ultrasonics 2011, 51, 667–674. [Google Scholar] [CrossRef]
- Ciampa, F.; Meo, M. Nonlinear elastic imaging using reciprocal time reversal and third order symmetry analysis. J. Acoust. Soc. Am. 2012, 131, 4316–4323. [Google Scholar] [CrossRef]
- Zumpano, G.; Meo, M. A new damage detection technique based on wave propagation for rails. Int. J. Solids Struct. 2006, 43, 1023–1046. [Google Scholar] [CrossRef]
- Amerini, F.; Barbieri, E.; Meo, M.; Polimeno, U. Detecting loosening/tightening of clamped structures using nonlinear vibration techniques. Smart Mater. Struct. 2010, 19, 085013. [Google Scholar] [CrossRef]
- Harput, S.; Arif, M.; Freear, S. Experimental investigation of the subharmonic emission from microbubbles using linear and nonlinear frequency modulated signals. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010; pp. 1724–1727. [Google Scholar]
- Cantrell, J.H. Fundamentals and Applications of Nonlinear Ultrasonic Nondestructive Evaluation. In Ultrasonic Nondestructive Evaluation; CRC Press: Boca Raton, FL, USA, 2003; pp. 377–448. [Google Scholar]
- Ciampa, F.; Onder, E.; Barbieri, E.; Meo, M. Detection and Modelling of Nonlinear Elastic Response in Damaged Composite Structures. J. Nondestruct. Eval. 2014, 33, 515–521. [Google Scholar] [CrossRef]
- Ohara, Y.; Mihara, T.; Sasaki, R.; Ogata, T.; Yamamoto, S.; Kishimoto, Y.; Yamanaka, K. Imaging of closed cracks using nonlinear response of elastic waves at subharmonic frequency. Appl. Phys. Lett. 2007, 90, 011902. [Google Scholar] [CrossRef]
- Park, C.-S.; Kim, J.-W.; Cho, S.; Seo, D.-C. A high resolution approach for nonlinear sub-harmonic imaging. NDT E Int. 2016, 79, 114–122. [Google Scholar] [CrossRef]
- Potter, J.N.; Croxford, A.J.; Wilcox, P.D. Nonlinear Ultrasonic Phased Array Imaging. Phys. Rev. Lett. 2014, 113, 144301. [Google Scholar] [CrossRef]
- Oralkan, O.; Ergun, A.S.; Johnson, J.A.; Karaman, M.; Demirci, U.; Kaviani, K.; Lee, T.; Khuri-Yakub, B.T. Capacitive micromachined ultrasonic transducers: Next-generation arrays for acoustic imaging? IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 1596–1610. [Google Scholar] [CrossRef]
- Chiao, R.Y.; Thomas, L.J. Analytic evaluation of sampled aperture ultrasonic imaging techniques for NDE. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1994, 41, 484–493. [Google Scholar] [CrossRef]
- Kim, K.-B.; Hsu, D.K.; Barnard, D.J. Estimation of porosity content of composite materials by applying discrete wavelet transform to ultrasonic backscattered signal. NDT E Int. 2013, 56, 10–16. [Google Scholar] [CrossRef]
- Neppiras, E.A.; Noltingk, B.E. Cavitation Produced by Ultrasonics: Theoretical Conditions for the Onset of Cavitation. Proc. Phys. Soc. Sect. B 1951, 64, 1032–1038. [Google Scholar] [CrossRef]
- Neppiras, E.A. Acoustic cavitation. Phys. Rep. 1980, 61, 159–251. [Google Scholar] [CrossRef]
- Minnaert, M. On musical air-bubbles and the sounds of running water. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1933, 16, 235–248. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Johnson, P.A. Dynamic nonlinear elasticity in geomaterials. Riv. Nuovo Cimento 2001, 24, 1–46. [Google Scholar] [CrossRef]
- Karabutov, A.A.; Podymova, N.B.; Belyaev, I.O. The influence of porosity on ultrasound attenuation in carbon fiber reinforced plastic composites using the laser-ultrasound spectroscopy. Acoust. Phys. 2013, 59, 667–673. [Google Scholar] [CrossRef]
- Eller, A.; Flynn, H.G. Generation of Subharmonics of Order One-Half by Bubbles in a Sound Field. J. Acoust. Soc. Am. 1969, 46, 722–727. [Google Scholar] [CrossRef]
- Krishna, P.D.; Shankar, P.M.; Newhouse, V.L. Subharmonic generation from ultrasonic contrast agents. Phys. Med. Biol. 1999, 44, 681–694. [Google Scholar] [CrossRef]
- Forsberg, F.; Shi, W.T.; Goldberg, B.B. Subharmonic imaging of contrast agents. Ultrasonics 2000, 38, 93–98. [Google Scholar] [CrossRef]
- Biagi, E.; Breschi, L.; Vannacci, E.; Masotti, L. Subharmonic emissions from microbubbles: Effect of the driving pulse shape. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 2174–2182. [Google Scholar] [CrossRef] [PubMed]





| Sample | C-Maps | S-Maps | D-Maps |
|---|---|---|---|
| 1 | 2.26 | 9.17 (406%) | 3.75 (166%) |
| 2 | 1.4 | 7.99 (570%) | 3.13 (224%) |
| 3 | 1.13 | 2.7 (239%) | 2.18 (193%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Simone, M.E.; Boccardi, S.; Fierro, G.P.M.; Meo, M. Nonlinear Ultrasonic Imaging for Porosity Evaluation. Sensors 2023, 23, 6319. https://doi.org/10.3390/s23146319
De Simone ME, Boccardi S, Fierro GPM, Meo M. Nonlinear Ultrasonic Imaging for Porosity Evaluation. Sensors. 2023; 23(14):6319. https://doi.org/10.3390/s23146319
Chicago/Turabian StyleDe Simone, Mario Emanuele, Salvatore Boccardi, Gian Piero Malfense Fierro, and Michele Meo. 2023. "Nonlinear Ultrasonic Imaging for Porosity Evaluation" Sensors 23, no. 14: 6319. https://doi.org/10.3390/s23146319
APA StyleDe Simone, M. E., Boccardi, S., Fierro, G. P. M., & Meo, M. (2023). Nonlinear Ultrasonic Imaging for Porosity Evaluation. Sensors, 23(14), 6319. https://doi.org/10.3390/s23146319







