Decision Levels and Resolution for Low-Power Winner-Take-All Circuit †
Abstract
:1. Introduction
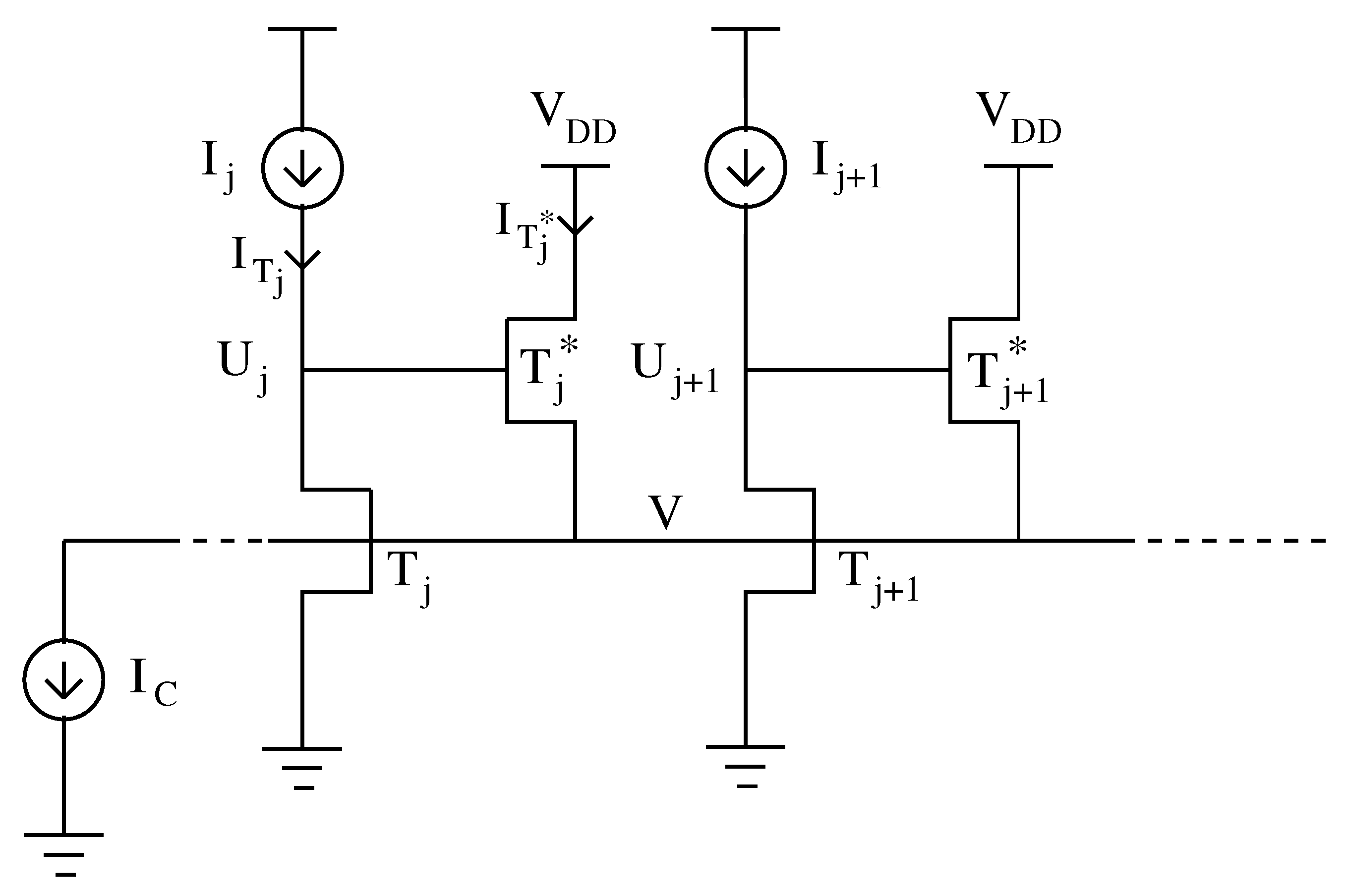
2. The Circuit Model
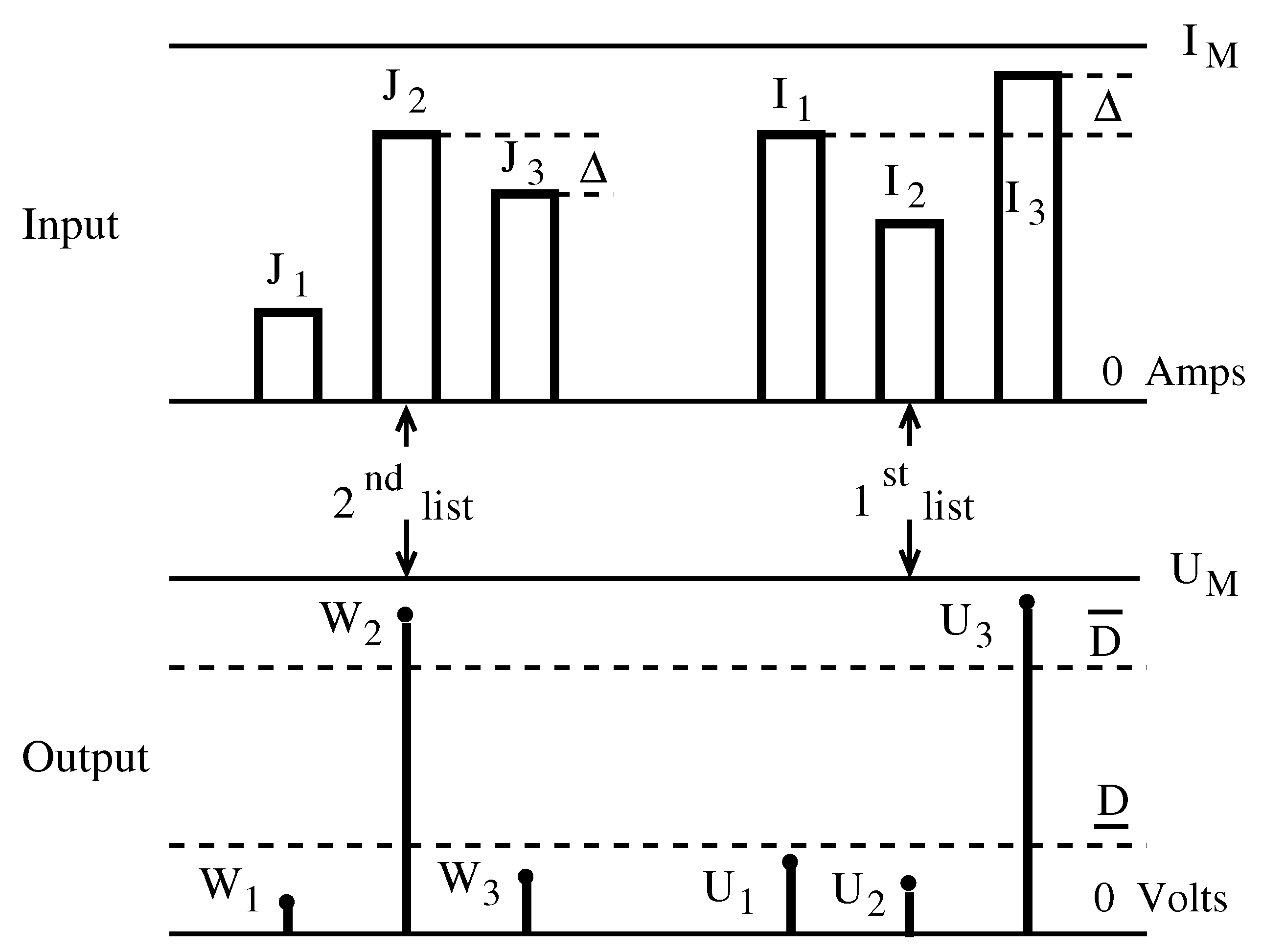
3. Decision Levels
4. Resolutions
5. Exploring the Mismatch
6. Numerical Checks–Discussion
6.1. Decision Levels
6.2. Mismatch
6.3. List Processing
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Badel, S.; Schmid, A.; Leblebici, Y. CMOS realization of two-dimensional mixed analog-digital Hamming distance discriminator circuits for real-time imaging applications. Microelectron. J. 2008, 39, 1817–18280. [Google Scholar] [CrossRef]
- Bigas, M.; Cabruja, E.; Forest, J.; Salvi, J. Review of CMOS image sensors. Microelectron. J. 2006, 37, 433–451. [Google Scholar] [CrossRef] [Green Version]
- Brink, S.; Nease, S.; Hasler, P.; Ramakrishnan, S.; Wunderlich, R.; Basu, A.; Degnan, B. A learning-enabled neuron array IC based upon transistor channel models of biological phenomena. IEEE Trans. Biomed. Circuits Syst. 2012, 7, 71–81. [Google Scholar] [CrossRef] [PubMed]
- Gomes, J.G.R.C.; Petraglia, A.; Mitra, S.K. Sensitivity analysis of multilayer perceptrons applied to focal-plane image compression. IET Circuits Devices Syst. 2007, 1, 79–86. [Google Scholar] [CrossRef]
- Indiveri, G. Neuromorphic Selective Attention Systems. In Proceedings of the International Symposium on Circuits and Systems, Bangkok, Thailand, 25–28 May 2003; Volume III, pp. 770–773. [Google Scholar]
- Izak, R.; Scarbata, G.; Paschke, P. Sound source localization with an integrate-and-fire neural system. In Proceedings of the Seventh International Conference on Microelectronics for Neural, Fuzzy and Bio-Inspired Systems, Granada, Spain, 9 April 1999; pp. 103–109. [Google Scholar]
- Sgrott, O.; Mosconi, D.; Perenzoni, M.; Pedretti, G.; Gonzo, L.; Stoppa, D. A 134-Pixel CMOS Sensor for Combined Time-of-Flight and Optical Triangulation 3-D Imaging. IEEE J. Solid-State Circuits 2010, 45, 1354–1364. [Google Scholar] [CrossRef]
- Koton, J.; Lahiri, A.; Herencsar, N.; Vrba, K. Current-mode precision full-wave rectifier using two WTA cells. In Proceedings of the 2011 34th International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 18–20 August 2011; pp. 324–327. [Google Scholar]
- Koton, J.; Lahiri, A.; Herencsar, N.; Vrba, K. Current-Mode Dual-Phase Precision Full-Wave Rectifier Using Current-Mode Two-Cell Winner-Takes-All (WTA) Circuit. Radioengineering 2011, 20, 428–432. [Google Scholar]
- Prommee, P.; Chattrakun, K. CMOS WTA maximum and minimum circuits with their applications to analog switch and rectifiers. Microelectron. J. 2011, 42, 52–62. [Google Scholar] [CrossRef]
- Ramirez-Angulo, J.; Molinar-Solis, J.E.; Gupta, S.; Carvajal, R.G.; Lopez-Martin, A.J. A High-Swing, High-Speed CMOS WTA Using Differential Flipped Voltage Followers. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 668–672. [Google Scholar] [CrossRef]
- Carvajal, R.G.; Ramirez-Angula, J.; Tombs, J. High-speed high-precision voltage-mode MIN/MAX circuits in CMOS technology. In Proceedings of the 2000 IEEE International Symposium on Circuits and Systems (ISCAS), Geneva, Switzerland, 28–31 May 2000; Volume 5, pp. 13–16. [Google Scholar]
- Baishnab, K.L.; Rahaman, M.; Talukdar, F. A 200 µv resolution and high speed VLSI Winner-take-all circuit for self-organising neural network. In Proceedings of the 2009 International Conference on Methods and Models in Computer Science (ICM2CS), New Delhi, India, 14–15 December 2009; pp. 1–4. [Google Scholar]
- Fish, A.; Milrud, V.; Yadid-Pecht, O. High-speed and high-precision current winner-take-all circuit. IEEE Trans. Circuits Syst. II Exp. Briefs 2005, 52, 131–135. [Google Scholar] [CrossRef]
- Indiveri, G. A Current-Mode Hysteretic Winner-take-all Network, with Excitatory and Inhibitory Coupling. Analog Integr. Circuits Signal Process. 2001, 28, 279–291. [Google Scholar] [CrossRef]
- Massari, N.; Gottardi, M. Low power WTA circuit for optical position detector. Electron. Lett. 2006, 42, 1373–1374. [Google Scholar] [CrossRef]
- Sarpeshkar, R. Ultra Low Power Bioelectronics: Fundamentals, Biomedical Applications, and Bio-Inspired Systems; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Kim, M.; Twigg, C.M. Rank determination by winner-take-all circuit for rank modulation memory. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 326–330. [Google Scholar] [CrossRef]
- Mead, C.A. Neuromorphic electronic systems. Proceeding IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef]
- Andreou, A.G.; Boahen, K.A.; Pouliquen, P.O.; Pavasovic, A.; Jenkins, R.E.; Strohbehn, K. Current-mode subthreshold MOS circuits for analog VLSI neural systems. IEEE Trans. Neural Netw. 1991, 2, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Lazzaro, J.; Ryckebush, S.; Mahowald, M.A.; Mead, C.A. Winner-take-all networks of O(N) complexity. In Advances In Neural Information Processing Systems; Touretzky, D.S., Ed.; Morgan Kaufmann: San Mateo, CA, USA, 1989; Volume 1, pp. 703–711. [Google Scholar]
- Sundararajan, G.; Winstead, C. A winner-take-all circuit with improved accuracy and tolerance to mismatch and process variations. In Proceedings of the 2013 IEEE 56th International Midwest Symposium on Circuits and Systems (MWSCAS), Columbus, OH, USA, 4–7 August 2013; pp. 265–268. [Google Scholar]
- Rahiminejad, E.; Saben, M.; Lotfi, R.; Taherzadeh-Sani, M.; Nabki, F. A low-voltage high-precision time-domain winner-take-all circuit. IEEE Trans. Circuits Syst. Express Briefs 2020, 67, 4–8. [Google Scholar] [CrossRef]
- Sekerkiran, B.; Cilingiroglu, U. Improving the resolution of Lazzaro winner-take-all circuit. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 12 June 1997; Volume 2, pp. 1005–1008. [Google Scholar]
- Benjamin, B.V.; Smith, R.L.; Boahen, K.A. An Analytical MOS Device Model with Mismatch and Temperature Variation for Subthreshold Circuits. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 1826–1830. [Google Scholar] [CrossRef]
- Marinov, C.A.; Costea, R.L. Designing a Winner–Loser Gap for WTA in Subthreshold. Resolution Performance Revisited. Circuits Syst. Signal Process. 2022, 41, 7145–7171. [Google Scholar] [CrossRef]
- Costea, R.L. Checking Over the Separation Performance for Winner Take All in Subthreshold Regime. In Proceedings of the 2022 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 10–11 November 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Tsividis, Y. Mixed Analog Digital VLSI Devices and Technology; World Scientific: Singapore, 2002. [Google Scholar]
- Costea, R.L.; Marinov, C.A. A Consistent Model for Lazzaro Winner-Take-All Circuit With Invariant Subthreshold Behavior. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2375–2385. [Google Scholar] [CrossRef] [PubMed]
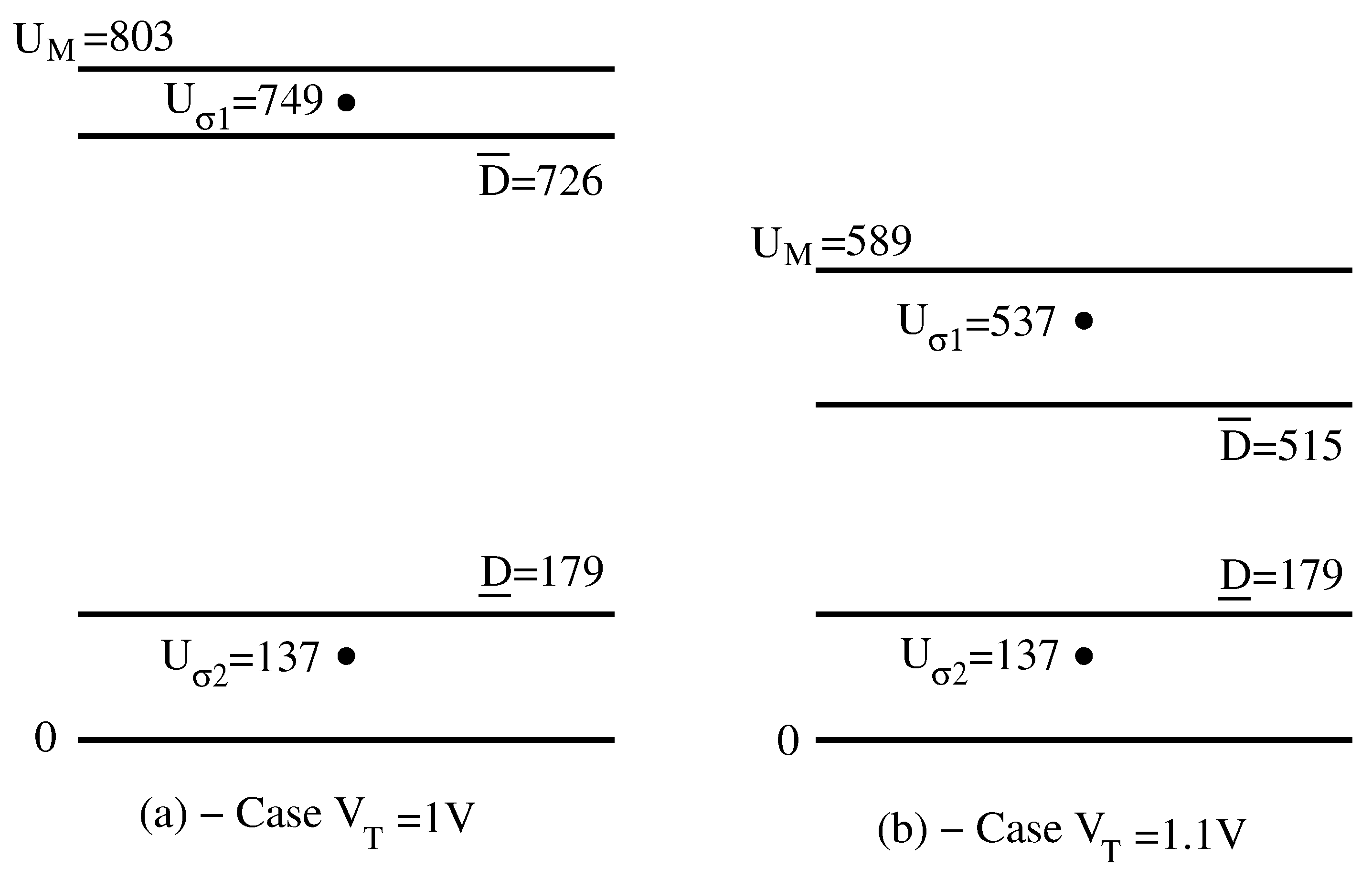
| 1000 | 1020 | 1040 | 1060 | 1080 | 1100 | |
| 803 | 759 | 719 | 674 | 632 | 589 | |
| 726 | 684 | 642 | 600 | 557 | 515 | |
| 179 | 179 | 179 | 179 | 179 | 179 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costea, R.L. Decision Levels and Resolution for Low-Power Winner-Take-All Circuit. Sensors 2023, 23, 6247. https://doi.org/10.3390/s23146247
Costea RL. Decision Levels and Resolution for Low-Power Winner-Take-All Circuit. Sensors. 2023; 23(14):6247. https://doi.org/10.3390/s23146247
Chicago/Turabian StyleCostea, Ruxandra L. 2023. "Decision Levels and Resolution for Low-Power Winner-Take-All Circuit" Sensors 23, no. 14: 6247. https://doi.org/10.3390/s23146247
APA StyleCostea, R. L. (2023). Decision Levels and Resolution for Low-Power Winner-Take-All Circuit. Sensors, 23(14), 6247. https://doi.org/10.3390/s23146247





