Dynamic Modeling of Carbon Dioxide Transport through the Skin Using a Capnometry Wristband
Abstract
1. Introduction
2. Materials and Methods
2.1. Continuous Space–Time Model of the Transport
- A convective flux which is the media’s convective flow, transporting the species with a speed in m·s−1:
- Distributed source. If, in addition, we have a distributed source or sink within the volume that is, respectively, generating or absorbing moles at a constant rate, an additional term can be added to the right-hand side of convection–diffusion differential Equation (6) as a distributed source/sink term (in mol⋅m−3⋅s−1). If the system interacts with the external world, modeled as exogeneous fluxes entering or leaving the system through the surface as a flux (in mol⋅m−2⋅s−1), this can be added in the conservation equation as
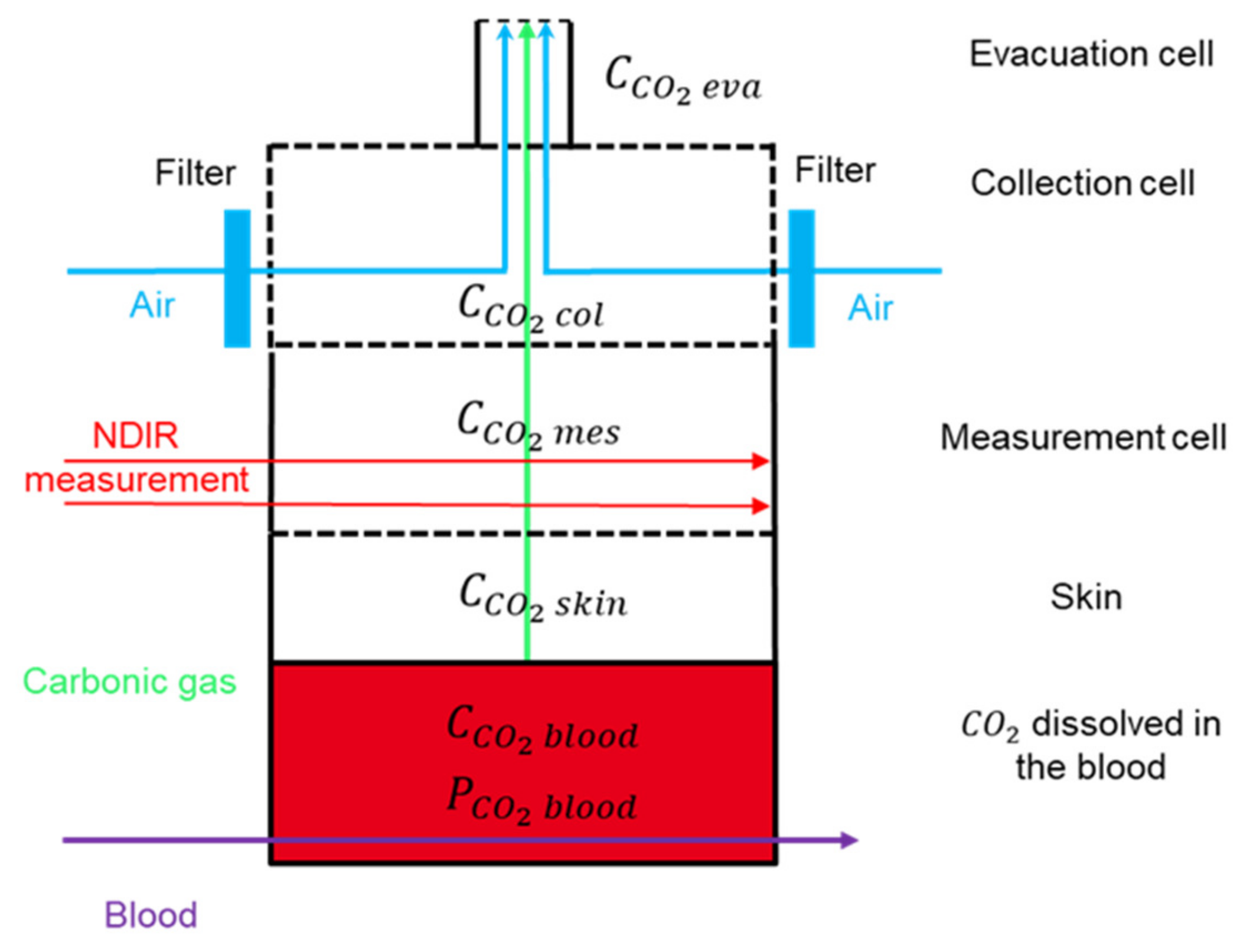
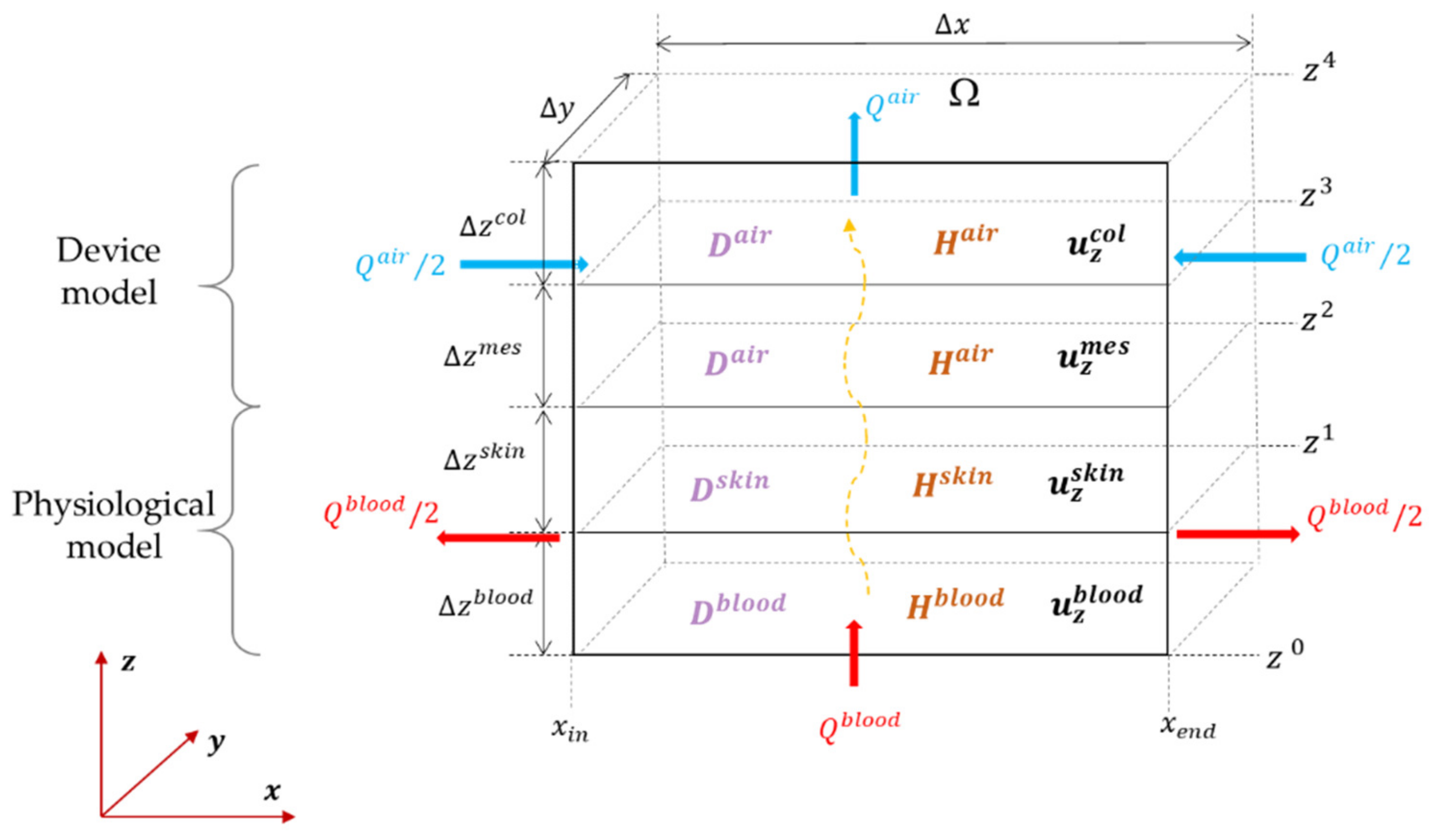
2.1.1. Introducing the Four Compartments
2.1.2. Measuring Concentration with Dual-Wavelength IR Thermopiles
2.1.3. Boundary Conditions for the System
2.1.4. Physical Parameters for the Transcutaneous Transport
Physical Parameters for Blood Medium
- is the blood flow (;
- is the surface of the transverse section of the blood compartment );
- is the average blood velocity along the axis (;
- is the length of the blood compartment ();
- is the width of the blood compartment ().
| Variable | Symbol | Measurement Unit | Value | Reference |
|---|---|---|---|---|
| Height | ||||
| Length | ||||
| Width | ||||
| Diffusion coefficient At 42 °C | −1 | Ghasem [58], Al Marzouqi [38], and Cao [59] | ||
| Average velocity | −1 | Formaggia [60], Vlachopoulos [61], and Guyton [62] | ||
| Henry coefficient | ||||
| Ostwald’s solubility coefficient of the carbon dioxide at 42 °C | 0.0275 | |||
| Temperature | 315.15 | |||
| Blood flow | −1 | Chatterjee [16] | ||
| Blood surface | 10 |
- is the ideal gas constant—;
- is the Ostwald’s solubility coefficient of the carbon dioxide in the blood at 42 °C (;
- is the blood temperature (K).
Physical Parameters for the Skin
| Variable | Symbol | Measurement Unit | Value | Reference |
|---|---|---|---|---|
| Height | ||||
| Length | ||||
| Width | ||||
| Diffusion coefficient | −1 | |||
| Average velocity | −1 | |||
| Henry coefficient | Scheuplein [33] | |||
| Transcutaneous carbon dioxide flow rate per exchange surface area at 42 °C | 290 | |||
| Bunsen carbon dioxide solubility at 42 °C | [33,64,65,66] | |||
| Skin conductance (volume flow rate) at 42 °C | Itoh [69] | |||
| Mass transfer coefficient | ||||
| Krogh’s diffusion constant |
- is the Bunsen carbon dioxide solubility in the stratum corneum ( (STPD stands for standard temperature, pressure, and dryness);
- is the Krogh’s diffusion constant ().
- is the Henry coefficient of the skin;
- is the total air pressure at skin or membrane temperature.
- is the mass transfer coefficient of the stratum corneum ;
- is the width of the stratum corneum (.
- is the conductance of the skin with respect to pressure difference for the surface area of the device ();
- is the volumic conductance of the skin with respect to pressure difference per surface area (;
- is the exchange surface area ().
- is the flow rate coming out of the skin ();
- is the carbon dioxide pressure in the blood (;
- is the carbon dioxide pressure in the ambient air (;
- is the exchange surface area ().
- mass transfer coefficient of the stratum corneum: ;
- Krogh’s diffusion constant: ;
- diffusion coefficient: .
Physical Parameters for the Gaseous Media in the Column of the Capnometry Device
| Variable | Symbol | Measurement Unit | Value | Reference |
|---|---|---|---|---|
| Length | ||||
| Width | ||||
| Height | ||||
| 0.25 | ||||
| Diffusion coefficient at 42 °C | −1 | Qazi [36] and Eslami Faiz [39] | ||
| Average velocity | −1 | 0 | ||
| −1 | 1.67 · | |||
| Henry coefficient | ||||
| Air flow | −1 | Typically, | ||
| Carbon dioxide concentration in the ambient air | 0.01613 | |||
| Carbon dioxide pressure in the ambient air at 42 °C | 0.32 |
2.2. A Discrete Space–Time CO2 Transportation Model
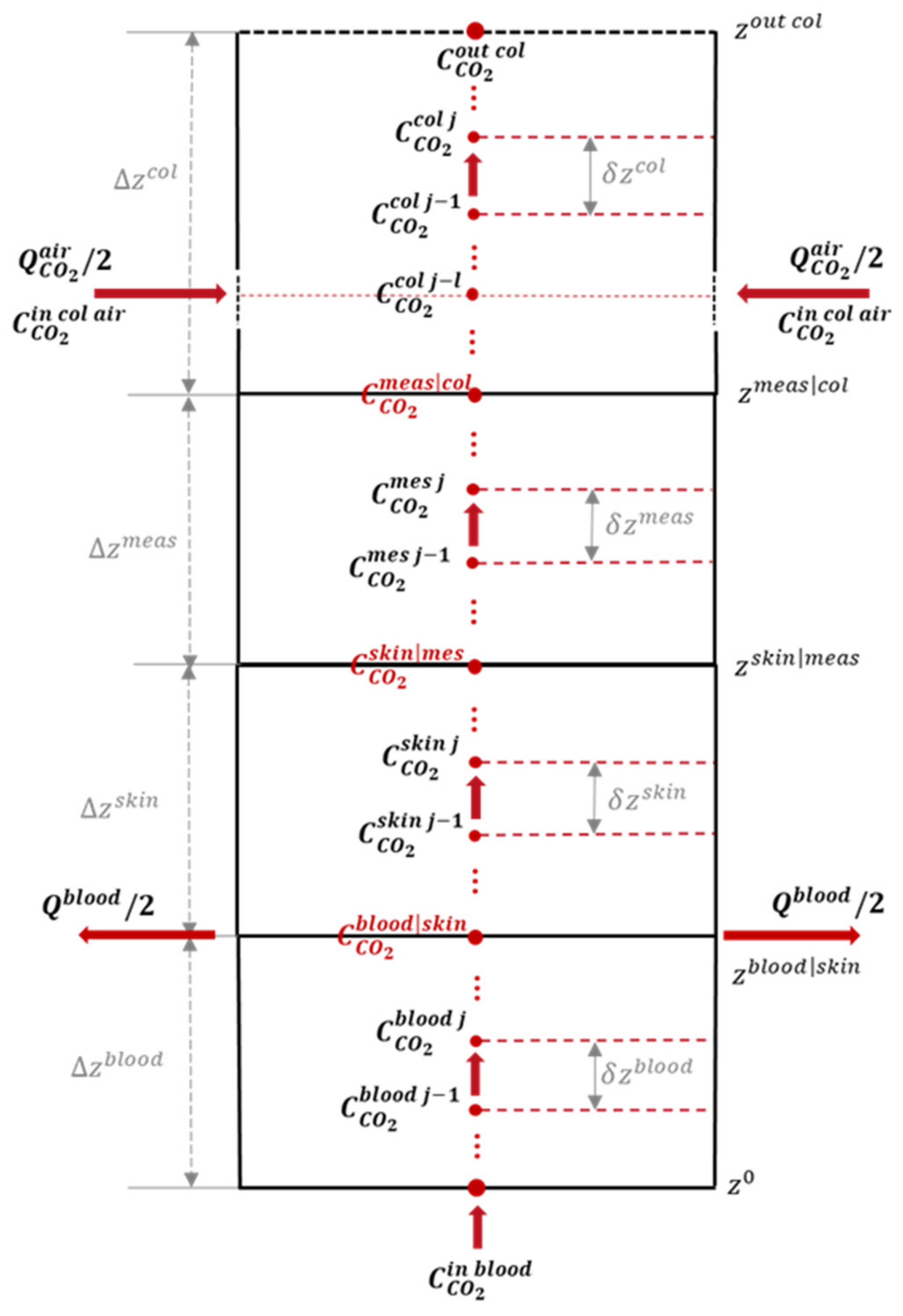
2.2.1. Spatial Discretization
2.2.2. Temporal Discretization
2.2.3. Exogenous Inputs
2.2.4. State-Space Model and Noise
- is a canonical vector for which sole non-zero entry is associated with the position of the NDIR optical measurement (the last grid point in the measurement cell before the interface with the collection cell);
- is the observation noise with a variance–covariance matrix that describes the inaccuracies of sensor outputs as measurements are taken.
- is the input noise model used to generate the input signal ; it is a white Gaussian noise process of variance .
- is a signal regularity parameter of a first-order autoregressive signal model.
2.3. Estimation of Blood Concentration Using Kalman Filter
2.3.1. Kalman Filter Algorithm
- Algorithm initialization:
- During the initialization phase, at the time step , is initialized to null vector, and is initialized to identity matrix.
- 2.
- Prediction step: Extrapolation (prediction) of the state and uncertainty covariance matrix at time step from the current state (at time step ). We present below the equations for the implicit method used for time integration scheme. Equation (44) is for state extrapolation, and Equation (45) is for covariance extrapolation:
- 3.
- Correction step: State vector and uncertainty covariance matrix update using the estimates computed at time step , and , and the current measurement .
- The Kalman gain given in Equation (46) expresses the weights given to the new noisy measurement or the estimated state, which is also subject to different external disturbances:
- The estimation of the current state (a posteriori state estimator) of the system is performed by taking a linear combination between the estimate made at the previous moment (a priori state estimator) and the new recorded data, as shown in Equation (47) below. Knowing the Kalman gain expression, we can give the expression to estimate the concentration at time based on the difference between the current measurement and the estimated measurement from the previous state estimate. This difference defines the prediction error (), which evaluates the amount of new information brought by the current measurement:
- The estimation of the covariance matrix of the estimate error at time from the estimated covariance matrix at time is based on Equation (48):
- 4.
- End of iteration:
- The steps are iterated until either the end is decided by the user or the measurements are stopped.
- The output of the algorithm is the estimated blood concentration corresponding to the first element of vector , at each time step.
2.3.2. Estimation of Blood Pressure
2.4. Methods of Evaluation
2.4.1. Evaluation of the Direct Approach
2.4.2. Evaluation of the Complete Model for Quantification
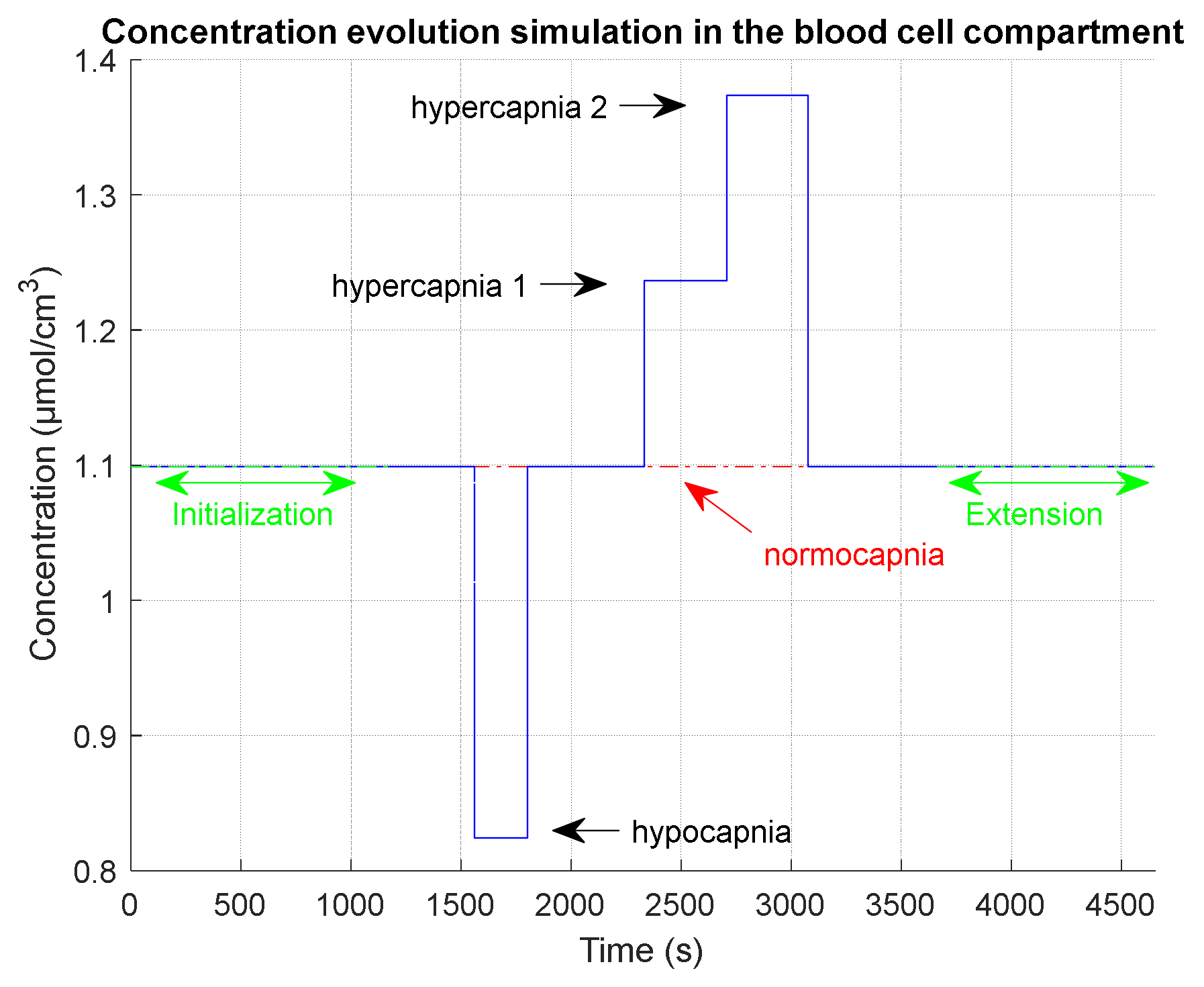
2.4.3. Evaluation on a Realistic Simulated Clinical Case
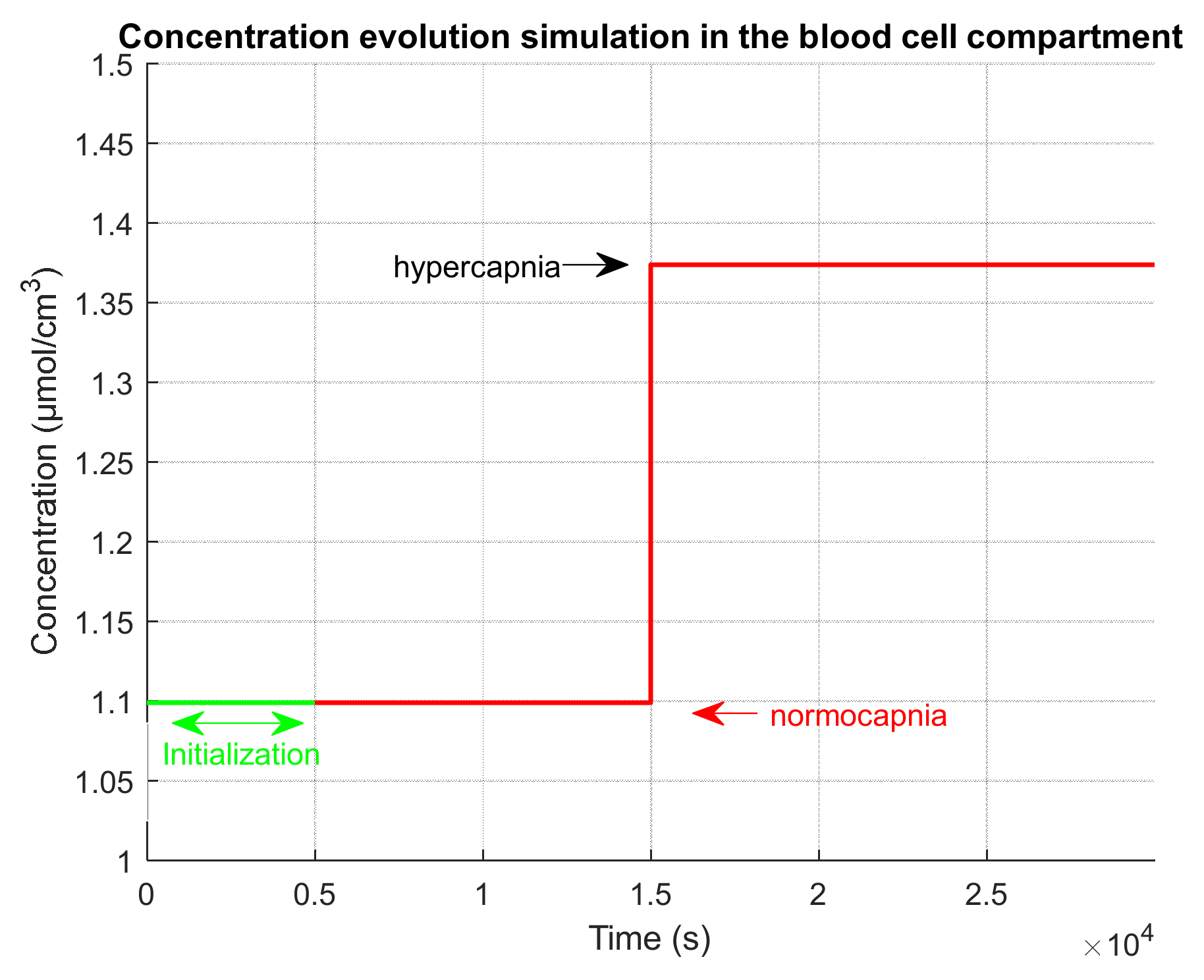
- An initialization phase to simulate the time that was used in the clinical test after installation of the device on the patient and before the test recording. During this initialization phase, we simulate a normocapnia level.
- An extension phase in order to observe on simulations the return to normocapnia equilibrium. During this extension phase, we simulate a normocapnia level.
| Phase Name | Phase Start Time (s) | Duration (s) | |
|---|---|---|---|
| Initialization | 1 | 1188 | 1.099/40 |
| Normocapnia 1 | 1189 | 374 | 1.099/40 |
| Hypocapnia | 1563 | 240 | 0.824/30 |
| Normocapnia 2 | 1803 | 531 | 1.099/40 |
| Hypercapnia 1 | 2334 | 375 | 1.236/45 |
| Hypercapnia 2 | 2709 | 368 | 1.374/50 |
| Normocapnia 3 | 3077 | 587 | 1.099/40 |
| Extension (end of measurement) | 3664 | 990 | 1.099/40 |
| End of simulation | 4654 |
3. Results
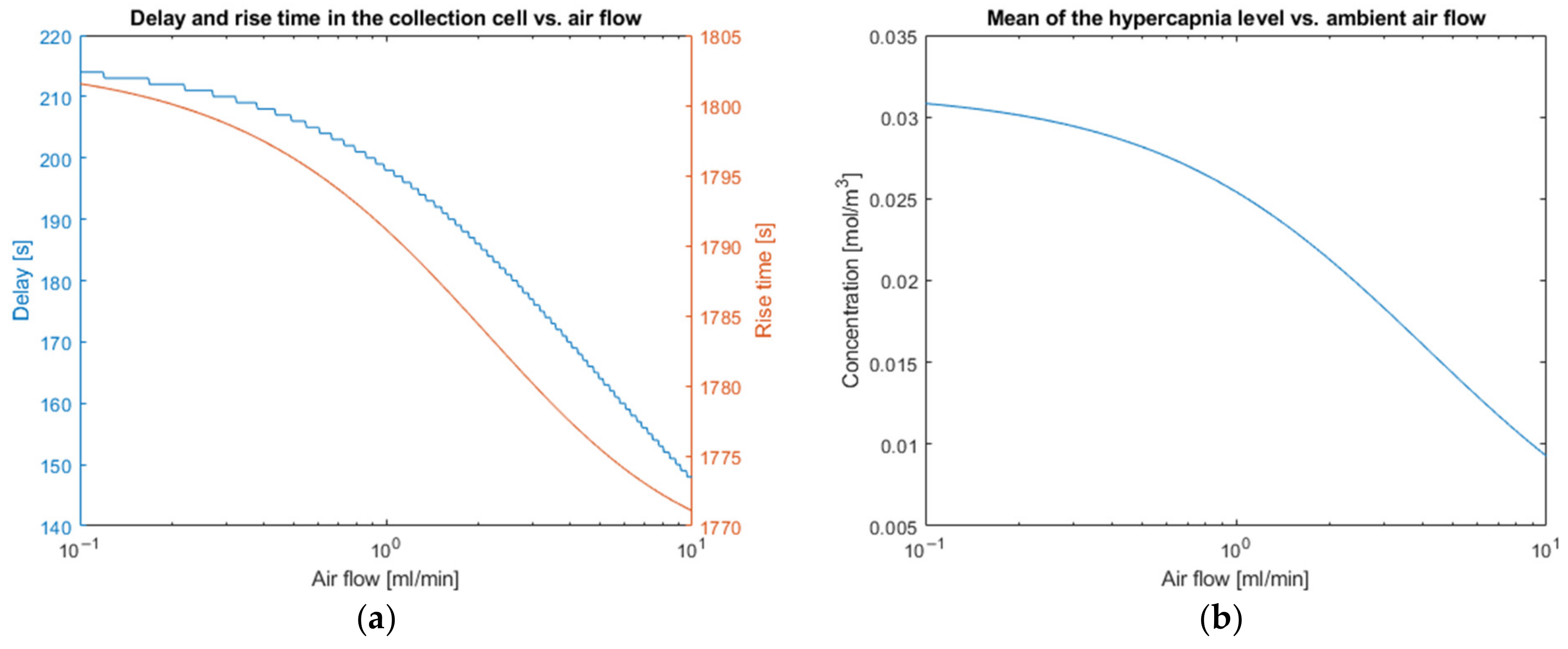
3.1. Performance Parameters for the Direct Model
3.2. Performance Parameters for the Inverse Model
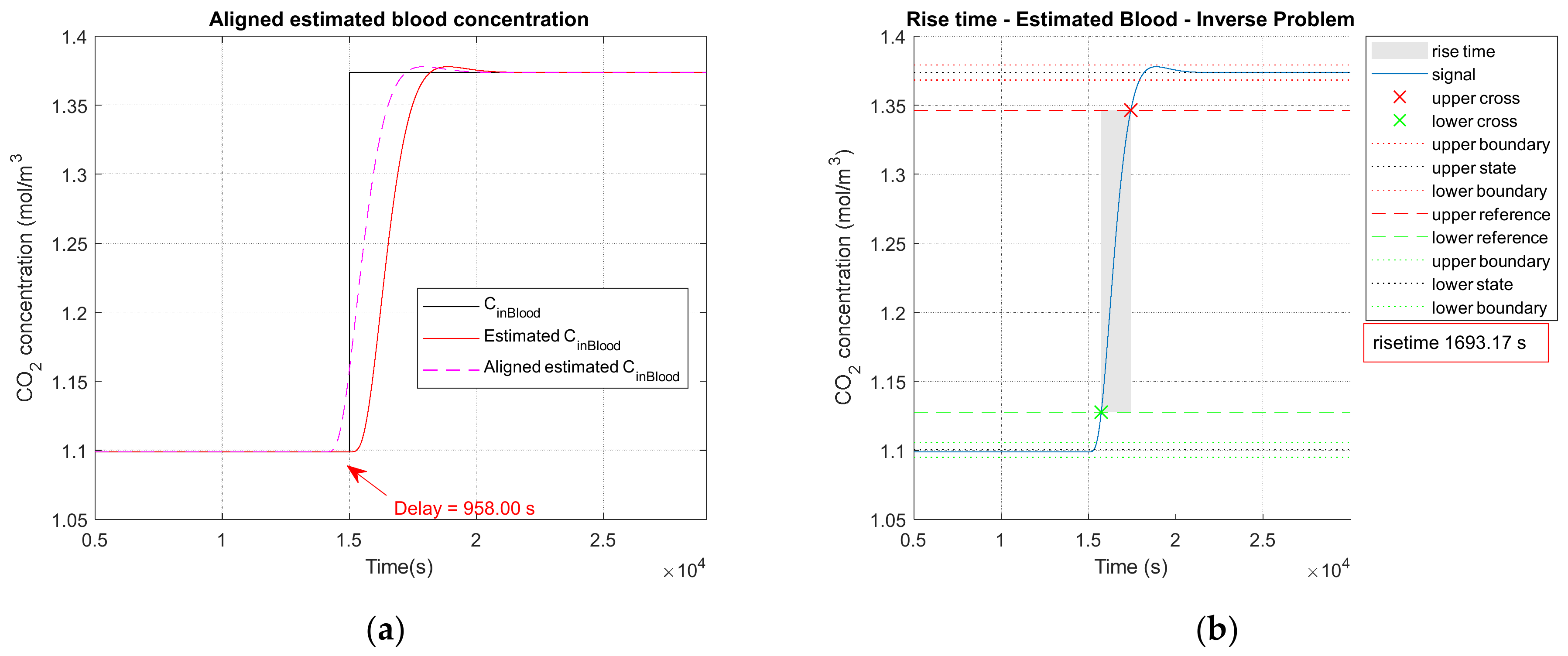
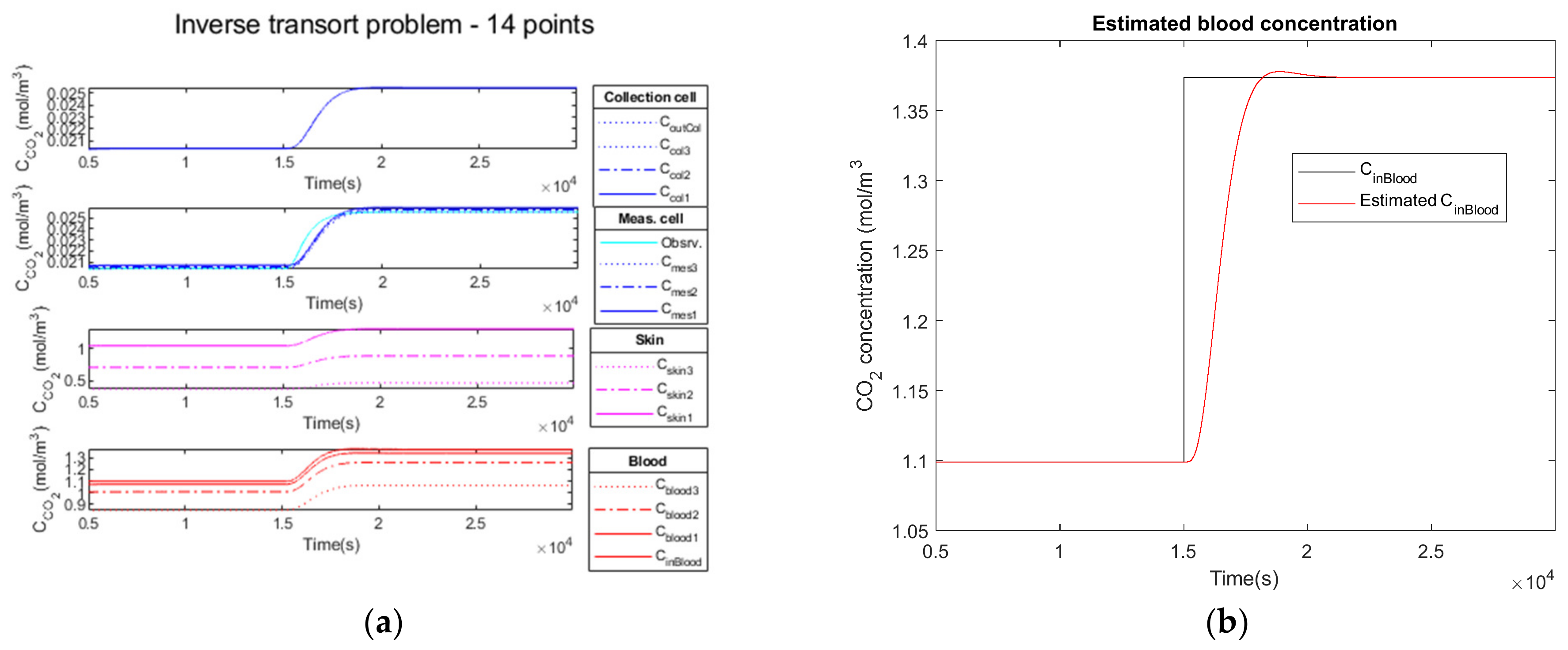
3.2.1. Noiseless Observation of a Step Function as Input
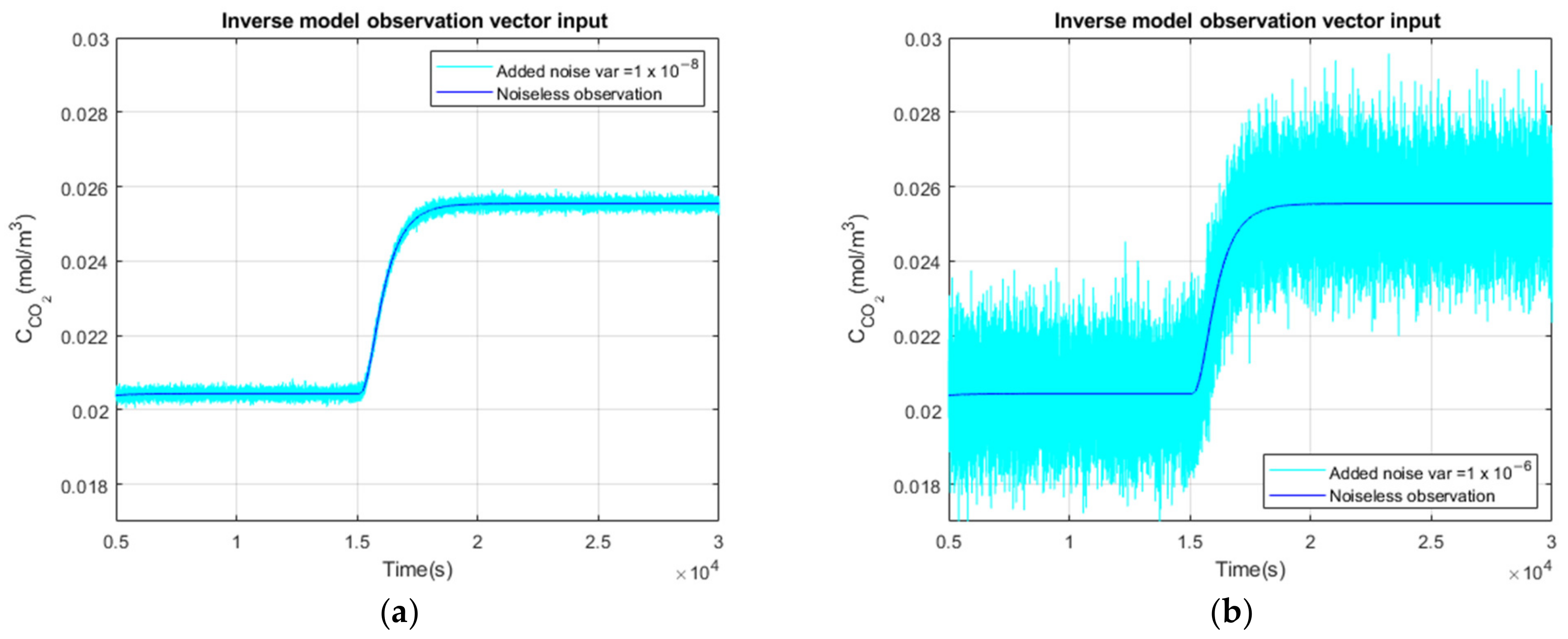
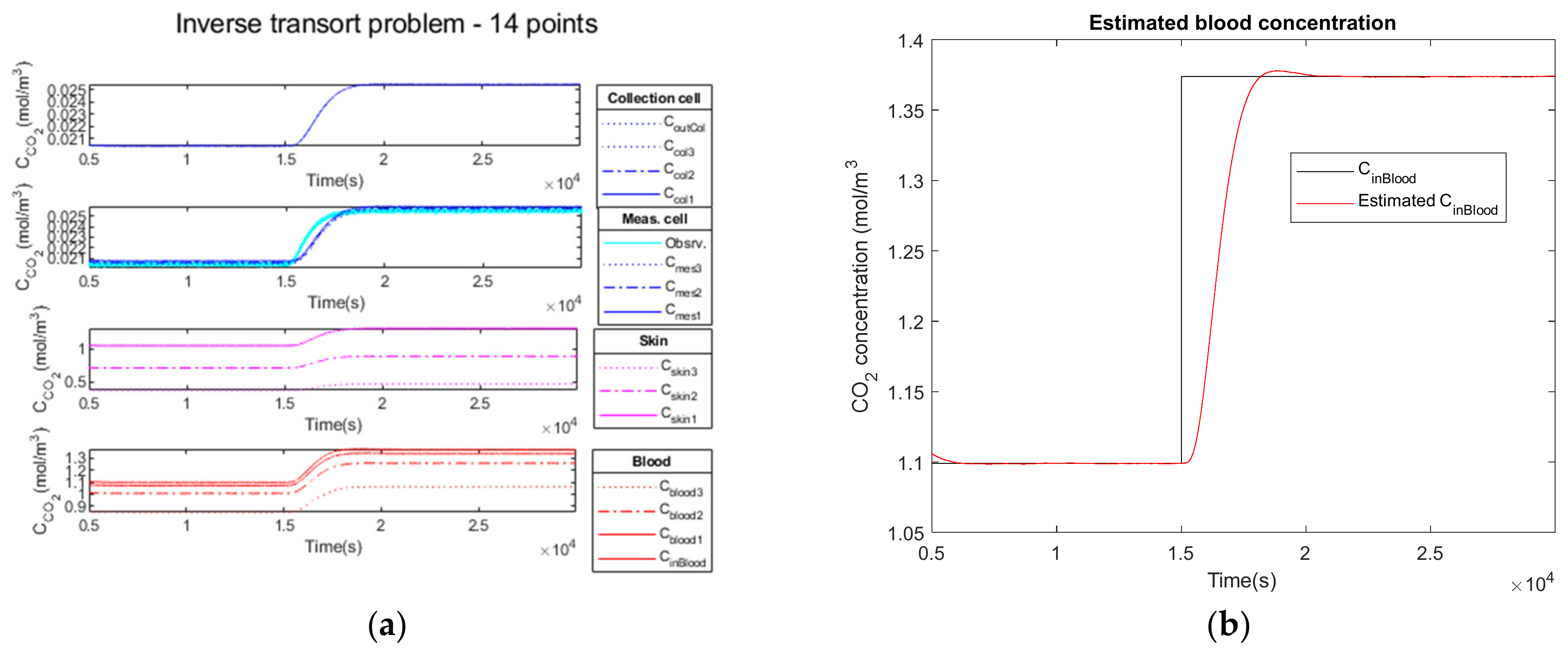
3.2.2. Low Noise Observation of a Step Function as Input
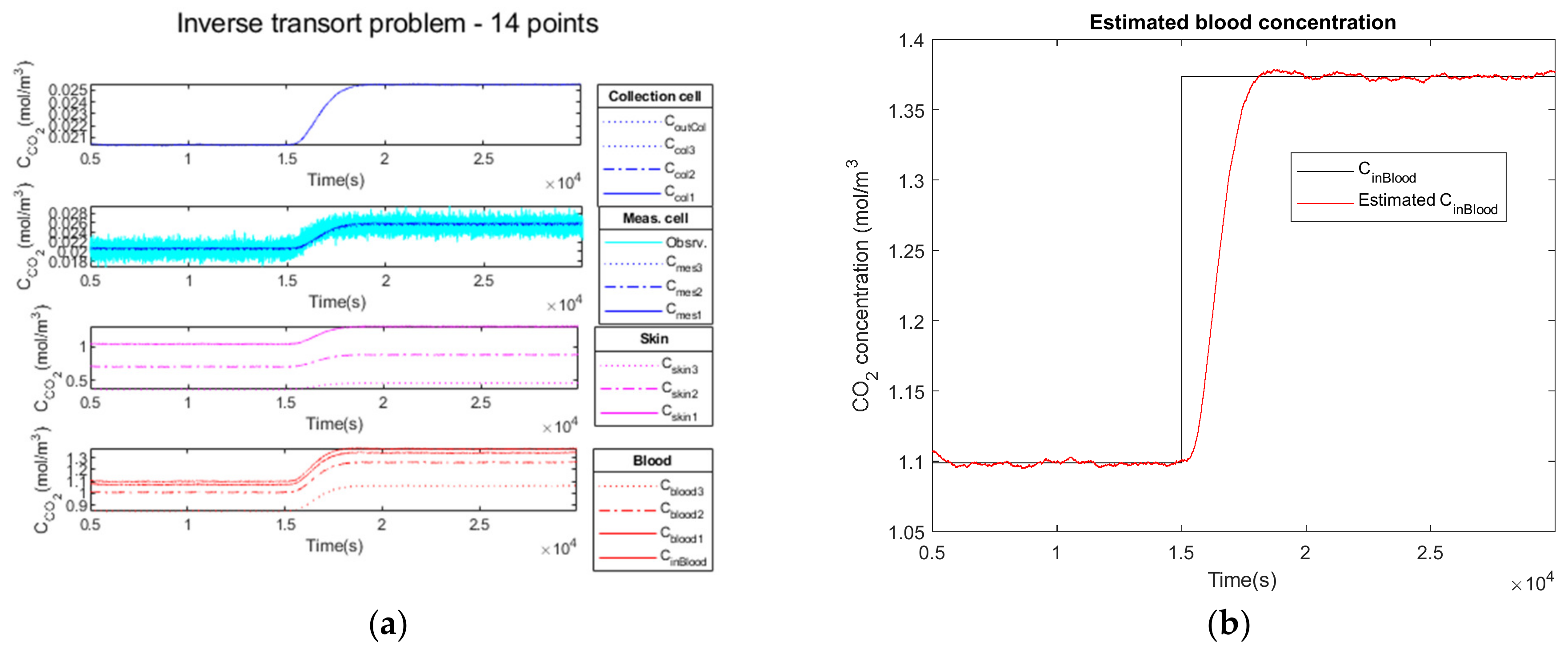
3.2.3. High Observation Noise of a Step Function as Input
3.2.4. Performance Parameters
3.3. Performance Parameters for the Complete Model on a Realistic Clinical Test
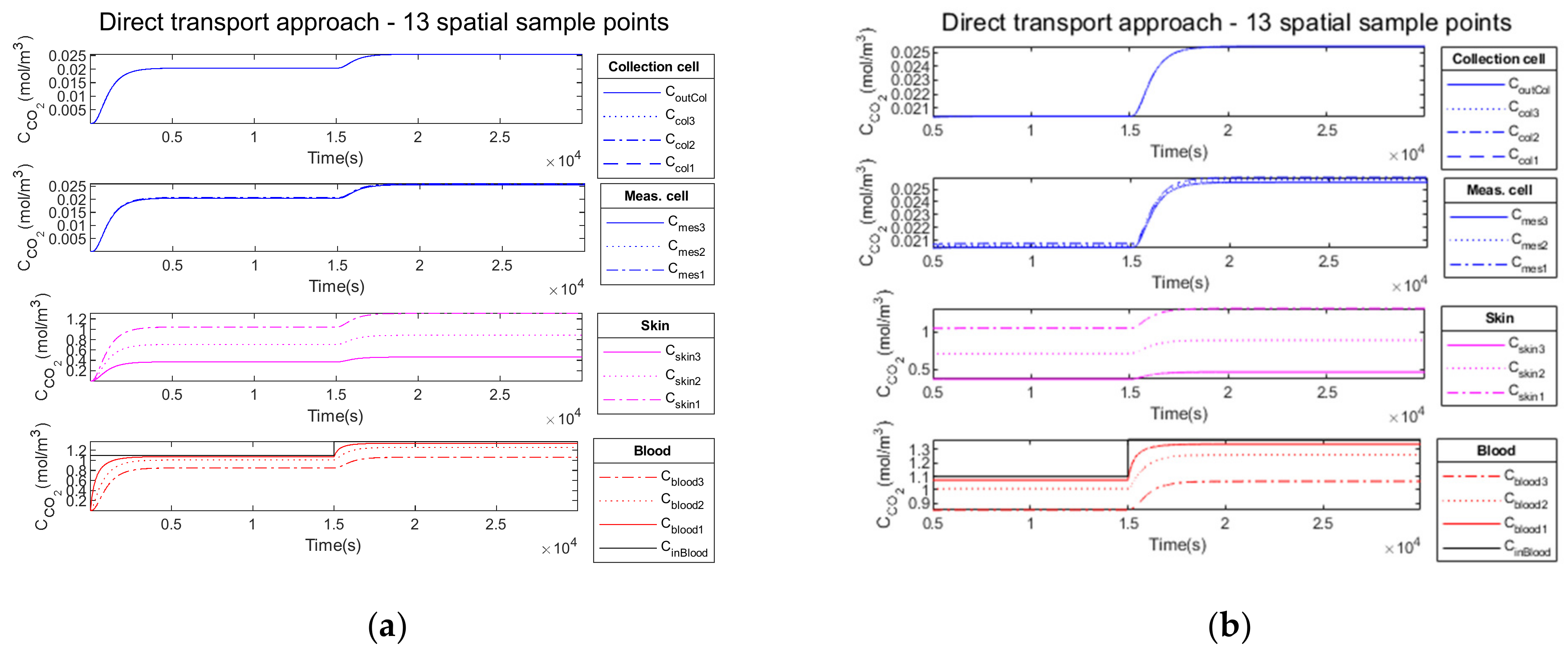
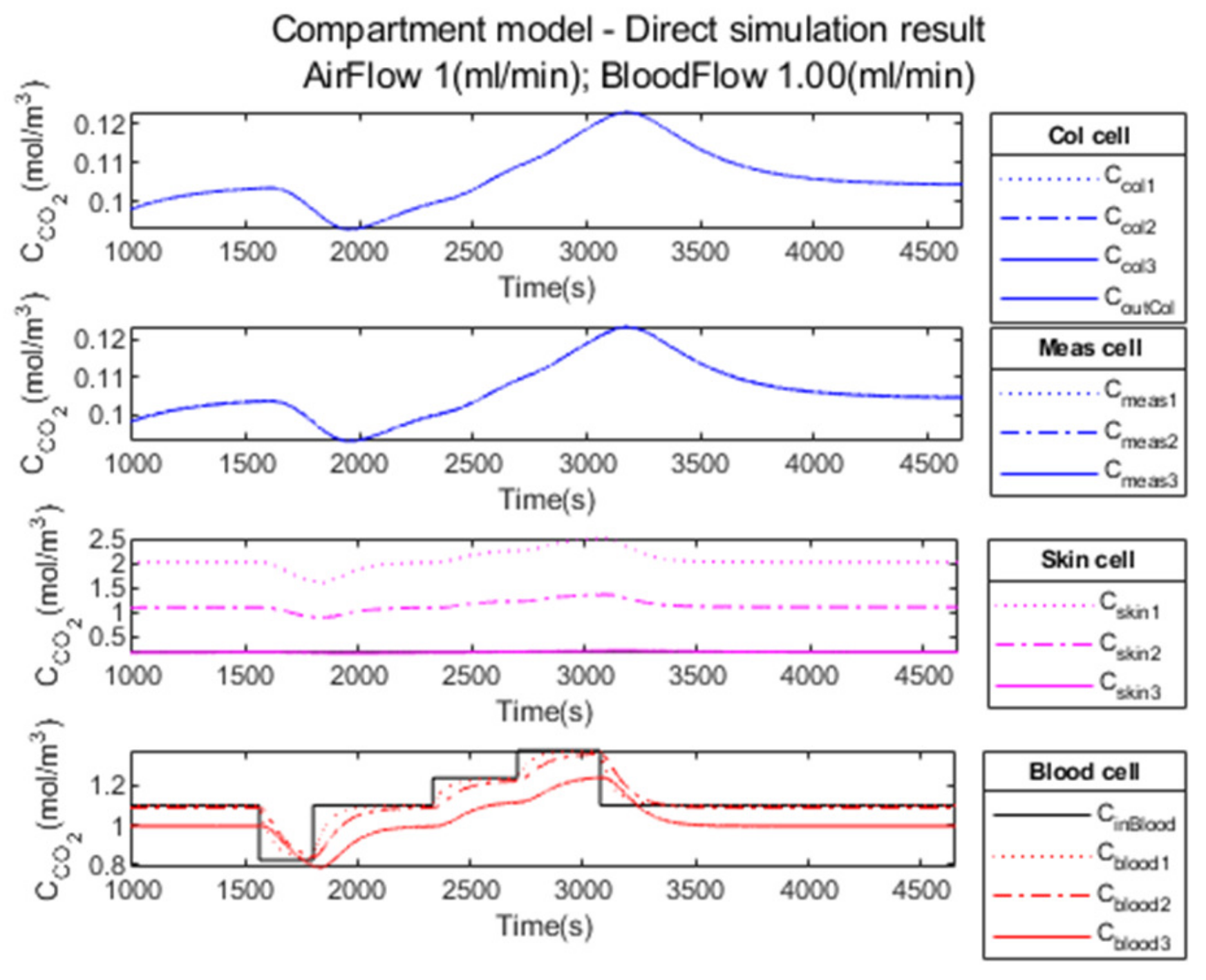
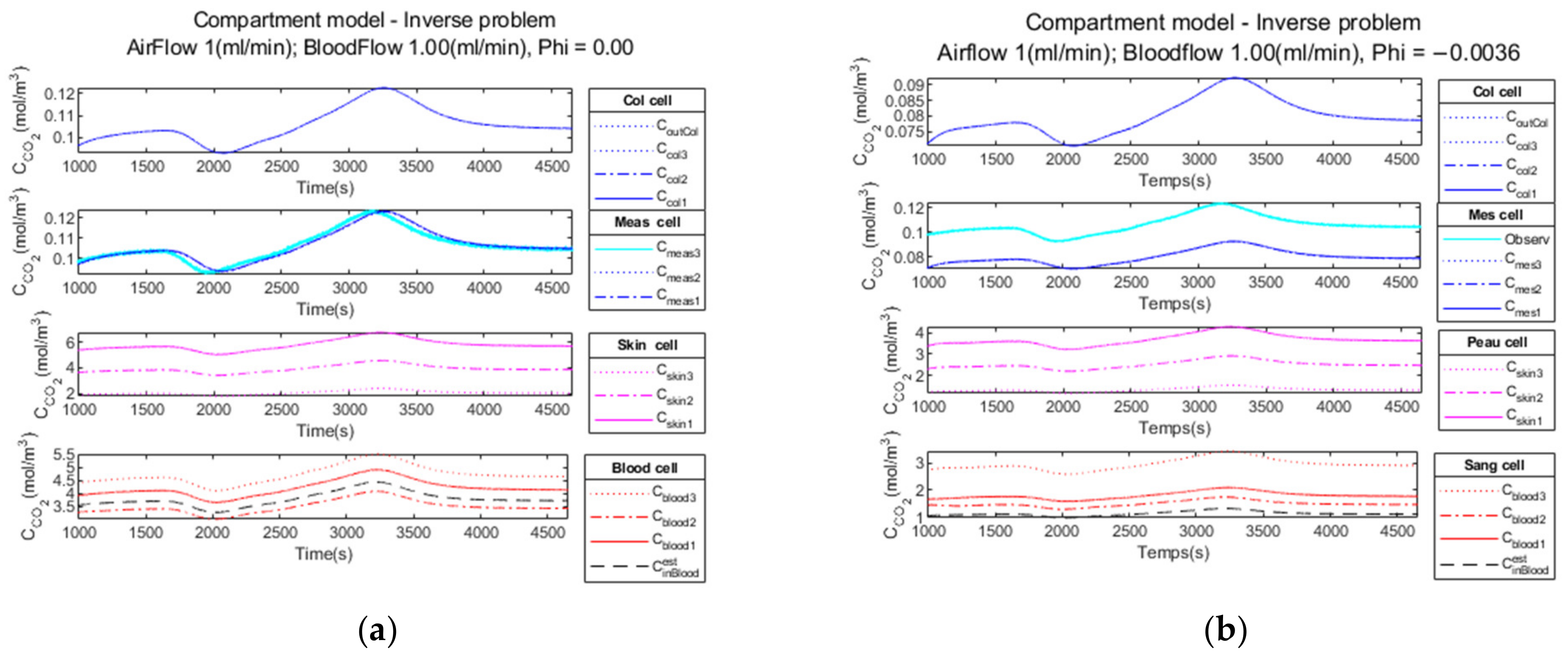
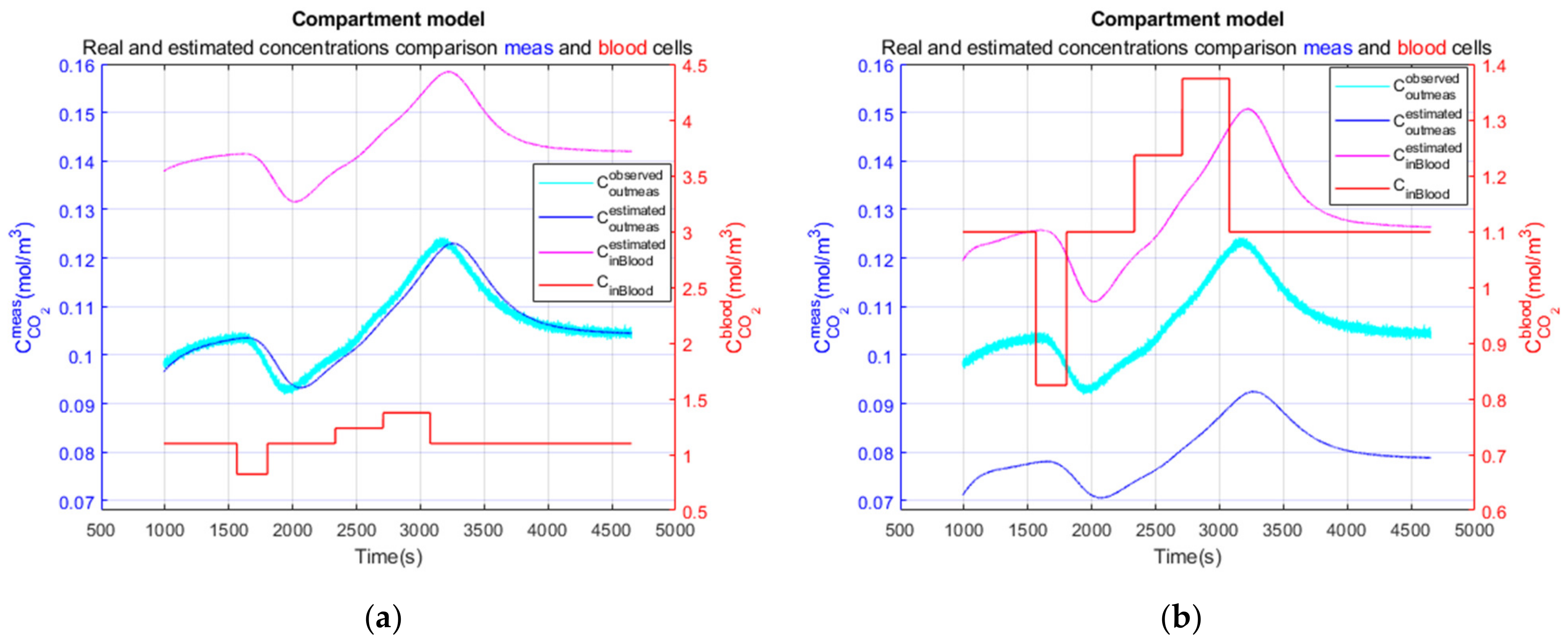
3.3.1. Compartment Model Simulation
3.3.2. Compartment Model Simulation
3.3.3. Performance Parameters
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agache, P. Carbon Dioxide Transcutaneous Pressure. In Agache’s Measuring the Skin; Humbert, P., Maibach, H., Fanian, F., Agache, P., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 587–590. ISBN 978-3-319-26594-0. [Google Scholar]
- Higgins, C. An Introduction to Acid-Base Balance in Health and Disease. 2004. Available online: https://acutecaretesting.org/en/articles/an-introduction-to-acidbase-balance-in-health-and-disease (accessed on 15 June 2022).
- Higgins, C. Parameters That Reflect the Carbon Dioxide Content of Blood. 2008. Available online: https://acutecaretesting.org/en/articles/parameters-that-reflect-the-carbon-dioxide-content-of-blood (accessed on 15 June 2022).
- Seifter, J.L.; Chang, H.-Y. Disorders of Acid-Base Balance: New Perspectives. Kidney Dis. 2016, 2, 170–186. [Google Scholar] [CrossRef]
- Huttmann, S.E.; Windisch, W.; Storre, J.H. Techniques for the Measurement and Monitoring of Carbon Dioxide in the Blood. Ann. Am. Thorac. Soc. 2014, 11, 645–652. [Google Scholar] [CrossRef]
- Hahn, C.E.W. Blood Gas Measurement. Review Article. Clin. Phys. Physiol. Meas. 1987, 8, 3–38. [Google Scholar] [CrossRef]
- Rithalia, S.V.S. Developments in Transcutaneous Blood Gas Monitoring: A Review. J. Med. Eng. Technol. 1991, 15, 143–153. [Google Scholar] [CrossRef]
- Severinghaus, J.W. The Current Status of Transcutaneous Blood Gas Analysis and Monitoring. Blood Gas News 1998, 7, 4–9. [Google Scholar]
- Zosel, J.; Oelßner, W.; Decker, M.; Gerlach, G.; Guth, U. The Measurement of Dissolved and Gaseous Carbon Dioxide Concentration. Meas. Sci. Technol. 2011, 22, 072001. [Google Scholar] [CrossRef]
- Dervieux, E.; Théron, M.; Uhring, W. Carbon Dioxide Sensing—Biomedical Applications to Human Subjects. Sensors 2021, 22, 188. [Google Scholar] [CrossRef]
- Severinghaus, J.W.; Stafford, M.; Bradley, A.F. TcPCO, Electrode Design, Calibration and Temperature Gradient Problems. Acta Anaesthesiol. Scand. 1978, 22, 118–122. [Google Scholar] [CrossRef]
- Thiele, F.A.J.; Kempen, L.H.J. A Micro Method for Measuring the Carbon Dioxide Release by Small Skin Areas. Br. J. Dermatol. 1972, 86, 463–471. [Google Scholar] [CrossRef]
- Eletr, S.; Jimison, H.; Ream, A.K.; Dolan, W.M.; Rosenthal, M.H. Cutaneous Monitoring of Systemic PCO2 on Patients in the Respiratory Intensive Care Unit Being Weaned from the Ventilator. Acta Anaesthesiol. Scand. 1978, 22, 123–127. [Google Scholar] [CrossRef]
- Gehrich, J.L.; Lubbers, D.W.; Opitz, N.; Hansmann, D.R.; Miller, W.W.; Tusa, J.K.; Yafuso, M. Optical Fluorescence and Its Application to an Intravascular Blood Gas Monitoring System. IEEE Trans. Biomed. Eng. 1986, BME-33, 117–132. [Google Scholar] [CrossRef]
- Tufan, T.B.; Sen, D.; Guler, U. An Infra-Red-Based Prototype for a Miniaturized Transcutaneous Carbon Dioxide Monitor. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Guadalajara, Mexico, 1–5 November 2021; pp. 7132–7135. [Google Scholar]
- Chatterjee, M.; Ge, X.; Kostov, Y.; Luu, P.; Tolosa, L.; Woo, H.; Viscardi, R.; Falk, S.; Potts, R.; Rao, G. A Rate-Based Transcutaneous CO2 Sensor for Noninvasive Respiration Monitoring. Physiol. Meas. 2015, 36, 883–894. [Google Scholar] [CrossRef]
- Ge, X.; Adangwa, P.; Lim, J.Y.; Kostov, Y.; Tolosa, L.; Pierson, R.; Herr, D.; Rao, G. Development and Characterization of a Point-of Care Rate-Based Transcutaneous Respiratory Status Monitor. Med. Eng. Phys. 2018, 56, 36–41. [Google Scholar] [CrossRef]
- Iitani, K.; Tyson, J.; Rao, S.; Ramamurthy, S.S.; Ge, X.; Rao, G. What Do Masks Mask? A Study on Transdermal CO2 Monitoring. Med. Eng. Phys. 2021, 98, 50–56. [Google Scholar] [CrossRef]
- Grangeat, P. Nanoscience: Nanobiotechnology and Nanobiology—Chap 13 Data Processing; Boisseau, P., Houdy, P., Lahmani, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-88632-7. [Google Scholar]
- Marco, S.; Gutierrez-Galvez, A. Signal and Data Processing for Machine Olfaction and Chemical Sensing: A Review. IEEE Sens. J. 2012, 12, 3189–3214. [Google Scholar] [CrossRef]
- Candy, J.V. Model-Based Signal Processing; Wiley-IEEE Press: Hoboken, NJ, USA, 2006; ISBN 978-0-471-73266-2. [Google Scholar]
- Al Fahoum, A.S.; Abu Al-Haija, A.O.; Alshraideh, H.A. Identification of Coronary Artery Diseases Using Photoplethysmography Signals and Practical Feature Selection Process. Bioengineering 2023, 10, 249. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Chui, C.K.; Chen, G. Kalman Filtering with Real-Time Applications; Springer Series in Information Sciences; Springer: Berlin/Heidelberg, Germany, 1987; Volume 17, ISBN 978-3-662-02510-9. [Google Scholar]
- Anderson, B.D.O.; Moore, J.B. Optimal Filtering; Dover Publications: New York, NY, USA, 2004; ISBN 978-1-62198-604-1. [Google Scholar]
- Haykin, S.; Widrow, B. Least-Mean-Square Adaptive Filters, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Piiper, J. Respiratory Gas Exchange at Lungs, Gills and Tissues: Mechanisms and Adjustments. J. Exp. Biol. 1982, 100, 5–22. [Google Scholar] [CrossRef]
- Piiper, J.; Scheid, P. Blood—Gas Equilibration in Lung. In Pulmonary Gas Exchange; West, J.B., Ed.; Academic Press: New York, NY, USA, 1980; ISBN 978-0-12-744501-4. [Google Scholar]
- Farhi, L.E. Elimination of Inert Gas by the Lung. Respir. Physiol. 1967, 3, 1–11. [Google Scholar] [CrossRef]
- King, J.; Unterkofler, K.; Teschl, G.; Teschl, S.; Koc, H.; Hinterhuber, H.; Amann, A. A Mathematical Model for Breath Gas Analysis of Volatile Organic Compounds with Special Emphasis on Acetone. J. Math. Biol. 2011, 63, 959–999. [Google Scholar] [CrossRef]
- Unterkofler, K.; King, J.; Mochalski, P.; Jandacka, M.; Koc, H.; Teschl, S.; Amann, A.; Teschl, G. Modeling-Based Determination of Physiological Parameters of Systemic VOCs by Breath Gas Analysis: A Pilot Study. J. Breath Res. 2015, 9, 036002. [Google Scholar] [CrossRef]
- Piiper, J.; Scheid, P. Gas Transport Efficacy of Gills, Lungs and Skin: Theory and Experimental Data. Respir. Physiol. 1975, 23, 209–221. [Google Scholar] [CrossRef]
- Scheuplein, R.J.; Blank, I.H. Permeability of the Skin. Physiol. Rev. 1971, 51, 702–747. [Google Scholar] [CrossRef]
- Scheuplein, R.J. Mechanism of Percutaneous Adsorption. J. Investg. Dermatol. 1965, 45, 334–346. [Google Scholar] [CrossRef]
- Rosli, A.; Shoparwe, N.F.; Ahmad, A.L.; Low, S.C.; Lim, J.K. Dynamic Modelling and Experimental Validation of CO2 Removal Using Hydrophobic Membrane Contactor with Different Types of Absorbent. Sep. Purif. Technol. 2019, 219, 230–240. [Google Scholar] [CrossRef]
- Qazi, S.; Gómez-Coma, L.; Albo, J.; Druon-Bocquet, S.; Irabien, A.; Younas, M.; Sanchez-Marcano, J. Mathematical Modeling of CO2 Absorption with Ionic Liquids in a Membrane Contactor, Study of Absorption Kinetics and Influence of Temperature. J. Chem. Technol. Biotechnol. 2020, 95, 1844–1857. [Google Scholar] [CrossRef]
- Darabi, M.; Pahlavanzadeh, H. Mathematical Modeling of CO2 Membrane Absorption System Using Ionic Liquid Solutions. Chem. Eng. Process.-Process Intensif. 2020, 147, 107743. [Google Scholar] [CrossRef]
- Al-Marzouqi, M.; El-Naas, M.; Marzouk, S.; Abdullatif, N. Modeling of Chemical Absorption of CO2 in Membrane Contactors. Sep. Purif. Technol. 2008, 62, 499–506. [Google Scholar] [CrossRef]
- Faiz, R.; Al-Marzouqi, M. Mathematical Modeling for the Simultaneous Absorption of CO2 and H2S Using MEA in Hollow Fiber Membrane Contactors. J. Membr. Sci. 2009, 342, 269–278. [Google Scholar] [CrossRef]
- Li, X.L.; Karimi, H.; McLellan, P.J.; McAuley, K.B.; Jeffrey, C. Mathematical Model for a Point-of-Care Sensor for Measuring Carbon Dioxide in Blood. Sens. Actuators B Chem. 2016, 236, 635–645. [Google Scholar] [CrossRef]
- Grangeat, P.; Gharbi, S.; Koenig, A.; Comsa, M.-P.; Accensi, M.; Grateau, H.; Ghaith, A.; Chacaroun, S.; Doutreleau, S.; Verges, S. Evaluation in Healthy Subjects of a Transcutaneous Carbon Dioxide Monitoring Wristband during Hypo and Hypercapnia Conditions. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 4640–4643. [Google Scholar]
- Grangeat, P.; Gharbi, S.; Accensi, M.; Grateau, H. First Evaluation of a Transcutaneous Carbon Dioxide Monitoring Wristband Device during a Cardiopulmonary Exercise Test. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 3352–3355. [Google Scholar]
- Grangeat, P.; Gharbi, S.; Accensi, M.; Grateau, H. Dispositif Portable d’Estimation de La Pression Partielle de Gaz Sanguin. Portable Device fot Estimating the Partial Pressure of Blood. Gas. Patent WO 2020/249466A1, 17 December 2020. [Google Scholar]
- Lallemand, A. Écoulement des fluides—Équations de bilans. Tech. Ing. 1999, 1, BE8153.1–BE8153.18. [Google Scholar] [CrossRef]
- Anissimov, Y.G.; Jepps, O.G.; Dancik, Y.; Roberts, M.S. Mathematical and Pharmacokinetic Modelling of Epidermal and Dermal Transport Processes. Adv. Drug Deliv. Rev. 2013, 65, 169–190. [Google Scholar] [CrossRef]
- Couto, A.; Fernandes, R.; Cordeiro, M.N.S.; Reis, S.S.; Ribeiro, R.T.; Pessoa, A.M. Dermic Diffusion and Stratum Corneum: A State of the Art Review of Mathematical Models. J. Control. Release 2014, 177, 74–83. [Google Scholar] [CrossRef]
- Fick’s First Law. Available online: https://www.doitpoms.ac.uk/tlplib/diffusion/fick1.php (accessed on 22 June 2023).
- Darby, R.; Chhabra, R.P. Chemical Engineering Fluid Mechanics, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016; ISBN 978-1-315-37067-5. [Google Scholar]
- Fick’s Second Law. Available online: https://www.doitpoms.ac.uk/tlplib/diffusion/fick2.php (accessed on 22 June 2023).
- Mitragotri, S.; Anissimov, Y.G.; Bunge, A.L.; Frasch, H.F.; Guy, R.H.; Hadgraft, J.; Kasting, G.B.; Lane, M.E.; Roberts, M.S. Mathematical Models of Skin Permeability: An Overview. Int. J. Pharm. 2011, 418, 115–129. [Google Scholar] [CrossRef]
- Comsa, M.-P. Méthodes Numériques Pour Un Dispositif de Suivi Autonome Personnalisé Des Gaz Transcutanés. Numerical Methods for a Personalized Autonomous Transcutaneous Gas Monitoring Device. EEATS—Signal Image Parole Telecoms. Ph.D. Thesis, UGA—Université Grenoble Alpes, Grenoble, France, 2022. [Google Scholar]
- Grangeat, P.; Gharbi, S.; Accensi, M.; Grateau, H. Etude d’un modèle linéaire quadratique appliqué à la mesure optique infrarouge du gaz carbonique sanguin émis par la peau. In Proceedings of the 27° Colloque sur le Traitement du Signal et des Images, Lille, France, 29 August 2019. [Google Scholar]
- Madrolle, S.; Grangeat, P.; Jutten, C. A Linear-Quadratic Model for the Quantification of a Mixture of Two Diluted Gases with a Single Metal Oxide Sensor. Sensors 2018, 18, 1785. [Google Scholar] [CrossRef]
- Madrolle, S.; Duarte, L.T.; Grangeat, P.; Jutten, C. A Bayesian Blind Source Separation Method for a Linear-Quadratic Model. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 1242–1246. [Google Scholar]
- Madrolle, S.; Duarte, L.T.; Grangeat, P.; Jutten, C. Supervised Bayesian Source Separation of Nonlinear Mixtures for Quantitative Analysis of Gas Mixtures. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; pp. 1230–1233. [Google Scholar]
- Madrolle, S. Méthodes de Traitement du Signal Pour L’analyse Quantitative de Gaz Respiratoires à Partir d’un Unique Capteur MOX. Signal Processing for Quantitative Analysis of Exhaled Breath Using a Single MOX Sensor. EEATS—Signal Image Parole Telecoms. Ph.D. Thesis, UGA—Université Grenoble Alpes, Grenoble, France, 2016. [Google Scholar]
- Vaidya, D.S.; Nitsche, J.M.; Diamond, S.L.; Kofke, D.A. Convection-Diffusion of Solutes in Media with Piecewise Constant Transport Properties. Chem. Eng. Sci. 1996, 51, 5299–5312. [Google Scholar] [CrossRef]
- Ghasem, N. Modeling and Simulation of CO2 Absorption Enhancement in Hollow-Fiber Membrane Contactors Using CNT–Water-Based Nanofluids. J. Membr. Sci. Res. 2019, 5, 295–302. [Google Scholar] [CrossRef]
- Cao, F.; Gao, H.; Ling, H.; Huang, Y.; Liang, Z. Theoretical Modeling of the Mass Transfer Performance of CO2 Absorption into DEAB Solution in Hollow Fiber Membrane Contactor. J. Membr. Sci. 2020, 593, 117439. [Google Scholar] [CrossRef]
- Formaggia, L.; Quarteroni, A.; Veneziani, A. Cardiovascular Mathematics; MS&A: Modeling, Simulation and Applications; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-88-470-1151-9. [Google Scholar]
- Vlachopoulos, C.; O’Rourke, M.; Nichols, W.W. McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles, 6th ed.; CRC Press: London, UK, 2012; ISBN 978-0-429-16692-1. [Google Scholar]
- Guyton, A.C.; Hall, J.E.; Cuculici, G.P.; Gheorghiu, A.W. Tratat de Fiziologie a Omului. Bucureşti; Editura Medicală; Callisto: Bucureşti, Romania, 2007. [Google Scholar]
- Chappell, M.; Payne, S. Physiology for Engineers; Biosystems & Biorobotics; Springer International Publishing: Cham, Switzerland, 2016; Volume 13, ISBN 978-3-319-26195-9. [Google Scholar]
- Agache, P. Main Skin Physical Constants. In Agache’s Measuring the Skin: Non-Invasive Investigations, Physiology, Normal Constants; Humbert, P., Fanian, F., Maibach, H.I., Agache, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1607–1622. ISBN 978-3-319-32383-1. [Google Scholar]
- Severinghaus, J.W.; Stafford, M.; Thunstrom, A.M. Estimation of Skin Metabolism and Blood Flow with TcPo2 and TcPco2 Electrodes by Cuff Occlusion of the Circulation. Acta Anaesthesiol. Scand. 1978, 22, 9–15. [Google Scholar] [CrossRef]
- Agache, P. Physical, Biological and General Constants of the Skin. In Agache’s Measuring the Skin: Non-Invasive Investigations, Physiology, Normal Constants; Humbert, P., Fanian, F., Maibach, H.I., Agache, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1623–1626. ISBN 978-3-319-32383-1. [Google Scholar]
- Severinghaus, J.W.; Stupfel, M.; Bradley, A.F. Accuracy of Blood PH and Pco, Determination. J. Appl. Physiol. 1956, 9, 189–196. [Google Scholar] [CrossRef]
- Lumb, A.B. Nunn’s Applied Respiratory Physiology—Chapter 10 Carbon Dioxide; Elsevier Health Sciences: Amsterdam, The Netherlands, 2012; ISBN 978-0-7020-5416-7. [Google Scholar]
- Itoh, S.; Yamamoto, K.; Mikami, T. [Measurement of skin conductance to gas in adults]. Iyo Denshi Seitai Kogaku/Jpn. J. Med. Electron. Biol. Eng. 1987, 25, 227–231. [Google Scholar]
- Janssens, K.G.F.; Raabe, D.; Kozeschnik, E.; Miodownik, M.A.; Nestler, B. (Eds.) Computational Materials Engineering; Academic Press: Burlington, NJ, USA, 2007; p. iii. ISBN 978-0-12-369468-3. [Google Scholar]
- Kozeschnik, E. 5—Modeling Solid-State Diffusion. In Computational Materials Engineering; Janssens, K.G.F., Raabe, D., Kozeschnik, E., Miodownik, M.A., Nestler, B., Eds.; Academic Press: Burlington, NJ, USA, 2007; pp. 151–177. ISBN 978-0-12-369468-3. [Google Scholar]
- Langtangen, H.P.; Linge, S. Finite Difference Computing with PDEs: A Modern Software Approach; Texts in Computational Science and Engineering; Springer International Publishing: Cham, Switzerland, 2017; Volume 16, ISBN 978-3-319-55455-6. [Google Scholar]
- Linge, S.; Langtangen, H.P. Diffusion Equations. In Finite Difference Computing with PDEs: A Modern Software Approach; Langtangen, H.P., Linge, S., Eds.; Texts in Computational Science and Engineering; Springer International Publishing: Cham, Switzerland, 2017; pp. 207–322. ISBN 978-3-319-55456-3. [Google Scholar]
- Scherer, P.O.J. Computational Physics: Simulation of Classical and Quantum Systems; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-13989-5. [Google Scholar]
- Scherer, P.O.J. Advection. In Computational Physics: Simulation of Classical and Quantum Systems; Scherer, P.O.J., Ed.; Graduate Texts in Physics; Springer International Publishing: Cham, Switzerland, 2017; pp. 427–454. ISBN 978-3-319-61088-7. [Google Scholar]
- Scherer, P.O.J. Diffusion. In Computational Physics: Simulation of Classical and Quantum Systems; Graduate Texts in Physics; Scherer, P.O.J., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 479–491. ISBN 978-3-319-61088-7. [Google Scholar]
- Crank, J.; Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 1979; ISBN 978-0-19-853411-2. [Google Scholar]
- Comsa, M.-P.; Phlypo, R.; Grangeat, P. Inverting the Diffusion-Convection Equation for Gas Desorption through an Homogeneous Membrane by Kalman Filtering. In Proceedings of the 2022 30th European Signal Processing Conference (EUSIPCO), Belgrade, Serbia, 28 August–2 September 2022; pp. 1318–1322. [Google Scholar]
- Amarah, A.A.; Petlin, D.G.; Grice, J.E.; Hadgraft, J.; Roberts, M.S.; Anissimov, Y.G. Compartmental Modeling of Skin Transport. Eur. J. Pharm. Biopharm. 2018, 130, 336–344. [Google Scholar] [CrossRef]
- Dias, D.; Paulo Silva Cunha, J. Wearable Health Devices—Vital Sign Monitoring, Systems and Technologies. Sensors 2018, 18, 2414. [Google Scholar] [CrossRef]
- Jin, H.; Abu-Raya, Y.S.; Haick, H. Advanced Materials for Health Monitoring with Skin-Based Wearable Devices. Adv. Healthc. Mater. 2017, 6, 1700024. [Google Scholar] [CrossRef]
- Kireev, D.; Sel, K.; Ibrahim, B.; Kumar, N.; Akbari, A.; Jafari, R.; Akinwande, D. Continuous Cuffless Monitoring of Arterial Blood Pressure via Graphene Bioimpedance Tattoos. Nat. Nanotechnol. 2022, 17, 864–870. [Google Scholar] [CrossRef]
- Akinwande, D.; Kireev, D. Wearable Graphene Sensors Use Ambient Light to Monitor Health. Nature 2019, 576, 220–221. [Google Scholar] [CrossRef]
- Tricoli, A.; Nasiri, N.; De, S. Wearable and Miniaturized Sensor Technologies for Personalized and Preventive Medicine. Adv. Funct. Mater. 2017, 27, 1605271. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, S.; Zhang, D.; Yang, Y.; Zhao, J.; Yu, H.; Wang, T.; Wang, T.; Dong, X. Conductometric Room Temperature NOx Sensor Based on Metal-Organic Framework-Derived Fe2O3/Co3O4 Nanocomposite. Sens. Actuators B Chem. 2023, 390, 133894. [Google Scholar] [CrossRef]
- Tomasic, I.; Tomasic, N.; Trobec, R.; Krpan, M.; Kelava, T. Continuous Remote Monitoring of COPD Patients-Justification and Explanation of the Requirements and a Survey of the Available Technologies. Med. Biol. Eng. Comput. 2018, 56, 547–569. [Google Scholar] [CrossRef]
- Mochalski, P.; King, J.; Unterkofler, K.; Hinterhuber, H.; Amann, A. Emission Rates of Selected Volatile Organic Compounds from Skin of Healthy Volunteers. J. Chromatogr. B Analyt. Technol. Biomed. Life Sci. 2014, 959, 62–70. [Google Scholar] [CrossRef]
- Arakawa, T.; Suzuki, T.; Tsujii, M.; Iitani, K.; Chien, P.-J.; Ye, M.; Toma, K.; Iwasaki, Y.; Mitsubayashi, K. Real-Time Monitoring of Skin Ethanol Gas by a High-Sensitivity Gas Phase Biosensor (Bio-Sniffer) for the Non-Invasive Evaluation of Volatile Blood Compounds. Biosens. Bioelectron. 2019, 129, 245–253. [Google Scholar] [CrossRef] [PubMed]
- Ohkuwa, T.; Mizuno, T.; Kato, Y.; Nose, K.; Itoh, H.; Tsuda, T. Effects of Hypoxia on Nitric Oxide (NO) in Skin Gas and Exhaled Air. Int. J. Biomed. Sci. IJBS 2006, 2, 279–283. [Google Scholar] [PubMed]
- Sekine, Y.; Nikaido, N.; Sato, S.; Todaka, M.; Oikawa, D. Measurement of Toluene Emanating from the Surface of Human Skin in Relation to Toluene Inhalation. J. Skin Stem Cell 2019, 6, e99392. [Google Scholar] [CrossRef]
| Parameter | Explanation | Set Member |
|---|---|---|
| Total number of points considered to discretize the continuous spatial space (state vector dimension) | ||
| Total number of interior points considered in each compartment | ||
| Thickness value of each compartment | ||
| State vector | ||
| A | Transition matrix applied to state | |
| Slack variable for compartment boundaries | ||
| Command vector | ||
| Data observation vector | ||
| Command matrix | ||
| Observation vector of observation response function | ||
| Modelization noise vector | ||
| Observation noise | ||
| Modelization noise covariance matrix | ||
| Observation noise covariance matrix | ||
| Kalman gain matrix | ||
| Differential spatial operator | ||
| Signal regularity parameter |
| Parameter | Explanation |
|---|---|
| state vector at time step predicted at previous time step | |
| state vector at time step computed at time step | |
| prediction of the state vector at the next time step, | |
| uncertainty covariance matrix at time step predicted at previous time step | |
| uncertainty covariance matrix computed at the current state | |
| predicted uncertainty covariance matrix at the next time step, | |
| Kalman gain computed at the current state | |
| measurement at time step |
| Parameters | Noiseless Observation | Low Noise Observation | High Noise Observation |
|---|---|---|---|
| 1.3738 | 1.3738 | 1.3738 | |
| 1.3736 | 1.3736 | 1.3733 | |
| 0.0306 | 0.0306 | 0.0313 | |
| 0.011 | 0.014 | 0.036 | |
| 32.34 | 32.34 | 32.16 | |
| 1693 | 1694 | 1685 | |
| 618 | 618 | 618 | |
| 0 | 0 | 0 | |
| 958 | 959 | 931 |
| Parameters | Phase 1 Normocapnia | Phase 2 Hypocapnia | Phase 3 Normocapnia | Phase 4 Hypercapnia 1 | Phase 5 Hypercapnia 2 | Phase 6 Normocapnia | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.099 | 1.099 | 0.825 | 0.825 | 1.099 | 1.099 | 1.236 | 1.236 | 1.374 | 1.374 | 1.099 | 1.099 | |
| 3.668 | 1.094 | 3.416 | 1.019 | 3.583 | 1.069 | 4.003 | 1.19 | 4.42 | 1.317 | 3.841 | 1.145 | |
| (%) | −234 | 0.45 | −313 | −23.49 | −226 | 2.74 | −224 | 3.71 | −222 | 4.16 | −249 | −4.17 |
| 214.36 | 215.70 | 251.90 | 264.16 | 264.37 | 254.01 | 225.39 | 225.61 | 519.61 | 529.53 | |||
| Parameters | Values | Values |
|---|---|---|
| 2.68 | 0.065 | |
| (dB) | −7.48 | 24.82 |
| 330.03 | 330.03 | |
| 32.09 | 41.2 | |
| 369.65 | 369.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grangeat, P.; Duval Comsa, M.-P.; Koenig, A.; Phlypo, R. Dynamic Modeling of Carbon Dioxide Transport through the Skin Using a Capnometry Wristband. Sensors 2023, 23, 6096. https://doi.org/10.3390/s23136096
Grangeat P, Duval Comsa M-P, Koenig A, Phlypo R. Dynamic Modeling of Carbon Dioxide Transport through the Skin Using a Capnometry Wristband. Sensors. 2023; 23(13):6096. https://doi.org/10.3390/s23136096
Chicago/Turabian StyleGrangeat, Pierre, Maria-Paula Duval Comsa, Anne Koenig, and Ronald Phlypo. 2023. "Dynamic Modeling of Carbon Dioxide Transport through the Skin Using a Capnometry Wristband" Sensors 23, no. 13: 6096. https://doi.org/10.3390/s23136096
APA StyleGrangeat, P., Duval Comsa, M.-P., Koenig, A., & Phlypo, R. (2023). Dynamic Modeling of Carbon Dioxide Transport through the Skin Using a Capnometry Wristband. Sensors, 23(13), 6096. https://doi.org/10.3390/s23136096






