Abstract
Payload weight detection plays an important role in condition monitoring and automation of cranes. Crane cells and scales are commonly used in industrial practice; however, when their installation to the hoisting equipment is not possible or costly, an alternative solution is to derive information about the load weight indirectly from other sensors. In this paper, a static payload weight is estimated based on the local strain of a crane’s girder and the current position of the trolley. Soft-computing-based techniques are used to derive a nonlinear input–output relationship between the measured signals and the estimated payload mass. Data-driven identification is performed using a novel variant of genetic programming named grammar-guided genetic programming with sparse regression, multi-gene genetic programming, and subtractive fuzzy clustering method combined with the least squares algorithm on experimental data obtained from a laboratory overhead crane. A comparative analysis of the methods showed that multi-gene genetic programming and grammar-guided genetic programming with sparse regression performed similarly in terms of accuracy and both performed better than subtractive fuzzy clustering. The novel approach was able to find a more parsimonious model with its direct implantation having a lower execution time.
1. Introduction
Cranes are material-handling machines widely used in the industrial, construction, and logistic sectors. Monitoring the static and dynamic load of material handling systems is important to satisfy safety, reliability, performance, and cost requirements [1,2,3,4]. The weight of the payload is crucial input information in crane applications, such as control, condition monitoring, maintenance planning, prediction of failures, and remaining useful life of crane equipment. Crane cells and scales are commonly used in industrial practice and implemented in different forms in load monitoring systems, such as Load Moment Indicator (LMI) and Rated Capacity Indicator (RCI) [1,2]. For hydraulic cranes, the payload weight is usually determined based on the hydraulic pressures in the lift cylinders [5]. When the load transportation is performed by cranes using ropes, cables, or chains, it requires an additional installation, usually of a strain-gauge-based sensor, onto the hoisting equipment.
The development of controllers for the safe and efficient operation of cranes in terms of crane positioning and payload sway suppression is an active area of research. There have been several control strategies [6] such as partial feedback linearization [7], sliding mode control [8], and nonlinear model predictive control [9] that require information about the operating point of the crane such as payload mass. Payload weight detection also plays an important role in condition monitoring [1,2]. However, in industrial practice there are a variety of crane configurations, thus, when the crane scale installation to the hoisting equipment is not possible, difficult, and costly, deteriorates crane maneuverability, or when the complementary measurement devices for hybrid payload monitoring are required, an alternative solution is to derive information about the load weight indirectly from other sensors. The problem of load estimation for material handling lifting systems in several papers is studied through analytical modeling of their static and/or dynamics. A review of model-based methods of payload estimations in hydraulic excavators and a discussion of their applicability is provided in [10]. The model-based static and dynamic load estimation for hydraulically actuated material handling machines is commonly performed based on information obtained from the hydraulic pressure (pressure difference across the boom) and angular position sensors, while the model parameters are estimated offline and/or online usually using least square [11] or recursive least square method [12]. A variety of models addressing the dynamics of a hoisted load are developed in the literature mostly using the Lagrangian approach, such as a dynamic model of the hoisting motion of a hydraulic lattice mobile crane [13] and an overhead crane hoist with a crane’s structure dynamic model [14,15,16]. An overhead crane hoist with an asynchronous electric motor model is developed and analyzed in numerical simulations to determine the relationship between the weight of a payload and the deviation in the amplitude of the electric motor current [17]. A digital-twin approach with a CAD model of a knuckle boom crane was proposed for real-time monitoring of a payload weight in [18]. A virtual strain gauge sensor was implemented with a nonlinear finite element model of a crane to find a linear relationship between the payload weight input and strain output signals, then the load weight is estimated through the inverse modeling approach applying the input signal from the physical strain gauge used in the experimental setup. The idea to estimate a payload weight using data-driven models identified using machine learning techniques based on data collected from available sensors is implemented in several recent papers. The ANN model trained using the Levenberg–Marquardt algorithm is developed in [19] for payload weight detection of the John Deere 644J hydraulic four-wheel-drive loader based on the differential pressure across the boom cylinder, boom and bucket strokes, and vibration acceleration of the frame. The ANN model is used to estimate a payload mass for a hydraulic forestry crane based on the hydraulic pressure of the inner boom cylinder and the grapple position [20,21]. The vision system and convolutional neural network are reported to recognize a wood log weight for a forestry crane [22]. The quay crane load identification method based on the signals from an accelerometer and strain gauge sensors installed on the crane’s structure parts is reported in [23].
Strain gauge sensors are used in a variety of crane applications. Strain-gauge-based methods are applied to fatigue life prediction of existing crane runway girders and to evaluate the residual operating life of a bridge crane girder [24,25,26]. A combination of strain-gauge measurement and finite element analysis is used to identify crane wheel load for a quay ship-to-shore crane [27]. Strain sensing is used to identify the occurrence and intensity of the overhead crane skewing [28] and in the new technique of payload sway angle measurement [29].
In this paper, a static payload weight is estimated based on the local strain of a crane’s girder and the current displacement of the trolley. The problem of the crane girder’s deformation due to a moving trolley with a rope-suspended payload is studied in the literature mostly using analytical models developed based on the Euler-Bernoulli or Timoshenko beam deformation theories [30,31,32,33,34], or through applying finite elements methods [35,36,37,38]. The analytical models can be used to solve a nonlinear static inverse problem: knowing the deformation of the crane’s girder and trolley displacement, determine the payload mass. However, obtaining an accurate mathematical model can be a challenging process and there are many factors, complexity characteristics, nonlinearities, parameters’ uncertainty, etc., affecting the deviation between a mathematical model and the physical system. Thus, in this paper data-driven techniques are adapted to model-based estimation of a static payload weight. This work follows the previous paper [39], in which a payload weight is estimated for an overhead crane based on a local strain of a girder and the trolley position using a data-driven Takagi–Sugeno fuzzy (TSF) model identified through the subtractive clustering method and least square algorithm, thus, the nonlinear relation between the payload weight, strain, and trolley’s position is approximated by linear models expressed in fuzzy rule consequents. In comparison to the previous work, this paper addresses the issue of improving estimation accuracy and increasing interpretability using genetic-programming-based model structure optimization. Genetic programming is an evolutionary-based method whose outputs are computer programs. This makes genetic programming well suited to find a mathematical function that relates the input to the output, which is interpretable by the user and can be directly implemented reducing execution time. The reduction in execution time of the model is a significant advantage since the payload estimation is carried out online. Two variants of genetic programming, multi-gene genetic programming (MGGP) and grammar-guided genetic programming with sparse regression (G3PSR) are applied to obtain a static data-driven input–output model. The G3PSR algorithm uses sparse regression on a fixed set of evolved candidate model terms that are obtained from a biased search of the function space and the l0 penalty is added for model selection, which results in reduced complexity and decreases the probability of overfitting. The subsequent sparse regression problem is solved by using the monotonically accelerated proximal gradient descent algorithm [40]. To the best of the authors’ knowledge, the only other evolutionary sparse regression algorithm is based on an elastic net regularization [41]. The contribution of this paper can be summarized as follows:
- Develop a novel genetic programming variant called G3PSR that can be used for symbolic regression problems that can be expressed as a linear in the parameters model.
- Apply genetic programming variants, namely G3PSR and MGGP, to identify a mathematical relationship between the payload mass and the trolley position and girder strain.
- Compare the genetic programming models for mass estimation with a method proposed in the literature [39].
The static model identification process was based on the experimental data obtained from a laboratory overhead crane. The comparative analysis of G3PSR, MGGP, and TSF models is presented in terms of accuracy and complexity. To the best of our knowledge, this is the first work on the crane’s payload weight estimation using a data-driven model identified using multi-gene genetic programming and grammar-guided genetic programming with sparse regression. The other genetic programming-based crane modeling approaches used the MGGP for payload sway prediction [42,43]. Crane dynamics modeling and control were also studied by using a genetic algorithm (GA) in [44,45,46,47].
The rest of the paper is organized as follows. In Section 2, the methods used to identify the models for payload weight estimation are described. Section 3 presents the experimental setup with a laboratory overhead crane, discusses the results of identification experiments, and compares the model performances, while the final conclusions are delivered in Section 4. The lists of symbols and abbreviations used in the paper with their definitions are exposed in Appendix A.
2. Methodology
Genetic programming is an evolutionary algorithm that is able to synthesize programs and was developed as an offshoot of genetic algorithms in the 1990s by Koza [48]. One of the important applications of genetic programming has been symbolic regression in which the aim is to identify a mathematical expression that best fits an input–output dataset. In traditional genetic programming, an individual is represented by an abstract syntax tree (AST) whose offspring, obtained by undergoing a variation operation, passes on to the next generation. Different variants of genetic programming have developed, such as multi-dimensional genetic programming, where an individual is composed of different subprograms such as in multi-gene genetic programming [49], linear genetic programming [50], grammatical evolution [51], Keizen programming [52], etc.
2.1. Multi-Gene Genetic Programming
Multi-gene genetic programming is a robust variant of genetic programming that was developed in [49]. In MGGP, each individual in the population is composed of a linear combination of functions called genes
where is the model output, is the coefficient of the i-th, gene and is the result of evaluating the function represented by the i-th gene. The expression in (1) allows MGGP to combine traditional genetic programming’s ability to evolve a sequence of functions together with the linear least squares algorithm to improve the performance in terms of speed of finding a solution to the symbolic regression problem as well as accuracy.
Selection in MGGP occurs in two stages, at first a parent is selected based on the individual’s fitness, then a gene within the parent is selected at random. Once the gene is selected, it undergoes one of four variation operators: subtree crossover, high-level crossover [53], subtree mutation, and point mutation as shown in Figure 1, Figure 2, Figure 3 and Figure 4. GPTIPS2 [53] an MGGP toolbox for MATLAB is used to obtain the model.
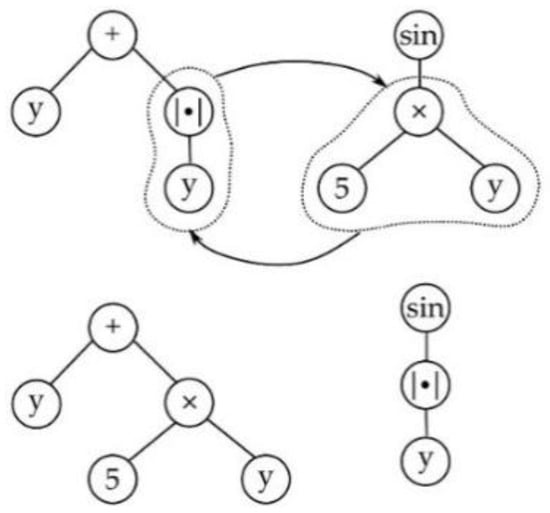
Figure 1.
Subtree crossover.
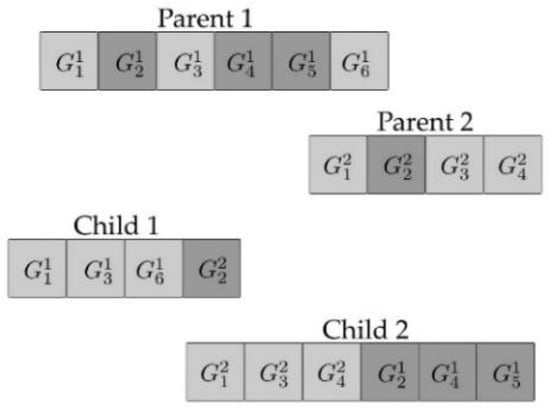
Figure 2.
High level crossover.
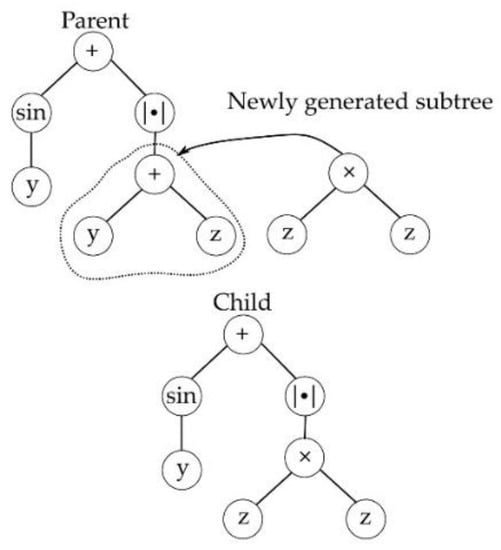
Figure 3.
Subtree mutation.
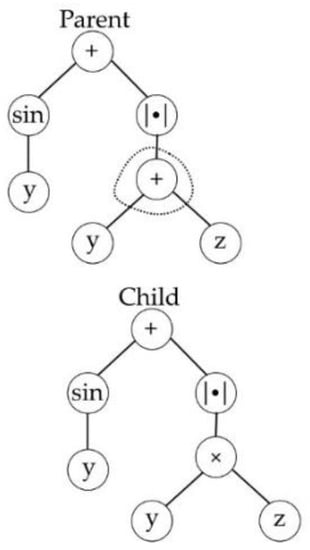
Figure 4.
Point mutation.
The configuration of the multi-gene genetic programming hyperparameters used to obtain the mathematical expression of the payload mass, , given the input data (trolley position) and strain were obtained using trial and error based on previously published values [54], with the exception of the maximum number of genes, which was chosen to be 25 in order to have a fair comparison between MGGP and G3PSR, is given in Table 1.

Table 1.
Configuration of the MGGP hyperparameters.
2.2. Grammar-Guided Genetic Programming with Sparse Regression
Grammar-guided genetic programming with sparse regression is a novel algorithm in which an individual is composed of functions, called model terms, and are the equivalent of genes in MGGP. The difference in representation between MGGP and G3PSR is that in MGGP an individual can have between 1— genes, while in G3PSR an individual always has candidate model terms. In order to select which model terms are included in the model an -penalty is added to the regression problem (2) which leads to a sparse solution vector
where the counts the number of nonzero elements in a vector, i.e., , is the measured output data, is a matrix whose columns, j, are composed of evaluating the functions represented by the model terms and normalized by , are the model term coefficients and is a constant that promotes the sparsification of the solution. The addition of the -penalty, which is nonconvex, makes solving (2) NP hard [55]. The solution to (2) is found using the monotone approximated gradient descent algorithm (mAPG) [40]. The pseudocode for mAPG is given in Algorithm 1, where the proximal operator for the -penalty is the hard thresholding operator (3). The algorithm runs until the maximum number of iterations has been reached or the objective function converges, i.e., is within a specified tolerance.
| Algorithm 1: mAPG. |
| Input: Initialize: while not converged do Initialize step size and using Barzilai-Borwein method while do end while while do end while end while Output: |
The variation operators used in G3PSR are similar to those used in MGGP with two main differences: the offspring should be admissible, as defined by the grammar, and in choosing the model terms that undergo crossover or mutation. Once an individual is selected from the population using tournament selection, the variation step is biased in the same manner as in [56] by setting the probability of choosing a model term from the individual proportional to its coefficient. The coefficients are first normalized using (4) and then the probability is calculated using (5), resulting in a higher chance of choosing model terms that have low or zero coefficients.
Grammars have been used in genetic programming to restrict the search space to increase interpretability and increase accuracy by incorporating prior knowledge about the problem. Several variants of grammar-based genetic programming, such as context-free grammar genetic programming [57] and grammatical evolution [51], have been applied successfully including the identification of nonparametric models of mechanical systems [58]. Context-free grammar is a four-tuple used in computer science to generate syntactically correct sentences, where is the start symbol, is the set of terminal symbols, is the set of all nonterminal symbols, and is the set of production rules. The configuration of the G3PSR hyperparameters is given in Table 2, and the production rules are given in Table 3.

Table 2.
Configuration of the G3PSR hyperparameters.

Table 3.
Grammar used to obtain the G3PSR model.
2.3. TS Fuzzy Model
TS fuzzy model [59,60] used in comparative study is defined as a set of R if-then rules with locally linear models in rule consequents:
where i = 1, 2, …, R, , and are the rule-consequent parameters estimated using the least square method. The model output is calculated through interpolations of linear models between centroids of fuzzy clusters in the input space corresponding to rule antecedents:
where is a weight of i-th rule calculated as a product of Gaussian membership functions of input variables x (trolley position) and ε (strain)
where , , , and are the rule antecedent parameters corresponding to the expected values ( and coordinates of fuzzy clusters centroids in the input Cartesian space) and their standard deviations ( and ).
The TSF model identification was performed using a combination of the fuzzy subtractive clustering algorithm [61] and the least square method. The subtractive algorithm was applied to derive the R rule’s antecedents from measurement data through an iterative procedure that starts with the calculation of the potential of each k-th data point to be a cluster center based on a squared distance to the other data points:
where is a positive constant called cluster radius. The data point with the highest potential is chosen as the first cluster center. In each next i-th step, the potential of all remaining data points is reduced according to their distance to the cluster center selected in the previous step:
where , and b is a positive parameter called the squash factor. The termination condition is defined twofold [61]. The upper and lower thresholds of data points’ potential are determined using and called the accept and reject ratio, respectively,
where P1 is the potential of the data point chosen as the first cluster center. Thus, the cluster centroid is either accepted if , or rejected if , and the algorithm is terminated. If condition (11) is satisfied, the shortest distance between and all previously found centroids is verified using condition (12). The data point is accepted as the centroid if condition (12) is satisfied, otherwise, the data point with the next highest potential is tested, and the algorithm is terminated if all data points violate condition (12).
3. Results of Identification Experiments
The data used in the identification procedure were obtained from experiments carried out on a double girder overhead crane installed in a laboratory (Figure 5). The trolley is driven by an AC gear motor with a gear ratio of 15.5, operating at 1400 rpm and output power of 0.12 kW. The girders’ length, trolley wheelbase, and traveling range are 2.4 m, 0.3 m, and 1.8 m, respectively. The trolley position x along the girders is measured using the incremental encoder installed on the trolley’s wheel with a resolution of 200 pulses per revolution (ppr). The strain gauge supplied by the ADAM 3016 input module is applied to measure the strain at the middle point of the girder. The data from sensors are sampled at 10 Hz using a PC with 16GB RAM and Quad Core 4GHz Intel Core i7-6700K CPU running Windows 10 and MATLAB R2020.

Figure 5.
The laboratory stand.
A series of experiments with different payload masses within the range of 20 kg and 100 kg were carried out to collect training and testing data for identification. It was assumed, that payload weight estimation is performed based on the signal from the strain gauge located at the midpoint of the girder and the trolley position ranging in x = [0.4 m, 1.4 m] (with the strain gauge sensor at the midpoint of this interval). Figure 6 presents the experimental data obtained in experiments in which the trolley transported payload along the girder. The experimental data used to identify G3PSR and MGGP models were partitioned into three sets, the training set, validation set, and testing set. The training set is used to minimize (2) for G3PSR and (1) for MGGP, and the root mean square error (RMSE) (13) on the training set is used as the fitness function in G3PSR and MGGP. The validation set is used for model selection, i.e., the model with the lowest RMSE on the validation set is stored as the best model, while the testing set is used to evaluate the performance of the obtained model. The testing set comprises data from experiments with payload masses of 30, 50, 70, and 90 kg (Figure 6), while the rest of the experimental data (payload mass: 20, 40, 60, 80, and 100 kg) are combined and split randomly with a 70:30 ratio into the training and validation sets, respectively. The performances of the models were compared using relative error (RE), mean relative error (MRE), and RMSE (13), where and are the real and model-estimated values of weight, respectively, and is the number of sample data.
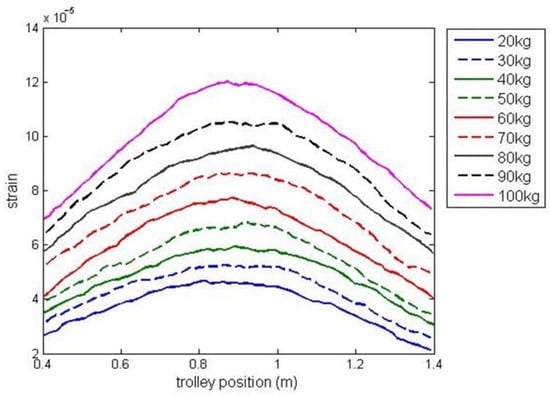
Figure 6.
Experimental data partition into training and validation data (solid line), and testing data (dashed line).
The model terms and their corresponding coefficients for G3PSR and MGGP static models obtained in identification experiments are given in Table 4. The value of the fitness function (RMSE) for both the training and validation data sets are shown in Figure 7 and Figure 8, for the G3PSR and MGGP models, respectively. Since both strategies use the performance on the validation set as the criteria for selection, the final models had RMSEs on the validation set of 1.2077 and 1.2565 by applying the G3PSR and MGGP techniques, respectively.

Table 4.
The model terms and coefficients generated by G3PSR and MGGP.
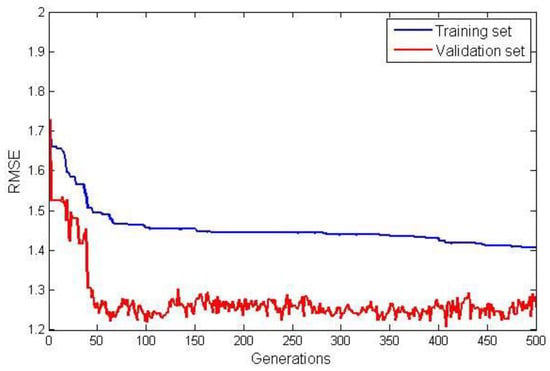
Figure 7.
RMSE for training and validation data for the G3PSR.
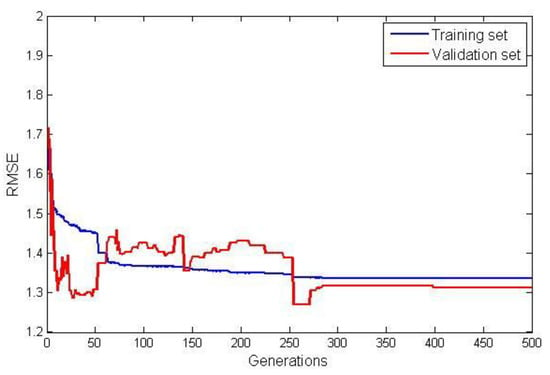
Figure 8.
RMSE for training and validation data for the MGGP.
In the case of the TSF model identified using the combination of subtractive clustering and least square methods, the best model was obtained by setting by trial and error the cluster radius and squash factor to and b = 1.1, respectively. For this setting, a clustering technique partitioned input space into eight clusters generating rules with premise and consequent parameters given in Table 5.

Table 5.
TSF model parameters.
The comparison of model performances for testing data in terms of accuracy and complexity is presented in Table 6. The G3PSR and MGGP models show similar performances for testing data: RMSE and MRE are 1.7813 and 0.0285 for G3PSR, while for MGGP they are 1.8069 and 0.0283, respectively. The TSF model performs slightly worse, as the RMSE and MRE are 1.8875 and 0.0294, respectively. In terms of the number of parameters to be estimated, the G3PSR and MGGP models have 14 and 17 parameters, respectively, while the number of parameters of the TSF model (56 parameters) is significantly greater. The G3PSR model notably outperforms the other models in terms of computational complexity, since the execution time (mean value from runs plus/minus standard deviation) is ms, while the MGGP and TSF models’ execution times are ms and ms, respectively.

Table 6.
Comparison of models complexity and performances for testing data.
Payload estimated mass along the test trajectories is compared in Figure 9, while the relative errors between the real and model-estimated values of weight for G3PSR, MGGP, and TSF models estimating mass 30 kg, 50 kg, 70 kg, and 90 kg are presented in Figure 10, Figure 11, Figure 12 and Figure 13, as well as in Table 7 where the models’ performances are compared using the MRE and maximum value of RE. Obviously, the accuracy in weight estimation increases with the increase in the payload mass. The models’ performances are similar for a payload mass of 90 kg. The maximum relative error is 0.0395, 0.0388, and 0.0402 for G3PSR, MGGP, and TSF models, respectively. The second obvious conclusion, which comes from Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 is that dividing a girder length into more sections with strain gauges at midpoints enhances estimation accuracy at the cost of more sensors and models to be used. It should be also noticed that the models were developed for the payload weight range of 20-100 kg, and we can expect that model complexity can rise with the increase in the range of the payload mass to be estimated. Thus, model optimization is necessary to save computational consumption.
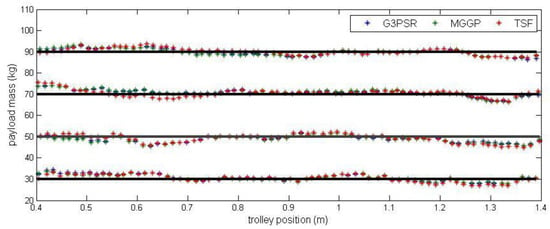
Figure 9.
Payload estimated mass along the test trajectories.
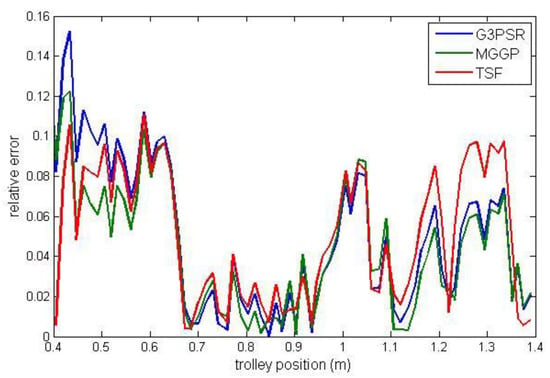
Figure 10.
Relative error for estimated mass 30 kg.
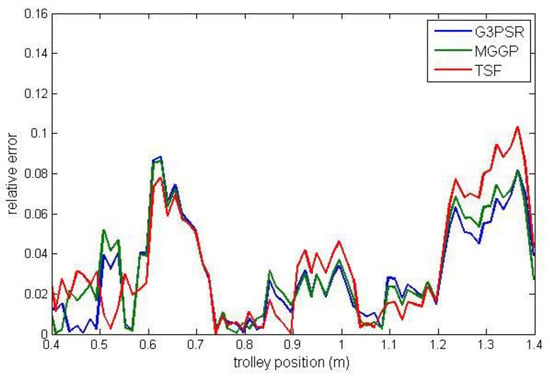
Figure 11.
Relative error for estimated mass 50 kg.
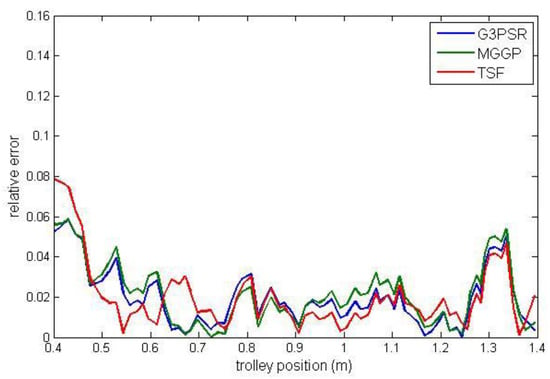
Figure 12.
Relative error for estimated mass 70 kg.
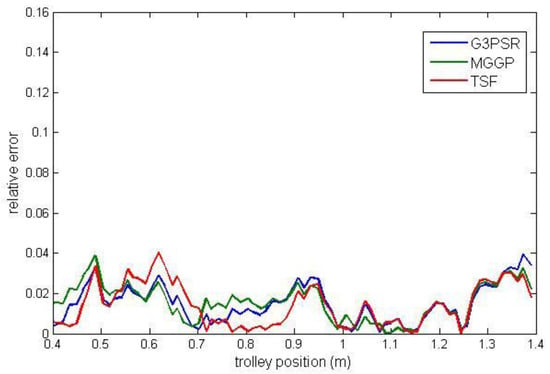
Figure 13.
Relative error for estimated mass 90 kg.

Table 7.
Models performances at testing operating points.
Uncertainty analysis is performed taking into account the effect of the strain signal variation. Another set of testing data obtained from eight experiments carried out on the laboratory stand was used to determine the standard deviation of strain signal with respect to the data used to identify the models assumed as the nominal data for comparison. The nominal strain input data used for models identification were then perturbed with a standard deviation of . The comparison of model performances at testing operating points for nominal input data ) and strain signal deviated by is presented in Table 8 using RMSE and MRE. All models exhibit a similar increase in RMSE (2.2115, 2.2104, and 2.2889 for G3PSR, MGGP, and TSF models, respectively) when the nominal trajectory of strain signal is deviated by , while the G3PSR model is slightly less affected by strain signal perturbation , since the RMSE is 2.0835, 2.2169, and 2.2169 for G3PSR, MGGP, and TSF models, respectively. Taking into account the nominal and deviated strain signal, the uncertainty of the models’ output (estimated payload weight) is expressed by standard error calculated according to (14), and the results are presented in Table 9 and Figure 14 (where the dotted line is a linear interpolation between testing points). The general tendency observed in Figure 14 and Table 9 is that the standard error decreases with the increase in the payload weight from 30 to 90 kg, from 2.2297 to 1.7460 for the G3PSR model, and from 2.0670 to 1.7786 and from 2.2066 to 1.7740 for MGGP and TSF models, with the exception of 50 kg.

Table 8.
Models performances at testing operating points for deviated strain input signal.

Table 9.
Standard error at testing operating points.
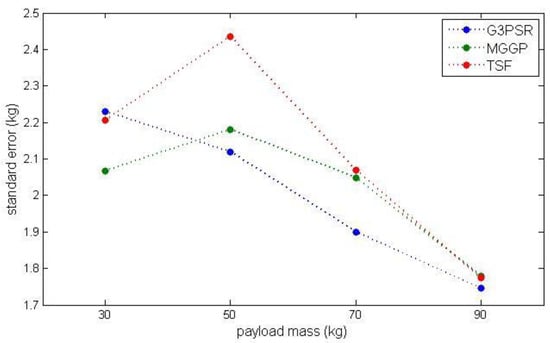
Figure 14.
Standard error at testing points.
4. Conclusions
The paper compares the data-driven soft-computing models for payload weight estimation for an overhead crane. The payload mass is estimated based on a local strain of a crane’s girder and the trolley position. Two genetic programming variants are used for model optimization, multi-gene genetic programming, a novel technique and grammar-guided genetic programming with sparse regression. The genetic programming methods are compared with the TSF model evolved using the fuzzy subtractive clustering and least square methods. The comparative study is presented in terms of accuracy and complexity. The G3PSR and MGGP models show similar estimation accuracy with an RMSE of 1.7813 and 1.8069 respectively, and slightly better than in the case of the TSF model with an RMSE of 1.8875. The relative error decreased for all models identified as the payload mass increased, this is due to the fact that the absolute error does not differ by a significant amount depending on the payload mass while the relative error is normalized by the payload mass, which, when increased, results in a decrease in the relative error. The model complexity expressed as the number of model parameters to be estimated is lowest for the G3PSR model (14 parameters) in comparison to the MGG and TSF models at 17 and 56 parameters, respectively. The significant difference we observe in the model execution time is that the G3PSR outperforms the other models with a mean execution time of ms, while the MGGP model and the TSF model had mean execution times of ms and ms, respectively. The direct implementation of the input–output function decreased the computational time by approximately 98.6% and 78.1% for the G3PSR and MGGP models, respectively, when compared to the TSF model. Future works will be focused on testing the proposed approach on a crane system with a larger girder length and payload weight range. The G3PSR algorithm would also be applied to the inverse modeling approach to estimate the strain/stress of a girder [18] for a given payload mass, as well as in other static and dynamic model optimization problems [62,63].
Author Contributions
T.K. and J.S. conceived, designed, and performed the experiments; analyzed the data; and wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
The work has been financially supported by the Polish Ministry of Education and Science.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Symbols and Definitions
This appendix consists of a list of all the symbols used in this paper along with their definitions (Table A1) in addition to abbreviations (Table A2).

Table A1.
List of symbols and their definitions.
Table A1.
List of symbols and their definitions.
| Variable | Definition |
|---|---|
| Squash factor, cluster center, distance between cluster centers | |
| Suspended payload mass | |
| Rule consequent parameters | |
| Cluster radius | |
| Weights of i-th rule | |
| Trolley position | |
| Set of all nonterminal symbols | |
| Set of production rules (also potential of chosen datapoint as cluster center and probability of selection) | |
| Start symbol | |
| Strain | |
| Accept ratio, reject ratio | |
| Step size | |
| Model term coefficients | |
| Normalized coefficients | |
| Sparsification parameter | |
| Regressor matrix | |
| Set of all terminal symbols |

Table A2.
List of abbreviations and their definitions.
Table A2.
List of abbreviations and their definitions.
| Abbreviation | Definition |
|---|---|
| GP | Genetic programming |
| G3PSR | Grammar guided genetic programming with sparse regression |
| mAPG | Monotone accelerated proximal gradient descent |
| MGGP | Multi-gene genetic programming |
| PTC2 | Probability tree creation 2 |
| TSF | Takagi–Sugeno fuzzy |
References
- Neitzel, R.L.; Seixas, N.S.; Ren, K.K. A review of crane safety in the construction industry. Appl. Occup. Environ. Hyg. 2001, 16, 1106–1117. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Cho, Y.K.; Chen, J. A framework for real-time pro-active safety assistance for mobile crane lifting operations. Autom. Constr. 2016, 72, 367–379. [Google Scholar] [CrossRef]
- Świder, J.; Szewerda, K.; Herbuś, K.; Jura, J. Testing the impact of braking algorithm parameters on acceleration and braking distance for a suspended monorail with regard to acceptable travel speed in hard coal mines. Energies 2021, 14, 7275. [Google Scholar] [CrossRef]
- Świder, J.; Szewerda, K.; Tokarczyk, J.; Plewa, F.; Grodzicka, A.; Kędzia, K. An overview of possibilities of increasing the permissible speed of underground suspended monorails for transporting people in the conditions of polish underground mining. Energies 2023, 16, 3703. [Google Scholar] [CrossRef]
- Kalairassan, G.; Boopathi, M.; Mohan, R.M. Analysis of load monitoring system in hydraulic mobile cranes. IOP Conf. Ser. Mater. Sci. Eng. 2017, 263, 062045. [Google Scholar] [CrossRef]
- Ramli, L.; Mohamed, Z.; Abdullahi, A.M.; Jaafar, H.I.; Lazim, I.M. Control strategies for crane systems: A comprehensive review. Mech. Syst. Signal Process. 2017, 95, 1–23. [Google Scholar] [CrossRef]
- Hamdy, M.; Shalaby, R.; Sallam, M. A hybrid partial feedback linearization and deadbeat control scheme for a nonlinear gantry crane. J. Frankl. Inst. 2018, 355, 6286–6299. [Google Scholar] [CrossRef]
- Guo, Q.; Chai, L.; Liu, H. Anti-swing sliding mode control of three-dimensional double pendulum overhead cranes based on extended state observer. Nonlinear Dyn. 2023, 111, 391–410. [Google Scholar] [CrossRef]
- Krupa, F.; Nemcik, J.; Ozana, S.; Slanina, Z. NMPC design and embedded application for overhead crane: Case study. IFAC-PapersOnLine 2022, 55, 356–361. [Google Scholar] [CrossRef]
- Bennett, N.; Walawalkar, A.; Schindler, C. Payload estimation in excavators: Model-based evaluation of current payload estimation systems. In Proceedings of the 3rd Commercial Vehicle Technology Symposium (CTV 2014), University of, Kaiserslautern, Kaiserslautern, Germany, 11–13 March 2014; pp. 333–346. [Google Scholar]
- Ferlibas, M.; Ghabcheloo, R. Load weight estimation on an excavator in static and dynamic motions. In Proceedings of the 17th Scandinavian International Conference on Fluid Power (SICFP’21), Linkoping, Sweden, 1–2 June 2021. [Google Scholar]
- Renner, A.; Wind, H.; Sawodny, O. Online payload estimation for hydraulically actuated manipulators. Mechatronics 2020, 66, 102322. [Google Scholar] [CrossRef]
- Sun, G.; Kleeberger, M.; Liu, J. Complete dynamic calculation of lattice mobile crane during hoisting motion. Mech. Mach. Theory 2005, 40, 447–466. [Google Scholar] [CrossRef]
- Bogdevičius, M.; Vik, A. Investigation of the dynamics of an overhead crane lifting process in a vertical plane. Transport 2005, 20, 176–180. [Google Scholar] [CrossRef]
- Gąska, D.; Margielewicz, J.; Haniszewski, T.; Matyja, T.; Konieczny, Ł.; Chróst, P. Numerical identification of the overhead traveling crane’s dynamic factor caused by lifting the load off the ground. J. Meas. Eng. 2015, 3, 34–35. [Google Scholar]
- Haniszewski, T. Modeling the dynamics of cargo lifting process by overhead crane for dynamic overload factor estimation. J. Vibroengineering 2017, 19, 75–86. [Google Scholar] [CrossRef]
- Semykina, I.Y.; Kipervasser, M.V.; Gerasimuk, A.V. Study of drive currents for lifting bridge cranes of metallurgical enterprises or early diagnosis of load excess weight. J. Min. Inst. 2021, 247, 122–131. [Google Scholar] [CrossRef]
- Moi, T.; Cibicik, A.; Rolvag, T. Digital twin based condition monitoring of a knuckle boom crane: An experimental study. Eng. Fail. Anal. 2020, 112, 104517. [Google Scholar] [CrossRef]
- Hindman, J.J. Dynamic Payload Estimation in Four Wheel Drive Loaders. Ph.D. Dissertation, University of Saskatchewan, Saskatoon, SK, Canada, 2008. [Google Scholar]
- Geiger, C.; Greff, D.; Geimer, M.; Starke, M.; Ziesak, M. The potential of a weight detection system for forwarders using an artificial neural network. In Proceedings of the 51st International Symposium on Forestry Mechanization: Improved Forest Mechanisation: Mobilizing Natural Resources and Preventing Wildfires, Madrid, Spain, 25–27 September 2018; pp. 157–164. [Google Scholar]
- Starke, M.; Geiger, C. Field setup and assessment of a cloud-data based crane scale (CCS) considering weight and local green wood density-related volume references. Croat. J. For. Eng. 2022, 43, 29–45. [Google Scholar] [CrossRef]
- Geiger, C.; Maier, N.; Kalinke, F.; Geimer, M. Assistance system for an automated log-quality and assortment estimation based on data-driven approaches using hydraulic signals of forestry machines. In Proceedings of the 12th International Fluid Power Conference (IFK 2020), Dresden, Germany, 12–14 October 2020; pp. 83–92. [Google Scholar]
- Zhou, X.; Hu, X. Load identification method of crane based on vibration acceleration signal and stress signal. Int. Core J. Eng. 2022, 8, 741–747. [Google Scholar]
- Pástor, M.; Lengvarsky, P.; Hagara, M.; Kulka, J. Experimental investigation of the fatigue life of a bridge crane girder using S-N method. Appl. Sci. 2022, 12, 10319. [Google Scholar] [CrossRef]
- Frankovský, P.; Delyová, I.; Sivák, P.; Kurylo, P.; Pivarčiová, E.; Neumann, V. Experimental assessment of time-limited operation and rectification of a bridge crane. Materials 2020, 13, 2708. [Google Scholar] [CrossRef]
- Rettenmeier, P.; Roos, E.; Weihe, S.; Schuler, X. Assessment of mixed mode crack propagation of crane runway girders subjected to cyclic loading. Eng. Fract. Mech. 2016, 153, 11–24. [Google Scholar] [CrossRef]
- Starykov, M.; Kokoshko, E. Approach for measuring a ship to shore crane actual wheel load. J. Marit. 2022, 1, 25–28. [Google Scholar] [CrossRef]
- Mantič, M.; Kuľka, J.; Grega, R.; Virostko, M.; Kopas, M. Application of sensors for incorrect behavior identification in a transport system. Sensors 2023, 23, 1635. [Google Scholar] [CrossRef] [PubMed]
- Grosinger, P.; Rybář, J.; Dunaj, Š.; Ďuriš, S.; Hučko, B. A new payload swing angle sensing device and its accuracy. Sensors 2021, 21, 6612. [Google Scholar] [CrossRef] [PubMed]
- Michaltsos, G.T.; Sophianopoulos, D.; Kounadis, A.N. The effect of a moving mass and other parameters on the dynamic response of a simply supported beam. J. Sound Vib. 1996, 191, 357–362. [Google Scholar] [CrossRef]
- Oguamanam, D.C.D.; Hansen, J.S.; Heppler, G.R. Dynamic response of an overhead crane system. J. Sound Vib. 1998, 213, 889–906. [Google Scholar] [CrossRef]
- Dyniewicz, B.; Bajer, C.I. New feature of the solution of a Timoshenko beam carrying the moving mass particle. Arch. Mech. 2010, 62, 327–341. [Google Scholar]
- Xin, Y.; Xu, G.; Su, N.; Dong, Q. Nonlinear vibration of ladle crane due to a moving trolley. Math. Probl. Eng. 2018, 2018, 5756180. [Google Scholar] [CrossRef]
- Chen, Q.; Cheng, W.; Gao, L.; Du, R. Dynamic response of a gantry crane’s beam subjected to a two-axle moving trolley. Math. Probl. Eng. 2020, 2020, 3096213. [Google Scholar] [CrossRef]
- Wu, J.J. Transverse and longitudinal vibrations of a frame structure due to a moving trolley and the hoisted object using moving finite element. Int. J. Mech. Sci. 2008, 50, 613–625. [Google Scholar] [CrossRef]
- Zrnic, N.D.; Hoffmann, K.; Bosnjak, S.M. Modelling of dynamic interaction between structure and trolley for mega container cranes. Math. Comput. Model. Dyn. Syst. 2009, 15, 295–311. [Google Scholar] [CrossRef]
- Jaafar, H.I.; Mohamed, Z.; Jamian, J.J.; Abidin, A.F.Z.; Kassim, A.M.; Ghani, Z.A. Dynamic behavior of a nonlinear gantry crane system. Proc. Technol. 2013, 11, 419–425. [Google Scholar] [CrossRef]
- Milana, G.; Banisoleiman, K.; González, A. An investigation into the moving load problem for the lifting boom of a ship unloader. Eng. Struct. 2021, 234, 111899. [Google Scholar] [CrossRef]
- Smoczek, J.; Hyla, P.; Kusznir, T. Machine learning based approach to a crane load estimation. J. KONBiN 2021, 51, 1–10. [Google Scholar] [CrossRef]
- Huan, L.; Zhouchen, L. Accelerated proximal gradient methods for nonconvex programming. In Proceedings of the NIPS15 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 379–387. [Google Scholar]
- Goharoodi, S.K.; Dekemele, K.; Loccufier, M.; Dupre, L.; Crevecoeur, G. Evolutionary-based sparse regression for the experimental identification of Duffing oscillator. Math. Probl. Eng. 2020, 2020, 7286575. [Google Scholar]
- Kusznir, T.; Smoczek, J. Genetic programming based identification of an overhead crane. J. KONBiN 2021, 51, 123–133. [Google Scholar] [CrossRef]
- Kusznir, T.; Smoczek, J. Multi-gene genetic programming-based identification of a dynamic prediction model of an overhead traveling crane. Sensors 2022, 22, 339. [Google Scholar] [CrossRef] [PubMed]
- Kawada, K.; Yamamoto, T. Evolutionary identification using closed-loop data for a mechanical system. In Proceedings of the SICE Annual Conference, IEEE, Taipei, Taiwan, 18–21 August 2010; pp. 1065–1070. [Google Scholar]
- Duong, S.C.; Uezato, E.; Kinjo, H.; Yamamoto, T. A hybrid evolutionary algorithm for recurrent neural network control of a three-dimensional tower crane. Autom. Constr. 2012, 23, 55–63. [Google Scholar] [CrossRef]
- Smoczek, J.; Szpytko, J. Evolutionary algorithm-based design of a fuzzy TBF predictive model and TSK fuzzy anti-sway crane control system. Eng. Appl. Artif. Intell. 2014, 28, 190–200. [Google Scholar] [CrossRef]
- Çakan, A.; Önen, U. Anti-swing control of an overhead crane by using genetic algorithm based LQR. Int. J. Eng. Comput. Sci. 2017, 6, 21612–21616. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Willis, M.; Hiden, H.; Hinchliffe, M.; McKay, B.; Barton, G.W. Systems modelling using genetic programming. Comput. Chem. Eng. 1997, 21, 1161–1166. [Google Scholar] [CrossRef]
- Banzhaf, W. Genetic programming for pedestrians. In Proceedings of the Fifth International Conference on Genetic Algorithms (ICGA’93), San Mateo, CA, USA, 17–22 July 1993; Forrest, S., Ed.; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Ryan, C.; Collins, J.; Neill, M.O. Grammatical evolution: Evolving programs for an arbitrary language. In Genetic Programming, Proceedings of the First European Workshop, EuroGP’98, Paris, France, 14–15 April 1998; Banzhaf, W., Poli, R., Schoenauer, M., Fogarty, T.C., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 83–96. [Google Scholar]
- De Melo, V.V. Kaizen programming. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, ACM, Vancouver, BC, Canada, 12–16 July 2014; pp. 895–902. [Google Scholar]
- Searson, D.P. Chapter 22—GPTIPS 2: An open-source software platform for symbolic data mining. In Handbook of Genetic Programming Applications; Gandomi, A.H., Alavi, A.H., Ryan, C., Eds.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Riahi-Madvar, H.; Dehghani, M.; Seifi, A.; Singh, V.P. Pareto optimal multigene genetic programming for prediction of longitudinal dispersion coefficient. Water Resour. Manag. 2019, 33, 905–921. [Google Scholar] [CrossRef]
- Natarajan, B.K. Sparse approximate solutions to linear systems. SIAM J. Comput. 1995, 24, 227–234. [Google Scholar] [CrossRef]
- La Cava, W.; Moore, J.H. Learning feature spaces for regression with genetic programming. Genet. Program. Evolvable Mach. 2020, 21, 433–467. [Google Scholar] [CrossRef]
- Whigham, P.A. Grammatically-based genetic programming. In Proceedings of the Workshop on Genetic Programming: From Theory to Real-World Applications, Tahoe City, CA, USA, 9 July 1995; Rosca, J., Ed.; University of Rochester: Rochester, NY, USA, 1995; pp. 33–41. [Google Scholar]
- Ratle, A.; Sebag, M. Grammar-guided genetic programming and dimensional consistency: Application to non-parametric identification in mechanics. Appl. Soft Comput. 2001, 1, 105–118. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its application to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Sugeno, M.; Kang, T. Structure identification of fuzzy model. Fuzzy Sets Syst. 1988, 28, 15–33. [Google Scholar] [CrossRef]
- Chiu, S.L. Fuzzy model identification based in cluster estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar] [CrossRef]
- Efkolidis, N.; Markopoulos, A.; Κarkalos, N.; Hernández, C.G.; Talón, J.L.H.; Kyratsis, P. Optimizing models for sustainable drilling operations using genetic algorithm for the optimum ANN. Appl. Artif. Intell. 2019, 33, 881–901. [Google Scholar] [CrossRef]
- Karkalos, N.E.; Efkolidis, N.; Kyratsis, P.; Markopoulos, A.P. A comparative study between regression and neural networks for modeling Al6082-T6 alloy drilling. Machines 2019, 7, 13. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).