Robust Stabilization of Linear Time-Delay Systems under Denial-of-Service Attacks
Abstract
1. Introduction
- Notations:
- and denote the transpose, inverse, and induced norm of any square matrix W, respectively. stands for an asymmetrical and positive (negative) definite matrix W. The n-dimensional Euclid n space is denoted by and I stands for the identity matrix with appropriate dimension. The symbol ∗ is used in some matrix expressions to induce a symmetrical structure.
2. Problem Definition
- (1)
- Matrix has full rank.
- (2)
- The following PID-like state feedback controller is proposedwhere is the upper bound on the time delay produced by DoS attacks, is a proportional gain designed to ensure internal stability, and and are to meet the control objectives.
- Case 1
- (Delay-independent): The time delay caused by DoS attack is continuous and satisfies
- Case 2
- (Delay-dependent): The time delay caused by DoS attack is continuous, differentiable and satisfieswhere the bounds and are known. From ref. [11], the usual bounding relation , but in this work it is expanded to . This new upper bound on is shown later in the proof of Theorem 2, contributing to others’ work.
3. Ltd under DoS Attack Control Design
3.1. DoS Attacks Causing Unknown Time-Delay Design
- Remarks:
- The solution to inequality (10) will result in a sub-optimal one. The optimal gains of the delay-independent asymptotically stabilized controller can be determined by solving the following convex minimization problem
- The conventional state feedback stabilization controlleris obtained as stated by the next lemma.
3.2. DoS Attacks Causing Time-Varying Delay Design
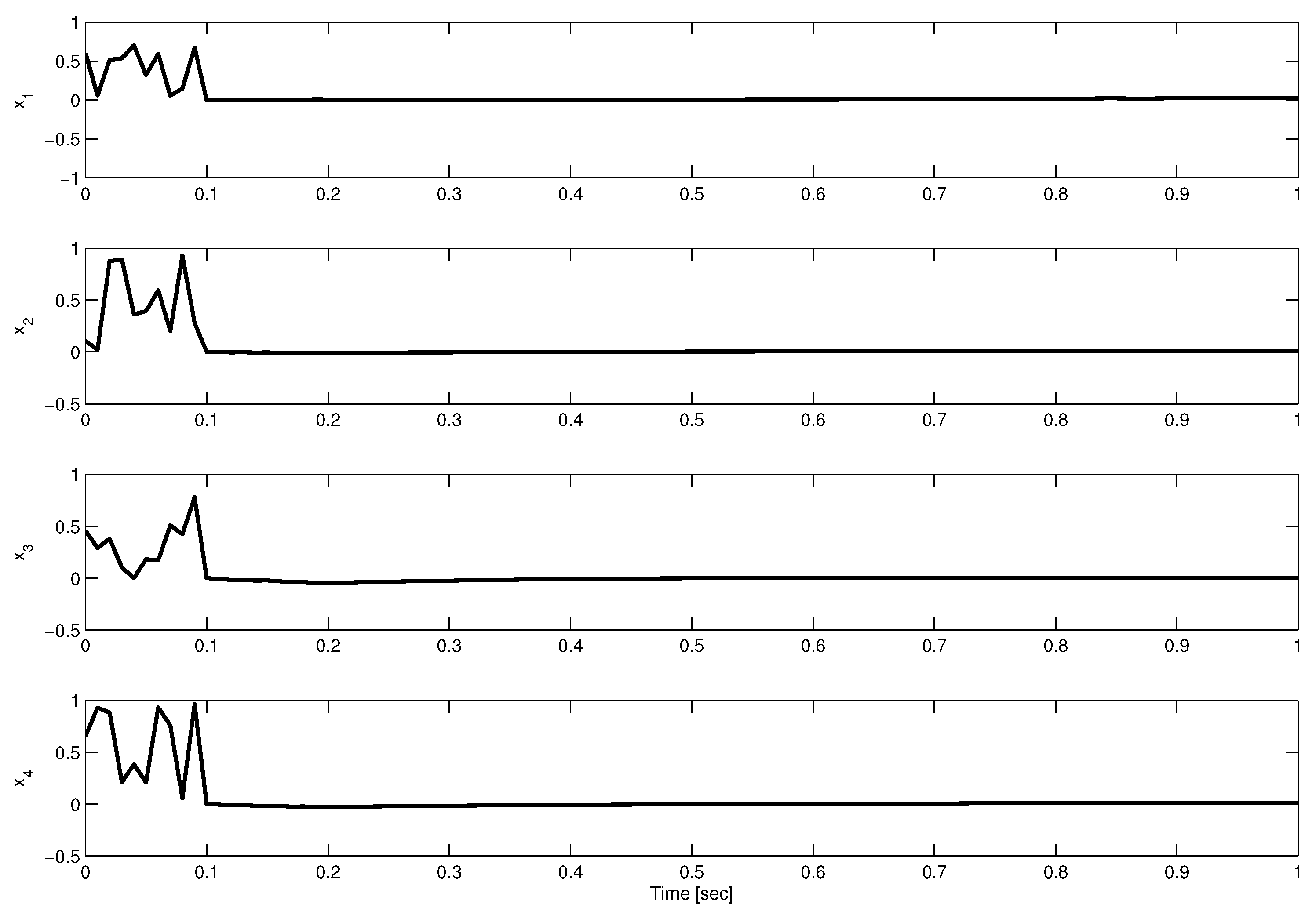
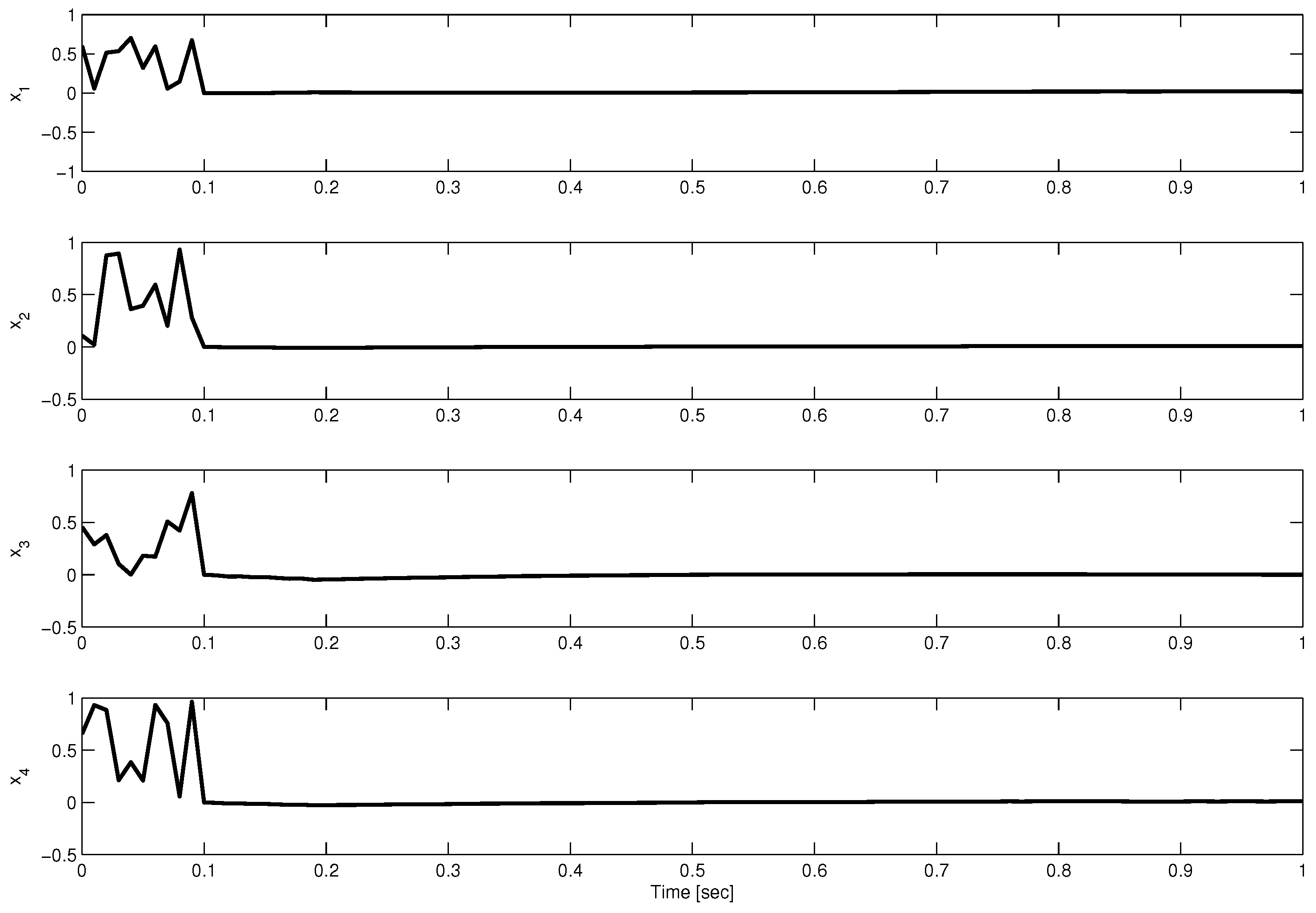
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Michiels, W.; Niculescu, S.-I. (Eds.) Stability, Control, and Computation for Time-Delay Systems: An Eigenvalue-Based Approach, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014; pp. 407–435. [Google Scholar]
- Abdelaziz, T.H.S.; Valas’ek, M. Pole-Placement for SISO Linear Systems by State Derivative Feedback. IEE Proc. Control Theory Appl. 2004, 151, 377–385. [Google Scholar] [CrossRef]
- Duan, G.R.; Zhang, X. Regularizability of Linear Descriptor Systems via Output plus Partial State-Derivative Feedback. Asian J. Control 2003, 5, 334–340. [Google Scholar] [CrossRef]
- Assuncao, E.; Teixeira, M.C.M.; Faria, F.A.; Da Silva, N.A.P.; Cardim, R. Robust State Derivative Feedback LMI-Based Designs for Multivariable Linear Systems. Int. J. Control 2007, 80, 1260–1270. [Google Scholar]
- Reithmeier, E.; Leitmann, G. Robust Vibration Control of Dynamical Systems based on the Derivative of the State. Arch. Appl. Mech. 2003, 72, 856–864. [Google Scholar] [CrossRef]
- Delibasi, A.; Kucukdemiral, I.B.; Cansever, G. A robust PID like state-feedback control via LMI a pproach: An application on a Double Inverted Pendulum System. In Proceedings of the 2007 IEEE International Symposium on Computational Intelligence in Robotics and Automation, Jacksonville, FL, USA, 20–23 June 2007. [Google Scholar]
- Sujitjorn, S.; Wiboonjaroen, W. State-PID Feedback for Pole Placement of LTI Systems. Math. Probl. Eng. 2011, 2011, 929430. [Google Scholar] [CrossRef]
- Lee, C.S.; Leitmann, G. Continuous Feedback Guaranteeing Uniform Ultimate Boundedness for Uncertain Linear Delay Systems: An Application to River Pollution Control. Comput. Math. Model. 1988, 16, 929–938. [Google Scholar] [CrossRef]
- Wang, Z.W.; Zhou, R.; Wen, C. Load-Frequency Controller Design for Power Systems. Proc. IEE Part C 1993, 140, 11–17. [Google Scholar] [CrossRef]
- Zheng, F.; Frank, P.M. Robust Control of Uncertain Distributed Delay Systems with Application to the Stabilization of Combustion in Rocket Motor Chambers. Automatica 2002, 38, 487–497. [Google Scholar] [CrossRef]
- Madsen, J.M.; Shieh, L.-S.; Guo, S.-M. State-Space Digital PID Controller Design for Multivariable Analog Systems with Multiple Time Delays. Asian J. Control 2006, 8, 161–173. [Google Scholar] [CrossRef]
- Liu, G.; Hua, C.; Liu, P.X.; Xu, H.; Guan, X. Stabilization and Data-Rate Condition for Stability of Networked Control Systems With Denial-of-Service Attacks. IEEE Trans. Cybern. 2022, 52, 700–711. [Google Scholar] [PubMed]
- Cao, R.; Wu, J.; Long, C.; Li, S. Stability analysis for networked control systems under denial-of-service attacks. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015. [Google Scholar]
- Zhang, J.; Peng, C.; Masroor, S.; Sun, H.; Chai, L. Stability analysis of networked control systems with denial-of-service attacks. In Proceedings of the 2016 UKACC 11th International Conference on Control (CONTROL), Belfast, UK, 31 August–2 September 2016. [Google Scholar]
- Peng, C.; Sun, H. Switching-Like Event-Triggered Control for Networked Control Systems Under Malicious Denial of Service Attacks. IEEE Trans. Autom. Control 2020, 65, 3943–3949. [Google Scholar] [CrossRef]
- Tian, Y.; Li, X.; Dong, B.; Gao, Y.; Wu, L. Event-based sliding mode control under denial-of-service attacks. Sci. China Inf. Sci. 2022, 65, 162203. [Google Scholar] [CrossRef]
- Hu, S.; Yue, D.; Han, Q.-L.; Xie, X.; Chen, X.; Dou, C. Observer-Based Event-Triggered Control for Networked Linear Systems Subject to Denial-of-Service Attacks. IEEE Trans. Cybern. 2020, 50, 1952–1964. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Wang, Z.; Ho, D.W.C.; Wei, G. Observer-Based PID Security Control for Discrete Time-Delay Systems under Cyber-Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3926–3938. [Google Scholar] [CrossRef]
- Sun, H.; Peng, C.; Yang, T.; Zhang, H.; He, W. Resilient control of networked control systems with stochastic denial of service attacks. Neurocomputing 2017, 270, 170–177. [Google Scholar] [CrossRef]
- Jeong, J.; Lim, Y.; Parivallal, A. An asymmetric Lyapunov-Krasovskii functional approach for event-triggered consensus of multi-agent systems with deception attacks. Appl. Math. Comput. 2023, 439, 127584. [Google Scholar] [CrossRef]
- Elkhider, S.M.; El-Ferik, S.; Saif, A.-W.A. Denial of Service Attack of QoS-Based Control of Multi-Agent Systems. Appl. Sci. 2022, 12, 4315. [Google Scholar] [CrossRef]
- Elkhider, S.M.; El-Ferik, S.; Saif, A.-W.A. Containment Control of Multiagent Systems Subject to Denial of Service Attacks. IEEE Access 2022, 10, 48102–48111. [Google Scholar] [CrossRef]
- Parivallal, A.; Lim, Y.; Jeong, J. Hybrid-Triggered Hoo Control for Parabolic PDE Systems Under Deception Attacks. IEEE Access 2022, 10, 80289–80299. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saif, A.-W.A.; El-Ferik, S.; Elkhider, S.M. Robust Stabilization of Linear Time-Delay Systems under Denial-of-Service Attacks. Sensors 2023, 23, 5773. https://doi.org/10.3390/s23135773
Saif A-WA, El-Ferik S, Elkhider SM. Robust Stabilization of Linear Time-Delay Systems under Denial-of-Service Attacks. Sensors. 2023; 23(13):5773. https://doi.org/10.3390/s23135773
Chicago/Turabian StyleSaif, Abdul-Wahid A., Sami El-Ferik, and Siddig M. Elkhider. 2023. "Robust Stabilization of Linear Time-Delay Systems under Denial-of-Service Attacks" Sensors 23, no. 13: 5773. https://doi.org/10.3390/s23135773
APA StyleSaif, A.-W. A., El-Ferik, S., & Elkhider, S. M. (2023). Robust Stabilization of Linear Time-Delay Systems under Denial-of-Service Attacks. Sensors, 23(13), 5773. https://doi.org/10.3390/s23135773




