Edge-Supervised Linear Object Skeletonization for High-Speed Camera
Abstract
1. Introduction
- We propose a novel edge-supervised skeletonization approach, specifically designed for high-speed skeleton extraction that does not need to scrutinize every pixel in a binary image.
- We introduce a branch detector and an intersection center detector to enhance the quality of our skeletonization outcomes by identifying branches and intersection centers of the object for skeleton searching.
- We develop an innovative skeleton detection framework to facilitate high-speed applications for binary images.
2. Related Work
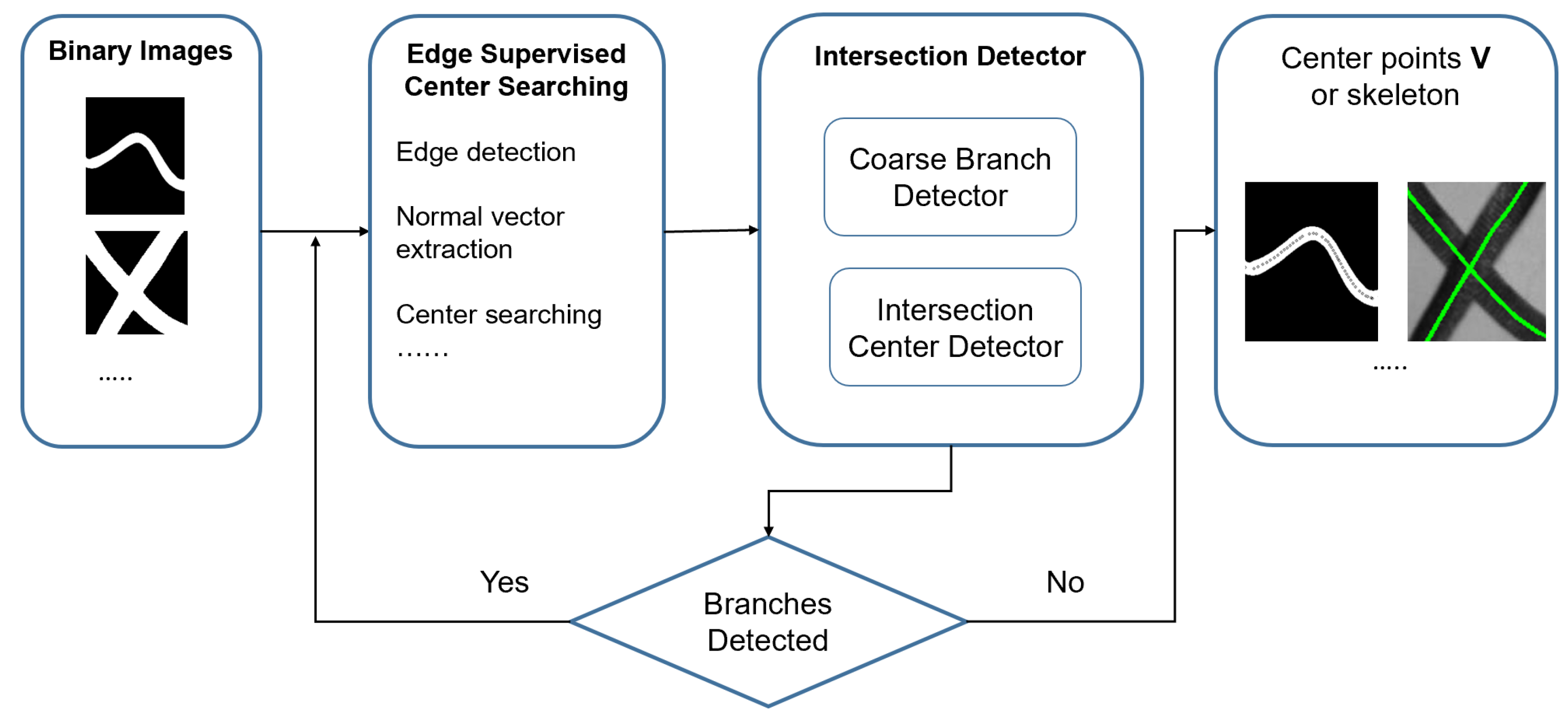
3. Edge-Supervised Skeletonization System
3.1. Edge Supervised Center Searching
3.2. Intersection Detector
3.2.1. Coarse Branch Detector
| Algorithm 1 Edge Supervised Skeletonization for Linear Object. |
Input: binary image I Output: skeleton points V
|
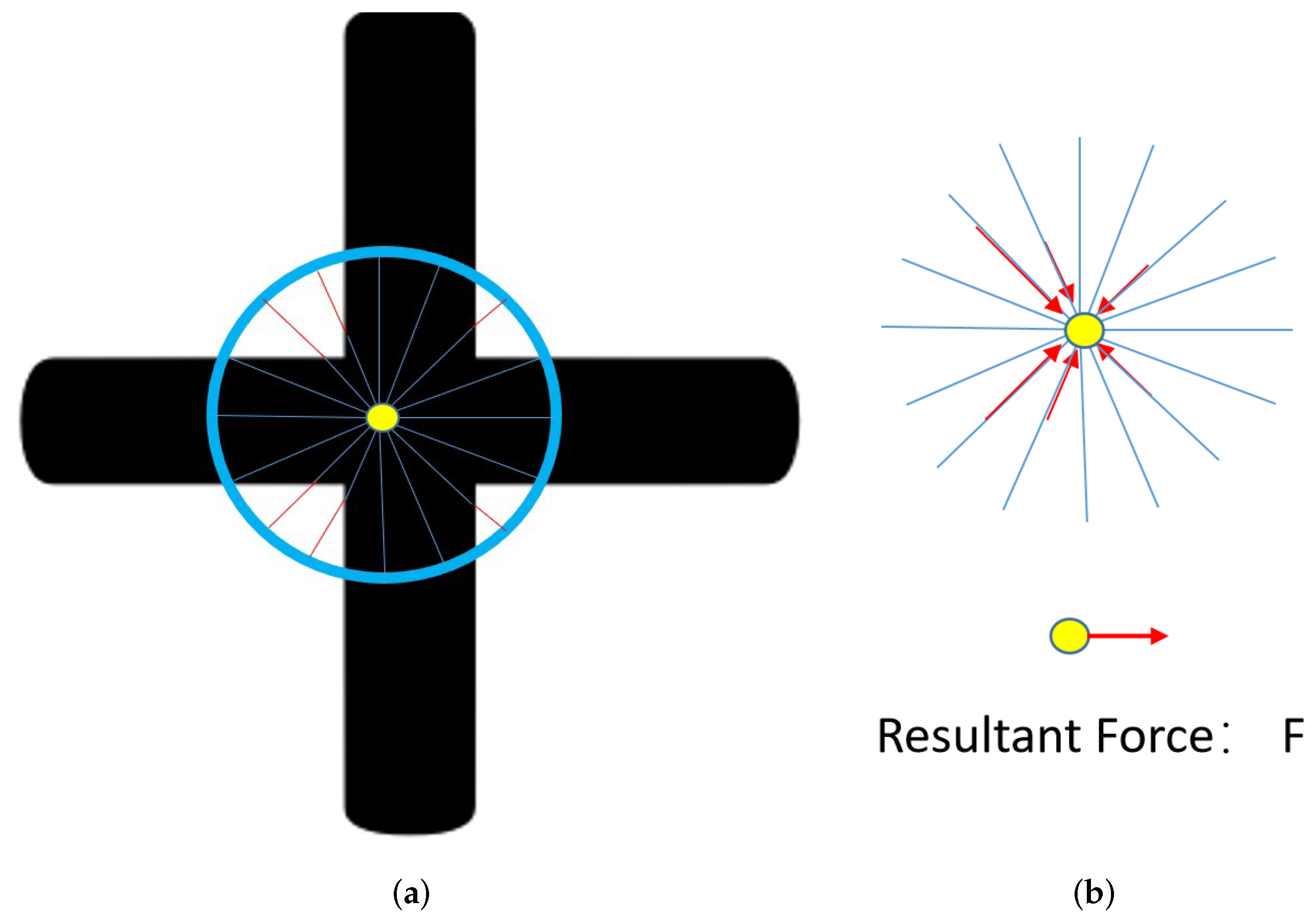
3.2.2. Intersection Center Detector
3.2.3. Edge Supervised Searching with Branch Detection
| Algorithm 2 Edge Supervised Skeletonization for the Linear Object with Branch Detector. |
Input: binary image I Output: skeleton points V
|
4. Experiments and Results
4.1. Experiments of Time Consumption
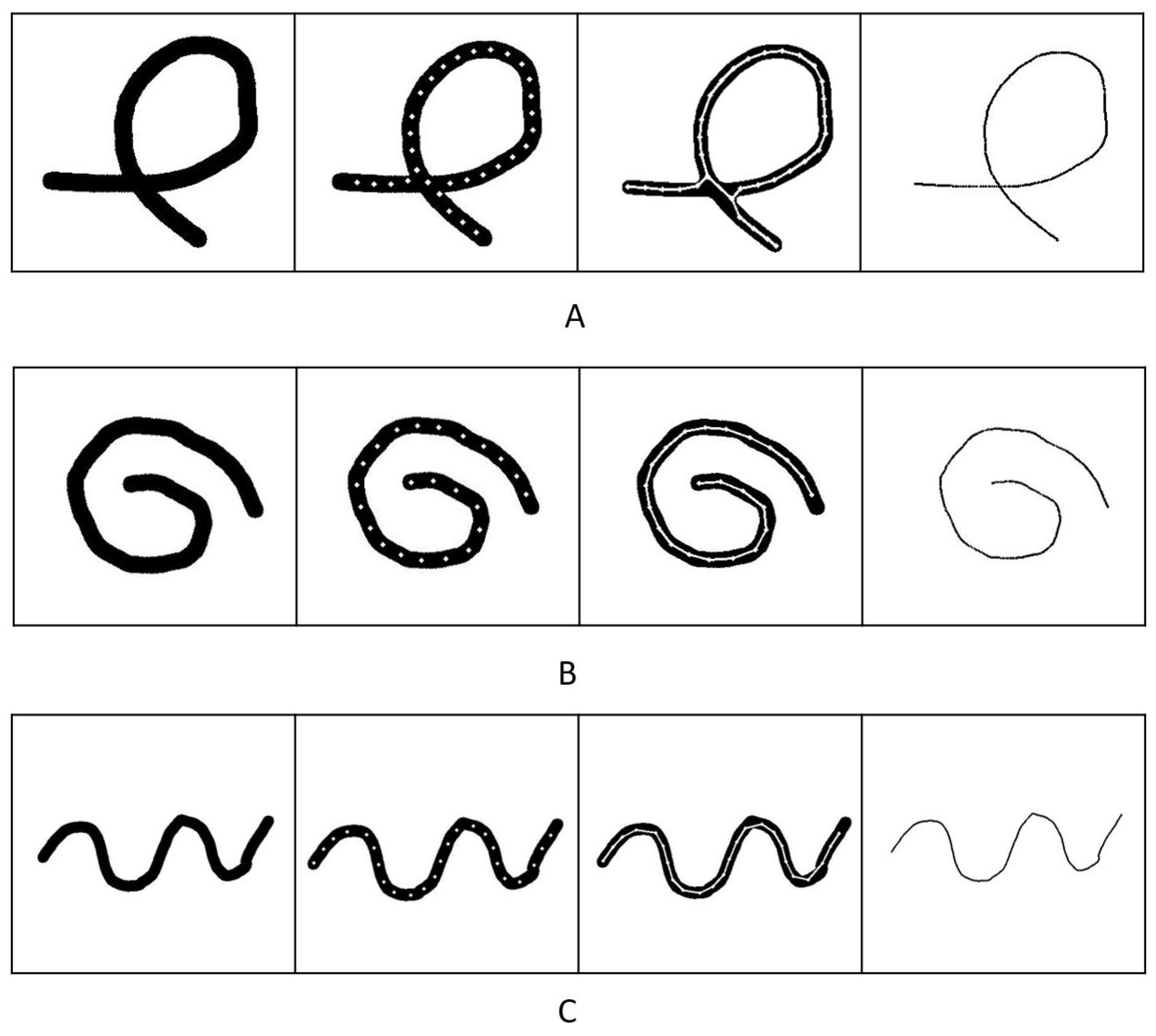
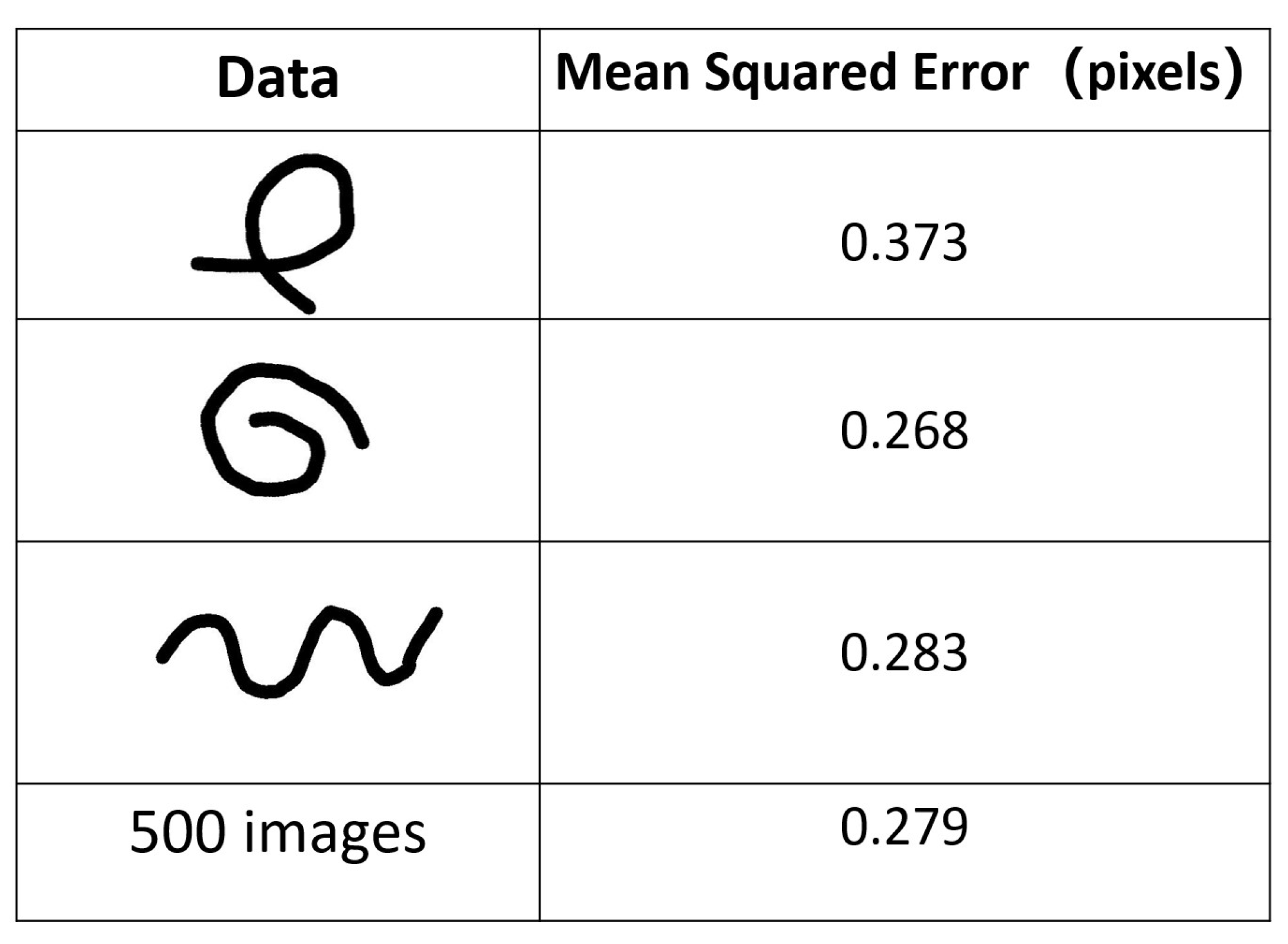
4.2. Experiments with Simulation Data
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Minimal Number of the Points

References
- Blum, H. A transformation for extracting new descriptions of shape. In Models for the Perception of Speech and Visual Form; MIT Press: Cambridge, MA, USA, 1967; pp. 362–380. [Google Scholar]
- Blum, H.; Nagel, R.N. Shape description using weighted symmetric axis features. Pattern Recognit. 1978, 10, 167–180. [Google Scholar] [CrossRef]
- Brandt, J.W.; Algazi, V.R. Continuous skeleton computation by Voronoi diagram. CVGIP Image Underst. 1992, 55, 329–338. [Google Scholar] [CrossRef]
- Ogniewicz, R.L.; Ilg, M. Voronoi skeletons: Theory and applications. In Proceedings of the CVPR, Champaign, IL, USA, 15–18 June 1992; Volume 92, pp. 63–69. [Google Scholar]
- Dey, T.K.; Zhao, W. Approximating the medial axis from the Voronoi diagram with a convergence guarantee. Algorithmica 2004, 38, 179–200. [Google Scholar] [CrossRef]
- Saha, P.K.; Borgefors, G.; di Baja, G.S. Skeletonization and its applications—A review. Skeletonization 2017, 3–42. [Google Scholar] [CrossRef]
- Shen, W.; Zhao, K.; Jiang, Y.; Wang, Y.; Bai, X.; Yuille, A. Deepskeleton: Learning multi-task scale-associated deep side outputs for object skeleton extraction in natural images. IEEE Trans. Image Process. 2017, 26, 5298–5311. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Li, X.; Shen, J. MSB-FCN: Multi-scale bidirectional fcn for object skeleton extraction. IEEE Trans. Image Process. 2020, 30, 2301–2312. [Google Scholar] [CrossRef]
- Atienza, R. Pyramid U-network for skeleton extraction from shape points. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Panichev, O.; Voloshyna, A. U-net based convolutional neural network for skeleton extraction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Ko, D.H.; Hassan, A.U.; Majeed, S.; Choi, J. Skelgan: A font image skeletonization method. J. Inf. Process. Syst. 2021, 17, 1–13. [Google Scholar]
- Nathan, S.; Kansal, P. Skeletonnet: Shape pixel to skeleton pixel. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Liu, C.; Ke, W.; Jiao, J.; Ye, Q. Rsrn: Rich side-output residual network for medial axis detection. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 1739–1743. [Google Scholar]
- Tang, W.; Su, Y.; Li, X.; Zha, D.; Jiang, W.; Gao, N.; Xiang, J. Cnn-based chinese character recognition with skeleton feature. In Proceedings of the Neural Information Processing: 25th International Conference, ICONIP 2018, Siem Reap, Cambodia, 13–16 December 2018; Proceedings, Part V 25. Springer: Berlin/Heidelberg, Germany, 2018; pp. 461–472. [Google Scholar]
- Wu, F.; Yang, Z.; Mo, X.; Wu, Z.; Tang, W.; Duan, J.; Zou, X. Detection and counting of banana bunches by integrating deep learning and classic image-processing algorithms. Comput. Electron. Agric. 2023, 209, 107827. [Google Scholar] [CrossRef]
- Saha, P.K.; Borgefors, G.; di Baja, G.S. A survey on skeletonization algorithms and their applications. Pattern Recognit. Lett. 2016, 76, 3–12. [Google Scholar] [CrossRef]
- Amenta, N.; Choi, S.; Kolluri, R.K. The power crust, unions of balls, and the medial axis transform. Comput. Geom. 2001, 19, 127–153. [Google Scholar] [CrossRef]
- Näf, M.; Székely, G.; Kikinis, R.; Shenton, M.E.; Kübler, O. 3D Voronoi skeletons and their usage for the characterization and recognition of 3D organ shape. Comput. Vis. Image Underst. 1997, 66, 147–161. [Google Scholar] [CrossRef]
- Kiraly, A.P.; Helferty, J.P.; Hoffman, E.A.; McLennan, G.; Higgins, W.E. Three-dimensional path planning for virtual bronchoscopy. IEEE Trans. Med. Imaging 2004, 23, 1365–1379. [Google Scholar] [CrossRef]
- Kimia, B.B.; Tannenbaum, A.R.; Zucker, S.W. Shapes, shocks, and deformations I: The components of two-dimensional shape and the reaction-diffusion space. Int. J. Comput. Vis. 1995, 15, 189–224. [Google Scholar] [CrossRef]
- Leymarie, F.; Levine, M.D. Simulating the grassfire transform using an active contour model. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 56–75. [Google Scholar] [CrossRef]
- Bitter, I.; Kaufman, A.E.; Sato, M. Penalized-distance volumetric skeleton algorithm. IEEE Trans. Vis. Comput. Graph. 2001, 7, 195–206. [Google Scholar] [CrossRef]
- Arcelli, C.; Di Baja, G.S. A width-independent fast thinning algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1985, PAMI-7, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Bertrand, G. A parallel thinning algorithm for medial surfaces. Pattern Recognit. Lett. 1995, 16, 979–986. [Google Scholar] [CrossRef]
- Saha, P.K. Skeletonization and Its Application to Quantitative Structural Imaging. In Proceedings of the International Conference on Frontiers in Computing and Systems: COMSYS 2021, Rupnagar, India, 18–20 December 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 233–243. [Google Scholar]
- Lü, H.; Wang, P.S.P. A comment on “A fast parallel algorithm for thinning digital patterns”. Commun. ACM 1986, 29, 239–242. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, X.; Zhang, X. Parallel thinning and skeletonization algorithm based on cellular automaton. Multimed. Tools Appl. 2020, 79, 33215–33232. [Google Scholar] [CrossRef]
- Ma, J.; Ren, X.; Tsviatkou, V.Y.; Kanapelka, V.K. A novel fully parallel skeletonization algorithm. Pattern Anal. Appl. 2022, 25, 169–188. [Google Scholar] [CrossRef]
- Lee, T.C.; Kashyap, R.L.; Chu, C.N. Building skeleton models via 3-D medial surface axis thinning algorithms. CVGIP Graph. Model. Image Process. 1994, 56, 462–478. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef]
- Tang, T.; Tomizuka, M. Track deformable objects from point clouds with structure preserved registration. Int. J. Robot. Res. 2022, 41, 599–614. [Google Scholar] [CrossRef]
- Wang, T.; Yamakawa, Y. Real-Time Occlusion-Robust Deformable Linear Object Tracking with Model-Based Gaussian Mixture Model. Front. Neurorobotics 2022, 16, 886068. [Google Scholar] [CrossRef] [PubMed]
- Prewitt, J.M. Object enhancement and extraction. Pict. Process. Psychopictorics 1970, 10, 15–19. [Google Scholar]




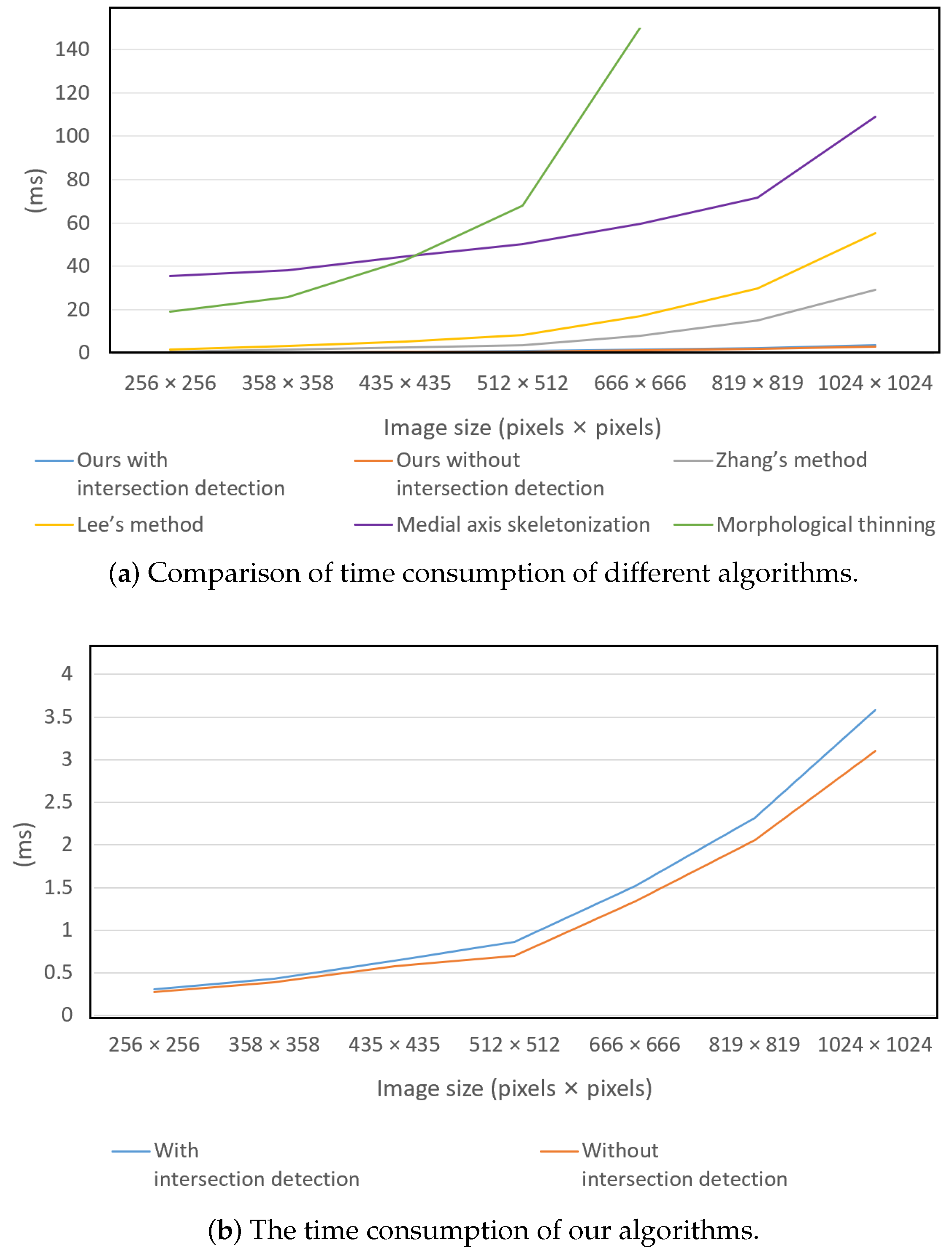
| Image Size | Ours with Inter- Section Detector | Ours Without Intersection Detector | Zhang’s Method | Lee’s Method | Medial Axis Skeletonization | Morphological Thinning |
|---|---|---|---|---|---|---|
| 0.31283 | 0.275 | 0.7511 | 1.544 | 35.565 | 19.120 | |
| 0.43038 | 0.388 | 1.529 | 3.260 | 38.250 | 25.816 | |
| 0.64367 | 0.581 | 2.565 | 5.332 | 44.685 | 42.815 | |
| 0.86207 | 0.701 | 3.804 | 8.375 | 50.191 | 68.088 | |
| 1.52092 | 1.334 | 8.137 | 17.174 | 59.705 | 150.337 | |
| 2.31342 | 2.057 | 15.175 | 29.789 | 71.856 | 279.808 | |
| 3.58309 | 3.102 | 29.126 | 55.387 | 109.202 | 431.654 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Yamakawa, Y. Edge-Supervised Linear Object Skeletonization for High-Speed Camera. Sensors 2023, 23, 5721. https://doi.org/10.3390/s23125721
Wang T, Yamakawa Y. Edge-Supervised Linear Object Skeletonization for High-Speed Camera. Sensors. 2023; 23(12):5721. https://doi.org/10.3390/s23125721
Chicago/Turabian StyleWang, Taohan, and Yuji Yamakawa. 2023. "Edge-Supervised Linear Object Skeletonization for High-Speed Camera" Sensors 23, no. 12: 5721. https://doi.org/10.3390/s23125721
APA StyleWang, T., & Yamakawa, Y. (2023). Edge-Supervised Linear Object Skeletonization for High-Speed Camera. Sensors, 23(12), 5721. https://doi.org/10.3390/s23125721





