Optimization of Tungsten Heavy Alloy Cutting Parameters Based on RSM and Reinforcement Dung Beetle Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Workpiece and Cutting Tool
2.2. Experimental Work
2.2.1. Experimental Setup
2.2.2. Experimental Design
2.3. RSM Modeling
2.4. Multi-Objective Optimization Algorithm
2.4.1. Dung Beetle Optimization Algorithm
- (a)
- Dung ball
- (b)
- Dance
- (c)
- Breed
- (d)
- Foraging
- (e)
- Pilfer
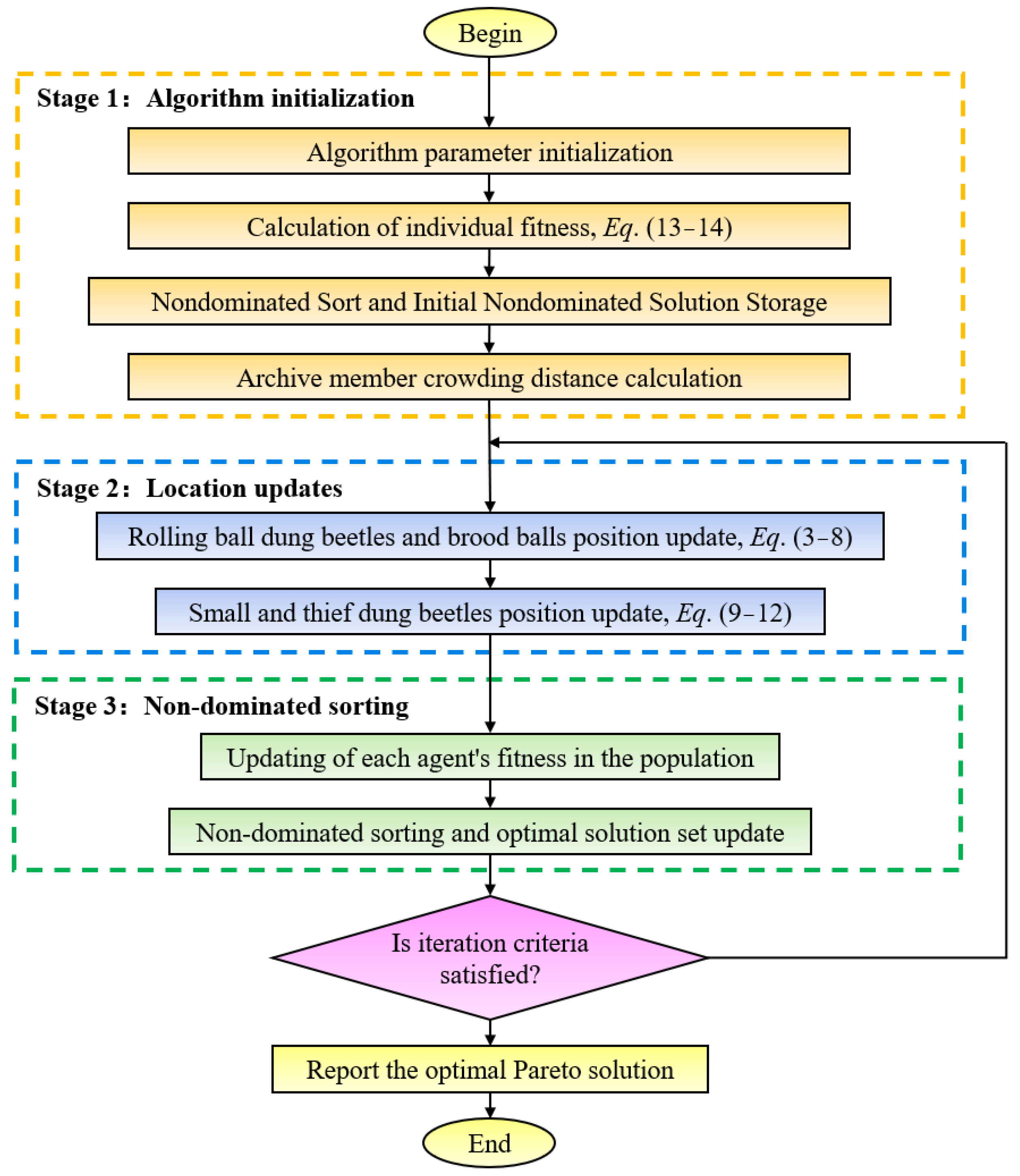
2.4.2. Multi-Objective Dung Beetle Optimization Algorithm Based on Non-Dominant Ordering
3. Results and Discussion
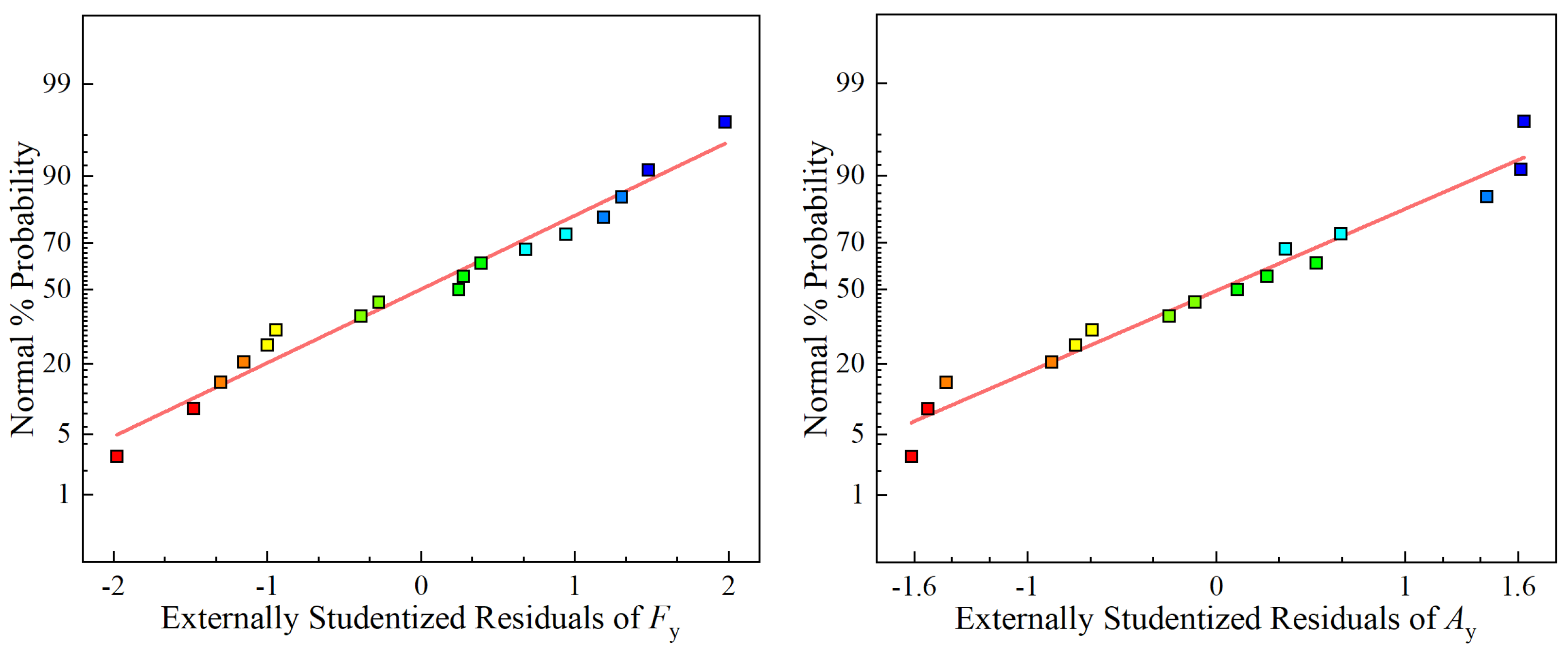
3.1. Analysis of Experimental Results Based on RSM
3.2. Optimization of Turning Parameters Based on NSDBO
4. Conclusions
- A second-order polynomial regression model using response surface methodology (RSM) was established to correlate cutting speed, feed rate, cutting depth, cutting force, and vibration. ANOVA analysis results indicated that all of the constructed regression models could be used to quantify the relationship between cutting parameters and corresponding responses.
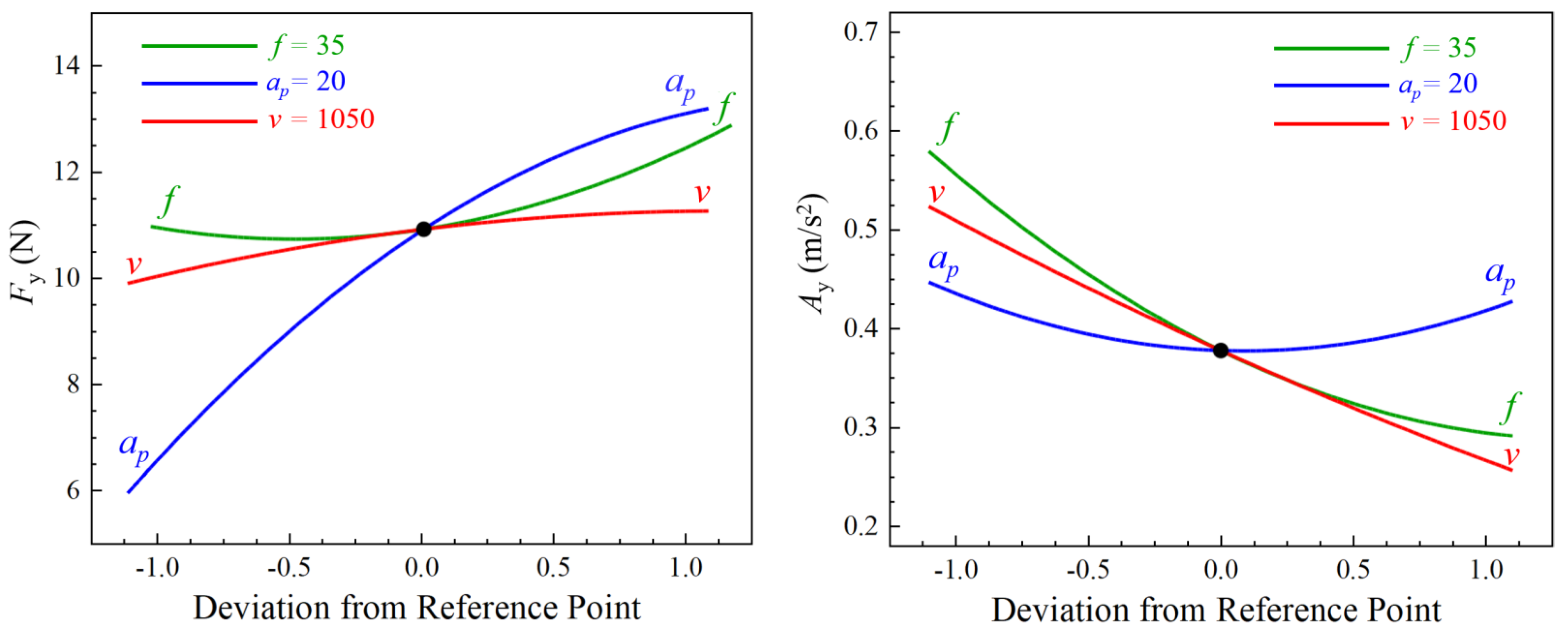
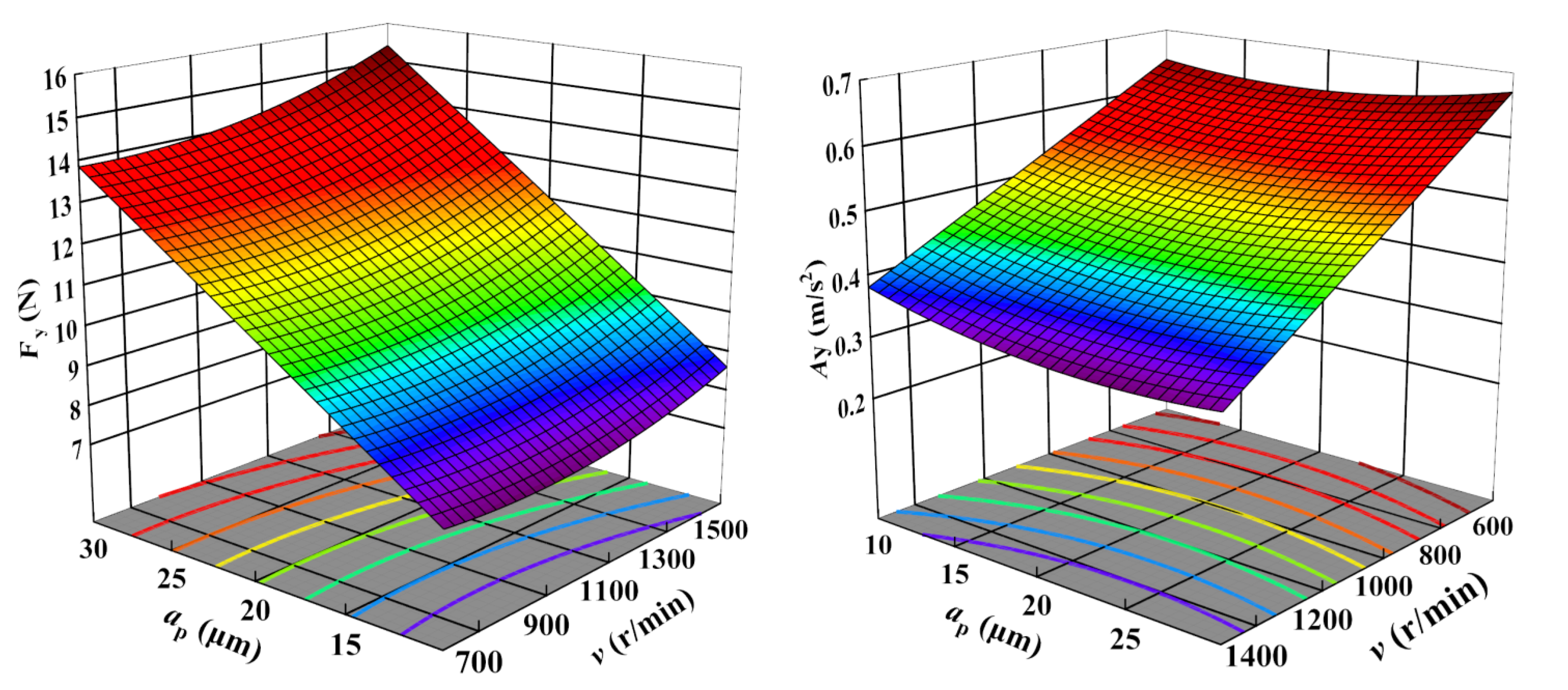
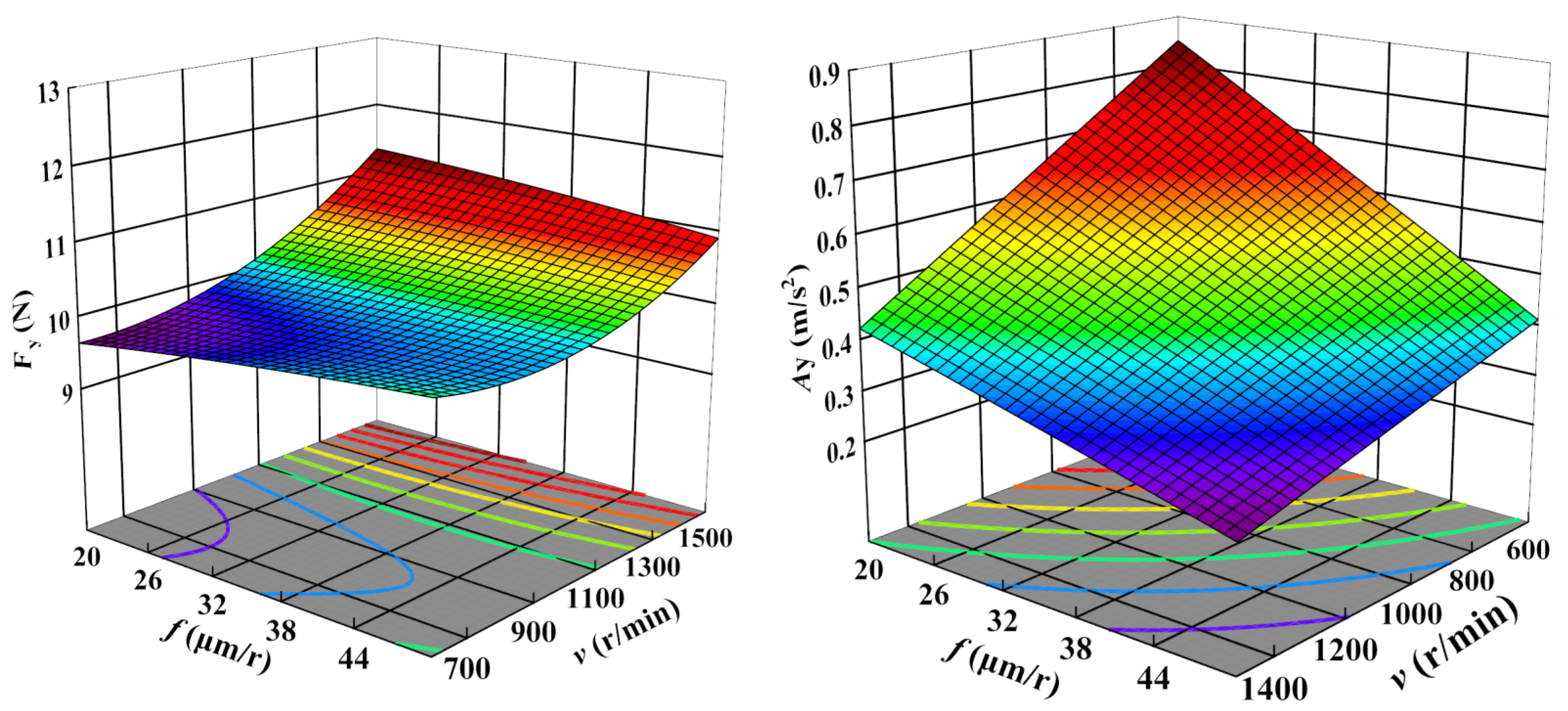
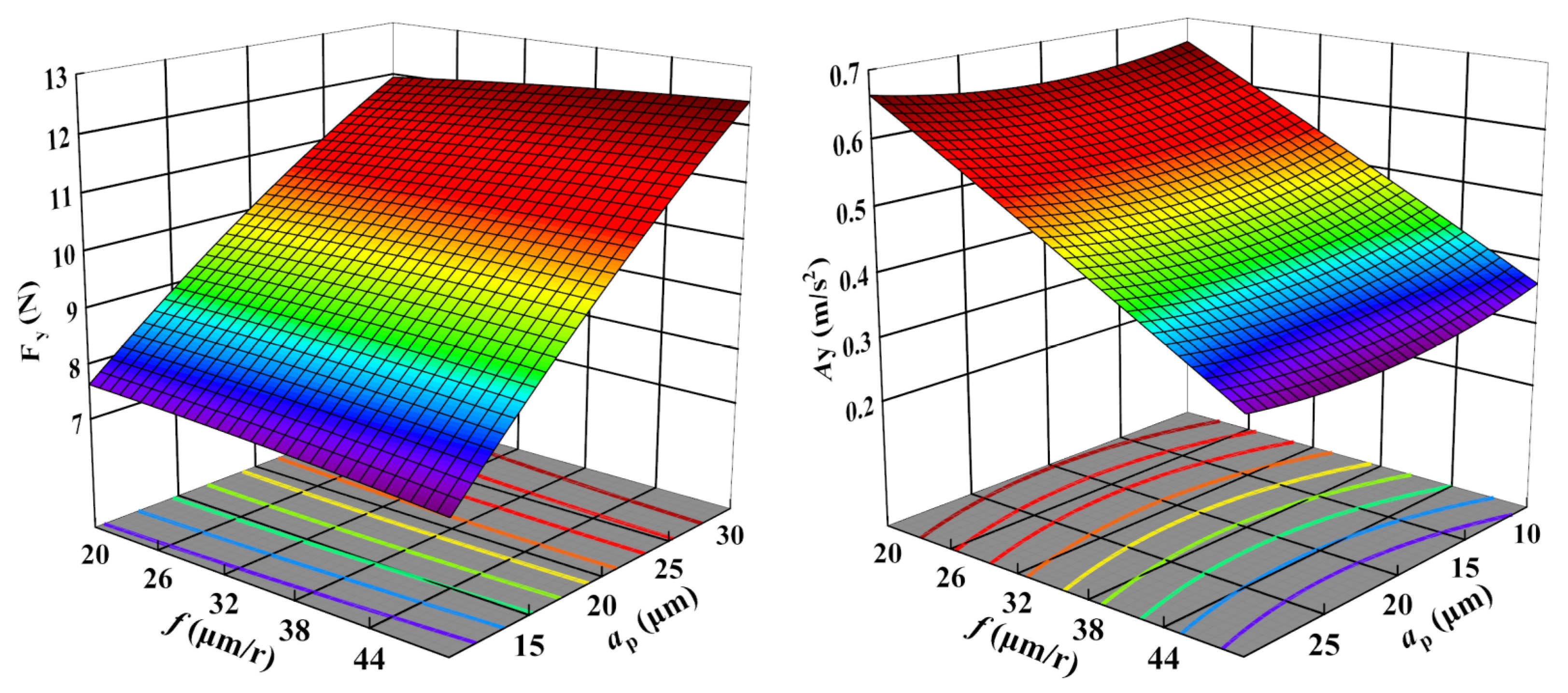
- The influence of cutting parameters on cutting force and vibration was analyzed via RSM. The influence of depth of cut on cutting forces is the most significant, the influence of cutting speed is second, and the influence of feed rate is the smallest. For vibration, the cutting parameter with the most significant impact is the cutting speed, followed by the feed rate, and the depth of cut has the least influence.
- A multi-objective dung beetle optimization algorithm was realized by introducing the non-dominated sorting technology. The results show that the proposed algorithm has a faster convergence speed and better global optimization ability than the multi-objective genetic and cuckoo algorithms.
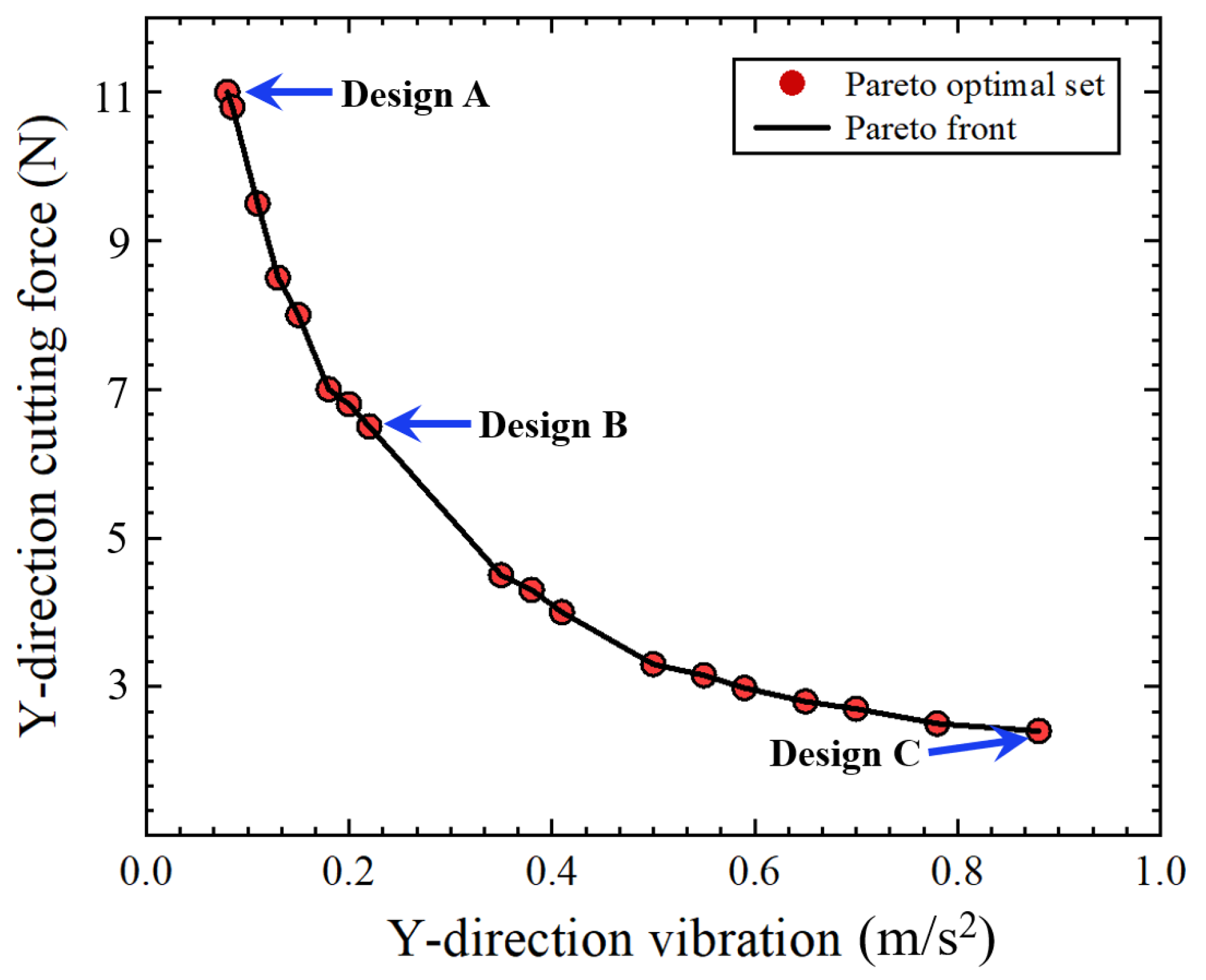
- Combining the RSM and NSDBO methods, the cutting parameters of the tungsten alloy were optimized. After the optimized parameters, the cutting force was reduced by 9.7%, and the vibration was reduced by 46.47%. The surface roughness of the final workpiece was reduced by 18.2%. This means that the method proposed in this text can guide the turning of tungsten alloys.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kiran, U.R.; Panchal, A.; Sankaranarayana, M.; Nageswara Rao, G.V.S.; Nandy, T.K. Effect of alloying addition and microstructural parameters on mechanical properties of 93% tungsten heavy alloys. Mater. Sci. Eng. A 2015, 640, 82–90. [Google Scholar] [CrossRef]
- Zhong, L.; Li, L.; Wu, X.; He, N. Micro cutting of pure tungsten using self-developed polycrystalline diamond slotting tools. Int. J. Adv. Manuf. Technol. 2017, 89, 2435–2445. [Google Scholar] [CrossRef]
- Marschnigg, S.; Gierl-Mayer, C.; Danninger, H.; Weirather, T.; Granzer, T.; Zobl, P. Non-destructive measurement of the tungsten content in the binder phase of tungsten heavy alloys. Int. J. Refract. Met. Hard Mater. 2018, 73, 215–220. [Google Scholar] [CrossRef]
- Zhuo, L.; Zhang, Y.; Zhao, Z.; Luo, B.; Chen, Q.; Liang, S. Preparation and properties of ultrafine-grained W-Cu composites reinforced with tungsten fibers. Mater. Lett. 2019, 243, 26–29. [Google Scholar] [CrossRef]
- Jiao, Z.; Kang, R.; Dong, Z.; Guo, J. Microstructure characterization of W-Ni-Fe heavy alloys with optimized metallographic preparation method. Int. J. Refract. Met. Hard Mater. 2019, 80, 114–122. [Google Scholar] [CrossRef]
- Niu, L.; Jin, Z.; Han, X.; Zhou, Z.; Guo, J. Modification of tungsten heavy alloy by selective electrochemical etching in sodium carbonate electrolyte. J. Electrochem. Soc. 2019, 166, E496. [Google Scholar] [CrossRef]
- Jawahir, I.S.; Brinksmeier, E.; M’saoubi, R.; Aspinwall, D.K.; Outeiro, J.C.; Meyer, D.; Umbrello, D.; Jayal, A.D. Surface integrity in material removal processes: Recent advances. CIRP Ann. 2011, 60, 603–626. [Google Scholar] [CrossRef]
- Yin, S.; Bao, Y.; Pan, Y.; Dong, Z.; Jin, Z.; Kang, R. Design of ultrasonic elliptical vibration cutting system for tungsten heavy alloy. Front. Mech. Eng. 2022, 17, 59. [Google Scholar] [CrossRef]
- Pan, Y.; Kang, R.; Dong, Z.; Du, W.; Yin, S.; Bao, Y. On-line prediction of ultrasonic elliptical vibration cutting surface roughness of tungsten heavy alloy based on deep learning. J. Intell. Manuf. 2022, 33, 675–685. [Google Scholar] [CrossRef]
- Pan, Y.; Bai, J.; Xu, Z. Theoretical and numerical studies of surface microstructural transformation in ultrasonic elliptical vibration cutting tungsten heavy alloys. Int. J. Adv. Manuf. Technol. 2022, 123, 3943–3953. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Z.; Lv, Y.; Wang, J.; Shao, L.; Iqbal, A. Wear behavior of natural diamond tool in cutting tungsten-based alloy. Int. J. Adv. Manuf. Technol. 2013, 69, 329–335. [Google Scholar] [CrossRef]
- Olsson, M.; Bushlya, V.; Lenrick, F.; Ståhl, J.-E. Evaluation of tool wear mechanisms and tool performance in machining single-phase tungsten. Int. J. Refract. Met. Hard Mater. 2021, 94, 105379. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, Z.; Zhao, Y.; Niu, L.; Guo, J. A comparative study on tool life and wear of uncoated and coated cutting tools in turning of tungsten heavy alloys. Wear 2021, 482, 203929. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, L.; Wang, X.Z. Additive manufacturing of W-12Ta (wt.%) alloy: Processing and resulting mechanical properties. J. Alloys Compd. 2021, 868, 159193. [Google Scholar] [CrossRef]
- Guo, J.; Shi, X.; Song, C.; Niu, L.; Cui, H.; Guo, X.; Tong, Z.; Yu, N.; Jin, Z.; Kang, R. Theoretical and experimental investigation of chemical mechanical polishing of W–Ni–Fe alloy. Int. J. Extrem. Manuf. 2021, 3, 025103. [Google Scholar] [CrossRef]
- Guo, J.; Song, C.; Niu, L.; Shi, X.; Jin, Z.; Guo, C.; Namba, Y. Suppression of grain boundary steps in chemical mechanical polishing of W-Ni-Fe alloy by a citric acid-based slurry. Manuf. Lett. 2020, 25, 40–43. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.; Hou, L.; Wang, K.; Chao, C.; Zhang, H. A hybrid MCDM-based optimization method for cutting-type energy-absorbing structures of subway vehicles. Struct. Multidiscip. Optim. 2022, 65, 228. [Google Scholar] [CrossRef]
- Tanvir, M.H.; Hussain, A.; Rahman, M.M.T.; Ishraq, S.; Zishan, K.; Rahul, S.T.T.; Habib, M.A. Multi-objective optimization of turning operation of stainless steel using a hybrid whale optimization algorithm. J. Manuf. Mater. Process. 2020, 4, 64. [Google Scholar] [CrossRef]
- Vukelic, D.; Simunovic, K.; Kanovic, Z.; Saric, T.; Tadic, B.; Simunovic, G. Multi-objective optimization of steel AISI 1040 dry turning using genetic algorithm. Neural Comput. Appl. 2021, 33, 12445–12475. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Abbas, A.T.; Al-Abduljabbar, A.A.; El Rayes, M.M.; Benyahia, F.; Abdelgaliel, I.H.; Elkaseer, A. Multi-Objective Optimization of Performance Indicators in Turning of AISI 1045 under Dry Cutting Conditions. Metals 2023, 13, 96. [Google Scholar] [CrossRef]
- Tseng, L.W.; Hu, T.S.; Hu, Y.C. A Smart Tool Holder Calibrated by Machine Learning for Measuring Cutting Force in Fine Turning and Its Application to the Specific Cutting Force of Low Carbon Steel S15C. Machines 2021, 9, 190. [Google Scholar] [CrossRef]
- Segreto, T.; Caggiano, A.; Karam, S.; Teti, R. Vibration sensor monitoring of nickel-titanium alloy turning for machinability evaluation. Sensors 2017, 17, 2885. [Google Scholar] [CrossRef] [PubMed]
- Jangir, P.; Jangir, N. Non-dominated sorting whale optimization algorithm (NSWOA): A multi-objective optimization algorithm for solving engineering design problems. Glob. J. Res. Eng. 2017, 17, 15–42. [Google Scholar]


| Properties | Values |  |
| Density (g/cm3) | 18.3 | |
| Hardness (HV) | 380 | |
| Tensile strength (Mpa) | 800 | |
| Yield strength (Mpa) | 400 | |
| Young’s modulus (Gpa) | 450 | |
| Deflective strength (Mpa) | 1176 | |
| Thermal conductivity (W/(m·K)) | 89.2 | |
| Thermal expansion coefficient (ppm/k) | 4.8 |
| Symbol | Factors | Unit | Level | ||
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| Cutting speed | r/min | 800 | 1100 | 1400 | |
| Feed rate | μm/r | 20 | 35 | 50 | |
| Depth of cut | μm | 2 | 4 | 6 | |
| Exp. No. | v (r/min) | ap (μm) | f (μm/r) | Fy (N) | Ay (m/s2) | Ra (nm) |
|---|---|---|---|---|---|---|
| 1 | 600 | 30 | 35 | 11.79 | 0.662 | 461 |
| 2 | 600 | 20 | 20 | 9.588 | 0.851 | 557 |
| 3 | 600 | 10 | 35 | 7.716 | 0.653 | 454 |
| 4 | 600 | 20 | 50 | 10.15 | 0.415 | 332 |
| 5 | 1050 | 30 | 50 | 12.57 | 0.343 | 289 |
| 6 | 1050 | 20 | 35 | 9.904 | 0.488 | 321 |
| 7 | 1050 | 30 | 20 | 12.10 | 0.672 | 411 |
| 8 | 1050 | 10 | 20 | 7.492 | 0.656 | 438 |
| 9 | 1050 | 10 | 50 | 7.128 | 0.355 | 193 |
| 10 | 1050 | 20 | 35 | 9.879 | 0.498 | 346 |
| 11 | 1050 | 20 | 35 | 10.25 | 0.485 | 355 |
| 12 | 1050 | 20 | 35 | 10.16 | 0.472 | 368 |
| 13 | 1050 | 20 | 35 | 10.34 | 0.488 | 329 |
| 14 | 1500 | 30 | 35 | 13.29 | 0.332 | 398 |
| 15 | 1500 | 10 | 35 | 8.496 | 0.389 | 409 |
| 16 | 1500 | 20 | 50 | 10.97 | 0.236 | 206 |
| 17 | 1500 | 20 | 20 | 11.37 | 0.416 | 478 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 43.34 | 9 | 5.48 | 106.97 | <0.0001 | Significant |
| 2.98 | 1 | 2.98 | 58.13 | 0.0001 | ||
| 44.74 | 1 | 44.74 | 872.95 | <0.0001 | ||
| 0.009 | 1 | 0.009 | 0.1752 | 0.6881 | ||
| 0.1296 | 1 | 0.1296 | 2.53 | 0.1558 | ||
| 0.2314 | 1 | 0.2341 | 4.51 | 0.0712 | ||
| 0.1739 | 1 | 0.1739 | 3.39 | 0.1080 | ||
| 0.8782 | 1 | 0.8782 | 17.14 | 0.0044 | ||
| 0.2431 | 1 | 0.2431 | 4.74 | 0.0658 | ||
| 0.0081 | 1 | 0.0081 | 0.1576 | 0.7032 | ||
| Residual | 0.3587 | 7 | 0.0512 | |||
| Cor total | 40.70 | 16 | ||||
| Standard deviation | 0.2264 | 0.9729 | ||||
| Mean | 10.19 | Adjusted | 0.9620 | |||
| Coefficient of variation | 2.22 | Predicted | 0.9341 | |||
| Predicted residual of sum of squares | 3.27 | Adequate precision | 35.6818 | |||
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 0.3975 | 9 | 0.0442 | 289.12 | <0.0001 | Significant |
| 0.1824 | 1 | 0.1824 | 1194.1 | <0.0001 | ||
| 0.0002 | 1 | 0.0002 | 1.58 | 0.2485 | ||
| 0.1914 | 1 | 0.1914 | 1270.41 | <0.0001 | ||
| 0.0011 | 1 | 0.0011 | 7.13 | 0.0320 | ||
| 0.0164 | 1 | 0.0164 | 107.26 | <0.0001 | ||
| 0.0002 | 1 | 0.0002 | 1.28 | 0.2946 | ||
| 0.0001 | 1 | 0.0001 | 0.0003 | 0.9872 | ||
| 0.0031 | 1 | 0.0031 | 20.24 | 0.0028 | ||
| 0 | 1 | 0 | 0.1588 | 0.7022 | ||
| Residual | 0.0011 | 7 | 0.0002 | |||
| Cor total | 0.3986 | 16 | ||||
| Standard deviation | 0.0124 | 0.9930 | ||||
| Mean | 0.4935 | Adjusted | 0.9939 | |||
| Coefficient of variation | 2.5 | Predicted | 0.9809 | |||
| Predicted residual of sum of squares | 0.0076 | Adequate precision | 64.7200 | |||
| Exp. No. | Design Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (r/min) | (μm) | (μm/r) | Exp. | Predicted | Error (%) | Exp. | Predicted | Error (%) | |
| 1 | 600 | 35 | 30 | 11.735 | 12.48 | 6.34% | 0.839 | 0.7863 | 6.28% |
| 2 | 600 | 20 | 20 | 9.432 | 9.630 | 2.09% | 0.892 | 0.8500 | 4.70% |
| 3 | 1050 | 50 | 30 | 13.75 | 14.80 | 7.63% | 0.717 | 0.7672 | 7.01% |
| 4 | 1050 | 35 | 20 | 13.15 | 12.71 | 3.34% | 0.657 | 0.6981 | 6.25% |
| Parameters | v (r/min) | ap (μm) | f (μm/r) | ||
|---|---|---|---|---|---|
| Design A | 1032 | 25.85 | 22.85 | 13.87 | 0.0921 |
| Design B | 1452 | 20.5 | 31.25 | 6.43 | 0.19 |
| Design C | 897 | 12.8 | 21.52 | 5.62 | 0.92 |
| Experimental | 1050 | 30 | 20 | 7.128 | 0.355 |
| Method | Maximum Iterations | Optimized Result | |
|---|---|---|---|
| NSDBO | 87 | 6.43 | 0.19 |
| NAGA-II | 112 | 8.92 | 0.27 |
| CSO | 95 | 9.1 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Ni, C.; Chen, G.; Guo, J. Optimization of Tungsten Heavy Alloy Cutting Parameters Based on RSM and Reinforcement Dung Beetle Algorithm. Sensors 2023, 23, 5616. https://doi.org/10.3390/s23125616
Zhu X, Ni C, Chen G, Guo J. Optimization of Tungsten Heavy Alloy Cutting Parameters Based on RSM and Reinforcement Dung Beetle Algorithm. Sensors. 2023; 23(12):5616. https://doi.org/10.3390/s23125616
Chicago/Turabian StyleZhu, Xu, Chao Ni, Guilin Chen, and Jiang Guo. 2023. "Optimization of Tungsten Heavy Alloy Cutting Parameters Based on RSM and Reinforcement Dung Beetle Algorithm" Sensors 23, no. 12: 5616. https://doi.org/10.3390/s23125616
APA StyleZhu, X., Ni, C., Chen, G., & Guo, J. (2023). Optimization of Tungsten Heavy Alloy Cutting Parameters Based on RSM and Reinforcement Dung Beetle Algorithm. Sensors, 23(12), 5616. https://doi.org/10.3390/s23125616







