Calibration of a Structured Light Imaging System in Two-Layer Flat Refractive Geometry for Underwater Imaging †
Abstract
1. Introduction
- The coplanarity constraint proposed by Agrawal et al. [19] and used in our previous work [9] was extended to the case of multiple cameras and projectors that share a single flat glass interface and was then applied to the estimation of the axial camera’s axis. The proposed axis estimation was more stable than the method of [19] as demonstrated by the performed experiments.
- The proposed optimization of the 3D cost function from our previous work [9] was extended to the whole SL imaging system, and we also introduced boundaries on allowed system parameters.
- Calibration using the extended coplanarity constraint and the proposed 3D cost function were thoroughly evaluated on four different glass types, and the obtained results verify that the proposed method can cope with differing glass thicknesses.
2. Related Work
3. Calibration Method
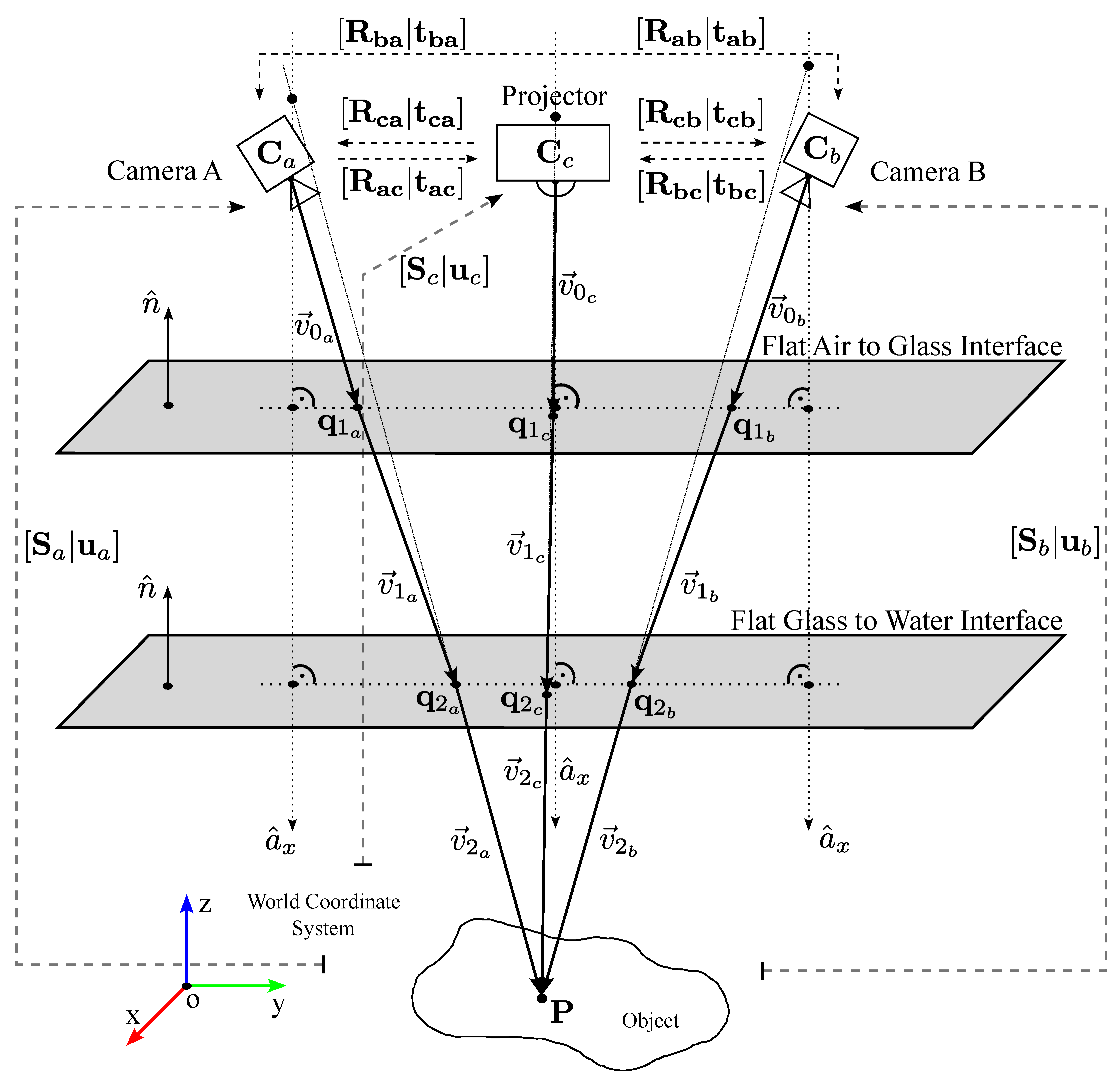
3.1. Imaging Geometry
3.2. The Coplanarity Constraint for a Camera/Projector Using a Single Interface
3.3. Unified Coplanarity Constraint for a System Using a Single Interface
3.4. In-the-Air Calibration
- Create an image of a planar calibration board in many positions;
- Extract the image coordinates of the calibration points;
- Optimize all the parameters by minimizing the re-projection error.
3.5. Numerical Optimization
3.5.1. Coplanarity Error
3.5.2. Frustum Error
3.5.3. Backprojection Error
3.5.4. Total Error
3.5.5. Boundary Constraints
3.6. SL System Calibration
- Calibrate all cameras and projectors in-the-air using a standard pinhole model with distortions as described in Section 3.4.
- Acquire as many images of the calibration board in the water as is practical and process the data using the procedure of [21] to extract the calibration data.
- Estimate the axis using Equation (14). In addition, for each position of the calibration board, estimate the initial pose of the calibration board w.r.t. the camera/projector frame using central approximation.
- Use a numerical optimization with the objective function comprising the coplanarity error and of the frustum error (see Section 3.5) to estimate true relative poses and to refine the axis; this is performed separately for each position of the calibration board.
- Use the numerical optimization with the complete objective function comprising the backprojection, the coplanarity, and the frustum errors to refine all parameters (see Section 3.5).
4. Evaluation
4.1. Laboratory Setup
4.2. Data Acquisition
4.3. Axis Estimation
4.4. Errors in 2D and 3D
5. Discussion
6. Conclusions
Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ROV | Remotely Operated Vehicle |
| UAV | Underwater Autonomous Vehicle |
| SL | Structured Light |
| FRC | Flat Refraction Constraint |
| POR | Plane of Refraction |
| MPS | Multiple Phase Shift |
| SVD | Single Value Decomposition |
| AFP | Analytical Forward Projection |
| CPL | Coplanarity |
| BPR | Backprojection |
| FRS | Frustum |
| FOV | Field of View |
Appendix A
Appendix A.1. Coplanarity Constraint for Camera (Projector) Using a Single Interface
Appendix A.2. Unified Coplanarity Constraint for System Using a Single Interface
References
- Roman, C.; Inglis, G.; Rutter, J. Application of structured light imaging for high resolution mapping of underwater archaeological sites. In Proceedings of the OCEANS’10 IEEE SYDNEY, Sydney, Australia, 4–27 May 2010; pp. 1–9. [Google Scholar] [CrossRef]
- Shortis, M.; Ravanbakskh, M.; Shaifat, F.; Harvey, E.; Mian, A.; Seager, J.; Culverhouse, P.; Cline, D.; Edgington, D. A review of techniques for the identification and measurement of fish in underwater stereo-video image sequences. In Videometrics, Range Imaging, and Applications XII and Automated Visual Inspection; SPIE: Bellingham, WA, USA, 2013; Volume 8791, p. 87910G. [Google Scholar] [CrossRef]
- Lopes, F.; Silva, H.; Almeida, J.; Martins, A.; Silva, E. Structured light system for underwater inspection operations. In Proceedings of the OCEANS 2015–Genova, Genova, Italy, 18–21 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Castillón, M.; Forest, J.; Ridao, P. Underwater 3D Scanner to Counteract Refraction: Calibration and Experimental Results. IEEE/ASME Trans. Mechatronics 2022, 27, 1–9. [Google Scholar] [CrossRef]
- Castillón, M.; Palomer, A.; Forest, J.; Ridao, P. Underwater 3D Scanner Model Using a Biaxial MEMS Mirror. IEEE Access 2021, 9, 50231–50243. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Zhou, C.; Ou, Y.; Jing, F.; Hou, Z. Development, Calibration, and Image Processing of Underwater Structured Light Vision System: A Survey. IEEE Trans. Instrum. Meas. 2023, 72, 1–18. [Google Scholar] [CrossRef]
- Shortis, M. Camera Calibration Techniques for Accurate Measurement Underwater. In 3D Recording and Interpretation for Maritime Archaeology; McCarthy, J.K., Benjamin, J., Winton, T., van Duivenvoorde, W., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 11–27. [Google Scholar] [CrossRef]
- Maas, H.G. On the Accuracy Potential in Underwater/Multimedia Photogrammetry. Sensors 2015, 15, 18140–18152. [Google Scholar] [CrossRef] [PubMed]
- Zoraja, D.; Petković, T.; Pribanić, T.; Forest, J. Projector Calibration in a Two-Layer Flat Refractive Geometry for Underwater Imaging. In Proceedings of the 2022 45th Jubilee International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 23–27 May 2022; pp. 930–935. [Google Scholar] [CrossRef]
- Hartley, R.I.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; ISBN 0521540518. [Google Scholar]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photon. 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A state of the art in structured light patterns for surface profilometry. Pattern Recognit. 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Bruno, F.; Bianco, G.; Muzzupappa, M.; Barone, S.; Razionale, A. Experimentation of structured light and stereo vision for underwater 3D reconstruction. ISPRS J. Photogramm. Remote Sens. 2011, 66, 508–518. [Google Scholar] [CrossRef]
- Sarafraz, A.; Haus, B.K. A structured light method for underwater surface reconstruction. ISPRS J. Photogramm. Remote Sens. 2016, 114, 40–52. [Google Scholar] [CrossRef]
- Narasimhan, S.; Nayar, S.; Sun, B.; Koppal, S. Structured light in scattering media. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 1, pp. 420–427. [Google Scholar] [CrossRef]
- Bräuer-Burchardt, C.; Munkelt, C.; Heinze, M.; Gebhart, I.; Kühmstedt, P.; Notni, G. Underwater 3D measurements with advanced camera modelling. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2022, 90, 55–67. [Google Scholar] [CrossRef]
- Young, M. The pinhole camera: Imaging without lenses or mirrors. Phys. Teach. 1989, 27, 648–655. [Google Scholar] [CrossRef]
- Sedlazeck, A.; Koch, R. Perspective and Non-perspective Camera Models in Underwater Imaging—Overview and Error Analysis. In Outdoor and Large-Scale Real-World Scene Analysis, Proceedings of the 15th International Conference on Theoretical Foundations of Computer Vision: Outdoor and Large-Scale Real-World Scene Analysis, Dagstuhl Castle, Germany, 26 June–1 July 2011; Dellaert, F., Frahm, J.M., Pollefeys, M., Leal-Taixé, L., Rosenhahn, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 212–242. [Google Scholar]
- Agrawal, A.; Ramalingam, S.; Taguchi, Y.; Chari, V. A Theory of Multi-Layer Flat Refractive Geometry. Available online: http://www.amitkagrawal.com/cvpr12/FlatRefraction.html (accessed on 28 November 2022).
- Ramalingam, S.; Sturm, P.; Lodha, S. Theory and Calibration for Axial Cameras. In Proceedings of the Computer Vision—ACCV 2006: 7th Asian Conference on Computer Vision, Hyderabad, India, 13–16 January 2006; Volume 3851. [Google Scholar] [CrossRef]
- Petković, T.; Gasparini, S.; Pribanić, T. A Note on Geometric Calibration of Multiple Cameras and Projectors. In Proceedings of the 2020 43rd International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 28 September–2 October 2020; pp. 1157–1162. [Google Scholar] [CrossRef]
- Łuczyński, T.; Pfingsthorn, M.; Birk, A. The Pinax-model for accurate and efficient refraction correction of underwater cameras in flat-pane housings. Ocean. Eng. 2017, 133, 9–22. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, P. Novel method for structured light system calibration. Opt. Eng. 2006, 45, 083601. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Kawahara, R.; Nobuhara, S.; Matsuyama, T. A Pixel-Wise Varifocal Camera Model for Efficient Forward Projection and Linear Extrinsic Calibration of Underwater Cameras with Flat Housings. In Proceedings of the 2013 IEEE International Conference on Computer Vision Workshops, Sydney, Australia, 1–8 December 2013; pp. 819–824. [Google Scholar] [CrossRef]
- Bouguet, J.Y. Camera Calibration Toolbox for Matlab. Available online: http://robots.stanford.edu/cs223b04/JeanYvesCalib/ (accessed on 29 November 2022).
- Silvatti, A.P.; Salve Dias, F.A.; Cerveri, P.; Barros, R.M. Comparison of different camera calibration approaches for underwater applications. J. Biomech. 2012, 45, 1112–1116. [Google Scholar] [CrossRef]
- Demazure, M. Sur Deux Problemes de Reconstruction. Ph.D. Thesis, National Institute for Research in Digital Science and Technology, Paris, France, 1988. [Google Scholar]
- Nister, D. An efficient solution to the five-point relative pose problem. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 756–770. [Google Scholar] [CrossRef]
- Li, B.; Karpinsky, N.; Zhang, S. Novel calibration method for structured-light system with an out-of-focus projector. Appl. Opt. 2014, 53, 3415–3426. [Google Scholar] [CrossRef]
- Petković, T.; Pribanić, T. Multiprojector Multicamera Structured Light Surface Scanner. IEEE Access 2022, 10, 90321–90337. [Google Scholar] [CrossRef]
- Petković, T.; Pribanić, T.; Đonlić, M. Temporal phase unwrapping using orthographic projection. Opt. Lasers Eng. 2017, 90, 34–47. [Google Scholar] [CrossRef]
- Mathworks. Optimization Toolbox. Available online: https://www.mathworks.com/help/optim/ug/lsqnonlin.html (accessed on 2 December 2022).







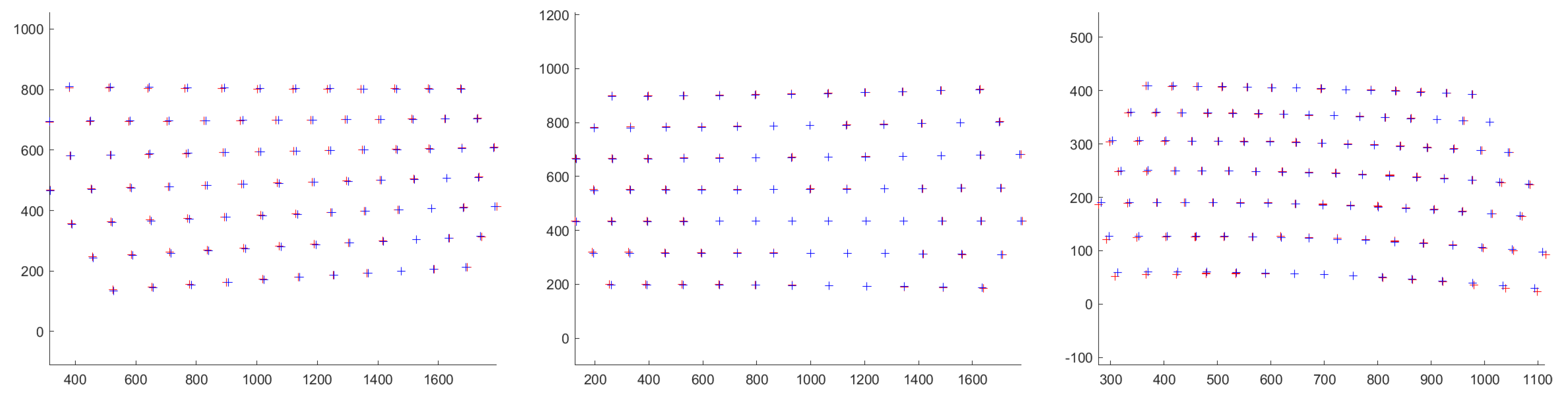
| i | Ours | Agrawal et al. [19] | ||||
|---|---|---|---|---|---|---|
| [mm] | [] | [] | [] | [] | [] | |
| I | 8 | |||||
| II | 10 | |||||
| III | 10 | |||||
| IV | 12 | |||||
| i | Total Error | Re-Projection Error | Re-Projection Error | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (Mean) [mm] (23) | (Mean) [px] | (Median) [px] | |||||||
| [mm] | e | e | |||||||
| I | 8 | 0.63 | 0.17 | 5.11 | 2.38 | 1.91 | 5.24 | 1.99 | 1.32 |
| II | 10 | 0.47 | 0.13 | 4.22 | 2.01 | 1.80 | 4.47 | 1.72 | 1.23 |
| III | 10 | 2.72 | 0.78 | 16.33 | 6.88 | 5.20 | 18.54 | 6.00 | 2.64 |
| IV | 12 | 0.50 | 0.14 | 4.12 | 2.19 | 1.66 | 4.16 | 1.97 | 1.24 |
| i | Fitting Error (Mean) [mm] | Fitting Error (Median) [mm] | ||
|---|---|---|---|---|
| [mm] | , | , | ||
| I | 8 | 7 | , , , , , , | , , , , , , |
| II | 6 | , , , , , | , , , , , | |
| III | 7 | , , , , , , | , , , , , , | |
| IV | 12 | 6 | , , , , , | , , , , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zoraja, D.; Petković, T.; Forest, J.; Pribanić, T. Calibration of a Structured Light Imaging System in Two-Layer Flat Refractive Geometry for Underwater Imaging. Sensors 2023, 23, 5444. https://doi.org/10.3390/s23125444
Zoraja D, Petković T, Forest J, Pribanić T. Calibration of a Structured Light Imaging System in Two-Layer Flat Refractive Geometry for Underwater Imaging. Sensors. 2023; 23(12):5444. https://doi.org/10.3390/s23125444
Chicago/Turabian StyleZoraja, Domagoj, Tomislav Petković, Josep Forest, and Tomislav Pribanić. 2023. "Calibration of a Structured Light Imaging System in Two-Layer Flat Refractive Geometry for Underwater Imaging" Sensors 23, no. 12: 5444. https://doi.org/10.3390/s23125444
APA StyleZoraja, D., Petković, T., Forest, J., & Pribanić, T. (2023). Calibration of a Structured Light Imaging System in Two-Layer Flat Refractive Geometry for Underwater Imaging. Sensors, 23(12), 5444. https://doi.org/10.3390/s23125444






